Ultrasonic Deicing Efficiency Prediction and Validation for a Flat Deicing System
Abstract
1. Introduction
2. Basic Theory and Model Establishment
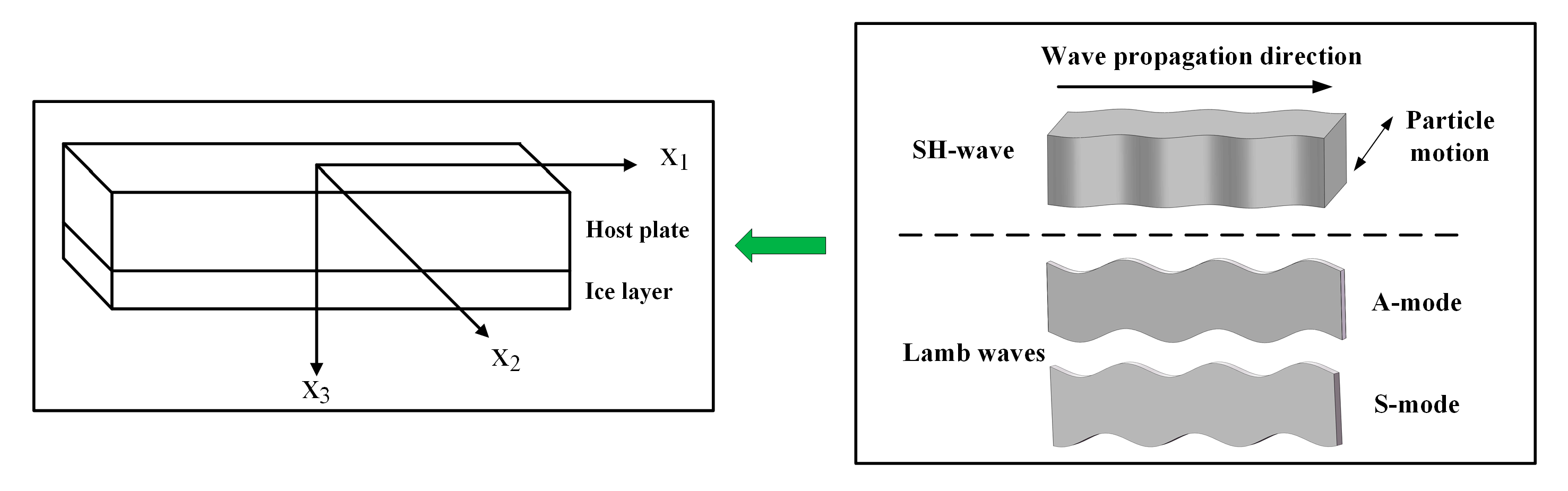
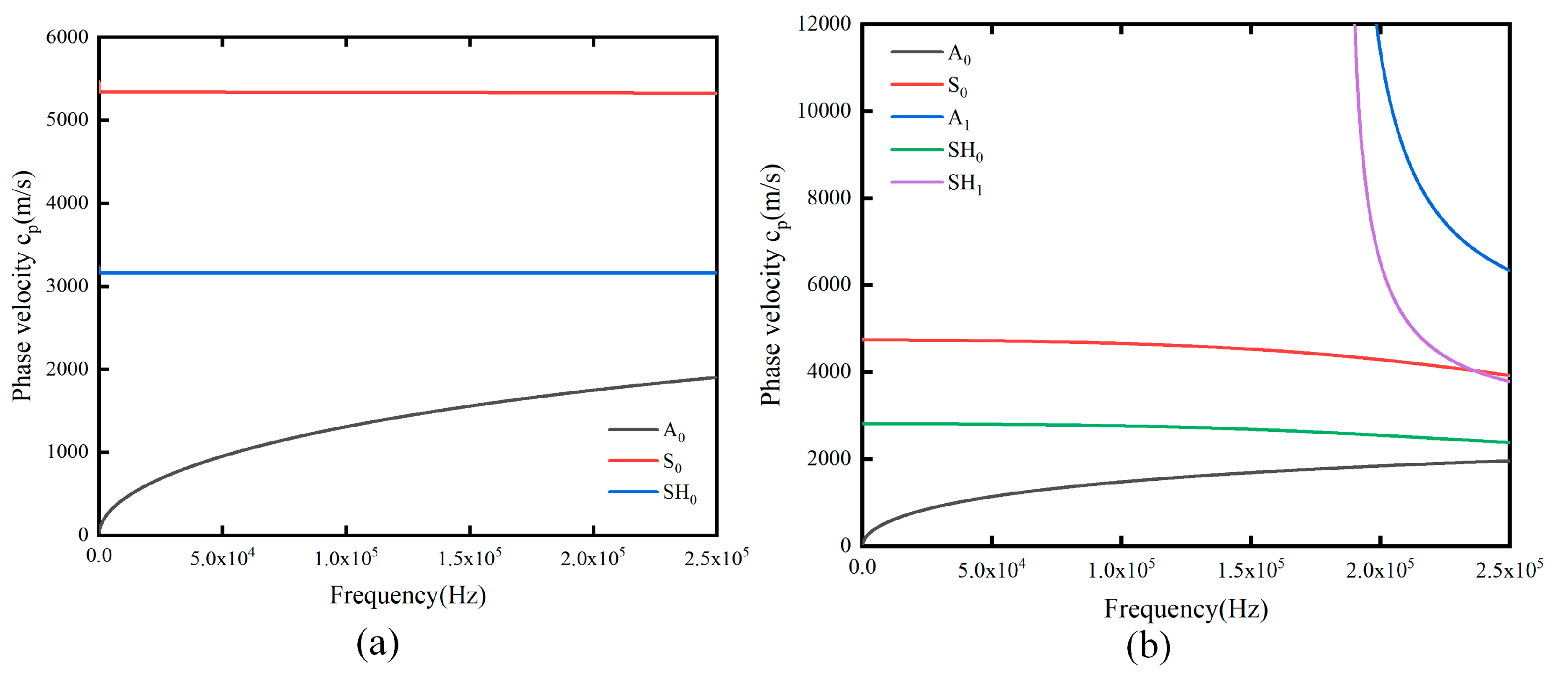
2.1. Ultrasonic Deicing Principle Interpretation
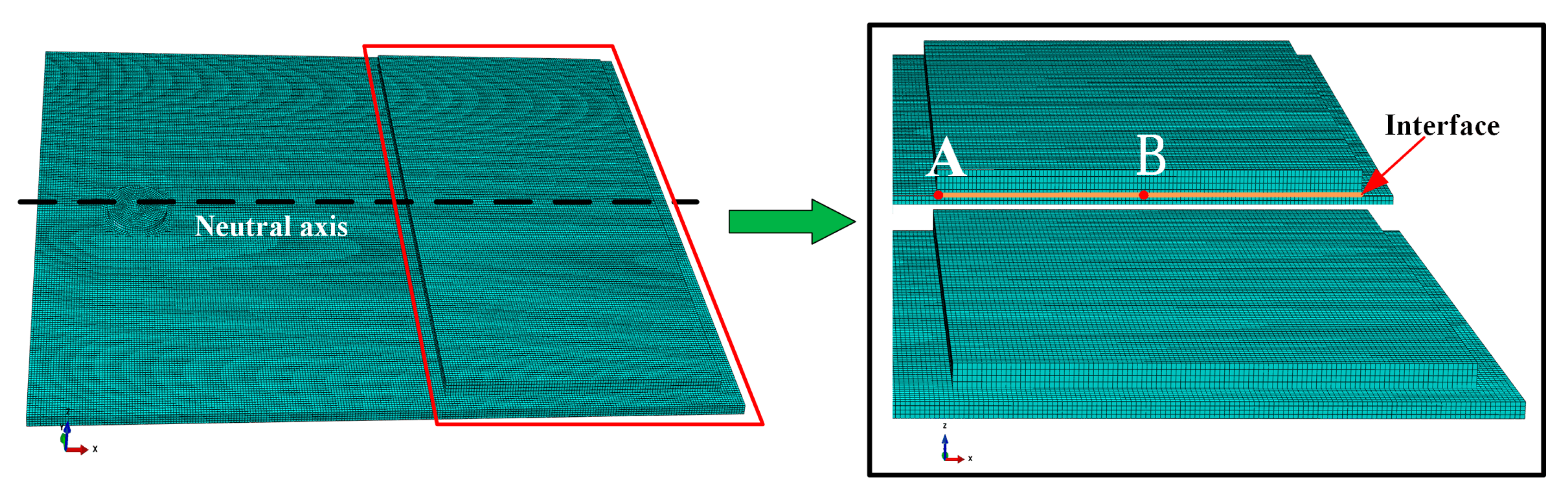
2.2. FE Model and Simulation
3. Deicing Experimental Setup and Schemes
4. Results and Discussion
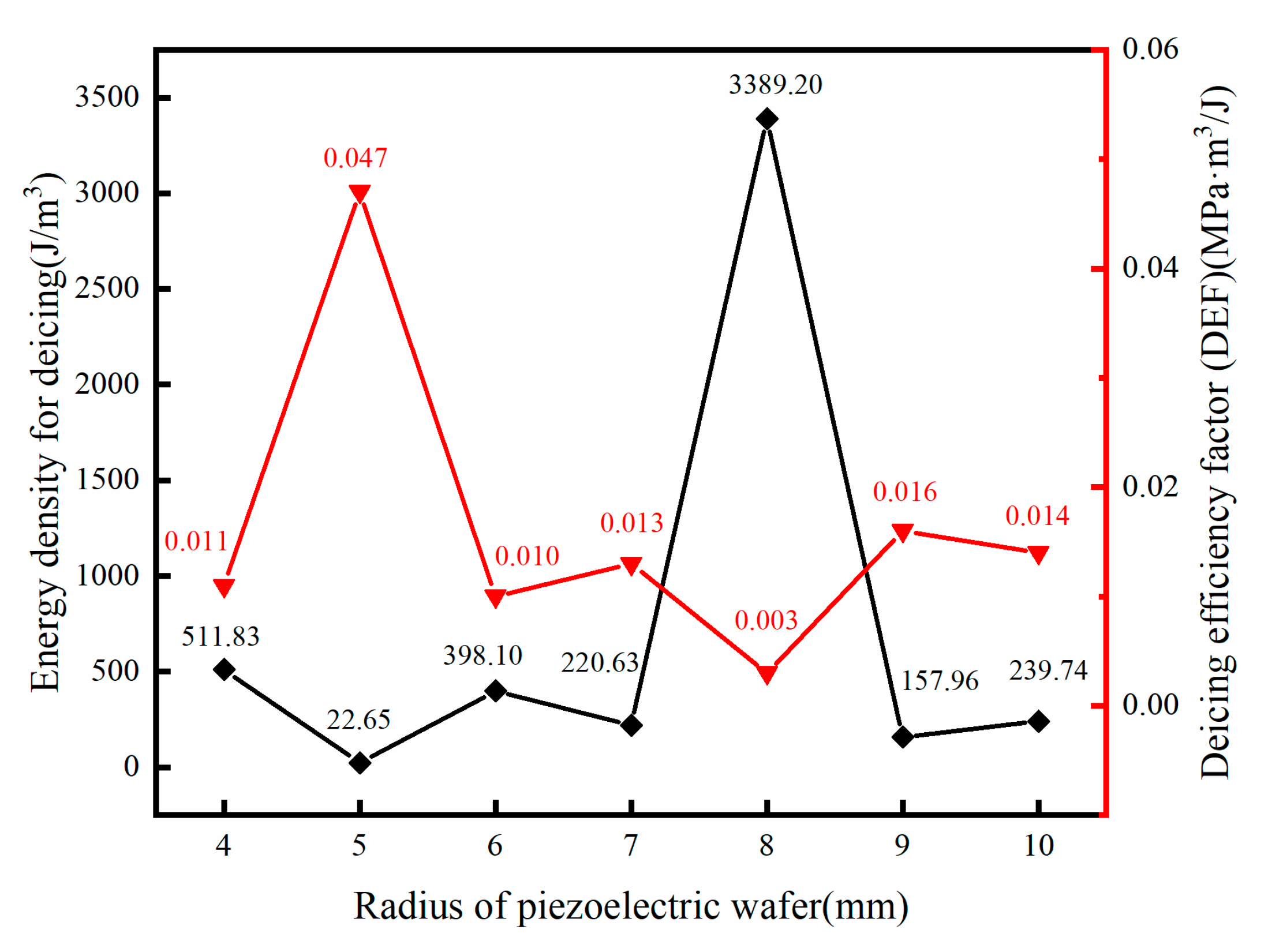
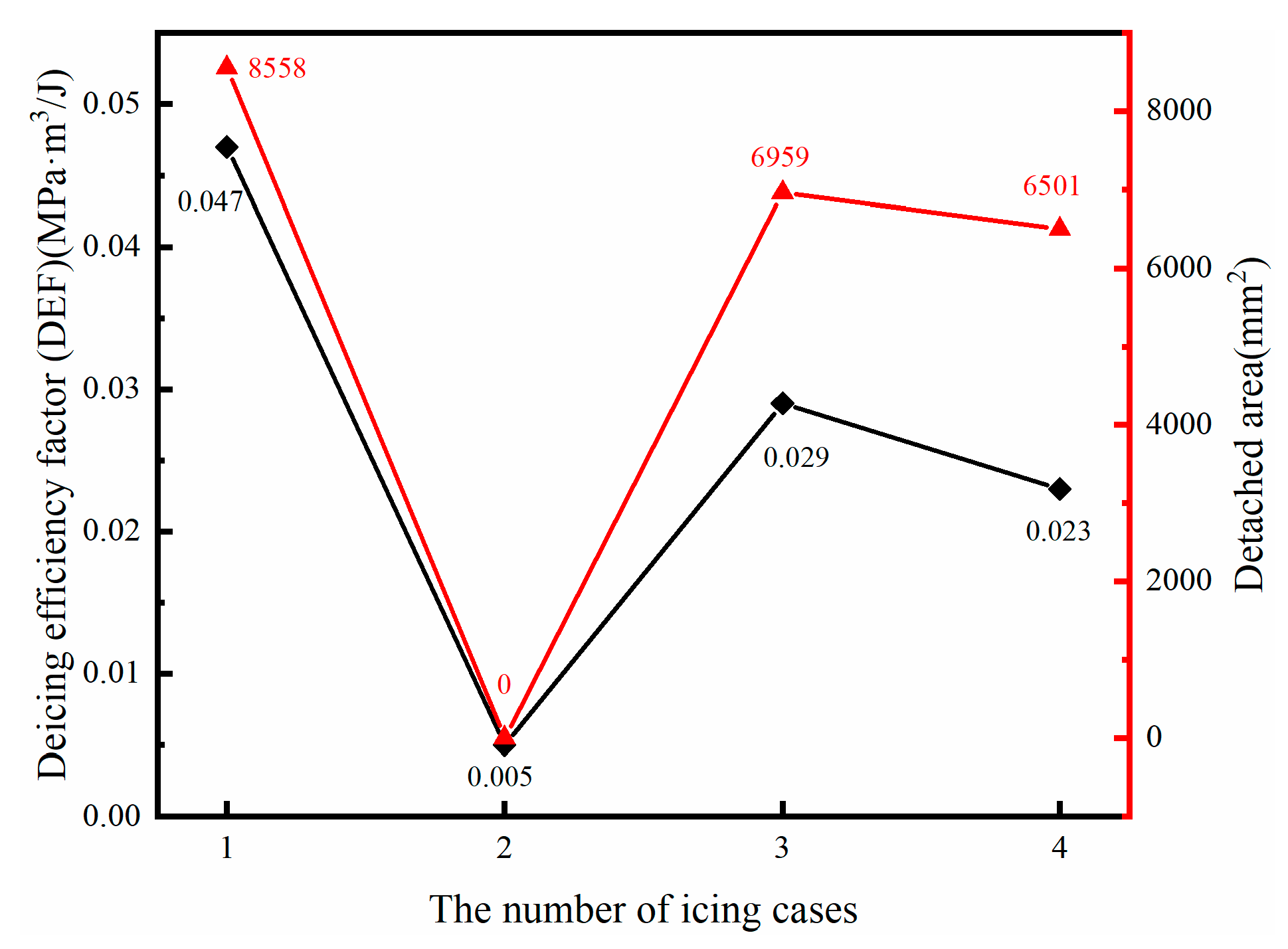
4.1. Deicing Energy Efficiency
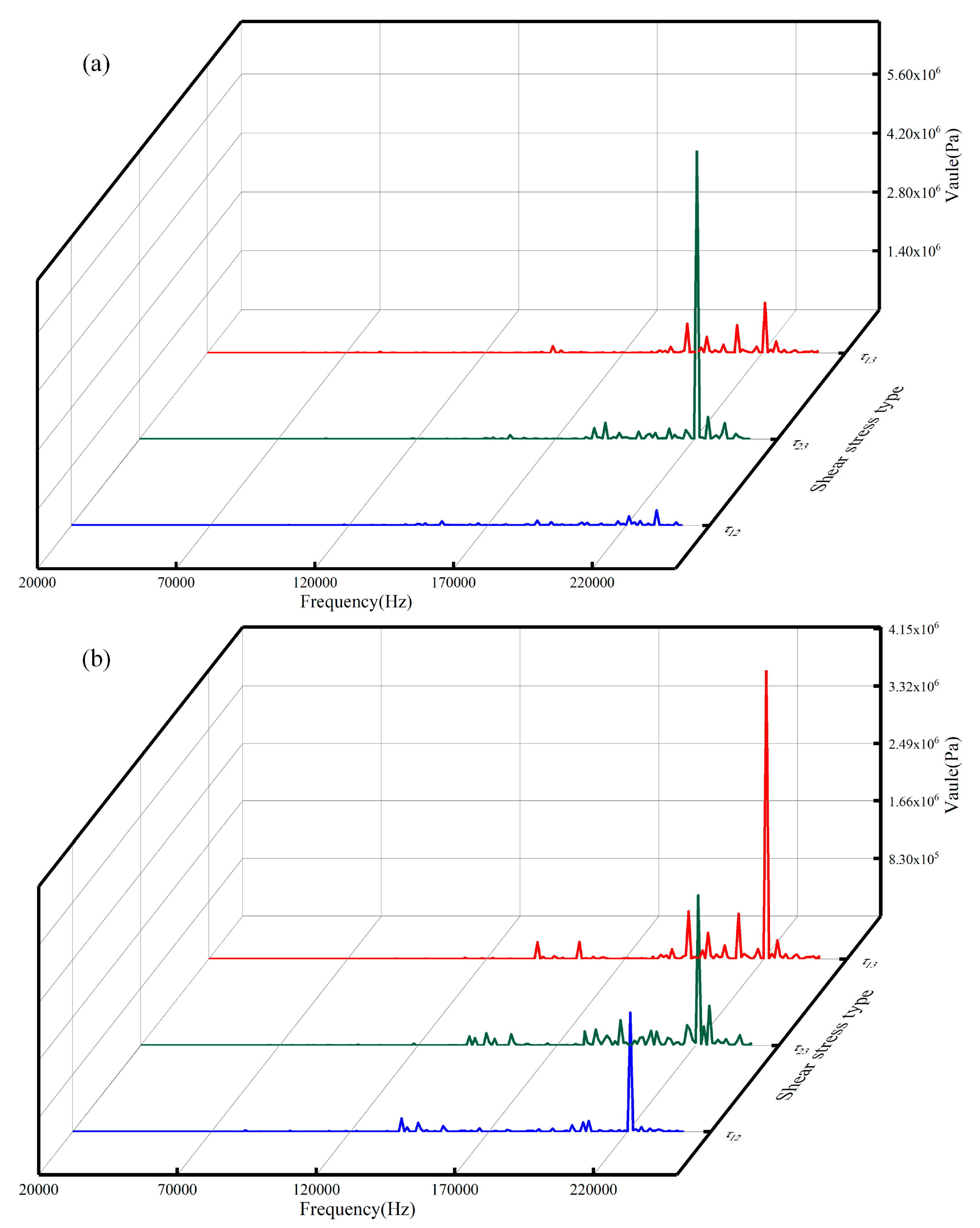
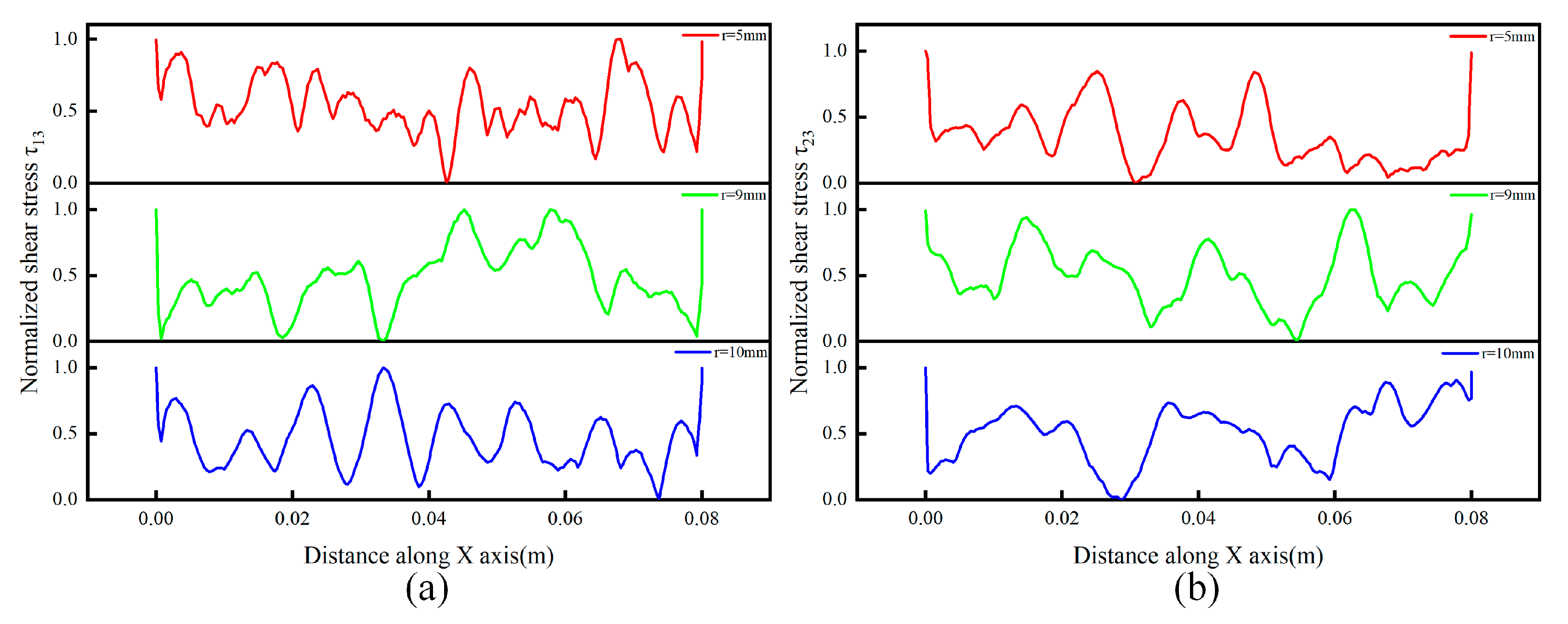
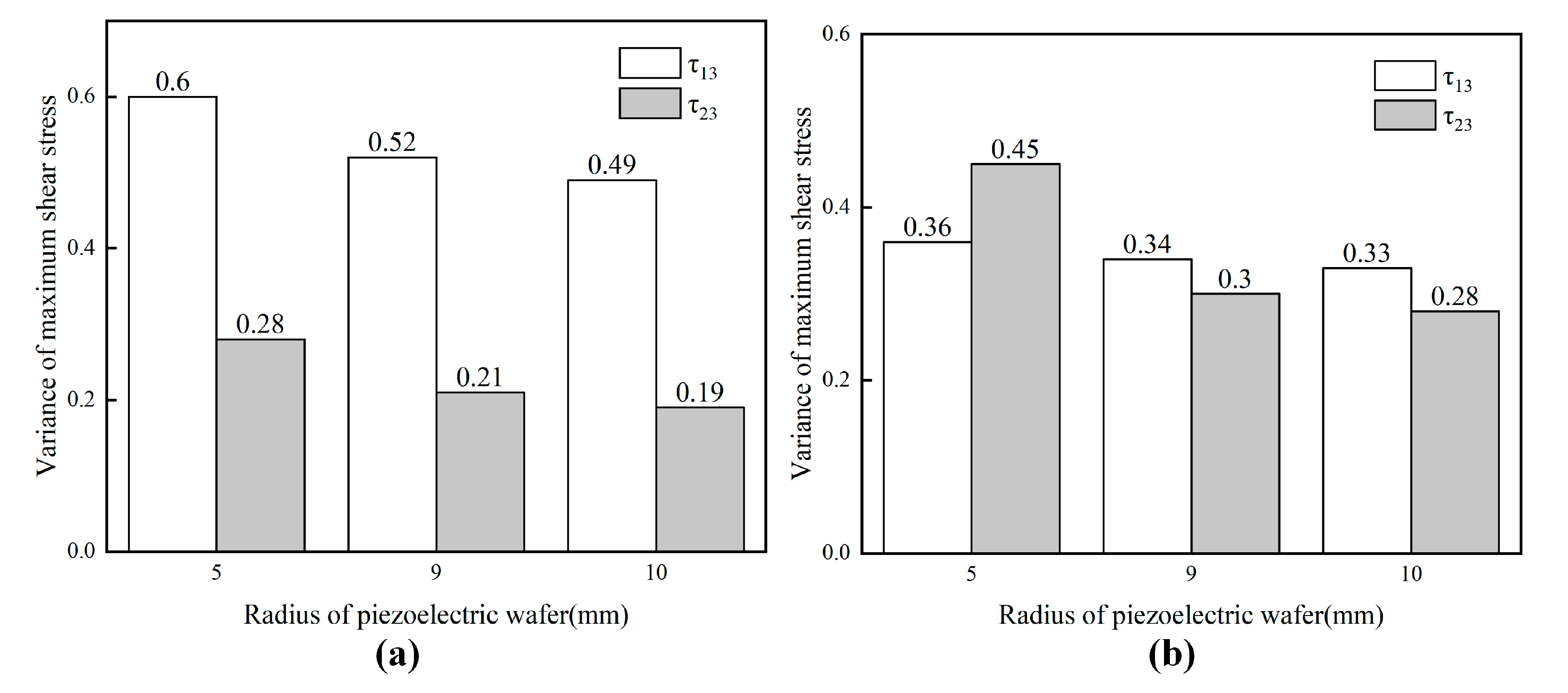
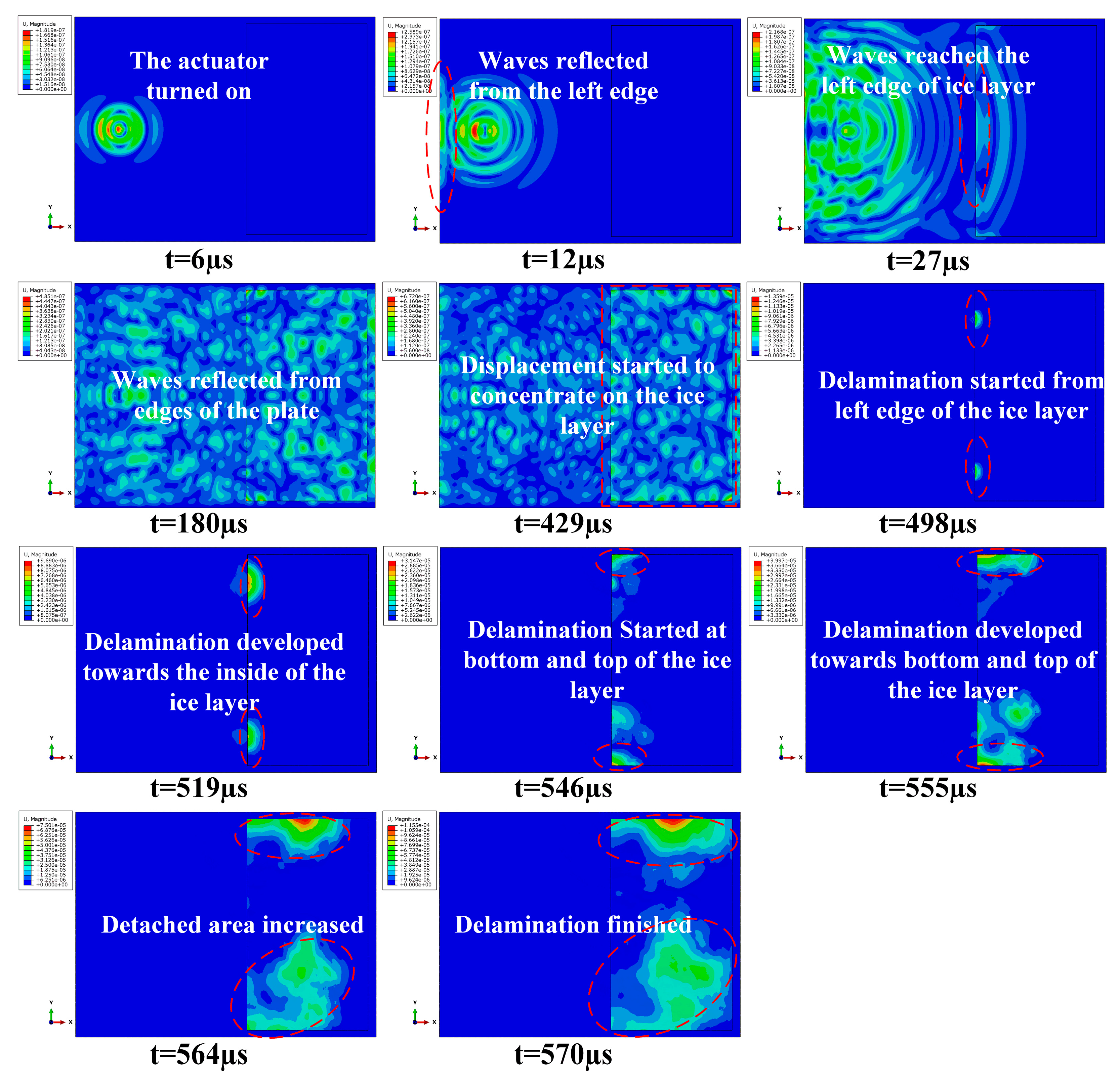
4.2. Stress Distribution and Deicing Affect Analysis
4.3. Standard-Explicit Co-Simulation Analysis
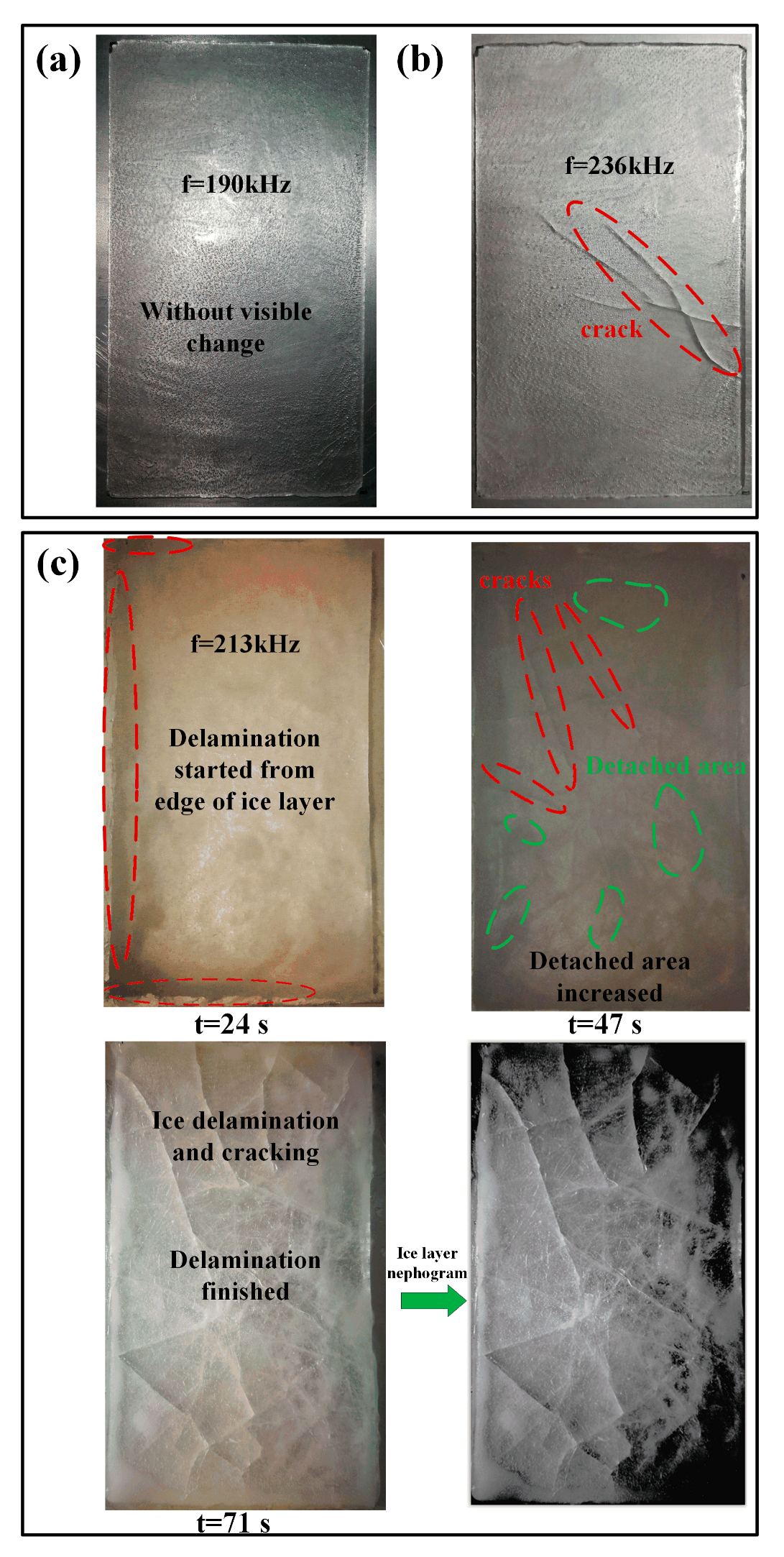
4.4. Experimental Verification
5. Conclusions
- A parameter design method was proposed according to simulation results on the supercomputer. The optimal configuration (the radius and the thickness of the PZT actuator) and deicing frequency were also given.
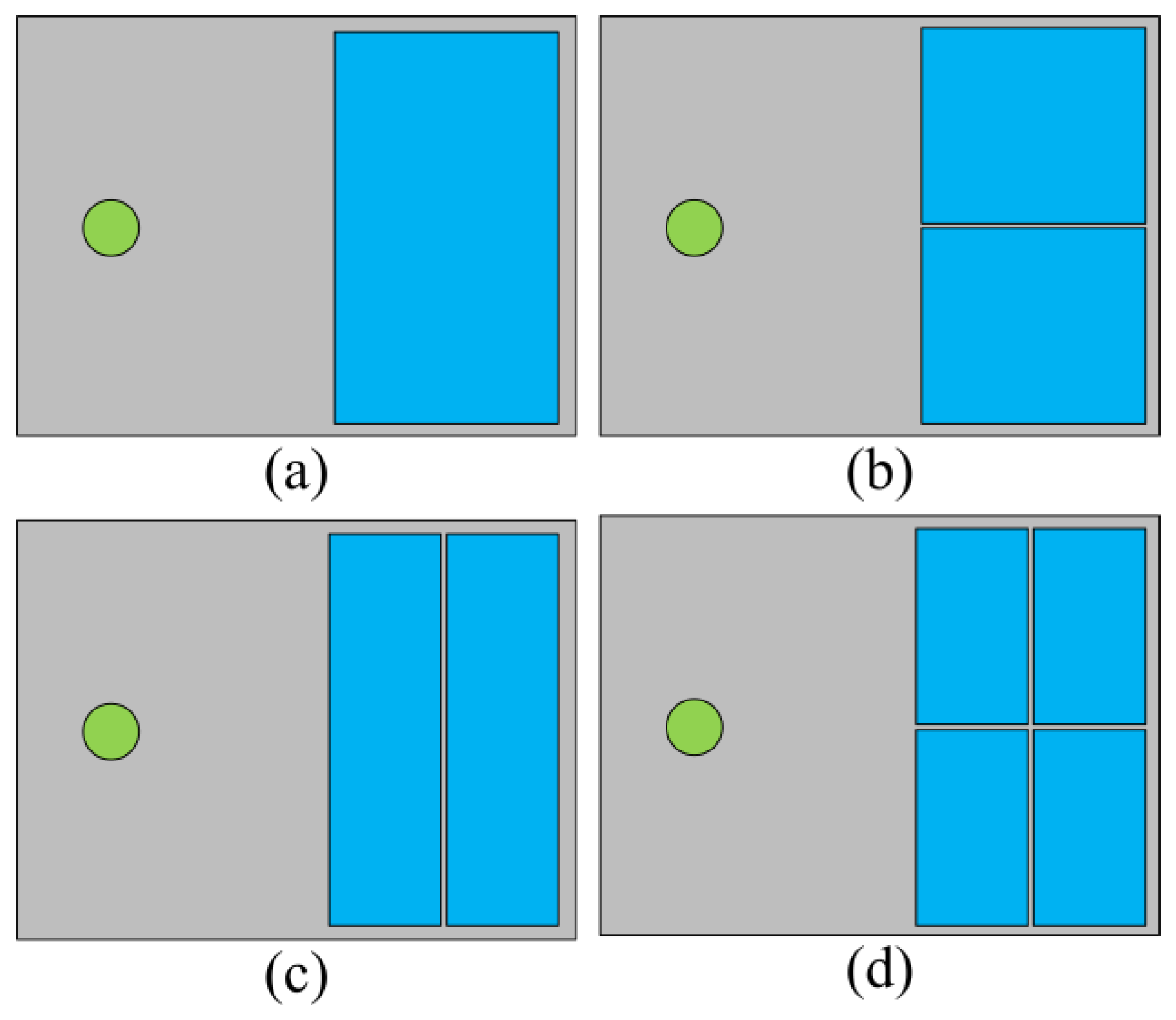
- The coefficient deicing efficiency factor (DEF) was proposed based on FE simulation, which can estimate and predict the deicing efficiency. With the help of this factor, the effect of the different model and deicing parameters on deicing efficiency can be calculated and compared. For shear stresses distributions, the more concentrated the shear stresses are on the edges of ice/substrate interface, the better for deicing. This can be one of the potential ways to achieve deicing more effectively.
- The calculation results of harmonic analysis and dynamic analysis are consistent. Harmonic analysis can obtain deicing stress and deicing results more concise and clearer. Wave propagation, reflection, superposition, and other processes are better displayed in dynamic analysis, which can help to understand the deicing process and provide guidance for further optimization. For different models and problems, these two analyses should be used rationally to achieve the purpose of obtaining the expected results with lower calculation costs.
Author Contributions
Funding
Conflicts of Interest
References
- Cao, Y.; Tan, W.; Wu, Z. Aircraft icing: An ongoing threat to aviation safety. Aerosp. Sci. Technol. 2018, 75, 353–385. [Google Scholar] [CrossRef]
- Nadeau, S.; Morency, F. De-icing of aircraft: Incorporating business risks and occupational health and safety. Int. J. Saf. Secur. Eng. 2017, 7, 247–266. [Google Scholar] [CrossRef]
- Yirtici, O.; Ozgen, S.; Tuncer, I.H. Predictions of ice formations on wind turbine blades and power production losses due to icing. Wind Energy 2019, 22, 945–958. [Google Scholar] [CrossRef]
- Jin, J.Y.; Virk, M.S. Study of ice accretion and icing effects on aerodynamic characteristics of DU96 wind turbine blade profile. Cold Reg. Sci. Technol. 2019, 160, 119–127. [Google Scholar] [CrossRef]
- Samuelsen, E.M. Ship-icing prediction methods applied in operational weather forecasting. Q. J. R. Meteorol. Soc. 2018, 144, 13–33. [Google Scholar] [CrossRef]
- Dehghani-Sanij, A.; Dehghani, S.; Naterer, G.; Muzychka, Y. Marine icing phenomena on vessels and offshore structures: Prediction and analysis. Ocean Eng. 2017, 143, 1–23. [Google Scholar] [CrossRef]
- Wei, K.; Yang, Y.; Zuo, H.; Zhong, D. A review on ice detection technology and ice elimination technology for wind turbine. Wind Energy 2020, 23, 433–457. [Google Scholar] [CrossRef]
- Fakorede, O.; Feger, Z.; Ibrahim, H.; Ilinca, A.; Perron, J.; Masson, C. Ice protection systems for wind turbines in cold climate: Characteristics, comparisons and analysis. Renew. Sustain. Energy Rev. 2016, 65, 662–675. [Google Scholar] [CrossRef]
- Goraj, Z. An overview of the deicing and anti-icing technologies with prospects for the future. In Proceedings of the 24th International Congress of the Aeronautical Sciences, Yokohama, Japan, 29 August–3 September 2004. [Google Scholar]
- Ramanathan, S. An Investigation on the Deicing of Helicopter Blades Using Shear Horizontal Guided Waves. Ph.D. Thesis, The Pennsylvania State University, University Park, PA, USA, 2004. [Google Scholar]
- Palacios, J.; Smith, E.; Rose, J.; Royer, R. Instantaneous de-icing of freezer ice via ultrasonic actuation. AIAA J. 2011, 49, 1158–1167. [Google Scholar] [CrossRef]
- Seppings, R.A. Investigation of Ice Removal from Cooled Metal Surfaces. Ph.D. Thesis, Imperial College London (University of London), London, UK, 2006. [Google Scholar]
- Yin, C.; Zhang, Z.; Wang, Z.; Guo, H. Numerical simulation and experimental validation of ultrasonic de-icing system for wind turbine blade. Appl. Acoust. 2016, 114, 19–26. [Google Scholar] [CrossRef]
- Budinger, M.; Pommier-Budinger, V.; Napias, G.; Costa da Silva, A. Ultrasonic Ice Protection Systems: Analytical and Numerical Models for Architecture Tradeoff. J. Aircr. 2016, 53, 680–690. [Google Scholar] [CrossRef]
- Kalkowski, M.K.; Waters, T.P.; Rustighi, E. Delamination of surface accretions with structural waves: Piezo-actuation and power requirements. J. Intell. Mater. Syst. Struct. 2017, 28, 1454–1471. [Google Scholar] [CrossRef]
- Shi, Z.; Zhao, Y.; Ma, C.; Zhang, J. Parametric Study of Ultrasonic De-Icing Method on a Plate with Coating. Coatings 2020, 10, 631. [Google Scholar] [CrossRef]
- Zhu, Y. Structural Tailoring and Actuation Studies for Low Power Ultrasonic De-Icing of Aluminum and Composite Plates. Ph.D. Thesis, The Pennsylvania State University, University Park, PA, USA, 2010. [Google Scholar]
- DiPlacido, N.; Soltis, J.; Palacios, J. Enhancement of ultrasonic de-icing via tone burst excitation. J. Aircr. 2016, 53, 1821–1829. [Google Scholar] [CrossRef]
- Wang, Z.; Xu, Y.; Gu, Y. A light lithium niobate transducer design and ultrasonic de-icing research for aircraft wing. Energy 2015, 87, 173–181. [Google Scholar] [CrossRef]
- Gao, H.; Rose, J.L. Ice detection and classification on an aircraft wing with ultrasonic shear horizontal guided waves. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2009, 56, 334–344. [Google Scholar]
- Palacios, J.; Zhu, Y.; Smith, E.; Rose, J. Ultrasonic shear and lamb wave interface stress for helicopter rotor de-icing purposes. In Proceedings of the 47th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Newport, RI, USA, 1–4 May 2006; p. 2282. [Google Scholar]
- Daniliuk, V.; Xu, Y.; Liu, R.; He, T.; Wang, X. Ultrasonic de-icing of wind turbine blades: Performance comparison of perspective transducers. Renew. Energy 2020, 145, 2005–2018. [Google Scholar] [CrossRef]
- Elices, M.; Guinea, G.; Gomez, J.; Planas, J. The cohesive zone model: Advantages, limitations and challenges. Eng. Fract. Mech. 2002, 69, 137–163. [Google Scholar] [CrossRef]
- Alfano, G.; Sacco, E. Combining interface damage and friction in a cohesive-zone model. Int. J. Numer. Methods Eng. 2006, 68, 542–582. [Google Scholar] [CrossRef]
- Li, S. Piezoelectric Fiber Composite Strip Health Monitoring Systems Based on Ultrasonic Guided Waves. Master’s Thesis, The Pennsylvania State University, University Park, PA, USA, 2011. [Google Scholar]
- Wang, T. Finite Element Modelling and Simulation of Guided Wave Propagation in Steel Structural Members. Ph.D. Thesis, University of Western Sydney, Sydney, Australia, 2014. [Google Scholar]
- Rose, J.L. Ultrasonic Guided Waves in Solid Media; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Centolanza, L.R.; Smith, E.C.; Munsky, B. Induced-shear piezoelectric actuators for rotor blade trailing edge flaps. Smart Mater. Struct. 2002, 11, 24. [Google Scholar] [CrossRef]
- Kandagal, S.; Venkatraman, K. Piezo-actuated vibratory deicing of a flat plate. In Proceedings of the 46th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Austin, TX, USA, 18–21 April 2005; p. 2115. [Google Scholar]
- Systèmes, D. Abaqus analysis user’s guide. Solid (Contin.) Elem. 2014, 6, 2019. [Google Scholar]
- Riahi, M.M.; Marceau, D.; Laforte, C.; Perron, J. The experimental/numerical study to predict mechanical behaviour at the ice/aluminium interface. Cold Reg. Sci. Technol. 2011, 65, 191–202. [Google Scholar] [CrossRef]
- Mlyniec, A.; Ambrozinski, L.; Packo, P.; Bednarz, J.; Staszewski, W.J.; Uhl, T. Adaptive de-icing system–numerical simulations and laboratory experimental validation. Int. J. Appl. Electromagn. Mech. 2014, 46, 997–1008. [Google Scholar] [CrossRef]
- Wei, Y.; Adamson, R.; Dempsey, J. Ice/metal interfaces: Fracture energy and fractography. J. Mater. Sci. 1996, 31, 943–947. [Google Scholar] [CrossRef]
- Guerin, F.; Laforte, C.; Farinas, M.-I.; Perron, J. Analytical model based on experimental data of centrifuge ice adhesion tests with different substrates. Cold Reg. Sci. Technol. 2016, 121, 93–99. [Google Scholar] [CrossRef]
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 2012, 9, 671–675. [Google Scholar] [CrossRef]








| Material | Density (kg/m3) | Young’s Modulus (GPa) | Poisson’s Ratio |
|---|---|---|---|
| Ice | 920 | 9 | 0.28 |
| Aluminum | 2700 | 70 | 0.30 |
| Parameters | Values |
|---|---|
| Cohesive layer modulus (penalty stiffness) in all 3 directions, Knn, Kss, Ktt | 1.0 × 106 N/mm3 |
| Ultimate strength in tensile, T | 0.8 MPa |
| Ultimate strength in mode II, S | 0.8 MPa |
| Ultimate strength in mode III, N | 0.8 MPa |
| Normal mode fracture, GIC | 1.0 × 10−3 N/mm |
| Normal mode fracture, GIIC | 2.0 × 10−3 N/mm |
| Normal mode fracture, GIIIC | 2.0 × 10−3 N/mm |
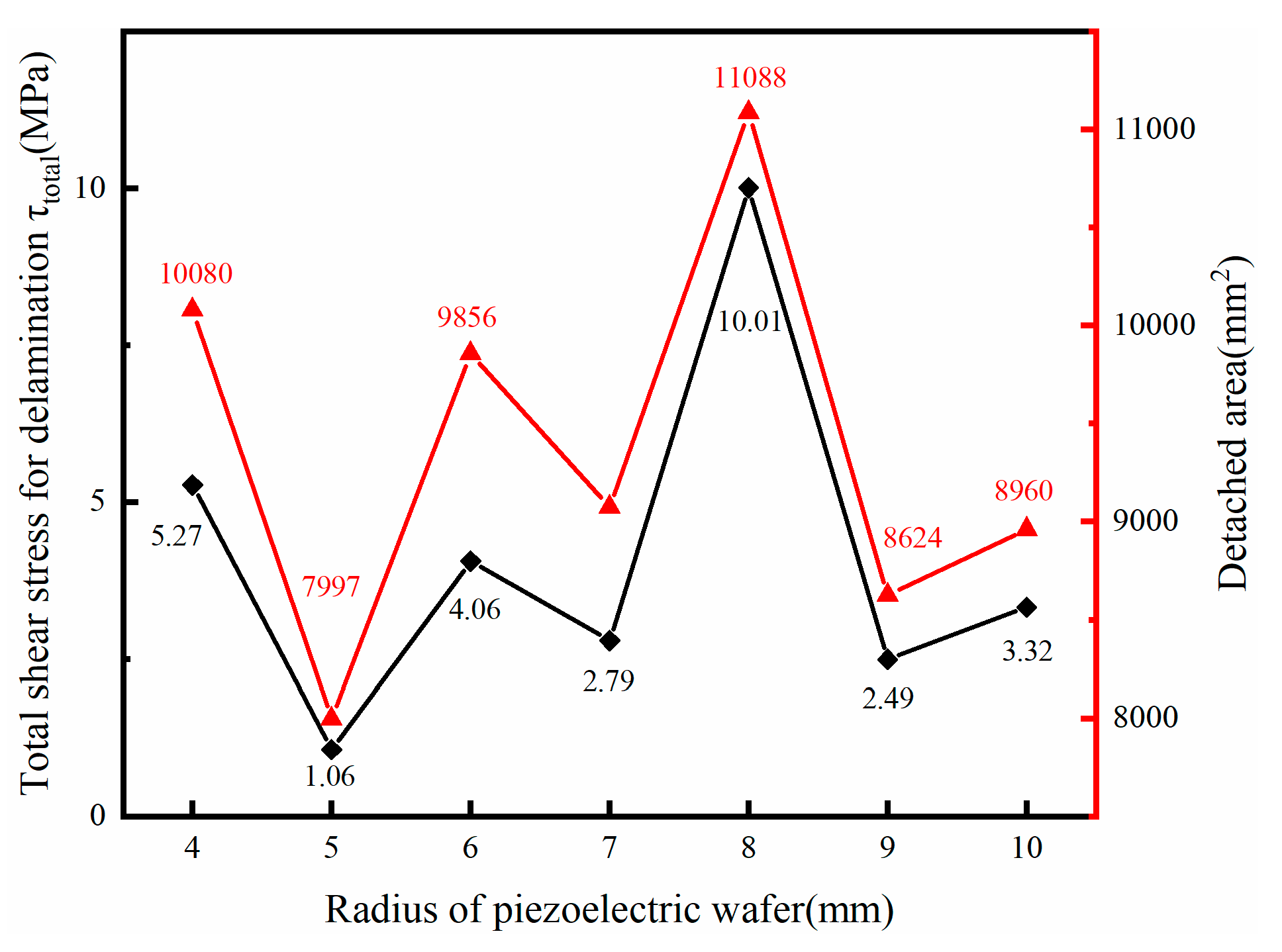
| Configuration Radius (mm) | Optimal Frequency (kHz) | τ13 (MPa) | τ23 (MPa) |
|---|---|---|---|
| 4 | 221 | 4.33 | 3.01 |
| 5 | 213 | 0.64 | 0.85 |
| 6 | 236 | 2.99 | 2.75 |
| 7 | 222 | 1.92 | 2.02 |
| 8 | 232 | 7.22 | 6.94 |
| 9 | 212 | 1.75 | 1.77 |
| 10 | 190 | 2.27 | 2.42 |
| Frequency (kHz) | Experimental Results | Simulation Results |
|---|---|---|
| 190 | Without visible change | Maximum τtotal = 0.23 MPa; Maximum τ12 = 0.11 MPa |
| 213 | Ice delamination and cracking | Maximum τ13 = 4.3 MP; Detached area is 83.3%; Maximum τ12 = 3.0 MPa |
| 236 | Cracks only | Maximum τtotal = 0.16 MPa; Maximum τ12 = 0.28 MPa |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, Z.; Kang, Z.; Xie, Q.; Tian, Y.; Zhao, Y.; Zhang, J. Ultrasonic Deicing Efficiency Prediction and Validation for a Flat Deicing System. Appl. Sci. 2020, 10, 6640. https://doi.org/10.3390/app10196640
Shi Z, Kang Z, Xie Q, Tian Y, Zhao Y, Zhang J. Ultrasonic Deicing Efficiency Prediction and Validation for a Flat Deicing System. Applied Sciences. 2020; 10(19):6640. https://doi.org/10.3390/app10196640
Chicago/Turabian StyleShi, Zhonghua, Zhenhang Kang, Qiang Xie, Yuan Tian, Yueqing Zhao, and Jifeng Zhang. 2020. "Ultrasonic Deicing Efficiency Prediction and Validation for a Flat Deicing System" Applied Sciences 10, no. 19: 6640. https://doi.org/10.3390/app10196640
APA StyleShi, Z., Kang, Z., Xie, Q., Tian, Y., Zhao, Y., & Zhang, J. (2020). Ultrasonic Deicing Efficiency Prediction and Validation for a Flat Deicing System. Applied Sciences, 10(19), 6640. https://doi.org/10.3390/app10196640





