Featured Application
This work is mainly applied in the optical element surface quality evaluation field.
Abstract
Defect size recognition is significant to the evaluation of optical element surface quality. Currently, it’s mainly achieved by the conventional image process, such as threshold segmentation. However, as the defect size gradually approaches the diffraction limit of the imaging system, the defect gray distribution changes from bimodal to unimodal, which makes it difficult to be accurately recognized. In this paper, an electromagnetic simulation model of the microscopic scattering dark-field imaging (MSDI) system is built based on the finite-difference time-domain (FDTD) method to research the defect imaging mechanism. The point spread function (PSF) of our MSDI system is measured to revise the far-field simulation light intensity distribution, and the mean value of the distance between three groups of feature points, whose intensity is 0.75, 0.5, and 0.25 of the light intensity distribution peak value, is taken as the feature parameter of the light intensity distribution. To obtain the defect size, the decision regression tree (DRT) is proposed to get the relationship between the feature parameter and the defect size. Besides, some scratches samples are made to verify the validity of the DRT. The results show the relative error of DRT is within 10%, which is better than the threshold segmentation.
1. Introduction
The optical integration level of sophisticated equipment is getting higher and higher in recent years. For instance, laser inertial confinement fusion equipment, a communication satellite, and optical quantum computer have integrated a large quantity of fine optical elements [1,2,3]. The existence of optical elements surface defects not only affects the performance of this sophisticated equipment but also causes the collapse of the whole equipment system in some extreme situations. Hence, it is necessary to carry out the quality evaluation of optical elements at an early age.
Defect size recognition is an important quantitative analysis basis of optical elements’ surface quality evaluation, and its accuracy directly affects the final quality evaluation result. At present, the defect size is mainly deduced from the defect image gray distribution collected by the optical imaging system. This process is also called the reverse recognition of defect size [4]. Conventional optical imaging systems for defect detection contains a dark-field imaging system [5,6], bright-field imaging system [7,8], etc. Since dark-field imaging system only captures the scattered light induced by the defect, the defect region will be brighter than the background in the image, which makes the defect to be detected at higher contrast and realizes super-resolution detection to a certain extent. Thus, a dark-field imaging system is more appropriate for detecting some tiny defects. When the size of the tiny defect is larger than the diffraction limit of the dark-field imaging system, the gray distribution of the defect has two peaks, and the defect size can be derived from the distance between two peaks. But as the defect size is close to the diffraction limit of the imaging system, its gray distribution becomes one peak, and the defect size cannot be recognized by the distance between two peaks anymore. To solve this problem, the commonly used image process method is image threshold segmentation, such as the Otsu method [9,10]. By setting or calculating an appropriate gray threshold, the defect size can be approximately extracted from the image. But its recognition accuracy is usually low, and it needs some additional calibration technique to ensure its accuracy. It is very inconvenient because some known size defects need to be prepared for calibration in advance. Thus, the current image process method for defect size recognition needs to be reconsidered.
Recently, with the development of the artificial intelligence field, machine learning is widely applied in the image process [11,12,13], and it has superior performance in defect detection, classification, etc. Yet, it has been rarely reported in defect size recognition. The main reason is that machine learning needs more known size defect images than the calibration procedure mentioned above to learn the relationship between the characteristic of the defect gray distribution and the defect size, which means a large quantity of known size defect samples needs to be made. This is extremely difficult to be achieved because the actual defect machining technique and machining accuracy cannot reach this condition, especially when the defect size is close to the diffraction limit of the imaging system. Hence, the scarce of the training data set limits the usage of machine learning.
In this paper, we propose a defect size recognition method based on the machine learning of the decision regression tree (DRT) [14,15,16], whose training data is from the simulation model of the dark-field imaging system. Here, we take scratch as an example, using the DRT algorithm to recognize the width of the scratch. Firstly, an electromagnetic simulation model of microscopic scattering dark-field imaging (MSDI) system is built based on the finite-difference time-domain (FDTD) method [17,18] to gain the far-field simulation light intensity distribution of the scratch. Since the diffraction effect exists in the MSDI system due to the limit of the aperture to the scattered light, the defect simulation light intensity distribution will be inconsistent with the defect actual gray distribution. This diffraction effect can be described by point spread function (PSF) in theory [19]. Hence, we measure the gray distribution of a step source in our MSDI system and get PSF by taking the derivative of the step source gray distribution. Then, we convolve the simulation light intensity distribution with the PSF as the revision of the simulation light intensity distribution. The mean value of the distance between three groups of feature points, whose intensity is 0.75, 0.5, and 0.25 of the revised simulation light intensity distribution peak value, is taken as the feature parameter. Finally, we use DRT to gain the relationship between the feature parameter of the revised light intensity distribution and the scratch width. To verify the effectiveness of DRT in scratch width recognition, the standard glass plates with the process of electron beam exposure and the ion beam etching are taken as the tested scratch samples, and the scanning electron microscope (SEM) is applied to measure the real width of the scratch. Moreover, the Otsu threshold segmentation method is also employed to recognize the scratch width on the standard glass plate in comparison to DRT, and the experiment result indicates that DRT has higher accuracy than the Otsu method, especially in the situation where the width of the scratch approaches to the diffraction limit of the MSDI system.
The remaining part of this paper is organized as follows. The layout of our MSDI system is presented, and the principle of dark-field imaging is illustrated in Section 2. In Section 3, the electromagnetic simulation model of MSDI is proposed, and the principle of the DRT for defect size recognition is described. Section 4 shows simulation and experiment results, and some conclusion is given in Section 5.
2. The Layout of the MSDI System
The layout of the MSDI system is shown in Figure 1. The optical element is put on the X and Y stage, and the movement of the stages is controlled by a motion controller. The incident light irradiates on the optical element surface from white light-emitting diode (LED) sources, which are in annular distribution. When there is no defect on the optical element surface, all incident light will be reflected, and almost no light will enter the MSDI system, which leads the collected image to be dark. But when there is a defect on the optical element surface, a part of the incident light will be scattered, and some scattered light will be collected by the charge coupled device (CCD) of the MSDI system. The defect region in the image will be brighter than the dark background region. Thus, the defect is detected. To further obtain defect size from the image, the gray distribution of the defect is extracted, as can be seen in the inset of Figure 1. Different size defects have different gray distribution. For example, the defect whose width is 4 μm or 8 μm, its gray distribution has two peaks. Thus, the defect width can be deduced from the distance between two peaks. However, when the defect size approaches to the diffraction limit of the MSDI system, the defect gray distribution has only one peak, as can be seen from the distribution of the defect whose width is 2 μm, and the defect size cannot be judged by the distance between two peaks.
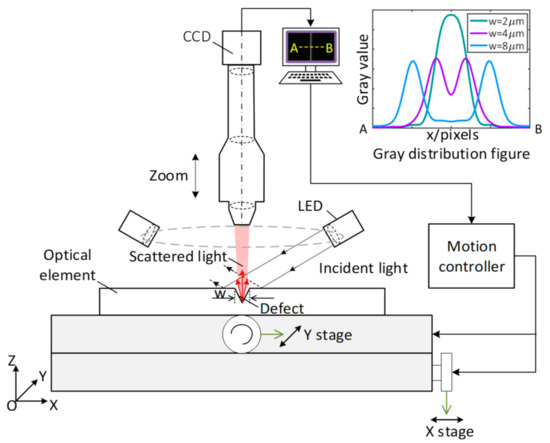
Figure 1.
The layout of the microscopic scattering dark-field imaging (MSDI) system.
3. The Principle of Defect Size Recognition
As discussed in Section 2, when the defect size approaches to the diffraction limit of the MSDI system, the gray distribution of the defect will change from bimodal to unimodal, which makes the defect size not to be recognized by the distance between two peaks. To solve this problem, we propose a defect size recognition method based on DRT. In order to obtain the defect size from the unimodal gray distribution, DRT needs much gray distribution of the known size defect to study the relationship between the defect gray distribution and the defect size. The gray distribution is also called the training data set of the DRT. Due to the limit of actual machining technique and machining accuracy, these tiny defects are too difficult to make. Thus, an electromagnetic simulation model of the MSDI system is built, and the far-field light intensity distribution of defects is acquired as the training data set of the DRT. Considering the simulation model cannot calculate the diffraction effect caused by the limit of the aperture to the scattered light, we measure the PSF of the MSDI system and use PSF to revise the light intensity distribution.
3.1. The Far Field Light Intensity Distribution of the Defect
To collect a series of known size defect gray distribution (i.e., light intensity distribution) as the training data set of the DRT, a simulation model based on the FDTD method is established in FDTD solution software to simulate the imaging environment of the MSDI system. As illustrated in Figure 2, the incident light irradiates on the optical element surface, and a part of them is scattered by the defect. The scattered light firstly travels to the near field and then is collected by the objective lens. Finally, it reaches the far-field where the dark-field image of the defect is obtained. The specific illustration is as follows.
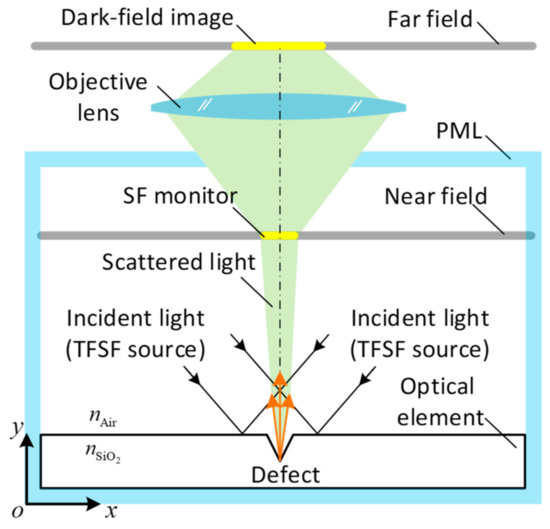
Figure 2.
Simulation model of MSDI based on the finite-difference time-domain (FDTD) method.
The total-field scattered-field (TFSF) source is chosen as the light source, and the medium around the optical element is set to air. The boundary is set to the perfectly matched layer (PML) to absorb the reflected light on the boundary, which can eliminate the effect of reflected light on the spatial distribution of the scattered light. Scattered field (SF) monitor is put in near field to acquire the electric field of scattered light.
The electric field in the far-field is solved by the built-in function of FDTD solution, and this procedure can be described as a Fourier transform from near field to far-field as follows,
where is a constant, and represents Fourier transform. Thus, the far-field light intensity distribution in far-field can be expressed as
Equation (2) is the ideal solution where the diffraction effect caused by the limit of the aperture to the scattered light in the actual MSDI system is not calculated. In the actual MSDI system, the objective lens has a certain numerical aperture. Limited by the aperture, the scattered light induced by the defect will generate diffraction during imaging in the MSDI system, which leads to the inconsistency between the simulation light intensity distribution and the actual gray distribution in the far-field. Thus, needs to be revised. Since the diffraction effect caused by the numerical aperture can be expressed by the PSF in theory, is revised by PSF as follows,
where is the revised result of , and is a convolution operator. By collecting the actual image gray distribution of the step source , PSF can be obtained as follows,
where the idea image gray distribution of the step source is expressed as,
3.2. Defect Size Recognition Based on DRT
3.2.1. Generation of DRT
DRT is a machine learning algorithm and is often used to solve classification and regression problems. The defect size recognition according to its far-field simulation light intensity distribution can be regarded as a regression problem. Hence, we employ the DRT to study the relationship between the defect size and its light intensity distribution, and its training data set (i.e., revised light intensity distribution of different size defects) can be obtained from the simulation model in Section 3.1. The schematic diagram of defect size recognition based on DRT is depicted in Figure 3. The mean value of the distance between three groups of feature points, whose intensity is 0.75, 0.5, and 0.25 of the peak value of , is taken as the feature parameter of the light intensity distribution as follows,
where , , and are the distance between points whose intensity is 0.75, 0.5, and 0.25 of the peak value of , respectively. Hence, the relationship between the defect size and the light intensity distribution feature parameter can be depicted by
where is the function of DRT. For the th light intensity distribution curve, its feature parameter is marked as , and its corresponding width is marked as . Hence, the training data set of DRT can be expressed as , where is the total number of the light intensity distribution curves.
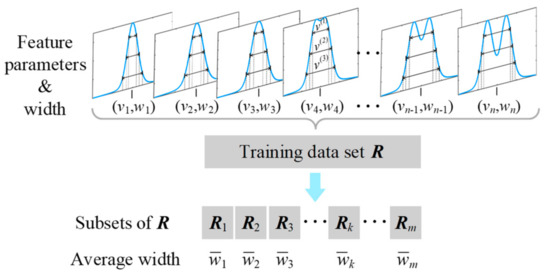
Figure 3.
Schematic diagram of defect size recognition based on the decision regression tree (DRT).
In Figure 3, DRT splits the training data set into subsets, and the mean width in each subset is taken as the prediction width of each subset. For example, if the feature parameter of a defect, whose width is unknown, belongs to a subset , then we will obtain its width recognition result , according to the mapping relationship as follows,
The specific defect size recognition process is shown in Figure 4. It mainly consists of three parts. The first part is to extract the feature parameter from the defect image. Our MSDI system mentioned in Section 2 is used to acquire the defect image. Considering there is inevitably some dirt and dust on the optical element surface, which will cause the noise to the defect gray distribution, we use image process methods, such as image filtering and outlier removal, to eliminate the noise of the image. Then, the gray distribution of the defect is extracted from the denoising image. After gray normalization, the feature parameter of the defect is obtained from the normalized gray distribution. The second part is about collecting training data for DRT. A simulation model of MDSI mentioned in Section 3.1 is built based on the FDTD method, and the simulation light intensity distribution revised by PSF is taken as the training data of DRT after normalization. The third part is about training DRT to recognize defect size, which is given as follows:
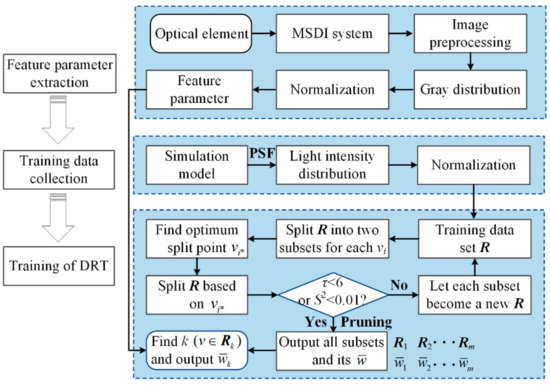
Figure 4.
Flow chart of the defect size recognition.
- Step 1.
- Arrange the training data set in ascending order according to the feature parameter , where and ;
- Step 2.
- Go through each in ascending order, and split into two subsets according to , which are and . Then, calculate the mean width of each subset, and use as the width estimation value of all in each subset. For instance, in the subset , the width estimation value of all and its error can be, respectively, expressed aswhere is a function for solving the mean value in the subset and ;
- Step 3.
- Find the optimum , where the value of is minimum, and mark this as . Take the two subsets and , which are split by as the two new sets . Go back to step 2 until the number of the feature parameter is less than 6 (i.e., ) or the variance of is less than 0.01 (i.e., ) in new set ;
- Step 4.
- Take the mean width as the prediction width of all in subset and denote this regression relationship as DRT . In case the overfitting of DRT occurs, DRT needs to be further optimized, and this optimization is called the DRT pruning [20], which is illustrated in Section 3.2.2.
3.2.2. The Pruning of DRT
As can be seen in Equation (10), the generation of DRT is based on the rule of minimizing the prediction error. However, like the high order polynomial fitting will lead to the overfitting, the continuous split of the set will also cause the same situation. The extreme situation is, each light intensity distribution curve is a subset of (i.e., ). Thus, the prediction error will be 0. This result is meaningless. Although the split termination condition () in Figure 4 will limit this extreme situation to some extent, will still be very close to 0. Hence, the DRT pruning must be taken to prevent this overfitting situation.
The pruning core strategy is to balance the prediction error in a small range. As discussed above, the small prediction error is what we expect, but the too-small value is not what we want. Since decreases with the increasing of the subset number (when increases to the total number of simulation curves , will be 0), decreasing the value of would be a good choice. It can be achieved by stopping the split of some subsets in , which makes some original split subsets be discarded (namely be pruned). The key question is how to decrease so that the prediction error won’t increase a lot. The solution has already been put forward in DRT pruning by solving an optimization problem as follows [20],
where () is a penalty factor. In Equation (11), we can see that reaches the minimum and is not the optimized result since will reach the maximum meanwhile. The optimization in Equation (11) is also called regularization in mathematics for preventing overfitting. Different values of will obtain different DRT optimized result . The equation of can be given as follows [20],
where is a subtree of (namely a subset of ). When subtree is selected to be pruned, all its subsets are discarded, so its subset number . is a subtree of , and its subset number is remarked as . Since the size of the original DRT , which is not be pruned, is finite, the number of values of is also finite. From the Equation (11), we can get a series of finite optimized DRT , where is the number of the values of . To get the final optimized DRT, the cross-validation is carried out among these DRT.
4. Results and Discussion
4.1. Simulation of MSDI System
To collect the far-field simulation light intensity distribution as the training data set of the DRT, an electromagnetic simulation model of MSDI is built in the FDTD solution software, as illustrated in Section 3.1. Here, we take the width recognition of scratch as an example. Since some research [21,22] has reported that the shape of the scratch cross-section is usually v-shaped in practice, a series of v-shaped scratches are designed in FDTD solution with the width in the range of 0.5 μm to 5 μm and the depth below 1 μm. A TFSF source with the wavelength in the range of 0.4 μm to 0.75 μm is taken as the white light source. The refractive index of air is set to 1, and the material of the optical element is set to SiO2. The SiO2 refractive is a built-in parameter in the FDTD solution, which is a function of the wavelength . The magnification of the objective lens is set to 9.7×. All settings of model parameters are shown in Table 1.

Table 1.
Parameters settings of the simulation model.
A series of the simulation light intensity distribution is obtained from the simulation model, as shown in Figure 5. The scratch width of 0.5 μm is close to the wavelength (0.4~0.75 μm), which will cause the scattered light diffraction. Thus, its distribution will be unimodal, as can be seen in Figure 5a. When the width of the scratch is slightly larger than the wavelength, the bimodal distribution of some scratch occurs, as shown in Figure 5b, which suggests that the diffraction caused by scratch weakens. In Figure 5c–f, the width of the scratch is in the range of 2~5 μm. The light intensity distribution of scratches is bimodal, and the distance between two peaks increases with the increase in the scratch width.
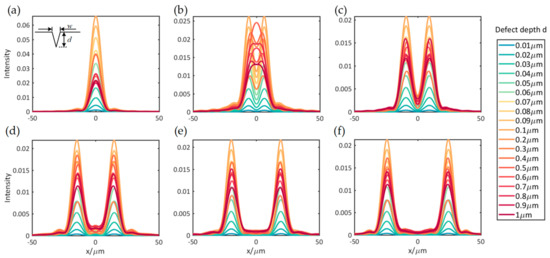
Figure 5.
The far field simulation light intensity distribution of scratches, where (a) w = 0.5 μm, (b) w = 1 μm, (c) w = 2 μm, (d) w = 3 μm, (e) w = 4 μm, and (f) w = 5 μm.
4.2. Revision of Simulation Light Intensity Distribution
The simulation light intensity distribution in Figure 5 are ideal results without calculating the diffraction effect caused by the aperture of the actual MSDI system. Hence, we measure the PSF of the MSDI system by the method mentioned in Section 3.1 and use PSF to revise the distribution. The measurement result of PSF is shown in Figure 6. Figure 6a is the ideal gray distribution of the step source, and its expression is given in Equation (5). In Figure 6a, there is a discontinuity point, where the gray value jumps from 0 to 255. To measure the PSF, the gray distribution of the actual step source is acquired by the MSDI system, as shown in Figure 6b. Slightly different from the ideal result in Figure 6a, the actual gray distribution is continuous and doesn’t have a discontinuity point. After taking the derivative of the actual gray distribution in Figure 6b, the PSF in a discrete form is shown in Figure 6c. Since the typical expression of the PSF is Gaussian type [23], we use the Gaussian fitting function to fit the discrete points, and the fitting expression result can be seen in Figure 6c.
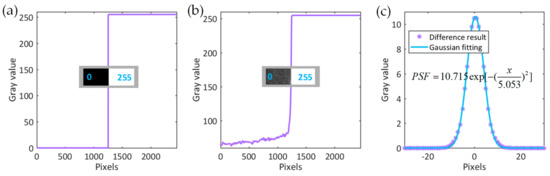
Figure 6.
(a) Gray distribution of ideal step source. Inset: Ideal image of step source; (b) Gray distribution of actual step source. Inset: Actual image of step source; (c) Gray distribution of point spread function (PSF).
Convolving the distribution in Figure 5 with the PSF, we get a revised distribution, as shown in Figure 7. The revised distribution is unimodal in Figure 7a–c and is bimodal in Figure 7d–f. Compared with Figure 5a–f, the span of the revised distribution in Figure 7a–f broadens. The bimodal distribution in Figure 5b,c becomes unimodal in Figure 7b,c, with the effect of the PSF. Figure 7d is the revised distribution of scratch, where w = 3 μm, and we can see that the bimodal distribution begins to appear, which means the actual diffraction limit resolution of our MSDI system is around 3 μm. With the increase in the scratch width, the distance between two peaks in bimodal distribution increases, as shown in Figure 7d–f.
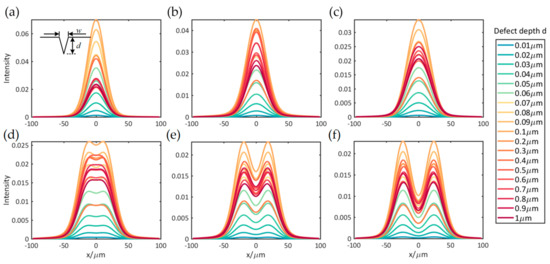
Figure 7.
The revised far field simulation light intensity distribution of scratches, where (a) w = 0.5 μm, (b) w = 1 μm, (c) w = 2 μm, (d) w = 3 μm, (e) w = 4 μm, and (f) w = 5 μm.
In order to validate the validity of the revision result by PSF, the images of five scratches are acquired by our MSDI system, and its width is measured by SEM. We utilize the simulation model to get the light intensity distribution of the scratch in the far-field whose width is equal to the value SEM measured. Figure 8 is the comparison between the revised simulation light intensity distribution and the actual gray distribution of the scratch at the same scratch width. Figure 8a corresponds to the scratch width of 1.17 μm; both the two kinds of distributions are unimodal, and the revised simulation light intensity distribution feature parameter is slightly larger than the experiment gray distribution feature parameter . For the scratch width of 2.23 μm, is almost the same with , as can be seen in Figure 8b. Figure 8c corresponds to the scratch width of 3.24 μm, and the difference between and is about 1.9 pixels. In Figure 8d,e, both two kinds of distributions are bimodal, and their feature parameter difference is within 1 pixel. The results in Figure 8a–e indicate that the simulation light intensity distribution revised by PSF is almost consistent with the experiment gray distribution of the scratch, and their feature parameter difference is within 2 pixels. Hence, taking simulation data instead of experiment data as the training data set of the DRT algorithm is practicable.
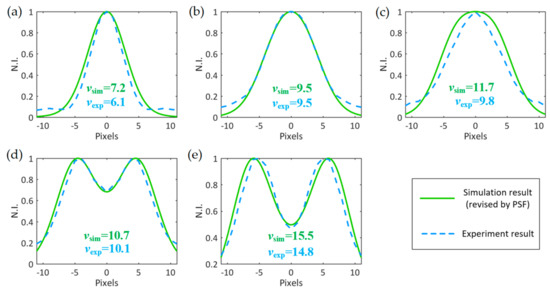
Figure 8.
The comparison between simulation and experiment results, where (a) w = 1.17 μm, (b) w = 2.23 μm, (c) w = 3.24 μm, (d) w = 4.22 μm, (e) w = 5.19 μm.
4.3. Simulation of Scratch Width Recognition
4.3.1. Training Result of DRT
Since the simulation light intensity distribution revised by PSF is almost consistent with the experiment gray distribution of the scratch, we take 600 simulation light intensity distribution curves from the simulation model to train and test the DRT in scratch width recognition. These curves are divided into two parts. Five hundred curves are randomly chosen as the training data set of DRT, and the remaining 100 curves are taken as the test data set to test the recognition accuracy of DRT. The root mean square error (RMSE) is taken as the parameter to represent the recognition accuracy. As mentioned in Section 3.2, the overfitting (i.e., width recognition result is too good in the training data set, while it is very poor in the testing data set) easily happens during the training of DRT. Thus, pruning optimization is carried out to avoid overfitting during the training of DRT. Table 2 is the width recognition result of the scratch by DRT under pruning and without pruning. As for the width recognition in the training data set, although the RMSE of unpruned DRT is 0.008 μm, which is smaller than the RMSE of 0.041 μm of pruned DRT, the width recognition in the test data set is totally opposite. The RMSE of unpruned DRT is 0.153 μm in the test data set; it is not only larger than the RMSE of 0.008 μm of unpruned DRT in the training data set but also larger than the RMSE of 0.045 μm of pruned DRT in the test data set. It indicates that the overfitting of the unpruned DRT will lead to a poor result in actual width recognition. Hence, the pruning optimization of the DRT is necessary. The RMSE of the pruned DRT in the training data set and test data set is 0.041 μm and 0.045 μm, respectively, which is better than the unpruned DRT.

Table 2.
Scratch width recognition results by DRT in simulation data.
4.3.2. Recognition Error Analysis for the Scratch Cross-Section Shape Deviation
For a standard v-shaped cross-section scratch, the DRT has good recognition accuracy, as shown in Table 2. However, the real cross-section shape of the scratch may not be so standard in practice. Hence, the recognition accuracy of the DRT needs to be further discussed. Here, we use the Monte Carlo method to generate a series of random like v-shaped scratches to verify the reliability of the DRT. Firstly, a rectangle ABCD is made in FDTD solution software as the original cross-section shape of the scratch. The original refractive index of the rectangle is set as . Then, the rectangle ABCD is divided into a large number of squares. Each square edge is 0.05 μm. Next, the built-in script in the software based on the Monte Carlo method is carried out to select some squares from the bottom edge DC to the top edge AB and override the refractive index of the selected squares with . Finally, the scratch cross-section AOB is obtained. A total of 150 random v-shaped cross-section scratches are generated. The width |AB| is set in the range of 0.5 μm to 5 μm. The DRT width recognition result is, as shown in Figure 9. For the scratch width of 0.5 μm, 1 μm, 2 μm, 3 μm, 4 μm, and 5 μm, the interquartile range (IQR) of the recognition absolute error is 0.17 μm, 0.34 μm, 0.41 μm,0.20 μm, 0.11 μm, and 0.08 μm, respectively. The scratch width of 1 μm and 2 μm has a relatively high IQR, and the IQR of the remaining width scratches is within 0.2 μm. It indicates that the inconsistency between the ideal and real shape of the scratch in the width of 1 μm and 2 μm has more influence on the scratch width recognition than other scratch width ranges.
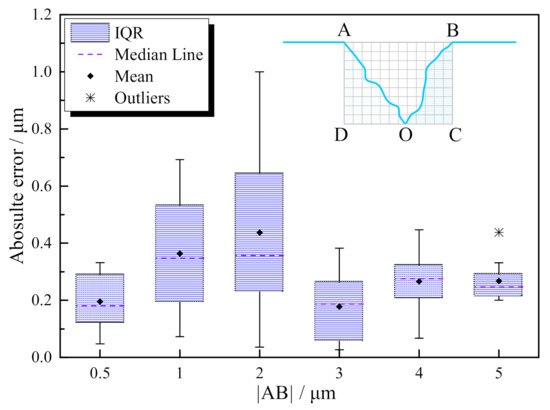
Figure 9.
The width recognition absolute error of the 150 random v-shaped cross-section scratches. Inset: the sketch of the random v-shaped scratch cross-section.
4.4. Experiment of Scratch Width Recognition
To further verify the training result of DRT in Section 4.3, the standard glass plate with the process of electron beam exposure and the ion beam etching is taken as the scratch samples, as shown in Figure 10, and the DRT, which has completed training from simulation data, is applied to recognize the width of these scratch samples. The actual scratch width is measured by a scanning electron microscope (SEM) as a reference. The scratches whose width is in the range of 0.61–5.19 μm are taken as the test samples. The experiment set up is introduced in Section 2. The incident light from the white LED irradiates on the optical element surface, and a part of them is scattered by the scratch. The scattered light is firstly focused on by the objective lens of our MSDI system with the magnification of 9.7× and the numerical aperture of 0.15 and then collected by CCD. The single-pixel size of CCD is 3.45 × 3.45 μm, and the photosensitive area of CCD is 8.47 × 7.10 mm. Finally, CCD transmits the image to the computer, and DRT is applied to recognize the width of these scratches. The scratch width recognition is executed on the MATLAB (R2017a), Windows 10 64-bit operating system (Intel Core i7-8550 CPU, 8G RAM).
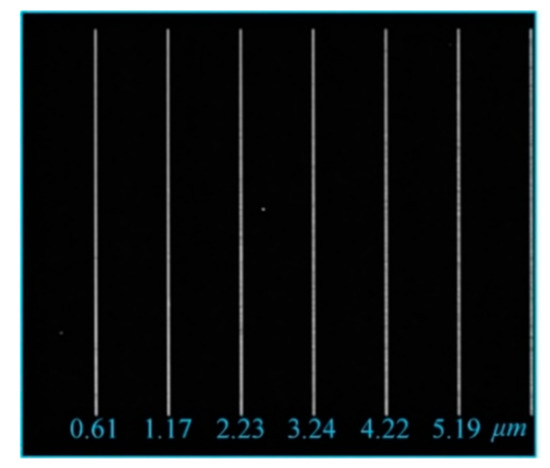
Figure 10.
Schematic diagram of standard glass plate scratches.
The width recognition result of the tested scratches samples is shown in Table 3. The conventional image processing method (Otsu threshold segmentation) is also employed as a comparison to the DRT. As for the scratches whose real width is 0.61 μm and 1.17 μm, the Otsu method has a large error, and the relative error of the Otsu method even exceeds 100% in recognition of the scratch width of 0.61 μm, while the relative error of DRT is between 5.1% and 10%. This is because the scratch width of 0.61~1.17 μm is close to the wavelength of the light source (0.4~0.75 μm), and the diffracted light will occur when the incident light is scattered by the scratch. Besides, the limit of the aperture to the scattered and diffracted light will cause the second diffraction. Thus, the gray distribution of the scratch will largely broaden, which leads to the recognition result of Otsu that is larger than the result in the situation where the gray distribution doesn’t broaden. Since the DRT is trained by learning the light intensity distribution of different width scratches, the gray distribution broadening caused by diffraction has less effect on DRT than the Otsu method. As for the scratches whose real width is 2.23 μm and 3.24 μm, the relative error of the Otsu method is between 11.4% and 31.4%, while the relative error of DRT is between 1.5% and 4.9%. It indicates that the effect of diffraction on the two methods decreases with the increase in the real width of the scratch. For the scratches whose real width is 4.22 μm and 5.19 μm, the relative error of the Otsu method is in the range of 2.1~2.9%, and the relative error of DRT is in the range of 1.2~2.1%.

Table 3.
Scratches width recognition result of the tested scratches samples.
Since DRT is essentially a regression method, the exponential nonlinear regression is carried out as a comparison to DRT. In Table 3, the exponential regression method shows good performance in the defect size range of 3.24 μm to 5.19 μm, and its relative error is between 2.7% and 3.4%, which is close to the DRT and is better than the Otsu method. However, for the defect size range of 0.61 μm to 2.23 μm, the relative error of the exponential method increases a lot and is far beyond the relative error of DRT. Hence, compared with the Otsu method and exponential regression method, the DRT can achieve relatively higher precision recognition.
5. Conclusions
A defect size recognition method based on DRT is proposed in this paper for the defect whose size is close to the diffraction limit of the MSDI system. To obtain the far-field simulation light intensity distribution of the defect as the training data set of the DRT, the FDTD electromagnetic simulation model of the MSDI system is built. Since the diffraction effect caused by the limit of the aperture to the scattered light isn’t calculated in the simulation model, the simulation light intensity distribution needs to be revised. Hence, the PSF of the actual MSDI system is measured, and the simulation light intensity distribution is convolved with the PSF as the revision. The mean value of the distance between three groups of feature points, whose intensity is 0.75, 0.5, and 0.25 of the peak value of the revised simulation light intensity distribution, is taken as the feature parameter, and the machine learning algorithm of DRT is applied to find the mapping relationship between the feature parameter and the defect size from the training data set. To validate the DRT, the standard glass plates with the process of electron beam exposure and the ion beam etching are taken as the tested defect samples. The experiment results show that the relative error of DRT is within 10%, which is far better than the conventional Otsu method and exponential regression method. In future work, the simulation database of more defect types will be built, and the defect depth recognition will be carried out.
Author Contributions
Conceptualization, Y.Y., P.C., and W.L.; methodology, W.L.; software, W.L.; validation, W.L., P.C., and D.Z.; formal analysis, W.L.; investigation, D.Z.; resources, P.C.; data curation, D.Z.; writing—original draft preparation, W.L.; writing—review and editing, Y.Y.; visualization, P.C.; supervision, Y.Y.; project administration, P.C.; funding acquisition, Y.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (NSFC,61627825, 61875173) and supported by the State Key Laboratory of Modern Optical Instrumentation of Zhejiang University and Zernike Optics Co., Ltd.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kim, J.-H.; Aghaeimeibodi, S.; Carolan, J.; Englund, D.; Waks, E. Hybrid integration methods for on-chip quantum photonics. Optica 2020, 7, 308. [Google Scholar] [CrossRef]
- Tao, H.; Veetil, S.P.; Pan, X.; Liu, C.; Zhu, J. Visualization of the influence of the air conditioning system to the high-power laser beam quality with the modulation coherent imaging method. Appl. Opt. 2015, 54, 6639. [Google Scholar] [CrossRef] [PubMed]
- Yang, M.; Xu, F.; Ren, J.-G.; Yin, J.; Li, Y.; Cao, Y.; Shen, Q.; Yong, H.-L.; Zhang, L.; Liao, S.-K.; et al. Spaceborne, low-noise, single-photon detection for satellite-based quantum communications. Opt. Express 2019, 27, 36128. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.Y.; Chai, H.T.; Li, C.; Zhang, Y.H.; Wu, F.; Bai, J.; Shen, Y.B. Surface defects evaluation system based on electromagnetic model simulation and inverse-recognition calibration method. Opt. Commun. 2017, 390, 88–98. [Google Scholar] [CrossRef]
- Liu, J.; Liu, J.; Liu, C.G.; Wang, Y.H. 3D dark-field confocal microscopy for subsurface defects detection. Opt. Lett. 2020, 45, 660–663. [Google Scholar] [CrossRef] [PubMed]
- Wu, F.; Cao, P.; Du, Y.; Hu, H.; Yang, Y. Calibration and Image Reconstruction in a Spot Scanning Detection System for Surface Defects. Appl. Sci. 2020, 10, 2503. [Google Scholar] [CrossRef]
- Forte, P.M.F.; Felgueiras, P.E.R.; Ferreira, F.P.; Sousa, M.A.; Nunes-Pereira, E.J.; Bret, B.P.J.; Belsley, M.S. Exploring combined dark and bright field illumination to improve the detection of defects on specular surfaces. Opt. Lasers Eng. 2017, 88, 120–128. [Google Scholar] [CrossRef]
- Kobayashi, H.; Lei, C.; Wu, Y.; Mao, A.L.; Jiang, Y.Y.; Guo, B.S.; Ozeki, Y.; Goda, K. Label-free detection of cellular drug responses by high-throughput bright-field imaging and machine learning. Sci. Rep. 2017, 7, 1–9. [Google Scholar] [CrossRef]
- Kurita, T.; Otsu, N.; Abdelmalek, N. Maxium-likelihood thresholding based on population mixture-models. Pattern Recognit. 1992, 25, 1231–1240. [Google Scholar] [CrossRef]
- Xu, X.Y.; Xu, S.Z.; Jin, L.H.; Song, E.M. Characteristic analysis of Otsu threshold and its applications. Pattern Recognit. Lett. 2011, 32, 956–961. [Google Scholar] [CrossRef]
- Jin, Y.; Zhang, D.D.; Li, M.Z.; Wang, Z.B.; Chen, Y.X. A Fuzzy Support Vector Machine-Enhanced Convolutional Neural Network for Recognition of Glass Defects. Int. J. Fuzzy Syst. 2019, 21, 1870–1881. [Google Scholar] [CrossRef]
- Li, C.; Tian, Y.; Li, W.J.; Tian, J.D.; Zhou, F. Low-Contrast Defects Recognition Using Low-Order Residual Network. IEEE Access 2019, 7, 91193–91201. [Google Scholar] [CrossRef]
- Mei, S.; Yang, H.; Yin, Z.P. Unsupervised-Learning-Based Feature-Level Fusion Method for Mura Defect Recognition. IEEE Trans. Semicond. Manuf. 2017, 30, 105–113. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- De’ath, G.; Fabricius, K.E. Classification and regression trees: A powerful yet simple technique for ecological data analysis. Ecology 2000, 81, 3178–3192. [Google Scholar]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Oskooi, A.F.; Roundy, D.; Ibanescu, M.; Bermel, P.; Joannopoulos, J.D.; Johnson, S.G. MEEP: A flexible free-software package for electromagnetic simulations by the FDTD method. Comput. Phys. Commun. 2010, 181, 687–702. [Google Scholar] [CrossRef]
- Wolf, E. Electromagnetic diffraction in optical systems I. An integral representation of the image field. Proc. R. Soc. Lond. Ser. A-Math. Phys. Sci. 1959, 253, 349–357. [Google Scholar]
- Marchand, E.W. Deriviation of point spread function from line spread function. J. Opt. Soc. Am. 1964, 54, 915. [Google Scholar] [CrossRef]
- Melnikov, G.A.; Melnikov, T.A.; Gubarev, V.V. Regression tree pruning algorithms: An overview and empirical comparison. Inf. Technol. 2016, 22, 669–675. [Google Scholar]
- Li, C.; Yang, Y.; Chai, H.; Zhang, Y.; Wu, F.; Zhou, L.; Yan, K.; Bai, J.; Shen, Y.; Xu, Q.; et al. Dark-field detection method of shallow scratches on the super-smooth optical surface based on the technology of adaptive smoothing and morphological differencing. Chin. Opt. Lett. 2017, 15, 1–5. [Google Scholar]
- Li, C.; Zhang, F.; Ding, Y.; Liu, L. Surface deformation and friction characteristic of nano scratch at ductile-removal regime for optical glass BK7. Appl. Opt. 2016, 55, 6547–6553. [Google Scholar] [CrossRef] [PubMed]
- Fan, C.; Li, G.; Tao, C. Slant edge method for point spread function estimation. Appl. Opt. 2015, 54, 4097–4103. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).