Abstract
Damping is one of the important issues related to isolated structures, including the newly proposed low-cost spring-asphalt isolation system. In this study, the damping properties of the system in terms of displacement dependence, frequency dependence and temperature dependence were studied by a cyclic simple shear experiment. Then, the direct least-square method was used to identify the damping properties from the experimental data. Furthermore, to validate the effectiveness of the damping device, a modal analysis was conducted based on multi-dimensional shaking table tests. The results indicate that (1) the hysteretic curves are similar to an ellipse, which means that the asphalt shows characteristics of viscoelastic materials; (2) the damping properties are positively related to the loading frequency and inversely related to the temperature and displacement; and (3) asphalt can provide adequate damping and reduce the displacements of the superstructure by nearly half. On the basis of the experimental test results, an analysis of the modal information with multi-dimensional input is also presented.
1. Introduction
Three-dimensional isolation systems have been studied by numerous scholars all over the world [1,2,3,4,5,6]. Most three-dimensional isolation systems use high-damping lead cores [1,2,3] or additional oil dampers [4] to provide damping. Therefore, these isolation systems usually have complex structures and high costs. Consequently, they are not often applied in residential buildings, especially in rural areas. To reduce costs and simplify structures, a low-cost three-dimensional spring-asphalt isolation bearing has been proposed. The system mainly consists of helical springs and Heavy Calcium Carbonate (HCC)-modified asphalt. The function of asphalt is to prevent the springs from eroding and impart a degree of damping to the system. In this system, HCC can be used as filler in the material, which can increase the volume of its products and thus reduce costs. A similar application of asphalt can also be found in other low-cost isolation systems [7]. However, it is not clear whether the damping properties of asphalt will be affected by adding HCC. Therefore, it is necessary to study the damping properties of HCC-modified asphalt and the damping effectiveness of low-cost isolation bearings.
The resonant column test, Dynamic Shear Rheometer (DSR) and cone-and-plate method are the main methods used to study the damping characteristics of asphalt. The resonate column test is widely used to study the properties of asphalt in main roads, so the asphalt is usually mixed with sand and stone. Wang and Zeng [8] studied the temperature-dependent properties of asphalt through a resonant column test. Their results showed that the damping ratio of all samples was highly dependent upon the temperature. Specifically, the damping ratio increased as the temperature of the sample increased. Tavassoti-Kheiry et al. [9] conducted resonant column tests of different asphalt mixtures to study the frequency-dependent characteristics of the modulus. The results showed that Young’s modulus increased with the input frequency. Islam, M. R et al. [10] utilized a concrete resonant column to study Poisson’s ratio with different input frequencies. This method is suitable for highway engineering, but not for isolated structures.
Another method to study the damping properties of asphalt is DSR. By adjusting the rotation speed and rotation angle of the instrument, the loading frequency and loading strain can be adjusted. Jiang and Hu et al. [11] utilized a dynamic shear rheometer to evaluate the damping performance of four types of asphalt using the temperature spectra of the loss factor (LF). The results revealed strong temperature-dependent properties, but there was less variation near the low-temperature area. In addition to temperature-dependent properties, frequency-dependent properties are also important. Makris [12,13] utilized the cone-and-plate method to determine the storage and loss shear moduli of asphalt with different loading frequencies and strains. They proposed the fractional derivative Maxwell model based on their experimental results. The results showed that asphalt has viscoelastic properties.
Using the DSR method, a cyclic simple shear instrument was used in the present study to directly change the loading frequency and displacement. The frequency dependence, temperature dependence and displacement dependence properties and the effect of the HCC mass ratio of asphalt were comprehensively studied by cyclic simple shear tests. Then, to validate the effectiveness of the damping properties of asphalt, time-domain, frequency-domain and modal analyses were conducted by using the experimental data of a multi-dimensional shaking table test. Furthermore, some additional work was conducted to identify the dynamic damping ratio with multi-dimensional input.
2. Experimental Study of HCC-Modified Asphalt
2.1. Test Design and Procedure
The purpose of this test was to investigate the damping properties of HCC-modified asphalt, which is used in low-cost spring-asphalt isolation bearings. The whole test was conducted in the structural experiment center at Hunan University. The experimental instrument is the cyclic simple shear system developed by the Wykeham Farrance company (see Figure 1a), and the schematic is shown in Figure 1b. The specimen used in the test is a round column with a diameter of 70 mm and a height of 25 mm (see Figure 1c). The material properties are shown in Table 1.
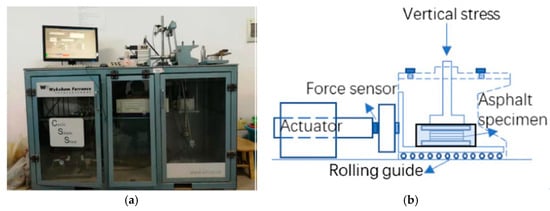

Figure 1.
Test instrument: (a) cyclic simple shear instrument; (b) illustration of the instrument; (c) asphalt specimen; (d) illustration of the cyclic shear.

Table 1.
Material properties of the asphalt.
The instrument can also apply a vertical force to the specimen, but the actual vertical stress of the asphalt in the isolation bearings is almost zero because the springs bear all of the gravity of the superstructure, as well as seismic forces. Therefore, vertical stress was not applied in this test.
To investigate the damping properties of the modified asphalt material, cyclic tests on the sinusoidal motion of specified amplitudes and frequencies were conducted using a cyclic simple shear instrument. The shear strain was induced by horizontal movement at the bottom of the sample relative to the top (see Figure 1d). During the test, the sensors of the instrument recorded the horizontal displacements and forces.
Dynamic tests were studied in the shear mode with a series of displacements (0.2–1 mm), loading frequencies (0.1–1 Hz), HCC mass ratios (0–0.3) and temperatures (5, 20 °C). Each specimen of the asphalt was subjected to 30 sinusoidal excitations cycles at a fixed temperature, loading displacement and loading frequency. The temperatures of the specimen were assumed to be equal to room temperature, given that the environment of the test room was relatively stable.
2.2. Parameter Identification
Hysteresis loops were plotted according to the data recorded by the instrument for each test condition. Then, the equal damping ratio and stiffness were calculated directly according to the hysteresis loops (see Figure 2). The equivalent damping ratio and stiffness can be expressed as follows [14]:
where ΔW is the total absorbed energy, W is the elastic energy, Fmax is the maximum force, and u0 is the maximum displacement.
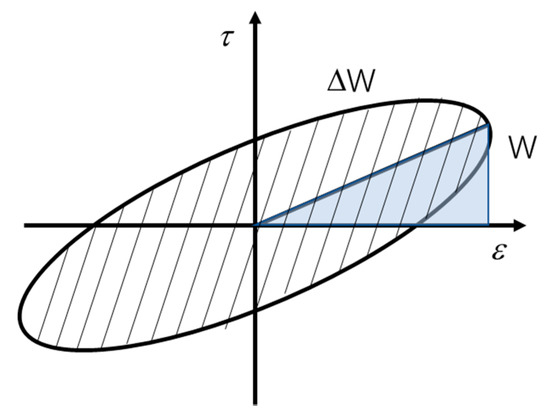
Figure 2.
Calculation of the equivalent damping ratio.
Under sinusoidal excitation, the relationship between the damping force and excitation displacement can be written as follows [15,16]:
where Fd and ud are the damping force and excitation displacement, respectively, u0 is the maximum displacement, η is the loss factor, and Ke is the storage stiffness. It is clear that the shape of the hysteretic loops for viscoelastic dampers should be an ellipse. Equation (3) can be expanded to get the implicit second-order polynomial:
where a, b and c are unknown parameters.
a *Fd2 + b * Fd * ud + c * ud 2 − 1 = 0
After generating the hysteretic loops from the experimental data, the unknown parameters can be identified by the direct least-square fitting method [17,18], and then the damping parameters can be calculated:
2.3. Effect of Repeated Loadings
Using Equations (8)–(10), the damping properties can be determined from the experimental data. All the parameters mentioned in the following sections were identified using the direct least-square fitting method.
The asphalt specimen was subjected to 30 cycles of repeated sinusoidal loadings under different frequencies and displacements. Parts of the hysteretic loops are shown in Figure 3a, and the fitting results of the experimental data are shown in Figure 3b. The fitting results show that the fitting values are in good agreement with the experimental values.
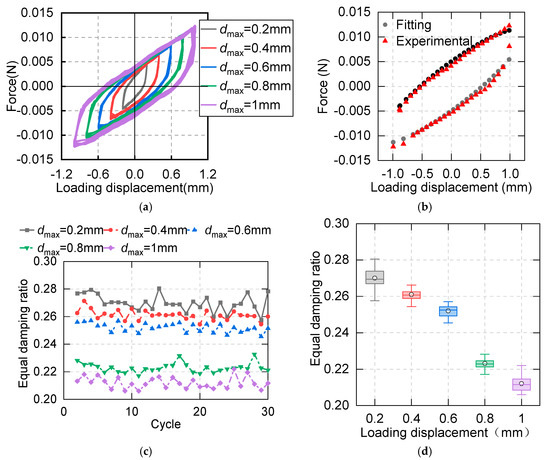
Figure 3.
Variance curves of the damping properties for cyclic simple shear tests under repeated excitation at 20 °C: (a) hysteretic loops of repeated loadings under a frequency of 0.1 Hz, HCC mass ratio of 0.2, and displacement amplitudes of 0.2–1 mm; (b) the fitting results of the hysteretic curves; (c) the equivalent damping ratios of different conditions; (d) box chart of the damping ratio with different frequencies over 30 cycles.
After 30 cycles of repeated loadings, the hysteretic curves remain stable and full, which means that the energy dissipation capability is adequate. From these hysteretic loops, the corresponding damping ratios can be calculated, and the results are shown in Figure 3c. In the figure, the damping ratio fluctuates around the mean value, and no noticeable change in the damping ratio can be observed. Furthermore, the results for the other damping parameters in different test conditions also show the same trend. Therefore, according to the data in this paper, the damping parameters are independent of the loading cycles, and the mean values of these parameters can be used to represent the damping properties in repeated tests (see Figure 3d).
2.4. Effect of the Loading Frequency
Usually, viscoelastic dampers have strong frequency-dependent properties, so it is necessary to investigate the performance under different loading frequencies. Figure 4 shows the displacement–force curves for loading frequencies of 0.1 Hz, 0.2 Hz, 0.5 Hz and 1 Hz at displacements of 0.2 mm, 0.4 mm, 0.6 mm, 0.8 mm and 1 mm. The hysteretic curves are full and round, which indicates that the asphalt can offer adequate damping. Meanwhile, the forces increase with the frequencies, which indicates that the equivalent stiffness is larger when subjected to high frequencies. At low frequencies, the hysteretic curves of the asphalt are not as full, and the slopes slightly decrease. Furthermore, the change rules of these curves under different frequencies are similar.
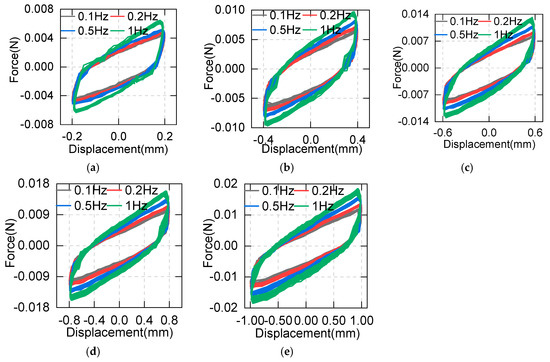
Figure 4.
Hysteretic curves of the asphalt specimen under different loading frequencies at 20 °C: (a) maximum displacement of 0.2 mm (maximum strain of 1%); (b) maximum displacement of 0.4 mm (maximum strain of 2%); (c) maximum displacement of 0.6 mm (maximum strain of 3%); (d) maximum displacement of 0.8 mm (maximum strain of 4%); (e) maximum displacement of 1 mm (maximum strain of 5%).
To reveal the effect of the loading frequency on the asphalt energy dissipation capacity, the storage stiffness (Ke), equivalent stiffness, loss factor (η), and equivalent damping ratio for the same displacements are plotted in Figure 5. It is apparent that all four parameters increase with increasing frequency.
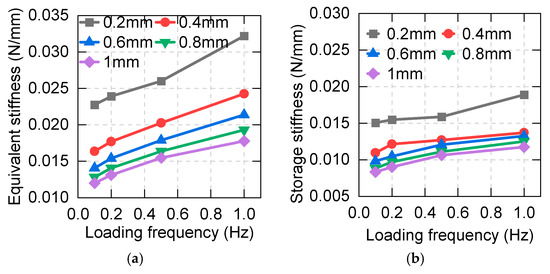
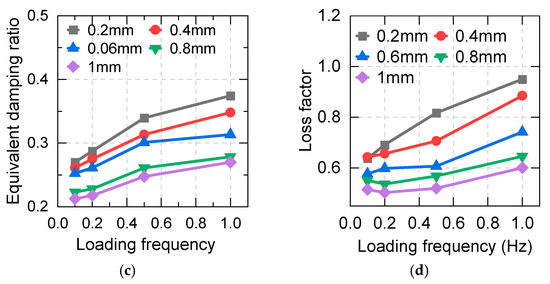
Figure 5.
Dependence of the damping properties of asphalt on the loading frequency: (a) equivalent stiffness; (b) storage stiffness; (c) equivalent damping ratio; (d) loss factor.
2.5. Effect of the Loading Displacement Amplitude
Figure 6 shows the hysteretic curves obtained from different loading frequencies. Overall, the asphalt specimens have good energy dissipation capacity. No strength degradation due to large displacements is evident, although degradation is common in some viscoelastic damping systems [15].
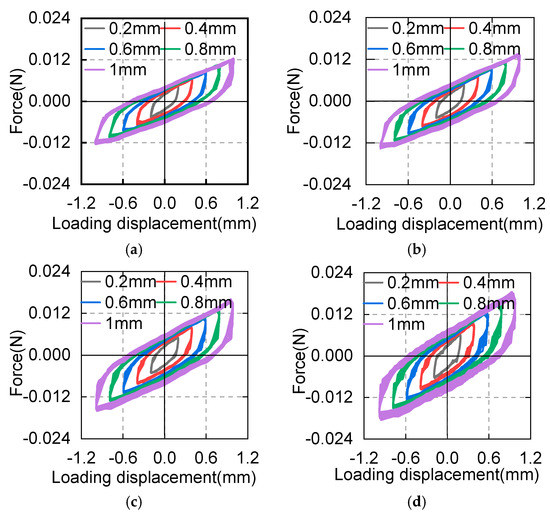
Figure 6.
Hysteretic curves of the asphalt specimen under different loading displacements at 20 °C: (a) loading frequency of 0.1 Hz; (b) loading frequency of 0.2 Hz; (c) loading frequency of 0.5 Hz; (d) loading frequency of 1 Hz.
The effect of loading displacement on damping properties is shown in Figure 7. The results show that all the parameters decrease with the increasing loading displacement. This means that isolation buildings possess larger stiffness and damping ratios at low vibration levels.
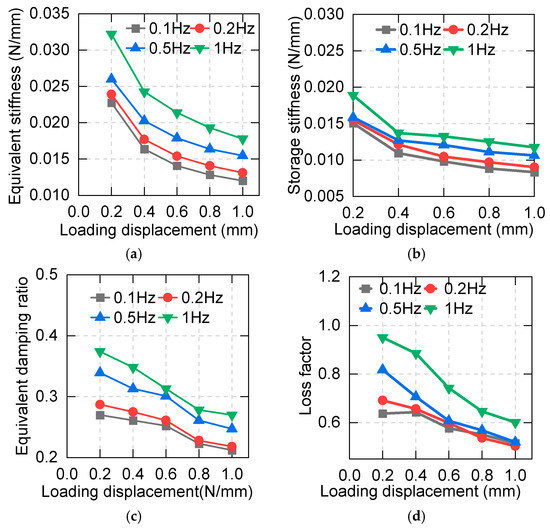
Figure 7.
Dependence of the damping properties of asphalt on loading displacement: (a) equivalent stiffness; (b) storage stiffness; (c) equivalent damping ratio; (d) loss factor.
2.6. Effect of the Temperature
The temperature dependence of damping properties was studied by analyzing the performance at 5 °C and 20 °C. Figure 8 shows that the area and plumpness of the hysteretic curves decrease with the increase in temperature. The results indicate that the isolation bearings have better energy dissipation capacity at low temperatures in the test range.
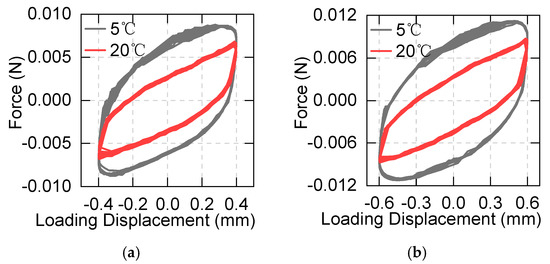
Figure 8.
Hysteretic curves of the asphalt specimen under different temperatures at 0.1 Hz: (a) maximum displacement of 0.4 mm; (b) maximum displacement of 0.6 mm.
The temperature can not only significantly affect the damping characteristics of asphalt but also affect the consistency of asphalt. A penetration experiment was conducted to investigate the consistency of asphalt with different HCC mass ratios at different temperatures (see Figure 9). The results show that the penetration of asphalt at high temperatures is much higher than that at low temperatures, which means that the asphalt has low consistency at low temperatures.
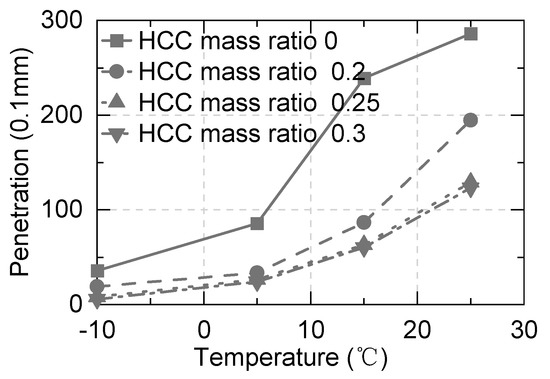
Figure 9.
Penetrations of asphalt of different HCC mass ratios at different temperatures.
Combined with the consistency and damping characteristics of asphalt, it can be concluded that the asphalt has good fluidity at high temperatures. Therefore, asphalt can be easily poured into the isolation bearing during the construction procedure, but the damping ratio of asphalt is lower at high temperatures.
2.7. Effect of the HCC Content
HCC is a contamination-free filler, so it does not change the chemical properties of asphalt; it only changes physical characteristics such as penetration and density. It is not clear whether it will affect its damping characteristics. To study the effect induced by the HCC mass ratio, a comparative experiment was conducted. The HCC ratio β is defined as follows:
where mHCC is the mass of HCC, and masphalt is the mass of base asphalt.
β = mHCC/masphalt
Figure 10 shows the hysteretic curves of four different HCC mass ratios. The results show that when the HCC mass ratio is 0, the corresponding hysteretic curve is the plumpest. When a small amount of HCC (β = 0.1) is added, the area of the hysteretic curve decreases slightly. Meanwhile, the area of hysteretic curves decreases significantly when a sufficient amount of HCC is added. However, there is no obvious difference when the HCC mass ratio is equivalent to 0.2 or 0.3.
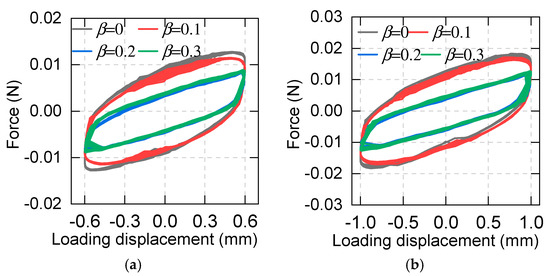
Figure 10.
Hysteretic curves of the asphalt specimen with different HCC mass ratios at 0.1 Hz and 20 °C: (a) maximum displacement of 0.6 mm; (b) maximum displacement of 1 mm.
The damping parameters are shown in Figure 11. The results indicate that all the parameters decrease with the increase in the HCC mass ratio, which means that the high HCC mass ratio could result in lower energy dissipation capability. Furthermore, a high HCC ratio could lead to the poor fluidity of asphalt. Therefore, on the basis of these test results, it is suggested that the HCC mass ratio be controlled at around a value of 0.2.
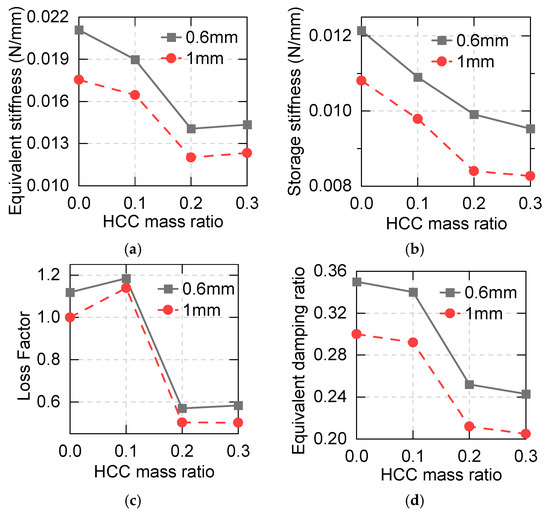
Figure 11.
Dependence of the damping properties of asphalt on the HCC mass ratio with a temperature of 20 °C and a loading frequency of 0.1 Hz: (a) equivalent stiffness; (b) storage stiffness; (c) loss factor; (d) equivalent damping ratio.
2.8. Discussion
The analytical results of cyclic simple shear tests are the basis of the application of spring-asphalt isolated structures and prove the potential feasibility of using asphalt as a damping material. The results show that the damping effect is evident in the test conditions. However, the size and shape of the isolation bearing can also influence the damping effect [12]. The damping effect has not been validated in actual buildings. Therefore, the test results of the cyclic simple shear tests cannot be directly applied to the design. However, the results of the experiment can qualitatively reveal the variation rules of the damping properties of isolation bearings that use this kind of asphalt as the damping material. Furthermore, these findings could serve as an important reference for practical application.
3. Shaking Table Test
The cyclic simple shear tests show that the asphalt specimens have full hysteretic curves, which means that asphalt has the potential to offer adequate damping for isolation structures. Therefore, a shaking table test was conducted to validate the effectiveness of the energy dissipation capability and the performance of the HCC-modified asphalt in the newly proposed low-cost three-dimensional isolation bearing and to study whether the spring has the ability to dissipate energy. Shang [19] has analyzed the isolation effect, but this paper focuses on the in-depth analysis of the damping effect.
3.1. Test Information
3.1.1. Model Information
The geometrical scale of the experimental model is 0.5. The structure is a reinforced concrete frame with asphalt-spring three-dimensional isolation bearings. The plane size of the model is 2.4 m by 2.4 m, and the elevation of the superstructure is 3.6 m. The isolation layer consists of 16 helical springs, and the height of the springs is 25.5 cm under the gravity of the superstructure. The theoretical horizontal frequency is 0.91 Hz, and the theoretical vertical frequency is 3.12 Hz. Note that the theoretical frequencies do not include the effect of asphalt on the stiffness. The elevation is shown in Figure 12. More details of the experiment can be found in Shang [19].
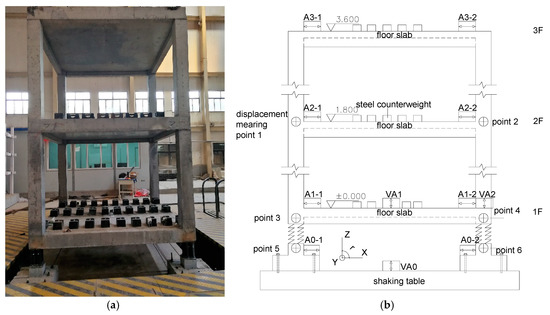
Figure 12.
Elevation of the experimental model: (a) photo of asphalt-spring three-dimensional isolation structures; (b) geometry of asphalt-spring three-dimensional isolation structures.
3.1.2. Loading Schedule
Horizontal, vertical and rocking shaking table tests were conducted with Pacoima and Wolong earthquake excitations. The detailed loading schedule, including Peak Ground Motion (PGA) and direction, is shown in Table 2. The test consists of two parts: non-asphalt tests and with-asphalt tests. In the non-asphalt tests, there is no asphalt in the isolation bearings. After finishing this part of the study, the isolation bearings were filled with asphalt with an HCC mass ratio of 0.2 (see Figure 13). The purpose of this set of comparative tests is to study the energy dissipation capability of HCC-modified asphalt. The time histories of the adopted ground motions are shown in Figure 14. The direction of the earthquake excitation is shown in Figure 12. In the reported results, “x” means uniaxial loading; “xz” means horizontal and vertical excitation; and “xzr” means loading horizontal, vertical and rocking ground motion simultaneously.

Table 2.
Loading schedule of the shaking table tests.

Figure 13.
Pouring the asphalt into the isolation bearings: (a) the procedure; (b) the isolation bearing with asphalt.
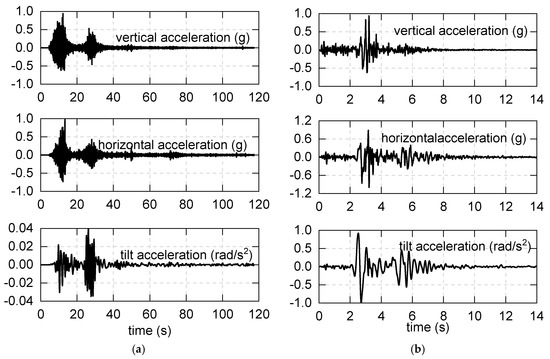
Figure 14.
Time histories of the adopted ground motions: (a) Wolong wave; (b) Pacoima wave.
3.1.3. Measurement Scheme
Horizontal acceleration sensors were set on both sides of each floor, and vertical sensors were installed at the center and corner of the first floor. Video image processing technology was used to record the displacement of the observed points in the XZ plane (see Figure 12b).
3.2. Experimental Results and Analysis
3.2.1. Acceleration and Displacement Responses
In this section, the damping ratio of the test model is the main research object. The constant damping ratio of the model during seismic excitation, which was studied using the parametric method, is reported. Then, a method to calculate the damping ratio of the structure under multi-dimensional ground motions is proposed.
The horizontal acceleration responses and corresponding frequency response functions in the phase of conditions No. 1 and No. 13 are shown in Figure 15. The Frequency Response Function (FRF) [20] and phase are defined in Equations (11) and (12). The PGAs are similar (78 gal and 93 gal, respectively). In the non-asphalt test, the acceleration decays slowly, while, in the with-asphalt test, the acceleration decays rapidly, which indicates that the springs cannot offer adequate damping but that asphalt can offer sufficient energy dissipation capability. Furthermore, according to the FRF and phase, in the with-asphalt test, there is only one main frequency, while, in the non-asphalt test, there are four main frequencies. According to a modal analysis based on the Finite Element Method (FEM), the four frequencies correspond to the first horizontal mode, torsional mode, rocking mode and the first vertical mode [19].
where Xi(ω) is the Fourier transformation of the ith floor, and Ftable(ω) is the Fourier transformation of the shaking table.
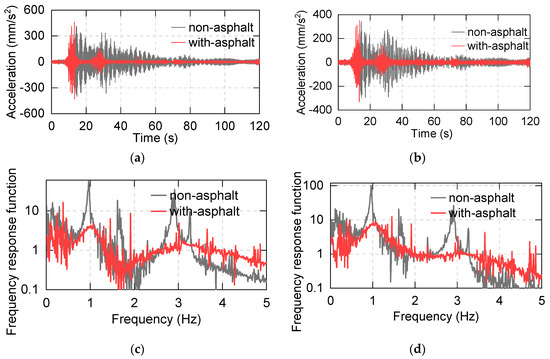
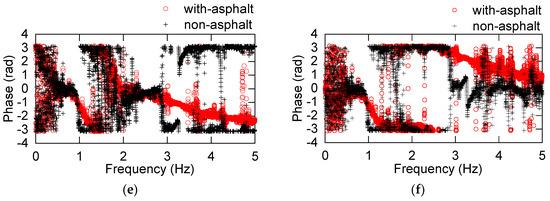
Figure 15.
Acceleration responses, Frequency Response Function and Phase spectra of non-asphalt and with-asphalt tests: (a) 1st floor acceleration responses of test condition Nos. 1, 13; (b) top floor acceleration responses of test condition Nos. 1, 13; (c) 1st floor FRF of test condition Nos. 1, 13; (d) top floor FRF of test condition Nos. 1, 13; (e) 1st floor phase of test condition Nos. 1, 13; (f) top floor phase of test condition Nos. 1, 13.
The phase is defined as follows:
denotes the imaginary part of the complex value, and denotes the real part of the complex value.
The displacements of measuring point 1 in the XZ plane are shown in Figure 16 and Figure 17. The results show that the vertical ground motions do not change the horizontal displacements significantly, whereas rocking ground motions can significantly increase the responses of the horizontal displacements. Furthermore, when the asphalt is added, the horizontal and vertical displacements are reduced by about 50%.
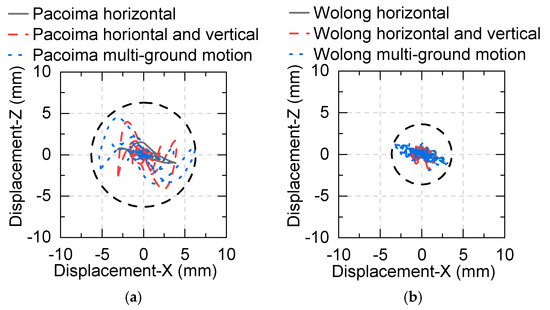
Figure 16.
Displacements of point 1 in XZ plane with different input directions: (a) No. 22, 23, 24 test conditions; (b) No. 19, 20, 21 test conditions.
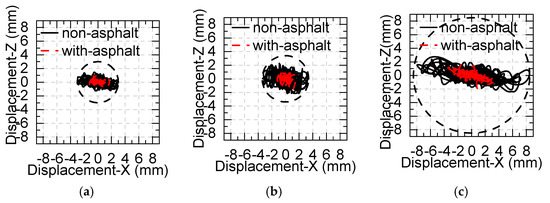
Figure 17.
Influence of asphalt on displacement: (a) test condition Nos. 7, 19; (b) test condition Nos. 8, 20; (c) test condition Nos. 9, 21.
3.2.2. Parameter Identification
Many methods can be used to identify the equivalent damping ratio of the test model based on the single degree of freedom [21,22,23,24]. To describe the damping ratio of the model more objectively, a parametric method based on multiple degrees of freedom [25] was used to calculate the constant damping ratio. In this method, the acceleration response is assumed to be composed of multiple vibration modes:
where ups is the sth mode contribution; a(t) is the ground motion accelerations; and qs(t) is the relative displacement of the sth mode, which satisfies the following equation:
Assuming that the starting and ending points of the time histories are both zero, the Fourier transformation is performed on both sides of Equation (14):
where hs is the damping ratio, ws is the natural frequency, and βsups is the effective participation factor at position p. In the following sections, the effective participation factor is simply called the participation factor.
The normalized error is defined as follows:
where Z(ω) is the Fourier transformation calculated by Equation (15), and Zobs(ω) is the Fourier transformation of the observed responses.
In the structural parameter identification procedure, the normalized error was used to determine the least-square fit of the modal responses to the observed responses in the frequency domain over a specific frequency band (ω1, ω2). For base-isolated structures, the structural vibration is mainly in the first mode. Therefore, in most cases, N equals 1, and the acceleration of the shaking table and the top of the structures can be used for Fourier transformation. The constant damping ratio and participation factor were calculated. The frequency band (0.6, 1.4) was used for horizontal parameter identification, and the frequency band (3, 3.5) was used for vertical parameter identification. The identified parameters are shown in Table 3 and Figure 18.

Table 3.
Horizontal parameter identification results.
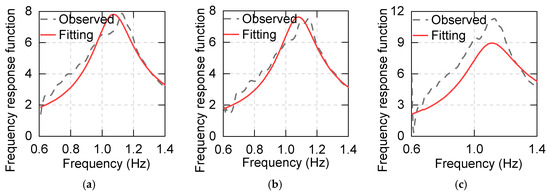
Figure 18.
Horizontal parameter identification results: (a) test condition No. 22; (b) test condition No. 23; (c) test condition No. 24.
The results show that the damping ratios of all with-asphalt tests are about 13%, while those of non-asphalt tests are less than 2%. This means that the springs cannot provide a sufficient damping ratio. At the same time, the errors and participation factors of multi-dimensional input conditions are significantly larger than those of horizontal, horizontal and vertical inputs. The reason for this is that when the rocking ground motions are input, the right side of the differential equation of motion has the effect of rocking ground motions. In this case, the differential equation of motion should be expressed as follows:
where is the rocking acceleration of the shaking table, and hi is the height of the ith floor.
Equation (17) was used to replace Equation (14), and the above modal analysis procedure was repeated to obtain the modal parameters under multi-dimensional ground motions.
The result of modal identification modified by Equation (17) is shown in Figure 19. The result shows that after modification, the frequency response function of the structure is basically the same as that under horizontal excitation.
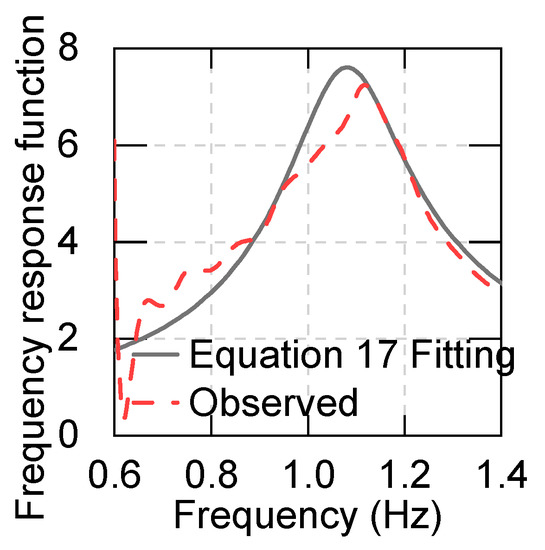
Figure 19.
Modified modal analysis using Equation (16).
Besides the damping ratio, the natural frequency is also an important characteristic of isolated structures. Table 3 shows that the natural frequency increases to about 1 Hz from 0.96 Hz after adding the asphalt. The relationships between the natural frequency and stiffness of the isolation structures can be expressed as . The increased natural frequency means that the stiffness of the isolation bearing increases after the addition of the asphalt. According to the definition of natural frequency, the stiffness of the isolated bearing is increased by 8.5%, which shows that the stiffness increase caused by asphalt paste cannot be ignored. If the stiffness increase caused by asphalt is too high, then the isolation effect will be affected.
4. Discussion
In this paper, the temperature dependence, displacement dependence and frequency dependence of asphalt damping properties are studied. A shaking table test was conducted to validate the effectiveness of asphalt damping. The results show the following:
- (1)
- According to the results of cyclic simple shear tests, the storage stiffness, the loss factor, equivalent stiffness and the equivalent damping ratio decrease with increasing displacement and temperature. Meanwhile, the above damping parameters increase with increasing frequency. These results demonstrate that when the ambient temperature is low, the displacement is small, the loading frequency is high, and the damping of the structure is larger.
- (2)
- Damping tests are qualitative tests, so the results are not the real parameters in practice because the test used scaled and simplified test specimens. However, the results can reveal the variation law of the damping characteristics of isolation bearings with this kind of asphalt.
- (3)
- The results of the modal analysis of the shaking table indicate that the damping effect is pronounced. Compared with non-asphalt tests, the duration and peak value of the acceleration responses in the with-asphalt tests are reduced by varying degrees, and the displacement is reduced to about 50% of that in the non-asphalt test.
- (4)
- A vertical earthquake will not change the frequency response function of the structure, but a rocking earthquake will markedly change it. Therefore, a modal analysis method for multi-dimensional seismic input is proposed. It is concluded that the analytical value agrees well with the experimental results.
- (5)
- The damping characteristics of the structure change with time, and a modal analysis method that is suitable for an invariant structure may cause errors. Therefore, the time-varying characteristics of the structure should be further studied in the future.
5. Patents
The three-dimensional isolation bearings described in this article have obtained the following Chinese invention patent:
Shang Shouping; Cui Xianglong. A Three-dimensional isolation pier. Patent No.: CN204059649U. (In Chinese.)
Author Contributions
Conceptualization, S.S. and Z.W.; methodology, Z.W.; software, Z.W.; validation, S.S.; formal analysis, Z.W.; investigation, Z.W.; resources, Z.W.; data curation, Z.W.; writing—original draft preparation, Z.W.; writing—review and editing, S.S. and Z.W.; supervision, S.S.; project administration, S.S.; funding acquisition, S.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministry of Science and Technology of the People’s Republic of China (Grant Nos. 2015BAL03B01).
Acknowledgments
The authors would like to express their sincere gratitude to the editor and the anonymous reviewers who significantly enhanced the contents of the study with their insightful comments. The authors also would like to thank Shimizu, Kunimatsu and Amano for their help and care in Nagoya University.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fujita, T.A. Three-Dimensional Isolation Floor for Earthquake and Ambient Micro-Vibration Using Multi-Stage Rubber Bearing. Trans. Jpn. Soc. Mech. Eng. 1995, 61, 1615–1622. [Google Scholar]
- Fujita, S.; Kato, E.; Kashiwazaki, A.; Kashiwazaki, A.; Shimoda, I.; Sakaki, K. Shake table tests on three-dimensional vibration isolation system comprising rubber bearing and coil springs. In Proceedings of the Eleventh World Conference on Earthquake Engineering, Acapulco, Mexico, 23–28 June 1996. [Google Scholar]
- Tsutsumi, H.; Yamada, H.; Mori, K.; Ebisawa, K.; Shibata, K. Characteristics and Dynamic Response of 3-D Component Base Isolation System Using Ball Bearings and Air Springs; Japan Atomic Energy Research Institute: Ibaraki, Japan, 2001.
- Mori, S.; Suhara, I.; Saruta, M.; Okada, K.; Tomizawa, T.; Tsuyuki, Y.; Fujita, T. Simulation analysis of free vibration test in a building “Chisuikan” using three-dimensional seismic base isolation system. In Proceedings of the 15th World Conference on Earthquake Engineering, Lisbon, Portugal, 24–28 September 2012. [Google Scholar]
- Lee, D.; Constantinou, M.C. Combined horizontal–vertical seismic isolation system for high-voltage–power transformers: Development, testing and validation. Bull. Earthq. Eng. 2018, 16, 4273–4296. [Google Scholar] [CrossRef]
- Makris, N.; Constantinou, M.C. Spring-viscous damper systems for combined seismic and vibration isolation. Earthq. Eng. Struct. Dyn. 1992, 21, 649–664. [Google Scholar] [CrossRef]
- Yao, F.; Shang, S.; Liu, K. Shake table tests of a new steel–asphalt composite layer system for the seismic base isolation of housing units. Soil Dyn. Earthq. Eng. 2014, 59, 1–7. [Google Scholar] [CrossRef]
- Wang, J.C.; Zeng, X. Influence of temperature and pressure on the dynamic properties of rubber-modified asphalt concrete. J. Mater. Civ. Eng. 2006, 18, 125–131. [Google Scholar] [CrossRef]
- Tavassoti-Kheiry, P.; Solaimanian, M.; Qiu, T. Characterization of high RAP/RAS asphalt mixtures using resonant column tests. J. Mater. Civ. Eng. 2016, 28, 04016143. [Google Scholar] [CrossRef]
- Islam, M.R.; Faisal, H.M.; Tarefder, R.A. Determining temperature and time dependent Poisson’s ratio of asphalt concrete using indirect tension test. Fuel 2015, 146, 119–124. [Google Scholar] [CrossRef]
- Jiang, Z.; Hu, C.; Easa, S.; Zheng, X.; Abd El Halim, A.O. Identifying optimal polymer type of modified asphalt based on damping characteristics. Constr. Build. Mater. 2018, 173, 308–316. [Google Scholar] [CrossRef]
- Makris, N.; Constantinou, M.C.; Reinhorn, A.M. Viscous Dampers: Testing, Modeling and Application in Vibration and Seismic Isolation; National Center for Earthquake Engineering Research: Buffalo, NY, USA, 1990. [Google Scholar]
- Makris, B.N.; Constantinou, M.C. Fractional-derivative Maxwell model for viscous dampers. J. Struct. Eng. 1992, 117, 2708–2724. [Google Scholar] [CrossRef]
- Clough, W.; Penzien, J. Dynamics of Structures, 3rd ed.; Computers & Structures, Inc. University Ave.: Berkeley, CA, USA, 1995; pp. 52–58. [Google Scholar]
- Xu, Z.D.; Gai, P.P.; Zhao, H.Y.; Huang, X.H.; Lu, L.Y. Experimental and theoretical study on a building structure controlled by multi-dimensional earthquake isolation and mitigation devices. Nonlinear Dynam 2017, 89, 723–740. [Google Scholar] [CrossRef]
- Xu, Z.D.; Liao, Y.X.; Ge, T.; Xu, C. Experimental and theoretical study of viscoelastic dampers with different matrix rubbers. J. Eng. Mech. 2016, 142, 04016051. [Google Scholar] [CrossRef]
- Fitzgibbon, A.; Pilu, M.; Fisher, R.B. Direct least square fitting of ellipses. IEEE Trans. Pattern Anal. 1999, 21, 476–480. [Google Scholar] [CrossRef]
- Ahn, S.J.; Rauh, W.; Warnecke, H.J. Least-squares orthogonal distances fitting of circle, sphere, ellipse, hyperbola, and parabola. Pattern Recognit. 2001, 34, 2283–2303. [Google Scholar] [CrossRef]
- Shang, S.; Wang, Z.; Xiao, Y.; Cui, X. Experimental and numerical study of the spring-asphalt 3D isolation structures under multi-component ground motions. Bull. Earthq. Eng. 2020, 18, 2461–2496. [Google Scholar] [CrossRef]
- Ewins, D.J. Modal Testing: Theory, Practice and Application; Research Studies Press: Taunton, UK, 1984; pp. 20–30. [Google Scholar]
- Xiao, S.J.; Xu, L.H.; Li, Z.X. Design and experimental verification of disc spring devices in self-centering reinforced concrete shear walls. Struct. Control Health Monit. 2020, 27, e2549. [Google Scholar] [CrossRef]
- Olmos, B.A.; Roesset, J.M. Evaluation of the half-power bandwidth method to estimate damping in systems without real modes. Earthq. Eng. Struct. Dyn. 2010, 39, 1671–1686. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Q. Identification of modal parameters of a 600-m-high skyscraper from field vibration tests. Earthq. Eng. Struct. Dyn. 2019, 48, 1678–1698. [Google Scholar] [CrossRef]
- Curadelli, R.O.; Riera, J.D.; Ambrosini, D.; Amani, M.G. Damage detection by means of structural damping identification. Eng. Struct. 2008, 30, 3497–3504. [Google Scholar] [CrossRef]
- Tobita, J. Evaluation of nonstationary damping characteristics of structures under earthquake excitations. J. Wind. Eng. Ind. Aerodyn. 1996, 59, 283–298. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).