4.1. Steady-State Model Tuning
The model was tuned with the experimental data of the 57-h steady-state test at a load of 845 kW
th (82% load). Various model parameters were adjusted and chosen to meet the pressure profile, the temperature profile, and the gas composition of the experiment. Other parameters were tuned to find the best values for high numerical stability and good agreement with the experimental data. The most relevant parameters are listed in
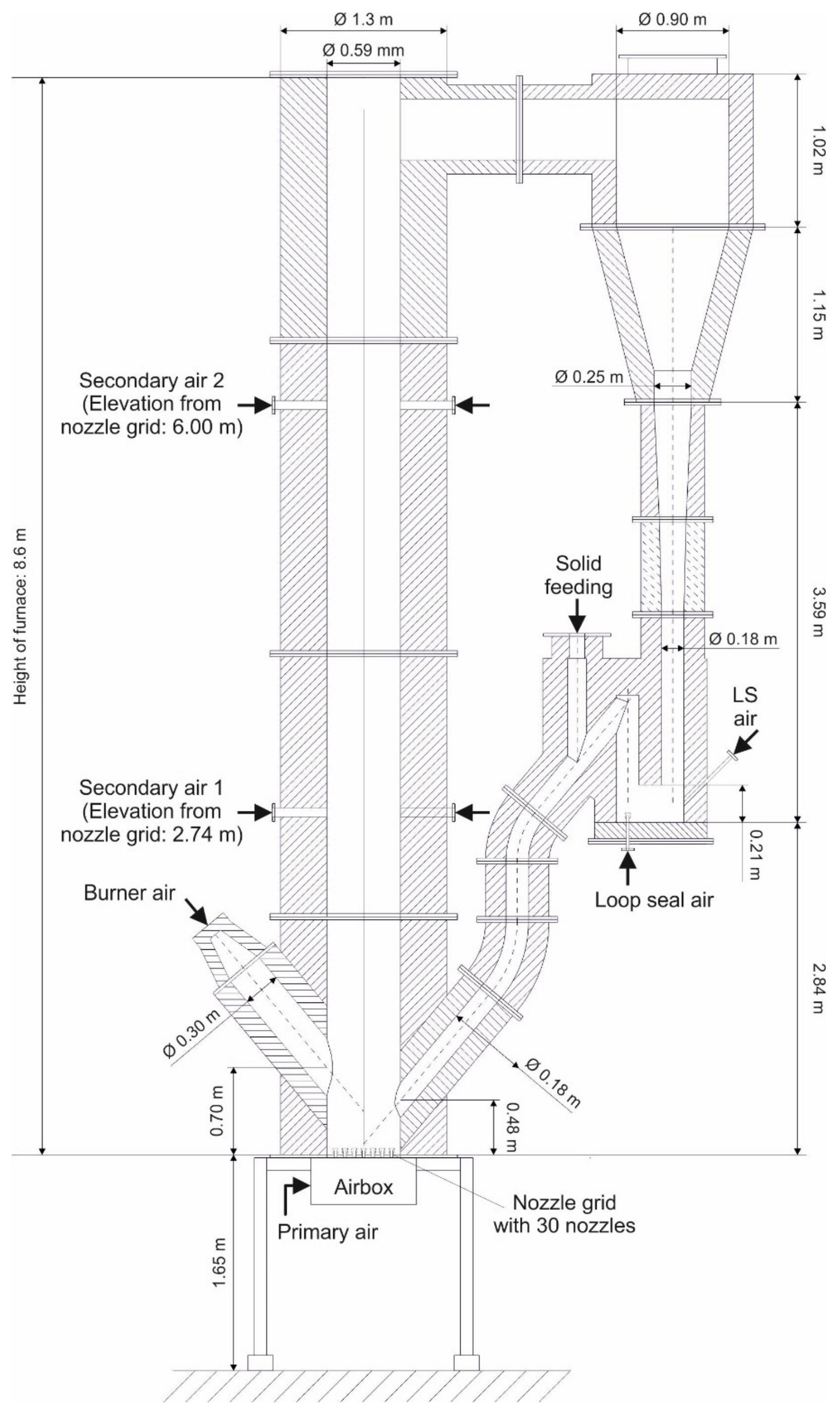
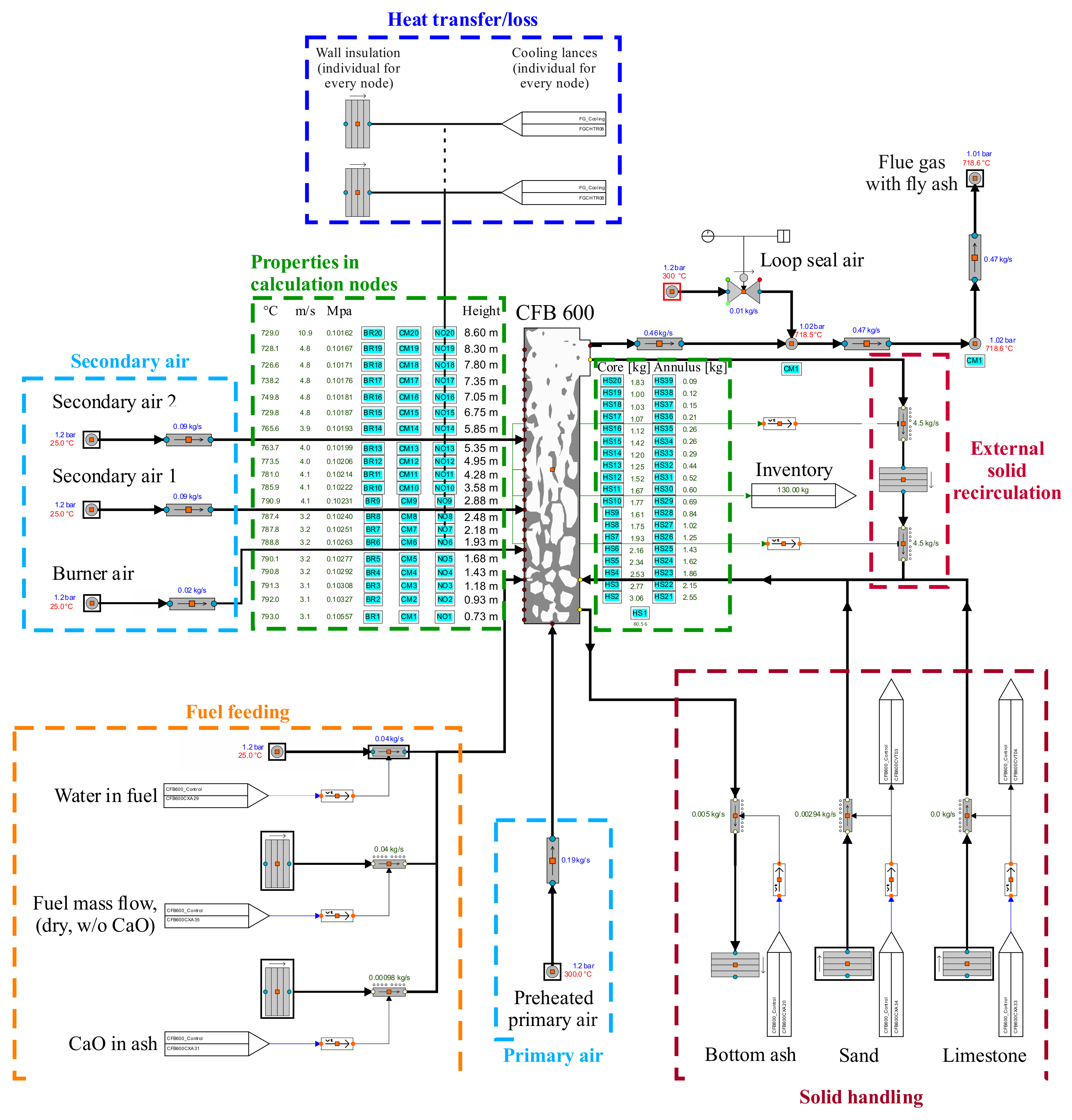
Table 10 with a short description. The riser is separated into 20 nodes. If the 20 nodes were equally distributed over the riser height, each node would have a height of 0.43 m. However, the bottom node of the riser has a height of 0.7 m. The bottom node represents the high-density bed zone. Here, no core-annulus approach is implemented due to the high inventory and the enhanced mixing of particles. For numerical stability, the bottom node must be higher than the bed height, which is calculated by APROS by dividing the mass of solid particles in the bed node by the average density of gas and solid particles in this node and the flow area of the node.
The heat transfer from the riser to the waterside depends on the temperature difference, the surface area, and the heat transfer coefficient. The heat transfer coefficient is calculated using the Mattman-Molerus-Wirth correlation. It takes into account the Archimedes number and the local pressure drop/particle fraction [
39]. This correlation is recommended for the prediction of heat transfer in circulating fluidized beds [
24].
The mass flow of particles from the core to the annulus and vice versa depends on the radial velocities and the mass of solids in the calculation nodes. Without further tuning, the radial velocities of the solids would be set equal to the axial velocities of the solids in the core/annulus. However, in reality, radial and axial velocities are not equal. To adjust the radial velocities and thereby the mass flow rates of the solids, so-called global split coefficients from the core to the annulus and from the annulus to the core are introduced. These coefficients have values between 0 and 1. With a value of e.g., 1, the radial velocity is equal to the axial velocity. With a value of e.g., 0.1, the radial velocity is ten times smaller than the axial velocity. Thereby, the global split coefficients have a great impact on the upflow/downflow of particles in the core/annulus and largely influence the pressure profile. The global split coefficients were adjusted to adapt the pressure profile according to the measurement data.
Another large influence on the pressure profile is given by the so-called interface density. The amount of particles that are entrained from the high-density bottom node to the first core node directly depends on the axial solid’s velocity and the interface density. The interface density is a theoretical value and can be set freely by the user. It represents the suspension density in the zone between the bed and the freeboard. Therefore, it physically represents the density in the splash zone of the fluidized bed. The density can be estimated from the experimental data by using the pressure drop in this area. From the experimental data, it is reasonable to define the location of the splash zone between the two pressure sensors at 0.58 m and 2.07 m, where the density of the bed changes from high-density zone to lean zone. In the steady-state case, the calculated splash zone density is 58.2 kg/m3. However, in the model, a value of 30 kg/m3 was chosen, as the entrainment was highly overestimated, when using a value of 58.2 kg/m3.
An average diameter has to be set to account for the particle size of the fluidized bed particles and no particle size distribution is implemented in the model. The average particle size is 0.211 mm, which is the average particle size of the bottom ash sample taken after the test period. To calculate the heat loss through the insulation to the environment, a boundary condition has to be set for the ambient temperature outside of the refractory lining. This temperature is set to 25 °C and is not adjusted during the simulations.
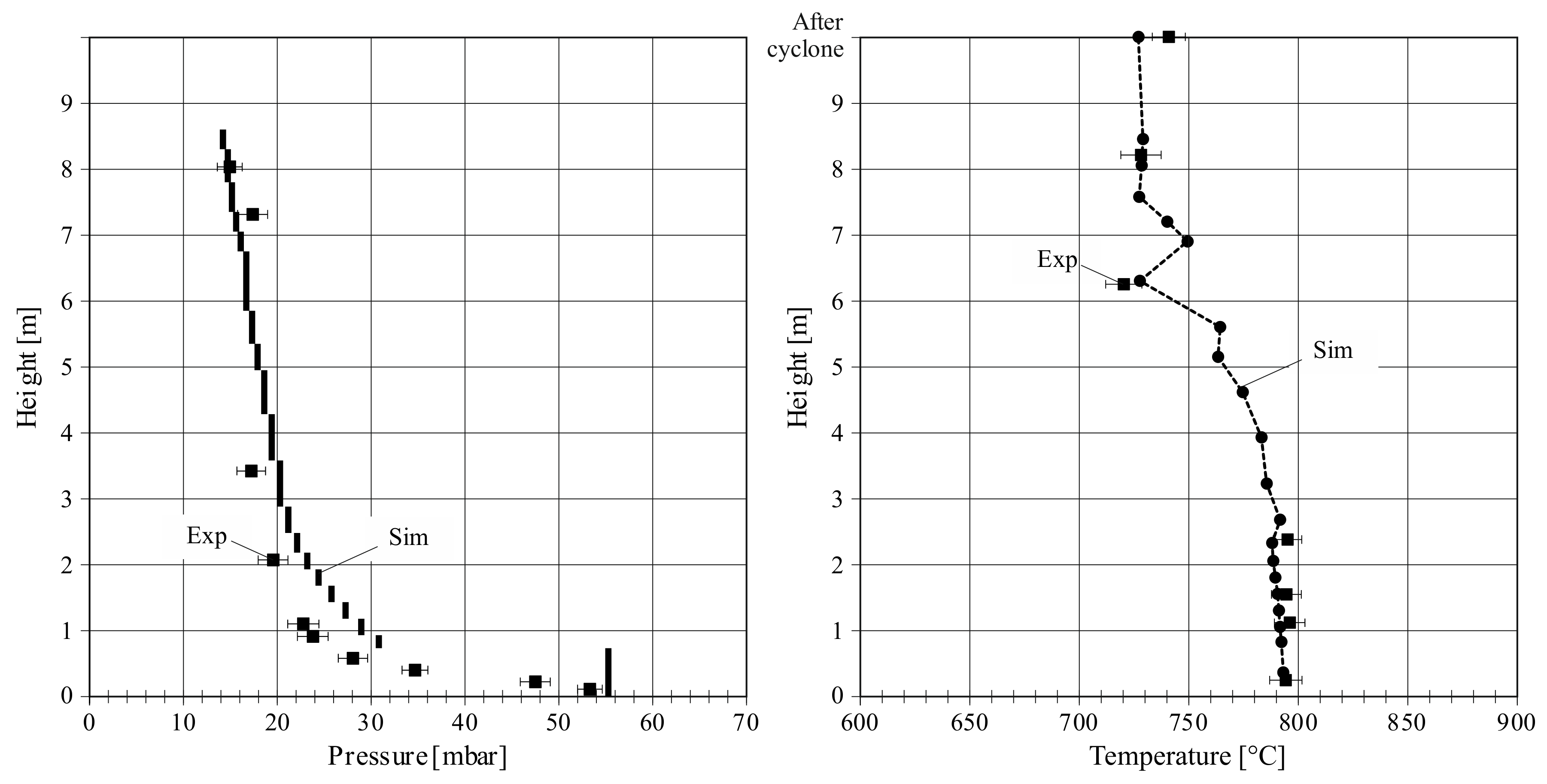
Figure 5 shows the pressure profile along with the furnace height during the long-term steady-state test with 845 kW
th load. The average velocity according to the description in
Section 2.2 is calculated to 4.2 m/s. In the model, the pressure drop in the freeboard is overestimated indicating that the entrainment is higher in the simulation compared to the experiment. The hydrodynamic conditions influence the chemical reactions, the heat transfer, and the temperature development in the furnace. Further improvements of the model are therefore useful to achieve better agreement in future studies—e.g., the interface density parameter can be set to smaller values. In this work, the interface density is already set 2 times smaller than the density in the splash zone. Therefore, it was chosen not to make the parameter even smaller, to have an appropriate compromise between the accuracy of the model and the physical foundation of the interface density. The agreement between experimental data and simulation is good both in terms of the total pressure drop and the reproduction of the typical CFB pressure profile. The figure also shows the standard errors for the experimental data calculated from the standard deviations in the measurement signals and the uncertainty of the measurement devices.
The temperature profile is shown on the right in
Figure 5. The temperatures in the simulation agree very well with the experiment. In the bed zone, the temperatures are almost constant due to the high level of mixing in the bottom region. At 2.7 m, secondary air is injected. However, the measurement shows decreasing temperatures from 2.4 to 6.3 m potentially for two reasons. Firstly, the cooling lances and the non-preheated secondary air might compensate for the combustion reactions. Secondly, no measurement is installed between these two locations. Therefore, the temperature might rise above the secondary air injection and it is just not shown by the available experimental data. However, the simulation does not show a temperature increase above 2.7 m either. In the experiment, the temperature increases above the secondary air injection at 6.0 m to the last measurement at 8.2 m. In the model, a temperature peak at 7.0 m is observed, before the temperature decreases again due to the impact of the cooling lances. At 8.2 m, experiment and simulation correspond. In addition to the riser temperatures, the temperature measurement after the cyclone is shown in
Figure 5. In the experiment, the temperature increases between riser and cyclone outlet. It is reasonable, that the mixing of secondary air, volatiles, and char is considerably smaller in the experiment, as the penetration depth of the secondary air is not optimized in the pilot. Thereby, the combustion reactions are shifted to the top of the reactor and the cyclone. In the cyclone, the high velocity and the turbulent flow ensure a strong mixing leading to the post-combustion of char. In the model, the mixing is very efficient, due to its 1-dimensional nature. Therefore, the combustion reactions are taking place only in the riser and the post-combustion is not reproduced sufficiently.
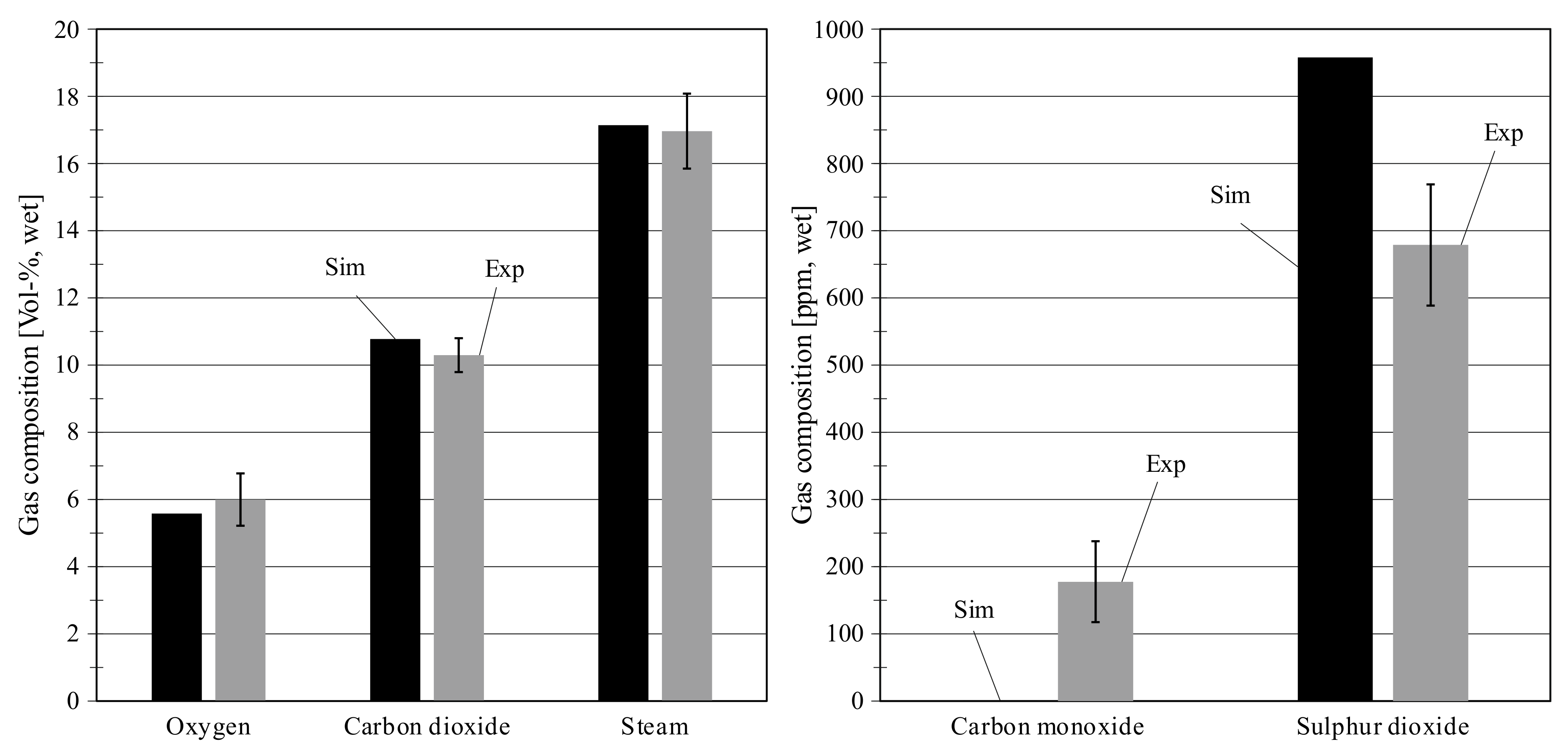
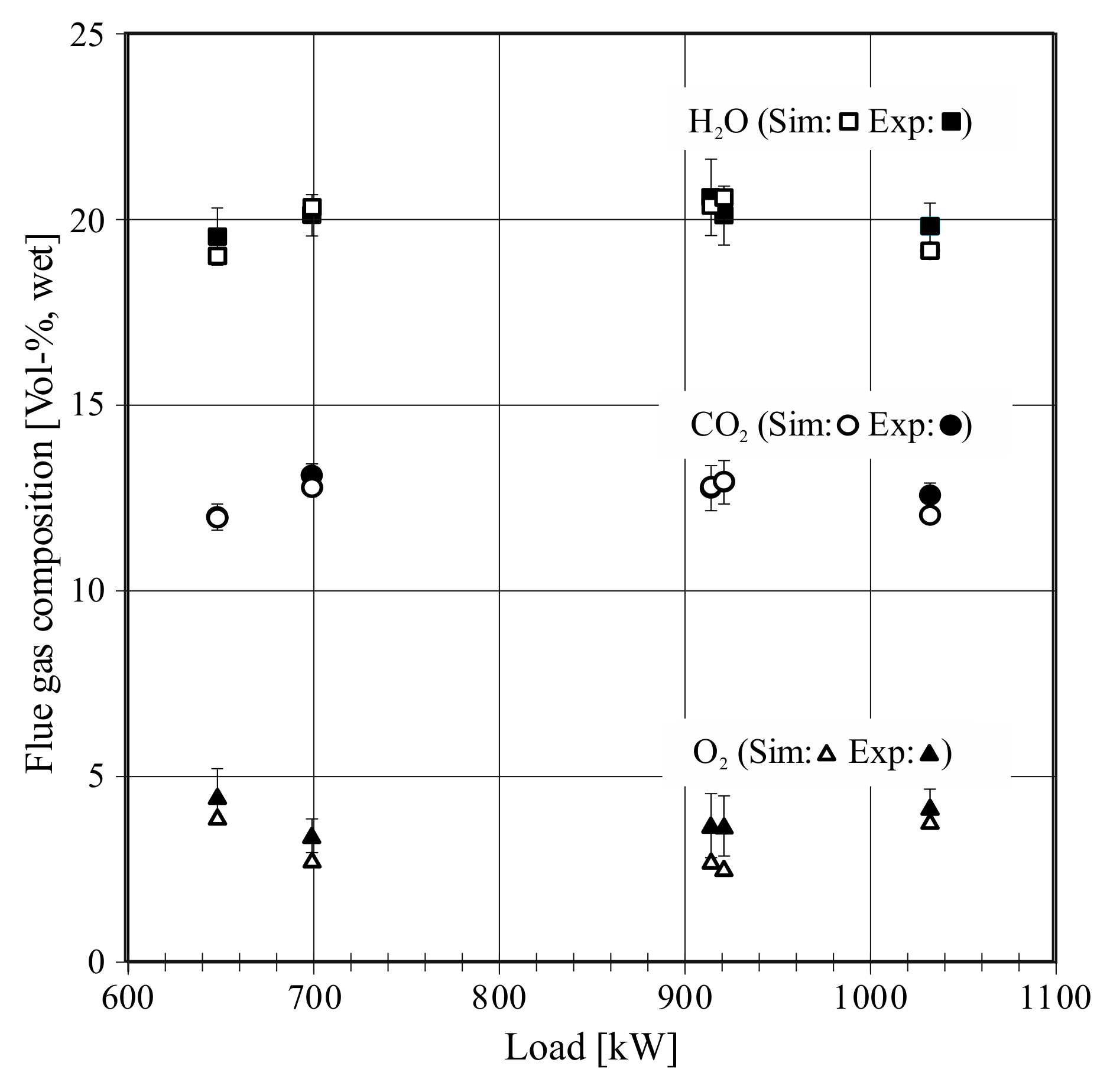
The flue gas composition is presented in
Figure 6. On the left-hand side, the main gas components O
2, CO
2, and H
2O are shown. The standard errors are presented, taking into account the measurement device uncertainty and the standard deviation of the fluctuating measurement signal. The simulation agrees very well with the experiment. Simulation results are always within the standard error of the experiment and the relative deviations are very small. Considering that the composition of the fuel is subject to fluctuations during the experiment, the agreement is considered very high.
On the right-hand side of
Figure 6, the content of the trace gases CO and SO
2 is presented. There is no CO in the flue gas in the simulation. This supports the findings from the temperature profile of the simulation, where all combustion reactions are completed in the riser. In the experiment, the CO content is around 200 ppm
wet, so the combustion reactions are not completed even after the post-combustion in the cyclone. The SO
2 content depends on the varying sulfur content in the fuel and on the efficiency of the sulfur capture with calcium oxide from the fuel ash. The sulfur capture in a CFB combustor is a complex process, which depends on many parameters, such as the flue gas composition (locally reducing conditions, water vapour content), the temperature, the residence times and the properties of the CaO-particles (porosity, size, shape) [
40,
41,
42,
43]. Taking into account all these uncertainties and the fact, that especially the particle properties cannot be defined to this extent in the APROS model, the relative deviation of 41% between model and experiment is in a comprehensible range. It should be mentioned at this point that no tuning was carried out concerning the desulphurization reactions in the model, besides the definition of the S-content in the fuel and the CaO content in the fuel ash.
4.2. Model Validation
After tuning with the steady-state test, no further tuning or modification of the model took place during the validation process. The model is validated with the measurement data of five test points, with a thermal load from 63% to 100%. The model validation focusses on the hydrodynamic conditions, the flue gas composition, and the dynamic behavior of the fluidized bed.
4.2.1. Hydrodynamic Condition in the Furnace
The hydrodynamic conditions in a CFB furnace depend on the load, the bed material properties, the fuel, the combustion air, the heat exchangers inside the furnace, and other parameters, such as the insulation of the furnace. All these parameters are considered in the presented APROS model. The temperature and pressure profiles are a suitable way to validate a process model in terms of the hydrodynamics.
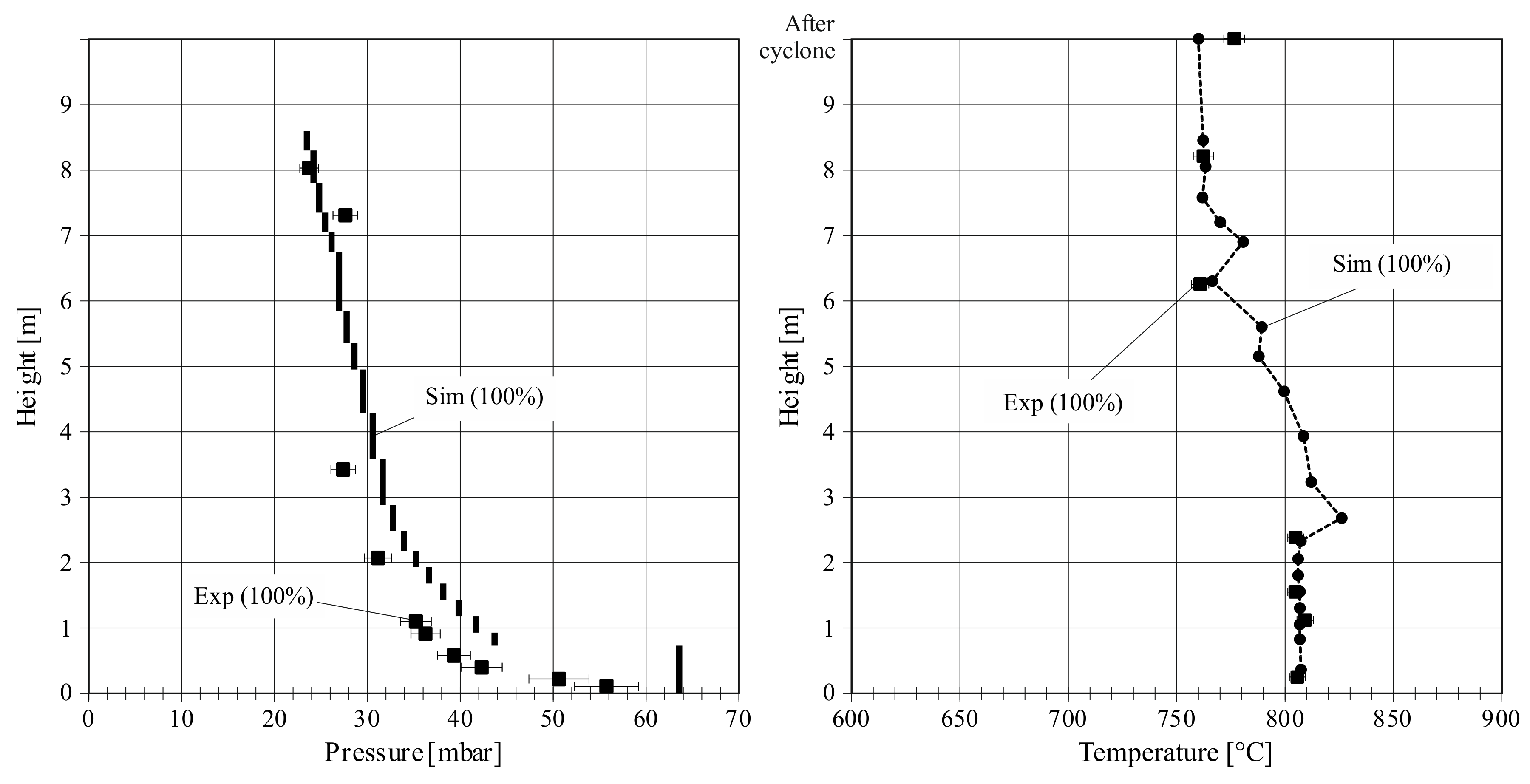
Figure 7 shows the pressure and temperature profile of the 100% load case (1032 kW) with a calculated average velocity of 4.60 m/s. The agreement between experiment and simulation is very good for the temperature profile. The bed temperature, as well as the temperature development along the reactor and the temperature at the riser top in the simulation, are within the standard errors of the experimental data. As in the steady-state case, the post-combustion in the cyclone does not happen in the model. Therefore, there is a temperature deviation of about 20 K between simulation and experiment for the temperature after the cyclone. The pressure profile shows greater deviations than the temperature profile. The overestimation of the pressure drop in the lean zone is similar to the steady-state test. However, the total pressure drop and the slope of the pressure profile in the upper reactor is still in good agreement.
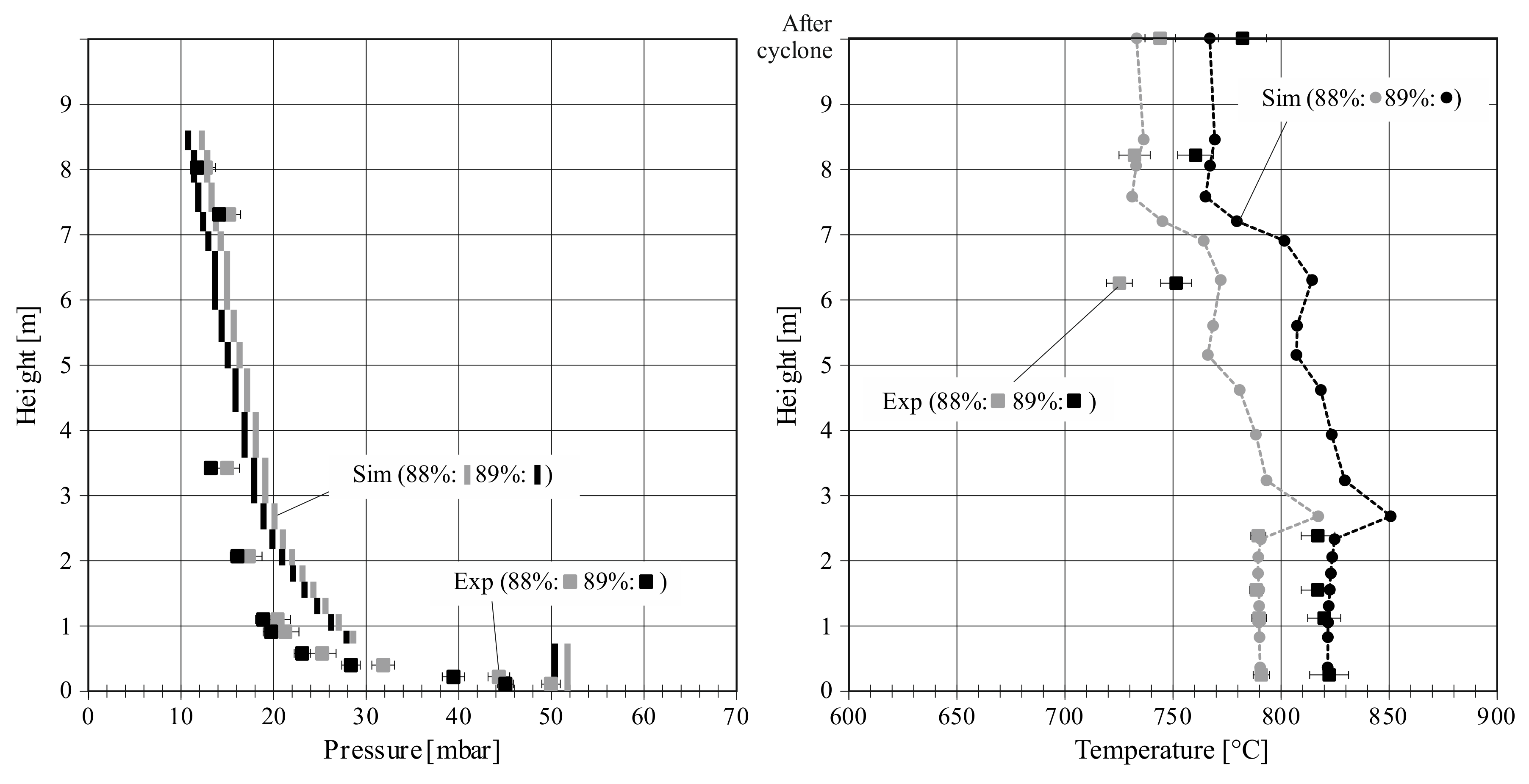
Figure 8 presents the hydrodynamics at medium load (88%, 89%). The average calculated velocities are 3.70 m/s (88%) and 3.77 m/s (89%). The pressure profile is similar for ascending and descending load. The load is slightly higher than in the steady-state tuning test point. However, the velocities are smaller, as the excess air factor is lower in these cases. The pressure drop in the freeboard is overestimated by the model, which could potentially be improved by adjusting the interface density in the model. However, the numerical simulation is capable of predicting the reduced entrainment at decreasing velocities/load cases on the same scale as in the experiment. The agreement between experiment and simulation is good regarding the total pressure drop and the bed density.
It is noticeable that the average temperature differs significantly at descending and ascending load changes, despite similar loads. The refractory and the inert bed material play a major role here. A large amount of energy is stored and is then slowly released when the load decreases. Therefore, the temperature level is higher in the case of descending load (89% load case), as long as steady-state conditions are not achieved. This mechanism is well shown also by the simulation, where this temperature difference is also present. It is necessary to mention here, that the walls of commercial CFB boilers are made of water walls. Therefore, the effect observed here will hardly affect industrial scale boilers.
Despite the different average temperatures, the temperature development along the riser is similar for both medium load tests. Partly, bed temperatures are higher at medium loads compared to high loads. Additionally, the temperature drop along the reactor increases at lower loads (see
Figure 7), due to several reasons. Less particles (e.g., char) are entrained from the bed at lower loads/velocities. Thereby the combustion reactions are shifted to the bed zone, which increases the bed temperatures and decreases the temperatures in the upper reactor. When the circulation of particles decreases, fewer particles are cooled by contact with the cooling lances and the surrounding flue gas. This lack of particle-cooling can result in an increased temperature of the solids and thereby an increasing bed temperature. These mechanisms, in combination with the heat stored in the insulation, can lead to an increase in the bed temperature, although the load is reduced. The simulated temperatures match the experiment very well in the high-density bed region and at the reactor top. At 6.3 m height, there is a larger deviation between model and experiment. Potentially, the heat transfer to the cooling lances is not correctly reproduced at this low load. As already discussed, also the combustion reactions with the secondary air, which is injected at a height of 6.0 m, are completed much faster in the model due to the idealized mixing. This leads to a higher temperature in this area.
The hydrodynamic profiles of the tests with 63% and 68% load are illustrated in
Figure 9. The calculated velocities are 2.78 m/s (63%) and 2.88 m/s (68%). In the experiment, there is only a minor pressure drop along the lean zone of the riser, while the simulation results still show significant entrainment. As discussed before, the model parameter interface density, which largely influences the entrainment, is kept constant for validation purposes. In the experiment, on the other hand, the density in the splash zone is slightly decreasing at lower loads (58.2 mbar at 82% load and 48.2 mbar at 63% load). It is therefore reasonable, that the deviation between the pressure profile of the simulation and the experiment may get worse at lower loads. The model gives a good indication of the total pressure loss of the experiment, even if the deviations are greater than at higher load.
Again, the temperature level is higher for the load reduction test (68% load) compared to the load elevation test (63%), which is partly due to the energy stored in the refractory and bed material. However, the load in the latter is also significantly lower, which is also responsible for the higher temperatures. There is an excellent agreement between experiment and simulation for the bed temperatures. The model also shows that the temperature along the reactor decreases much more than it did at higher loads, which matches the experimental data. At the top of the reactor and around 6 m, the deviation between experiment and simulation is higher than at high and medium load, whereby the agreement between experiment and model is much better for the temperature after the cyclone. In the experiment, there is a major level of post-combustion in the cyclone, which is not present in the model due to the reasons discussed before. As the combustion takes place entirely in the riser, the temperatures in the simulation are higher at 6.3 and 8.2 m.
4.2.2. Flue Gas Composition
The flue gas composition is measured at several positions in the pilot plant. The FTIR measurement after the flue gas cooler includes all main species including water vapor and many trace gases. This measurement data is compared to the simulation results for the validation of the model.
Figure 10 shows the flue gas composition of the part-load tests. In the simulation, the content of carbon dioxide and water vapor is within the standard error of the experiment for all tests. The oxygen content is always at or slightly below the lower limit of the standard error in the experiment. Regarding the fluctuating fuel composition, the model shows an excellent agreement with the experiment.
The CO content in dependency of the average riser temperature is shown in
Figure 11. Large fluctuations are present for the CO content in the experiment. The CO content tends to decrease with increasing temperature, as high temperatures accelerate the combustion reactions. However, more parameters influence the CO content, such as the oxygen content and the efficiency of the post-combustion in the cyclone for instance. In the simulation, no carbon monoxide remains in the flue gas and the combustion reactions are completed inside the riser for all tests. As discussed before, the mixing of oxygen and burnable components (CO, char) is modeled as ideal in the 1.5 D APROS model. In the experiment, the mixing depends on several parameters, such as the injection speed of the secondary air and the conditions in the riser.
4.2.3. Dynamic Evaluation
Besides the evaluation of the part-load tests with mean values for the temperature and pressure, also the dynamic behavior during load change is relevant to validate the process model. In this chapter, the dynamic response of the furnace is evaluated and the model prediction of this response is assessed.
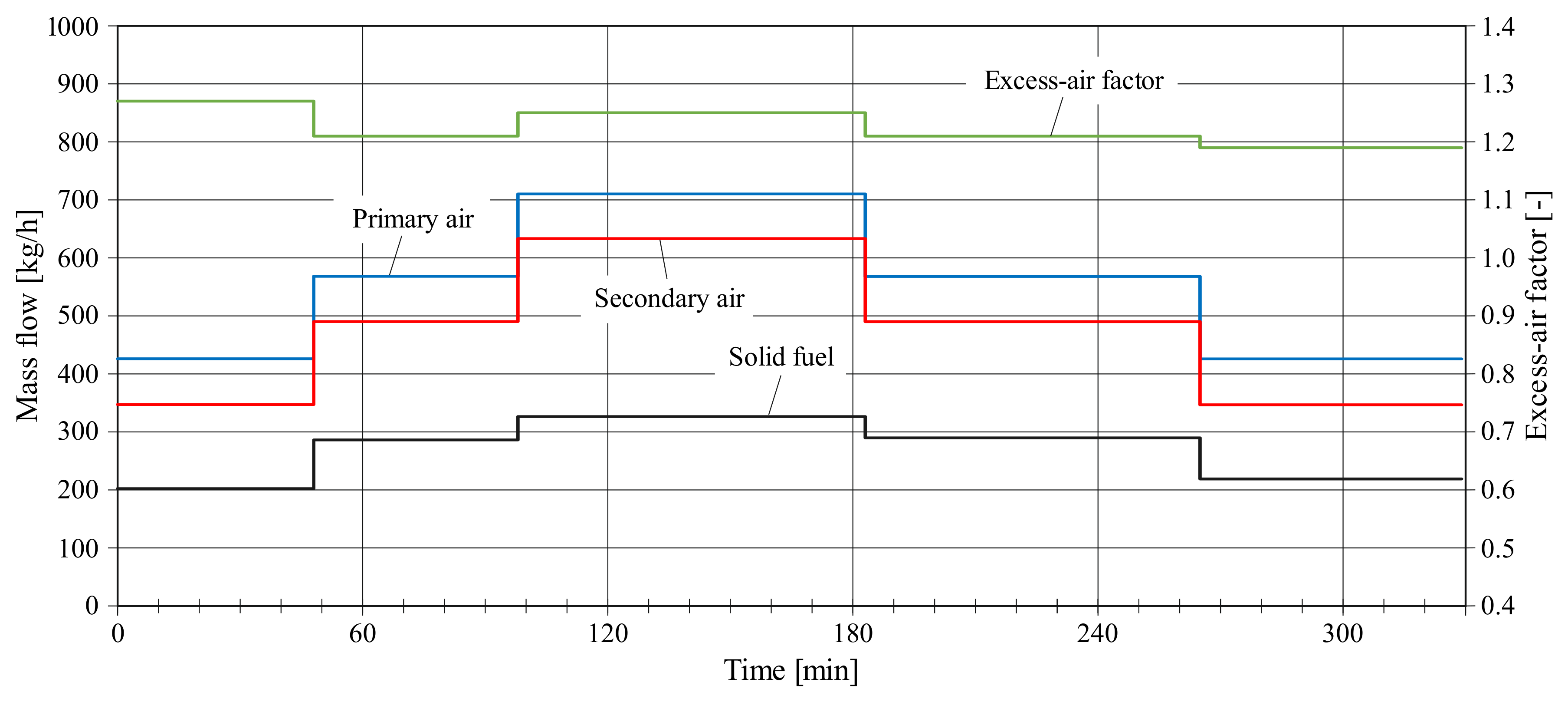
Figure 12 shows the development of the temperature in the bed and at 8.2 m, the pressure at several heights, and the flue gas composition. The fuel mass flow is varying, due to differences in the fuel properties such as particle size, shape, density, or moisture. In the simulation, these fluctuations are not modeled. This results in fluctuating values for the flue gas composition and the temperatures.
At the starting point at 63% load, the bed temperature of the numerical analysis and the experiment agree very well, while the temperature at the top of the reactor is significantly higher in the simulation. It is also apparent that the pressure above the bed (2.1 m) is overestimated, while the pressure in the bed and at the top, as well as the flue gas composition agree well with the experiment. The reasons for the deviations are discussed in detail in
Section 4.2.1. After 47 min, the load is increased to 88%. In the simulation, the temperatures oscillate shortly after the load changes, especially in the dense bed region. PI-controllers control the mass flows of combustion air in the model. These controllers cause a temporary excess/shortage of air and thus they are responsible for the temperature oscillation. Further optimization of the controller is necessary to match the air-flow of the experiment at all times. There is a very good agreement for the overall duration of the load change. In the experiment and the simulation, 75% of the absolute change in temperature is completed after 3–4 min. After 97 min, the load is increased to 100%. The load change duration is similar to the first load transient. Despite the oscillation after the load change in the numerical model, the furnace response is predicted well by the model and 75% of the new temperature level is reached after 2–3 min. As already discussed in
Section 4.2.1, the model is more accurate at higher loads with regard to the average pressure and temperature in the furnace.
The first load decreasing step (100–89%) is performed after 182 min. Due to the fuel mass flow fluctuations, shortly after the load change, there is a higher oxygen excess in the flue gas in the experiment compared to the simulation. When the fuel mass flow decreases slightly over time, the average oxygen excess decreases and is closer to the model prediction. This leads to a lower temperature level at the beginning of the 88% load test and an increasing temperature to the end of this test. For both, experiment and process model, the temperature difference between the 100% and 89% load test is low compared to the other tests. Therefore, and due to the fuel mass flow fluctuations, it is difficult to assess the duration of the temperature change in detail. After 264 min, the load changes from 89% to 68% load. The temperature response directly after the load change is reproduced well by the model. However, in the experiment, there is a long period (20–25 min), where the temperature converges to the final value, which is not observed in the simulation.
Compared to the partly slowly changing temperatures, the pressures are changing very fast (a few minutes) in all load transient tests—for the experiment and the numerical model. This is because the hydrodynamic condition mainly depends on the gas velocity and the solid particle properties. It depends only indirectly on the temperature—mainly by changing gas density and viscosity. On the other hand, the temperatures do of course depend strongly on the hydrodynamic conditions. However, the new temperature levels do not adjust as quickly as the pressure, due to the heat storage capacity of the bed material and the refractory. The large fluctuations of the pressure in the experiment in areas with high solid content (bed and splash zone) are typical for a CFB. The fluctuations decrease with the height of the reactor. The fluctuations are not given in the simulation, due to its one-dimensional nature.
Concluding this, the response of pressure and temperature on positive load changes can be predicted well by the model. It is not clear if this is also valid for negative load transients, but the first response after the load change seems to be predicted with good accuracy. In future studies, the fuel mass flow including the fluctuations should be modeled with higher details to further assess the dynamic properties of the model. However, with some improvements, the model seems to be suitable to predict the load transient response of a boiler very well. Therefore, core annulus models could be used to test novel concepts to increase the maximum load ramps of CFB combustors.