Cross-Layer Installed Cable-Bracing Inerter System for MDOF Structure Seismic Response Control
Abstract
:1. Introduction
2. Theoretical Analysis of CBIS
2.1. Basic Concept of the CBIS
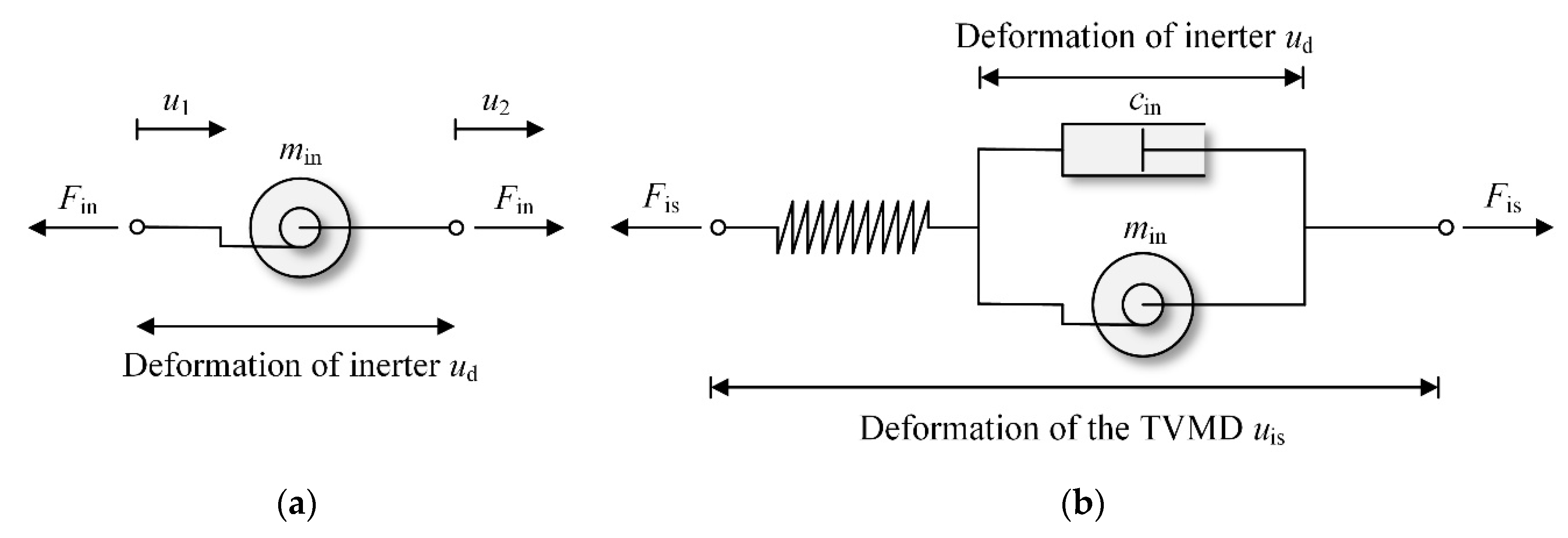
2.1.1. The Inerter System
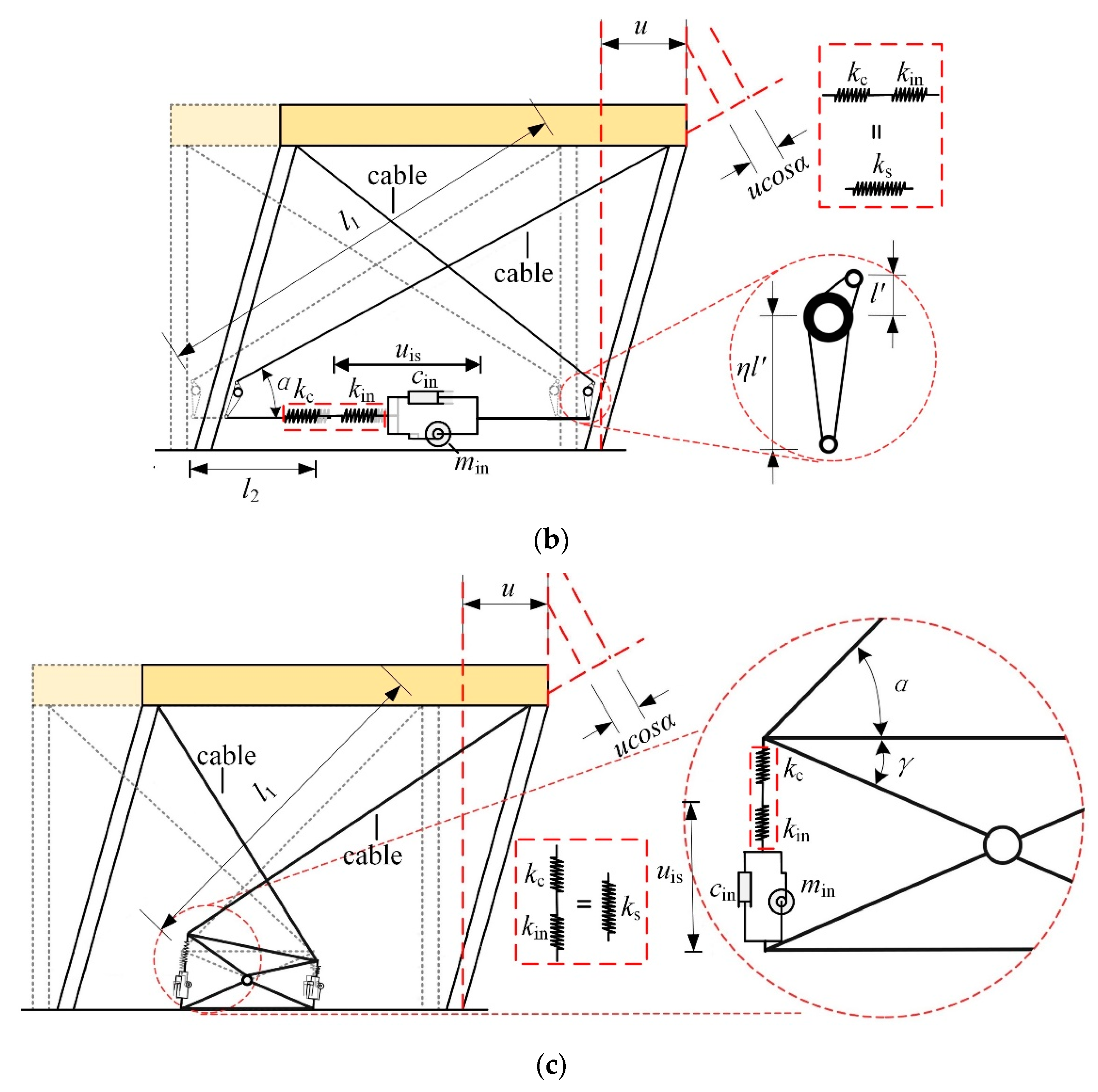
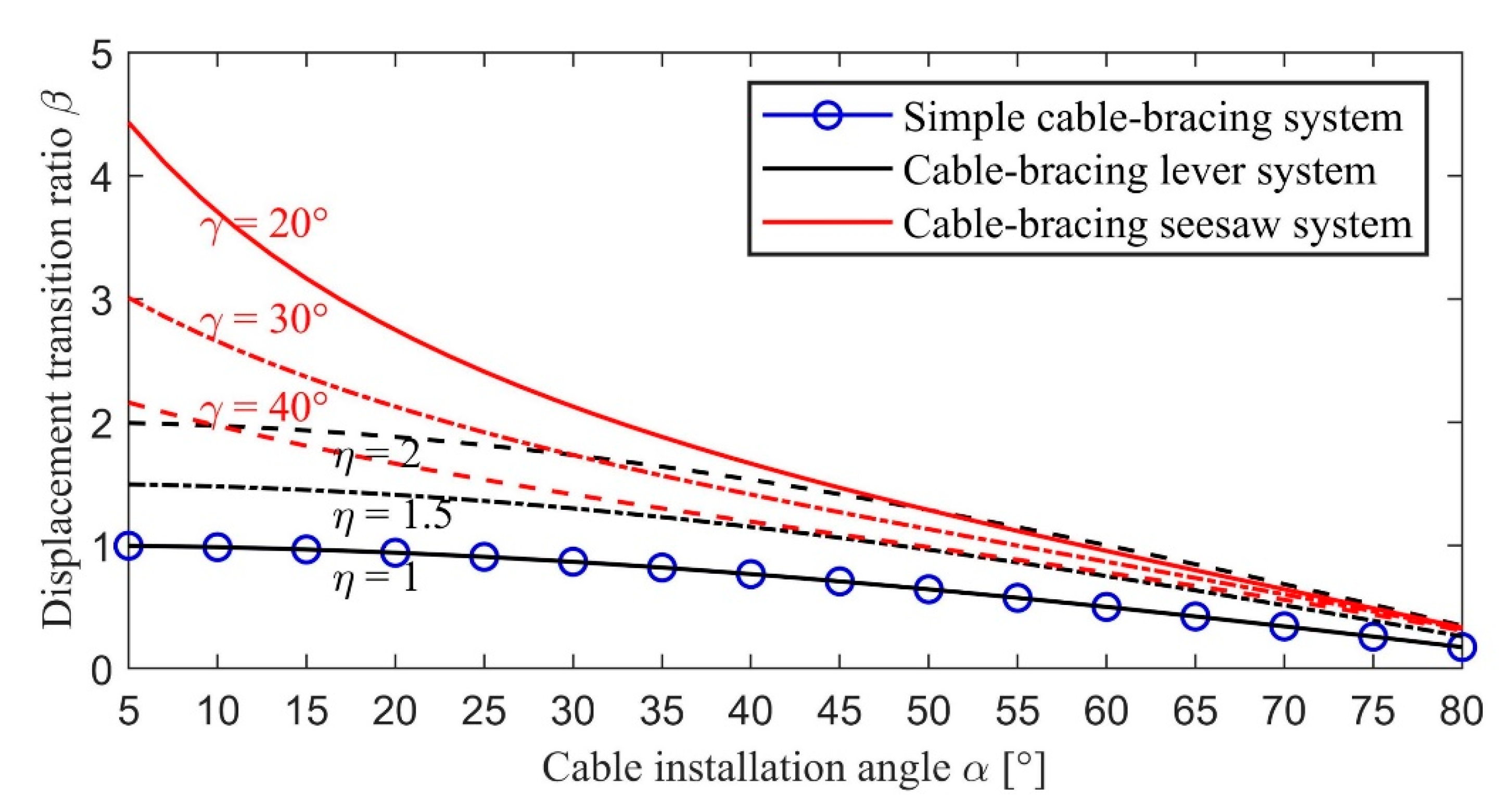
2.1.2. The Cable-Bracing System
2.2. Government Equations of the SDOF Structure of a CBIS
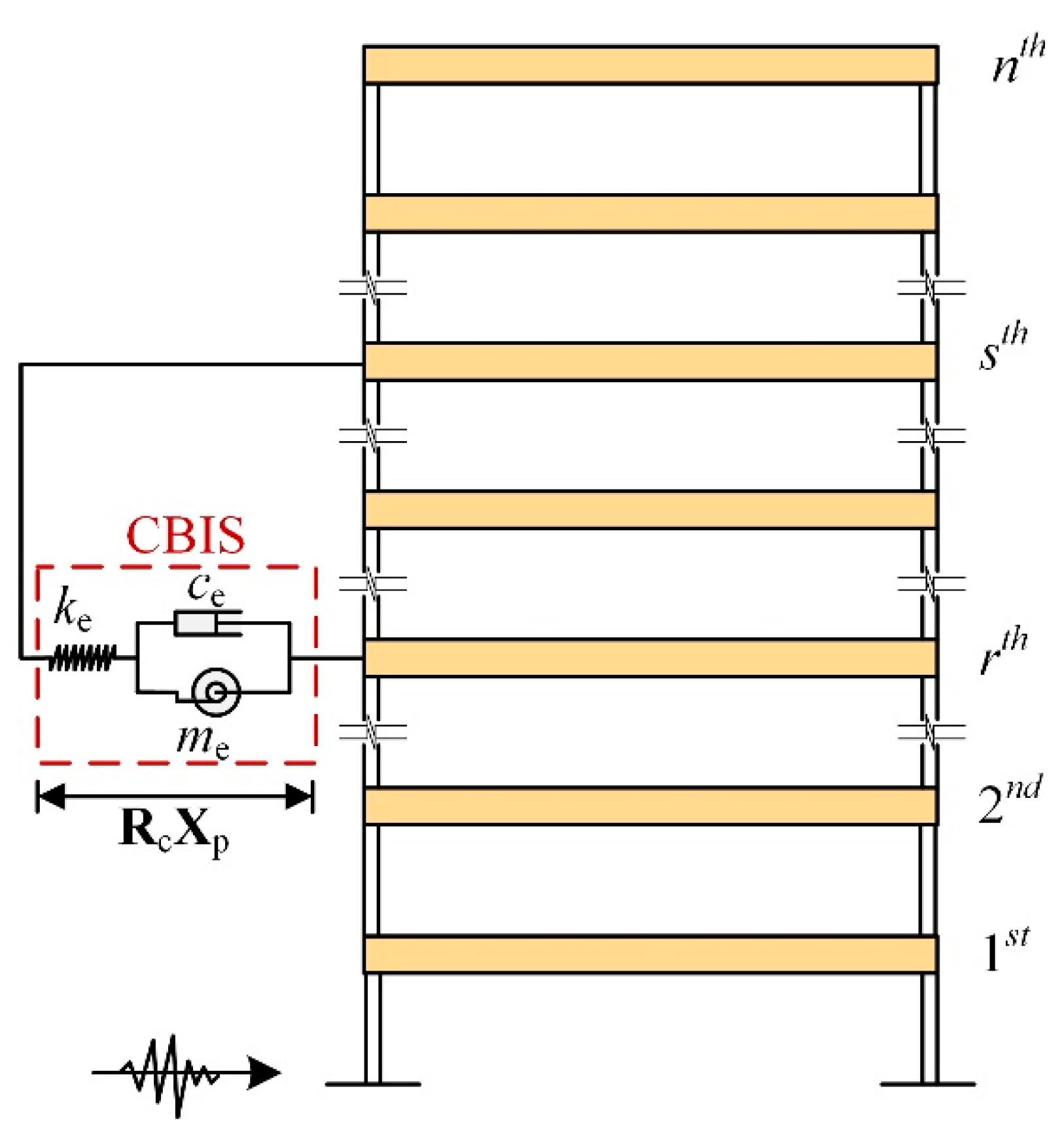
2.3. MDOF Structure with the CBISs
3. Optimum Seismic Control of an MDOF System with CBISs
3.1. Evaluation of the Seismic Response
3.2. Design Formulation and Procedure
4. An Illustrative Design Example
4.1. Analysis Model
4.2. Design of the CBISs
4.3. Effectiveness of the CICBISs
5. Conclusions
- The ability of the CICBIS to reduce the total apparent mass and damping coefficient requirements of the inerter systems without increasing the control force has been confirmed. Thus, the CICBIS with a high efficiency provides a feasible solution to attenuate the in-built or existing building’s seismic response.
- The demand-based CBIS design method proposed herein can exert the damping enhancement of the inerter system and the adjustability of the cable-bracing system. It allows the CBISs with the same inerter to realize an optimal vertical distribution, facilitating the manufacture and deployment of the inerter system.
- The effective inerter-mass ratio reflecting the influence of the installation location and layout of the CBIS on the inerter system’s utilization efficiency is used to explain the CICBIS’s high efficiency. It provides a reference for the further optimization of the installation location and layout of the inerter system.
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Symbol | Parameter Definition |
|---|---|
| TVMD | tuned viscous mass damper |
| SDOF | single-degree-of-freedom |
| MDOF | multiple-degree-of-freedom |
| TID | tuned inerter damper |
| CBIS | cable-bracing inerter system |
| CICBIS | cross-layer installed CBIS |
| IICBIS | inter-layer installed CBIS |
| RMS | root mean square |
| FRF | frequency response function |
| resisting force of the inerter | |
| , | displacement of the inerter two ends |
| , , | apparent mass, damping coefficient, and tuning spring stiffness of the TVMD |
| resisting force of the TVMD | |
| , | displacement differences at two ends of the TVMD and the inerter |
| cable stiffness | |
| , | elastic modulus and cross-section area of the cable |
| cable equivalent length | |
| , | one-side diagonal and horizontal cable length |
| cable installation angle | |
| lever arm ratio | |
| seesaw angle | |
| stiffness of the CBIS | |
| displacement transition ratio | |
| , , | mass, stiffness, and damping coefficient of the SDOF structure |
| control force applied to the structure | |
| ground motion displacement | |
| displacement of the structure relative to the ground | |
| equivalent inerter displacement | |
| , , | equivalent apparent mass, damping coefficient, and stiffness of the CBIS |
| relative displacement of the ith layer of the primary structure | |
| , , | mass, stiffness, and damping coefficient of the ith layer of the primary structure |
| number of MDOF structure layers | |
| , , | equivalent apparent mass, stiffness, and of damping coefficient the ith CBIS |
| equivalent inerter displacement of the ith CBIS | |
| total number of the CBIS | |
| generalized coordinates of the primary structure | |
| generalized coordinates of the inerter | |
| , , | kinetic energy, strain energy, and dissipated energy of the CBIS equipped n-DOF structure |
| generalized mass of the primary structure | |
| generalized apparent mass of the CBIS | |
| effective inerter-mass ratio | |
| , | frequency property and damping property of the supporting ground |
| intensity of the white noise excitation at the bedrock | |
| white noise input | |
| RMS structural responses | |
| RMS control forces | |
| , | designed apparent mass and damping coefficient of the inerter system |
| displacement transition ratio of the ith cable-bracing systems | |
| frequency of the CBIS | |
| designed stiffness of the CBISs | |
| drift reduction ratio | |
| ith RMS story drift of the controlled structure | |
| ith floor height of the structure | |
| maximum RMS story drift ratio of the uncontrolled structure | |
| cost index of installing CBISs | |
| RMS control force of the ith CBIS | |
| natural frequency of the uncontrolled structure | |
| first-order effective inerter-mass ratio | |
| first-order modal vector | |
| target drift reduction ratio |
References
- Mahmoodi, P. Structural dampers. J. Struct. Div. 1969, 95, 1661–1672. [Google Scholar]
- Housner, G.; Bergman, L.A.; Caughey, T.K.; Chassiakos, A.G.; Claus, R.O.; Masri, S.F.; Skelton, R.E.; Soong, T.; Spencer, B.; Yao, J.T. Structural control: Past, present, and future. J. Eng. Mech. 1997, 123, 897–971. [Google Scholar] [CrossRef]
- Yao, J. Concept of structural control. J. Struct. Div. 1972, 98, 1567–1574. [Google Scholar]
- Kawamata, S. Accelerated Liquid Mass Dampers as Tools of Structural Vibration Control. In Proceedings of the 9th World Conference on Earthquake Engineering, Tokyo-Kyoto, Japan, 2–9 August 1988; Volume 8, pp. 421–426. [Google Scholar]
- Ikago, K.; Saito, K.; Inoue, N. Seismic control of single-degree-of-freedom structure using tuned viscous mass damper. Earthq. Eng. Struct. Dyn. 2012, 41, 453–474. [Google Scholar] [CrossRef]
- Lazar, I.F.; Neild, S.A.; Wagg, D.J. Using an inerter-based device for structural vibration suppression. Earthq. Eng. Struct. Dyn. 2014, 43, 1129–1147. [Google Scholar] [CrossRef] [Green Version]
- Taflanidis, A.A.; Giaralis, A.; Patsialis, D. Multi-objective optimal design of inerter-based vibration absorbers for earthquake protection of multi-storey building structures. J. Frankl. Inst. 2019, 356, 7754–7784. [Google Scholar] [CrossRef]
- De Domenico, D.; Ricciardi, G.; Zhang, R. Optimal design and seismic performance of tuned fluid inerter applied to structures with friction pendulum isolators. Soil Dyn. Earthq. Eng. 2020, 132, 106099. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhang, R.; Jiang, Y.; De Domenico, D.; Pan, C. Displacement-Dependent Damping Inerter System for Seismic Response Control. Appl. Sci. 2020, 10, 257. [Google Scholar] [CrossRef] [Green Version]
- Kawamata, S. Development of a Vibration Control System of Structures by Means of Mass Pumps; Institute of Industrial Science, University of Tokyo: Tokyo, Japan, 1973. [Google Scholar]
- Arakaki, T.; Kuroda, H.; Arima, F.; Inoue, Y.; Baba, K. Development of seismic devices applied to ball screw. Part 1: Basic performance test of RD-series. AIJ J. Technol. Des. 1999, 5, 239–244. [Google Scholar] [CrossRef]
- Arakaki, T.; Kuroda, H.; Arima, F.; Inoue, Y.; Baba, K. Development of seismic devices applied to ball screw: Part 2 Performance test and evaluation of RD-series. AIJ J. Technol. Des. 1999, 9, 265–270. [Google Scholar] [CrossRef] [Green Version]
- Saito, K.; Sugimura, Y.; Inoue, N. A study on response control of a structure using viscous damper with inertial mass. J. Struct. Eng. 2008, 54, 623–648. [Google Scholar]
- Arai, T.; Aburakawa, T.; Ikago, K.; Hori, N.; Inoue, N. Verification on effectiveness of a tuned viscous mass damper and its applicability to non-linear structural systems. J. Struct. Constr. Eng. AIJ 2009, 645, 1993–2002. [Google Scholar] [CrossRef]
- Pan, C.; Zhang, R. Design of structure with inerter system based on stochastic response mitigation ratio. Struct. Control Health Monit. 2018, 25, e2169. [Google Scholar] [CrossRef]
- Pan, C.; Zhang, R.; Luo, H.; Li, C.; Shen, H. Demand-based optimal design of oscillator with parallel-layout viscous inerter damper. Struct. Control Health Monit. 2018, 25, e2051. [Google Scholar] [CrossRef]
- Shen, W.; Niyitangamahoro, A.; Feng, Z.; Zhu, H. Tuned inerter dampers for civil structures subjected to earthquake ground motions: Optimum design and seismic performance. Eng. Struct. 2019, 198, 109470. [Google Scholar] [CrossRef]
- Zhang, S.Y.; Li, Y.-Y.; Jiang, J.Z.; Neild, S.A.; Macdonald, J.H.G. A methodology for identifying optimum vibration absorbers with a reaction mass. Proc. R. Soc. A Math. Phys. Eng. Sci. 2019, 475, 20190232. [Google Scholar] [CrossRef] [Green Version]
- Zhang, R.; Zhao, Z.; Pan, C.; Ikago, K.; Xue, S. Damping enhancement principle of inerter system. Struct. Control Health Monit. 2020, e2523. [Google Scholar] [CrossRef]
- Marian, L.; Giaralis, A. Optimal design of a novel tuned mass-damper–inerter (TMDI) passive vibration control configuration for stochastically support-excited structural systems. Probabilistic Eng. Mech. 2014, 38, 156–164. [Google Scholar] [CrossRef]
- Giaralis, A.; Marian, L. Use of inerter devices for weight reduction of tuned mass-dampers for seismic protection of multi-story building: The Tuned Mass-Damper-Interter (TMDI). In Active and Passive Smart Structures and Integrated Systems; International Society for Optics and Photonics: Las Vegas, NA, USA, 2016; p. 97991G. [Google Scholar]
- Giaralis, A.; Taflanidis, A. Optimal tuned mass-damper-inerter (TMDI) design for seismically excited MDOF structures with model uncertainties based on reliability criteria. Struct. Control Health Monit. 2018, 25, e2082. [Google Scholar] [CrossRef]
- Garrido, H.; Curadelli, O.; Ambrosini, D. Improvement of tuned mass damper by using rotational inertia through tuned viscous mass damper. Eng. Struct. 2013, 56, 2149–2153. [Google Scholar] [CrossRef]
- De Domenico, D.; Ricciardi, G. Improving the dynamic performance of base-isolated structures via tuned mass damper and inerter devices: A comparative study. Struct. Control Health Monit. 2018, 25, e2234. [Google Scholar] [CrossRef]
- De Domenico, D.; Ricciardi, G. An enhanced base isolation system equipped with optimal tuned mass damper inerter (TMDI). Earthq. Eng. Struct. Dyn. 2018, 47, 1169–1192. [Google Scholar] [CrossRef]
- Angelis, M.; Giaralis, A.; Petrini, F.; Pietrosanti, D. Optimal tuning and assessment of inertial dampers with grounded inerter for vibration control of seismically excited base-isolated systems. Eng. Struct. 2019, 196. [Google Scholar] [CrossRef]
- Ikago, K.; Sugimura, Y.; Saito, K.; Inoue, N. Seismic displacement control of multiple-degree-of-freedom structures using tuned viscious mass dampers system. In Proceedings of the 8th International Conference on Structural Dynamics EURODYN, Leuven, Belgium, 4–6 July 2011; Volume 7, pp. 1800–1807. [Google Scholar]
- Ikago, K.; Sugimura, Y.; Saito, K.; Inoue, N. Simple design method for a tuned viscous mass damper seismic control system. In Proceedings of the 15th World Conference on Earthquake Engineering, Lisbon, Portugal, 24–28 September 2012; Volume 9. [Google Scholar]
- Wen, Y.; Chen, Z.; Hua, X. Design and evaluation of tuned inerter-based dampers for the seismic control of MDOF structures. J. Struct. Eng. 2017, 143, 04016207. [Google Scholar] [CrossRef]
- Zhang, S.Y.; Jiang, J.Z.; Neild, S. Optimal configurations for a linear vibration suppression device in a multi-storey building. Struct. Control Health Monit. 2017, 24, e1887. [Google Scholar] [CrossRef] [Green Version]
- Asai, T.; Watanabe, Y. Outrigger tuned inertial mass electromagnetic transducers for high-rise buildings subject to long period earthquakes. Eng. Struct. 2017, 153, 404–410. [Google Scholar] [CrossRef] [Green Version]
- Ogino, M.; Sumiyama, T. Structural design of a high-rise building using tuned viscous mass dampers installed across three consecutive sotreys. In Proceedings of the Twelveth International Conference on Computational Structures Technology, Naples, Italy, 2–5 September 2014. [Google Scholar]
- Hwang, J.-S.; Kim, J.; Kim, Y.-M. Rotational inertia dampers with toggle bracing for vibration control of a building structure. Eng. Struct. 2007, 29, 1201–1208. [Google Scholar] [CrossRef]
- Xie, L.; Ban, X.; Xue, S.; Ikago, K.; Kang, J.; Tang, H. Theoretical Study on a Cable-Bracing Inerter System for Seismic Mitigation. Appl. Sci. 2019, 9, 4096. [Google Scholar] [CrossRef] [Green Version]
- Sorace, S.; Terenzi, G. The damped cable system for seismic protection of frame structures—Part I: General concepts, testing and modeling. Earthq. Eng. Struct. Dyn. 2012, 41, 915–928. [Google Scholar] [CrossRef]
- Sorace, S.; Terenzi, G. The damped cable system for seismic protection of frame structures—Part II: Design and application. Earthq. Eng. Struct. Dyn. 2012, 41, 929–947. [Google Scholar] [CrossRef]
- Aly, A.M. The Use of Bracing Systems with MR Dampers in Super Tall Buildings. Int. J. High Rise Build. 2016, 5, 31–41. [Google Scholar] [CrossRef]
- Kang, J.-D.; Tagawa, H. Seismic performance of steel structures with seesaw energy dissipation system using fluid viscous dampers. Eng. Struct. 2013, 56, 431–442. [Google Scholar] [CrossRef]
- Sugimura, Y.; Goto, W.; Tanizawa, H.; Saito, K.; Nimomiya, T. Response control effect of steel building structure using tuned viscous mass damper. In Proceedings of the 15th World Conference on Earthquake Engineering, Lisbon, Portugal, 24–28 September 2012; Volume 9, pp. 24–28. [Google Scholar]
- Lutes, L.D.; Sarkani, S. Random Vibrations: Analysis of Structural and Mechanical Systems; Butterworth-Heinemann: Oxford, UK, 2004. [Google Scholar]
- Kanai, K. Semi-empirical formula for the seismic characteristics of the ground. Bull. Earthq. Res. Inst. Univ. Tokyo 1957, 35, 309–325. [Google Scholar]
- JSSI Manual. Design and Construction Manual for Passively Controlled Buildings, 2nd ed.; Japan Society of Seismic Isolation: Tokyo, Japan, 2005. (In Japanese) [Google Scholar]



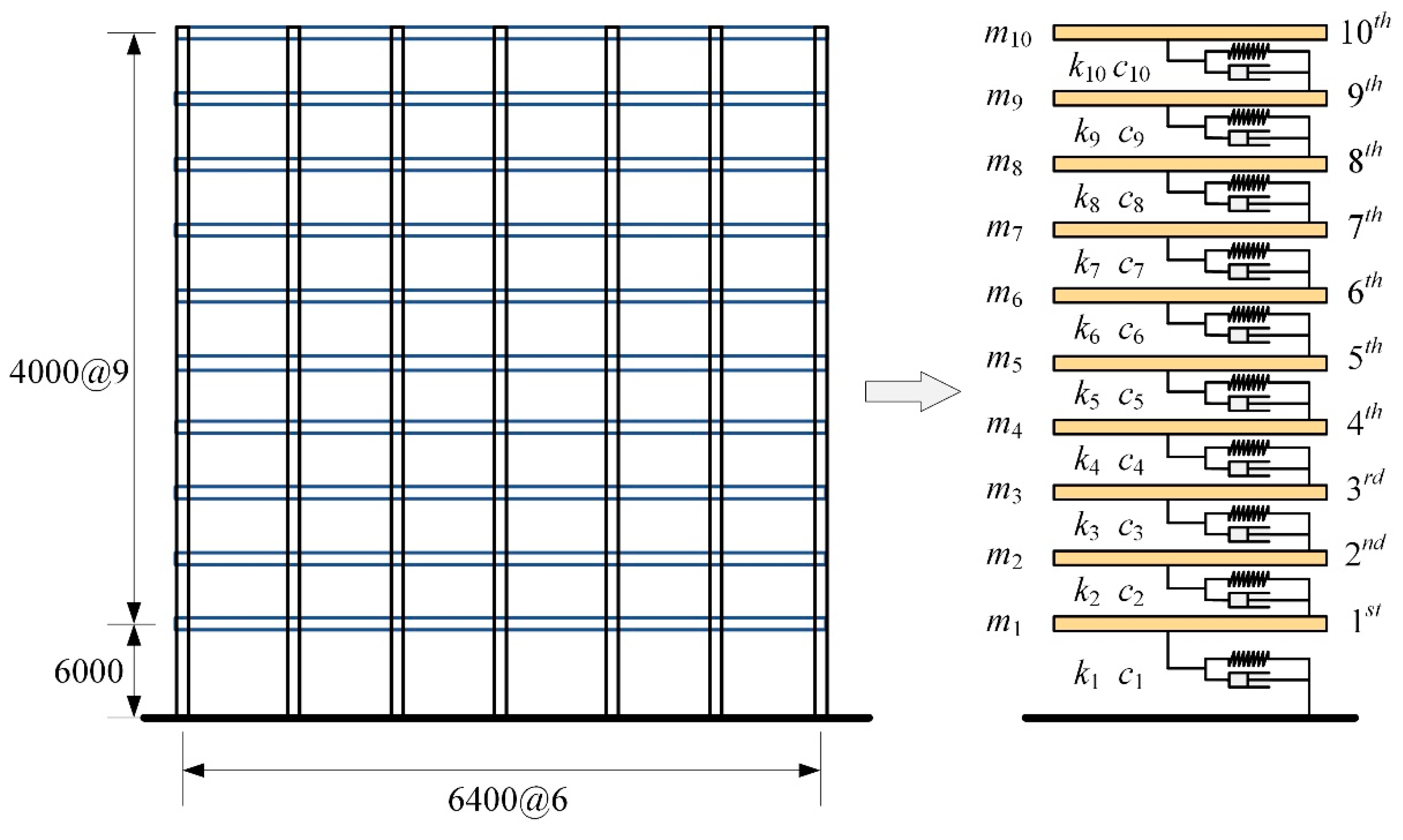
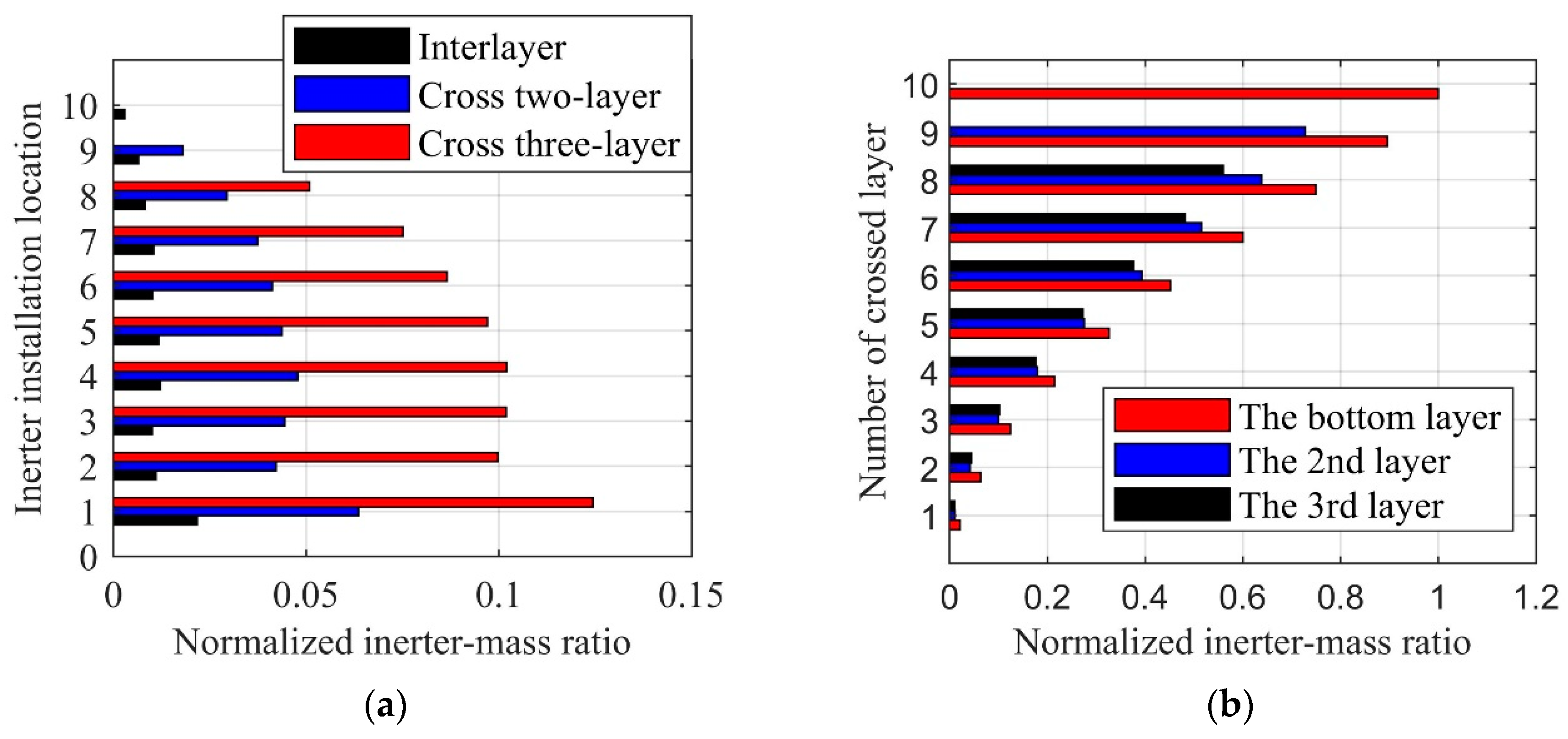

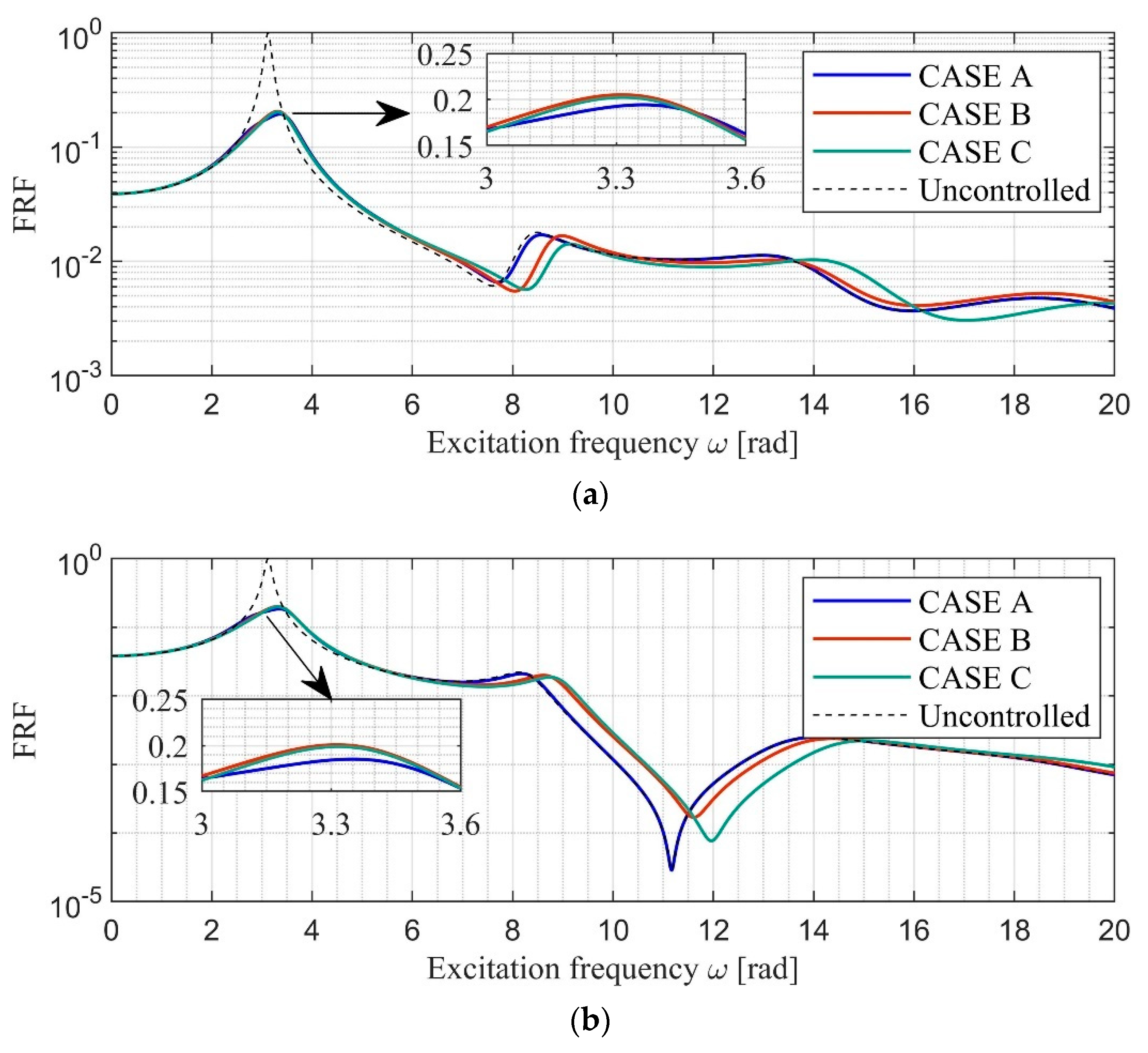
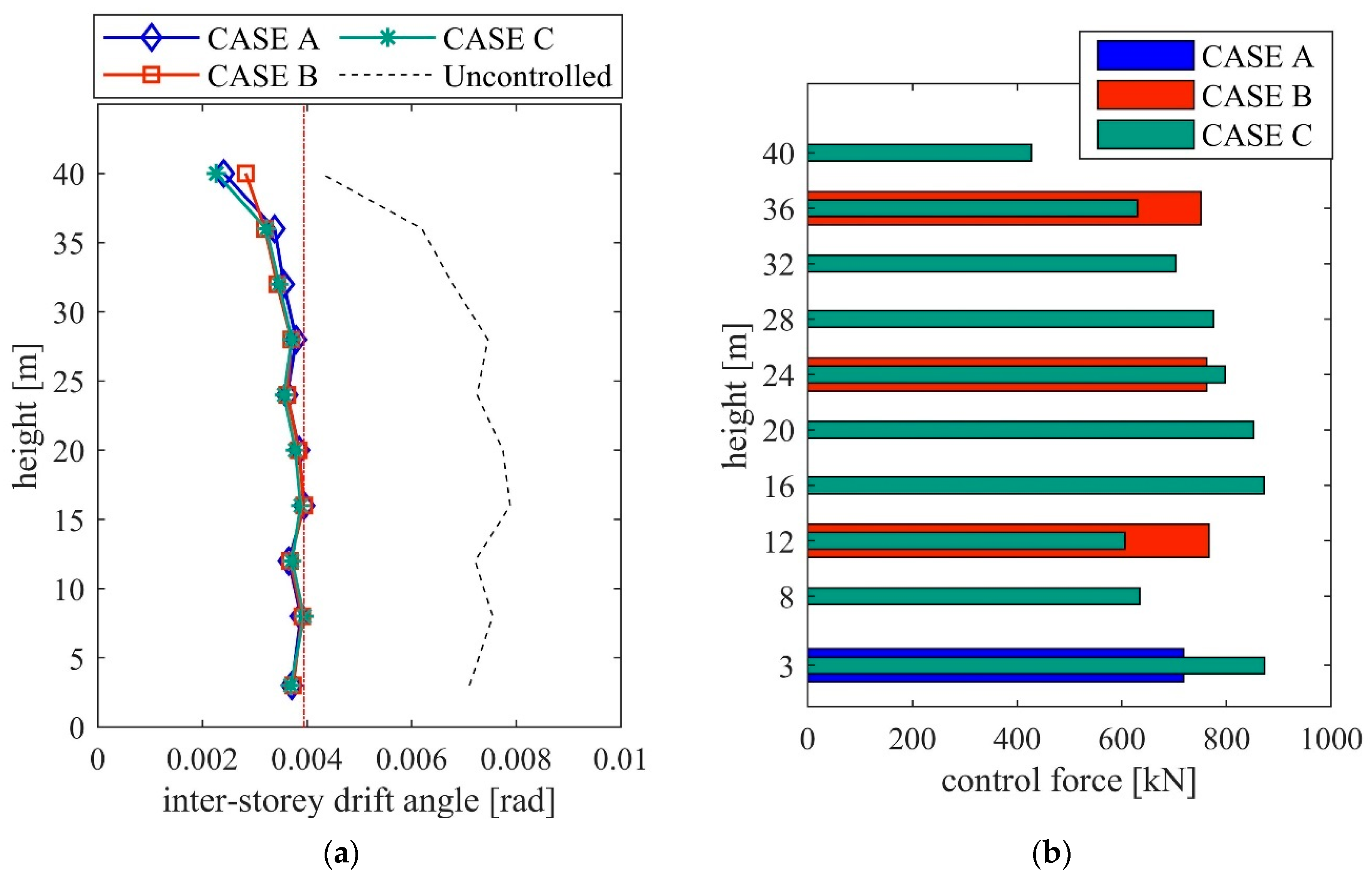
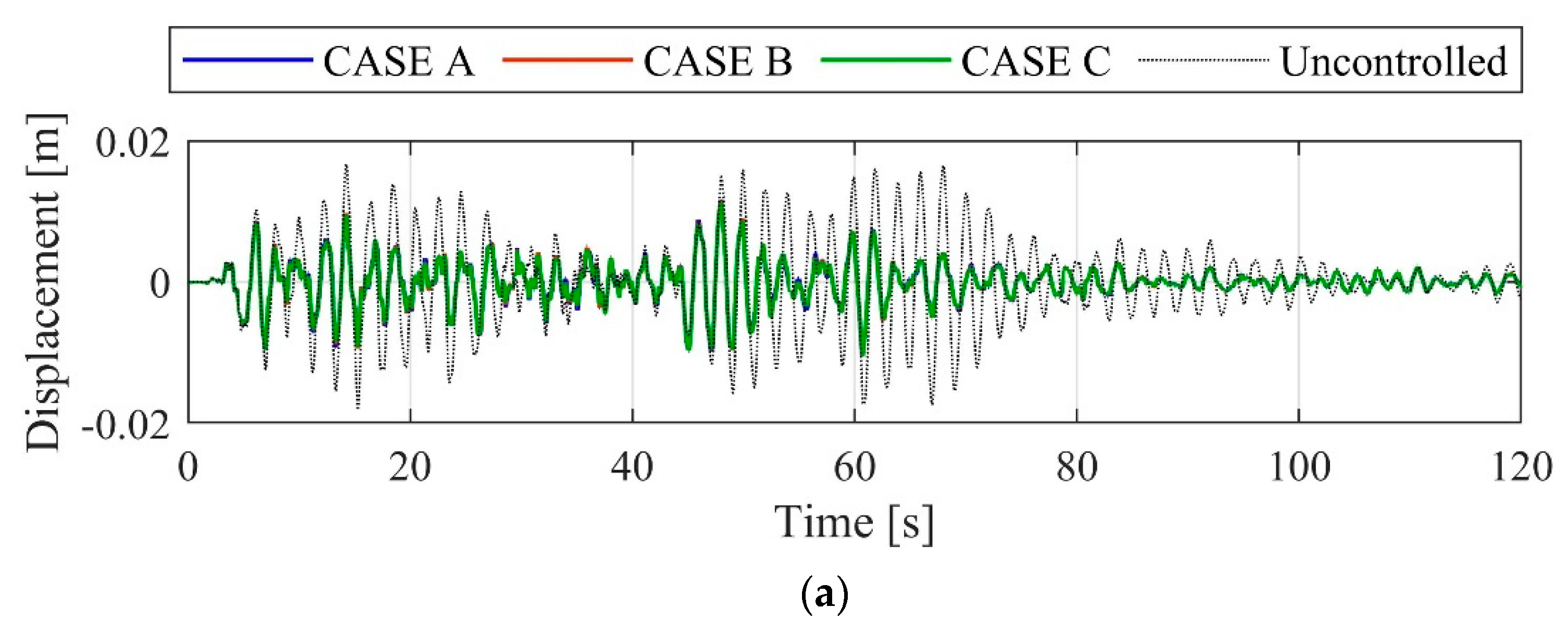

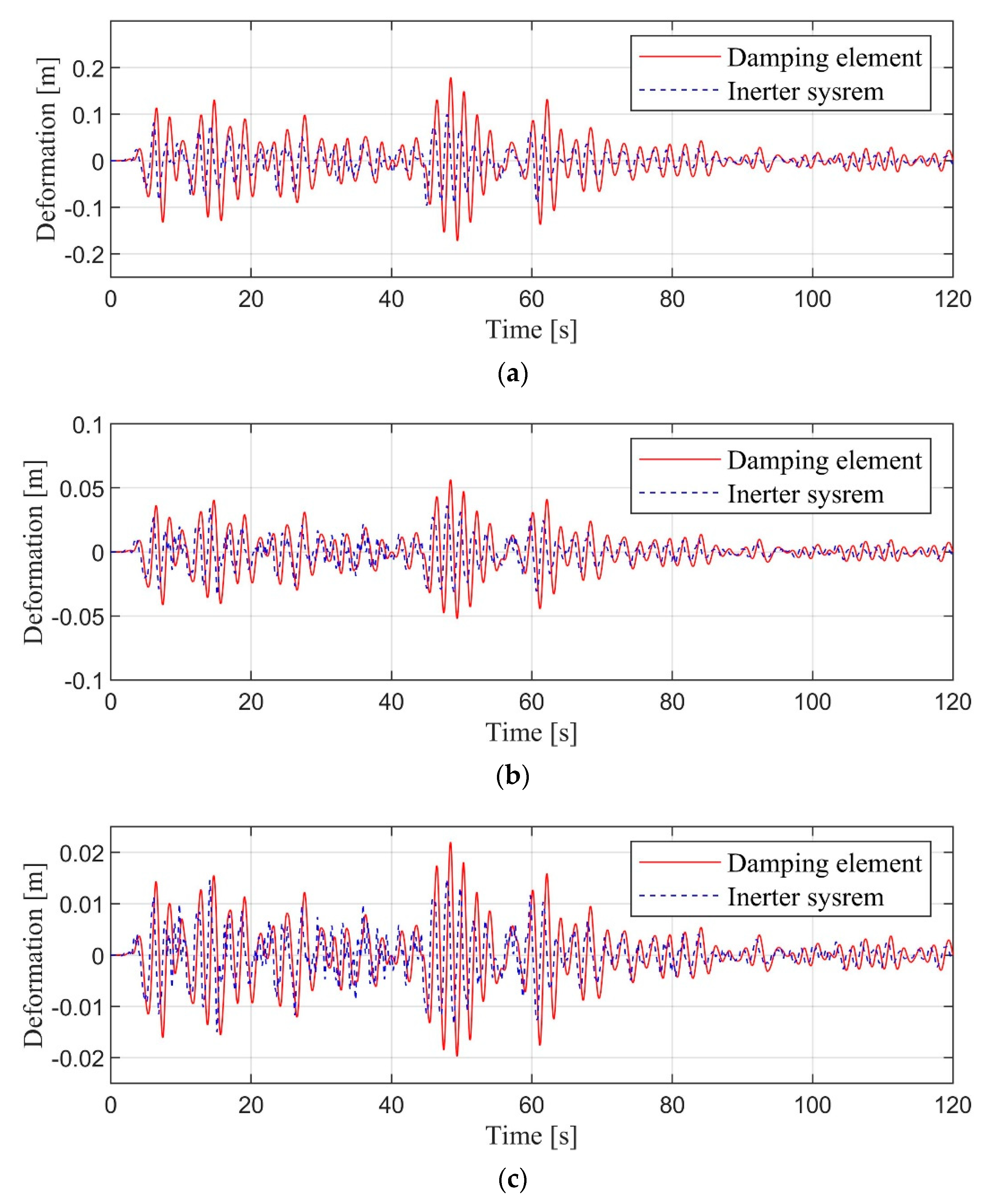
| Story | Mass mi (×103 kg) | Stiffness ki (kN/m) | Height (m) |
|---|---|---|---|
| 10 | 875.4 | 158,550 | 4 |
| 9 | 649.5 | 180,110 | 4 |
| 8 | 656.2 | 220,250 | 4 |
| 7 | 660.2 | 244,790 | 4 |
| 6 | 667.2 | 291,890 | 4 |
| 5 | 670.1 | 306,160 | 4 |
| 4 | 675.7 | 328,260 | 4 |
| 3 | 680.0 | 383,020 | 4 |
| 2 | 681.6 | 383,550 | 4 |
| 1 | 699.9 | 279,960 | 6 |
| md (kg) | cd (kN/m/s) | ωr | β | kd (kN/m) | ||
|---|---|---|---|---|---|---|
| CASE A | CICBIS-All | 1,000,000 | 1605.899 | 3.259 | 0.508 | 10,620.172 |
| CASE B | CICBIS-1 | 1,000,000 | 1970.397 | 3.270 | 0.909 | 10,695.612 |
| CICBIS-2 | 0.964 | |||||
| CICBIS-3 | 1.040 | |||||
| CASE C | IICBIS-1 | 1,000,000 | 2129.588 | 3.281 | 1.535 | 10,766.132 |
| IICBIS-2 | 1.799 | |||||
| IICBIS-3 | 1.754 | |||||
| TVMD-1 | 2,354,898 | 5014.963 | 3.281 | 1.000 | 25,353.142 | |
| TVMD-2 | 3,234,898 | 6889.000 | 3.281 | 1.000 | 34,827.336 | |
| TVMD-3 | 3,078,151 | 6555.193 | 3.281 | 1.000 | 33,139.778 |
| α (°) | η | β | |
|---|---|---|---|
| CICBIS-All | 46.009 | 1.116 | 0.508 |
| CICBIS-1 | 20.054 | 0.968 | 0.909 |
| CICBIS-2 | 17.361 | 1.010 | 0.964 |
| CICBIS-3 | 17.361 | 1.090 | 1.040 |
| IICBIS-1 | 5.959 (8.881 1) | 1.543 (1.554 1) | 1.535 |
| IICBIS-2 | 5.959 | 1.809 | 1.799 |
| IICBIS-3 | 5.959 | 1.764 | 1.754 |
| CASE A | CASE B | CASE C | |
|---|---|---|---|
| cost index (kN) | 718.234 | 2299.150 | 8727.719 |
| Title 1 | BCJ-L2 Artificial Accelerogram | Kobe Accelerogram | Chi-chi Accelerogram | El Centro Accelerogram |
|---|---|---|---|---|
| CASE A | 0.4714 | 0.4081 | 0.4906 | 0.4416 |
| CASE B | 0.4690 | 0.4182 | 0.4953 | 0.4469 |
| CASE C | 0.4600 | 0.4111 | 0.4874 | 0.4393 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, S.; Kang, J.; Xie, L.; Zhang, R.; Ban, X. Cross-Layer Installed Cable-Bracing Inerter System for MDOF Structure Seismic Response Control. Appl. Sci. 2020, 10, 5914. https://doi.org/10.3390/app10175914
Xue S, Kang J, Xie L, Zhang R, Ban X. Cross-Layer Installed Cable-Bracing Inerter System for MDOF Structure Seismic Response Control. Applied Sciences. 2020; 10(17):5914. https://doi.org/10.3390/app10175914
Chicago/Turabian StyleXue, Songtao, Jianfei Kang, Liyu Xie, Ruifu Zhang, and Xinlei Ban. 2020. "Cross-Layer Installed Cable-Bracing Inerter System for MDOF Structure Seismic Response Control" Applied Sciences 10, no. 17: 5914. https://doi.org/10.3390/app10175914
APA StyleXue, S., Kang, J., Xie, L., Zhang, R., & Ban, X. (2020). Cross-Layer Installed Cable-Bracing Inerter System for MDOF Structure Seismic Response Control. Applied Sciences, 10(17), 5914. https://doi.org/10.3390/app10175914






