1.1. General Context
Electrical distribution networks represent the most significant portion of the power system and are entrusted with providing electricity to end-users at medium- and low-voltage levels by connecting the transmission/sub-transmission system with consumers [
1,
2]. Typical voltages in these electrical networks oscillate between 4.16 kV and 33 kV [
3], and these networks are typically operated with a radial structure to minimize installation, operation, and maintenance costs, including protective devices coordination simplifications [
4,
5,
6]. To determine the behavior of electrical networks under well-defined voltage conditions, power flow methodologies are used, which facilitate the calculation of the voltage profiles at all the nodes of the network for a particular load condition [
7,
8]. The main challenge in the power-flow analysis of distribution networks is the constant power loads that produce nonlinear relationships between the voltages and powers [
9,
10], which makes the use of numerical methods for solving the power-flow problem necessary [
11]. A typical tendency in the power-flow analysis of electrical distribution networks is the use of graph-based methods to address the power-flow problem based on the radial structure of the grid [
12,
13]. However, these methodologies are not useful in the case of weakly or strongly meshed distribution networks [
14], which can cause major issues in modern power systems where meshed structures can help with grid performance in terms of realizing lower power losses and improvement voltage profiles [
15]. In the case of commercial solutions for a distribution system analysis such as the DigSILENT and ETAP software, the Newton–Raphson (NR) method is the most-used approach [
16] as it can be used with radial and meshed structures as well as multiple slack and voltage-controlled nodes [
17]. In this research, we tackle the power-flow problem in electrical distribution networks while considering a unique slack node and radial and meshed configurations by reformulating the conventional backward–forward power flow using the branch-to-nodal admittance matrix [
18].
1.2. Motivation
The power-flow analysis in electrical distribution networks is one of the most classical and largely studied problems in power-system analysis [
14] as the power-flow is a necessary calculation in the determination of grid performance [
10]. A power-flow method is a tool that is used to determine, via an iterative procedure, the final values of all the voltages in an electrical network with a certain tolerance acceptance in order to determine the complete operative state [
14], i.e., currents through lines, voltage regulation in all the nodes, active and reactive power losses, and voltage stability. To solve the power-flow problem, the most classical methods used are the NR and Gauss–Seidel (GS) approaches, which guarantee convergence based on the Kantarovich and Banach fixed-point theorems [
19]. In addition, some graph-based methods such as triangular formulation and quasi-symmetric matrices have also been reported for handling radial grid configurations [
12,
20]. However, this research is motivated by the fact that the classical backward–forward power-flow method is commonly formulated via sequential steps that require that the grid is ordered in layers [
21]. It has a radial structure as, all the currents are calculated in the backward stage, while all the voltages are defined in the forward stage [
13]. As this operation can be efficient, these stages exclude meshed configurations, which implies that it is not applicable to weakly or strongly meshed distribution networks. Therefore, herein, a reformulation of the backward–forward power flow in distribution networks is presented based on the branch-to-nodal incidence matrix [
13], which permits the handling of radial and meshed distribution networks that include voltage-controlled nodes. Furthermore, the convergence of the proposed method is demonstrated by applying the Banach fixed-point theorem [
22].
1.3. Literature Review
Power-flow solutions in the literature present a vast universe of possibilities based on iterative procedures, linearization methods, and convex reformulations. Some of these approaches are presented below.
The most classical power-flow methods in power-systems analysis correspond to the Gauss-Seidel (GS) and NR approaches [
14]. The GS approach can be easily implemented using any programming language with its main advantage being that it can be used with complex numbers. However, it exhibits the worse performance in terms of processing time and number of iterations. With the purpose of improving the efficiency of the GS method, an accelerating factor
that reduces the total number of iterations and the required overall processing time is used [
17]. In the case of the NR approach, it is a methodology that is more commonly used in commercial software and is widely adopted by utilities [
23]. The main advantage of the NR approach is that it converges in a few iterations, has low processing times, and can possibly be used with radial and meshed networks comprising multiple voltage-controlled nodes. The main problem with using the NR approach in distribution networks is the high dispersion of the Jacobian matrix, which may cause convergence problems when the matrix is inverted for updating the voltage magnitude and angle variables [
19]. The authors of [
24] proposed the use of the Levenberg–Marquardt (LM) algorithm for solving power-flow problems in electrical networks; this approach essentially comprises an alternative manner of presenting the NR formulation with the main advantage that a factor is added to the Jacobian in order to reduce the possible singularities in this matrix.
For distribution networks, some of the most recognized approaches for addressing the power-flow problem are graph-based methodologies known as backward–forward and triangular methods [
12,
20]. The backward–forward method is typically designed with an algorithmic structure using an iterative sweep based on currents in the backward stage to update the voltages in the forward stage [
21]. An important improvement in the backward–forward approach was presented by [
13], wherein radial and meshed structures were included in a matricial formulation. The triangular approach works for radial and meshed structures [
12]; however, the related convergence analysis is not provided. It should be noted that in these methods, the authors do not present an analysis of the inclusion of voltage-controlled nodes, which we proposed in our matricial reformulation. A new approach based on successive approximations was recently reported in [
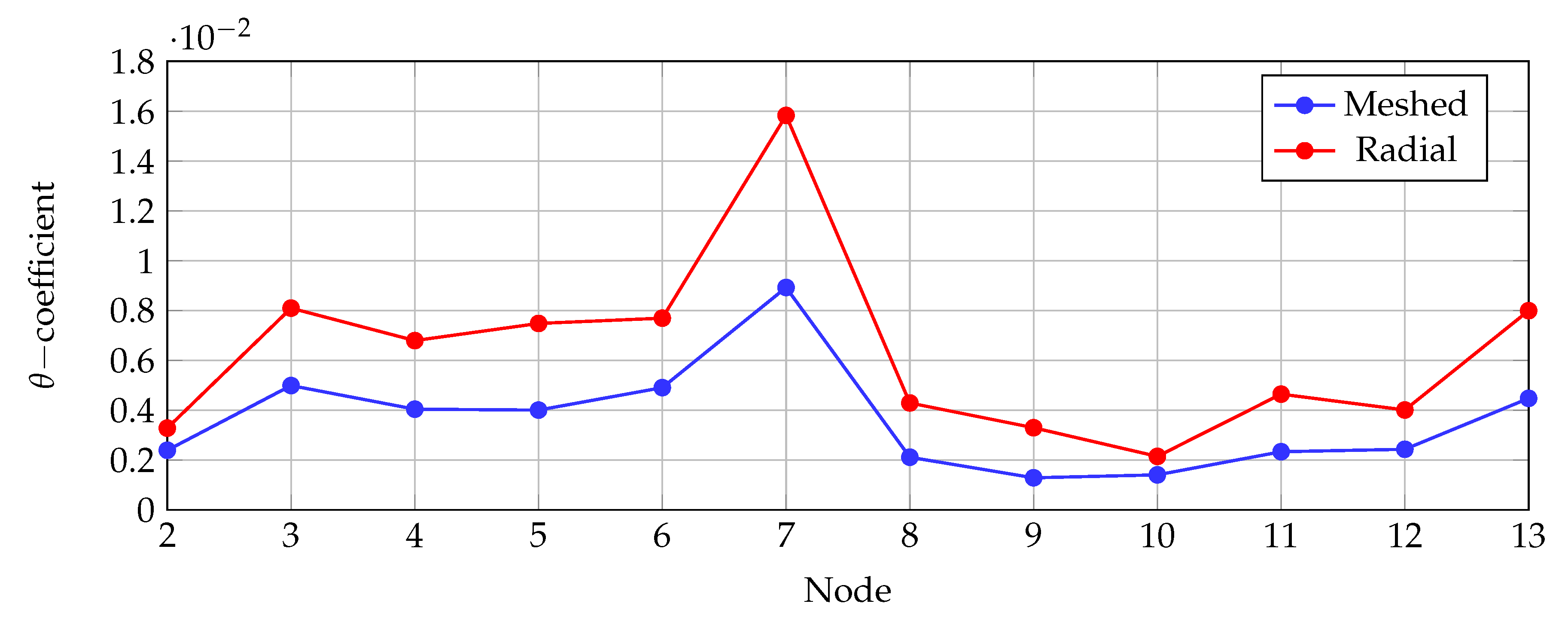
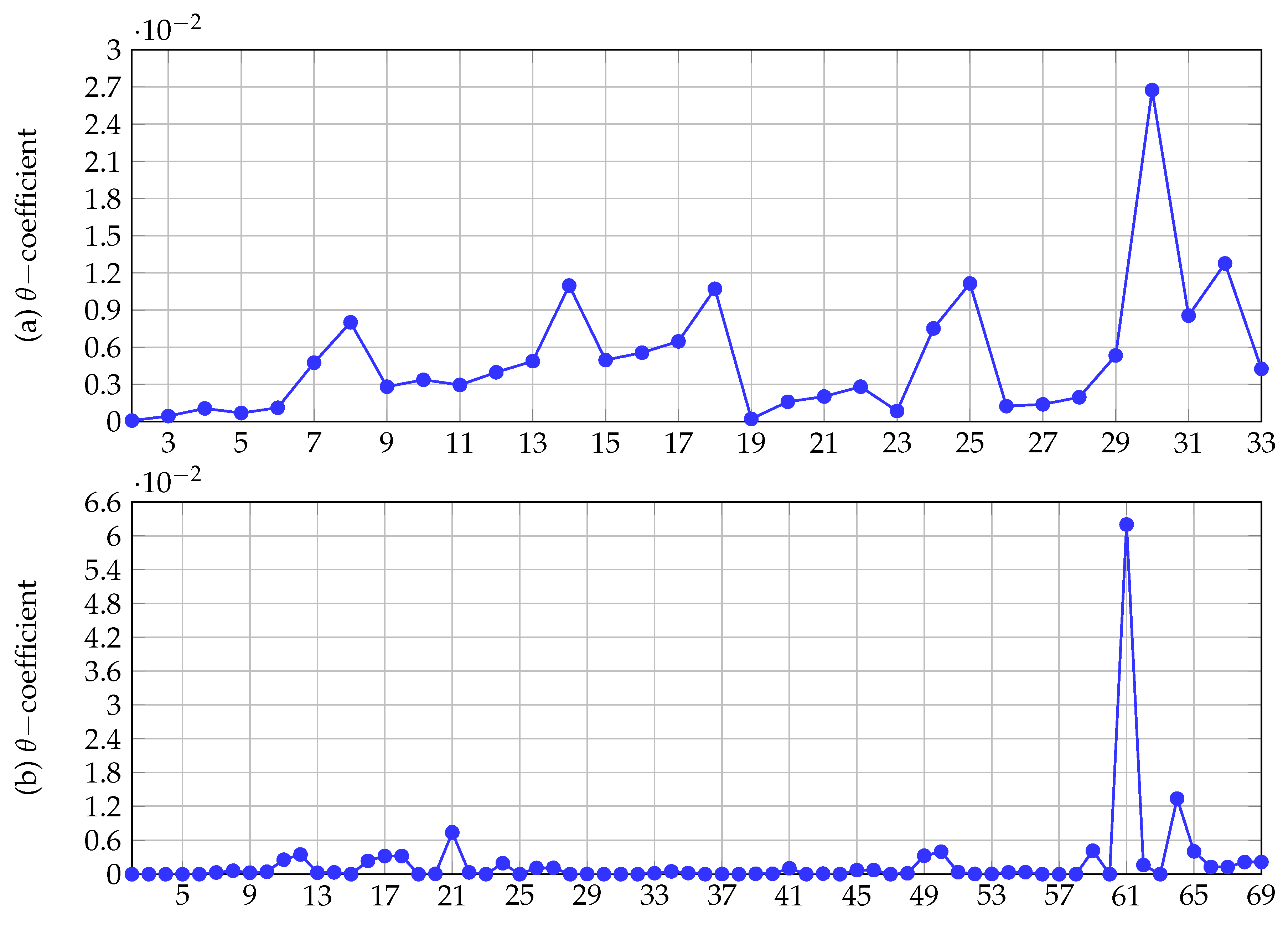
25]. This approach demonstrates the convergence of the recursive formulation for radial and meshed networks using the Banach fixed-point theorem. However, voltage-controlled sources were not considered in this formulation, and the behavior of the
-coefficient was not determined to confirm the convergence at well-defined voltage conditions. Two additional important power flow contributions have been reported in specialized literature by [
26,
27] regarding secondary distribution networks to study the problem of the harmonic penetration caused by higher penetration of photovoltaic sources. The authors in these approaches have proposed a harmonic power flow analysis using affine arithmetic which allows reaching better results regarding harmonic distortion estimations with low-computational effort when compared with classical Monte-Carlo simulations; in addition, these methods were validate in real secondary distribution networks with promissory results for utilities.
Other approaches have also been presented in specialized literature in relation to linear and convex approximations for power-flow solutions in distribution networks. In [
11], a convex approximation for a power-flow analysis of radial and meshed distribution networks was presented while considering a semidefinite programming approximation by using a rectangular representation of the power-balance equations. In [
8], a second-order cone programming approximation was described while considering branch variables related to currents and powers in all the lines. It is essential to mention that the main disadvantage of these approaches is the low rate of convergence when the number of nodes (
n) increases as these formulations create
variables related to voltages, which increase the required processing times to reach the optimal solution in the iterative procedure [
28]. In the case of linear methodologies, the authors of [
7] proposed a Taylor’s series expansion of the hyperbolic relation between the voltage and powers to reach a linear formulation that can be used to solve directly without the use of iterative procedures. In [
10], an improvement of this linear approximation was presented using the straight equation to include the minimum expected voltage in the approximation and improve the final result of the power-loss calculation. The authors of [
29] described a linear approximation based on a logarithmic transformation of the voltage magnitudes added to the Taylor’s series expansion for applications in power systems. It should be noted that these linear approximations have speed responses; however, the final result of the power-loss estimation varies in the range of 1% and 10%.
1.5. Organization of the Document
The remainder of this paper is arranged as follows.
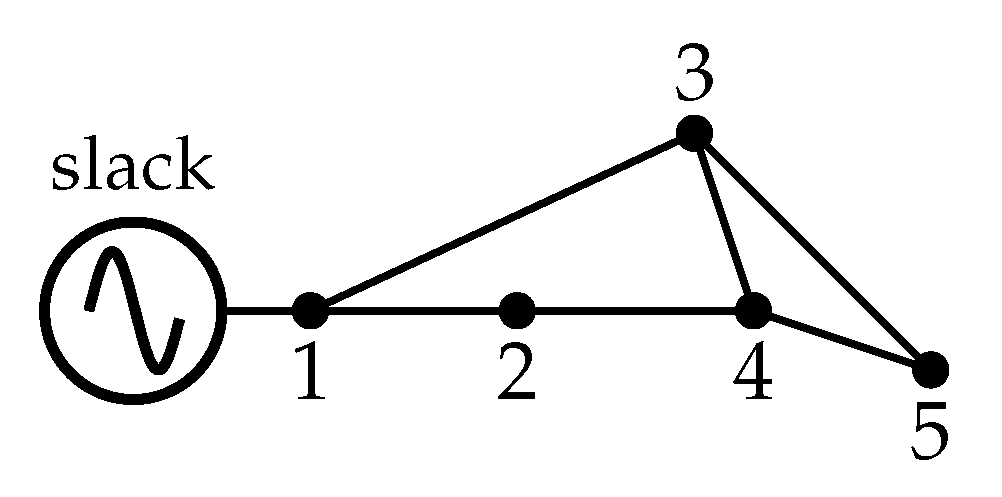
Section 2 presents the matricial formulation of the classical backward–forward power flow method using a small distribution test feeder with multiple meshes. In
Section 3, the convergence analysis is presented based on the Banach fixed-point theorem, which results in the maximum load current divided by the minimum short-circuit current per node.
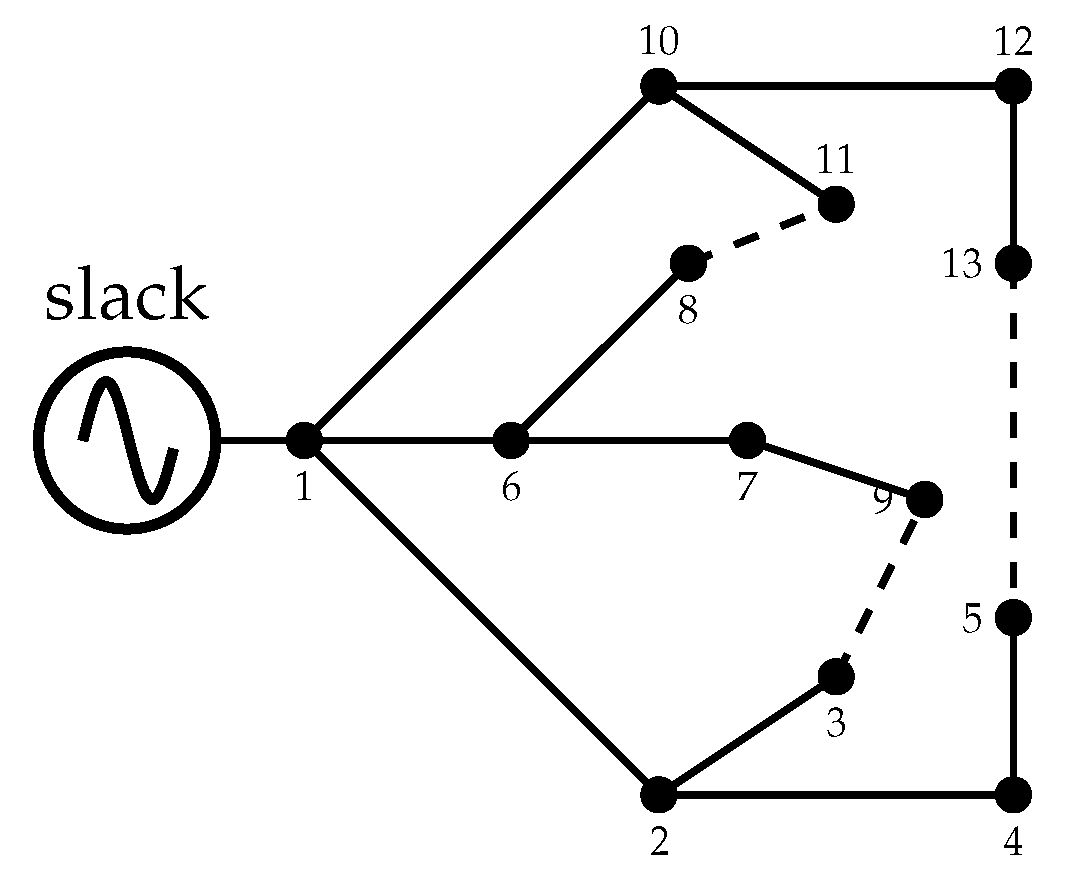
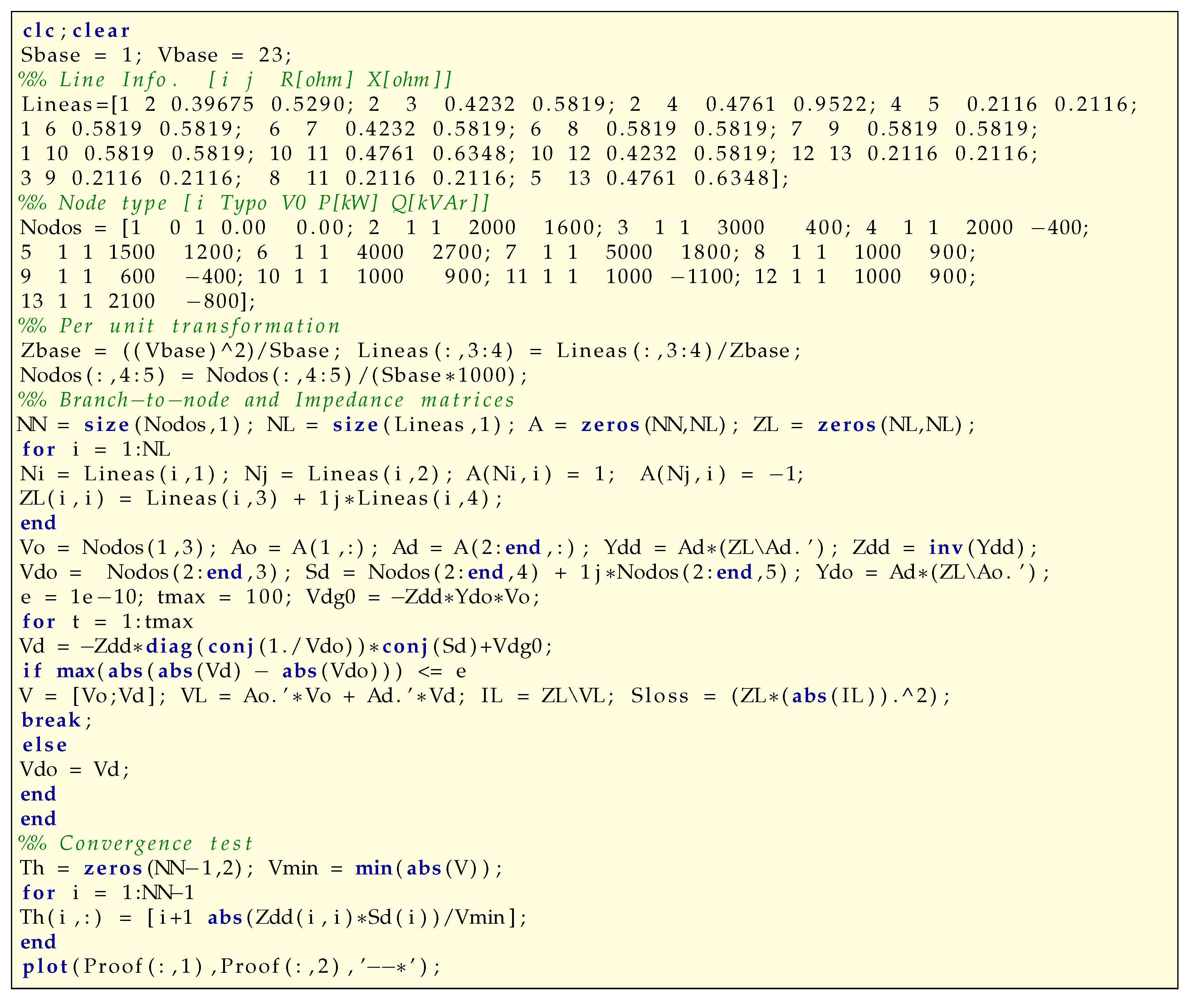
Section 4 presents a small numerical example comprising a 13-node test feeder with mesh and radial topologies and presents the MATLAB/OCTAVE implementation that can be used as a power-flow analysis tutorial for beginners. In
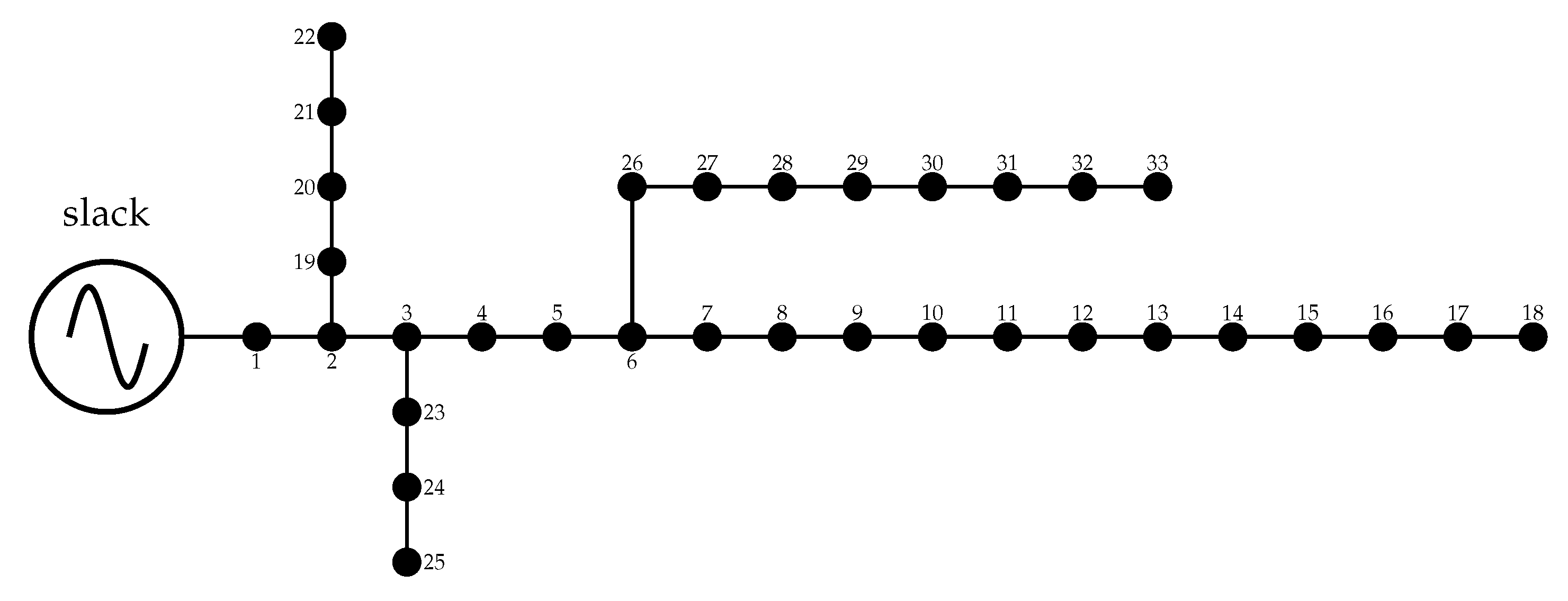
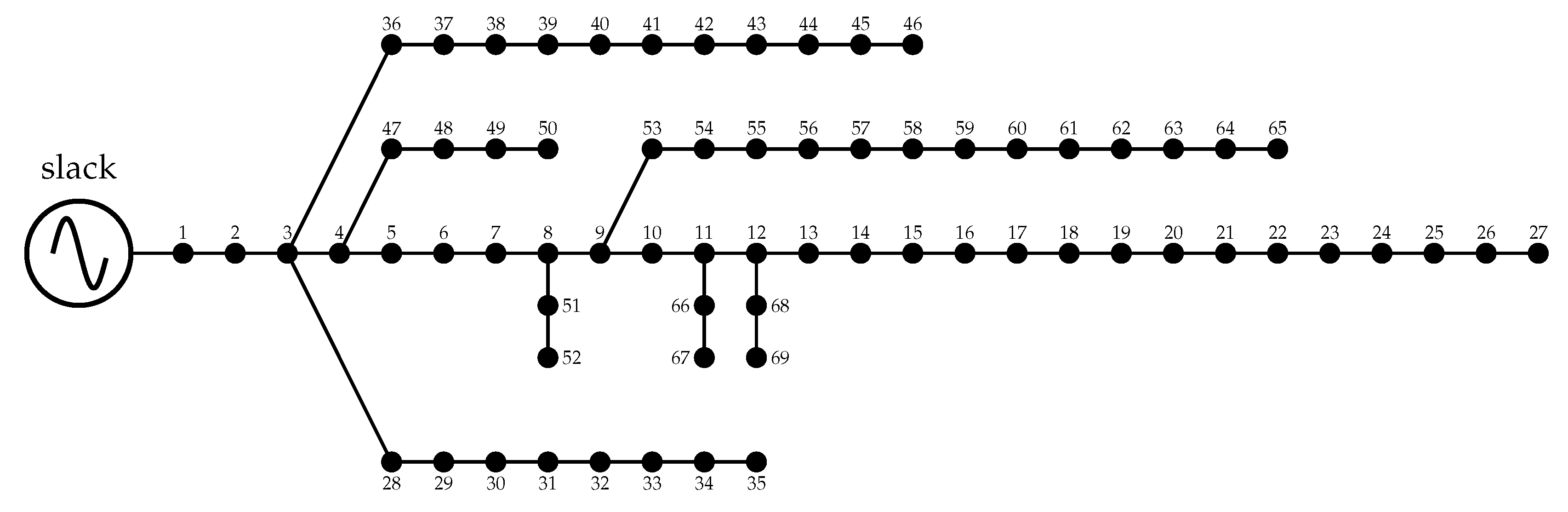
Section 4, the configurations of two classical distribution test feeders comprising 33 and 69 nodes are presented.
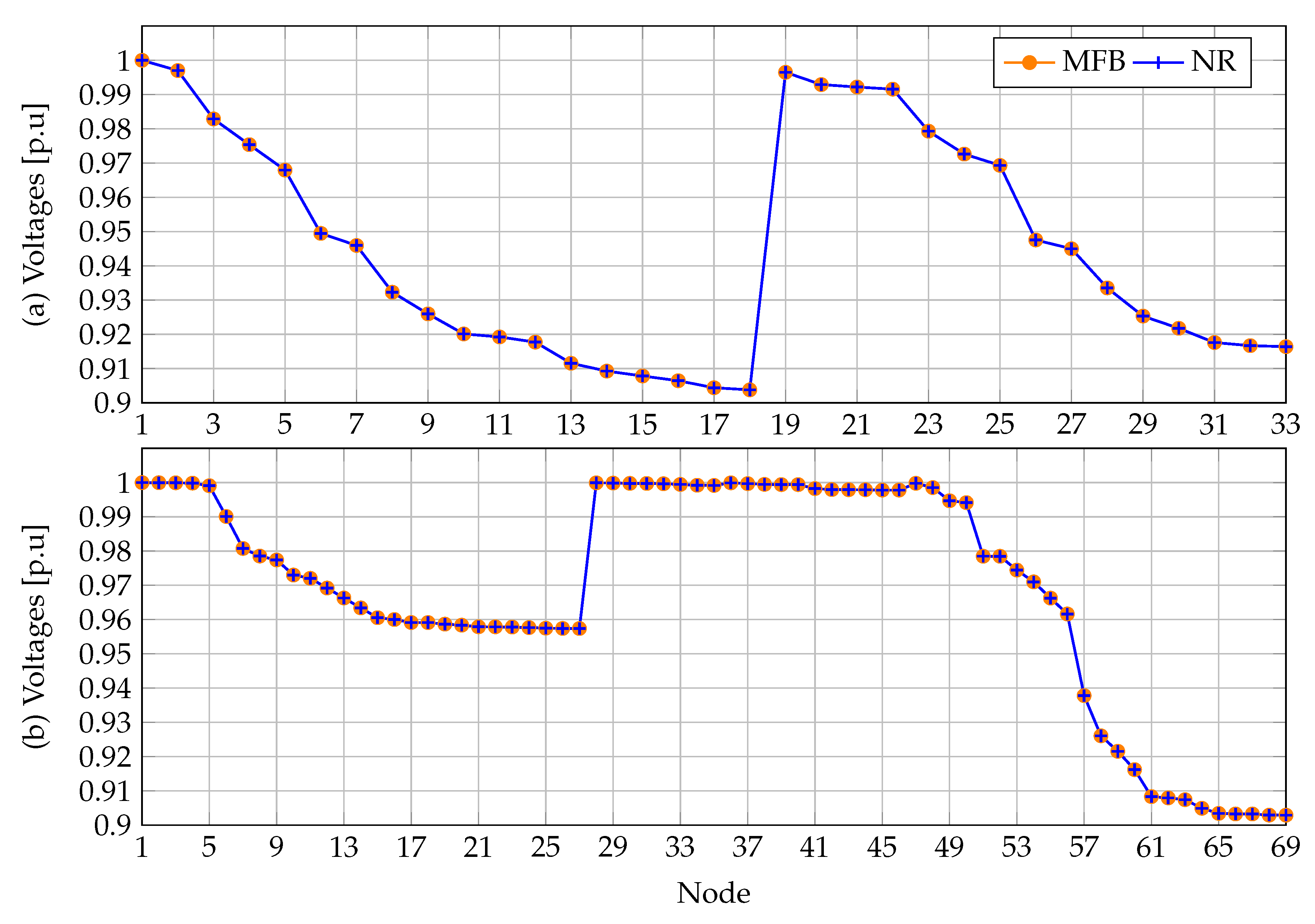
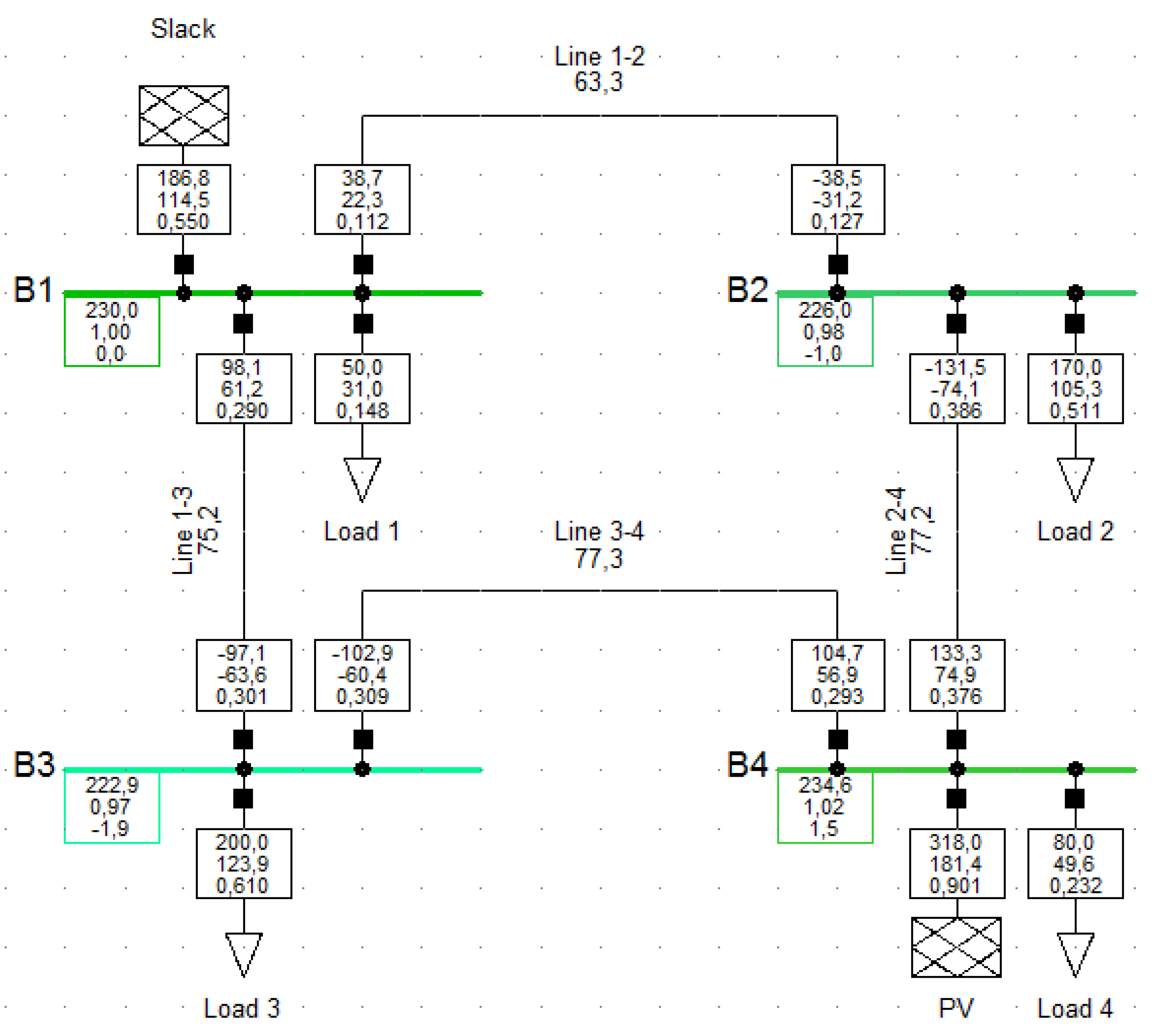
Section 6 presents the numerical results obtained for these test feeders on comparing the proposed matricial formulation with the classical power- flow methods such as the GS, NR, and LM methods; in addition, a small transmission network comprising four nodes that comprise a meshed structure with a voltage-controlled node is presented, which aids in understanding the extension of the proposed formulation to power-system analyses.
Section 7 presents the main conclusions derived from this work as well as its possible future improvements.