Towards the Use of Novel Materials in Shipbuilding: Assessing Thermal Performances of Fire-Doors by Self-Consistent Numerical Modelling
Abstract
1. Introduction
2. Materials and Methods
2.1. Material Properties
2.1.1. Mechanical Tests
2.1.2. Thermal Conductivity
2.1.3. Incombustibility
2.2. Numerical Modelling of Fire Resistance Test
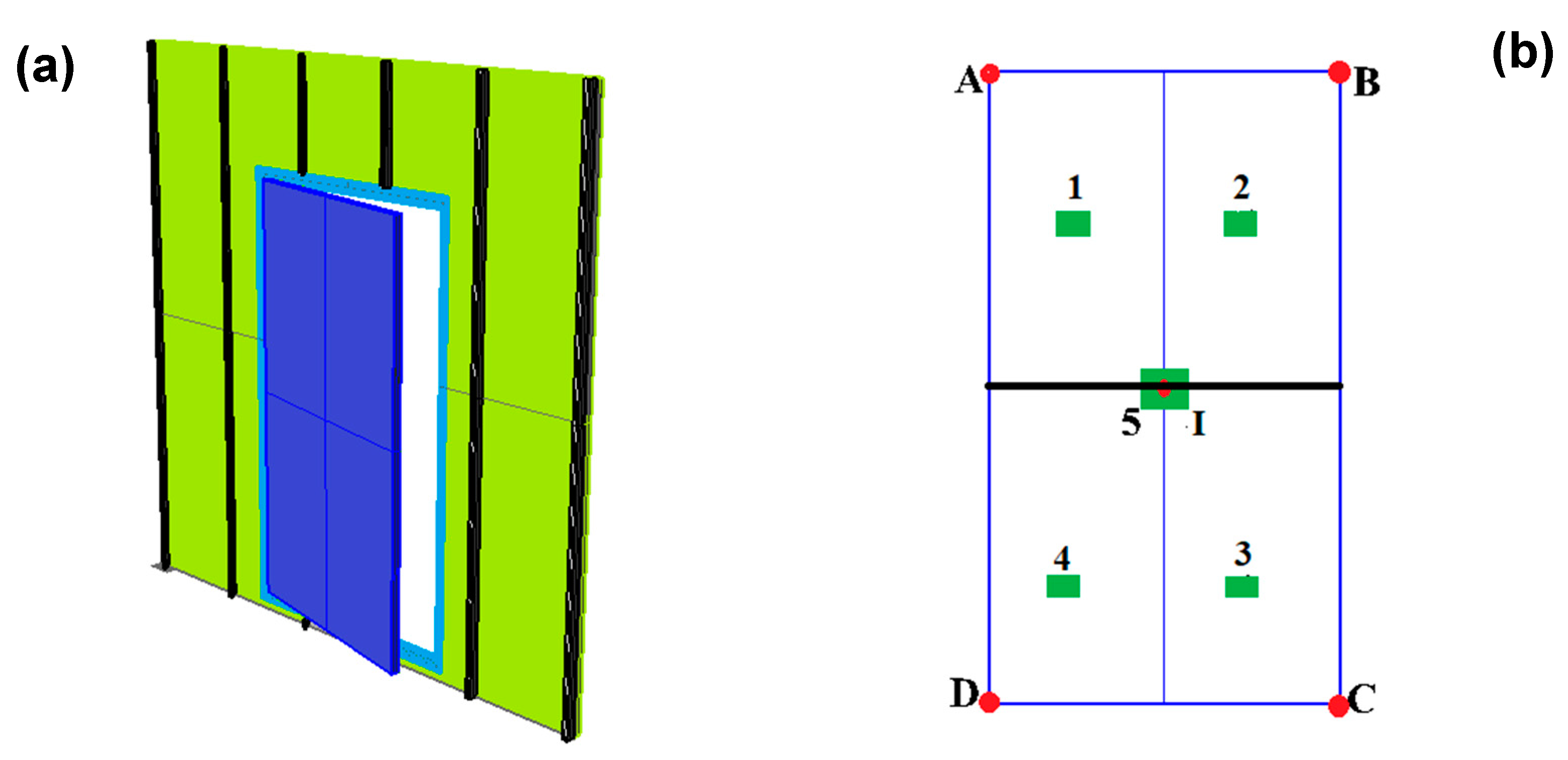
2.2.1. Fire-Proof Door Characteristics and Test Conditions
- (i)
- The final temperature of each thermocouple must not exceed 180 °C above T0;
- (ii)
- The medium temperature of the five thermocouples must not exceed 140 °C above T0.
2.2.2. FEM Modelling
3. Results
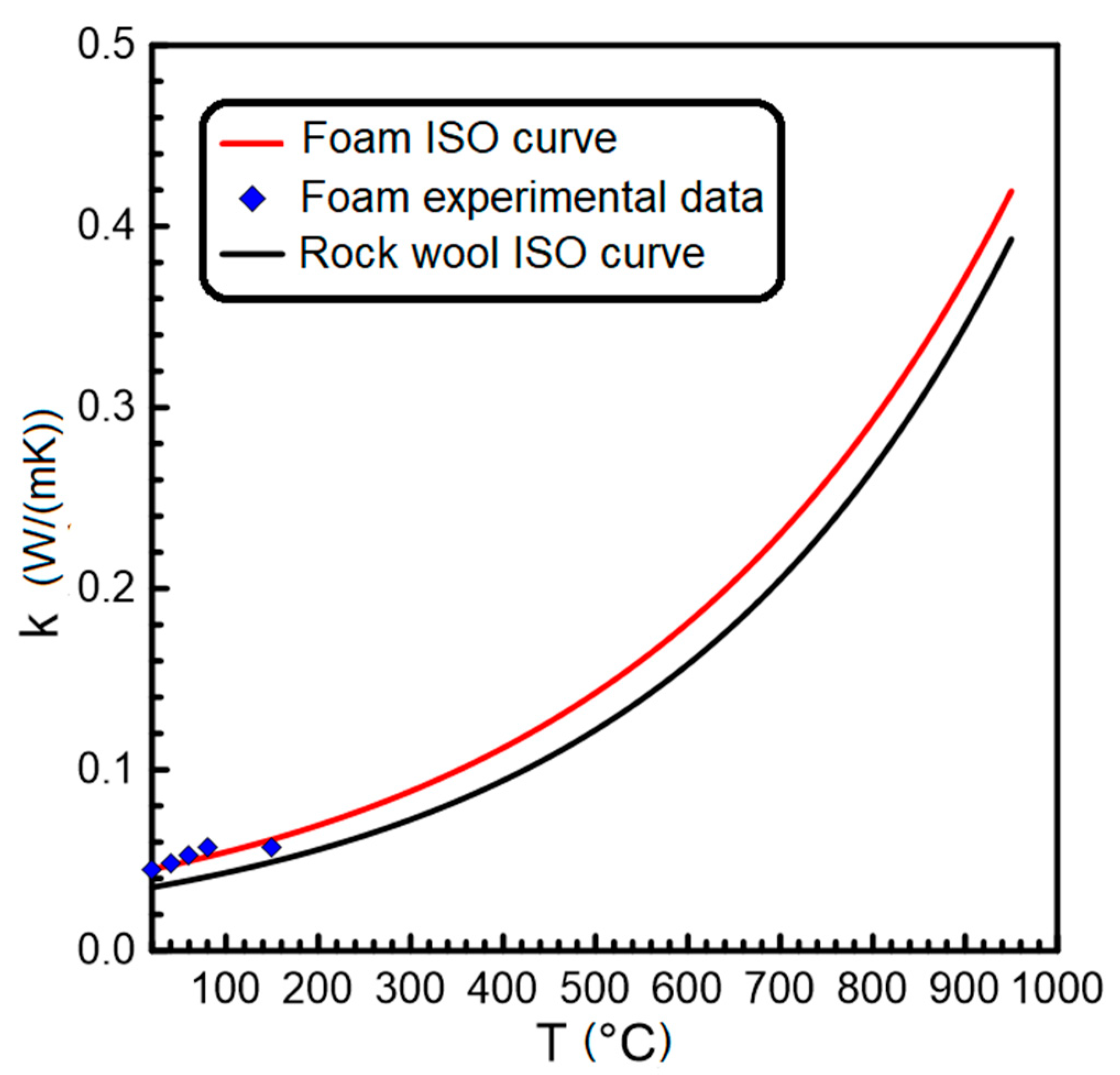
3.1. Foam Characterization
3.2. Numerical Model Assessment
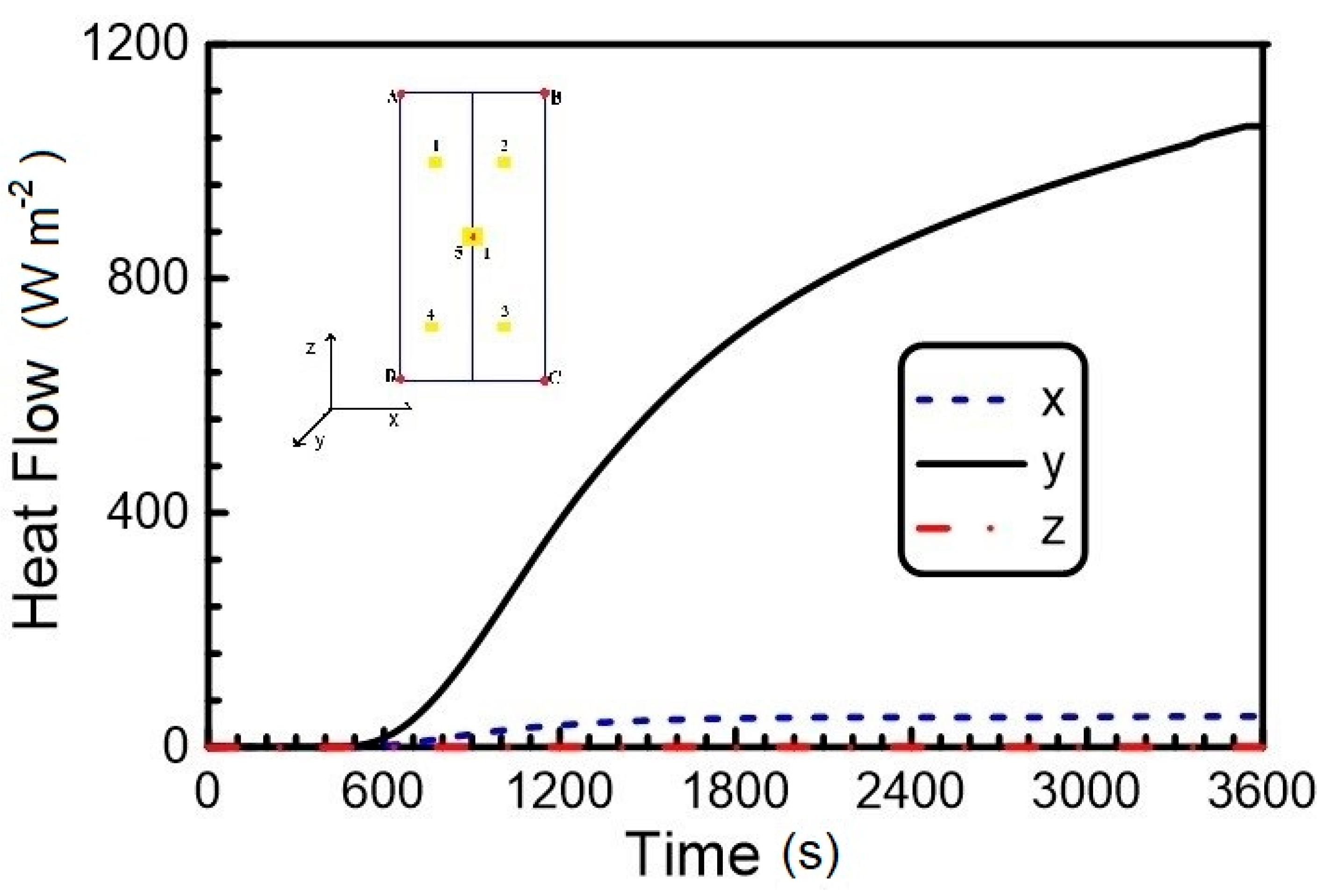
3.2.1. Boundary Conditions for Thermal Analysis
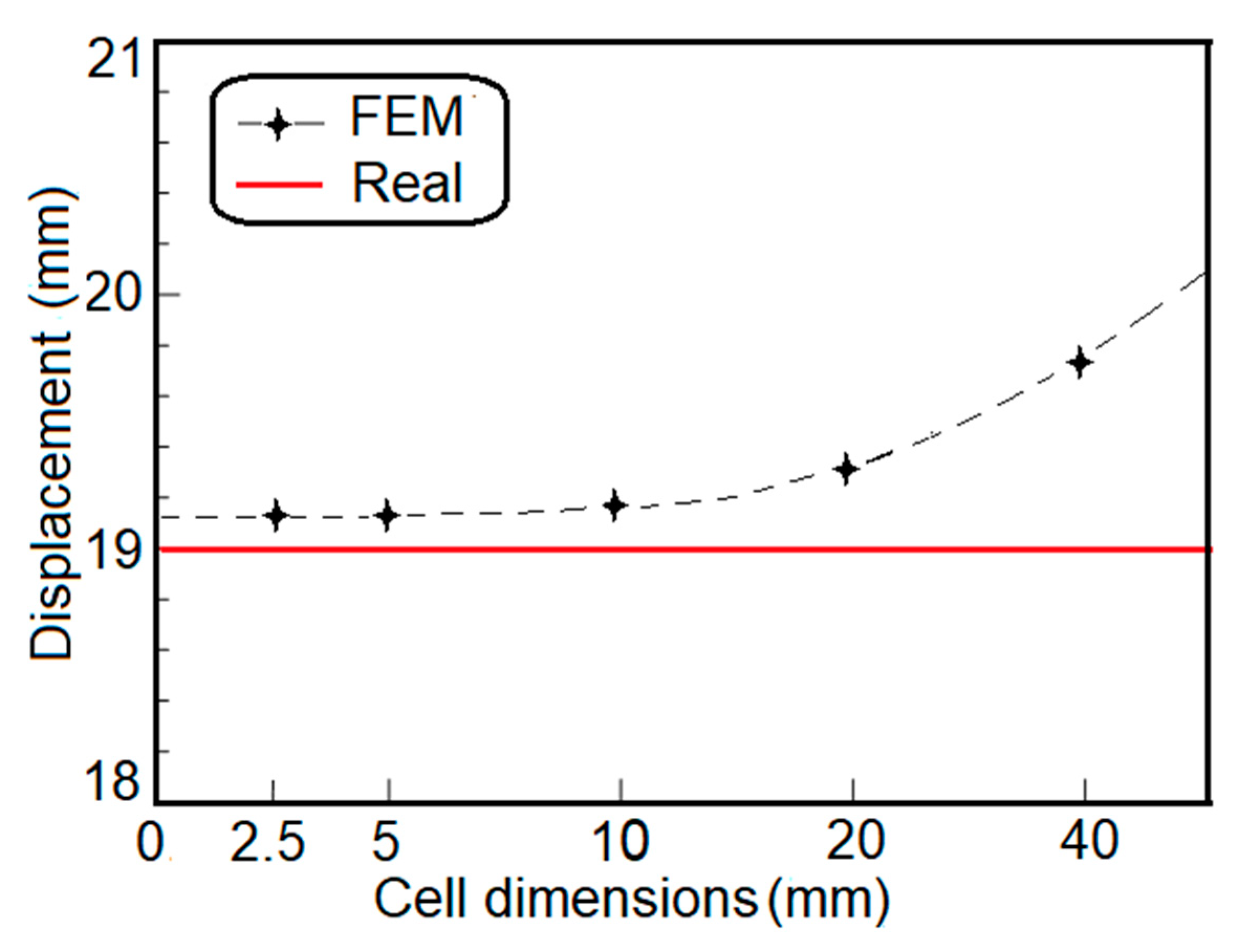
3.2.2. Mesh Sensitivity Study
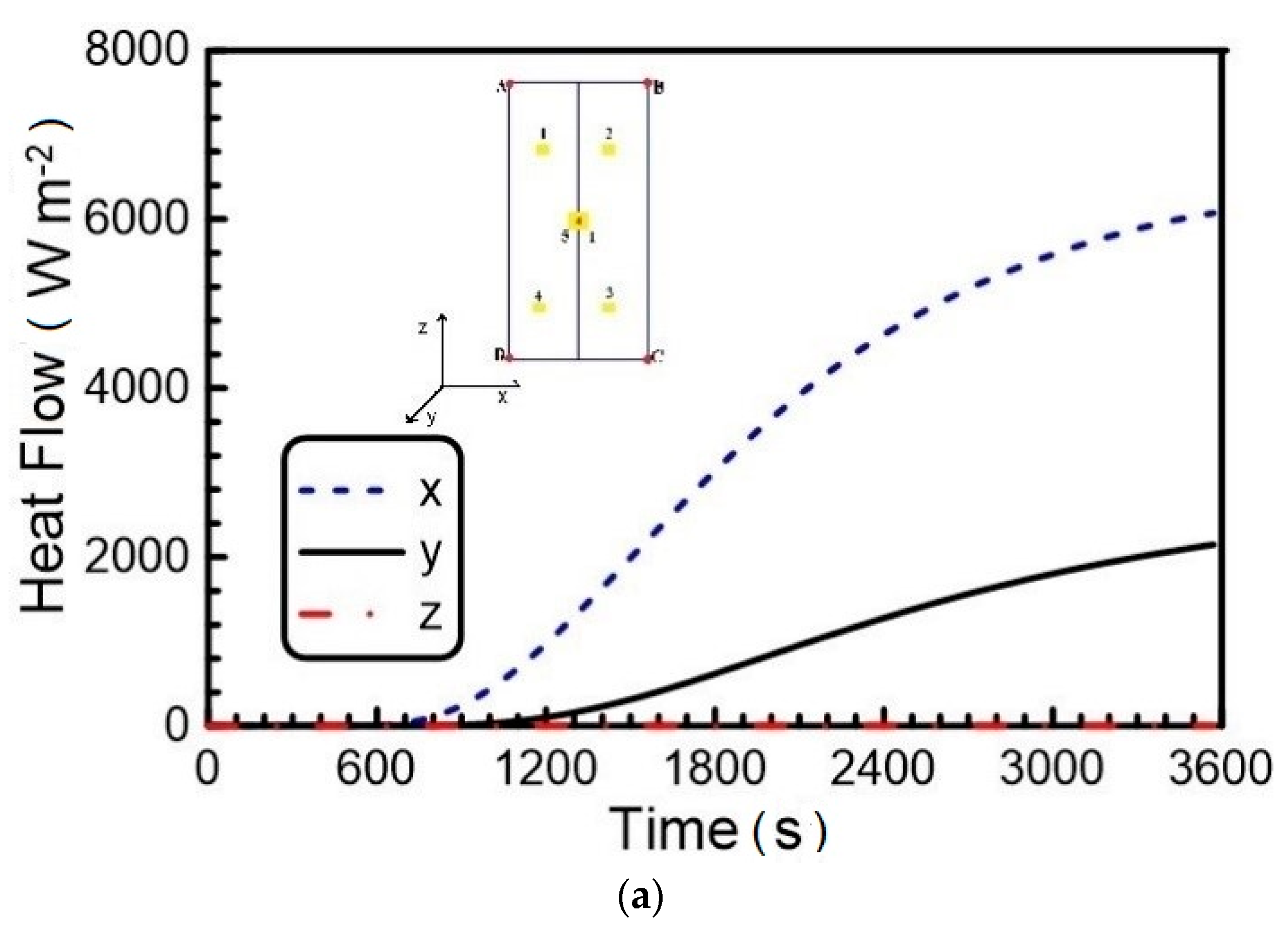
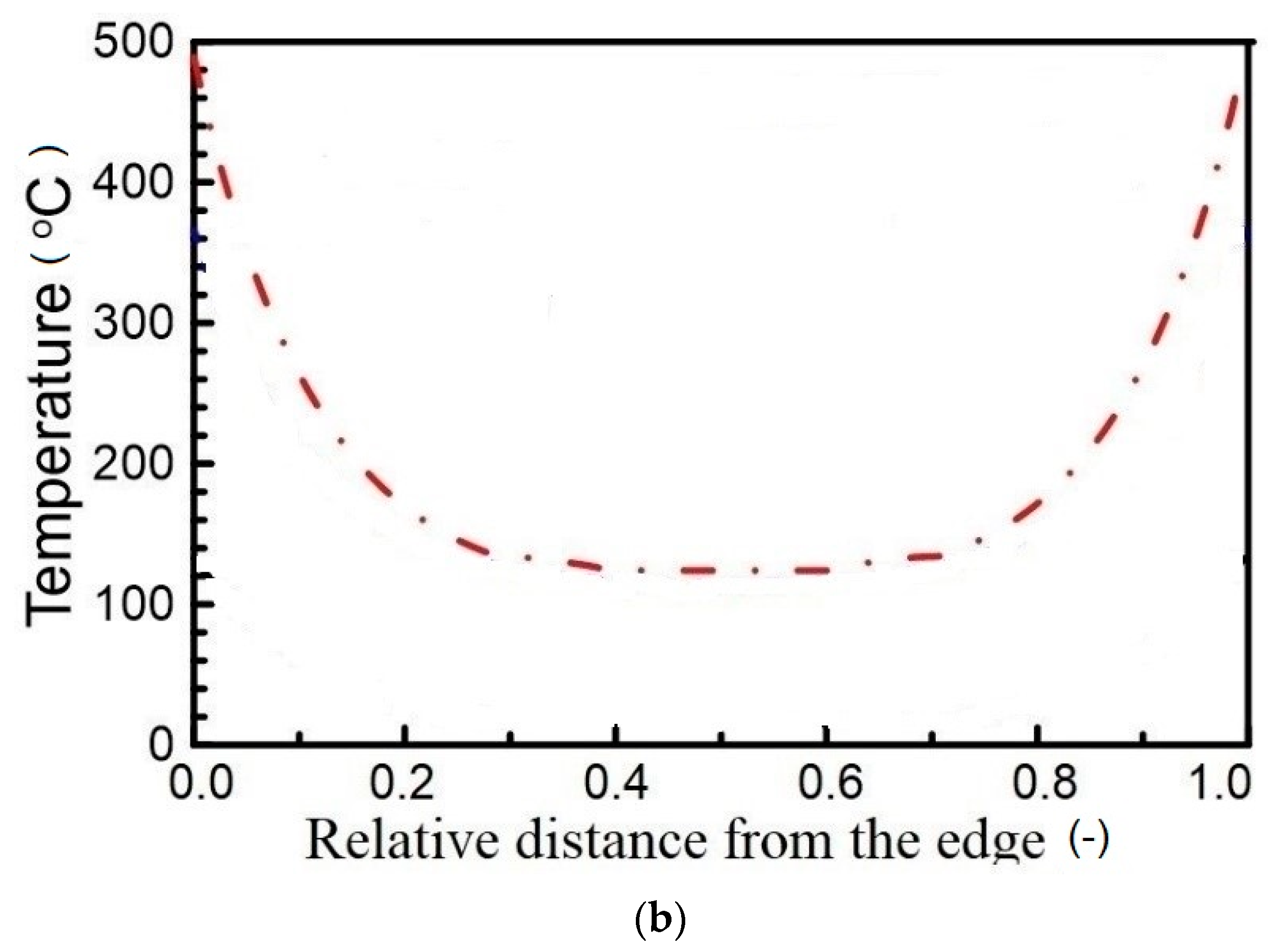
3.2.3. Validation of the Model
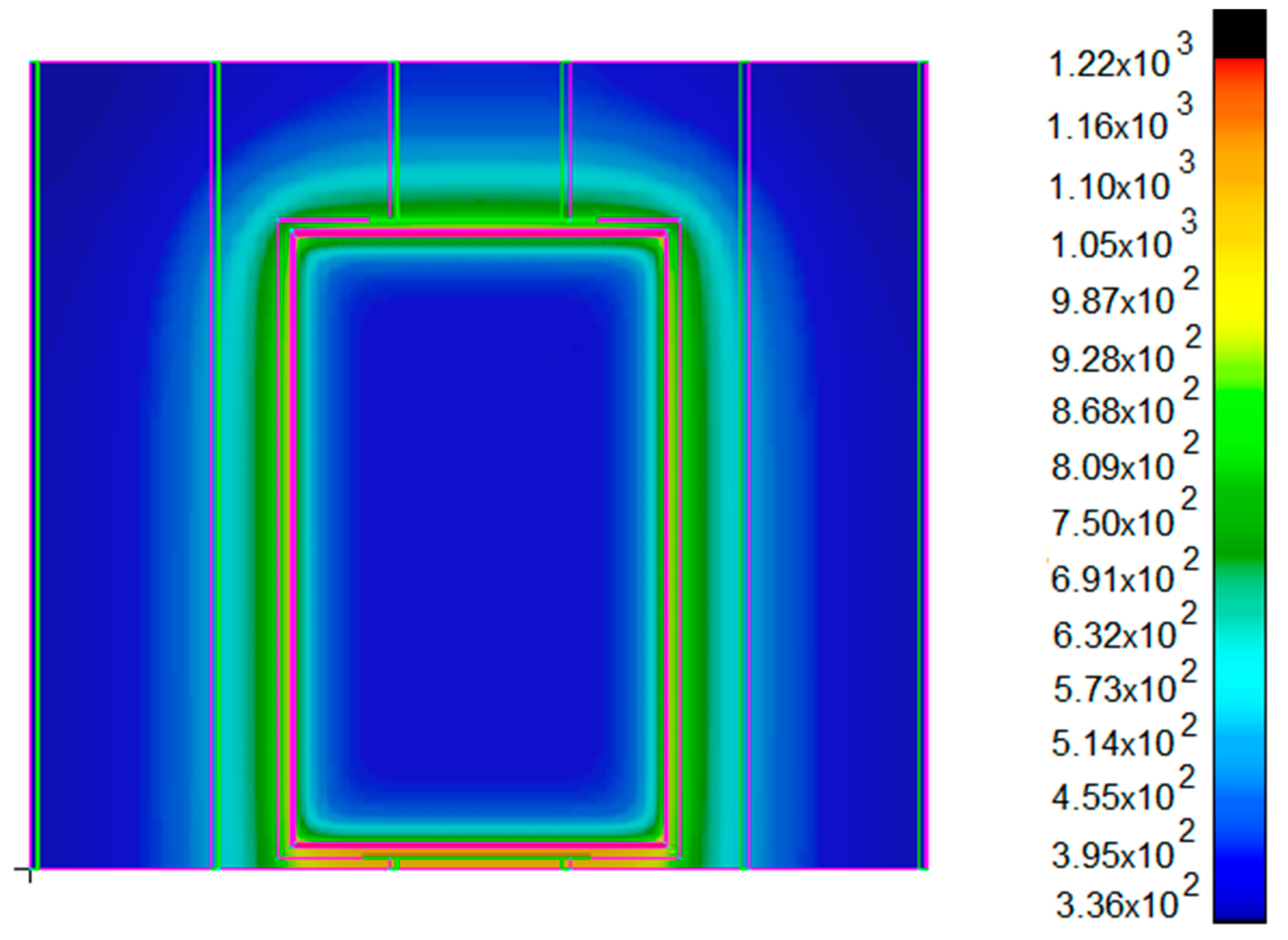
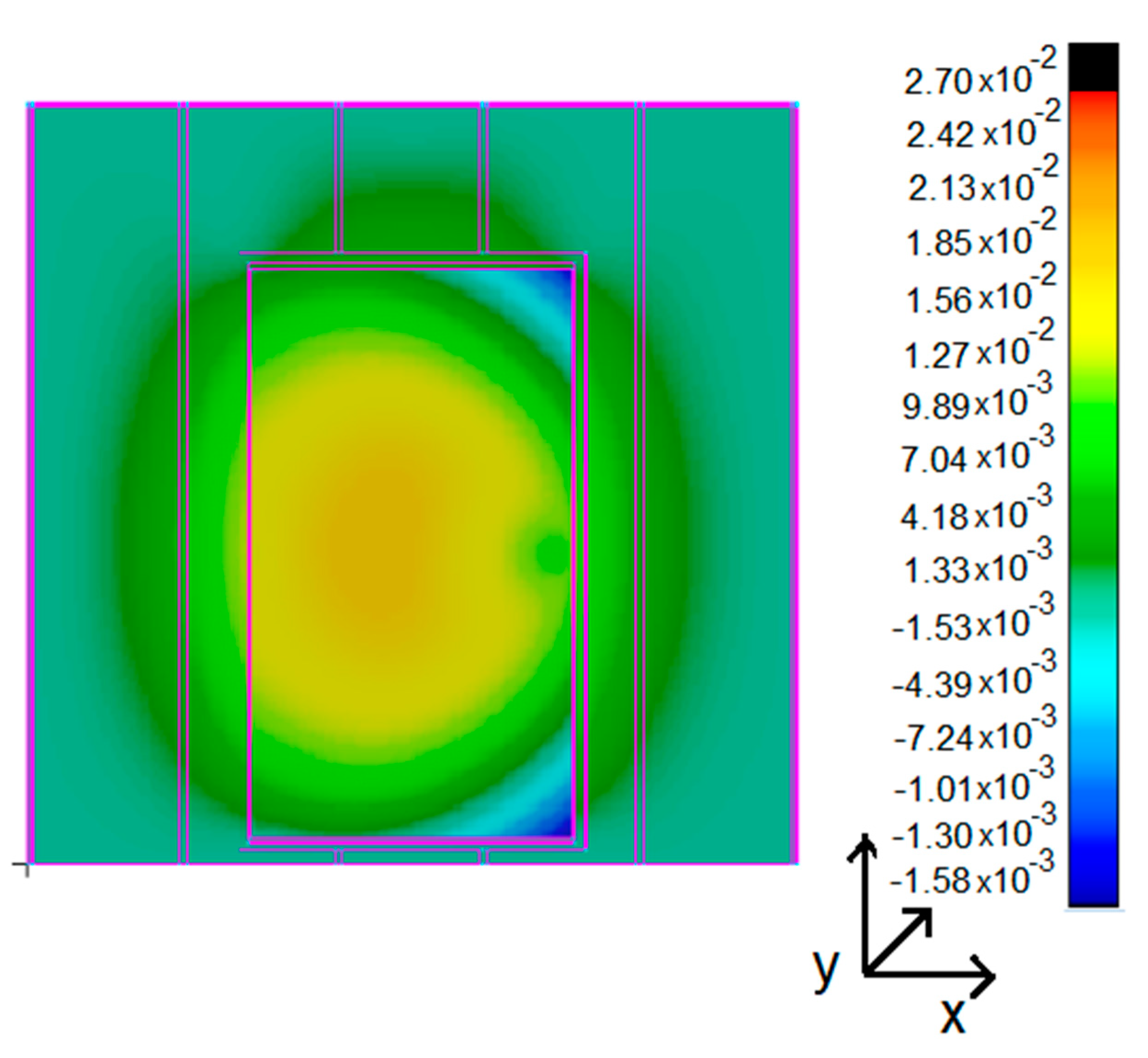
3.2.4. Effect of the Thermal Bridge
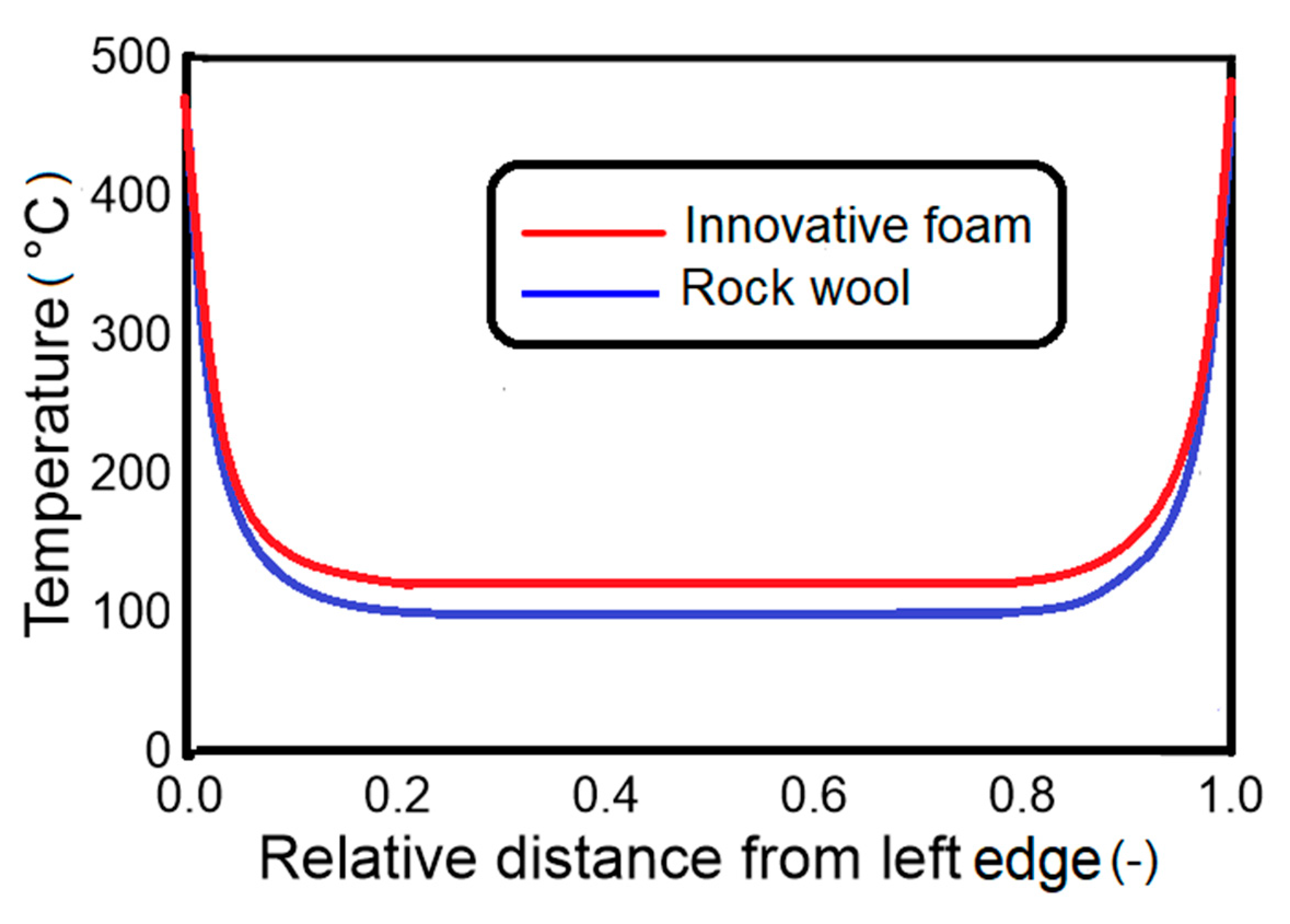
3.2.5. Fire-Door with the Foam
4. Discussion
4.1. Assessment of the FE Model
4.2. Effect of the Construction Geometry and Use of Innovative Insulation Material
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- International Code for Application of Fire Test Procedures (FTP Code); Annex 1, Part 3; International Maritime Organization (IMO): London, UK, 2010.
- Moro, L.; De Bona, F.; Gasparetto, A.; Novak, J.S.; Boscariol, P. Innovative design of fire doors: Computational modeling and experimental validation. Fire Technol. 2017, 53, 1833–1846. [Google Scholar] [CrossRef]
- Asdrubali, F.; D’Alessandro, F.; Schiavoni, S. A review of unconventional sustainable building insulation materials. Sustain. Mater. Technol. 2015, 4, 1–17. [Google Scholar] [CrossRef]
- Papadopoulos, A.M. State of the art in thermal insulation materials and aims for future developments. Energy Build. 2005, 37, 77–86. [Google Scholar] [CrossRef]
- Harrison, P.; Holmes, P.; Bevan, R.; Kamps, K.; Levy, L.; Greim, H. Regulatory risk assessment approaches for synthetic mineral fibres. Regul. Toxicol. Pharm. 2015, 73, 425–441. [Google Scholar] [CrossRef]
- Tang, X.; Yan, X. Acoustic energy absorption properties of fibrous materials: A review. Compos. Part A 2017, 101, 360–380. [Google Scholar] [CrossRef]
- Wang, C.-N.; Torng, J.-H. Experimental study of the absorption characteristics of some porous fibrous materials. Appl. Acoust. 2001, 62, 447–459. [Google Scholar] [CrossRef]
- Caniato, M.; Kyaw Oo D’Amore, G.; Kaspar, J.; Gasparella, A. Sound absorption performance of sustainable foam materials: Application of analytical and numerical tools for the optimization of forecasting models. Appl. Acoust. 2020, 161. [Google Scholar] [CrossRef]
- Boscariol, P.; De Bona, F.; Gasparetto, A.; Moro, L. Thermo-mechanical analysis of a fire door for naval applications. J. Fire Sci. 2015, 33, 142–156. [Google Scholar] [CrossRef]
- Tabaddor, M.; Gandhi, P.D.; Jones, G. Thermo-mechanical analysis of fire doors subjected to a fire endurance test. J. Fire. Prot. Eng. 2009, 19, 51–71. [Google Scholar] [CrossRef]
- Capote, J.A.; Alvear, D.; Abreu, O.; Lazaro, M.; Boffill, Y.; Manzanares, A.; Maamar, M. Assessment of physical phenomena associated to fire doors during standard tests. Fire Technol. 2013, 49, 357–378. [Google Scholar] [CrossRef]
- Teytelman, L. No more excuses for non-reproducible methods. Nature 2018, 560, 411. [Google Scholar] [CrossRef] [PubMed]
- Hugi, E.; Wakili, K.G.; Wullschleger, L. Measured and calculated temperature evolution on the room side of a butted steel door frame subjected to the standard fire of ISO 834. Fire Saf. J. 2009, 44, 808–812. [Google Scholar] [CrossRef]
- D’Amore, G.K.O.; Marinò, A.; Kašpar, J. Numerical modeling of fire resistance test as a tool to design lightweight marine fire doors: A preliminary study. J. Marine Sci. Eng. 2020, 8, 520. [Google Scholar] [CrossRef]
- Eurocode 3: Design of Steel Structures—Part 1–2: General rules—Structural Fire Design; European Committee for Standardization: Brussels, Belgium, 2005.
- Caniato, M.; Travan, A. Method for Recycling Waste Material. European Patent EP 3216825 B1, 28 August 2019. [Google Scholar]
- ASTM. D1621: Standard Test Method for Compressive Properties of Rigid Cellular Plastics; ASTM International: West Conshohocken, PA, USA, 2000. [Google Scholar]
- ASTM. C518: Standard Test Method for Steady-State Thermal Transmission Properties by Means of the Heat Flow Meter Apparatus; ASTM International: West Conshohocken, PA, USA, 2017. [Google Scholar]
- Incropera, F.P.; DeWitt, D.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer, 6th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2007; ISBN 13:978-0471457282. [Google Scholar]
- ISO 10456: Building Materials and Products, Hygrothermal Properties, Tabulated Design Values and Procedures for Determining Declared and Design Hermal Values; International Organization for Standardization: Geneva, Switzerland, 2007.
- ISO 1182: Reaction to Fire Tests for Products—Non-Combustibility Test; International Organization for Standardization: Geneva, Switzerland, 2010.
- Test Report No. 2016CS011021/14; Registro Navale Italiano (RINA): Genoa, Italy, 2017.
- Green, D.W.; Perry, R.H. Section 5: Heat and mass transfer. In Perry’s Chemical Engineers’ Handbook; McGraw-Hill Professional: New York, NY, USA, 2008; pp. 1–83. ISBN 0-07-154212-4. [Google Scholar]
- Dry Air Properties. Available online: https://www.engineeringtoolbox.com/dry-air-properties-d_973.html (accessed on 10 September 2019).
- Eurocode 1: Actions on Structures—Part 1–2: General Actions—Actions on Structures Exposed to Fire; European Committee for Standardization: Brussels, Belgium, 2002.
- Bergman, T.L.; Incropera, F.P.; Dewitt, D.P.; Lavine, A.S. Fundamentals of Heat and Mass Transfer, 7th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011; ISBN 978-0-470-50197-9. [Google Scholar]
- Kwaśniewski, L. Application of grid convergence index in FE computation. Bull. Pol. Acad. Sci. Tech. Sci. 2013, 61, 123–128. [Google Scholar] [CrossRef]
- Mauro, F.; Cerni, P.; Nabergoj, R. Rans calculations on submerged bodies. In Proceedings of the 23rd International Conference Engineering Mechanics, Svratka, Czech Republic, 15–18 May 2017; pp. 630–633. [Google Scholar]
- Richardson, L.F. The Approximate Arithmetical Solution by Finite Differences of Physical Problems Involving Differential Equations, with an Application to the Stresses in a Masonry Dam. Philos. Trans. R. Soc. A 1911, 210, 307–357. [Google Scholar]
- Roache, P.J. Verification and Validation in Computational Science and Engineering; Hermosa Pub: Sierra County, NM, USA, 1998; ISBN 13 978-0913478080. [Google Scholar]
- Batty, W.J.; Probert, S.D.; Lane, J.W. Convection and radiation in layers of low-density fibrous insulants. Appl. Energy 1984, 18, 143–161. [Google Scholar] [CrossRef]
- Dyrbøl, S.; Svendsen, S.; Elmroth, A. Experimental investigation of the effect of natural convection on heat transfer in mineral wool. J. Therm. Envel. Build. Sci. 2002, 26, 153–164. [Google Scholar] [CrossRef]
- Fang, H.; Wong, M.B.; Bai, Y. Heating rate effect on the thermophysical properties of steel in fire. J. Constr. Steel Res. 2017, 128, 611–617. [Google Scholar] [CrossRef]
- Sadiq, H.; Wong, M.B.; Tashan, J.; Al-Mahaidi, R.; Zhao, X.-L. Determination of steel emissivity for the temperature prediction of structural steel members in fire. J. Mater. Civ. Eng. 2013, 25, 167–173. [Google Scholar] [CrossRef]
- MSC 91/22/Add.1 Adoption of the Code on Noise Levels on Board Ships; International Maritime Organization (IMO): London, UK, 2014.
- Borelli, D.; Gaggero, T.; Rizzuto, E.; Schenone, C. Analysis of noise on board a ship during navigation and manoeuvres. Ocean Eng. 2015, 105, 256–269. [Google Scholar] [CrossRef]
- Goujard, B.; Sakout, A.; Valeau, V. Acoustic comfort on board ships: An evaluation based on a questionnaire. Appl. Acoust. 2005, 66, 1063–1073. [Google Scholar] [CrossRef]
- Lind-Nordgren, E.; Göransson, P. Optimising open porous foam for acoustical and vibrational performance. J. Sound Vib. 2010, 329, 753–767. [Google Scholar] [CrossRef]


| Material | Young Modulus E (GPa) | Poisson Ratio ν (-) | Density ρ (kg m−3) | Thermal Conductivity k (W (m K)−1) |
|---|---|---|---|---|
| Carbon steel | 190 | 0.3 | 7800 | 27.29 |
| Rock wool | 1.0 × 10−3 | 0.0 | 150 | 0.035 |
| Foam | 3.4 × 10−3 | 0.0 | 130 | 0.045 |
| Point | T Eurocode Model (°C) | T Self-Consistent Model (°C) | T Measured * (°C) | |E| | U |
|---|---|---|---|---|---|
| 1 | 206.0 | 100.0 | 99.0 | 1.0 | 1.4 |
| 2 | 206.0 | 100.0 | 100.0 | 0.0 | 1.0 |
| 5 | 204.0 | 99.0 | 99.0 | 0.0 | 1.0 |
| 3 | 206.0 | 100.0 | 101.0 | 1.0 | 1.4 |
| 4 | 206.0 | 100.0 | 101.0 | 1.0 | 1.4 |
| Point | d Model (mm) | d Measured * (mm) | |E| | U |
|---|---|---|---|---|
| A | 0.5 | 0.0 | 0.5 | 1.0 |
| B | 19.2 | 19.0 | 0.2 | 1.0 |
| C | 19.2 | ND | / | / |
| D | 0.5 | ND | / | / |
| I | 17.9 | 17.0 | 0.9 | 1.3 |
| Position | T Foam Model (°C) | T Rock Wool Model (°C) | ∆T (°C) |
|---|---|---|---|
| 1 | 120 | 100 | 20 |
| 2 | 120 | 100 | 20 |
| 5 | 119 | 99 | 20 |
| 3 | 120 | 100 | 20 |
| 4 | 120 | 100 | 20 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kyaw Oo D’Amore, G.; Mauro, F.; Marinò, A.; Caniato, M.; Kašpar, J. Towards the Use of Novel Materials in Shipbuilding: Assessing Thermal Performances of Fire-Doors by Self-Consistent Numerical Modelling. Appl. Sci. 2020, 10, 5736. https://doi.org/10.3390/app10175736
Kyaw Oo D’Amore G, Mauro F, Marinò A, Caniato M, Kašpar J. Towards the Use of Novel Materials in Shipbuilding: Assessing Thermal Performances of Fire-Doors by Self-Consistent Numerical Modelling. Applied Sciences. 2020; 10(17):5736. https://doi.org/10.3390/app10175736
Chicago/Turabian StyleKyaw Oo D’Amore, Giada, Francesco Mauro, Alberto Marinò, Marco Caniato, and Jan Kašpar. 2020. "Towards the Use of Novel Materials in Shipbuilding: Assessing Thermal Performances of Fire-Doors by Self-Consistent Numerical Modelling" Applied Sciences 10, no. 17: 5736. https://doi.org/10.3390/app10175736
APA StyleKyaw Oo D’Amore, G., Mauro, F., Marinò, A., Caniato, M., & Kašpar, J. (2020). Towards the Use of Novel Materials in Shipbuilding: Assessing Thermal Performances of Fire-Doors by Self-Consistent Numerical Modelling. Applied Sciences, 10(17), 5736. https://doi.org/10.3390/app10175736






