Abstract
The nonlinearity of a mechanical oscillator may lead to the generation of the macroscopic quantum states, which are useful for precision measurement. Measuring the nonlinearity of a mechanical oscillator becomes important in order to effectively assess its performance. In this paper, we study the electromagnetically induced transparency (EIT) in an optomechanical system with a cubic nonlinear movable mirror. In the presence of the nonlinearity of the movable mirror, we show that the intensity of the output probe field exhibits an asymmetric shape with the transparency peak shifted to a frequency lower than the cavity resonance frequency. This shift can be used to measure the nonlinearity strength of the movable mirror. We also show that the mechanical nonlinearity gives rise to the enhancement of the intensity of the second-order upper sideband generation.
1. Introduction
In recent years, cavity optomechanics, exploring the interaction between optical and mechanical modes via radiation pressure [1], has received considerable attention owing to its possible applications in ultrasensitive force measurement [2] and quantum information processing [3]. It is an outstanding challenge in cooling a macroscopic mechanical oscillator of an optomechanical system to its quantum ground state. With the rapid development of the experimental technologies, it is now possible to reduce the average phonon occupancy number of the macroscopic mechanical oscillator to below unity [4,5]. This enables us to observe numerous quantum optical phenomena in the optomechanical system, such as the mechanical squeezed state below zeropoint fluctuations [6,7,8], entanglement between optical and mechanical resonators [9,10], non-classical correlations between single photons and phonons [11], normal mode splitting [12,13], and electromagnetically induced transparency (EIT) [14,15,16,17]. The EIT has been theoretically studied in the Fabry–Perot-type optomechanical system [14], and has been displayed experimentally in different optomechanical systems, including a toroid microresonator [15], an optomechanical crystal nanocavities [16], and a silica microsphere [17]. The EIT plays an important role in realizing slow light and fast light [18], storage and retrieval of an optical pulse [19], and light switching [20]. The review of the EIT in the optomechanical systems can be seen in [21,22]. Up to date, almost all of the EIT studies in the optomechanical systems have been done with linear mechanical oscillators since the intrinsic nonlinearity of a mechanical oscillator is generally weak, and it can be ignored. However, the recent works have shown that the strong nonlinearity of the mechanical oscillator can be achieved by geometrical and material effects of the mechanical oscillators [23], electrostatic coupling mechanism [23], strong driving [24], and coupling a linear mechanical oscillator to an auxiliary system [25]. Hence, a nonlinear mechanical oscillator has been recently introduced into the optomechanical system. It has been analyzed that a quartic nonlinear mechanical oscillator which includes a quartic term in its potential energy in the optomechnical system can be prepared in a Fock state [26] and a squeezed state [27]. Moreover, a cubic nonlinear mechanical oscillator which includes a cubic term in its potential energy in the optomechnical system can also be prepared in a squeezed state, which is shown in Appendix B in Ref. [27].
On the other hand, when an intense coherent coupling field with frequency and a weak coherent probe field with frequency are combined in an optomechanical system, many sidebands at frequencies (n is an integer representing the sideband order and ) are created in the output field due to the nonlinear optomechanical coupling. It has been shown that the second-order upper sideband generation in the output field is much weaker than the input probe field [28]. The enhancement of the second-order upper sideband generation has potential applications in precise measurements of electrical charges [29] and the effective mass of the mechanical resonator [30]. It has been shown that the enhancement of the second-order upper sideband generation in the optomechanical system can be achieved by using Coulomb-interaction [29], a degenerate parametric amplifier [30], a nonlinear Kerr medium [31], and two-level atoms [32].
As mentioned above, the nonlinearity of a mechanical oscillator can be used to prepare nonclassical mechanical states [26,27]. In order to better assess its performance, different methods have been proposed to measure the nonlinearity strength of the mechanical oscillator [33,34]. It has been proposed that the nonlinearity strength of a mechanical oscillator in an optomechanical system can be estimated by measuring the phase shift of a cavity field after interacting with a nonlinear mechanical oscillator based on a pulsed scheme [34]. In this work, we study the optical response of the optomechanical system with a cubic anharmonic oscillator to a weak coherent probe field. We find that the nonlinearity of the mechanical oscillator gives rise to the asymmetric line shape in the output field at the probe frequency, and the transparency peak is shifted. The shift of the transparency peak can be employed to measure the mechanical nonlinearity strength. We also find that the second-order upper sideband generation is enhanced by the mechanical nonlinearity.
The paper is divided as follows. In Section 2, we present the model, give the equations of the expectation values for the system operators, and obtain the expressions for the output probe field and the second-order upper sideband generation. In Section 3, we discuss the effect of the nonlinearity strength of the mechanical oscillator on the intensity of the output probe field. In Section 4, we analyze how the mechanical nonlinearity modifies the intensity of the second-order upper sideband generation. We briefly summarize the results in Section 5.
2. Model
We consider a Fabry–Perot optical cavity with a moving-end mirror, as depicted in Figure 1. The movable mirror is a cubic anharmonic oscillator. An intense coupling field with frequency and a weak probe field with frequency are sent into the optical cavity through the left fixed mirror.

Figure 1.
Schematic diagram of the studied system. A coupling field with frequency and a probe field with frequency enter the cavity through the left fixed mirror. The right movable mirror is a cubic anharmonic oscillator.
We assume that a single-mode cavity field having a resonant frequency of is generated inside the optical cavity. The moving mirror with effective mass m and resonance frequency makes one-dimensional motion along the cavity axis due to the radiation pressure force exerted by the photons within the cavity. By moving to a rotating frame at the coupling frequency , the Hamiltonian of the system reads
where c and denote the annihilation and creation operators of the cavity mode, satisfying the commutation relation , g is the optomechanical coupling constant, q and p are the displacement and momentum operators of the movable mirror, obeying the relation . The is the probe tuning from the coupling field. The amplitudes and of the coupling and probe fields are determined by their respective powers and by and . The is the cavity coupling parameter defined by , where is the total cavity decay rate, and are the photon loss rates due to the intrinsic dissipation of the cavity and the transmission of the left fixed mirror, respectively. In Equation (1), the first term gives the energy of the cavity field, the second term describes the coupling between the optical cavity field and the movable mirror, the third term is the energy of the movable mirror which is modeled as a cubic anharmonic oscillator, the four terms give the interaction between the coupling field and the cavity field, the last term describes the interaction between the probe field and the cavity field. The has two terms, the first term corresponds to the energy of the simple harmonic oscillator, the second term proportional to the third order of the mechanical displacement q is the potential energy generated by the mechanical nonlinearity, and the parameter represents the nonlinearity strength of the mechanical oscillator. The cubic potential is assumed to be much smaller than the quadratic potential , thus the cubic potential is a small perturbation.
A cubic anharmonic oscillator is a typical example of the simplest perturbation to the harmonic oscillator in quantum mechanics [35]. Different aspects of a cubic anharmonic oscillator have been investigated, including the behavior of the resonance eigenvalues of a cubic anharmonic oscillator with a real nonlinearity strength [36], the periodic motion of a cubic anharmonic oscillator with a real parameter [37], the real spectrum of a cubic anharmonic oscillator with a complex nonlinearity strength [38], the ground-state energy of a cubic anharmonic oscillator with a complex parameter [39,40], the eigenenergies and eigenfunctions of a cubic anharmonic oscillator with a real parameter or a complex parameter [41], and the Stark effect in a cubic anharmonic oscillator with a real parameter or a complex parameter [42]. For simplicity, here we consider the case that the parameter is real and positive.
The equations for the time evolutions of the expectation values of the system operators can be found from the Heisenberg equations of motion, which are given by
where we have included the optical and mechanical dissipations, we have used the factorization assumption , and is the mechanical damping rate. It is worth mentioning that this factorization assumption is not valid when both the coupling and probe fields are weak [43,44,45].
When the power of the probe field is much smaller than that of the coupling field, in the limit where , the steady state solution of Equation (2) can be truncated to second order in
where , and () indicate the nth-order upper and lower sidebands, respectively. In addition, and () correspond to the nth-order anti-Stokes and Stokes fields, respectively. The solution has five components oscillating at the frequencies , , , , , respectively. Combining Equation (3) with Equation (2), and equating coefficients belonging to the same frequency, we find the amplitudes of the components oscillating at the frequency of the coupling field
the amplitudes of the first-order sideband generations
and the amplitude of the second-order anti-Stokes field
where is the displacement-dependent effective cavity detuning, , . The and represent the steady-state values of the displacement and momentum of the movable mirror, respectively. It is seen that the steady-state displacement of the mechanical oscillator is related to the mechanical nonlinearity . Moreover, we note that the amplitudes and of the first-order and second-order anti-Stokes fields depend on the mechanical nonlinearity strength and the steady-state displacement of the movable mirror. In addition, the amplitude of the second-order anti-Stokes field is dependent on the amplitudes and of the first-order anti-Stokes and Stokes fields and the amplitude of the mechanical excitation.
Furthermore, the output field is connected with the cavity field and the two input fields via the standard input–output relation [15,46], which yields
The output field consists of five components
where , , , , are the amplitudes of the five components of the output field, respectively, and their frequencies are , , and , , , respectively. From Equations (7) and (8), we obtain
Next, the output probe field at frequency is rescaled by , which gives
Without the coupling field (), is given by
which is independent of the oscillation of the movable mirror. Moreover, the outgoing field from the cavity at the second-order upper sideband is renormalized as
Without the coupling field (), , no second-order upper sideband is generated.
3. The Effect of the Mechanical Nonlinearity on the EIT
In this section, we discuss the influence of the nonlinearity strength of the movable mirror on the intensity of the output probe field at frequency .
The parameters we use are from the experimental work focusing on slowing, advancing, and switching of the weak probe field [18]. The frequency of the coupling field is GHz. The cavity decay rate is kHz. The effective mass of the movable mirror is pg, the mechanical frequency MHz, and the mechanical damping rate is Hz. The optomechanical coupling strength is Hz/m. The cavity field is driven by a red-sideband coupling field with . We consider the critically coupled cavity with . The power of the coupling field is W. For the nonlinearity strength N/m, the cubic potential energy is much smaller than the quadratic potential energy since .
The intensity of the output probe field is plotted against the normalized probe detuning for different values of the nonlinearity strength in Figure 2. In the absence of the coupling field (), it is seen that the intensity curve exhibits an inverted Lorentzian shape, and the value of near is close to zero, thus the input weak probe field is almost completely absorbed by the optomechanical system. In the presence of the coupling field (), for the linear mechanical oscillator (), the intensity curve is symmetric, it has an EIT peak near , and the value of near is close to unity, thus the weak probe field is almost totally reflected to the left-hand output port. This is the result of the destructive interference between the input probe field and the first-order anti-Stokes field produced by the interaction of the strong coupling field with the linear mechanical oscillator. For the nonlinear mechanical oscillator (), the intensity curve becomes asymmetric, and the transparency peak is shifted to the left, i.e., the output probe frequency is lower than the cavity resonance frequency . Increasing the nonlinearity strength will increase the shift of the transparency peak. The dependence of the transparency peak position of the output probe field on the mechanical nonlinearity strength is shown in Figure 3. From Figure 3, it is seen that the mechanical nonlinearity strength can be easily probed via measuring the transparency peak position of the output probe field. Moreover, in Figure 2, it is seen that the mechanical nonlinearity strength can broaden the full width at half maximum (FWHM) of the transparency peak. In the absence of the mechanical nonlinearity (), the FWHM of the transparency peak is about 0.1 . In the presence of the mechanical nonlinearity with N/m, the FWHM of the transparency peak is about 0.1761 , which is less than the shift of about 0.257 of the transparency peak position. Therefore, when the linewidth of the transparency peak is considered, it is still possible to estimate the mechanical nonlinearity strength by detecting the transparency peak position of the output probe field.
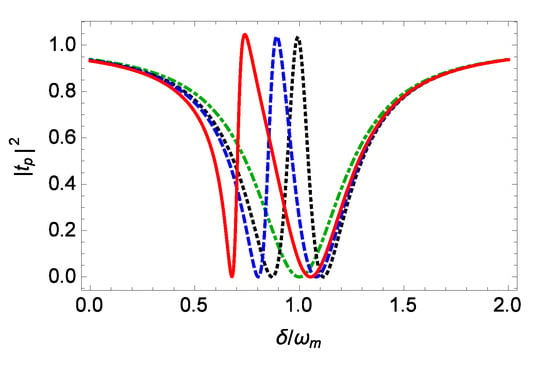
Figure 2.
The intensity of the output probe field versus the normalized probe detuning for different values of the nonlinearity strength N/m. The black dotted, blue dashed, and red solid lines correspond to , N/m, N/m, respectively. The dot-dashed green line is the intensity without the coupling laser.
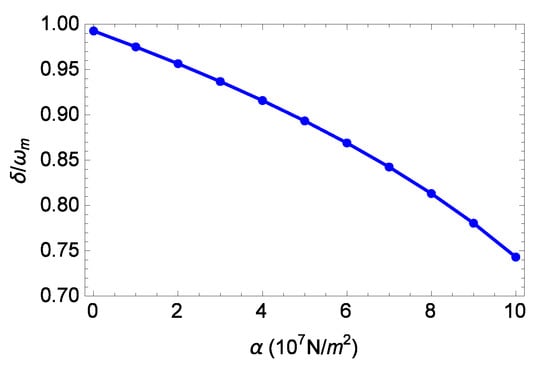
Figure 3.
The transparency peak position of the output probe field as a function of the nonlinearity strength .
It is worth noting that the optomechanical response of a cubic nonlinear mechanical oscillator is different from that of a quartic nonlinear mechanical oscillator whose potential energy includes a term with N/m in the experimental paper [18]. It has been shown that a quartic nonlinear mechanical oscillator could also lead to the shift of the transparency peak of a weak probe field, but the transmission of the probe field exhibits the bistable behavior, which indicates that there are two values of the intensity of the output probe field for a given probe detuning [18].
4. The Enhancement of the Second-Order Upper Sideband Generation by the Mechanical Nonlinearity
In this section, we discuss the influence of the mechanical nonlinearity on the second-order upper sideband generation at frequency generated by the four wave-mixing process. In the four wave-mixing process, two photons at frequency are absorbed and one photon at frequency is emitted.
The intensity of the second-order upper sideband generation in the output field is plotted against the normalized probe detuning for different values of the nonlinearity strength when the power of the probe field is in Figure 4. Without the mechanical nonlinearity (), a dip is observed near in the intensity of the second-order upper sideband generation. The value of at the dip near is about zero. For , we have mentioned above that the value of at the transparency peak near in the first-order upper sideband generation in Figure 2 is about unity. Hence, when the input probe field is completely reflected to the left-hand output port, the second-order anti-Stokes field vanishes. This is consistent with the result in [28]. Moreover, as the nonlinearity strength is increased, the maximum intensity of the second-order upper sideband generation is increased. When , N/m, the maximum values of are about 0.0063, 0.1003, respectively. Thus, the intensity of the second-order upper sideband generation with the mechanical nonlinearity N/m is enhanced by a factor of about 15.9 compared to that without the mechanical nonlinearity . In addition, the intensity of the second-order upper sideband generation can be largely enhanced by further increasing the mechanical nonlinearity strength . For example, for N/m, the cubic potential energy is still much smaller than the quadratic potential energy due to , the maximum value of is about 0.4886. Hence, the intensity of the second-order upper sideband generation with the mechanical nonlinearity N/m is enhanced by a factor of about 77.5 compared to that without the mechanical nonlinearity . Therefore, the mechanical nonlinearity can enhance the intensity of the second-order upper sideband generation. This is because the mechanical nonlinearity enhances the four-wave mixing process in the optical cavity.
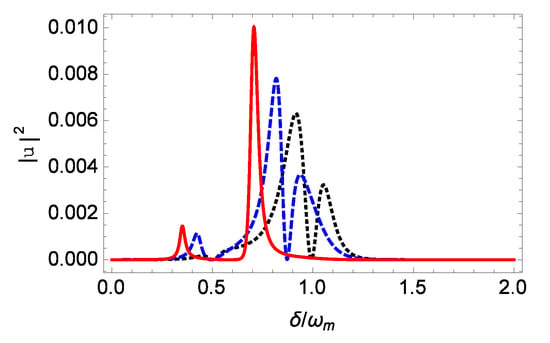
Figure 4.
The intensity of the second-order upper sideband generation in the output field versus the normalized probe detuning for different values of the nonlinearity strength N/m when . The other parameters are the same as those in Figure 2. The black dotted, blue dashed, and red solid lines correspond to , N/m, N/m, respectively. Here, the red solid line for N/m has been divided by 10.
5. Conclusions
We have investigated that the propagation of a weak probe field in an optomechanical system with a cubic anharmonic oscillator. When the optomechanical cavity is pumped by a strong red-sideband laser, the nonlinearity of the movable mirror causes an asymmetric line shape to appear in the intensity of the output probe field. We show that the nonlinearity strength of the movable mirror can be detected by measuring the shift of the transparency peak of the output probe field. We also show that the mechanical nonlinearity results in the enhancement of the intensity of the second-order upper sideband generation. Thus, compared to the optomechanical system with a mechanical harmonic oscillator, the optomechanical system with a cubic anharmonic oscillator offers more efficient conversion from the incident lights (the coupling light and the probe light) to the second-order upper sideband generation; this is useful in frequency conversion in all-optical communication networks. Future work will extend these studies to the single-photon strong-coupling regime [47,48], where the nonlinear coupling between the optical cavity field and the movable mirror could not be neglected.
Finally, we briefly discuss the possibility of the generation of a strong cubic mechanical nonlinearity. It has been reported that a cubic anharmonic oscillator can be realized by coupling a linear mechanical oscillator to a three-level auxiliary via the linear interaction [25], where is the interaction strength, x is the dimensionless displacement operator of the mechanical oscillator and is related to the mechanical displacement operator q via , and V is the operator of the three-level auxiliary. The auxiliary system has a diagonal Hamiltonian , whose three energy levels are given by , , and is the energy difference between adjacent energy levels. By placing the auxiliary in the eigenstate corresponding to the energy level , choosing the appropriate operator V, a cubic potential in the form of could be created. By choosing GHz, MHz, , we have . By using , we find that the cubic nonlinearity strength is about N/m, which is close to the parameter we use in the numerical calculations.
Author Contributions
Conceptualization, S.H. and A.C.; methodology, S.H. and A.C.; software, S.H. and H.H.; formal analysis, S.H. and H.H.; writing—original draft preparation, S.H. and H.H.; writing—review and editing, S.H., H.H., and A.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Science Foundation of Zhejiang Sci-Tech University (Grant Nos. 18062121-Y, 17062071-Y), by the National Natural Science Foundation of China (Grant Nos. 11775190,91636108), and by the Zhejiang Provincial Natural Science Foundation of China (Grant No. LZ20A040002).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Aspelmeyer, M.; Kippenberg, T.J.; Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 2014, 86, 1391. [Google Scholar] [CrossRef]
- Gavartin, E.; Verlot, P.; Kippenberg, T.J. A hybrid on-chip opto-nanomechanical transducer for ultra-sensitive force measurements. Nat. Nanotechnol. 2012, 7, 509–514. [Google Scholar] [PubMed]
- Stannigel, K.; Rabl, P.; Sørensen, A.S.; Zoller, P.; Lukin, M.D. Optomechanical transducers for long-distance quantum communication. Phys. Rev. Lett. 2010, 105, 220501. [Google Scholar] [CrossRef] [PubMed]
- Teufel, J.D.; Donner, T.; Li, D.; Harlow, J.W.; Allman, M.S.; Cicak, K.; Sirois, A.J.; Whittaker, J.D.; Lehnert, K.W.; Simmonds, R.W. Sideband cooling of micromechanical motion to the quantum ground state. Nature (London) 2011, 475, 359–363. [Google Scholar] [CrossRef]
- Chan, J.; Alegre, T.P.M.; Safavi-Naeini, A.H.; Hill, J.T.; Krause, A.; Gröblacher, S.; Aspelmeyer, M.; Painter, O. Laser cooling of a nanomechanical oscillator into its quantum ground state. Nature (London) 2011, 478, 89–92. [Google Scholar] [CrossRef]
- Jähne, K.; Genes, C.; Hammerer, K.; Wallquist, M.; Polzik, E.S.; Zoller, P. Cavity-assisted squeezing of a mechanical oscillator. Phys. Rev. A 2009, 79, 063819. [Google Scholar] [CrossRef]
- Agarwal, G.S.; Huang, S. Strong mechanical squeezing and its detection. Phys. Rev. A 2016, 93, 043844. [Google Scholar] [CrossRef]
- Wollman, E.E.; Lei, C.U.; Weinstein, A.J.; Suh, J.; Kronwald, A.; Marquardt, F.; Clerk, A.A.; Schwab, K.C. Quantum squeezing of motion in a mechanical resonator. Science 2015, 349, 952–955. [Google Scholar] [CrossRef]
- Paternostro, M.; Vitali, D.; Gigan, S.; Kim, M.S.; Brukner, C.; Eisert, J.; Aspelmeyer, M. Creating and probing multipartite macroscopic entanglement with light. Phys. Rev. Lett. 2007, 99, 250401. [Google Scholar] [CrossRef]
- Palomaki, T.A.; Teufel, J.D.; Simmonds, R.W.; Lehnert, K.W. Entangling mechanical motion with microwave fields. Science 2013, 342, 710–713. [Google Scholar] [CrossRef]
- Riedinger, R.; Hong, S.; Norte, R.A.; Slater, J.A.; Shang, J.; Krause, A.G.; Anant, V.; Aspelmeyer, M.; Gröblacher, S. Nonclassical correlations between single photons and phonons from a mechanical oscillator. Nature (London) 2016, 530, 313–316. [Google Scholar] [CrossRef] [PubMed]
- Gröblacher, S.; Hammerer, K.; Vanner, M.R.; Aspelmeyer, M. Observation of strong coupling between a micromechanical resonator and an optical cavity field. Nature (London) 2009, 460, 724–727. [Google Scholar] [CrossRef] [PubMed]
- Dobrindt, J.M.; Wilson-Rae, I.; Kippenberg, T.J. Parametric normal-mode splitting in cavity optomechanics. Phys. Rev. Lett. 2008, 101, 263602. [Google Scholar] [CrossRef] [PubMed]
- Agarwal, G.S.; Huang, S. Electromagnetically induced transparency in mechanical effects of light. Phys. Rev. A 2010, 81, 041803(R). [Google Scholar] [CrossRef]
- Weis, S.; Rivière, R.; Deléglise, S.; Gavartin, E.; Arcizet, O.; Schliesser, A.; Kippenberg, T.J. Optomechanically induced transparency. Science 2010, 300, 1520–1523. [Google Scholar] [CrossRef]
- Safavi-Naeini, A.H.; Mayer Alegre, T.P.; Chan, J.; Eichenfield, M.; Winger, M.; Lin, Q.; Hill, J.T.; Chang, D.E.; Painter, O. Electromagnetically induced transparency and slow light with optomechanics. Nature 2011, 472, 69–73. [Google Scholar] [CrossRef]
- Dong, C.; Fiore, V.; Kuzyk, M.C.; Wang, H. Transient optomechanically induced transparency in a silica microsphere. Phys. Rev. A 2013, 87, 055802. [Google Scholar] [CrossRef]
- Zhou, X.; Hocke, F.; Schliesser, A.; Marx, A.; Huebl, H.; Gross, R.; Kippenberg, T.J. Slowing, advancing and switching of microwave signals using circuit nanoelectromechanics. Nat. Phys. 2013, 9, 179–184. [Google Scholar] [CrossRef]
- Fiore, V.; Yang, Y.; Kuzyk, M.C.; Barbour, R.; Tian, L.; Wang, H. Storing optical information as a mechanical excitation in a silica optomechanical resonator. Phys. Rev. Lett. 2011, 107, 133601. [Google Scholar] [CrossRef]
- Agarwal, G.S.; Huang, S. Optomechanical systems as single-photon routers. Phys. Rev. A 2012, 85, 021801(R). [Google Scholar] [CrossRef]
- Liu, Y.C.; Li, B.B.; Xiao, Y.F. Electromagnetically induced transparency in optical microcavities. Nanophotonics 2017, 6, 789–811. [Google Scholar] [CrossRef]
- Xiong, H.; Wu, Y. Fundamentals and applications of optomechanically induced transparency. Appl. Phys. Rev. 2018, 5, 031305. [Google Scholar] [CrossRef]
- Kaajakari, V.; Mattila, T.; Oja, A.; Seppä, H. Nonlinear limits for single-crystal silicon microresonators. J. Microelectromech. Syst. 2004, 13, 715–724. [Google Scholar] [CrossRef]
- Huang, P.; Zhou, J.W.; Zhang, L.; Hou, D.; Lin, S.C.; Deng, W.; Meng, C.; Duan, C.K.; Ju, C.Y.; Zheng, X.; et al. Generating giant and tunable nonlinearity in a macroscopic mechanical resonator from a single chemical bond. Nat. Commun. 2016, 7, 11517. [Google Scholar] [CrossRef] [PubMed]
- Jacobs, K.; Landahl, A.J. Engineering giant nonlinearities in quantum nanosystems. Phys. Rev. Lett. 2009, 103, 067201. [Google Scholar] [CrossRef]
- Rips, S.; Kiffner, M.; Wilson-Rae, I.; Hartmann, M.J. Steady-state negative Wigner functions of nonlinear nanomechanical oscillators. New J. Phys. 2012, 14, 023042. [Google Scholar] [CrossRef]
- Lü, X.Y.; Liao, J.Q.; Tian, L.; Nori, F. Steady-state mechanical squeezing in an optomechanical system via Duffing nonlinearity. Phys. Rev. A 2015, 91, 013834. [Google Scholar] [CrossRef]
- Xiong, H.; Si, L.G.; Zheng, A.S.; Yang, X.; Wu, Y. Higher-order sidebands in optomechanically induced transparency. Phys. Rev. A 2012, 86, 013815. [Google Scholar] [CrossRef]
- Kong, C.; Xiong, H.; Wu, Y. Coulomb-interaction-dependent effect of high-order sideband generation in an optomechanical system. Phys. Rev. A 2017, 95, 033820. [Google Scholar] [CrossRef]
- Liu, S.; Liu, B.; Wang, J.; Sun, T.; Yang, W. Realization of a highly sensitive mass sensor in a quadratically coupled optomechanical system. Phys. Rev. A 2019, 99, 033822. [Google Scholar] [CrossRef]
- Li, J.; Li, J.; Xiao, Q.; Wu, Y. Giant enhancement of optical high-order sideband generation and their control in a dimer of two cavities with gain and loss. Phys. Rev. A 2016, 93, 063814. [Google Scholar] [CrossRef]
- Liu, Z.X.; Xiong, H.; Wu, Y. Generation and amplification of a high-order sideband induced by two-level atoms in a hybrid optomechanical system. Phys. Rev. A 2018, 97, 013801. [Google Scholar] [CrossRef]
- Paris, M.G.A.; Genoni, M.G.; Shammah, N.; Teklu, B. Quantifying the nonlinearity of a quantum oscillator. Phys. Rev. A 2014, 90, 012104. [Google Scholar] [CrossRef]
- Latmiral, L.; Armata, F.; Genoni, M.G.; Pikovski, I.; Kim, M.S. Probing anharmonicity of a quantum oscillator in an optomechanical cavity. Phys. Rev. A 2016, 93, 052306. [Google Scholar] [CrossRef]
- Davydov, A. Quantum Mechanics; Pergamon: New York, NY, USA, 1965. [Google Scholar]
- Alvarez, G. Coupling-constant behavior of the resonances of the cubic anharmonic oscillator. Phys. Rev. A 1988, 37, 4079. [Google Scholar] [CrossRef] [PubMed]
- Cveticanin, L.; Zukovic, M.; Mester, G.; Biro, I.; Sarosi, J. Oscillators with symmetric and asymmetric quadratic nonlinearity. Acta Mech. 2016, 227, 1727–1742. [Google Scholar] [CrossRef]
- Bender, C.M.; Boettcher, S. Real spectra in non-Hermitian Hamiltonians having PT symmetry. Phys. Rev. Lett. 1998, 80, 5243. [Google Scholar] [CrossRef]
- Bender, C.M.; Dunne, G.V. Large-order perturbation theory for a non-Hermitian PT-symmetric Hamiltonian. J. Math. Phys. 1999, 40, 4616–4621. [Google Scholar] [CrossRef]
- Bender, C.M.; Weniger, E.J. Numerical evidence that the perturbation expansion for a non-Hermitian PT-symmetric Hamiltonian is Stieltjes. J. Math. Phys. 2001, 42, 2167–2183. [Google Scholar] [CrossRef]
- Ferreira, E.M.; Sesma, J. Global solution of the cubic oscillator. J. Phys. A Math. Theor. 2014, 47, 415306. [Google Scholar] [CrossRef]
- Mera, H.; Pedersen, T.G.; Nikolić, B.K. Nonperturbative quantum physics from low-order perturbation theory. Phys. Rev. Lett. 2015, 115, 143001. [Google Scholar] [CrossRef] [PubMed]
- Kronwald, A.; Marquardt, F. Optomechanically induced transparency in the nonlinear quantum regime. Phys. Rev. Lett. 2013, 111, 133601. [Google Scholar] [CrossRef] [PubMed]
- Lemonde, M.A.; Didier, N.; Clerk, A.A. Nonlinear interaction effects in a strongly driven optomechanical Cavity. Phys. Rev. Lett. 2013, 111, 053602. [Google Scholar] [CrossRef] [PubMed]
- Børkje, K.; Nunnenkamp, A.; Teufel, J.D.; Girvin, S.M. Signatures of nonlinear cavity optomechanics in the weak coupling regime. Phys. Rev. Lett. 2013, 111, 053603. [Google Scholar] [CrossRef] [PubMed]
- Walls, D.F.; Milburn, G.J. Cavity modes. In Quantum Optics; Springer: Berlin, Germany, 1998; pp. 121–124. [Google Scholar]
- Rabl, P. Photon blockade effect in optomechanical systems. Phys. Rev. Lett. 2011, 107, 063601. [Google Scholar] [CrossRef]
- Nunnenkamp, A.; Børkje, K.; Girvin, S.M. Single-photon optomechanics. Phys. Rev. Lett. 2011, 107, 063602. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).