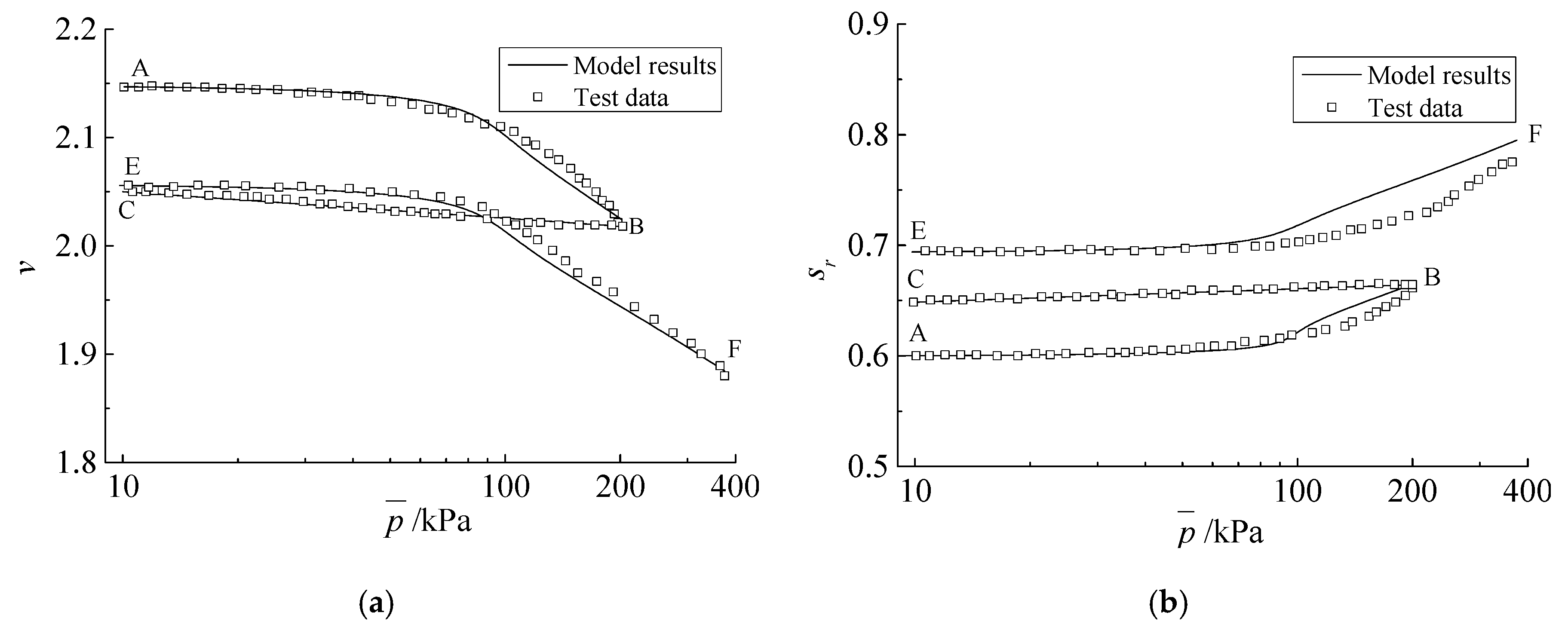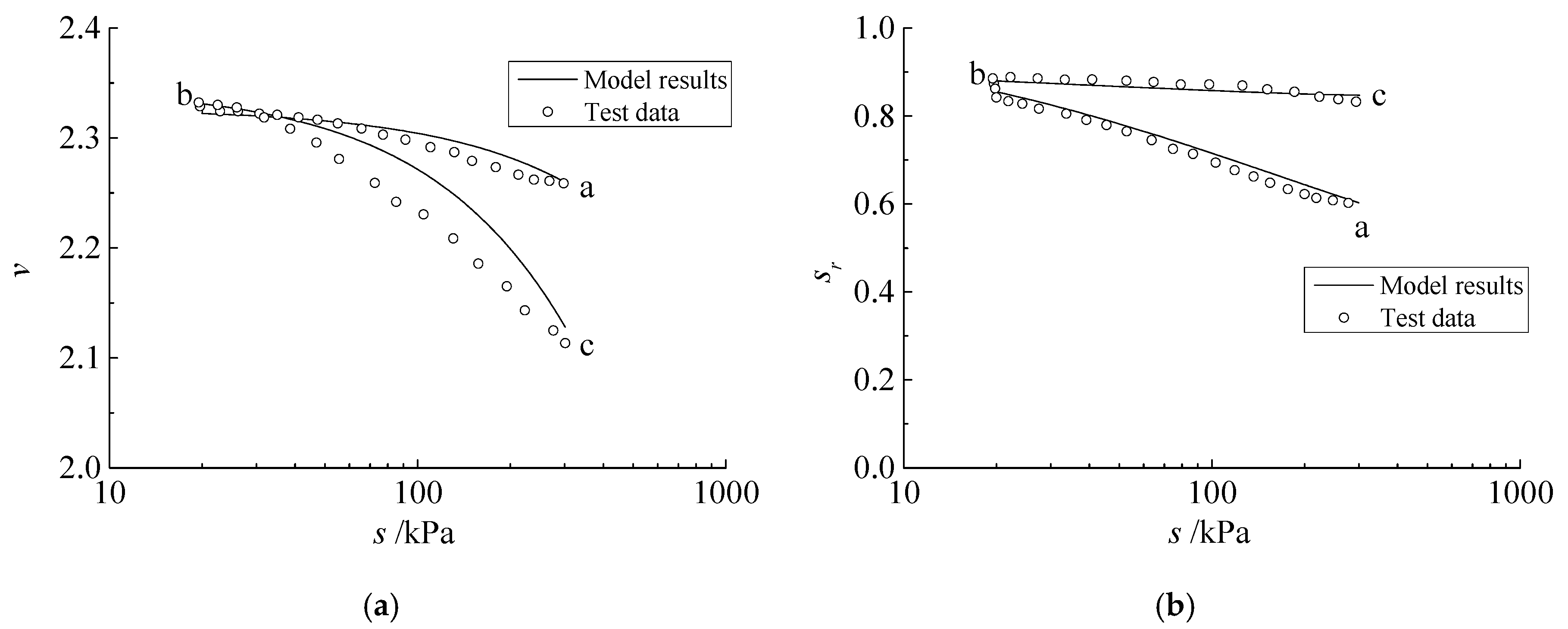Modeling the Hydro-Mechanical Coupling Behavior of Unsaturated Geotechnical Materials Based on Non-Equilibrium Thermodynamic Theory

Abstract

A new hydro-mechanical model for unsaturated geotechnical materials based on the non-equilibrium thermodynamic theory is presented in this paper. Common concepts, such as yield criterion and flow rules, are not involved in the constitutive relationships, and are replaced with the thermodynamic concepts of granular temperature, granular entropy, migration coefficients, and energy functions. The dissipation system and the migration coefficient relationships are theoretically determined, and the constitutive relations of non-elastic deformation and granular temperature are obtained by dissipation relations and thermodynamic identity. Thus, the relationship between dissipation mechanism and macro mechanical behavior can be established by migration coefficients and energy functions. The model can reflect the complex hydro-mechanical coupling behavior of unsaturated geotechnical materials subjected to various mechanical paths. The validity of the model is verified by comparing the modeling results with experimental data, and reasonable agreement is achieved.

1. Introduction

The development of hydro-mechanical models of unsaturated geotechnical materials plays an important role in solving the problems in geotechnical engineering [1,2,3]. Numbers of elastoplastic models were developed for unsaturated geotechnical materials based on critical state theory [4,5,6,7,8]. For example, Alonso et al. [4] proposed a Barcelona basic model (BBM) based on the modified Cam-clay model [9] and derived a loading collapse yield function (LC curve) to describe the collapse phenomenon when wetting. Wheeler and Sivakumar [5] proposed an elastoplastic model similar to BBM while using a different LC yield function. As a classical model, BBM has been widely quoted and modified by researchers [10,11,12]. In addition, Sheng et al. [13] presented a volumetric model, called SFG (Sheng-Fredlund-Gens), for describing the volume change of unsaturated soils during the wetting and drying processes. These models adopt the double-stress variables, mean net stress, and suction, but ignore the effect of saturation on strength and deformation. Lots of experimental data shows that geotechnical materials with different saturation present different mechanical properties, even when the suction and mean net stress are identical. Some authors introduce saturation into the constitutive model to describe the effect of saturation on unsaturated geotechnical materials characteristics [14,15,16]. In addition, soil-water characteristic curves (SWCC) have obvious hysteresis characteristics, which has been considered when establishing the hydro-mechanical coupling models of unsaturated geotechnical materials [13,17,18,19].

Many existing coupling models of geotechnical materials are based on classical elastoplastic theory, which is also the most widely used constitutive theory. However, most of the constitutive equations used in these models are empirical equations obtained by fitting the experimental results [20], which lack a strict theoretical basis. With the help of thermodynamic theory, some authors established the corresponding hyper-plasticity constitutive models by defining the free energy function and the dissipative potential function to overcome the theoretical defects of the classical elastic-plastic model [21,22,23,24]. Although these models still follow the theoretical framework of the classical elastoplastic model, they provide a clear physical meaning for the concepts of yield criteria and flow rules. Recently, based on the physical conservation laws and non-equilibrium thermodynamic theory, the granular solid hydrodynamics modeling method has been successfully applied to the constitutive model of geotechnical materials [25,26,27]. The constitutive relations of geotechnical materials are established by constructing thermodynamic identity and combining free energy function and energy dissipation law. The dissipative system, which causes the system to deviate from the equilibrium state, can be determined theoretically. Energy dissipation has a great influence on the mechanical behavior of geotechnical materials. It is most convenient and reliable to describe these contents with entropy and thermodynamic language, and it can also ensure that the model does not conflict with the basic physical principles. For multi-scale geotechnical materials, this method is simple and effective and it can grasp the essential characteristics of multi-scale behavior of materials from the perspective of energy dissipation.

In this paper, a new hydro-mechanical coupling model for unsaturated geotechnical materials is established based on the non-equilibrium thermodynamic theory. The dissipative system and thermodynamic relationships are determined theoretically, and the constitutive relationships of non-elastic strain and granular temperature are obtained by constructing thermodynamic identity and dissipative relations. The relationship between dissipation mechanism and macro mechanical behavior is established by migration coefficients and energy functions. The parameter calibration method is also described, and the ability of the model to capture the hydro-mechanical coupling behavior of unsaturated geotechnical materials is verified by laboratory experimental data.

2. Non-Equilibrium Thermodynamic-Based Model Framework

2.1. Thermodynamic State Variables

From the point of view of material structure, geotechnical materials are significantly different to ordinary fluids or solids, such as crystals and metals [28]. In addition to macro and micro space levels, geotechnical materials also have a granular level, also called the mesoscopic level. The interaction at this level is the contact force between particles. There is also irregular motion at the mesoscopic level, such as particle sliding, collision, and rolling, which is also called the granular fluctuation motion. Condensed-matter physicists use the concept of granular entropy S_g or granular temperature T_g to describe the fluctuation motion at the mesoscopic level by analogy with the irregular motion of molecules at the micro level [29]. Additionally, solids, including geotechnical materials, have a special feature of spatial translational symmetry breaking [30], which will cause the material to add a state variable in relation to deformation, i.e., elastic strain ${\epsilon }_{\mathit{ij}}^e$. It is worth noting that the total strain ${\epsilon }_{\mathit{ij}}$ is not directly used as the state variable, because it may contain plastic strain ${\epsilon }_{\mathit{ij}}^p$ and cannot correspond to the thermodynamic state.

Thus, $\left\{{\rho ,m,S,\epsilon }_{\mathit{ij}}^e,S_g\right\}$ can be taken as thermodynamic state variables for geotechnical materials, where $\rho$, m, and S are density, momentum, and entropy, respectively, which are the common state variables for ordinary fluids and solids. Since unsaturated geotechnical materials are a mixture of solid (S), liquid (L), and gas (G), its thermodynamic state variables can be written as bulk density ${\rho }^a=n^a{\rho }_a$, momentum $m_i^a={\rho }^a{v}_i^a$, total entropy ${S=n}^S{S}_S+n^L{S}_L+n^G{S}_G$, granular entropy S_g, and elastic strain ${\epsilon }_{\mathit{ij}}^e$, where ${\rho }_a$, $n^a$, and $v_i^a$ are intrinsic density, porosity, and velocity, respectively, and $a=\left[S,L,G\right]$. Additionally, its corresponding conjugate variables are $\left\{{\mu }_{\mathit{ca}},v_i^a,T,{\pi }_{\mathit{ij}},T_g\right\}$, where ${\mu }_{\mathit{ca}}$ is the chemical potential, T is the temperature, T_g is thee granular temperature, and ${\pi }_{\mathit{ij}}$ is the interaction force between particles, respectively [31].

2.2. Thermodynamic Relationships

The thermodynamic total differential form of unsaturated geotechnical materials is obtained as follows:

$$\dot{w}={\pi }_{\mathit{ij}}{\dot{\epsilon }}_{\mathit{ij}}^e+T_g{\dot{S}}_g+T\dot{S}+{\displaystyle \sum _{a=S,L,G}\left({\mu }_{\mathit{ca}}{\dot{\rho }}^a+v_i^a{\dot{m}}_i^a\right)},a\in \left[S,L,G\right],$$

(1)

where w is the total energy density. According to the Equation (1), some relationships can be obtained, such as ${\pi }_{\mathit{ij}}=\frac{\partial w}{\partial {\epsilon }_{\mathit{ij}}^e}$, $T_g=\frac{\partial w}{\partial S_g}$.

Since mass $\rho$, momentum m, and energy w are conserved quantities, the total mass, the total momentum, and the total energy of a unit of unsaturated geotechnical materials remain constant when there is no heat exchange with the outside world. The dissipative system of the unsaturated geotechnical materials can be obtained by $\delta S=0$ and ${\delta }^{2}S<0$, based on the maximum entropy principle. Therefore, it can be obtained that the dissipation forces of unsaturated geotechnical materials are $\left\{{\pi }_{\mathit{ij}},T_g,{\nabla }_{i}T,{\dot{\epsilon }}_{\mathit{ij}},{\psi }_{\mathit{ij}}^L,{\psi }_{\mathit{ij}}^G\right\}$ and the corresponding dissipation flows are $\left\{{\dot{\epsilon }}_{\mathit{ij}}^p,I_g,q_k/T,{\sigma }_{\mathit{ij}}^{\mathit{vS}},{\sigma }_{\mathit{ij}}^{\mathit{vL}},{\sigma }_{\mathit{ij}}^{\mathit{vG}}\right\}$, where ${\dot{\epsilon }}_{\mathit{ij}}$, ${\psi }_{\mathit{ij}}^L$, and ${\psi }_{\mathit{ij}}^G$ are the strain rate, ${\dot{\epsilon }}_{\mathit{ij}}^p$ is the plastic strain rate of solid phase, ${\sigma }_{\mathit{ij}}^{\mathit{va}}$ is the viscous stress, and $q_k$ is the heat conduction.

The Onsager relationship [32] indicates that the entropy production rate R can be written as the sum of the product of dissipative forces and dissipation flows.

$${R=\dot{\epsilon }}_{\mathit{ij}}^p{\pi }_{\mathit{ij}}+I_g{T}_g+\frac{q_k}{T}{\nabla }_i{T+\sigma }_{\mathit{ij}}^{\mathit{vS}}{\dot{\epsilon }}_{\mathit{ij}}+{\sigma }_{\mathit{ij}}^{\mathit{vL}}{\psi }_{\mathit{ij}}^L+{\sigma }_{\mathit{ij}}^{\mathit{vG}}{\psi }_{\mathit{ij}}^G$$

(2)

Moreover, the dissipative flow can be written as a linear function of the dissipative force [33], followed by:

$$\left[\begin{array}{l}{\dot{\epsilon }}_{\mathit{ij}}^p\\ I_g\\ q_i\\ {\sigma }_{\mathit{ij}}^{\mathit{vS}}\\ {\sigma }_{\mathit{ij}}^{\mathit{vL}}\\ {\sigma }_{\mathit{ij}}^{\mathit{vG}}\end{array}\right]=\left[\begin{array}{cccccc}{\eta }_{\mathit{ijkl}}& 0& 0& 0& 0& 0\\ 0& \gamma & 0& 0& 0& 0\\ 0& 0& {\kappa }_{\mathit{ik}}& 0& 0& 0\\ 0& 0& 0& {\lambda }_{\mathit{ijkl}}^S& 0& 0\\ 0& 0& 0& 0& {\lambda }_{\mathit{ijkl}}^L& 0\\ 0& 0& 0& 0& 0& {\lambda }_{\mathit{ijkl}}^G\end{array}\right]\left[\begin{array}{l}{\pi }_{\mathit{kl}}\\ T_g\\ {\nabla }_{k}T\\ {\dot{\epsilon }}_{\mathit{kl}}\\ {\psi }_{\mathit{kl}}^L\\ {\psi }_{\mathit{kl}}^G\end{array}\right]$$

(3)

The intermediate matrix is a positive definite matrix, also known as the transfer coefficient matrix, and should satisfy the reciprocity of Onsager and the Curie principle. However, the interaction between each dissipative flow in Equation (3) is not obvious, so the non-diagonal phases are considered to be 0.

2.3. Energy Dissipation at a Mesoscopic Level

Entropy is similar to conserved quantities and has superposition and non-zero properties. However, the difference is that it can be produced, also known as entropy production. It is found that the behavior of entropy is also effective when deviating from thermodynamic equilibrium [30]. Thus, the total entropy balance equation can be written as:

$${\displaystyle \sum _{a=S,L,G}\left({\rho }^a{\dot{\vartheta }}_a\right)}=R/T+{\nabla }_k{f}_k-{\rho }^L{v}_k^{\mathit{LS}}{\nabla }_k{\vartheta }_L-{\rho }^G{v}_k^{\mathit{GS}}{\nabla }_k{\vartheta }_G$$

(4)

where $\vartheta =S/\rho$ is specific entropy.

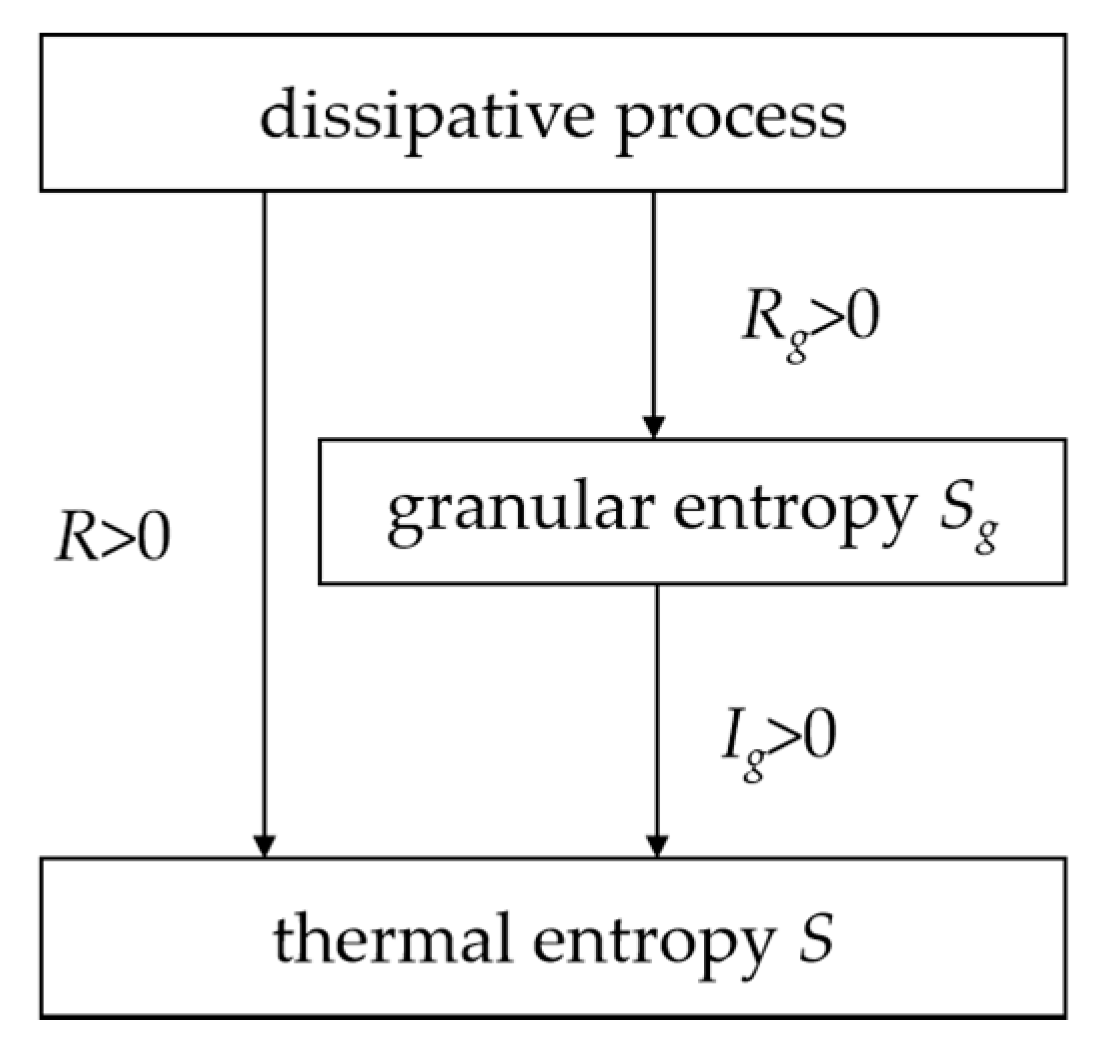
Different to the irregular motion of micro molecules, the interaction between particles (fluctuation motion) is generally non-elastic, which will lead to energy dissipation [34]. If there is no sustained excitation, the fluctuation motion of particles will decay in the form of macro energy dissipation until the fluctuation disappears and reaches equilibrium again. As shown in Figure 1, the dissipation process of geotechnical materials will produce granular entropy S_g and thermal entropy S. Since the interaction between particles is non-elastic, entropy production will be generated along with it and finally granular entropy S_g will decay to thermal entropy S.

The granular entropy balance equation can be obtained by analogy in Equation (4)

$${\rho }^S{\dot{\vartheta }}_g=R_g/T_g-I_g$$

(5)

where ${\vartheta }_g=S_g/{\rho }^S$ is specific granular entropy, R_g is granular entropy production, and I_g is the granular entropy decay rate, which is the entropy production of the system caused by the granular temperature.

For unsaturated geotechnical materials containing water and gas, the change of saturation will change the attraction force and cementation between particles, which will cause the recombination movement between particles [17,35], such as the wetting collapsibility phenomenon. Therefore, the change rate of saturation is also a driving force of particle fluctuation, which should be attributed to the dissipation mechanism at the mesoscopic level. Thus, the change rate of saturation ${\dot{s}}_r$ can be regarded as a dissipative force, and the suction s is the corresponding dissipative flow. Considering the viscosity at the mesoscopic level and the dissipation caused by saturation change, the granular entropy production rate R_g is expressed as:

$$R_g={\sigma }_{\mathit{ij}}^{\mathit{vg}}{\dot{\epsilon }}_{\mathit{ij}}+{\mathit{sT}}_g{\dot{S}}_r$$

(6)

where ${\mathit{sT}}_g{\dot{S}}_r$ is the dissipation at the mesoscopic level due to saturation changes, and when T_g=0, that is, no dissipation occurs at the mesoscopic level, ${\mathit{sT}}_g{\dot{S}}_r$ also disappears (multiplied by T_g to reflect this phenomenon).

Similarly, the viscous dissipation relationship at the mesoscopic level can also be expressed as:

$${\sigma }_{\mathit{ij}}^{\mathit{vg}}=T_g{\lambda }_{\mathit{ijkl}}^g{\dot{\epsilon }}_{\mathit{kl}}$$

(7)

where ${\sigma }_{\mathit{ij}}^{\mathit{vg}}$ is the viscous stress and ${\lambda }_{\mathit{ijkl}}^g$ is the migration coefficient at the mesoscopic level. Additionally, when T_g = 0, there is no dissipation at the mesoscopic level and the viscous dissipation disappears.

The energy density associated with the fluctuation motion of the particles w_g is expressed as $w_g={b\rho }^S{\left(T_g\right)}^2/2$, where $b$ is the material parameter [29]. According to Equation (1), there is

$${\rho }^S{\vartheta }_g=\frac{\partial w_g}{\partial T_g}={\rho }^S{\mathit{bT}}_g$$

(8)

Thus, ${\vartheta }_g={\mathit{bT}}_g$ can be obtained. Similarly, defining the tensor ${\lambda }_{\mathit{ijkl}}^g$ as

$${\lambda }_{\mathit{ijkl}}^g={\lambda }_{\mathit{sg}}{\delta }_{\mathit{il}}{\delta }_{\mathit{jk}}+\left({\lambda }_{\mathit{vg}}-\frac{{\lambda }_{\mathit{sg}}}{3}\right){\delta }_{\mathit{ij}}{\delta }_{\mathit{lk}}$$

(9)

where ${\lambda }_{\mathit{sg}}$ and ${\lambda }_{\mathit{vg}}$ are the migration coefficients at the mesoscopic level.

Combining Equations (5)–(9), the motion equation of granular temperature can be obtained:

$${\dot{T}}_{\mathit{gg}}=c_2{c}_5\frac{{\dot{\epsilon }}_s{\dot{\epsilon }}_s}{{\rho }^S}+c_3{c}_5\frac{{\dot{\epsilon }}_v{\dot{\epsilon }}_v}{{\rho }^S}+c_4\frac{{s\dot{s}}_r}{{\rho }^S}-c_5\frac{T_{\mathit{gg}}}{{\rho }^S}$$

(10)

where $T_{\mathit{gg}}={\left({\eta }_s\right)}^{1/\alpha }{T}_g$, $c_2={\left({\eta }_s\right)}^{1/\alpha }{\lambda }_{\mathit{sg}}/\gamma$, $c_3={\left({\eta }_s\right)}^{1/\alpha }{\lambda }_{\mathit{vg}}/\gamma$, $c_4={\left({\eta }_s\right)}^{1/\alpha }/b$, $c_5=\gamma /b$.

2.4. Expression of Stress and Strain

The elastic potential energy density function w_e is generally written as a function of elastic strain, such as the linear elastic model (generalized Hooke’s law). In addition, according to the influence of average effective stress on elastic bulk modulus K_e and elastic shear modulus G_e, some authors [29,36] constructed the elastic potential energy density functions, which have similar forms to the linear elastic model. By analogy with Hertz contact, Jiang and Liu [29] obtained the elastic potential energy density function of granular materials.

$$w_e=B{\left({\epsilon }_v^e\right)}^{0.5}\left[\frac{2}{5}{\left({\epsilon }_v^e\right)}^2+\frac{1}{\zeta }{\left({\epsilon }_s^e\right)}^2\right]$$

(11)

where ${\epsilon }_v^e$ is the elastic volume strain, ${\epsilon }_s^e$ is the elastic shear strain, $\zeta$ is the material parameters, $\zeta$ = 5/3 for dry sand, and $B$ describes the hardness of the material, the same dimension as the stress.

For unsaturated geotechnical materials, the cementation and the matrix suction has a great influence on the contact between particles, and cohesion between particles affects the elastic shear modulus. Following the method of describing the thermal expansion effect of solid [30], adding the contribution of suction ${\chi s\epsilon }_v^e$ into Equation (11), and considering the effect of cohesion, Equation (11) can be modified as follows:

$$w_e=B\left[\frac{2}{5}{\left({\epsilon }_v^e\right)}^{2.5}+\xi {\left({\epsilon }_v^e+c\right)}^{0.5}{\left({\epsilon }_s^e\right)}^2\right]+{\chi s\epsilon }_v^e$$

(12)

where $\xi =1/\zeta$; c is the material parameter to reflect the influence of cohesion on the elastic shear modulus and ${\chi =s}_r$, which is similar to Bishop’s effective stress of unsaturated soil.

${\pi }_{\mathit{ij}}$ is regarded as the mean effective stress of unsaturated geotechnical materials and is related to the elastic potential energy density w_e. According to Equation (1), there is

$${\pi }_{\mathit{ij}}=\frac{\partial w_e}{\partial {\epsilon }_{\mathit{ij}}^e}=B\left[{\left({\epsilon }_v^e\right)}^{1.5}{\delta }_{\mathit{ij}}+0.5\xi {\left({\epsilon }_v^e+c\right)}^{-0.5}{\left({\epsilon }_s^e\right)}^2{\delta }_{\mathit{ij}}+2\xi {\left({\epsilon }_v^e\right)}^{0.5}{e}_{\mathit{ij}}^e\right]+{\mathit{ss}}_r{\delta }_{\mathit{ij}}$$

(13)

Similar to the linear elastic model, ${\pi }_{\mathit{ij}}$ can be expressed as:

$${\pi }_{\mathit{ij}}=\left(K_e{\epsilon }_v^e+{\mathit{ss}}_r\right){\delta }_{\mathit{ij}}{+2G}_e{e}_{\mathit{ij}}^e$$

(14)

where the K_e and G_e can be expressed as:

$$K_e=B\left[{\left({\epsilon }_v^e\right)}^{0.5}+0.5\xi {\left({\epsilon }_v^e+c\right)}^{-0.5}\frac{{\left({\epsilon }_s^e\right)}^2}{{\epsilon }_v^e}\right]$$

(15)

$$G_e=B\xi {\left({\epsilon }_v^e\right)}^{0.5}$$

(16)

Additionally, the mean effective stress $p^{\prime }$ and shear stress q can be obtained:

$$p^{\prime }=\frac{{\pi }_{\mathit{kk}}}{3}=B\left[{\left({\epsilon }_v^e\right)}^{1.5}+0.5\xi {\left({\epsilon }_v^e+c\right)}^{-0.5}{\left({\epsilon }_s^e\right)}^2\right]+{\mathit{ss}}_r$$

(17)

$$q=\sqrt{\frac{3}{2}{s}_{\mathit{ij}}{s}_{\mathit{ji}}}=\sqrt{6}B\xi {\left({\epsilon }_v^e+c\right)}^{0.5}{\epsilon }_s^e$$

(18)

where $s_{\mathit{ij}}={\pi }_{\mathit{ij}}-\frac{{\pi }_{\mathit{kk}}}{3}{\delta }_{\mathit{ij}}$ is the deviator stress.

It can be seen that B is related to the density, and the greater the density, the greater the B. Thus, ${B=B}_0\exp \left(-\frac{e}{\lambda \left(s\right)}\right)$ can be obtained according to the compression curve (e-lnp′) of geotechnical materials [26], where e is the void ratio and $\lambda \left(s\right)$ is the slope of compression curve.

According to the migration coefficient matrix, the following relationship can be obtained:

$${\dot{\epsilon }}_{\mathit{ij}}^p={\eta }_{\mathit{ijkl}}{\pi }_{\mathit{kl}}$$

(19)

When the granular temperature T_g = 0, the plastic strain will not occur. For isotropic conditions, ${\eta }_{\mathit{ijkl}}$ can be defined as:

$${\eta }_{\mathit{ijkl}}={\left(T_g\right)}^{\alpha }\frac{{\eta }_s}{{2G}_e}{\delta }_{\mathit{il}}{\delta }_{\mathit{jk}}+{\left(T_g\right)}^{\alpha }\left(\frac{{\eta }_v}{{3K}_e}-\frac{{\eta }_s}{{6G}_e}\right){\delta }_{\mathit{ij}}{\delta }_{\mathit{lk}}$$

(20)

where ${\eta }_v$ and ${\eta }_s$ are migration coefficients, $\alpha$ is an exponential parameter, and $\alpha$ = 0.5 when it is assumed that the critical elastic shear strain is independent of the shear strain rate [25].

Combining Equations (14), (19), and (20), there is

$${\dot{\epsilon }}_{\mathit{ij}}^p={\eta }_{\mathit{ijkl}}{\pi }_{\mathit{kl}}={\eta }_v{\left(T_g\right)}^{\alpha }\left({\epsilon }_v^e+\frac{{\mathit{ss}}_r}{K_e}\right){\delta }_{\mathit{ij}}+{\eta }_s{\left(T_g\right)}^{\alpha }{e}_{\mathit{ij}}^e$$

(21)

The expressions of elastic volume strain rate ${\dot{\epsilon }}_v^e$ and elastic shear strain rate ${\dot{\epsilon }}_s^e$ can then obtained:

$${\dot{\epsilon }}_v^e={\dot{\epsilon }}_v-3c_1{\left({\eta }_s^{1/\alpha }{T}_g\right)}^{\alpha }\left({\epsilon }_v^e+\frac{{\mathit{ss}}_r}{K_e}\right),c_1={\eta }_v/{\eta }_s$$

(22)

$${\dot{\epsilon }}_s^e{=\dot{\epsilon }}_s-{\left({\eta }_s^{1/\alpha }{T}_g\right)}^{\alpha }{\epsilon }_s^e$$

(23)

2.5. Soil-Water Characteristic

The soil-water characteristic curve (SWCC) generally takes the form of the vG model [37], $s_r={\left[1+{\left(\frac{s}{a}\right)}^n\right]}^{-m}$, where $a$, $m$, and $n$ are the parameters associated with the curve. Since the saturation is also affected by the void ratio e, some authors [38,39] proposed modified SWCC models by adding the deformation factor into the vG model. For example, Tarantion [39] proposed a modified SWCC model to describe the effect of void ratio on soil-water characteristic behavior. He found that the pore water void ratio e_w can be described by a power function of suction s, $e_w{=a}_1{s}^{b_1}$, where a₁ and b₁ are related to the intercept and slope of the ${\mathit{lns}~\mathit{lne}}_w$ curve. The factor ${\left(\frac{e}{a_1}\right)}^{1/b_1}$ is added to indicate the effect of deformation, and the modified SWCC model is given as:

$$s_r={\left\{1+{\left[{\left(\frac{e}{a_1}\right)}^{1/b_1}s\right]}^n\right\}}^{-b_1/n}$$

(24)

where a₁, b₁, and n are the fitting parameters and $m=b_1/n$ is equal to the parameter m in vG model.

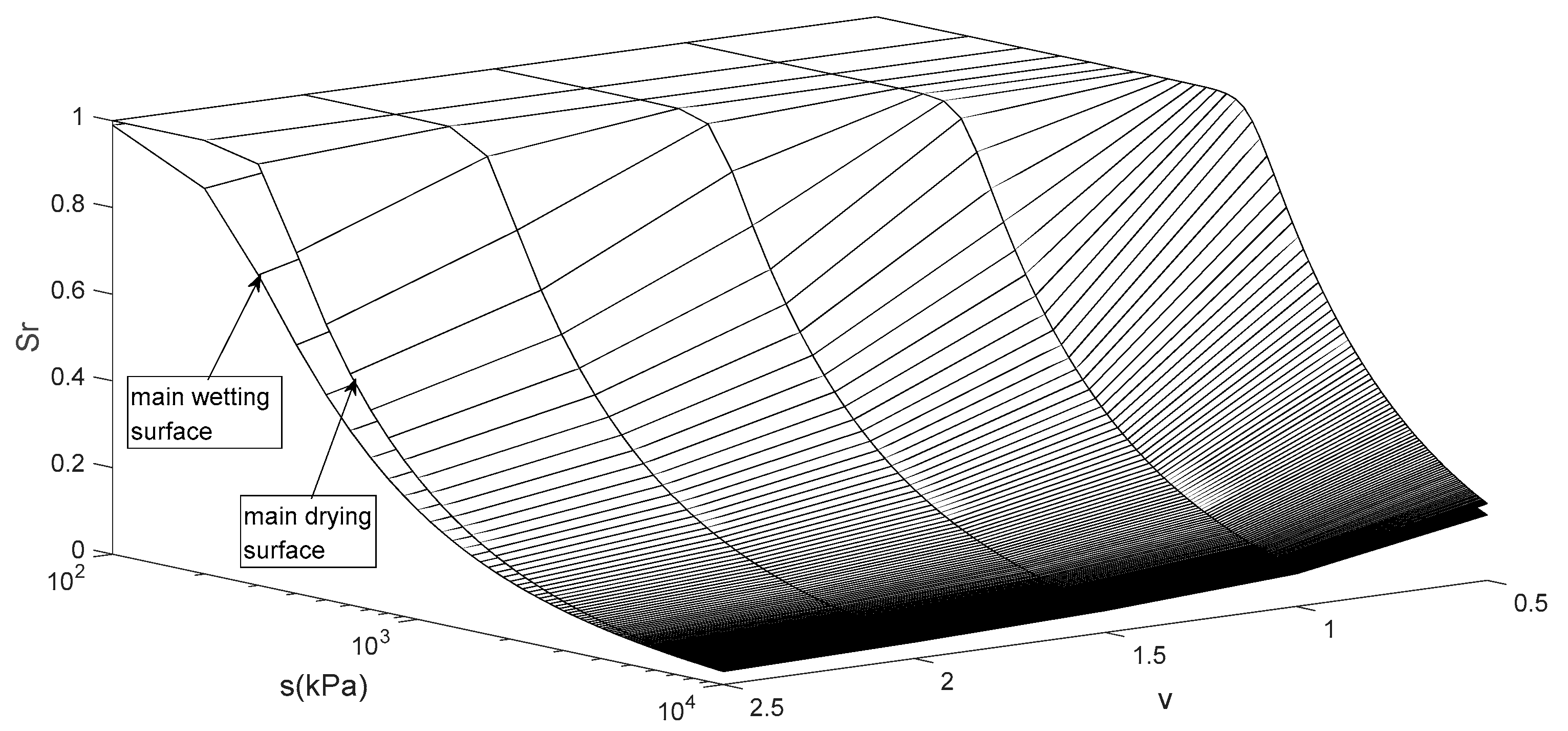
Figure 2 shows the main drying and wetting surfaces of Speswhite kaolin in ${e~\mathit{lns}~s}_r$ space based on the above modified SWCC model (Equation (24)). When the suction remains constant, the degree of saturation will decrease with the increase of void ratio, and when the degree of saturation is constant, the suction will increase with the increase of void ratio. Equation (24) can also be reduced to the vG model without considering the change of void ratio.

3. Model Characteristics and Calibration

The hydro-mechanical coupling behavior of unsaturated geotechnical materials can be described using the granular temperature motion equation (Equation (10)), mean effective stress equation (Equation (17)), shear stress equation (Equation (18)), strain evolution equation (Equations (22) and (23)), and SWCC equation (Equation (24)). This model does not involve yield criterion, flow rule, hardening criterion, or other classical concepts in elastoplastic mechanics. Instead, thermodynamic concepts, such as granular temperature, migration coefficients, and energy functions, are replaced. The dissipation system and migration coefficients are determined theoretically, especially the dissipation at the mesoscopic level. The constitutive relationship of non-elastic deformation is obtained by thermodynamic identity, and through the migration coefficients and energy functions, the dissipation mechanism is connected with macroscopic mechanical behavior. These mean that the model can reflect the energy dissipation mechanism and the macroscopic mechanical properties induced by it, and the multi field coupling characteristics of unsaturated geotechnical materials in a complex environment can be described in a unified thermodynamic theoretical framework.

The model involves some thermodynamic parameters, including ${\eta }_v$, ${\eta }_s$, ${\lambda }_{\mathit{vg}}$, ${\lambda }_{\mathit{sg}}$, b, and $\gamma$. However, it is not necessary to determine the value of each of the above coefficients, because the parameters required for the calculation of the model are c₁, c₂, c₃, c₄, and c₅, and they can be calibrated through laboratory tests. For example, c₅ can be calibrated through the stress relaxation test, that is, the stress applied to the sample decreases under the condition of zero strain, and the value of c₅ can be calibrated by the time of stress relaxation; c₂ and c can be determined by the stress-strain relationship at the critical state; c₁ can be determined by the stress paths and stress-strain relationship of the undrained shear test; c₃ is related to the volume deformation of soil, which can be calibrated through the isotropic compression test, and the value of B₀ can also be calibrated; c₄ can be determined by the wetting or drying test.

4. Modeling the Hydro-Mechanical Coupling Behavior of Unsaturated Geotechnical Materials

Test data are used to verify the effectiveness of the proposed model in describing the hydro-mechanical coupling behavior of unsaturated geotechnical materials, such as the irreversible compression in the drying stages of wetting–drying cycles and the effect of a wetting–drying cycle on subsequent behavior during isotropic loading. The test results of two typical geotechnical materials are compared with the modeling results, including non-expansive clay (Speswhite kaolin) [40] and highly expansive soil (bentonite/kaolin mixture) [41]. The geotechnical materials and the related model parameters are listed in

Table 1. Geotechnical materials types and model parameters. Soil-water characteristic curves (SWCC).

Thermodynamics Parameters
	Speswhite Kaolin	Bentonite/Kaolin Mixture		Speswhite Kaolin	Bentonite/Kaolin Mixture
B0	2.192 × 107 kPa	4.545 × 106 kPa	c2	6701.2	8536.4
ξ	0.6	0.6	c3	15,000	10,000
c	0.0022	0.0028	c4	0.15	0.17
c1	0.11	0.05	c5	37.3	20.6
SWCC Parameters
Drying			Wetting
	Speswhite Kaolin	Bentonite/Kaolin Mixture		Speswhite Kaolin	Bentonite/Kaolin Mixture
a1	631	1.46	a1	368	0.716
b1	0.963	0.243	b1	0.922	0.175
n	14.8	2.56	n	3.87	2.88

, and the SWCC parameters come from the literature [39].

4.1. Speswhite Kaolin (Non-Expansive Clay)

Ravenendiraraj [40] carried out a series of experiments to study the hydro-mechanical coupling behavior through various stress path tests, including wetting, drying, isotropic loading, and unloading. Here, using the data of Test A9 for comparison, the stress paths are shown in

Table 2. Stress paths of Test A9.

Stage			$\overline{p}$ (kPa)	s (kPa)
From	To	Description
A	B	Isotropic loading	10→200	300
B	C	Isotropic unloading	200→10	300
C	D	Wetting	10	300→10
D	E	Drying	10	10→300
E	F	Isotropic loading	10→375	300

. The mean net stress loading rate was 0.033 kPa/min, while the suction change rate was 0.0167 kPa/min in wetting or drying stages. The values of the slope of compression curve and unloading curve were 0.177 and 0.024, respectively.

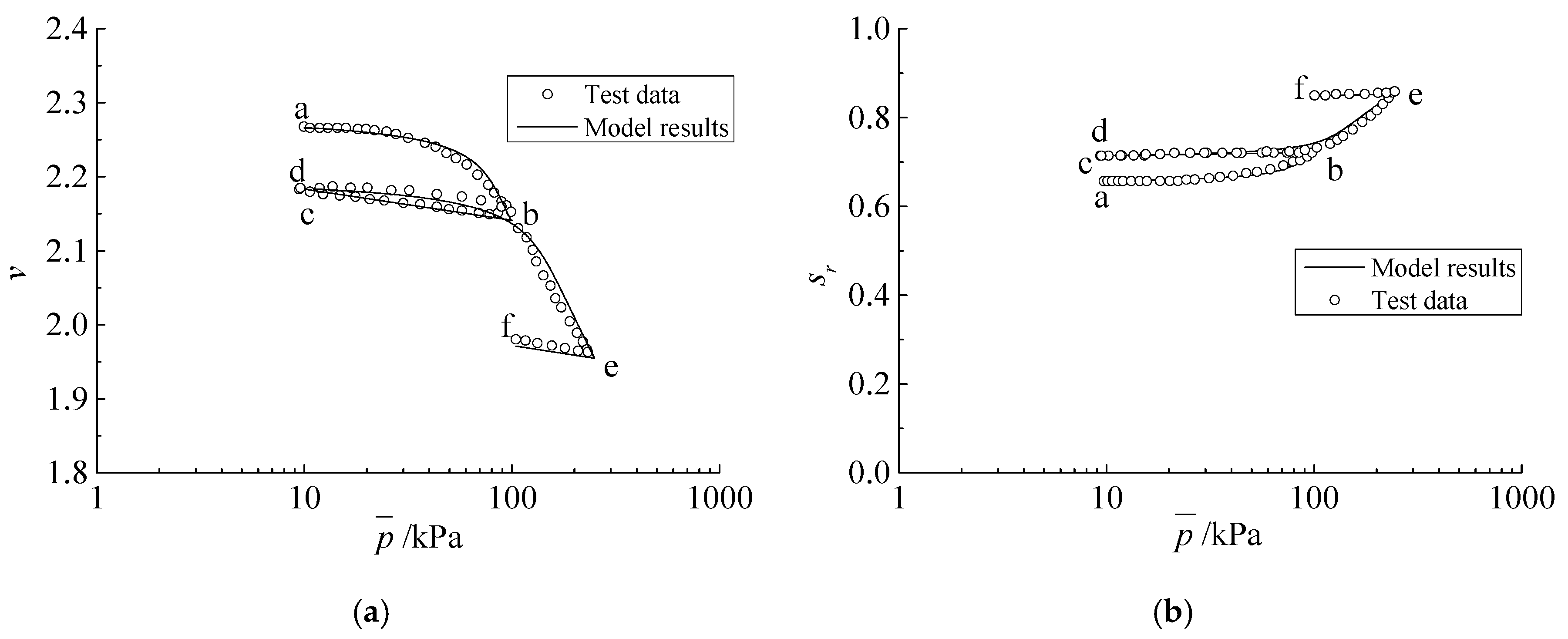
Figure 3 shows the comparison of modeling results and test data for isotropic loading and unloading stages. The isotropic loading–unloading cycle, A-B-C, performed at constant suction 300 kPa, is followed by a wetting–drying cycle, C-D-E, and then subsequent isotropic reloading, E-F, at the same suction 300 kPa. Due to the effect of hydraulic hysteresis, the saturation degree increases, while the specific volume is almost unchanged during the wetting–drying cycle (see points C and E). Additionally, the results show the degree of saturation changes irreversibly during the mechanical loading and unloading process, A-B-C. In addition, it can be seen that, during the second isotropic loading stage, E-F, yield occurs before the first loading, which can be interpreted as the increase of degree of saturation during the preceding wetting–drying cycle [5]. The modeling results are in good agreement with the test data.

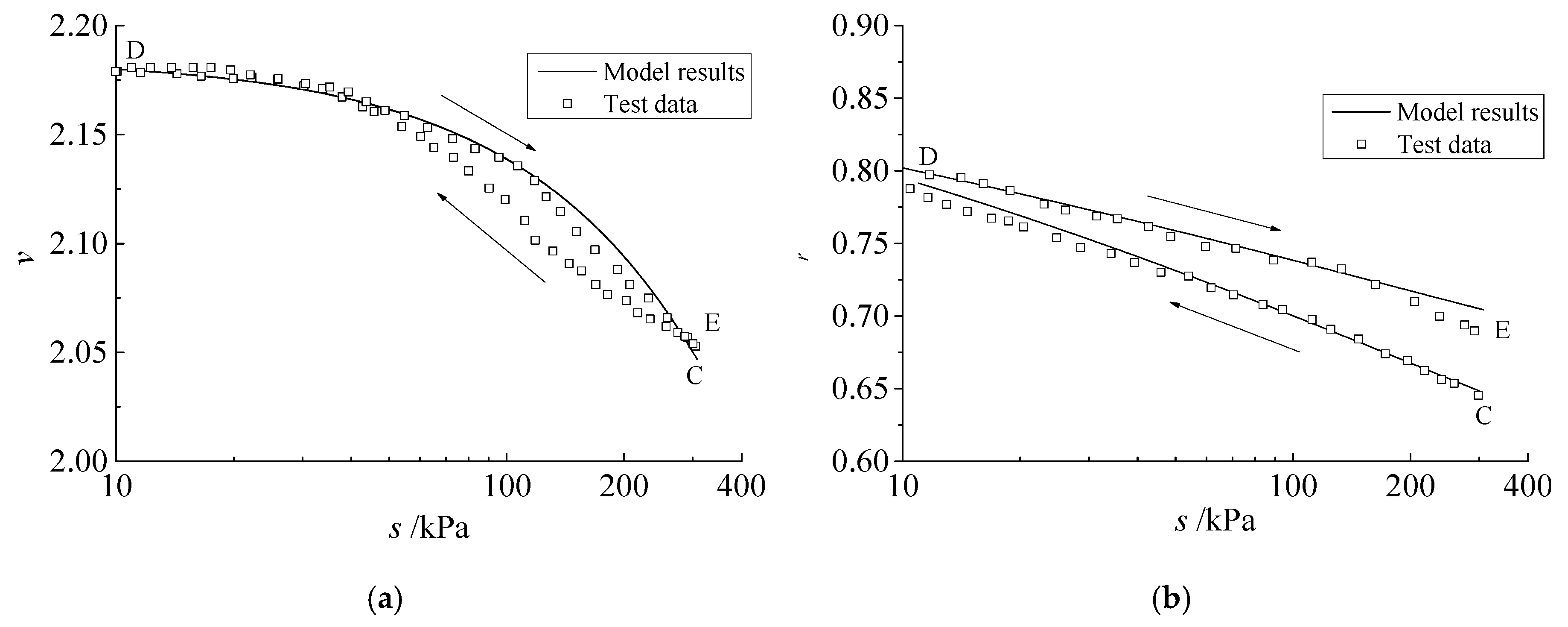
Figure 4 shows the modeling results and test data under the wetting–drying cycle, while the mean net stress remains constant during the process. It can be seen that the change of specific volume was almost the same during the wetting and drying process and changed little after a wetting–drying cycle due to a slight variation in the saturation degree (about 0.05). The modeling results were consistent with the test data.

4.2. Bentonite/Kaolin Mixture (Highly Expansive Doil)

The mixture include about 10% Wyoming sodium bentonite and 90% Speswhite kaolin [41], and the model parameters are also listed in Table 1. The data of Tests 8/9/10 were used to verify the efficiency of the model, and these behaviors were well simulated by the proposed model. The stress paths are as follows:

Test 8:

Wetting–drying at constant mean met stress $\overline{p}$ = 10 kPa;

Suction s(kPa) = 300(a)→20(b)→300(c)

Test 9:

Isotropic loading–unloading at constant suction s = 200 kPa;

Mean met stress $\overline{p}$ (kPa) = 10(a)→100(b)→10(c)→250(d)→100(e)

Test 10:

(1) Isotropic loading–unloading at constant suction s = 200 kPa;

Mean met stress $\overline{p}$ (kPa) = 10(a)→100(b)→10(c)

(2) Wetting–drying at constant mean met stress $\overline{p}$ = 10 kPa;

Suction s(kPa) = 200(c)→20(d)→200(e)

(3) Isotropic loading–unloading at constant suction s = 200 kPa

Mean met stress $\overline{p}$ (kPa) = 10(e)→250(f)→10(g)

Figure 5a shows that no collapse compression occurred in wetting path a→b and the irreversible shrinkage occurred in drying path b→c due to a greater change in saturation degree (about 0.27), i.e., a larger effective stress than the previous. Figure 5b provides the clear evidence for the hydraulic hysteresis behavior of the material.

Figure 6 shows the compressive and rebound characteristics of the material under isotropic loading–unloading cycles. The saturation degree increased with the increase of mean net stress during the loading process, while it changed a little during the unloading process, as shown in Figure 6b. In addition, the small mechanical hysteresis behavior could be seen during the unloading–reloading loop, and the yield point occurred near $\overline{p}$ = 100 kPa, corresponding to the maximum mean net stress previously applied (Figure 6a).

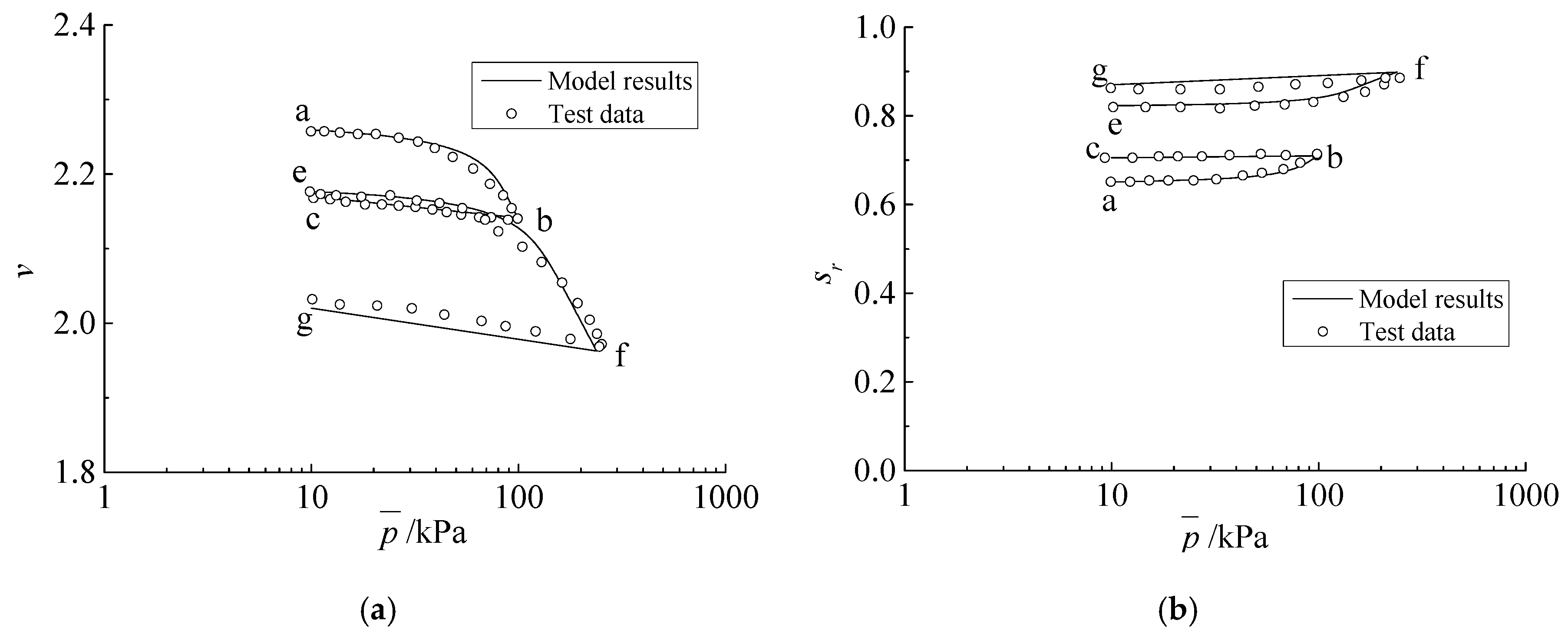
Test 10 differed from Test 9, only in that the wetting and drying cycle was added between the two loading–unloading cycles. The results show that there was no net shrinkage during the wetting–drying cycle (points c and e in Figure 7a), while in the second loading, e→f, the material yielded at a lower value of about 80 kPa due to the wetting–drying cycle. Additionally, the degree of saturation increased with the increasing value of mean net stress, as shown in Figure 7b. Although there is no net volume change, the points c and e were different due to the increase of saturation after the wetting–drying cycle. The model can well describe this phenomenon.

5. Conclusions

Based on the thermodynamic theory, a new hydro-mechanical coupled model for unsaturated geotechnical materials is developed in this paper. This model was quite different to the classical elastic-plastic theory model, and common concepts, such as yield criterion and flow rules, were not involved in the constitutive relations and were replaced with the concepts of granular entropy, granular temperature, migration coefficients, and energy functions, and dissipation at the mesoscopic level was considered. The dissipative system and thermodynamic relationships were determined theoretically, and the constitutive relationships of non-elastic strain and granular temperature were obtained by constructing thermodynamic identity and dissipative relations. The relationship between dissipation mechanisms and macro mechanical behavior can be established by migration coefficients and energy functions. For multi-scale geotechnical materials, this method was simple and effective, and it could grasp the essential characteristics of multi-scale behavior of materials from the perspective of energy dissipation. Therefore, the multi field coupling model of unsaturated geotechnical materials in a complex environment can be established in a unified theoretical framework.

Combining with SWCC model, considering deformation effect, the proposed model can well describe the hydro-mechanical coupling behavior of unsaturated geotechnical materials subjected to various mechanical paths, especially the influence of the wetting–drying cycle on subsequent behavior during isotropic loading and irreversible compression during the drying stages of a wetting–drying cycle, which have been verified by comparing modeling results with test data.