Spatial Domain-Based Nonlinear Residual Feature Extraction for Identification of Image Operations
Abstract
1. Introduction
2. Proposed Approach for Identification of Image Operations
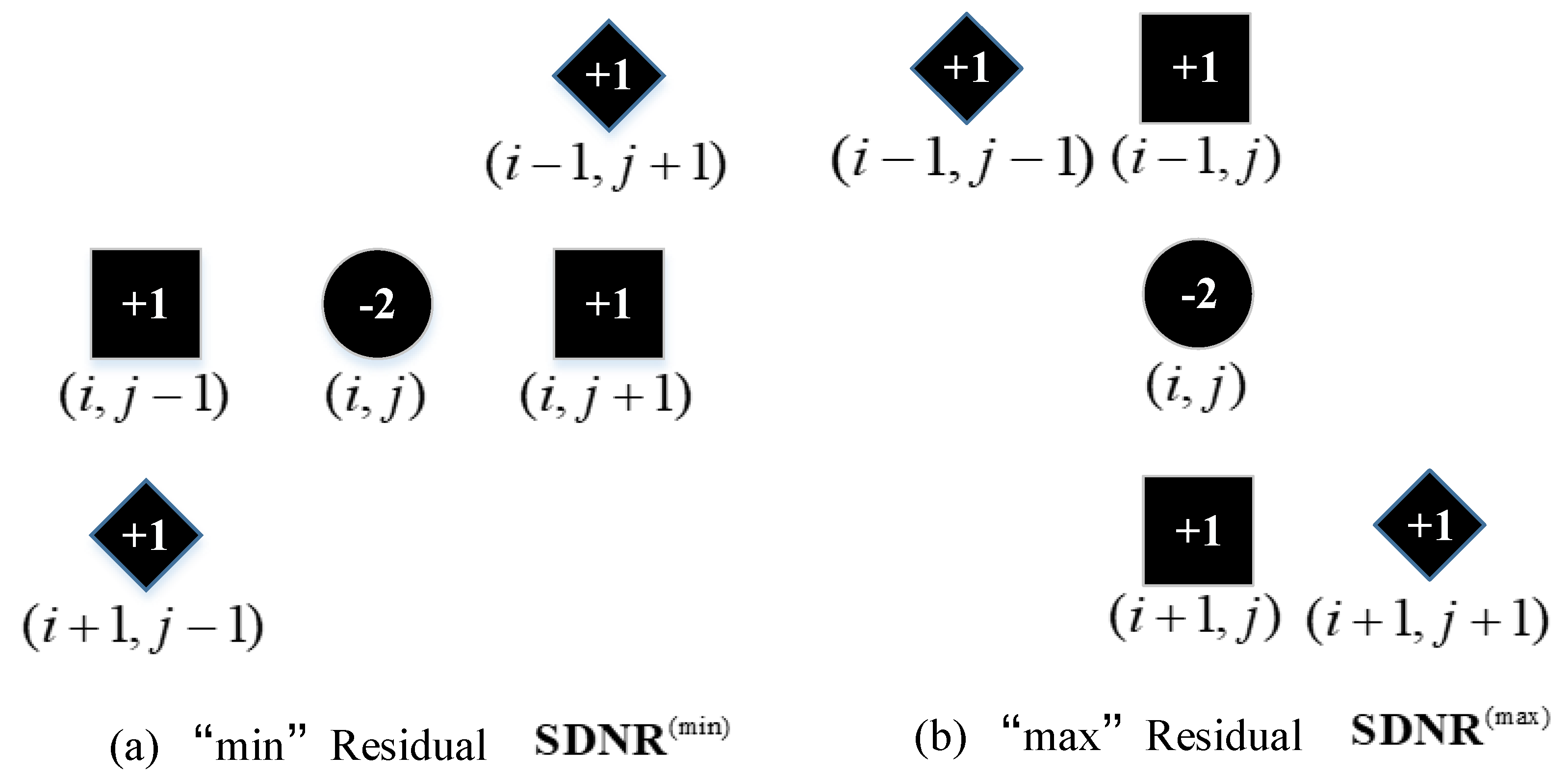
2.1. Spatial Domain-Based Nonlinear Residual (SDNR) Feature
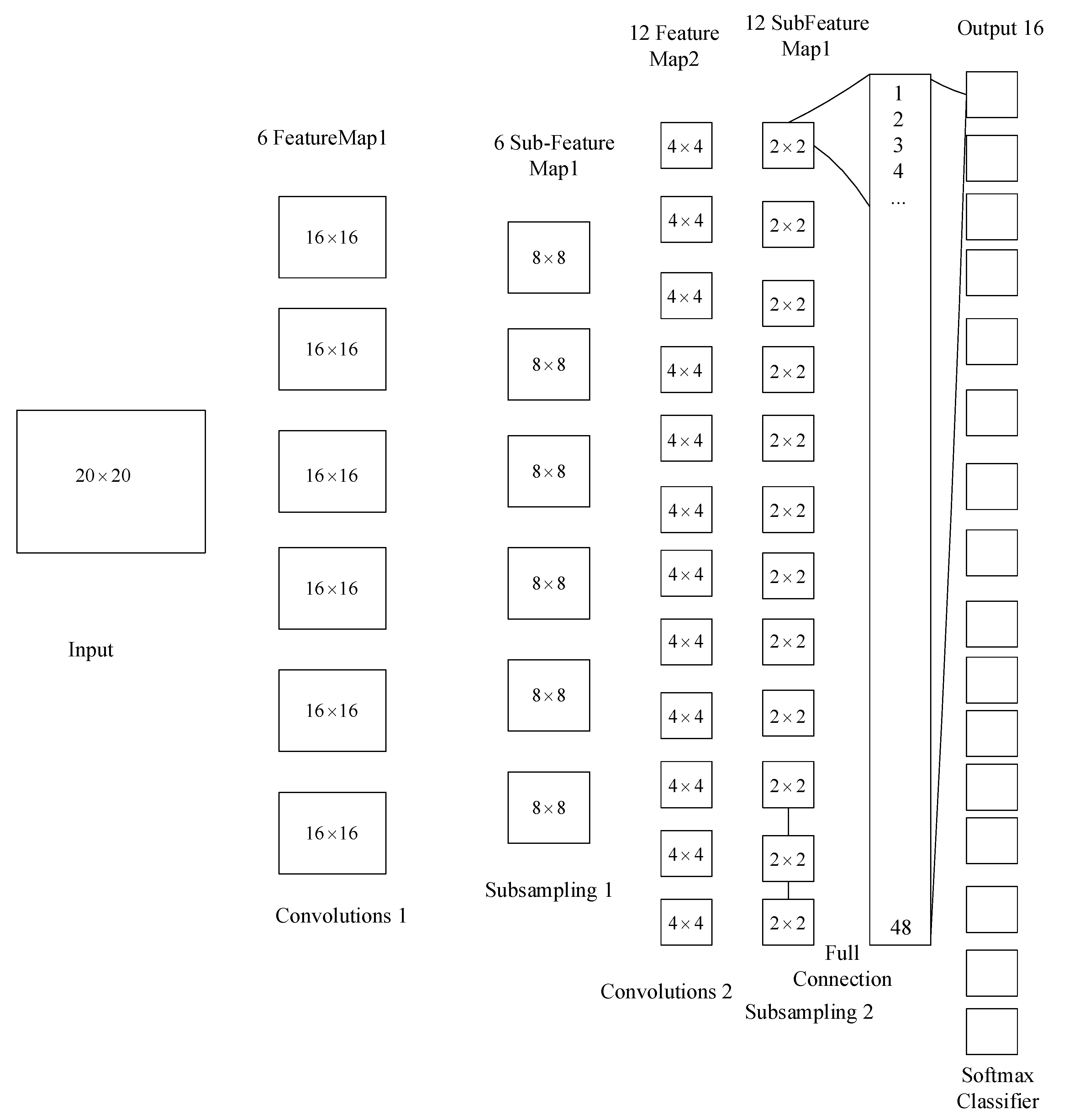
2.2. Employed Convolutional Neural Network Model for Classification
3. Experiments and Discussions
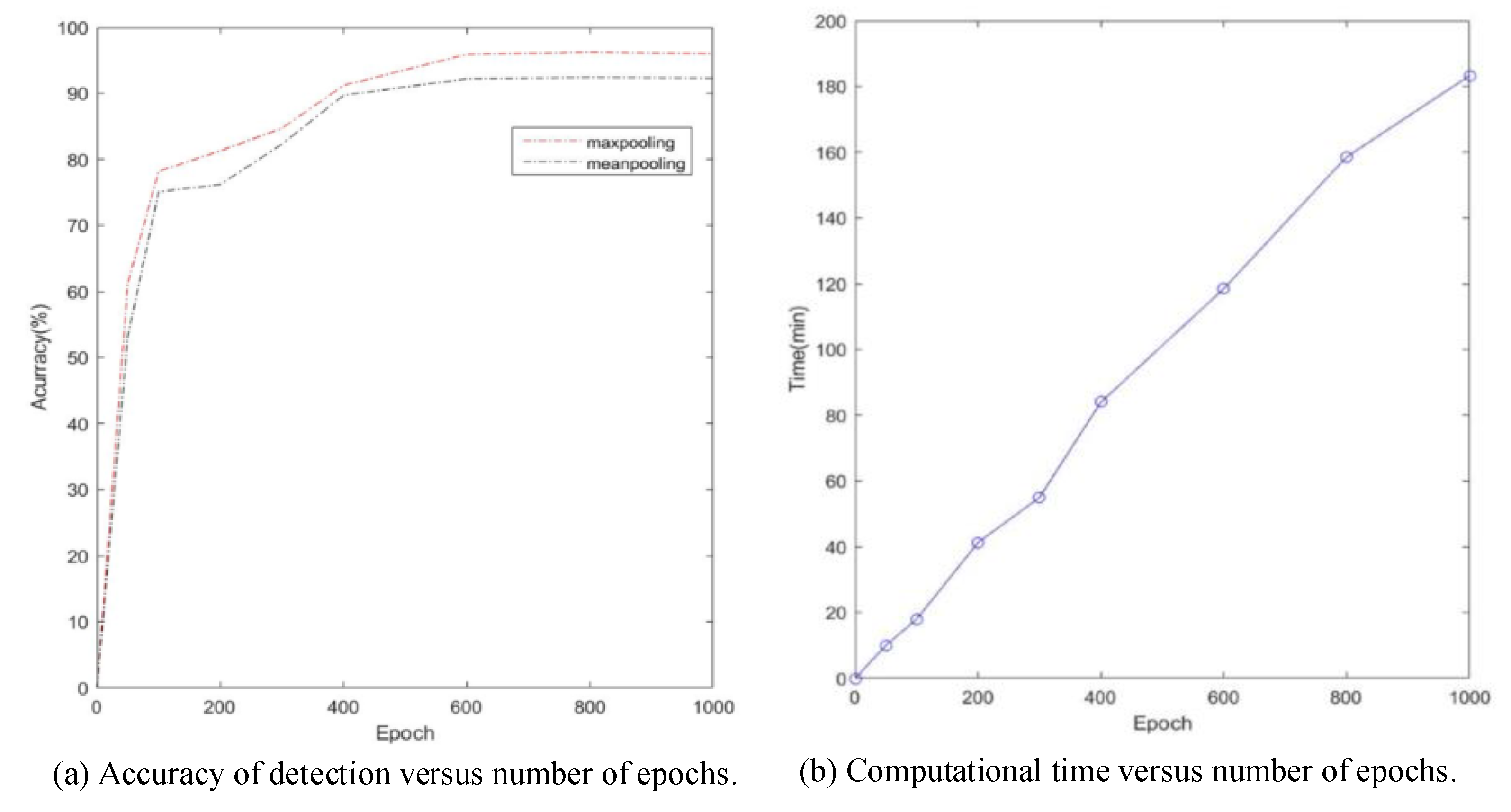
3.1. Parameter Settings
3.2. Detection and Classification of Various Image Postprocessing Operations
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Fan, Z.; Queiroz, R.L.D. Identification of bitmap compression history: JPEG detection and quantizer estimation. IEEE Trans. Image Process. 2003, 12, 230–235. [Google Scholar] [PubMed]
- Farid, H. Exposing digital forgeries from JPEG ghosts. IEEE Trans. Inf. Forensics Secur. 2009, 4, 154–160. [Google Scholar] [CrossRef]
- Luo, W.; Huang, J.; Qiu, G. JPEG Error Analysis and Its Applications to Digital Image Forensics. IEEE Trans. Inf. Forensics Secur. 2010, 5, 480–491. [Google Scholar] [CrossRef]
- Bianchi, T.; Piva, A. Detection of Nonaligned Double JPEG Compression Based on Integer Periodicity Maps. IEEE Trans. Inf. Forensics Secur. 2012, 7, 842–848. [Google Scholar] [CrossRef]
- Cao, G.; Zhao, Y.; Ni, R.; Li, X. Contrast Enhancement-Based Forensics in Digital Images. IEEE Trans. Inf. Forensics Secur. 2014, 9, 515–525. [Google Scholar] [CrossRef]
- Stamm, M.; Liu, K.J.R. Blind forensics of contrast enhancement in digital images. In Proceedings of the 15th IEEE International Conference on Image Processing, San Diego, CA, USA, 12–15 October 2008; pp. 3112–3115. [Google Scholar]
- Popescu, A.C.; Farid, H. Exposing digital forgeries by detecting traces of resampling. IEEE Trans. Signal Process. 2005, 53, 758–767. [Google Scholar] [CrossRef]
- Mahdian, B.; Saic, S. Blind Authentication Using Periodic Properties of Interpolation. IEEE Trans. Inf. Forensics Secur. 2008, 3, 529–538. [Google Scholar] [CrossRef]
- Li, L.; Xue, J.; Tian, Z.; Zheng, N. Moment feature based forensic detection of resampled digital images. In Proceedings of the 21st ACM International Conference on Multimedia, Barcelona, Spain, October 2013; pp. 569–572. [Google Scholar]
- Hou, X.; Zhang, T.; Xiong, G.; Lu, Z.; Xie, K. Resampling detection aided steganalysis of heterogeneous bitmap images. J. Electron. Imaging 2013, 22, 013037. [Google Scholar] [CrossRef]
- Chen, C.; Ni, J.; Huang, J. Blind Detection of Median Filtering in Digital Images: A Difference Domain Based Approach. IEEE Trans. Image Process. 2013, 22, 4699–4710. [Google Scholar] [CrossRef]
- Kang, X.; Stamm, M.C.; Peng, A.; Liu, K.J.R. Robust median filtering forensics based on the autoregressive model of median filtered residual. In Proceedings of the 2012 Asia Pacific Signal and Information Processing Association Annual Summit and Conference, Hollywood, CA, USA, 3–6 December 2012; pp. 1–9. [Google Scholar]
- Kirchner, M.; Fridrich, J. On detection of median filtering in digital images. In Media Forensics and Security II; SPIE: San Jose, CA, USA, 2010; 754110. [Google Scholar]
- Yuan, H.D. Blind Forensics of Median Filtering in Digital Images. IEEE Trans. Inf. Forensics Secur. 2011, 6, 1335–1345. [Google Scholar] [CrossRef]
- Shi, Y.Q.; Chen, C.; Xuan, G.; Su, W. Steganalysis versus Splicing Detection. Digit. Watermarking 2007, 5041, 158–172. [Google Scholar]
- He, Z.; Lu, W.; Sun, W.; Huang, J. Digital image splicing detection based on Markov features in DCT and DWT domain. Pattern Recognit. 2012, 45, 4292–4299. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, S.; Li, S.; Li, J. Passive Image-Splicing Detection by a 2-D Noncausal Markov Model. IEEE Trans. Circuits Syst. Video Technol. 2015, 25, 185–199. [Google Scholar] [CrossRef]
- Kao, H.-H.; Wen, C.-Y. An Offline Signature Verification and Forgery Detection Method Based on a Single Known Sample and an Explainable Deep Learning Approach. Appl. Sci. 2020, 10, 3716. [Google Scholar] [CrossRef]
- Hsu, C.-C.; Zhuang, Y.-X.; Lee, C.-Y. Deep Fake Image Detection Based on Pairwise Learning. Appl. Sci. 2020, 10, 370. [Google Scholar] [CrossRef]
- Rao, Y.; Ni, J. A deep learning approach to detection of splicing and copy-move forgeries in images. In Proceedings of the 2016 IEEE International Workshop on Information Forensics and Security, Abu Dhabi, UAE, 4–7 December 2016; pp. 1–6. [Google Scholar]
- Li, J.; Zhang, H.; Wan, W.; Sun, J. Two-class 3D-CNN classifiers combination for video copy detection. Multimed. Tools Appl. 2020, 79, 4749–4761. [Google Scholar] [CrossRef]
- Li, H.; Luo, W.; Qiu, X.; Huang, J. Identification of Various Image Operations Using Residual-based Features. IEEE Trans. Circuits Syst. Video Technol. 2016, 28, 31–45. [Google Scholar] [CrossRef]
- Fridrich, J.; Kodovsky, J. Rich Models for Steganalysis Digital Images. IEEE Trans. Inf. Forensics Secur. 2012, 7, 868–882. [Google Scholar] [CrossRef]
- Kodovsky, J.; Fridrich, J.; Holub, V. Ensemble Classifiers for Steganalysis of Digital Media. IEEE Trans. Inf. Forensics Secur. 2012, 7, 432–444. [Google Scholar] [CrossRef]
- Huang, T.; Yuan, X. Detection and Classification of Various Image Operations Using Deep Learning Technology. In Proceedings of the 2018 International Conference on Machine Learning and Cybernetics (ICMLC), Chengdu, China, 15–18 July 2018; pp. 50–55. [Google Scholar]
- Lippmann, R.P. Pattern classification using neural networks. IEEE Commun. Mag. 1989, 27, 47–50. [Google Scholar] [CrossRef]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. In NIPS’12: Proceedings of the 25th International Conference on Neural Information Processing Systems; Curran Associates Inc.: Red Hook, NY, USA, 2012; Volume 1, pp. 1097–1105. [Google Scholar]
- Bas, P.; Filler, T.; Pevný, T. Break our steganographic system: The ins and outs of organizing BOSS. In Information Hiding; IH 2011. Lecture Notes in Computer Science, Vol 6958; Filler, T., Pevný, T., Craver, S., Ker, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 59–70. [Google Scholar]
- Pevny, T.; Bas, P.; Fridrich, J. Steganalysis by Subtractive Pixel Adjacency Matrix. IEEE Trans. Inf. Forensics Secur. 2010, 5, 215–224. [Google Scholar] [CrossRef]
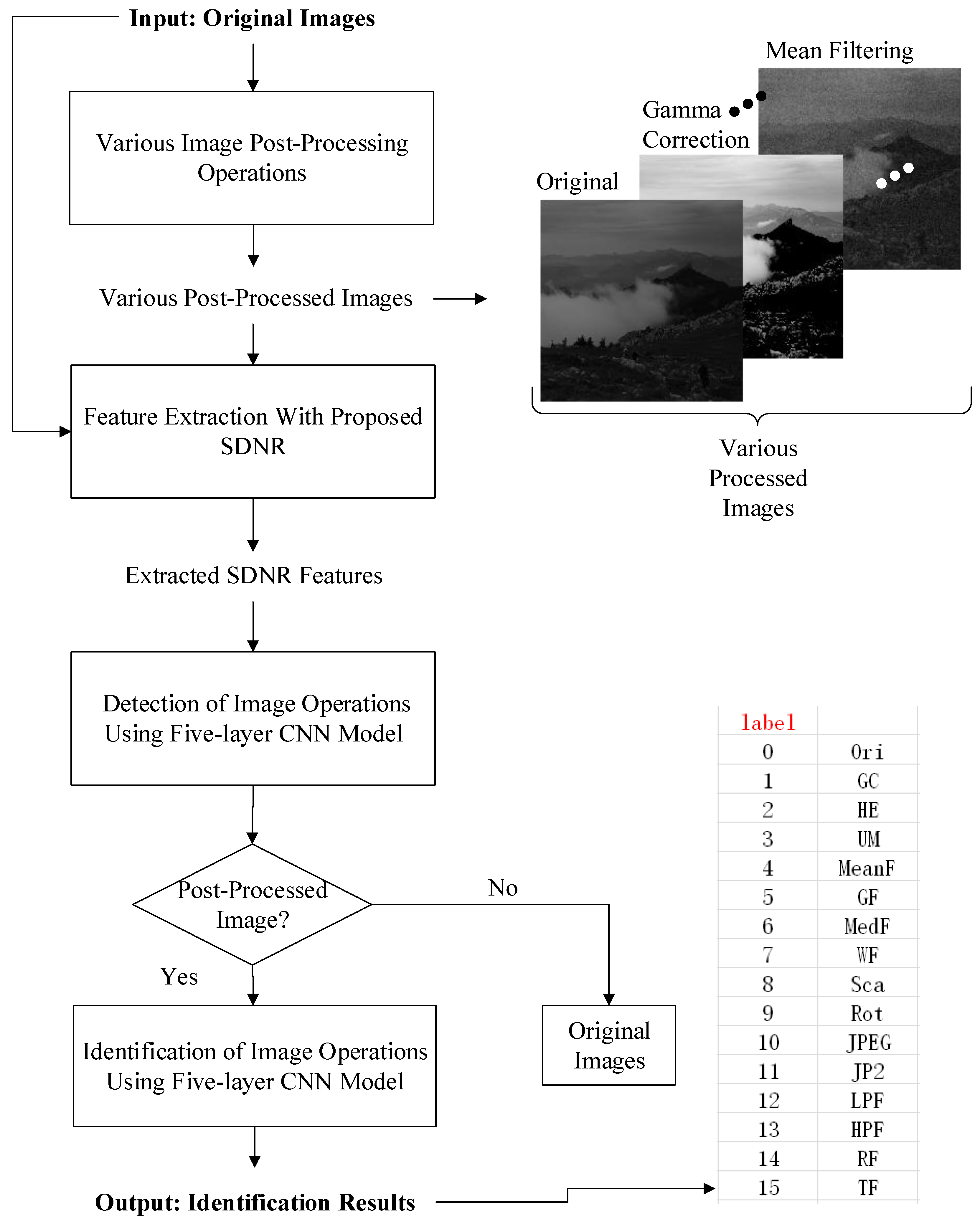
| Operation Categories | Operation Type | Parameter Setting |
|---|---|---|
| Spatial enhancement | Gamma Correction (GC) | γ: 1.0, 1.6, 1.8, 2.0 |
| Histogram Equalization (HE) | n/a | |
| Unsharp Masking Sharpening (UM) | σ: 0.5–1.5 τ: 0.5–1.5 | |
| Spatial filtering | Mean Filtering (MeanF) | Window sizes: 3 × 3, 5 × 5, 7 × 7 |
| Gaussian Filtering (GF) | Window sizes: 3 × 3, 5 × 5, 7 × 7 σ: 0.8–1.6 | |
| Median Filtering (MedF) | Windows size: 3 × 3, 5 × 5, 7 × 7 | |
| Wiener Filtering (WF) | Windows size: 3 × 3, 5 × 5, 7 × 7 | |
| Scaling | Scaling (Sca) | Down-sampling: 40%, 50%, 70% |
| Rotation | Rotation (Rot) | Angle: 30°, 35°, 40°, 45° |
| Lossy compression | JPEG | Quality factor: 80–90 |
| JPEG2000 (JP2) | Compression ratio: 4.0–6.0 | |
| Frequency filtering | Low-Pass Filtering (LPF) | Cutoff frequency: 80 Hz |
| High-Pass Filtering (HPF) | Cutoff frequency: 30 Hz | |
| Band-Stop Filtering (BF) | Stop band: 35–65 Hz | |
| Homomorphic Filtering (HF) | n/a |
| Classifier | Ensemble Classifier [24] | BPNN [26] | AlexNet [28] | Employed CNN | ||||
|---|---|---|---|---|---|---|---|---|
| Feature | SPAM [30] | Proposed SDNR | SPAM [30] | Proposed SDNR | SPAM [30] | Proposed SDNR | SPAM [30] | Proposed SDNR |
| GC | 96.2 | 96.4 | 92.1 | 93.1 | 95.3 | 96.7 | 96.5 | 97.6 |
| HE | 98.3 | 98.1 | 94.3 | 98.9 | 97.2 | 96.4 | 98.4 | 99.5 |
| UM | 97.2 | 98.3 | 96.4 | 96.2 | 98.6 | 98.7 | 97.6 | 99.3 |
| MeanF | 96.5 | 97.5 | 96.2 | 97.6 | 97.3 | 97.5 | 98.5 | 98.8 |
| MedF | 97.9 | 98.1 | 97.6 | 98.8 | 97.6 | 97.1 | 97.3 | 99.6 |
| WF | 98.8 | 99.6 | 96.2 | 97.1 | 98.5 | 96.5 | 97.1 | 97.6 |
| GF | 99.2 | 98.7 | 97.3 | 98.3 | 98.3 | 98.8 | 99 | 99.8 |
| SCA | 91.3 | 93.4 | 90.3 | 89.1 | 92.2 | 97.5 | 95.3 | 99.5 |
| ROT | 97.2 | 96.3 | 94.5 | 95.6 | 97.6 | 98.6 | 98.3 | 98.9 |
| JPEG | 95.3 | 96 | 96.8 | 97.4 | 98.5 | 99.2 | 97.8 | 98.2 |
| JP2 | 97.4 | 97.8 | 97.6 | 96.9 | 98.7 | 98.9 | 98.1 | 98.3 |
| LPF | 96.3 | 97.3 | 97.3 | 97.2 | 97.8 | 98.8 | 98.7 | 99.6 |
| HPF | 98.2 | 98.1 | 96.3 | 98.3 | 96.3 | 97.8 | 97.6 | 99.7 |
| BF | 93.3 | 95.3 | 84.2 | 86.7 | 94.6 | 95.6 | 97.2 | 98.2 |
| HF | 94.2 | 95.6 | 82.3 | 88.6 | 93.2 | 94.3 | 98 | 99 |
| Average | 96.5 | 97.1 | 94 | 95.3 | 96.8 | 97.5 | 97.7 | 98.9 |
| Actual/Predicted | Orig | GC | HE | UM | Rot | Sca | MeanF | MedF | WF | GF | JPEG | JP2 | LPF | HPF | HF | BF |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Orig | 90.3 | 0.4 | * | * | * | * | * | * | * | * | * | 1.6 | 3.3 | 1.6 | * | * |
| GC | 2 | 82.9 | 2.4 | 1.4 | 0.8 | * | * | 0.4 | * | * | 0.8 | 0.8 | * | * | * | * |
| HE | * | 0.2 | 99.3 | 0.3 | * | * | * | 0.1 | 0.2 | * | * | * | * | * | * | * |
| UM | 2.1 | 1.4 | 0.3 | 93.3 | * | * | * | 0.4 | 0.3 | * | * | 1 | * | * | * | * |
| Rot | 2.2 | 1.4 | * | * | 94.1 | 0.5 | * | * | * | * | * | * | 2 | * | 2 | * |
| Sca | 30.5 | 6.5 | * | 0.4 | * | 60.2 | * | * | * | * | 7.7 | * | 0.5 | 3 | * | 3 |
| MeanF | 0.3 | * | * | * | * | * | 98.8 | * | * | * | * | * | 0 | * | * | * |
| MedF | * | * | 0.8 | * | 0.4 | 0.4 | * | 97.7 | * | * | * | 0.2 | * | * | * | 0.2 |
| WF | * | * | * | * | * | * | * | * | 99.2 | * | * | * | * | * | * | * |
| GF | 1 | * | * | * | * | 0.4 | * | * | * | 99.9 | 2 | * | * | * | * | * |
| JPEG | * | 0.4 | * | 0.4 | * | 0.4 | * | 0.4 | 0.4 | * | 92.5 | 0.8 | 0.5 | 0.2 | 2 | 1 |
| JP2 | 1 | 0.4 | * | * | * | 0.4 | * | 0.4 | * | * | 2.4 | 87.4 | * | 0.2 | * | * |
| LPF | 0.3 | * | * | * | * | * | * | * | * | * | * | * | 98.6 | * | * | * |
| HPF | 0.2 | 0.1 | * | * | * | * | * | 0.1 | * | 0.2 | * | * | 0.1 | 98.4 | 0.1 | * |
| HF | 20.7 | * | * | * | * | 3.2 | 0.5 | 0.7 | 2.5 | 0.3 | * | 2.5 | * | * | 70.73 | * |
| BF | 30.5 | 10.7 | 4.2 | 1 | 5 | * | * | 0.5 | * | * | * | 3.5 | * | * | 1.6 | 59.4 |
| Actual/Predicted | Orig | GC | HE | UM | Rot | Sca | MeanF | MedF | WF | GF | JPEG | JP2 | LPF | HPF | HF | BF |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Orig | 87.5 | 0.4 | * | * | * | * | * | * | * | * | * | 2.4 | * | 1.6 | * | * |
| GC | 2 | 92.9 | 2.4 | 1.4 | 0.8 | * | * | 0.4 | * | * | 0.8 | 0.8 | * | * | * | * |
| HE | * | 0.2 | 98.7 | 0.3 | * | * | * | 0.1 | 0.2 | * | * | * | * | * | * | * |
| UM | 3.2 | 1.4 | 0.3 | 93.5 | * | * | * | 0.4 | 0.3 | * | * | 1 | * | * | * | * |
| Rot | 1.5 | 1.4 | * | * | 92.2 | 0.5 | * | * | * | * | * | * | 2 | * | 2 | * |
| Sca | 1.5 | * | * | 0.4 | * | 87.8 | * | * | * | * | * | * | 0.5 | 3 | * | 3 |
| MeanF | 0.3 | * | * | * | * | * | 99.7 | * | * | * | * | * | 0 | * | * | * |
| MedF | * | * | 0.8 | * | 0.4 | 0.4 | * | 97.1 | * | * | * | 0.2 | * | * | * | 0.2 |
| WF | * | * | * | * | * | * | * | * | 99.6 | * | * | * | * | * | * | * |
| GF | 1 | * | * | * | * | 0.4 | * | * | * | 94.8 | 2 | * | * | * | * | * |
| JPEG | * | 0.4 | * | 0.4 | * | 0.4 | * | 0.4 | 0.4 | * | 88.5 | 0.8 | 0.5 | 0.2 | 2 | 1 |
| JP2 | 1 | 0.4 | * | * | * | 0.4 | * | 0.4 | * | * | 2.4 | 89.7 | * | 0.2 | * | * |
| LPF | 0.3 | * | * | * | * | * | * | * | * | * | * | * | 97.5 | * | * | * |
| HPF | 0.2 | 0.1 | * | * | * | * | * | 0.1 | * | 0.2 | * | * | 0.1 | 98.2 | 0.1 | * |
| HF | 0.5 | * | * | * | * | 1 | 0.5 | 0.7 | 2.5 | 0.3 | * | * | * | * | 82.2 | * |
| BF | 1.1 | 0.8 | * | 1 | * | * | * | 0.5 | * | * | * | * | * | * | 1.6 | 81.1 |
| Actual/Predicted | Orig | GC | HE | UM | Rot | Sca | MeanF | MedF | WF | GF | JPEG | JP2 | LPF | HPF | HF | BF |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Orig | 94.6 | 0.4 | * | * | * | * | * | * | * | * | * | 2.4 | * | 1.6 | * | * |
| GC | 2 | 93.7 | 2.4 | 1.4 | 0.8 | * | * | 0.4 | * | * | 0.8 | 0.8 | * | * | * | * |
| HE | * | 0.2 | 99.1 | 0.3 | * | * | * | 0.1 | 0.2 | * | * | * | * | * | * | * |
| UM | 3.2 | 1.4 | 0.3 | 93.2 | * | * | * | 0.4 | 0.3 | * | * | 1 | * | * | * | * |
| Rot | 1.5 | 1.4 | * | * | 93.3 | 0.5 | * | * | * | * | * | * | 2 | * | 2 | * |
| Sca | 1.5 | * | * | 0.4 | * | 92.8 | * | * | * | * | * | * | 0.5 | 3 | * | 3 |
| MeanF | 0.3 | * | * | * | * | * | 99.7 | * | * | * | * | * | 0 | * | * | * |
| MedF | * | * | 0.8 | * | 0.4 | 0.4 | * | 98 | * | * | * | 0.2 | * | * | * | 0.2 |
| WF | * | * | * | * | * | * | * | * | 100 | * | * | * | * | * | * | * |
| GF | 1 | * | * | * | * | 0.4 | * | * | * | 96.6 | 2 | * | * | * | * | * |
| JPEG | * | 0.4 | * | 0.4 | * | 0.4 | * | 0.4 | 0.4 | * | 92.5 | 0.8 | 0.5 | 0.2 | 2 | 1 |
| JP2 | 1 | 0.4 | * | * | * | 0.4 | * | 0.4 | * | * | 2.4 | 92.5 | * | 0.2 | * | * |
| LPF | 0.3 | * | * | * | * | * | * | * | * | * | * | * | 99.7 | * | * | * |
| HPF | 0.2 | 0.1 | * | * | * | * | * | 0.1 | * | 0.2 | * | * | 0.1 | 99.2 | 0.1 | * |
| HF | 0.5 | * | * | * | * | 1 | 0.5 | 0.7 | 2.5 | 0.3 | * | * | * | * | 95.3 | * |
| BF | 1.1 | 0.8 | * | 1 | * | * | * | 0.5 | * | * | * | * | * | * | 1.6 | 94.6 |
| Classifier | BPNN [26] | AlexNet [28] | The Employed CNN Classifier | |||
|---|---|---|---|---|---|---|
| Feature | SPAM [30] | Proposed SDNR | SPAM [30] | Proposed SDNR | SPAM [30] | Proposed SDNR |
| ORI | 81.1% | 90.3% | 82.3% | 87.5% | 91.4% | 94.6% |
| GC | 82.1% | 82.9% | 91.3% | 92.9% | 87.5% | 93.7% |
| HE | 94.3% | 99.3% | 93.2% | 98.7% | 94.4% | 99.1% |
| UM | 96.4% | 93.3% | 91.6% | 93.5% | 69.1% | 93.2% |
| MeanF | 96.2% | 97.6% | 97.3% | 99.7% | 89.5% | 95.0% |
| MedF | 97.6% | 98.8% | 94.6% | 97.1% | 77.6% | 98.7% |
| WF | 96.2% | 99.7% | 96.5% | 99.6% | 92.1% | 100% |
| GF | 97.3% | 99.2% | 93.3% | 94.8% | 91.3% | 99.4% |
| SCA | 90.3% | 60.2% | 70.2% | 87.8% | 90.1% | 92.8% |
| ROT | 94.5% | 94.1% | 92.6% | 92.2% | 92.3% | 93.3% |
| JPEG | 96.8% | 92.5% | 91.5% | 88.5% | 80.4% | 92.5% |
| JP2 | 97.6% | 87.4% | 89.7% | 89.7% | 89.9& | 92.5% |
| LPF | 97.3% | 98.6% | 97.8% | 97.5% | 80.6% | 99.7% |
| HPF | 82.3% | 98.3% | 86.3% | 98.2% | 89.9% | 99.2% |
| HF | 64.2% | 59.4% | 84.6% | 82.2% | 61.1% | 95.3% |
| BF | 71.3% | 70.7% | 88.2% | 81.1% | 88.1% | 94.6% |
| Average | 89.7% | 88.89% | 90.6% | 92.2% | 85% | 95.9% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, X.; Huang, T. Spatial Domain-Based Nonlinear Residual Feature Extraction for Identification of Image Operations. Appl. Sci. 2020, 10, 5582. https://doi.org/10.3390/app10165582
Yuan X, Huang T. Spatial Domain-Based Nonlinear Residual Feature Extraction for Identification of Image Operations. Applied Sciences. 2020; 10(16):5582. https://doi.org/10.3390/app10165582
Chicago/Turabian StyleYuan, Xiaochen, and Tian Huang. 2020. "Spatial Domain-Based Nonlinear Residual Feature Extraction for Identification of Image Operations" Applied Sciences 10, no. 16: 5582. https://doi.org/10.3390/app10165582
APA StyleYuan, X., & Huang, T. (2020). Spatial Domain-Based Nonlinear Residual Feature Extraction for Identification of Image Operations. Applied Sciences, 10(16), 5582. https://doi.org/10.3390/app10165582





