Abstract
Underground structures can be vulnerable during strong earthquakes, and seismic mitigation systems designed for these structures are instrumental in improving multiple aspects of seismic performance. To deal with this problem, a novel isolation system is proposed for underground structures, employing the incorporation of a negative-stiffness amplification system (NSAS) and an isolator. The proposed NSAS consists of the subconfiguration of a spring with positive stiffness in parallel with a dashpot, which is then in series with a negative-stiffness device. The mechanical model and physical realization of the NSAS are presented, based on which the energy-dissipation-enhancement mechanism of NSAS is detailed. On this basis, comprehensive parameter analyses were conducted between the NSAS isolation system and a conventional isolation system. Analysis results showed that the NSAS exhibited a significant energy-dissipation-enhancement effect, in which the series connection of the negative and positive stiffnesses amplified the dashpot’s deformation for enhanced energy-dissipation capacity and efficiency. Compared with a conventional isolator, the NSAS isolation system provided the underground structure with a multiperformance and multilevel mitigation effect, particularly yielding lower responses of displacement and shear forces at the same time. More vibration energy could be dissipated by NSAS, thereby alleviating the energy-dissipation burden of underground structures.
1. Introduction
Underground structures are essential infrastructure of modern metropoles that can be vulnerable to strong earthquakes [1,2,3]. During the Great Hanshin earthquake in 1995, Daikai subway station suffered catastrophic damage [4,5]. Additionally, damages were also observed in underground structures after the Tang-Shan (Tang-Shan, China, 1976) [6], Parnitha (Parnitha, Athens, 1999) [7], Chi-Chi (Chi-Chi, China, 1999) [8] and Wen-Chuan earthquakes (Wen-Chuan, China, 2008) [9]. There is a broad need to improve the seismic safety of underground structures and develop innovative seismic-vibration control devices to protect underground structures from destruction during strong earthquakes [10,11,12]. Among the developed seismic-vibration control technologies, the seismic-isolation approach is definitely effective, involving installing an isolation system to reduce the seismic forces transferring from the foundation to the structure, and this approach has been used several decades for the earthquake protection of aboveground structures [13]. In recent years, seismic-isolation systems have been employed in underground structures to reduce or avoid excessive responses and seismic damage [14]. Existing studies on underground structures have reported that the central column is a key structural component whose failure leads to the collapse of the underground structure. Therefore, it was proposed that isolators be inserted at the top of central column to avoid excessive responses, especially with regard to shear forces. In employing conventional isolation systems (CISs) in underground structures, the implementation of flexible rubber joints [12], lead–rubber bearings [10] and sliding isolation bearings [11] has been proposed as an alternative selection. Despite the effectiveness of reducing shear force, the installation of the above CISs (flexible rubber joints, lead–rubber bearings, shear-panel dampers or sliding isolation bearings) cannot achieve high-level and multiperformance control, particularly the simultaneous control of both shear force and the relative displacement of underground structures.
Different from CISs with positive stiffness that resists the movement of the device, negative-stiffness control devices have the potential to improve structural dynamic performance by using their negative-stiffness mechanism. In an ideal scenario, a negative-stiffness device can produce negative resisting force that is proportional to its inner deformation. For the physical mechanisms of negative-stiffness elements, active [15], semiactive [16,17] and passive [18,19] negative-stiffness devices were developed, of which the passive type has attracted more attention, due to their stability and convenience. By utilizing precompressed springs [20,21], prebuckled columns [22] and friction pendulum sliding components [23], passive negative-stiffness devices yield satisfactory reaction forces to assist in the motion of the device [24]. Departing from the widely analyzed negative-stiffness effect, variants of negative-stiffness-based systems and the potential for improved energy-dissipation efficiency both remain unclear, especially in the vibration control of underground structures, which is of concern in this study. Resulting from the basic characteristic of a negative-stiffness spring, whereby it can assist in spring deformation, two spring devices with negative and positive stiffness in a series layout yielded an amplification effect [25]. As a consequence, a dashpot in parallel with a positive-stiffness spring can obtain amplified deformation for increased energy-dissipation efficiency and capacity, which provides improved seismic performance for the structures.
Therefore, a novel isolation system is proposed for the seismic-vibration control of underground structures, by incorporating a negative-stiffness amplification system (NSAS) and an isolator. The mechanical model, physical realization and energy-dissipation-enhancement mechanism of the NSAS are introduced and analyzed. Taking Daikai station as a typical example, comprehensive comparative analyses were conducted for the underground structure controlled with the NSAS and conventional isolation systems, of which the key performance, including the relative displacement of the central column, shear force and plastic-energy dissipation, was fully investigated. On the basis of the parametric analysis results, the effectiveness and suggested design parameters of the NSAS are provided for the seismic-vibration control of underground structures.
2. NSAS
2.1. NSAS Model
The NSAS was born from the combination of the typical Kelvin model (corresponding to the parallel configuration of the dashpot with damping coefficient and the spring with positive stiffness ) and a negative stiffness, , in a series layout. The series connection of two springs, respectively characterized by negative and positive stiffness, exhibited an amplification effect on the dashpot’s deformation for enhanced energy dissipation. The equivalent stiffness of this series connection of the two springs can also be evaluated as , which exhibits a negative-stiffness effect if the absolute value of is larger than that of . As an instructive example, a physical realization of the negative-stiffness device is presented as a frame-based component in Figure 1. A negative-stiffness device produces force that is in the same direction as that of the imposed displacement, thus the name “negative stiffness”. From a physical viewpoint, the negative-stiffness device is composed of a precompressed spring, shown in the center of the device, a pivot plate, lever, top and bottom chevron braces, and the two double-hinged columns. When the device is deformed, the precompressed spring rotates and exerts force in the direction of the displacement (introducing negative stiffness). Force in the precompressed spring is reduced as displacement is increased, so the negative-stiffness value is reduced with increasing displacement.
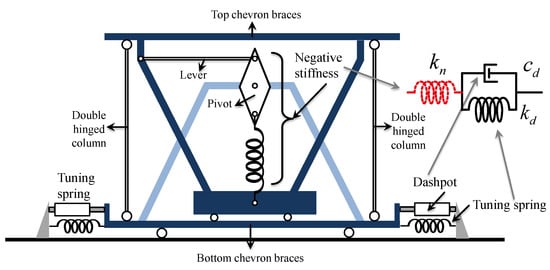
Figure 1.
Physical realization and mechanical model of a negative-stiffness amplification system (NSAS).
2.2. Governing Equation
The preliminary analysis of the NSAS was for a single-degree-of-freedom (SDOF) structure (Figure 2), consisting of mass , a spring with stiffness , and a viscous dashpot with damping coefficient . Subject to base excitation , an NSAS is equipped with the primary structure to mitigate the oscillating motion. The mechanical system is described in nondimensional form, including damping ratio , negative-stiffness ratio and stiffness ratio . The primary structure is characterized by circular frequency and inherent damping ratio . In the ultimate condition, where , the structural spring is in parallel with the proposed NSAS. The governing equation established for the NSAS–SDOF structure was
where the overdot signifies the derivative with respect to time . Displacement vector , excitation-location vector , the NSAS structure matrices of mass , stiffness and damping are given in detail as
where is the displacement of the primary structure relative to the ground, and is the inner deformation of the dashpot (equal to the deformation of the spring with positive stiffness). In the state-space form, where the state vector is , the governing equations can be rewritten as
where system matrix and the excitation-location vector in state-space can be determined as
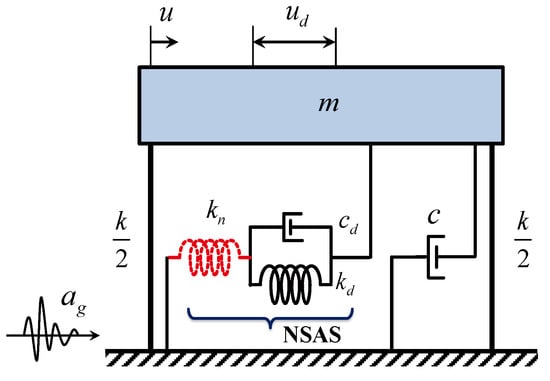
Figure 2.
Model of a single-degree-of-freedom (SDOF) structure with proposed NSAS.
The analytical solution to Equation (4) from time to is
2.3. Energy-Dissipation-Enhancement Effect
By utilizing the series connection of the two springs with negative and positive stiffnesses, the deformation of the dashpot (in parallel with ) could be amplified, as negative-stiffness device potentially supported the movement of the dashpot. As a result, in Figure 3, exhibited dashpot deformation could be larger than the entire deformation of the NSAS that was equal to the displacement of the SDOF structure. In this study, this dashpot-deformation amplification result is named as the energy-dissipation-enhancement effect, referring to the benefit that the NSAS presented in terms of enhanced energy-dissipation efficiency and capacity in comparison to that of a conventional dashpot. Especially for underground structures with limited deformation, this enhancement effect improves its seismic performance, which is explained in the following sections.
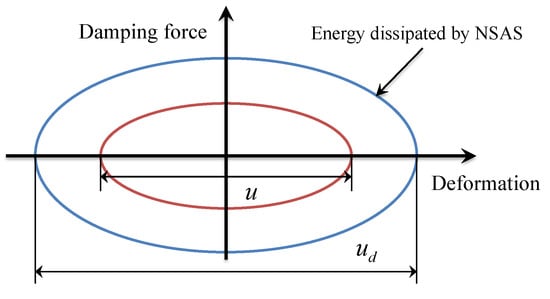
Figure 3.
Illustration of energy-dissipation-enhancement effect of NSAS.
3. NSAS-Based Underground Structure
3.1. Mechanical Model
This study proposes the idea that the NSAS is employed for the seismic-response control of underground structures, simultaneously utilizing the negative-stiffness behavior of the device and the energy-dissipation mechanism. Considering the dynamic interaction behavior between soil and underground structures, Figure 4 presents the soil–underground structure interaction system, wherein the rectangular underground structure consists of the upper slab, the bottom slab, the sidewall, and the central column. The NSAS is also applicable for other types of underground structures with more complex typology, including those of numerous stories and spans [7,26]. Dealing with the control problem of the vulnerable component, i.e., the central column, the proposed NSAS was set in parallel with a linear isolator, and then inserted between the top of the central column and the bottom of the upper slab (see Figure 4). The combination of the NSAS and isolator is ideally represented as the mechanical network in Figure 4 and in Figure 2 (). Conceptually, the combination of NSAS and isolator yielded an improved isolation effect, that more significantly reduced the shear force of the central column in comparison with the conventional isolator. At the same time, the NSAS also contributed to an enhanced mitigation effect for the displacement of the central column, which resulted from the enhanced damping effect.
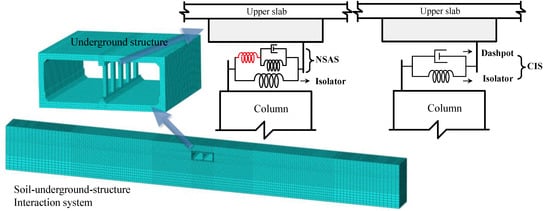
Figure 4.
Model of soil–underground structure interaction system controlled by conventional isolation system (CIS) and by NSAS combined with an isolator.
3.2. Soil and Boundary Conditions
For the analyzed underground structure with the control of the NSAS isolation system imbedded in the soil, numerical models were developed using ABAQUS [27]. For the sake of accuracy, the finite-element simulation techniques that were proven in previous studies were employed [28,29]. The mechanical properties of concrete and reinforced steel are represented by the classic concrete damaged plasticity model [30] and the bilinear plastic model [31], respectively. The classic Davidenkov model was proposed by Martin and Seed [32], and has been proven to be an effective model for describing the dynamic stress–strain relationship of soil [33]. Therefore, a constitutive model based on the classical Davidenkov method was developed and utilized to simulate the dynamic behavior of the surrounding soil. Details and validation of this model can be found elsewhere [34]; briefly, the tangent shear modulus for initial loading is
For unloading and reloading, it is
where superscripts and represent the tangent shear modulus at the end of the current and previous increments, respectively; is the maximal shear modulus of the soil; and are the shear stress and strain of soil, respectively; is the shear strain in the last load reversal, and is a shape function given by
where , and are fitting parameters of the model. To intuitively illustrate this model, its dynamic shear stress–shear strain curves are plotted in Figure 5, taking as an example.
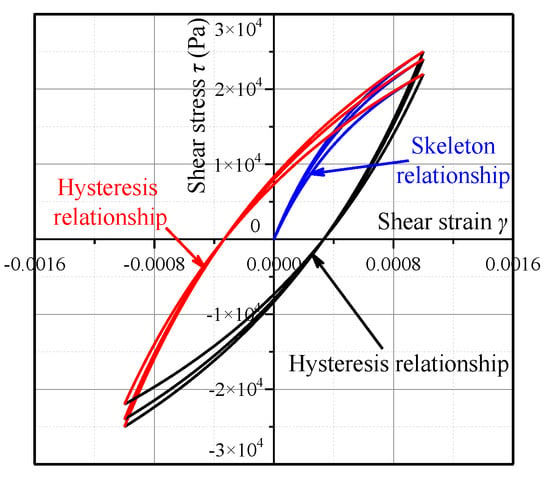
Figure 5.
Dynamic shear stress–strain relationship of the Davidenkov model.
In the finite-element simulation, a typical artificial constrained boundary [26], shown in Figure 6, was utilized to deal with the static–dynamic boundary-coupling conditions by using the classical procedure of finite-element software. In the geostatic step, the horizontal direction of the side boundary was constrained; then, reaction forces on the side boundaries were outputted after the geostatic step had been completed. Before conduct dynamic analysis, the side boundaries were converted by applying the horizontal outputted reaction forces in the direction of the side boundary, and the vertical direction was constrained.
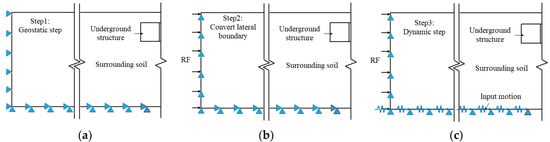
Figure 6.
Transformation of boundary condition during analysis: (a) geostatic step; (b) convert lateral boundary; and (c) dynamic step.
Referring to the design code [35], a stratum wherein shear-wave velocity is greater than 300 m/s can be selected as the artificial bedrock. At the same time, for the bottom boundary condition [36], the distance between the bottom of the soil and the underground structure should not be less than three times the height of the underground structure, which is selected in this study. The side boundary of soil is simulated by analyzing soil with 10 times the width of the soil depth, which was proven in previous studies to be effective in preventing propagating waves that reflect back to the model [28].
To simulate the contact behavior at interfaces during an earthquake, frictional surfaces were adopted as interfaces between the soil and the underground structure [37]. As given in Figure 7, in the normal direction, contact compressive stresses on different surfaces were mutually transferred through the contact constraint. In the tangential direction, the boundary constraint is represented by contact shear stress. In the case where contact shear stress exceeds critical stress , slipping can occur. Critical stress can be obtained with
where is the friction coefficient, and for interfaces between soil and underground structure [37]; is normal contact stress.
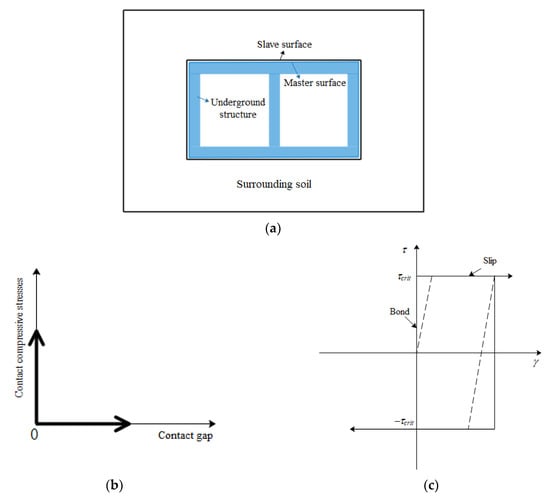
Figure 7.
Models of dynamic contact behavior between soil and underground structure: (a) master–slave surface relationship; contact behavior in (b) normal and (c) tangential directions.
4. NSAS Effectiveness for Underground Structures
4.1. Measurement Definition
Referring to Section 2.2, the NSAS isolation system is described in nondimensional form for underground structures, including damping ratio , negative-stiffness ratio , and stiffness ratio ; and denote the mass of the central column and the stiffness of the isolator inserted between the central column and the upper slab.
Dimensionless measurements are defined by comparing the seismic responses of the underground structure controlled by the NSAS isolation system or conventional isolation system (CIS, including the linear isolator in parallel with a dashpot, same as the NSAS isolation system) to those of the uncontrolled underground structure. The criteria of peak responses (represented by ) and root mean square (RMS, represented by ) were adopted in terms of the relative displacement between the top and the bottom of the central column, and the base shear force of the column, as
where and are the peak and RMS responses, respectively, of the relative displacement between the top and the bottom of the central column under the control of the NSAS or CIS, respectively. and are the peak and RMS responses, respectively, of the shear force of the central column under the control of the NSAS or CIS. Footnote “0” refers to a case of the uncontrolled underground structure without any control devices.
Given the established measurement system, Daikai station was adopted as a typical example [38] to demonstrate the seismic-vibration mitigation effect and the feasibility of the proposed NSAS isolation system. The obtained effectiveness and design can be used as guidelines for other typical underground structures with similar and more complex typologies. Daikai station was severely damaged during the 1995 Great Hanshin earthquake [4]. It is a typical two-span subway station with a cross-section, displayed in Figure 8. The dimensions of the central column are 0.40 × 1.0 m, and the space between central columns is 3.5 m. The density, Poisson’s ratio and Young’s modulus of the structural concrete in this model were 2500 kg/m3, 0.20 and 30 GPa, respectively. The initial compression yield stress, initial tensile yield stress and limited compression yield stress of the concrete material were 18.8, 2.4 and 26.8 MPa, respectively [11].
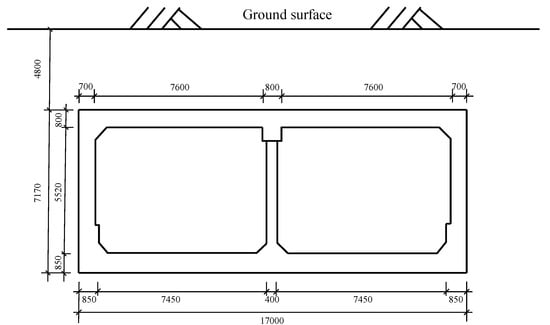
Figure 8.
Cross-section of Daikai station (unit: mm).
Daikai station was built on diluvial deposits and is overlain by alluvial deposits. The soil profile can be simplified into seven horizontally layered soil layers, and the characteristics and properties for each soil layer can be found in Table 1 [28]. Location between subway station and soil is shown in Figure 9. When using the Davidenkov model, outlined in Section 3.2, to simulate the dynamic behavior of soil, the fitting parameters , and in Equations (6)–(8) for different types of soil are referred to in [39].

Table 1.
Soil profile of Daikai station.
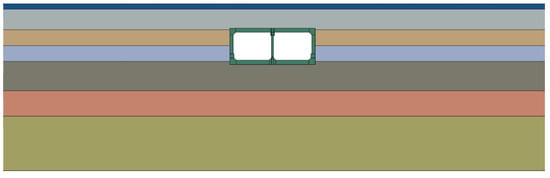
Figure 9.
Location between subway station and soil.
Widely accepted as representative of the ground motion (Figure 10a) at Daikai station [40], the north–south component of ground motion recorded at Port Island station during the 1995 Great Hanshin earthquake was used as the seismic input in this study. For this horizontal ground motion with a maximal value of 0.58 g, the strong motion lasted for about 10 to 15 s, and gradually decreased afterward. According to the design code [41], the seismic excitation in the vertical direction can be obtained by modulating the horizontal-acceleration amplitude of the recorded wave. Given the target that deals with the seismic performance of a horizontal isolator, the vertical input was simplified by following the code, and the maximal value was scaled as 0.16 g [10]. The ground motion (see Figure 10b) of the Great Hanshin earthquake recorded at the HIK station was selected for validation analysis.
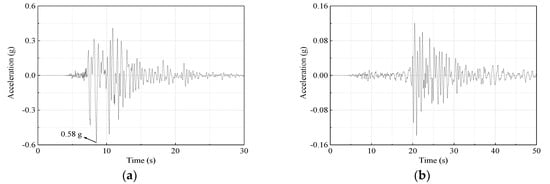
Figure 10.
Time series of input acceleration for Daikai station (horizontal direction). (a) Port Island and (b) HIK station records.
Before investigating the seismic performance of the underground structure controlled with the NSAS or CIS, nonlinear dynamic time-series analyses were performed for the original uncontrolled underground structure as a reference. As summarized, the maximal displacement, shear force and axial force of the central column without any seismic-vibration control systems were 38 mm, 767 kN and 4887 kN, respectively. Consistent with the results given by Huo et al. [37], Parra-Montesinos et al. [40] and Chen et al. [10], excessive seismic responses and failure of the central column caused the collapse of the Daikai subway station. Therefore, the NSAS and CIS were selected to be inserted between the top of the central column and the bottom of the upper slab to provide satisfactory performance for the central column.
4.2. Displacement Control
Dealing with the improvement of the NSAS isolation system compared with the CIS, the CIS stiffness and damping parameters were designed by referring to [10]. CIS stiffness was 18,000 kN/m, and the damping coefficient was 40 kNs/m. The maximal shear force under CIS control was 308 kN, potentially presenting about a 60% decrease of shear force response. The maximal displacement of the top relative to the bottom of the central column was 54 mm.
Given the same isolator and dashpot designed for CIS, the NSAS isolation system was further designed with variable negative-stiffness ratio and positive-stiffness ratio . Analysis results of and are plotted in Figure 11, for 0.30, 0.35, 0.40 and 0.50, respectively, and −0.10, −0.15, −0.20 and −0.25, respectively. Furthermore, the red, green, blue and light blue bars are used to represent different parameter sets of −0.10, −0.15, −0.20 and −0.25. These values are given in Table 2 and Table 3, respectively. For the majority of the parameter sets of and , and were lower than 1.0. In the sense of peak- and RMS response-based evaluation, the NSAS isolation system exhibited improved capacity for seismic-vibration control of the relative displacement of the central column in comparison with that of the CIS. Specifically, when and , the values of and were 0.85 and 0.87, respectively, which indicated about a 15% decrease in the relative displacement of the central column. On the basis of the enhanced energy-dissipation effect introduced in Section 2.3, the damping coefficient of the NSAS isolation system, the same as that of the CIS, provided a more effective mitigation of the relative displacement of the central column of the underground structure. As an intuitive illustration, the relative displacement responses of the central column were plotted for the uncontrolled underground structure, and the structures controlled with the NSAS isolation system (, ) and CIS, as shown in Figure 12. With the installation of the NSAS isolation system and CIS, the maximal displacement of the central column was increased from 38 to 46 and to 54 mm, respectively. Compared with the case of the original uncontrolled central column (38 mm), the maximal relative displacement of the central column was decreased from 16 (CIS) to 8 mm (NSAS isolation system), resulting in about a 50% reduction using the NSAS isolation system. At the end of the earthquake, the column exhibited permanent displacement in the uncontrolled underground structures, and in underground structures with CIS and NSAS isolation systems. This phenomenon was caused by the damage of the underground structure and the plastic soil deformations that had accumulated during the earthquake loading cycles.
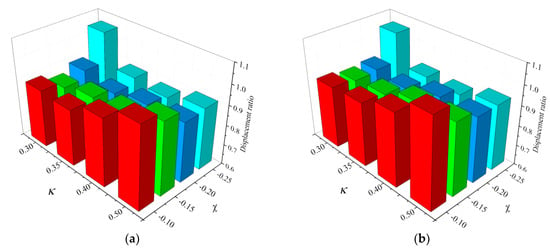
Figure 11.
Ratios of the relative displacements of the central column of the underground structures controlled with a negative-stiffness amplification-system (NSAS)-based isolation system, and a conventional isolation system (CIS): (a) ;(b) .

Table 2.
Values of

Table 3.
Values of
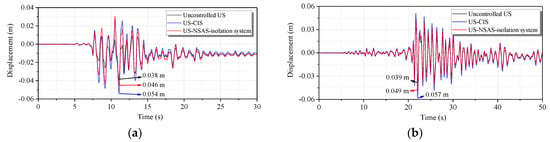
Figure 12.
Time series of relative displacements of central column for uncontrolled underground structure (US), controlled by conventional isolation system (US-CIS) and controlled by negative stiffness amplification system (US-NSAS)-based isolation system. (a) Port Island and (b) HIK station records.
4.3. Shear Force Control
With regard to the shear force control effect of the NSAS isolation system, compared to that of the CIS, the analysis results of and are plotted in Figure 13, for the same parameter sets of and as those in the above section. These values are given in Table 4 and Table 5, respectively. This is consistent with the concept that the negative-stiffness effect of NSAS provides an improved isolation effect to the isolator placed in parallel. For NSASs with different and parameters, and were much lower than 1.0. Specifically, when and , the values of and were 0.41 and 0.58, respectively, which indicated about 59% and 42% decreases in maximal and RMS shear force, in comparison with the case of CIS. Apart from the enhanced effectiveness of NSAS for displacement control, the negative-stiffness mechanism of NSAS yielded a more significant isolation effect in order to reduce the shear force of the central column. As an intuitive illustration, the shear force responses were plotted for the uncontrolled underground structure, as well as for the structures controlled with the NSAS isolation system (, ) and CIS, shown in in Figure 14. Compared with the case of the original uncontrolled central column, the maximal shear force decreased from 767 to 308 kN (for CIS), and to 127 kN (for NSAS isolation system), simultaneously reporting a significant reduction in shear force in the entire time domain.
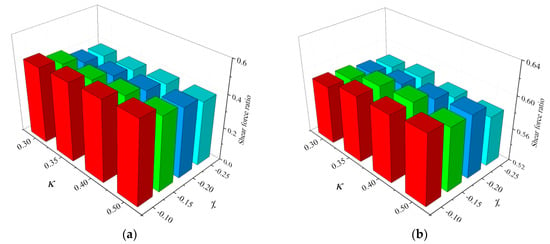
Figure 13.
Ratios of shear forces between NSAS-based isolation system and CIS: (a) ; (b) .

Table 4.
Values of

Table 5.
Values of
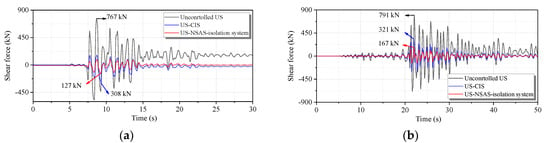
Figure 14.
Time series of shear force for uncontrolled underground structure (US), controlled by conventional isolation system (US-CIS) and controlled by negative-stiffness amplification system (US-NSAS)-based isolation system. (a) Port Island and (b) HIK station records.
At the end of the earthquake, as shown in Figure 14, the column exhibited a permanent load for uncontrolled underground structures due to the damage of the underground structure and the plastic soil deformations that accumulated during the earthquake loading cycles. However, for the underground structures controlled with the CIS and NSAS isolation system, the permanent load was released due to the use of isolation systems. The results are consistent with previous studies.
4.4. Energy-Based Damage Control
As a robust evaluation index for this type of seismic excitation [42,43,44,45,46], energy-dissipation distributions between different components of an uncontrolled underground structure and structures with a CIS or the NSAS isolation system are shown in Figure 15. Since the central column of the Daikai subway station was severely damaged in the uncontrolled structure, after the installation of the CIS and NSAS isolation system the proportion of energy dissipated by the central column was decreased from 20.42% to 3.18% and 1.61%, respectively. At the same time, the dissipated energy by the wall-slab structures (upper slab, bottom slab and sidewall) was increased by a small amount in the acceptable range. Quantitively, the maximal plastic-energy densities (plastic-energy dissipated by the unit volume of the structure) of the different structural components are listed in Table 6 in order to characterize the degree of unwanted damage. The maximal plastic-energy density of the central column was decreased from 2221 (uncontrolled) to 210 (CIS) and 138 J/m3 (NSAS isolation system). Benefitting from the energy-dissipation mechanism of the NSAS, the proposed NSAS isolation system undertook a heavier energy-dissipation burden to ensure the more effective protection effect of the central column. Particularly, the energy-dissipation proportions of the dashpots of the NSAS isolation system and CIS were, respectively, 4.2% and 1.2%. The NSAS isolation system proposed in this study had a better energy-dissipation effect than that of a conventional seismic-vibration control system. For the wall-slab structures, an increase of about 20% in maximal plastic-energy density was observed, which cannot significantly affect the seismic performance of wall-slab structures [10].
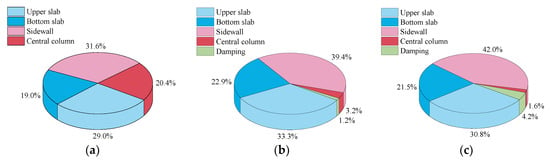
Figure 15.
Energy-dissipation proportion for (a) uncontrolled US, (b) US-CIS and (c) US-NSAS isolation system.

Table 6.
Maximal plastic-energy density for different parts of underground structure (US).
Moreover, the histograms of plastic-energy proportion for the uncontrolled underground structure and the structures controlled by the CIS and NSAS isolation system under seismic excitation, with increased intensities, are illustrated in Figure 16. Subject to excitation at variable intensities, the CIS and NSAS isolation system exhibited effectiveness in releasing the energy-dissipation burden of the central column. More importantly, the proportion of energy dissipated by the NSAS isolation system was always larger than that of CIS, which further stressed the energy enhancement of the NSAS isolation system. The dashpot hysteresis curves in the CIS and NSAS isolation system are illustrated in Figure 17. It is clear that the amplification of the dashpot deformation in the NSAS isolation system resulted in an obviously improved energy-dissipation capacity using the same damping ratio. In other words, only a lower damping ratio was required in the NSAS isolation system in order to satisfy the same energy-dissipation effect as that of the CIS. These results also demonstrated the robustness of the NSAS isolation system, which guarantees multilevel safety for underground structures.
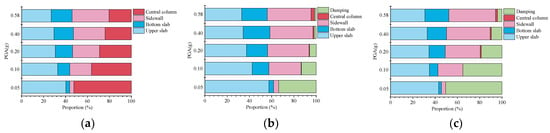
Figure 16.
Histogram of energy proportions for (a) uncontrolled US, (b) US-CIS and (c) US-NSAS isolation system.
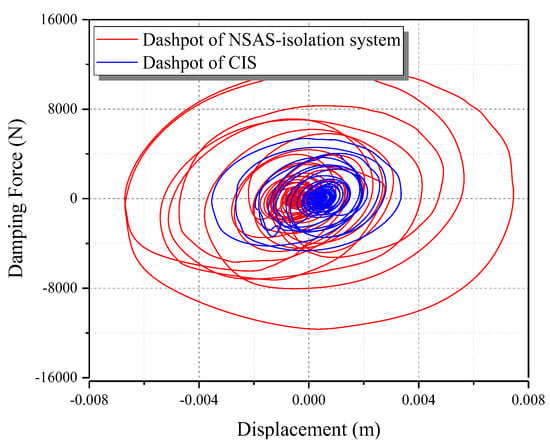
Figure 17.
Hysteresis curves of dashpots in CIS and NSAS isolation system.
5. Conclusions
This study proposed a novel isolation system for underground structures by employing the incorporation of a negative-stiffness amplification system (NSAS) and an isolator. Considering the energy-dissipation-enhancement effect, extensive parametric and comparative analysis was conducted to examine the effectiveness and design of the NSAS. The conclusions are summarized as follows:
- (1)
- The system is effective in the vibration control of underground structures, and it exhibited a significant energy-dissipation-enhancement effect in which the series connection of the negative and positive stiffnesses amplified dashpot deformation for enhanced energy-dissipation capacity and efficiency.
- (2)
- In comparison to a conventional isolator with the same damping coefficient, the NSAS isolation system provides underground structures with a multiperformance effect. Particularly, the simultaneous relative displacement of the central column and shear force responses can be mitigated more effectively by the NSAS.
- (3)
- Benefiting from the energy-dissipation-enhancement effect, more vibration energy can be dissipated by the NSAS, thereby reducing the energy-dissipation burden of the central column. Under seismic excitation with different intensity levels, the enhanced energy-dissipation capacity of the NSAS isolation system held true, which demonstrated the robustness of the proposed system for the multilevel safety of underground structures.
- (4)
- The objective of this study was to develop a novel isolation system, the NSAS, for the vibration mitigation of underground structures. In future studies, the parameter design of NSAS for underground structures should be detailed. Correspondingly, the design method and the energy-dissipation-enhancement effect of NSAS should be further verified by experiment analysis.
The proposed NSAS isolation system may bring some difficulties in manufacturing and installation in underground structures. In future studies, an experimental study of the NSAS isolation system for the seismic-vibration control of underground structures should be undertaken.
Author Contributions
Conceptualization: Q.C. and Z.Z.; methodology: Q.C., Y.W., and Z.Z.; software: Y.W. and Z.Z.; validation: Q.C., Z.Z., and Y.W.; formal analysis: Z.Z. and Y.W.; investigation: Q.C., Y.W., and Z.Z.; data curation: Y.W. and Z.Z.; writing—original draft preparation: Q.C., Y.W., and Z.Z.; writing—review and editing: Q.C., Y.W., Z.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the National Natural Science Foundation of China (grant number 51778489), the National Science and Technology Pillar Program of China (grant No. 2015BAK17B04), and the Basic Research Project of State Key Laboratory of Ministry of Science and Technology (grant number SLDRCE19A-02).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lanzano, G.; Bilotta, E.; Russo, G. Tunnels under seismic loading: A review of damage case histories and protection methods. In Strategies for Reduction of the Seismic Risk; StreGa: Ripalimosani (CB), Italy, 2008; pp. 65–75. [Google Scholar]
- Zhang, Z.M.; Bilotta, E.; Yuan, Y.; Yu, H.T.; Zhao, H.L. Experimental assessment of the effect of vertical earthquake motion on underground metro station. Appl. Sci. 2019, 9, 5182. [Google Scholar] [CrossRef]
- Pitilakis, K.; Tsinidis, G. Performance and Seismic Design of Underground Structures, Earthquake Geotechnical Engineering Design; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Iida, H.; Hiroto, T.; Yoshida, N.; Iwafuji, M. Damage to Daikai subway station. Soils Found. 1996, 36, 283–300. [Google Scholar] [CrossRef]
- An, X.; Shawky, A.A.; Maekawa, K. The collapse mechanism of a subway station during the Great Hanshin earthquake. Cem. Concr. Compos. 1997, 19, 241–257. [Google Scholar] [CrossRef]
- Ming, W.J.; Litehiser, J.J. The distribution of earthquake damage to underground facilities during the 1976 Tang-Shan earthquake. Earthq. Spectra 1985, 1, 741–757. [Google Scholar] [CrossRef]
- Gazetas, G.; Gerolymos, N.; Anastasopoulos, I. Response of three Athens metro underground structures in the 1999 Parnitha earthquake. Soil Dyn. Earthq. Eng. 2005, 25, 617–633. [Google Scholar] [CrossRef]
- Wang, W.L.; Wang, T.T.; Su, J.J.; Lin, C.H.; Seng, C.R.; Huang, T.H. Assessment of damage in mountain tunnels due to the Taiwan Chi-Chi Earthquake. Tunn. Undergr. Space Technol. 2001, 16, 133–150. [Google Scholar] [CrossRef]
- Lai, J.; He, S.; Qiu, J.; Chen, J.; Wang, L.; Wang, K.; Wang, J. Characteristics of seismic disasters and aseismic measures of tunnels in Wenchuan earthquake. Environ. Earth Sci. 2017, 76, 94. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Zhao, H.; Lou, M.L. Seismic performance and optimal design of framed underground structures with lead-rubber bearings. Struct. Eng. Mech. 2016, 58, 259–276. [Google Scholar] [CrossRef]
- Ma, C.; Lu, D.C.; Du, X.L. Seismic performance upgrading for underground structures by introducing sliding isolation bearings. Tunn. Undergr. Space Technol. 2018, 74, 1–9. [Google Scholar] [CrossRef]
- Mikami, A.; Konagai, K.; Sawada, T. Stiffness design of isolation rubber for center columns of tunnel. Doboku Gakkai Ronbunshu 2001, 415–420. [Google Scholar] [CrossRef]
- Buckle, I.G.; Mayes, R.L. Seismic isolation: History, application, and performance—A world view. Earthq. Spectra 1990, 6, 161–201. [Google Scholar] [CrossRef]
- Kiryu, S.; Murono, Y.; Morikawa, H. Seismic response of a cut-and-cover tunnel isolated by polymer material. Earthq. Eng. Struct. Dyn. 2012, 41, 2043–2057. [Google Scholar] [CrossRef]
- Li, H.; Liu, J.L.; Ou, J.P. Seismic response control of a cable-stayed bridge using negative stiffness dampers. Struct. Control Health Monit. 2011, 18, 265–288. [Google Scholar] [CrossRef]
- Iemura, H.; Pradono, M.H. Passive and semi-active seismic response control of a cable-stayed bridge. J. Struct. Control 2002, 9, 189–204. [Google Scholar] [CrossRef]
- Hogsberg, J.B. The role of negative stiffness in semi-active control of magneto-rheological dampers. Struct. Control Health Monit. 2011, 18, 289–304. [Google Scholar] [CrossRef]
- Sarlis, A.A.; Pasala, D.T.R.; Constantinou, M.C.; Reinhorn, A.M.; Nagarajaiah, S.; Taylor, D.P. Negative stiffness device for seismic protection of structures. J. Struct. Eng. 2013, 139, 1124–1133. [Google Scholar] [CrossRef]
- Pasala, D.T.R.; Sarlis, A.A.; Nagarajaiah, S.; Reinhorn, A.M.; Constantinou, M.C.; Taylor, D.P. Adaptive negative stiffness: New structural modification approach for seismic protection. J. Struct. Eng. 2013, 139, 1112–1123. [Google Scholar] [CrossRef]
- Kwon, I.Y.; Yang, H.T.; Hansma, P.K.; Randall, C. Implementable bio-inspired passive negative spring actuator for full-scale structural control under seismic excitation. J. Struct. Eng. 2016, 142, 04015079. [Google Scholar] [CrossRef]
- Attary, N.; Symans, M.D.; Nagarajaiah, S. Development of a rotation-based negative stiffness device for seismic protection of structures. J. Vib. Control 2017, 23, 853–867. [Google Scholar] [CrossRef]
- Kalathur, H.; Lakes, R.S. Column dampers with negative stiffness: High damping at small amplitude. Smart Mater. Struct. 2013, 22, 084013. [Google Scholar] [CrossRef]
- Iemura, H.; Pradono, M.H. Advances in the development of pseudo-negative-stiffness dampers for seismic response control. Struct. Control Health Monit. 2009, 16, 784–799. [Google Scholar] [CrossRef]
- Riosgarcia, G.; Benaventcliment, A. New rocking column with control of negative stiffness displacement range and its application to RC frames. Eng. Struct. 2020, 206, 110133. [Google Scholar] [CrossRef]
- Wang, M.; Sun, F.F.; Yang, J.Q.; Nagarajaiah, S. Seismic protection of SDOF systems with a negative stiffness amplifying damper. Eng. Struct. 2019, 190, 128–141. [Google Scholar] [CrossRef]
- Zhuang, H.Y.; Hu, Z.H.; Wang, X.J.; Chen, G.X. Seismic responses of a large underground structure in liquefied soils by FEM numerical modelling. Bull. Earthq. Eng. 2015, 13, 3645–3668. [Google Scholar] [CrossRef]
- ABAQUS. Theory and Analysis User’s Manual Version 6.12; Dassault Systems SIMULIA Corp: Providence, RI, USA, 2012. [Google Scholar]
- Li, W.; Chen, Q.J. Effect of vertical ground motions and overburden depth on the seismic responses of large underground structures. Eng. Struct. 2020, 205, 110073. [Google Scholar] [CrossRef]
- Li, W.; Chen, Q.J. Seismic damage evaluation of an entire underground subway system in dense urban areas by 3D FE simulation. Tunn. Undergr. Space Technol. 2020, 99, 103351. [Google Scholar] [CrossRef]
- Lee, J.; Fenves, G.L. Plastic-damage model for cyclic loading of concrete structures. J. Eng. Mech. 1998, 124, 892–900. [Google Scholar] [CrossRef]
- Chopra, A.K.; Chintanapakdee, C. Inelastic deformation ratios for design and evaluation of structures: Single-degree-of-freedom bilinear systems. J. Struct. Eng. 2004, 130, 1309–1319. [Google Scholar] [CrossRef]
- Martin, P.P.; Seed, H.B. One-dimensional dynamic ground response analyses. J. Geotech. Eng. Div. 1982, 108, 935–952. [Google Scholar] [CrossRef]
- Ge, Q.; Xiong, F.; Xie, L.W.; Chen, J.; Yu, M.J. Dynamic interaction of soil—Structure cluster. Soil Dyn. Earthq. Eng. 2019, 123, 16–30. [Google Scholar] [CrossRef]
- Chen, Q.J.; Wang, Y.C.; Zhao, Z.P. Energy spectrum study and optimal design of an inerter-based structure considering the underlying soil. Appl. Sci. 2020, 10, 2999. [Google Scholar] [CrossRef]
- JGS-4001-2004. Principles for Foundation Designs Grounded on a Performance-Based Design Concept; Japanese Geotechnical Society: Tokyo, Japan, 2006. [Google Scholar]
- GB/T-51336-2018. Standard for Seismic Design of Underground Structures; Architecture and Building Press: Beijing, China, 2018. [Google Scholar]
- Huo, H.; Bobet, A.; Fernández, G.; Ramirez, J. Load transfer mechanisms between underground structure and surrounding ground: Evaluation of the failure of the Daikai station. J. Geotech. Geoenviron. Eng. 2005, 131, 1522–1533. [Google Scholar] [CrossRef]
- Cai, X.S.; Yang, C.Y.; Yuan, Y. Hybrid simulation of seismic responses of a typical station with a reinforced concrete column. Appl. Sci. 2020, 10, 1331. [Google Scholar] [CrossRef]
- Wang, Y.C.; Chen, Q.J. Parametric fitting of soft soil sites’ Davidenkov model based on PSO algorithm and its application. J. Vib. Shock 2019, 38, 8–16. [Google Scholar]
- Parramontesinos, G.J.; Bobet, A.; Ramirez, J.A. Evaluation of soil-structure interaction and structural collapse in Daikai subway station during kobe earthquake. ACI Struct. J. 2006, 103, 113–122. [Google Scholar] [CrossRef]
- GB-50011-2010. Code for Seismic Design of Buildings; Architecture and Building Press: Beijing, China, 2016. [Google Scholar]
- Zhao, Z.P.; Chen, Q.J.; Zhang, R.F.; Pan, C.; Jiang, Y.Y. Energy dissipation mechanism of inerter systems. Int. J. Mech. Sci. 2020, 184, 105845. [Google Scholar] [CrossRef]
- Zhao, Z.P.; Zhang, R.F.; Jiang, Y.Y.; Pan, C. Seismic response mitigation of structures with a friction pendulum inerter system. Eng. Struct. 2019, 193, 110–120. [Google Scholar] [CrossRef]
- Zhao, Z.P.; Zhang, R.F.; Jiang, Y.Y.; Pan, C. A tuned liquid inerter system for vibration control. Int. J. Mech. Sci. 2019, 164, 105171. [Google Scholar] [CrossRef]
- Benavent-Climent, A.; Galelamuela, D.; Donaireavila, J. Energy capacity and seismic performance of RC waffle-flat plate structures under two components of far-field ground motions: Shake table tests. Earthq. Eng. Struct. Dyn. 2019, 48, 949–969. [Google Scholar] [CrossRef]
- Benavent-Climent, A. Design, testing, and evaluation of the web plastifying damper for the aseismic protection of buildings. In Encyclopedia of Earthquake Engineering; Springer: Berlin/Heidelberg, Germany, 2014; pp. 1–8. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).