Featured Application
Software for the purposes of determination of solar potential of rooftops.
Abstract
In the context of encouraging the development of renewable energy, this paper deals with the description of a software solution for mapping out solar potential in a large scale and in high resolution. We leverage the performance provided by Graphics Processing Units (GPUs) to accelerate shadow casting procedures (used both for direct sunlight exposure and the sky view factor), as well as use off-the-shelf components to compute an average weather pattern for a given area. Application of the approach is presented in the context of the solar cadaster of Greater Geneva (2000 km2). The results show that doing the analysis on a square tile of 3.4 km at a resolution of 0.5 m takes up to two hours, which is better than what we were achieving with the previous work. This shows that GPU-based calculations are highly competitive in the field of solar potential modeling.
1. Introduction
To be able to meet an increasing demand in renewable energies, due to the ubiquity of sunlight, the placement of photovoltaic (PV) panels on roofs is well indicated. As such, mapping out the places with the best solar potential can yield more solar power at a given cost. One of the main aspects of mapping out the solar potential is the determination of obstructions from the environment (buildings, trees, relief) in a straight line from any given point (which we will call “shadow casting”).
Shadow casting is a very computationally demanding effort. Each point must be treated independently, and obstructions must be determined in many directions in order to get a satisfactory result. Using conventional computing, which relies on the performance of Central Processing Units (CPUs) is expensive in terms of time and energy. However, Graphics Processing Units (GPUs), which traditionally have been used for rendering 3D scenes in real time, are very adapted by their massively parallel nature. They solve problems where the same computation is applied to different inputs, which is the case for shadow casting.
We define shadow casting broadly, as the determination of the existence of an obstruction from a given point of a scene along a given line, whether this line corresponds to the position of the physical sun or any other point in the sky. Shadow casting is used both for determining the direct sunlight exposure on a given day of the year and at a specific time, and for calculating the Sky View Factor, which is the proportion of sky that is visible from a given point.
Several approaches to shadow casting exist, and they can be broadly categorized into vector-based approaches and raster-based approaches. Some of these approaches, coupled with GPU techniques, are presented below.
Vector-based approaches look at an environment in terms of 3D shapes for each wall, floor, roof, and whatever other feature is desirable to include in the model. Many of those approaches related to shadow casting have been proposed. Robledo et al. [1] describe a pipeline that uses the GPU in a conventional manner, via 3D-rendered primitives, to determine obstruction of PV panels by representing the sun’s position as an orthographic camera. Liang et al. [2,3] present an interactive tool that is used for computing the solar potential on simplified vector-based buildings, with the processing being done with CUDA (Compute Unified Device Architecture) [4]. Seipel et al. [5] describe a pipeline based around GPU shaders to compute temporal maps for a given PV surface (with the time of day as the X-axis and the day of the year in the Y-axis). Those approaches have the advantage of allowing an arbitrary amount of detail, but have the disadvantage of being computationally expensive for large-scale analysis. Obtaining the data for a detailed vector-based model can be problematic as well, because it may require a significant amount of manual labor by 3D-modelling every building and feature.
Raster-based models on the other hand use the elevation map of the area as the definition of their environment. Even if lacking all the potential detail that a vector model can provide, a raster model can be acquired more easily with less human labor (for instance using LiDAR surveying), and can, due to the simplicity of the data structure, lead to performant algorithms that can be applied at a large scale and at high resolution. For these reasons, we went with the raster approach for the purposes of the solar cadaster in the Greater Geneva area as presented in this article.
Raster-based approaches that have been attempted by other authors include the following. Lukač and Žalik [6] perform an analysis of shadow casting on a graphical processing unit (GPU). Their analysis only computes the direct sunlight path and does not take into account the obstructions of the sky from a given point. The latter is used to compute the diffuse component of the solar irradiation. The authors also include multiresolution analysis (to take into account distant landscape features that may cause obstruction) via nearest-neighbor scaling. Their usage of CUDA for accelerating their shadow casting is similar to the approach proposed in the present paper. Tabik et al. [7] use a similar approach, but their goal is to compute the optimal tilt and orientation of the various points in the elevation model, in order to have solar panels that are not necessarily adherent to a roof, but at an optimal angle.
Calcabrini et al. [8] provide an approximation of the irradiance of all points in the elevation model by computing not only the sky view factor (the portion of the sky visible from a given point) but also the sun coverage factor (the ratio between the amount of time that the sun is obstructed and the total duration of sunlight the point would get if there were no surrounding geometry). This approximation allows for computing the sun coverage factor in parallel with the sky view factor at no additional computational expense, trading off some accuracy for speed. On this topic, our work does a more thorough analysis, by computing the direct illumination at each hour on representative days of each month (weighting them per the irradiation at the given time). However, it remains to be seen how much accuracy is gained by not performing the simplifications described in the latter article.
Huang et al. [9] have a very in-depth analysis of radiation, and use the GPU to compute final radiation parameters, while their obstruction analysis uses the Hillshade module of the ArcGIS software (ESRI, Redlands, CA, USA). In our tests, with our current setup, the most computationally challenging aspect is precisely shadow casting, so we preferred using the GPU for that rather than for the final irradiation calculation.
To summarize, GPU processing is widely used in several approaches, mainly raster-oriented. However, the way the GPU is used in the references mentioned above is generally incomplete and partial. In some cases, key parameters like the Sky View Factor are not processed; in others, simplifications are made to save computing time to the detriment of accuracy. The literature lacks a complete and integrated applicative approach using the GPU that performs the entire process of solar irradiation modeling in an hourly time scale, at a high raster resolution and large regional area.
This paper deals with an efficient and integrated computing solution to process solar energy potential in built areas. The proposed solution is implemented on GPU and relies on a shadow-casting algorithm and solar modelling, which leverage digital models at high resolution in large areas. The use of GPU is intended to boost computation time and enable processing wide areas. A new solar potential modelling architecture is proposed for this purpose.
The proposed solution consists in a suit of encoded algorithms that process digital elevation maps and some auxiliary inputs, and generates monthly and yearly solar irradiation values for each point in the area. It has been evaluated and applied in the real concrete situation of the Greater Geneva area as a case study. This trans-border region has an area of about 2000 km2 and contains nearly one million inhabitants, with Geneva as the main city in the middle. A first solar cadaster was developed for the Canton of Geneva only (280 km2), as presented in Desthieux et al. [10]. The goal now is to update and extend this solar cadaster for the whole of Greater Geneva area, with the aim of intensifying solar energy production. The specifics of the project require to produce a solar map at both a regional scale and in high resolution (50 cm) with a reasonable computation time, hence the need to use infrastructures like the GPU.
The next sections of the article will be structured as follows: Section 2 presents the previous work and the adopted methodology to calculate irradiance, both from algorithmic and technical standpoints. Section 3 deals with the new architecture and the scientific and technical improvements proposed to extend the solution to large scale deployments. Experimental results (quantifying computation time saving using GPU) are detailed in Section 4 in the context of the solar cadaster of the Greater Geneva area (as a case study) and the development of an online web interface. Finally, Section 5 concludes with a summary of the results, and potential future improvements to the approach.
2. Previous Related Work
Our previous work on solar modelling and mapping in a built environment [10,11,12] was for the Solar Cadaster of the canton of Geneva.
To summarize, the implemented solar modelling process is structured into 3 main steps (Figure 1):
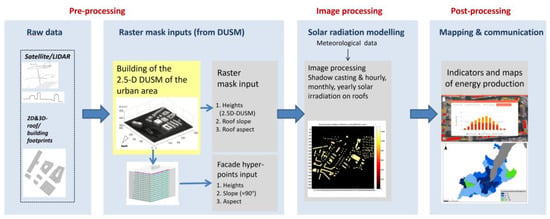
Figure 1.
The entire process of solar modelling and mapping from raw data acquisition to solar mapping. Adapted from [12]. DUSM: digital urban surface model.
- Pre-processing: collection and preparation of input data (meteorological data based on Meteonorm® (Meteotest AG, Bern, Switzerland); DUSM—digital urban surface model based on LIDAR survey of 50 cm resolution; slope and orientation maps derived from DUSM; model of the facade of buildings as hyper-points).
- Image processing: shadow casting and computation of hourly, monthly, yearly solar irradiation on each DUSM pixel.
- Post-processing: integration of irradiation outputs on building roofs and calculation of energy, economic, and environmental indicators at different scales.
Irradiation is the result of the image processing step. It has, as a physical property, 3 components. The first is the direct effect of sunlight in a straight line from the sun, the second is the effect of sunlight that is diffused by the atmosphere, the third is the reflected component of sunlight. Irradiation computation uses meteorological data from Meteonorm®, which gives statistical and representative data on global, diffuse, and direct irradiation on horizontal surfaces for a given location like Geneva Airport in the context of the solar cadaster. In order to save computation time, hourly data were averaged by month and a representative day of each month (around the 15th of the month) was chosen for the solar geometry as introduced by [10].
For the transposition of diffuse radiation on tilted surfaces, we opted for the Hay model [13], as it is the most suitable for using hourly irradiation data on horizontal surface averaged by month as demonstrated in [10] This model is structured into two parts: the circumsolar (anisotropic) that depends on the sun position and the isotropic that does not.
In order to compute shadow casting on the direct and diffuse components of irradiation, we need to compute: (i) the Sky View Factor (SVF), which is not time-sensitive, (ii) the shadow maps (Direct Illumination, DI) corresponding to each month and hour of a representative day of the given month. Hourly shadow maps are applied to both direct and circumsolar components, whereas SVF is applied to the isotropic one.
The SVF is a dimensionless parameter with values varying from 0 to 1, representing the fraction of the sky on a hemisphere that is visible from a given point (cf. Hämmerle et al. [14]). In the approach introduced by [10] used in this paper, the sky is subdivided into 580 equal solid angle light sources. In the SVF formula, sinus weighting factor is introduced in order to give more weight to light sources from the zenith (relative to the normal of the surface) than to those from the horizon, which is consistent with the purpose of solar potential analysis.
Both shadow maps and SVF are based on the same shadow casting algorithm introduced by Ratti and Richens [15,16], which, given a point on the DUSM and a direction, will determine whether there is an obstruction across the straight line from that point in the given direction.
The solar modelling process is also applied on building facades as introduced by Desthieux et al. [10]. Points are generated along the facades (called hyper-points) and shadow casting and irradiation are computed on each facade point in the same way as for horizontal or roof surfaces.
To integrate the solar modelling process into the solar cadaster, the Canton of Geneva (280 square kilometers in area) was split into about 55 square areas (called “tiles”) of 3 by 3 km, with a padding zone of 200 m on each side, and a resolution of 50 cm, for an image size of 6800 × 6800 pixels. The reason for the subdivision is that computation time and memory usage would be prohibitive if the whole canton were to be processed as a single unit. Several mountains surround Geneva (see Figure 2) and result in obstructions depending on areas and hours. Therefore, the approach separately calculates DI and SVF due to the relief at the regional scale, but using an elevation map or DTM (Digital Terrain Model) at lower resolution (50 m instead of 50 cm). Finally, for each data point of the tile, the resulting value, for both the DI and SVF, is defined as the minimum between the result calculated on the DUSM and the result calculated on the lower resolution DTM.
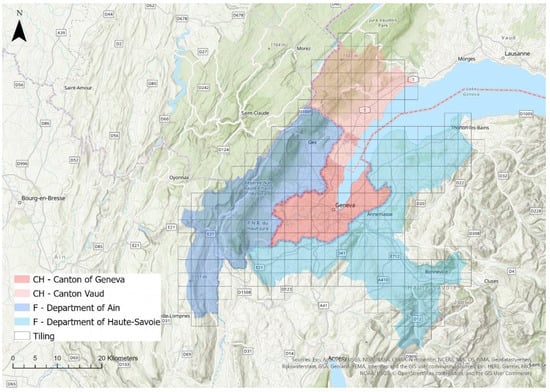
Figure 2.
Geographical context of Greater Geneva area (main administrative boundaries and tiling).
In terms of computing performance, the first solar cadaster of Geneva developed in 2012 used a single CPU machine, and the computation time took about 40 h for each of the 55 tiles (using a sky vault of only 137 light sources for the SVF). Solar modelling algorithms (in particular that of the SVF) were then refined and improved based on local comparison with specific models and measurements, as introduced by [12]. In parallel, a cloud computing solution were implemented in order to take advantage of the parallel processing of CPUs in order to reduce computation time (about 16 h hours by tile, in the updated solar cadaster of 2016, using a denser sky vault of 580 light sources). Boulmier et al [17] presents a cost and time analysis of the execution of the code in a cloud-based environment.
3. Methodological Developments and Application to the Greater Geneva Area
Based on the previous work presented in the last section, the methodology has evolved and has been adapted in the context of enlarging the solar cadaster from the canton of Geneva (280 km2) to the Greater Geneva area (2000 km2) as presented in Figure 2. The region includes three main territories: the canton of Geneva and the region of Nyon, which is part of the canton of Vaud, in Switzerland, and groups of municipalities of the departments of Ain and Haute-Savoie in France.
Increasing the scale of the zone of interest by over a factor of 7 (from 55 tiles to 294) creates the two following challenges. First of all, a more performant computational system based on GPU should be developed. Section 3.1 presents the workflow of the improved computational structure. Specific aspects have also been improved, as introduced in Section 3.2, related to the shadow casting formula for the integration of distant geometry, and introduction of masks to target a subset of positions on which to perform the analysis. Secondly, a large zone can have local variations in weather patterns, and it must be considered for an accurate analysis (Section 3.3).
3.1. Workflow
The workflow presented in Figure 3 deals with the image processing stage, as introduced earlier in Figure 1. The pipeline works as follows: for each tile, we compute both the Sky View Factor (SVF), which is not time-dependent, and the Direct Illumination (DI) value of each hour of sunlight of a representative day of each month. Both of these procedures derive from our shadow casting algorithm.
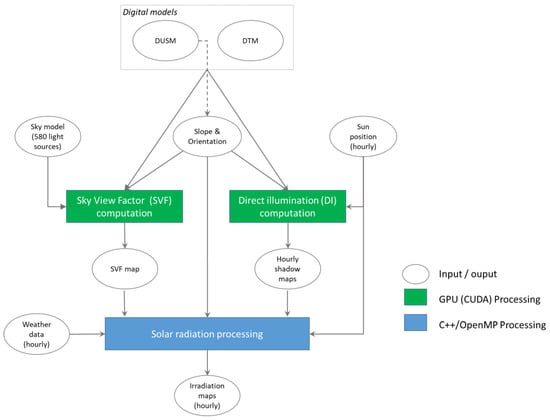
Figure 3.
A schematic view of the processing pipeline for a tile, detailing the image processing step of Figure 1. DTM: Digital Terrain Model; GPU: Graphics Processing Units; CUDA: Compute Unified Device Architecture.
The Sky View Factor Computation (left green box in Figure 3) uses as inputs: the Digital Urban Surface Model (DUSM) of the tile (for shadow casting in the immediate neighborhood of each point with high resolution of 50 cm), the Digital Terrain Model (DTM), which is a low-resolution (50 m) height map of the entire region (for shadow casting due to distant relief), a sky model of 580 points, the slope and orientation data for each point (for computing the weighting factor according to the normal of the roof). Slope and orientation derive themselves from the DUSM.
The Direct Illumination (DI) computation (right green box in Figure 3) uses as inputs the DUSM, DTM (for shadow casting to the distant relief), and the hourly solar position, which depends on the latitude of the center of the tile, time of day, and day of the year.
Finally, the solar radiation processing generates as output the irradiation maps of tiles. It takes as input (blue box in Figure 3): the DI values calculated for each hour of a representative day of each month, the SVF, the predicted meteorological data for the specific tile, the slope and orientation of each point, the sun position, as well as the latitude of the center of the tile. We apply the following irradiation formula adapted from [10] to compute the result. This Equation (1) is structured in three components: beam, diffuse, and reflected.
where:
| Igβγ: | Hourly global irradiation on the inclined surface (W/h/m2) |
| Ibβγ: | Hourly beam or direct irradiation on the inclined surface (W/h/m2) |
| rb: | cosθ/cosθz, transposition factor |
| DI: | Direct illumination (hourly shadowing effect on beam and diffuse circumsolar components, value = {0,1}, defined by the minimum value processed on DUMS and DTM) |
| Id: | Hourly diffuse radiation incident on the horizontal surface (W/h/m2) |
| Ig: | Hourly global irradiation on the horizontal surface (W/h/m2) |
| I0: | Hourly extraterrestrial irradiation (W/h/m2) |
| SVF: | Sky View Factor (shadowing effect on the isotropic part of the diffuse component processed on both DUMS and DTM, value = [0,1]) |
| a: | Albedo coefficient |
| β: | Slope angle of the inclined surface |
| γ: | Azimuth angle (orientation or aspect) of the inclined surface |
| Θ: | Angle of incidence of the inclined surface |
| θz: | Zenith angle of the light source |
Irradiation outputs are then post-processed in order to produce solar energy maps. This will be presented later in Section 4 through the application of the solar cadaster in Geneva.
Concerning the technological choices, given the considered total area (roughly 2000 km2), the previous approach of running the computation on conventional CPUs was prohibitive in terms of computation time and cost, if we wanted to keep the same surface model resolution (50 cm). Preliminary tests by Ben Bader [18] in 2016 demonstrated that GPUs, by their massively parallel nature, are adequate for problems in which the same computation must be performed on different inputs. They are thus particularly adapted to our shadow casting, which is the biggest time sink of the system.
Therefore, in order to take advantage of the performance provided by GPUs, both the DI and SVF computations have been implemented as CUDA kernels (i.e., the script language used for GPU), that distribute the workload of each point in the surface model across the available GPU cores. The irradiation module is coded in C++ using OpenMP directives, so we can benefit from the CPU cores we had access to, i.e., distributing the computation effort among the CPU cores.
3.2. Methodological Improvement on Shadow Casting Algorithms
If we are looking only at the local data provided by the DUSM, the shadow casting algorithm works by starting from a given point (P0, i.e., a cell of the DUSM), and incrementally looking in the direction provided for another point Pi that is higher (H) than the ray R that is traced from the sun or light source in that direction. The presence of such a point indicates an obstruction, and its absence the lack thereof. This concept illustrated in Figure 4 is presented more in detail in [10]. Listing 1 gives the pseudocode of this shadow casting algorithm.
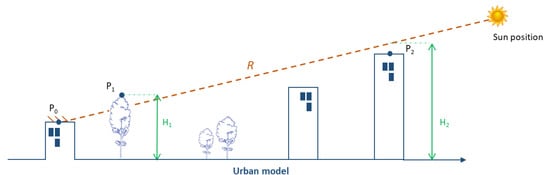
Figure 4.
Concept of shadow casting algorithm adapted from [10]. In this example P0 is shaded by P1, where the relative height (H1) is higher than the ray R, but not by P2.
As for the integration of remote obstruction, the new architecture supports now two main features that were not provided by the previous work detailed in Section 2.
The first one is a methodological change on how the distant terrain features were handled. Originally the calculation of the SVF and DI was done on both resolutions, then enlarging the low-resolution version (as explained in Section 2) and taking the minimum between the two. This does not give the correct result when local obstacles (for example buildings) defined on the DUSM are not situated in the same direction as remote relief features (for example mountains) defined on the DTM. In that case, cumulative shadowing effects from both relief and local obstacles should be considered on the SVF, instead of merely taking the minimum of both SVFs. Therefore, we integrate the multiresolution aspect in our main shadow casting loop by testing obstructions in both the resolutions in a given direction. The final result of that obstruction check will be the disjunction of both results (Listing 2 and Listing 3).
The second one is, while testing for obstructions on the low-resolution model, we ignore obstructions that occur within the boundaries of the tile, since we have access to more detailed information within the tile (due to the DUSM).
Listing 1. The pseudocode of the shadow casting algorithm on the DUSM, which, given a point and a direction (defined by azimuth and elevation), tells us whether there is an obstruction in that direction.
is_obstructed_1(DUSM, point, direction_azimuth, direction_elevation) -> dx = cos(direction_azimuth) dy = -sin(direction_azimuth)//(0,0) is top-left in the DUSM dz = tan(direction_elevation) * resolution(DUSM) current_point = point + [dx, dy] current_altitude = DUSM[point] + dz while current_point is not outside DUSM and current_altitude <= max(DUSM) if (DUSM[round(current_point)] > current_altitude) return TRUE current_point += [dx,dy] current_altitude += dz return FALSE
Listing 2. In counterpart to Listing 1, this is the pseudocode of the shadow casting algorithm that determines distant obstructions due to terrain features, that are determined by the lower resolution DTM.
is_obstructed_2(DTM, DUSM, point, direction_azimuth, direction_elevation) -> dtm_point = the conversion of “point” from DUSM to DTM coordinates dx = cos(direction_azimuth) dy = -sin(direction_azimuth)//(0,0) is top-left in the DTM dz = tan(direction_elevation) * resolution(DTM) current_point = dtm_point + [dx, dy] current_altitude = DUSM[point] + dz while current_point is not outside DTM and current_altitude <= max(DTM) if (DTM[current_point] > current_altitude and current_point is outside the boundaries of the tile ) return TRUE current_point += [dx,dy] current_altitude += dz return FALSE
Listing 3. We take the disjunction between Listing 1 and Listing 2 to get the final determination of obstruction.
is_obstructed(DTM,DUSM, point, direction_azimuth, direction_elevation) -> return is_obstructed_1(DUSM,point,direction_azimuth, direction_elevation) OR is_obstructed_2(DTM,DUSM,point,direction_azimuth, direction_elevation)
In addition, the CUDA kernels have also been written with the notion of “early termination” in mind, in that, as an implementation optimization, we actually combine both loops into one, and in the case of an obstruction in either resolution, declare an obstruction immediately.
Finally, we implemented an optional “masking” feature that allows to selectively apply the processing to only part of the tile, while still using the excluded areas for determining obstructions. There are many cases for which a mask can be useful, for instance to exclude the padding border of 200 m around each side, to exclude lakes, rivers, forests, fields, etc. from the solar potential analysis, or even for only computing the solar potential on building rooftops.
3.3. Meteorology at Large Scale
The large extent of the region covered by the solar cadaster of the Greater Geneva area accounts for significant variation of solar irradiance and temperature throughout the region. Conditions range from typical Swiss lowland conditions (372 m to sea level) to mountain climate (1500 m to sea level) with significant differences in cloud coverage and temperature. Yet, weather observations do not cover the whole Greater Geneva area (the number of meteorological stations is limited). Therefore, comparing several interpolation models and approaches, it results that Meteonorm® offers reliable estimated weather data in any point of the territory based on nearby weather stations and satellite imagery of cloud coverage. On this basis, specific weather input data are calculated for each tile. More details on the comparative study are presented in Appendix A.
4. Results
This section presents the experimental results from the new architecture detailed in Section 3 and compares them with those from our previous work.
4.1. Application to the Solar Cadaster of the Greater Geneva Area
From monthly and yearly irradiation raster outputs, post-processing is carried out with GIS to calculate indicators by roof section for solar PV, and by building for solar heating and domestic hot water purposes. Indicators include: geometry (orientation, slope, available and not shadowed roof surface area, potential solar panels areas), monthly and yearly solar energy production, building energy needs coverage ratio, peak power for PV, investment and yearly maintenance costs, subsidies, and CO2 savings.
GIS layers of the results are displayed through two systems:
- Official “geoportail” of the canton of Geneva [19] (also centralized data for the Greater Geneva area) that displays and delivers the full set of the spatial layers. Experts and professionals can download them for their own use in GIS.
- The online web interface [20] illustrated in Figure 5 is addressed to the broader public (building owners, public authorities, policymakers, etc.). It displays the main indicators and key information about the thermal and solar photovoltaic potential and gives the best and unshaded locations for solar installations. It aims at raising awareness among building owners about the existing solar potential and motivating them to invest in solar energy.
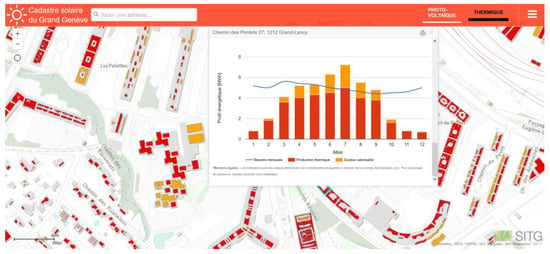 Figure 5. Screenshot of the web interface of the solar cadaster of the Greater Geneva area (with an example of a monthly solar thermal profile for a given building).
Figure 5. Screenshot of the web interface of the solar cadaster of the Greater Geneva area (with an example of a monthly solar thermal profile for a given building).
Results can be also aggregated to areas like municipalities as illustrated in Figure 6, supporting policy makers in devising energy planning and strategies at different scales. For example, urban centers with a higher number of building roofs often have the highest potential, but also some peripheral and rural areas may offer interesting potential on farm roofs.
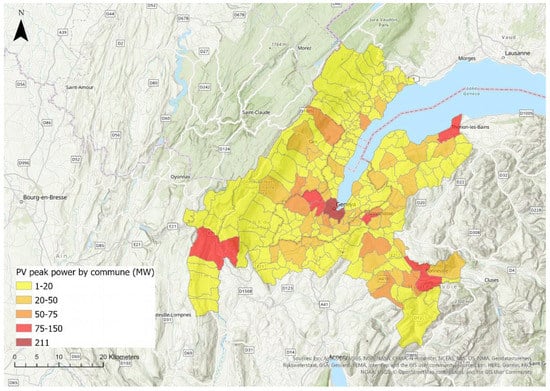
Figure 6.
Potential total photovoltaic (PV) peak power by commune (i.e., municipality) of the Greater Geneva area.
As an example of helpful information for energy planers and public authorities, overall in the Greater Geneva area, potential PV peak power on building roofs totals 3800 MW. Based on statistics on electricity consumption in the Canton of Geneva, PV solar panels on roofs could potentially cover 38% of the consumption (with a potential of 1000 MW over the 62 MW already installed in 2019).
4.2. Presentation of Timing Results
The experiments were run on a GPU-enabled workstation with its technical characteristics given in Appendix B.
Given that our shadow casting algorithm uses an “early termination” criterion (as explained earlier in Section 3.2), tiles of different nature can lead to different run times. As such, tiles with more obstructions (typically urban areas) will have shorter processing times than tiles with fewer obstructions in more open areas.
For our timing experiments, we selected 2 representative tiles for 3 types of environment (6 tiles total). The types of environment that were chosen were “urban”, “rural”, and “mountainous”.
For the purposes of the timing evaluation, we defined appropriate masks for each tile (Figure 7). Masks of urban tiles exclude everything that is not the roof of a building. In rural and mountainous areas, we exclude forested areas as well as water bodies (rivers) from the analysis.

Figure 7.
Illustration of the 6 tiles with different types of masks (0—black: excluded pixel, 1—white: included pixel).
From each mask, we deduced a coverage ratio, i.e., the number of image pixels included (i.e., mask = 1) for the analysis divided by the total number of pixels in the tile, expressed as a percentage.
As we can observe from the results (Table 1), the relevance of applying masks, when it is a matter of assessing solar radiation on buildings only, is particularly evident in urban areas where the coverage ratio is low and the computing time saving is therefore important (factor 2). The same observation can be made when it is appropriate to remove forested areas (as in particular in the tile Mountainous 1).

Table 1.
Measured run times of representative tiles, with and without the usage of a mask.
Overall, the processing time for the tiles (without using a mask) ranges between 1 and 2 h, which is notably less than the first experiments (40 h per tile with a simpler sky model in the first attempts in 2012, and 16 h per tile for our cloud computing experiments in 2016).
For the purposes of the solar cadaster of the Greater Geneva area (that spans 294 tiles, although some tiles on the border have a significant amount of missing data), the entire analysis was completed in roughly 15 days (without usage of a mask), tiles being processed in sequence.
It is also apparent, according to these results that using a mask, in the presence of areas that are not needed for analysis can lead to significant speedups. This is the case when it is appropriate to remove water (except if solar installations are planned on water surfaces) and forested portions in mostly unbuilt areas or focus on actual rooftops in heavily urbanized areas.
We should also note that, since the processing of each tile is independent from each other, the workload can be distributed across multiple GPU-enabled machines, for a theoretically linear speedup (minus input-output overhead).
5. Perspectives and Conclusions
Our methodology brings a fast system that can scale to any number of GPU-enabled machines. Computational run time results show increased performance compared to both conventional CPU usage (including cloud computing). Using masks in order to target the analysis on specific surfaces like building roofs significantly reduces calculation time. The application of the tool, as illustrated in the Greater Geneva area, enables estimating the solar energy potential of an arbitrary zone on the surface of the earth, at a high resolution, around the order of magnitude of the size of a regular photovoltaic panel. The proposed approach can be easily replicated everywhere in the world, provided that reliable input data, in particular DUSM, DTM, and building or roof spatial layers (for calculating energy indicators) are available. Weather data can be based on local meteorological stations or on statistical databases like Meteonorm® that are available for areas around the world.
Some limitations of our approach include the use of a raster model; by representing the environment by an elevation map, we cannot take into account overhanging structures, such as bridges, balconies, and arches. Such structures would be important to take into account if we were to adapt our model for determining the solar potential of vertical walls (facades). A vector model would be a lot more appropriate for this purpose but will require more computationally intensive resources. A vector model would also allow for modeling sunlight bounces, for a more accurate determination of reflected solar energy, which, while negligible for rooftops, is a very important source of irradiation for facades.
On the theoretical side, future perspectives can include the validation of our model with respect to ground truth (measured) data, by replacing our meteorological predictions by the actual a posteriori data corresponding to the weather that occurred. Performing benchmarks of the GPU-based systems referenced in Section 1 would be useful for the purpose of comparing shadow casting, irradiation and time calculation results, identify the most performant approach, and consider the effect of some simplifications. Another important analysis to be done is a sensitivity analysis, to determine to what extent increasing or decreasing the spatial or temporal resolution would have an effect on the final results.
On the computational side and from an engineering perspective, further improvements to our method include taking into account the internal details of how the threading model of the GPU works, to make sure no processing potential is wasted. Such optimizations may be well indicated if we were to work on an area that is one or more orders of magnitude larger than what we are now processing. Another improvement would be to compute multiple direct illumination passes (for each hour of a given day for instance) in parallel on a GPU, saving the results in individual bits of a 32-bit integer, which will allow to save even more time, not only in terms of the actual computation, but also in terms of input/output speed.
In conclusion, our research has shown that Graphics Processing Units can be leveraged in an efficient manner for the purposes of Solar Energy Modelling, and many useful applications for the planning of solar installations can be devised based on this information.
Author Contributions
N.S. performed the literature survey, conceptualized and implemented the computing environment based on GPU technology, wrote the pseudocode scripts, co-designed figures, contributed the methodological improvement of solar modelling, wrote and edited the paper. G.D. supervised and coordinated the work, acquired the funds, worked on solar modelling and outputs, co-designed figures, wrote the paper. N.A. provided the computing environment resources, defined the global architecture of the system (parallel programming, tasks allocation), supervised the work, and reviewed the paper. P.G. worked on meteorological data and methodology, and wrote the dedicated chapter/appendix. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by EU-INTERREG V France-Suisse program (G2-SOLAIRE Ref: 4610), and co-funded, for the Swiss part of this program, by the Cantons of Geneva (SAEF, OCEN, DIT) and Vaud (DIREN), SIG (state-owned energy company for the Canton of Geneva) and Region of Nyon.
Acknowledgments
The authors would like to thank the above-mentioned funders and the French-Swiss technical and scientific partners of the INTERREG G2-Solaire project for their technical support: Université de Savoie Mont-Blanc (USMB/FRESBE), Université Claude Bernard Lyon 1 (CETHIL), Institut national d’énergie solaire (INES), CAUE-74, Innovales, Enedis, arx iT.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had a role in the decision to publish the results, but not in the design of the study, in the collection, analyses, or interpretation of data, and in the writing of the manuscript.
Appendix A. Methodological Approach Dealing with Weather Data at Regional Level
The large extent of the region covered by the solar cadaster of the Greater Geneva area accounts for significant variation of solar irradiance and temperature throughout the region. Conditions range from typical Swiss lowland conditions (372 m to sea level) to mountain climate (1500 m to sea level) with significant differences in cloud coverage and temperature.
Two typical situations qualify the region:
During summer (Figure A1 left), cumulus formations occur on mountainous landforms, typically beginning during the early afternoon and evolving occasionally into thunderstorms by the end of the day.
During winter (Figure A1 right), when high pressure prevails over central Europe, stratus coverage and temperature inversion may occur for longer periods, thus impacting solar access below 800 m altitude.

Figure A1.
Typical stratus during winter (left), typical cumulus coverage above mountain summits during summer (right); the dot points representing the center of the tiles (credit: https://worldview.earthdata.nasa.gov/).
Since weather observations do not cover the whole area (the number of meteorological stations is limited), methods using satellite data to calculate solar radiation have been considered. Methods have been described in a number of scientific papers (e.g., [21,22]), but an implementation from scratch would have been too time consuming and useless since these methods have been implemented into readily available tools.
To choose the appropriate tool, inter-comparisons of two distinct databases providing calculation algorithms have been made. The graphs in Figure A2 show relative irradiation as calculated by PVGIS (https://ec.europa.eu/jrc/en/pvgis) and Meteonorm®. Two calculated stations with significantly different geographic situations (St. Cergue, a settlement in the Jura mountains and Bellegarde, a small town located on the opposite side of the Jura) were compared to a reference station (Airport—Cointrin reference station close to Geneva in the lowlands). While PVGIS shows little effect due to topography, Meteonorm® shows more solar radiation during winter and less during summer for St. Cergue. The same effect but attenuated can be observed for Bellegarde. This is consistent with cloud coverage schemes related to typical meteorological situations described earlier.
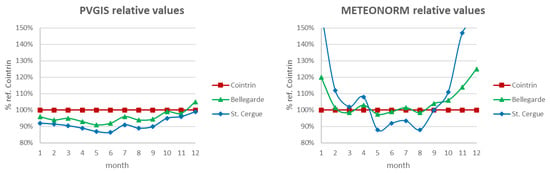
Figure A2.
Comparison between PVGIS (left) and Meteonorm® (right) in terms of relative irradiation.
Appendix B. Technical Characteristics of the GPU-Enabled Workstation
The experiments were run on GPU-enabled workstation with the following characteristics:
- 2 processorsIntel Xeon E5-2650v2 (8 cores) 2.6Ghz
- 2 coprocessors Intel Xeon Phi 5110P (8GBm 1.053Ghz, 60 core)
- 2 GPU nVidia Tesla K20 (Active Thermal)
- Memory: 256Gb DDR3 1600 Mhz ECC
- CentOS 7, CUDA 10.1
References
- Robledo, J.; Leloux, J.; Lorenzo, E.; Gueymard, C.A. From Video Games to Solar Energy: 3D Shading Simulation for PV Using GPU. Solar Energy 2019, 193, 962–980. [Google Scholar] [CrossRef]
- Liang, J.; Gong, J.; Li, W.; Ibrahim, A.N. A Visualization-Oriented 3D Method for Efficient Computation of Urban Solar Radiation Based on 3D–2D Surface Mapping. Int. J. Geogr. Inf. Sci. 2014, 28, 780–798. [Google Scholar] [CrossRef]
- Liang, J.; Gong, J.; Zhou, J.; Ibrahim, A.N.; Li, M. An Open-Source 3D Solar Radiation Model Integrated with a 3D Geographic Information System. Environ. Model. Softw. 2015, 64, 94–101. [Google Scholar] [CrossRef]
- About CUDA. Available online: https://developer.nvidia.com/about-cuda (accessed on 2 April 2020).
- Seipel, S.; Lingfors, D.; Widén, J. Dual-Domain Visual Exploration of Urban Solar Potential. Eurographics Workshop Urban Data Model. Vis. 2013, 21–24. [Google Scholar] [CrossRef]
- Lukač, N.; Žalik, B. GPU-Based Roofs’ Solar Potential Estimation Using LiDAR Data. Comput. Geosci. 2013, 52, 34–41. [Google Scholar] [CrossRef]
- Tabik, S.; Villegas, A.; Zapata, E.L.; Romero, L.F. Optimal Tilt and Orientation Maps: A Multi-Algorithm Approach for Heterogeneous Multicore-GPU Systems. J. Supercomput. 2013, 66, 135–147. [Google Scholar] [CrossRef]
- Calcabrini, A.; Ziar, H.; Isabella, O.; Zeman, M. A Simplified Skyline-Based Method for Estimating the Annual Solar Energy Potential in Urban Environments. Nat. Energy 2019, 4, 206–215. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, Z.; Wu, B.; Chen, L.; Mao, W.; Zhao, F.; Wu, J.; Wu, J.; Yu, B. Estimating Roof Solar Energy Potential in the Downtown Area Using a GPU-Accelerated Solar Radiation Model and Airborne LiDAR Data. Remote Sens. 2015, 7, 17212–17233. [Google Scholar] [CrossRef]
- Desthieux, G.; Carneiro, C.; Camponovo, R.; Ineichen, P.; Morello, E.; Boulmier, A.; Abdennadher, N.; Dervey, S.; Ellert, C. Solar Energy Potential Assessment on Rooftops and Facades in Large Built Environments Based on LiDAR Data, Image Processing, and Cloud Computing. Methodological Background, Application, and Validation in Geneva (Solar Cadaster). Front. Built Environ. 2018, 4. [Google Scholar] [CrossRef]
- Magalhães Carneiro, C. Extraction of Urban Environmental Quality Indicators using LiDAR-Based Digital Surface Models. Available online: https://infoscience.epfl.ch/record/164437 (accessed on 18 March 2020).
- Desthieux, G.; Carneiro, C.; Susini, A.; Abdennadher, N.; Boulmier, A.; Dubois, A.; Camponovo, R.; Beni, D.; Bach, M.; Leverington, P.; et al. Solar Cadaster of Geneva: A Decision Support System for Sustainable Energy Management. In From Science to Society; Otjacques, B., Hitzelberger, P., Naumann, S., Wohlgemuth, V., Eds.; Progress in IS.; Springer International Publishing: Cham, Switzerland, 2018; pp. 129–137. [Google Scholar] [CrossRef]
- Hay, J.E. Calculation of Monthly Mean Solar Radiation for Horizontal and Inclined Surfaces. Solar Energy 1979, 23, 301–307. [Google Scholar] [CrossRef]
- Hämmerle, M.; Gál, T.; Unger, J.; Matzarakis, A. Comparison of Models Calculating the Sky View Factor Used for Urban Climate Investigations. Theor. Appl. Climatol. 2011, 105, 521–527. [Google Scholar] [CrossRef]
- Ratti, C.; Richens, P. Urban Texture Analysis with Image Processing Techniques. In Computers in Building: Proceedings of the CAADfutures’99 Conference, Proceedings of the Eighth International Conference on Computer Aided Architectural Design Futures held at Georgia Institute of Technology, Atlanta, GA, USA, 7–8 June 1999; Augenbroe, G., Eastman, C., Eds.; Springer: Boston, MA, USA, 1999; pp. 49–64. [Google Scholar] [CrossRef]
- Ratti, C.; Richens, P. Raster Analysis of Urban Form. Environ. Plan. B Plan. Des. 2004, 31, 297–309. [Google Scholar] [CrossRef]
- Boulmier, A.; White, J.; Abdennadher, N. Towards a Cloud Based Decision Support System for Solar Map Generation. In Proceedings of the 2016 IEEE International Conference on Cloud Computing Technology and Science (CloudCom), Luxembourg, 12–15 December 2016; pp. 230–236. [Google Scholar] [CrossRef]
- Ben Bader, S. ICeBOUND Project—Porting a Solar Energy Potential Algorithm on GPU. Master’s Thesis, EPFL, Lausanne, Switzerland, 2016. [Google Scholar]
- SITG | Carteprofessionnelle. Available online: https://www.etat.ge.ch/geoportail/pro/?mapresources=GEOTHERMIE%2CENERGIE_SOLAIRE%2CENERGIE&hidden=GEOTHERMIE%2CENERGIE_SOLAIRE (accessed on 10 April 2020).
- SITG Lab Solaire (Online Web Interface of the Solar Cadaster of the Greater Geneva). Available online: https://sitg-lab.ch/solaire/ (accessed on 1 July 2020).
- Mueller, R.W.; Matsoukas, C.; Gratzki, A.; Behr, H.D.; Hollmann, R. The CM-SAF Operational Scheme for the Satellite Based Retrieval of Solar Surface Irradiance—A LUT Based Eigenvector Hybrid Approach. Remote Sens. Environ. 2009, 113, 1012–1024. [Google Scholar] [CrossRef]
- Mueller, R.; Behrendt, T.; Hammer, A.; Kemper, A. A New Algorithm for the Satellite-Based Retrieval of Solar Surface Irradiance in Spectral Bands. Remote Sens. 2012, 4, 622–647. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).