Time-Aware Music Recommender Systems: Modeling the Evolution of Implicit User Preferences and User Listening Habits in A Collaborative Filtering Approach
Abstract
1. Introduction
- A method to induce music implicit ratings that addresses the evolution of user preferences.
- A way of incorporating time-dependent user listening behavior in user-based collaborative filtering models.
- An approach for providing context-aware recommendations that combine the evolution of user preferences, user listening behavior and the time of day as a contextual factor.
2. Background and Related Work
2.1. Collaborative Filtering
2.2. Time-Aware Recommender Systems
2.2.1. Evolution of User Preferences
2.2.2. Temporal Context
3. Modeling the Time Effect on Music Recommendations
3.1. Problem Statement
3.2. Time-Aware Music Recommendation Method
3.2.1. Modeling the Evolution of Preferences
| Algorithm 1 Computation of decay plays, implicit ratings and the average time of day attribute. |
| U = {u1, u2, . . ., un} S = {s1, s2, . . ., sm} , R, DT // R: Rating matrix, DT: Vector of average time of day for every user 1.: , 2: 3: 4: for do 5: 6: for do 7: 8: 0 9: for do 10: 11: 12: end for 13: 14: 15: end for 16: end for 17: for do 18: for do 19: 20: end for 21: end for 22: for do 23: 24: for do 25: 26: Set value 27: for do 28: 29: end for 30: 31: end for 32: end for 33: for do 34: 35: for do 36: for do 37: 38: end for 39: end for 40: 41: end for 42: |
3.2.2. Modeling Time Context
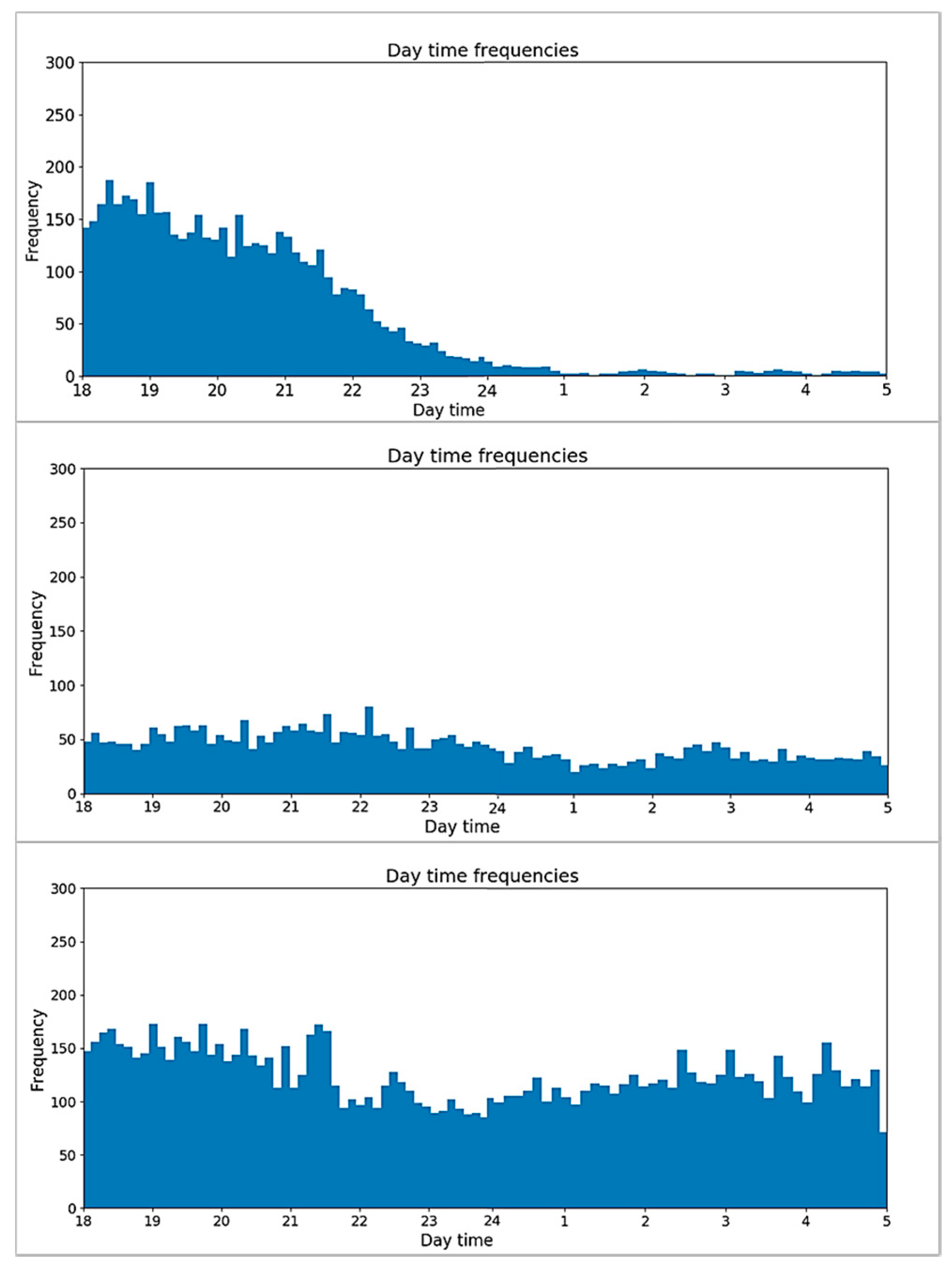
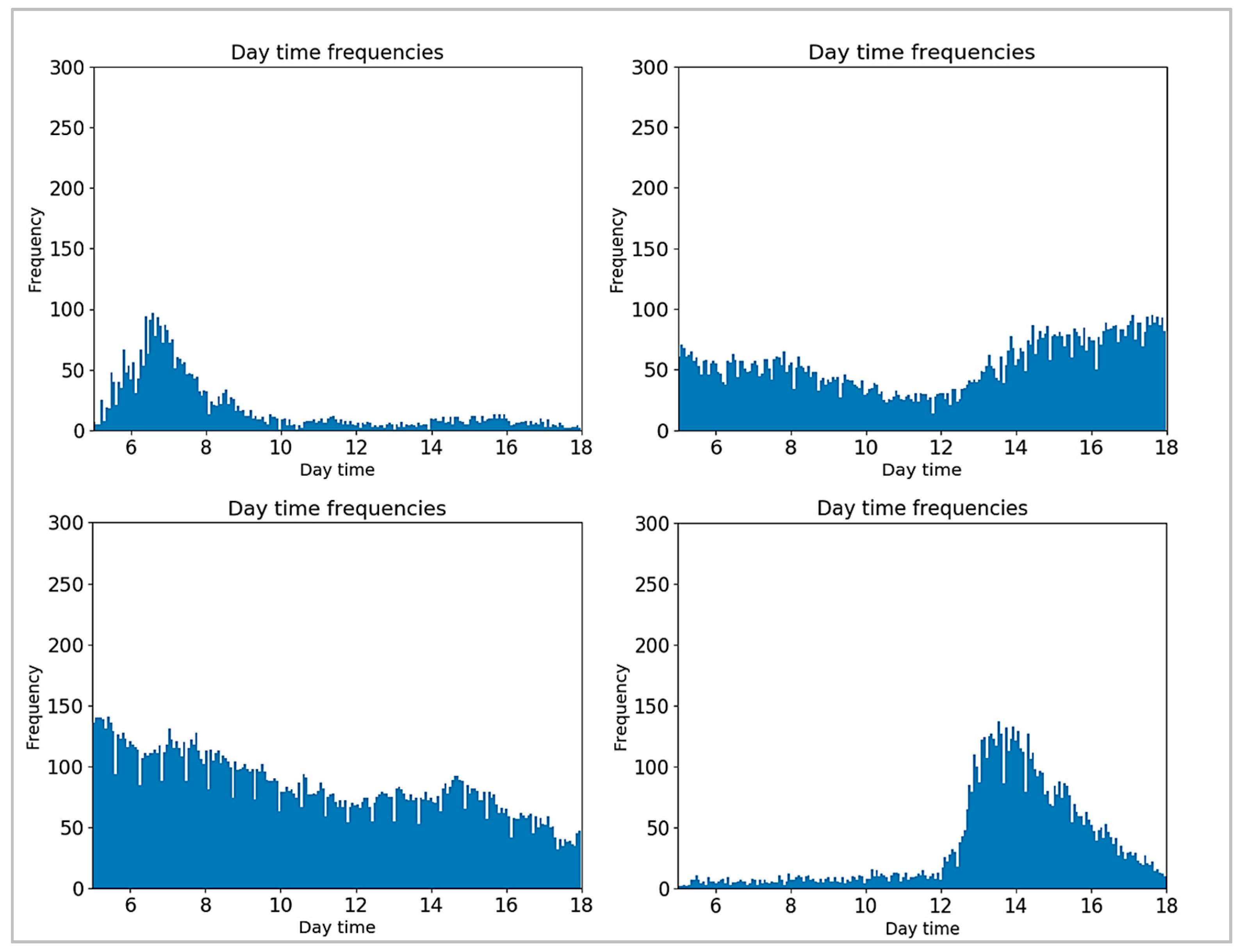
3.2.3. Modeling User Listening Behavior
4. Experimental Study and Validation
4.1. Validation Metrics
4.2. Baseline Methods
4.3. Modeling Temporal Evolution of Preferences
4.3.1. Rating Prediction
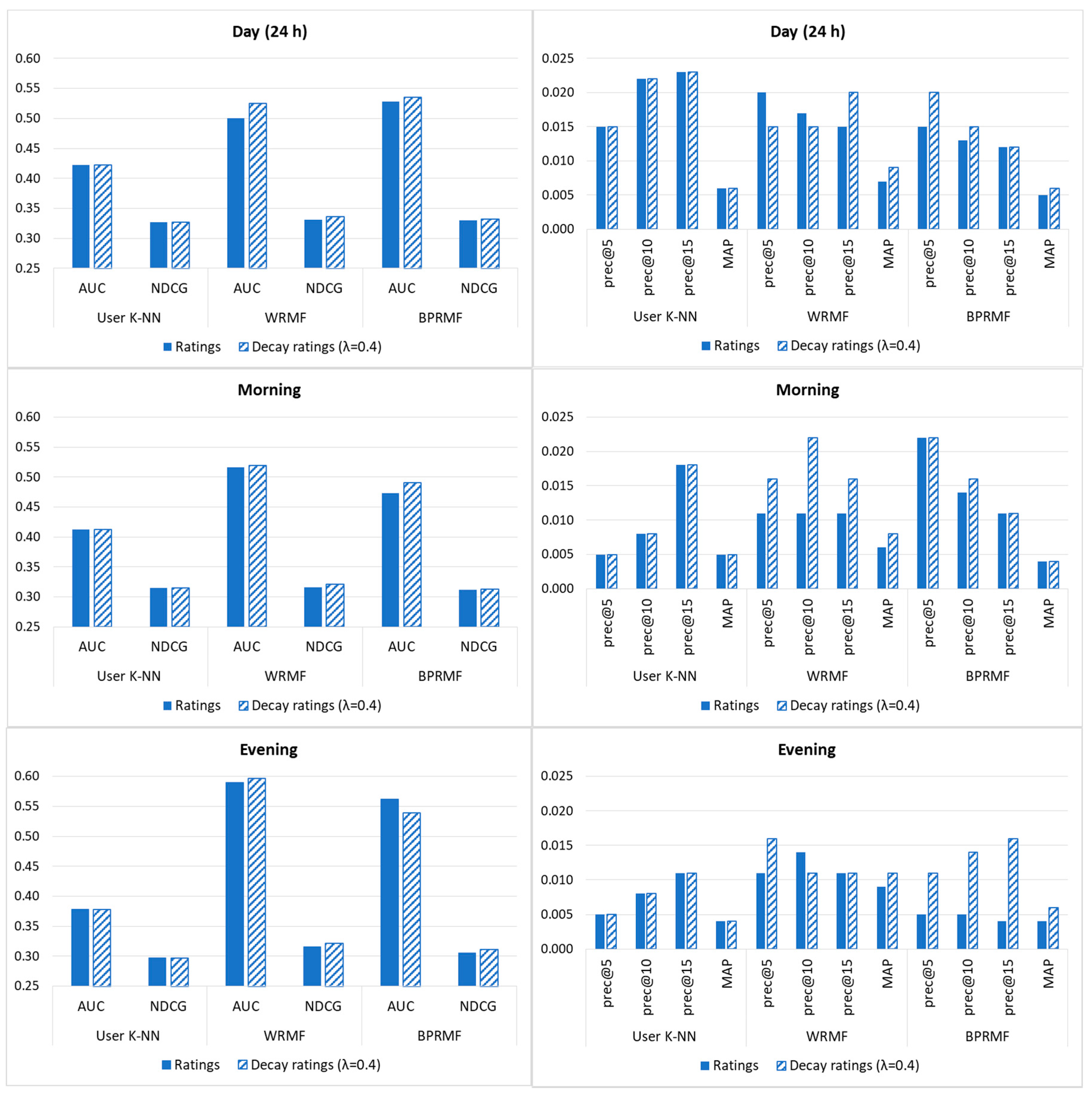
4.3.2. Top-N Recommendation
4.4. Modeling Listening Habits of Users
4.4.1. Rating Prediction
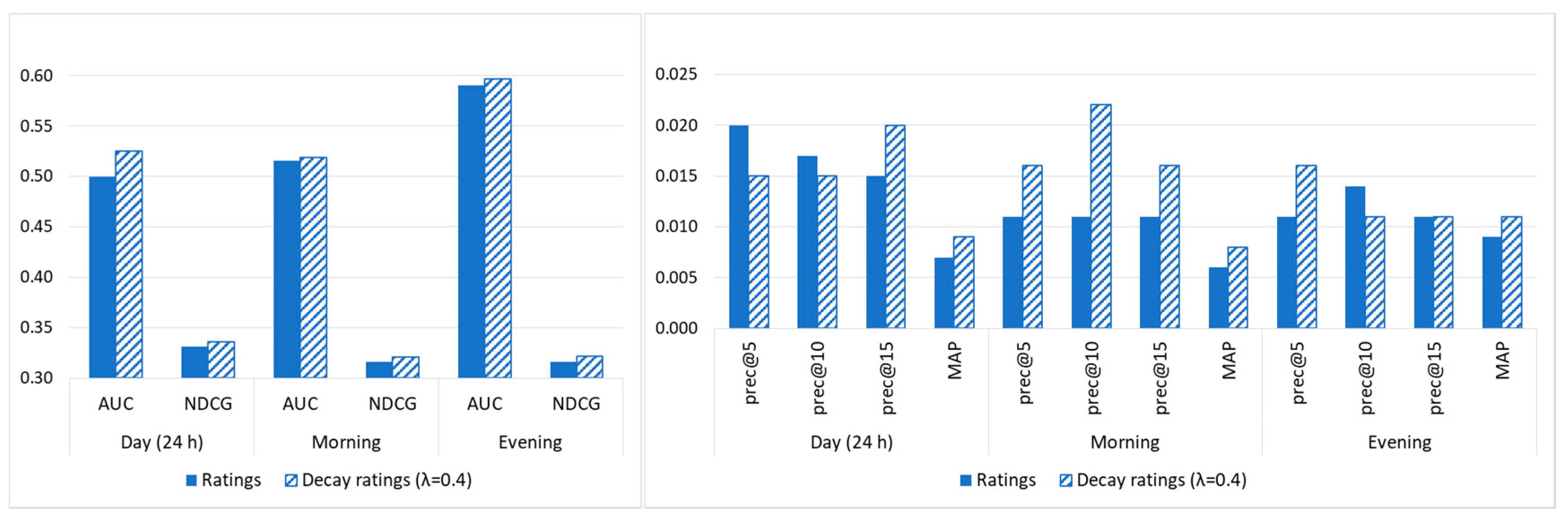
4.4.2. Top-N Recommendations
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Iqbal, M. Spotify Usage and Revenue Statistics. 2020. Available online: https://www.businessofapps.com/data/spotify-statistics (accessed on 24 July 2020).
- Sánchez-Moreno, D.; Zheng, Y.; Moreno-García, M.N. Incorporating Time Dynamics and Implicit Feedback into Music Recommender Systems. In Proceedings of the 2018 IEEE/WIC/ACM International Conference on Web Intelligence (WI), Santiago, Chile, 3–6 December 2018; pp. 580–585. [Google Scholar]
- Sarkar, M.; Banerjee, S.; Badr, Y.; Sangaiah, A.K. Configuring a trusted cloud service model for smart city exploration using hybrid intelligence. Int. J. Ambient Comput. Intell. 2017, 8, 21. [Google Scholar] [CrossRef]
- Yamin, M.; Abi Sen, A.A. Improving privacy and security of user data in location based services. Int. J. Ambient Comput. Intell. 2018, 9, 19–42. [Google Scholar] [CrossRef]
- Desrosiers, C.; Karypis, G. A Comprehensive Survey of Neighborhood-based Recommendation Methods. In Recommender Systems Handbook; Springer US: Boston, MA, USA, 2011; pp. 107–144. [Google Scholar]
- Sarwar, B.; Karypis, G.; Konstan, J.A.; Riedl, J. Incremental Singular Value Decomposition Algorithms for Highly Scalable Recommender Systems. In Proceedings of the 5th International Conference in Computers and Information Technology, Rousse, Bulgaria, 27 December 2002; ACM: New York, NY, USA, 2002. [Google Scholar]
- Shardanand, U.; Maes, P. Social Information Filtering: Algorithms for Automating ‘Word of Mouth’. In Proceedings of the CHI, Denver, CO, USA, 7–11 May 1995; ACM Press: New York, NY, USA, 1995; pp. 210–217. [Google Scholar]
- Breese, J.S.; Heckerman, D.; Kadie, C. Empirical Analysis of Predictive Algorithms for Collaborative Filtering. In Technical Report Microsoft Research; Morgan Kaufmann Publishers: Burlington, MA, USA, 1998. [Google Scholar]
- Cremonesi, P.; Koren, Y.; Turrin, R. Performance of Recommender Algorithms on Top-N Recommendation Tasks. In Proceedings of the Fourth ACM conference on Recommender Systems, Barcelona, Spain, 26–30 September 2010; ACM: New York, NY, USA, 2010; pp. 39–46. [Google Scholar]
- Valcarce, D.; Parapar, J.; Barreiro, Á. Language Models for Collaborative Filtering Neighbourhoods. In European Conference on Information Retrieval; Springer: Berlin/Heidelberg, Germany, 2016; pp. 614–625. [Google Scholar]
- Howe, A.; Forbes, R. Re-considering neighborhood-based collaborative filtering parameters in the context of new data. In Proceedings of the 17th ACM Conference on Information and Knowledge Management, Napa Valley, CA, USA, 26–30 October 2008; pp. 1481–1482. [Google Scholar]
- Burke, R. Hybrid Web recommender systems. In The Adaptive Web; Springer: Berlin/Heidelberg, Germany, 2007; pp. 377–406. [Google Scholar]
- Basilico, J.; Hofmann, T. Unifying collaborative and content-based filtering. In Proceedings of the Twenty-First International Conference on Machine Learning, Alberta, Canada, 4–8 July 2004. [Google Scholar]
- Tso, K.; Schmidt-Thieme, L. Attribute-aware Collaborative Filtering. In From Data and Information Analysis to Knowledge Engineering. Studies in Classification, Data Analysis, and Knowledge Organization; Spiliopoulou, M., Kruse, R., Borgelt, C., Nürnberger, A., Gaul, W., Eds.; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Sánchez-Moreno, D.; Pérez-Marcos, J.; Gil, A.B.; López, V.F.; Moreno-García, M.N. Social influence-based similarity measures for user-user collaborative filtering applied to music recommendation. In Distributed Computing and Artificial Intelligence, Special Sessions, 15th International Conference, 2018; Rodríguez, S., Prieto, J., Faria, P., Kłos, S., Fernández, A., Mazuelas, S., Jiménez-López, M.D., Moreno, M.N., Navarro, E., Eds.; Advances in Intelligent Systems and Computing; Springer: Berlin/Heidelberg, Germany, 2019; Volume 801, pp. 1–8. [Google Scholar]
- Pérez-Marcos, J.; Martín-Gómez, L.; Jimenez-Bravo, D.M.; López, V.F.; Moreno-García, M.N. Hybrid system for video game recommendation based on implicit ratings and social networks. J. Ambient Intell. Human. Comput. 2020. [Google Scholar] [CrossRef]
- Sánchez-Moreno, D.; Muñoz, M.D.; López, V.F.; Gil, A.B.; Moreno, M.N. A session-based song recommendation approach involving user characterization along the play power-law distribution. Complexity 2020, 7309453. [Google Scholar] [CrossRef]
- Aggarwal, C.C. Recommender Systems. The Testbook; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Moreno, M.N.; García, F.J.; Polo, M.J.; López, V. Using Association Analysis of Web Data in Recommender Systems. Lect. Notes Comput. Sci. 2004, LNCS 3182, 11–20. [Google Scholar]
- Sarwar, B.; Karypis, G.; Konstan, J.; Riedl, J. Item-based collaborative filtering recommendation algorithms. In Proceedings of the 10th International Conference on World Wide Web, Hong Kong, 1–5 May 2001; pp. 285–295. [Google Scholar]
- Shyu, M.L.; Haruechaiyasak, C.; Chen, S.C.; Zhao, N. Collaborative filtering by mining association rules from user access sequences. In Proceedings of the International Workshop on Challenges in Web Information Retrieval and Integration, Tokyo, Japan, 8–9 April 2005; pp. 128–135. [Google Scholar]
- Miyahara, K.; Pazzani, M.J. Collaborative filtering with the simple Bayesian classifier. In Pacific Rim International Conference on Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Xia, Z.; Dong, Y.; Xing, G. Support vector machines for collaborative filtering. In Proceedings of the 44th Annual Southeast Regional Conference, Melbourne, FL, USA, 10–12 March 2006; pp. 169–174. [Google Scholar]
- Salakhutdinov, R.; Mnih, A.; Hinton, G. Restricted Boltzmann machines for collaborative filtering. In Proceedings of the 24th International Conference on Machine Learning, Corvalis, ORE, USA, 20–24 June 2007; pp. 791–798. [Google Scholar]
- Aggarwal, C.; Parthasarathy, S. Mining massively incomplete data sets by conceptual reconstruction. In Proceedings of the Seventh ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 26–29 August 2001; pp. 227–232. [Google Scholar]
- Baltrunas, L.; Ludwig, B.; Ricci, F. Matrix factorization techniques for context aware recommendation. In Proceedings of the Fifth ACM Conference on Recommender Systems, Chicago, IL, USA, 23–27 October 2011; pp. 301–304. [Google Scholar]
- Billsus, D.; Pazzani, M. Learning collaborative information filters. In Proceedings of the International Conference on Machine Learning, San Francisco, CA, USA, 24–27 July 1998; Morgan Kaufmann: Burlington, MA, USA, 1998; pp. 46–54. [Google Scholar]
- Su, X.; Khoshgoftaar, T.M. A survey of collaborative filtering techniques. Adv. Artif. Intell. 2009, 2009, 421425. [Google Scholar] [CrossRef]
- Hofmann, T. Latent semantic models for collaborative filtering. ACM Trans. Inf. Syst. 2004, 22, 89–115. [Google Scholar] [CrossRef]
- Hu, Y.; Koren, Y.; Volinsky, C. Collaborative filtering for implicit feedback datasets. In Proceedings of the 2008 Eighth IEEE ICDM, Pisa, Italy, 15–19 December 2008; pp. 263–272. [Google Scholar]
- Rendle, S.; Freudenthaler, C.; Gantner, Z.; Schmidt-Thieme, L. BPR: Bayesian Personalized Ranking from Implicit Feedback. In Proceedings of the Twenty-Fifth Conference on Uncertainty in Artificial Intelligence, Montreal, QC, Canada, 18–21 June 2009; pp. 452–461. [Google Scholar]
- Koren, Y. Factor in the neighbors: Scalable and accurate collaborative filtering. ACM Trans. Knowl. Discov. Data 2010, 4, 1. [Google Scholar] [CrossRef]
- Campos, P.G.; Díez, F.; Cantador, I. Time-aware recommender systems: A comprehensive survey and analysis of existing evaluation protocols. User Model. User-Adapt. Interact. 2014, 24, 67–119. [Google Scholar] [CrossRef]
- Chen, J.; Wang, C.; Wang, J. Will you reconsume the near past? Fast prediction on short-term reconsumption behaviors. In Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015; pp. 23–29. [Google Scholar]
- Chen, J.; Wang, C.; Wang, J.; Yu, P.S. Recommendation for Repeat Consumption from User Implicit Feedback. IEEE Trans. Knowl. Data Eng. 2016, 28, 3083–3097. [Google Scholar] [CrossRef]
- Wang, Y.; Han, L. Personalized recommendation via network-based inference with time. Phys. A 2020, 550, 123917. [Google Scholar] [CrossRef]
- Tuan, C.-C.; Hung, C.-F.; Wu, Z.-H. Collaborative location recommendations with dynamic time Periods. Pervasive Mob. Comput. 2017, 35, 1–14. [Google Scholar] [CrossRef]
- Ding, Y.; Li, X. Time weight collaborative filtering. In Proceedings of the 14th ACM International Conference on Information and Knowledge Management, Bremen, Germany, 31 October–5 November 2005; ACM: New York, NY, USA, 2005; pp. 485–492. [Google Scholar]
- Campos, P.; Bellogin, A.; Diez, F.; Chavarriaga, J. Simple time-biased KNN-based recommendations. In Proceedings of the Workshop on Context-Aware Movie Recommendation, Barcelona, Spain, 30 September 2010; pp. 20–23. [Google Scholar]
- Gordea, S.; Zanker, M. Time filtering for better recommendations with small and sparse rating matrices. In Proc. WISE; Springer: Berlin/Heidelberg, Germany, 2007; pp. 171–183. [Google Scholar]
- Zhang, Y.; Liu, Y. A collaborative filtering algorithm based on time period partition. In Proceedings of the IEEE 2010 Third IITSI, Jinggangshan, China, 2–4 April 2010; pp. 777–780. [Google Scholar]
- Wang, C.; Zhang, M.; Ma, W.; Liu, Y.; Ma, S. Modeling Item-Specific Temporal Dynamics of Repeat Consumption for Recommender Systems. In Proceedings of the World Wide Web Conference, San Francisco, CA, USA, 13–17 May 2019; pp. 1977–1987. [Google Scholar]
- Hermann, C. Time-Based Recommendations for Lecture Materials. In Proceedings of the ED-MEDIA, Toronto, ON, Canada, 29 June 2010; pp. 1028–1033. [Google Scholar]
- Zhang, H.; Zhang, X.; Tian, Z.; Li, Z.; Yu, J.; Li, F. Incorporating temporal dynamics into LDA for one-class collaborative filtering. Knowl.-Based Syst. 2018, 150, 49–56. [Google Scholar] [CrossRef]
- Rezaeimehr, F.; Moradi, P.; Ahmadian, S.; Qader, N.N.; Jalili, M. TCARS: Time- and Community-Aware Recommendation System. Future Gener. Comp. Syst. 2018, 78, 419–429. [Google Scholar] [CrossRef]
- Koren, Y. Collaborative Filtering with Temporal Dynamics. In Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Paris, France, 28 June–1 July 2009; pp. 447–456. [Google Scholar]
- Xiong, L.; Chen, X.; Huang, T.; Schneider, J.; Carbonell, J.G. Temporal collaborative filtering with bayesian probabilistic tensor factorization. In Proceedings of the 2010 SIAM International Conference on Data Mining, Columbus, OH, USA, 29 April–1 May 2010; pp. 211–222. [Google Scholar]
- Li, X.; Xu, G.; Chen, E.; Zong, Y. Learning recency based comparative choice towards point-of-interest recommendation. Expert Syst. Appl. 2015, 42, 4274–4283. [Google Scholar] [CrossRef]
- Zafari, F.; Moser, I.; Baarslag, T. Modelling and analysis of temporal preference drifts using a component-based factorised latent approach. Expert Syst. Appl. 2019, 116, 186–208. [Google Scholar] [CrossRef]
- Tong, C.; Qi, J.; Lian, Y.; Niu, J.; Rodrigues, J.J.P.C. TimeTrustSVD: A collaborative filtering model integrating time, trust and rating information. Future Gener. Comp. Syst. 2019, 93, 933–941. [Google Scholar] [CrossRef]
- Koenigstein, N.; Dror, G.; Koren, Y. Yahoo! Music Recommendations: Modeling Music Ratings with Temporal Dynamics and Item Taxonomy. In Proceedings of the Fifth ACM Conference on Recommender Systems, Chicago, IL, USA, 23–27 October 2011; pp. 165–172. [Google Scholar]
- Chen, J.; Wang, C.; Wang, J. Modeling the Interest-Forgetting Curve for Music Recommendation. In Proceedings of the 22nd ACM International Conference on Multimedia, Orlando, FL, USA, 3–7 November 2014; ACM: New York, NY, USA, 2014; pp. 921–924. [Google Scholar]
- Larrain, S.; Trattner, C.; Parra, D.; Graells-Garrido, E.; Nørvåg, K. Good times bad times: A study on recency effects in collaborative filtering for social tagging. In Proceedings of the 9th ACM Conference on Recommender Systems, Vienna, Austria, 16–20 September 2015; ACM: New York, NY, USA, 2015; pp. 269–272. [Google Scholar]
- Yan, C.; Zhang, Q. Merging visual features and temporal dynamics in sequential recommendation. Neurocomputing 2019, 362, 11–18. [Google Scholar] [CrossRef]
- Khosravy, M.; Gupta, N.; Patel, N.; Senjyu, T. (Eds.) Frontier Applications of Nature Inspired Computation; Springer: Singapore, 2020. [Google Scholar]
- Khosravy, M.; Gupta, N.; Patel, N.; Senjyu, T.; Duque, C.A. Particle Swarm Optimization of Morphological Filters for Electrocardiogram Baseline Drift Estimation. In Applied Nature-Inspired Computing: Algorithms and Case Studies; Dey, N., Ashour, A., Bhattacharyya, S., Eds.; Springer Tracts in Nature-Inspired Computing; Springer: Singapore, 2020. [Google Scholar]
- Sedaaghi, M.H.; Daj, R.; Khosravi, M. Mediated morphological filters. In Proceedings of the IEEE 2001 International Conference on Image Processing, Thessaloniki, Greece, 7–10 October 2001; pp. 692–695. [Google Scholar]
- Panniello, U.; Tuzhilin, A.; Gorgoglione, M.; Palmisano, C.; Pedone, A. Experimental comparison of pre- vs. post-filtering approaches in context-aware recommender systems. In Proceedings of the Third ACM Conference on Recommender Systems, New York, NY, USA, 23–25 October 2009; ACM: New York, NY, USA, 2009; pp. 265–268. [Google Scholar]
- Qi, L.; Wang, R.; Hu, C.; Li, S.; He, Q.; Xu, X. Time-aware distributed service recommendation with privacy-preservation. Inf. Sci. 2019, 480, 354–364. [Google Scholar] [CrossRef]
- Adomavicius, G.; Sankaranarayanan, R.; Sen, S.; Tuzhilin, A. Incorporating contextual information in recommender systems using a multidimensional approach. ACM Trans. Inf. Syst. 2005, 23, 103–145. [Google Scholar] [CrossRef]
- Adomavicius, G.; Mobasher, B.; Ricci, F.; Tuzhilin, A. Context-aware recommender systems. Ai Mag. 2011, 32, 67–80. [Google Scholar] [CrossRef]
- Baltrunas, L.; Ludwig, B.; Peer, S.; Ricci, F. Context-aware places of interest recommendations for mobile users. In Proceedings of the International Conference on Human-Computer Interaction, Orlando, FL, USA, 9–14 July 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 531–540. [Google Scholar]
- Lu, J.; Indeche, M.A. Multi-Context-Aware Location Recommendation Using Tensor Decomposition. IEEE Access 2020, 8, 61327–61339. [Google Scholar] [CrossRef]
- Zhao, S.; King, I.; Lyu, M.R. Aggregated temporal tensor factorization model for point-of-interest recommendation. Neural Process. Lett. 2018, 47, 975–992. [Google Scholar] [CrossRef]
- Hosseini, S.; Yin, H.; Zhou, X.; Sadiq, S.; Kangavari, M.R.; Cheung, N.M. Leveraging multi-aspect time-related influence in location recommendation. World Wide Web 2019, 22, 1001–1028. [Google Scholar] [CrossRef]
- Reddy, S.; Mascia, J. Lifetrak: Music in tune with your life. In Proceedings of the 1st ACM International Workshop on Human-centered Multimedia, Santa Barbara, CA, USA, 23–27 October 2006; pp. 25–34. [Google Scholar]
- Baltrunas, L.; Amatriain, X. Towards time-dependant recommendation based on implicit feedback. In Proceedings of the Workshop on Context-Aware Recommender Systems, New York, NY, USA, 25 October 2009. [Google Scholar]
- Tkalcic, M.; Kosir, A.; Tasic, J. Affective recommender systems: The role of emotions in recommender systems. Proc. Ceur Workshop 2011, 811, 9–13. [Google Scholar]
- Liu, C.L.; Chen, Y.C. Background music recommendation based on latent factors and moods. Knowl.-Based Syst. 2018, 159, 158–170. [Google Scholar] [CrossRef]
- Hariri, N.; Mobasher, B.; Burke, R. Context-aware Music Recommendation Based on Latent Topic Sequential Patterns. In Proceedings of the Sixth ACM Conference on Recommender Systems, Dublin, Ireland, 9–13 September 2012; pp. 131–138. [Google Scholar]
- Aghdam, M.H.; Hariri, N.; Mobasher, B.; Burke, R. Adapting Recommendations to Contextual Changes Using Hierarchical Hidden Markov Models. In Proceedings of the 9th ACM Conference on Recommender Systems, Vienna, Austria, 16–20 September 2015; pp. 241–244. [Google Scholar]
- Wang, D.; Deng, S.; Xu, G. Sequence-based context-aware music recommendation. Inf. Retr. 2018, 21, 230–252. [Google Scholar] [CrossRef]
- Yang, D.; Zhang, J.; Wang, S.; Zhang, X. A Time-Aware CNN-Based Personalized Recommender System. Complexity 2019, 2019, 9476981. [Google Scholar] [CrossRef]
- Pacula, M. A Matrix Factorization Algorithm for Music Recommendation Using Implicit User Feedback. Available online: http://www.mpacula.com/publications/lastfm.pdf (accessed on 2 July 2020).
- Vargas, S.; Castells, P. Rank and relevance in novelty and diversity metrics for recommender systems. In Proceedings of the Fifth ACM Conference on Recommender Systems, Chicago, IL, USA, 23–27 October 2011; pp. 109–116. [Google Scholar]
- Bellogin, A.; Castells, P.; Cantador, I. Precision-oriented evaluation of recommender systems: An algorithmic comparison. In Proceedings of the Fifth ACM Conference on Recommender Systems, Chicago, IL, USA, 23–27 October 2011; ACM: New York, NY, USA, 2011; pp. 333–336. [Google Scholar]
- Herlocker, J.L.; Konstan, J.A.; Terveen, L.G.; Riedl, J.T. Evaluating collaborative filtering recommender systems. ACM Trans. Inf. Syst. 2004, 22, 5–53. [Google Scholar] [CrossRef]
- Jarvelin, K.; Kekalainen, J. Cumulated gain-based evaluation of IR techniques. ACM Trans. Inf. Syst. 2002, 20, 422–446. [Google Scholar] [CrossRef]
- Gemulla, R.; Haas, P.J.; Nijkamp, E.; Sismanis, Y. Large-scale matrix factorization with distributed stochastic gradient descent. In Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data mining, San Diego, CA, USA, 21–24 August 2011; ACM: New York, NY, USA, 2011; pp. 69–77. [Google Scholar]
- Bell, R.; Koren, Y.; Volinsky, C. Modeling Relationships at Multiple Scales to Improve Accuracy of Large Recommender Systems. In Proceedings of the 13th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Jose, CA, USA, 12–15 August 2007; ACM: New York, NY, USA, 2007; pp. 95–104. [Google Scholar]
- Pan, R.; Zhou, Y.; Cao, B.; Liu, N.N.; Lukose, R.M.; Scholz, M.; Yang, Q. One-class collaborative filtering. In Proceedings of the 2008 Eighth IEEE ICDM, Pisa, Italy, 15–19 December 2008; pp. 502–511. [Google Scholar]
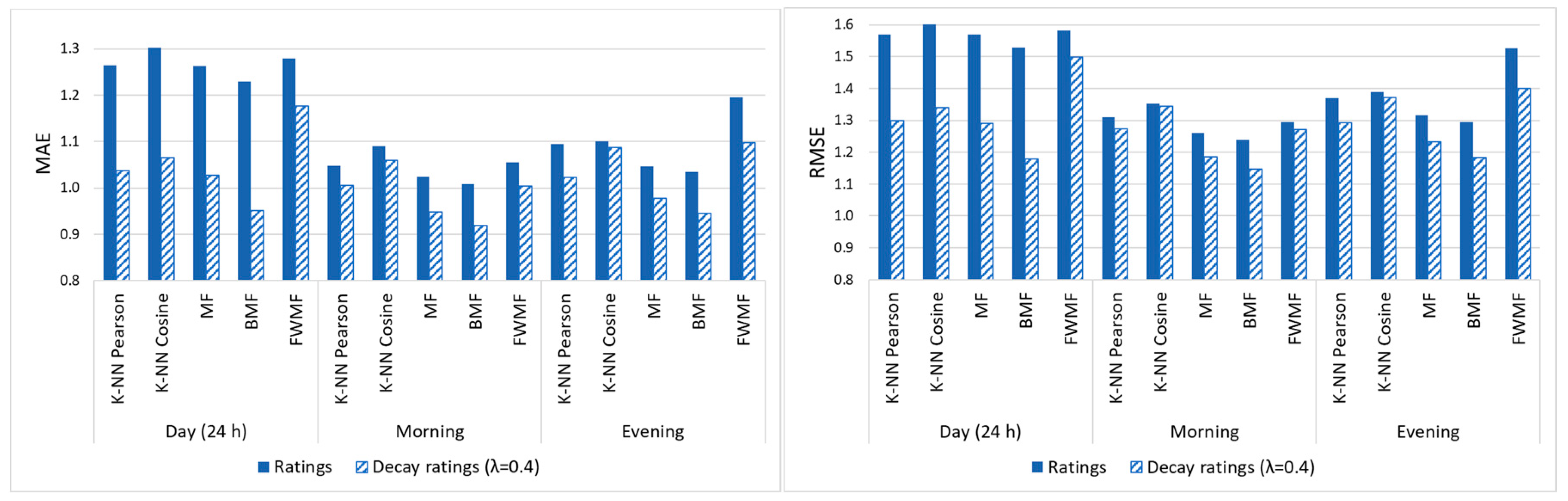

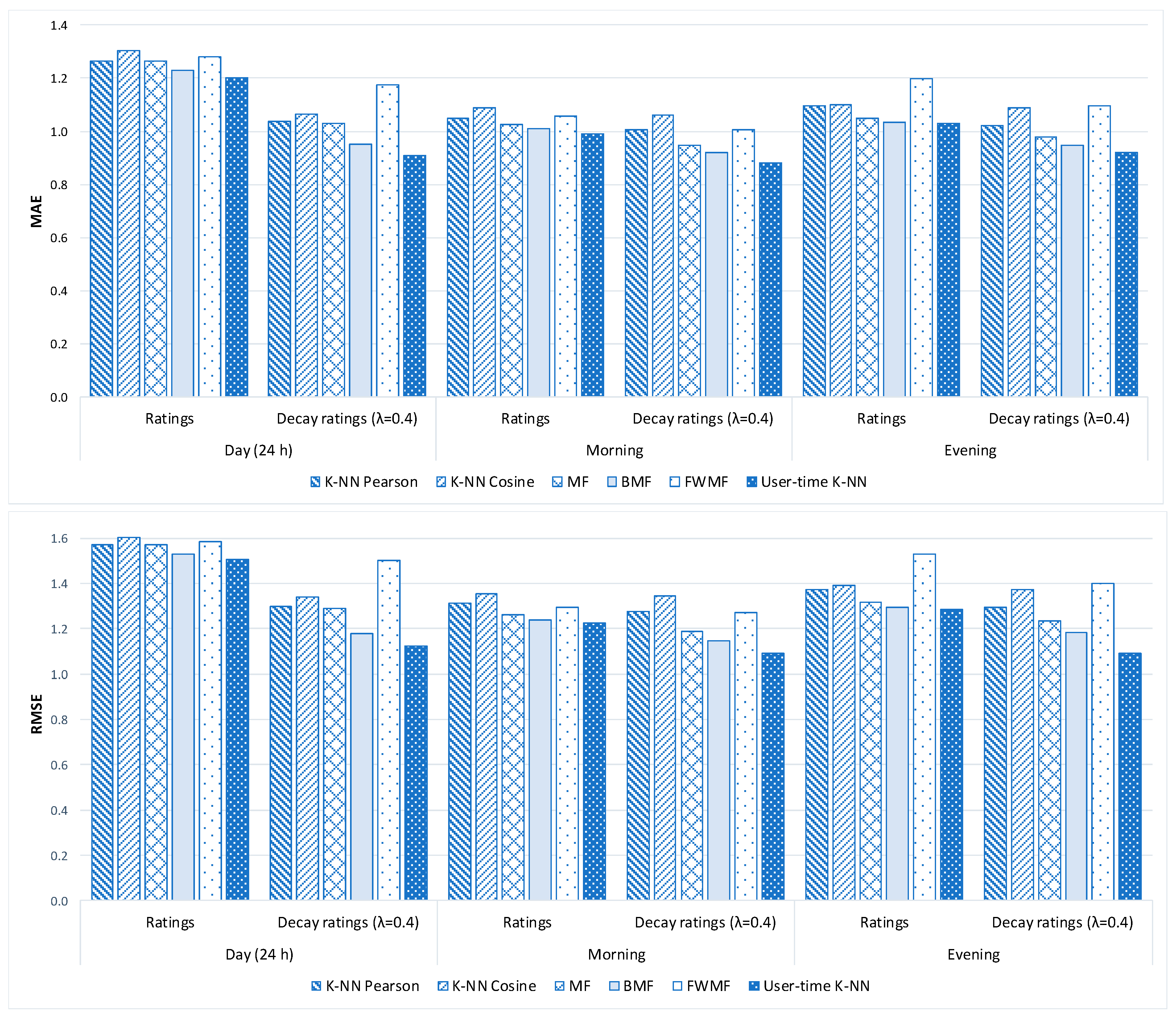
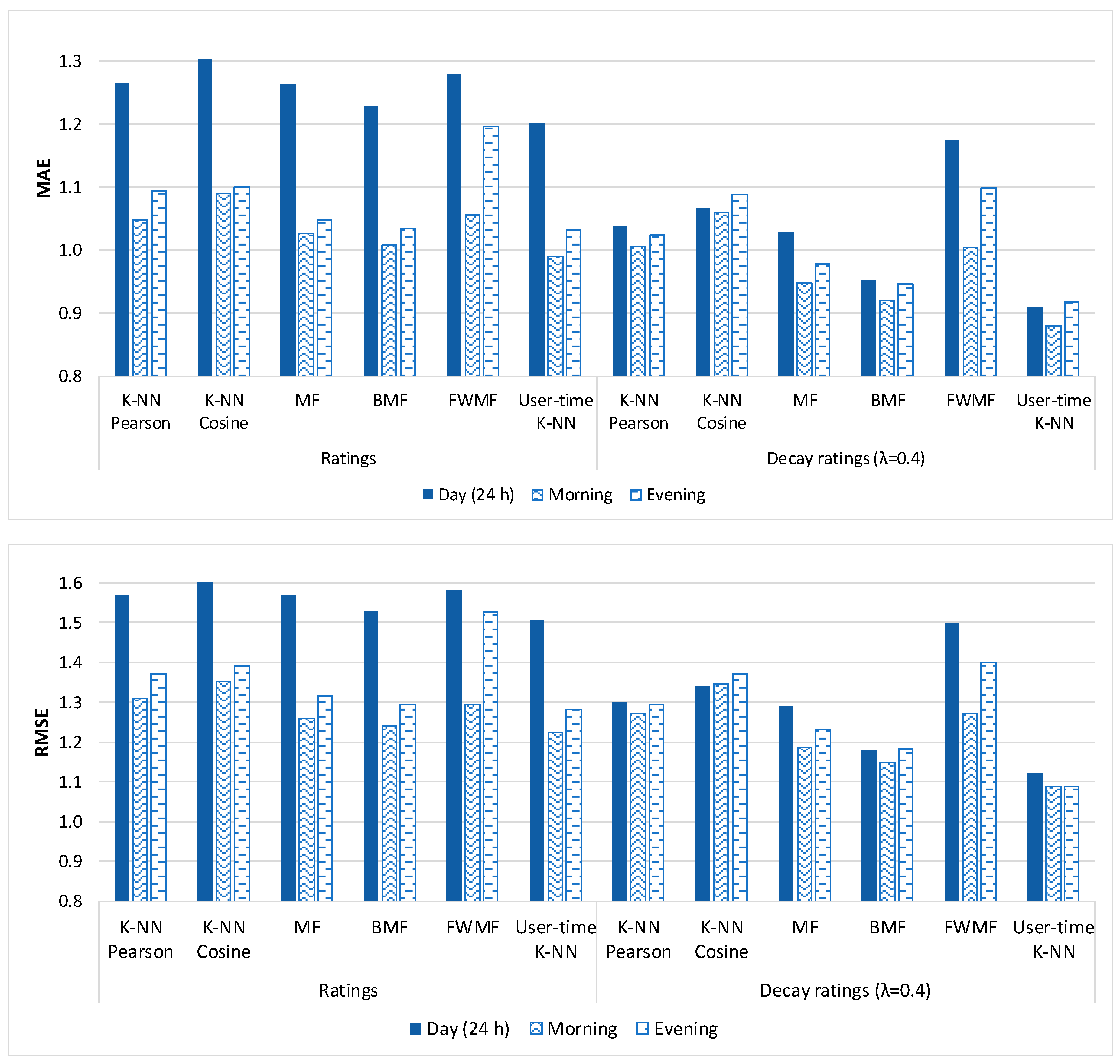

| MAE | RMSE | NMAE | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Ratings | Decay Ratings | Improv. | Ratings | Decay Ratings | Improv. | Ratings | Decay Ratings | ||
| Day (24 h.) | K-NN Pearson | 1.265 | 1.037 | 18.02% | 1.570 | 1.299 | 17.26% | 0.316 | 0.259 |
| K-NN Cosine | 1.303 | 1.066 | 18.19% | 1.601 | 1.340 | 16.30% | 0.326 | 0.267 | |
| MF | 1.263 | 1.028 | 18.61% | 1.569 | 1.291 | 17.72% | 0.316 | 0.257 | |
| BMF | 1.229 | 0.952 | 22.54% | 1.529 | 1.179 | 22.89% | 0.307 | 0.238 | |
| FWMF | 1.279 | 1.176 | 8.05% | 1.582 | 1.499 | 5.25% | 0.320 | 0.294 | |
| Morning | K-NN Pearson | 1.048 | 1.006 | 4.01% | 1.310 | 1.273 | 2.82% | 0.262 | 0.251 |
| K-NN Cosine | 1.090 | 1.060 | 2.75% | 1.353 | 1.345 | 0.59% | 0.273 | 0.265 | |
| MF | 1.025 | 0.948 | 7.51% | 1.260 | 1.186 | 5.87% | 0.256 | 0.237 | |
| BMF | 1.008 | 0.919 | 8.83% | 1.240 | 1.147 | 7.50% | 0.252 | 0.230 | |
| FWMF | 1.055 | 1.004 | 4.83% | 1.294 | 1.271 | 1.78% | 0.264 | 0.251 | |
| Evening | K-NN Pearson | 1.094 | 1.023 | 6.49% | 1.370 | 1.293 | 5.62% | 0.274 | 0.256 |
| K-NN Cosine | 1.100 | 1.088 | 1.09% | 1.389 | 1.371 | 1.30% | 0.275 | 0.272 | |
| MF | 1.047 | 0.978 | 6.59% | 1.317 | 1.232 | 6.45% | 0.262 | 0.245 | |
| BMF | 1.034 | 0.946 | 8.51% | 1.294 | 1.183 | 8.58% | 0.258 | 0.237 | |
| FWMF | 1.196 | 1.097 | 8.28% | 1.527 | 1.399 | 8.38% | 0.256 | 0.227 | |
| MAE | RMSE | NMAE | ||||||
|---|---|---|---|---|---|---|---|---|
| Ratings | Decay Ratings | Improv. | Ratings | Decay Ratings | Improv. | Ratings | Decay Ratings | |
| K-NN Pearson | 0.898 | 0.890 | 0.89% | 1.162 | 1.153 | 0.77% | 0.225 | 0.222 |
| K-NN Cosine | 0.985 | 0.948 | 3.76% | 1.228 | 1.212 | 1.30% | 0.246 | 0.237 |
| MF | 0.788 | 0.777 | 1.40% | 0.999 | 0.998 | 0.10% | 0.197 | 0.194 |
| BMF | 0.785 | 0.775 | 1.27% | 0.977 | 0.982 | 0.51% | 0.196 | 0.194 |
| FWMF | 0.803 | 0.792 | 1.37% | 0.995 | 0.993 | 0.20% | 0.201 | 0.198 |
| AUC | NDCG | MAP | |||||
|---|---|---|---|---|---|---|---|
| Ratings | Decay Ratings | Ratings | Decay Ratings | Ratings | Decay Ratings | ||
| Day (24 h.) | K-NN | 0.422 | 0.422 | 0.327 | 0.327 | 0.006 | 0.006 |
| WRMF | 0.500 | 0.525 | 0.331 | 0.336 | 0.007 | 0.009 | |
| BPRMF | 0.528 | 0.535 | 0.330 | 0.332 | 0.005 | 0.006 | |
| Morning | K-NN | 0.413 | 0.413 | 0.315 | 0.315 | 0.005 | 0.005 |
| WRMF | 0.516 | 0.519 | 0.316 | 0.321 | 0.006 | 0.008 | |
| BPRMF | 0.473 | 0.491 | 0.312 | 0.313 | 0.004 | 0.004 | |
| Evening | K-NN | 0.378 | 0.378 | 0.297 | 0.297 | 0.004 | 0.004 |
| WRMF | 0.590 | 0.597 | 0.316 | 0.322 | 0.009 | 0.011 | |
| BPRMF | 0.562 | 0.539 | 0.306 | 0.311 | 0.004 | 0.006 | |
| User-Time K-NN | MAE | RMSE | NMAE | |||||
|---|---|---|---|---|---|---|---|---|
| Ratings | Decay Ratings | Improv. | Ratings | Decay Ratings | Improv. | Ratings | Decay Ratings | |
| Day (24 h) | 1.202 | 0.909 | 24.38% | 1.506 | 1.121 | 25.56% | 0.301 | 0.227 |
| Morning | 0.990 | 0.879 | 11.21% | 1.223 | 1.089 | 10.96% | 0.247 | 0.220 |
| Evening | 1.031 | 0.918 | 10.96% | 1.282 | 1.089 | 15.05% | 0.258 | 0.229 |
| User-time K-NN | AUC | NDCG | MAP |
|---|---|---|---|
| Ratings/Decay Ratings | Ratings/Decay Rating | Ratings/Decay Rating | |
| Day (24 h) | 0.708 | 0.348 | 0.009 |
| Morning | 0.662 | 0.331 | 0.008 |
| Evening | 0.692 | 0.551 | 0.001 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sánchez-Moreno, D.; Zheng, Y.; Moreno-García, M.N. Time-Aware Music Recommender Systems: Modeling the Evolution of Implicit User Preferences and User Listening Habits in A Collaborative Filtering Approach. Appl. Sci. 2020, 10, 5324. https://doi.org/10.3390/app10155324
Sánchez-Moreno D, Zheng Y, Moreno-García MN. Time-Aware Music Recommender Systems: Modeling the Evolution of Implicit User Preferences and User Listening Habits in A Collaborative Filtering Approach. Applied Sciences. 2020; 10(15):5324. https://doi.org/10.3390/app10155324
Chicago/Turabian StyleSánchez-Moreno, Diego, Yong Zheng, and María N. Moreno-García. 2020. "Time-Aware Music Recommender Systems: Modeling the Evolution of Implicit User Preferences and User Listening Habits in A Collaborative Filtering Approach" Applied Sciences 10, no. 15: 5324. https://doi.org/10.3390/app10155324
APA StyleSánchez-Moreno, D., Zheng, Y., & Moreno-García, M. N. (2020). Time-Aware Music Recommender Systems: Modeling the Evolution of Implicit User Preferences and User Listening Habits in A Collaborative Filtering Approach. Applied Sciences, 10(15), 5324. https://doi.org/10.3390/app10155324






