Combining Internal- and External-Training-Loads to Predict Non-Contact Injuries in Soccer
Abstract
1. Introduction
2. Materials and Methods
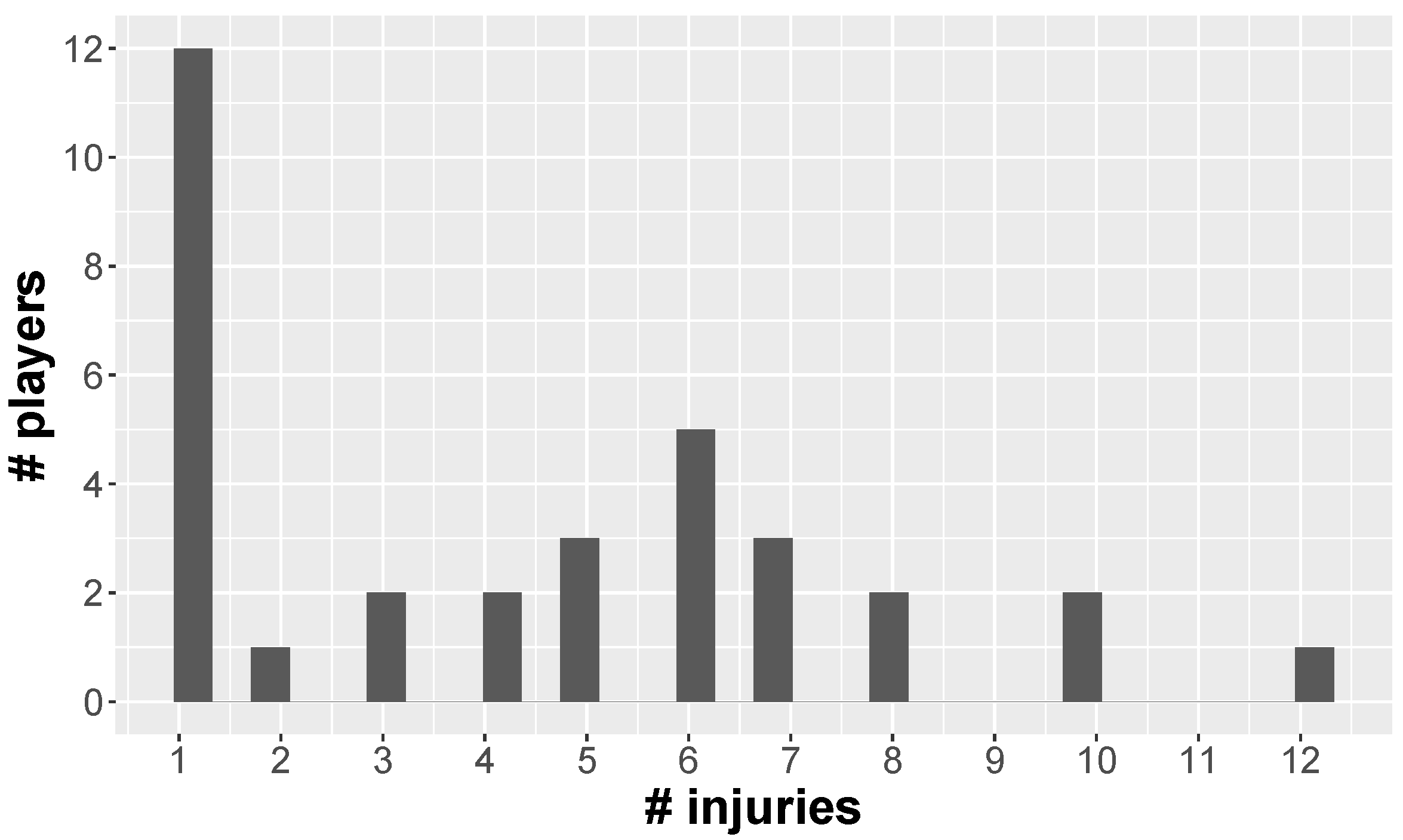
2.1. Procedures and Data Collection
2.2. Predicting Injuries
2.3. Data Pre-Processing and Evaluation Protocol
2.4. Predictive Models
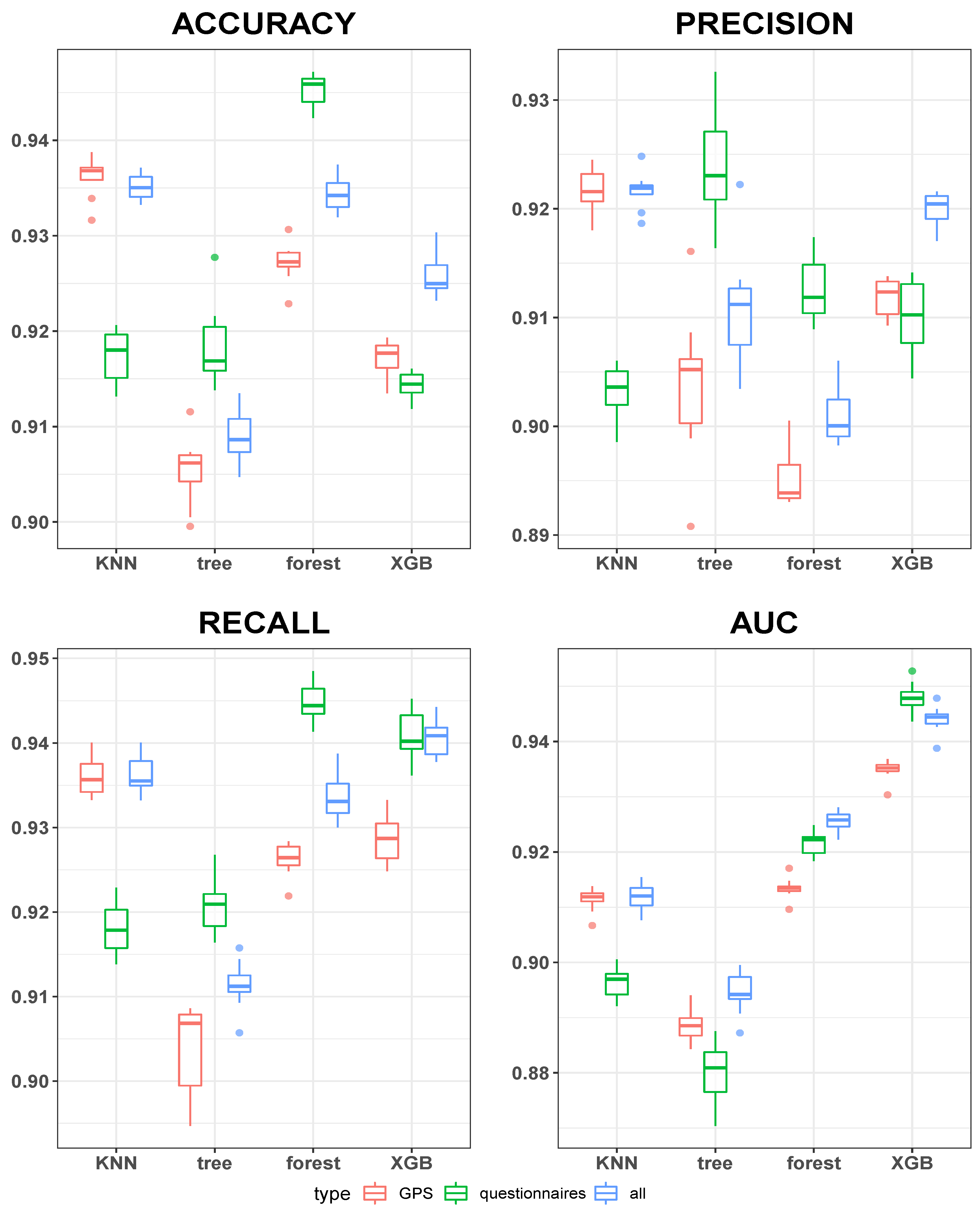
3. Results
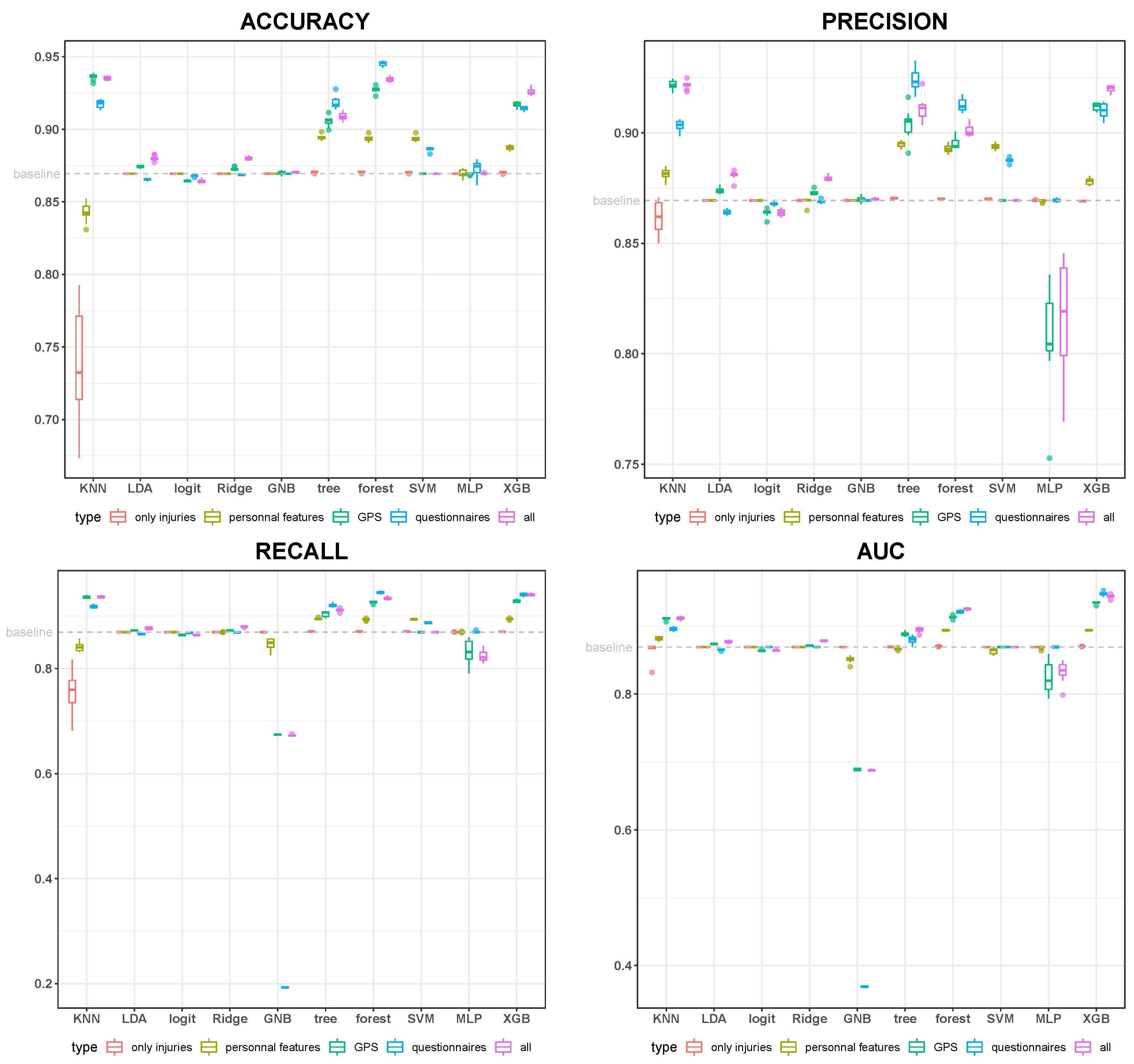
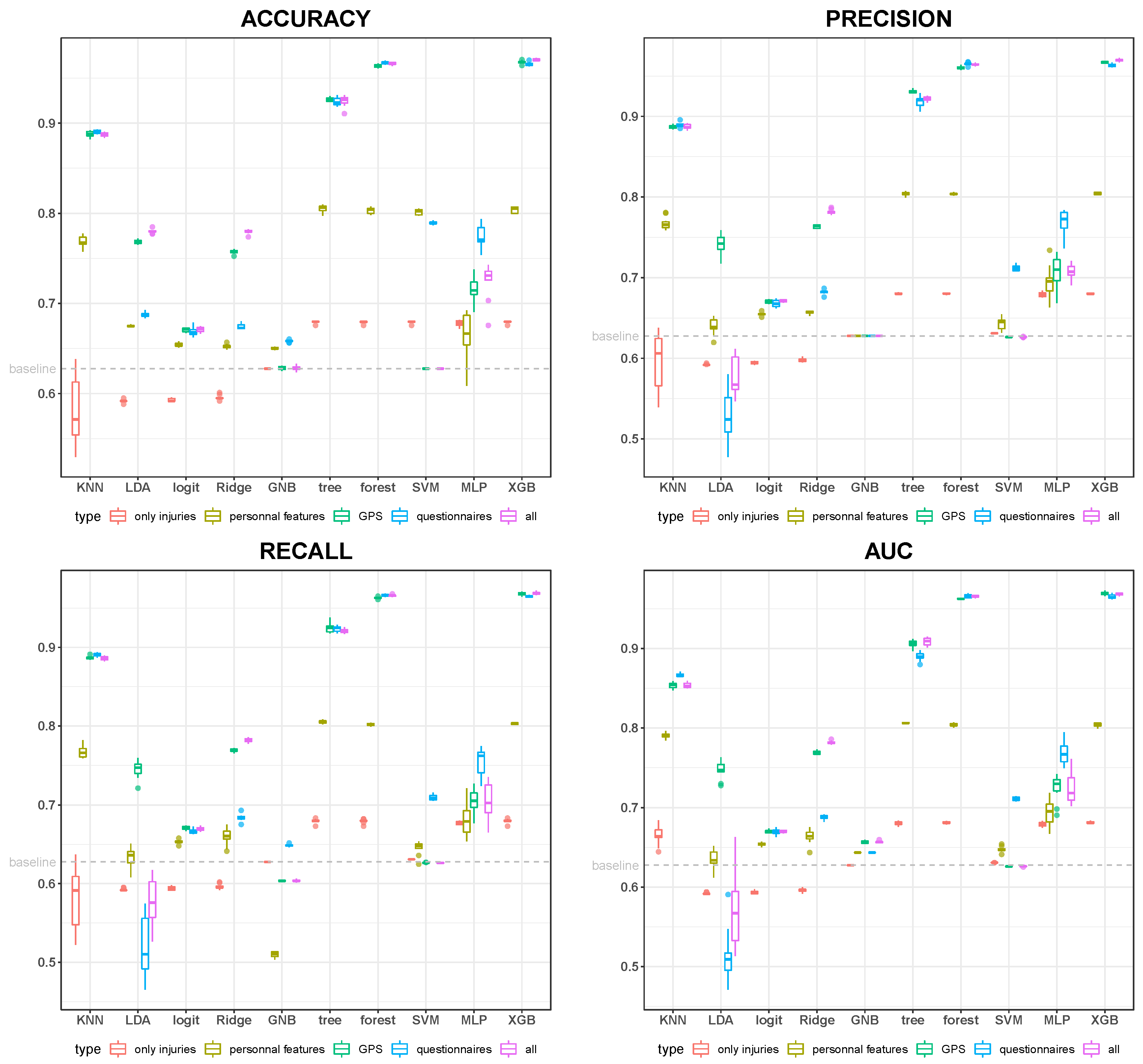
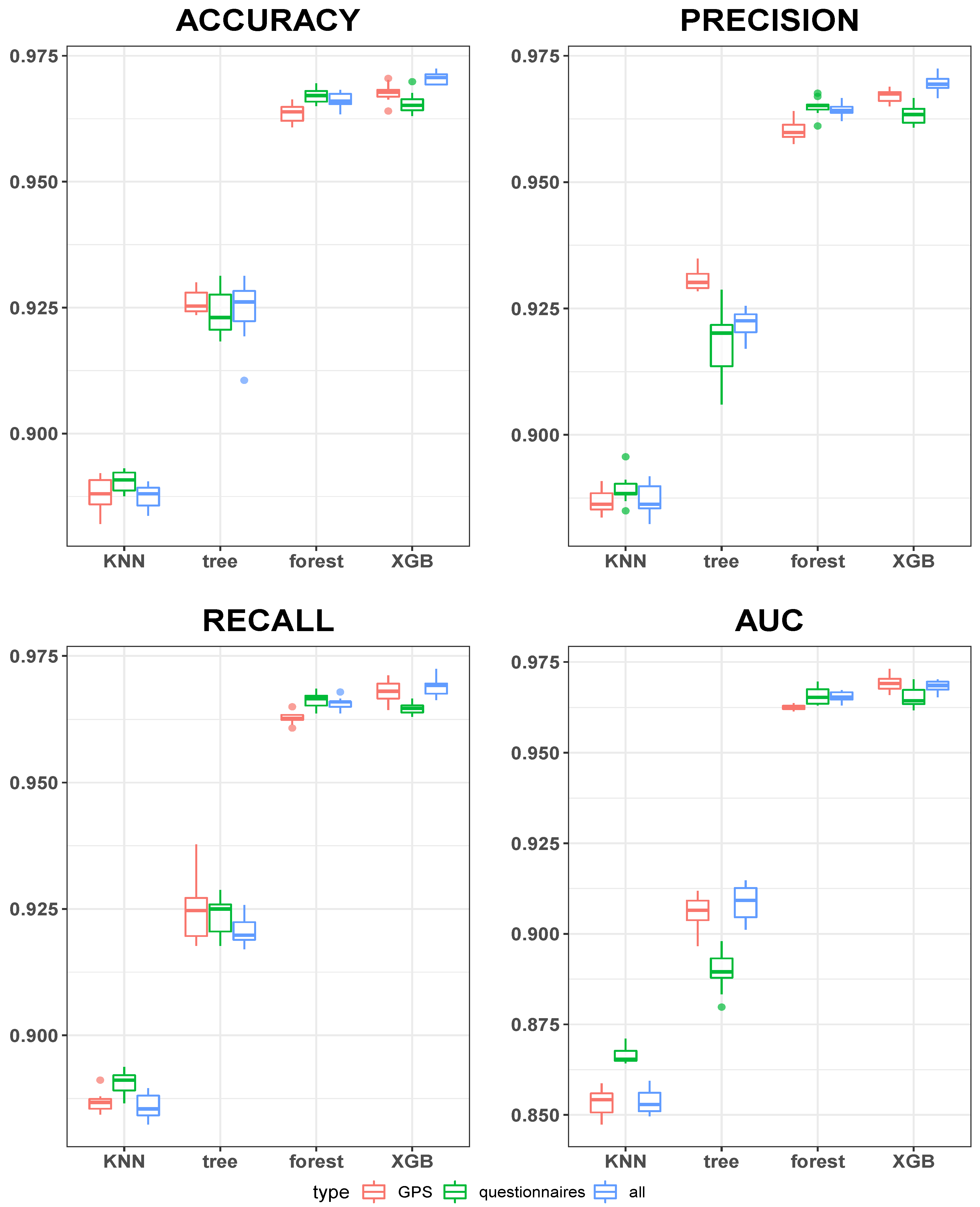
3.1. Predictive Performance
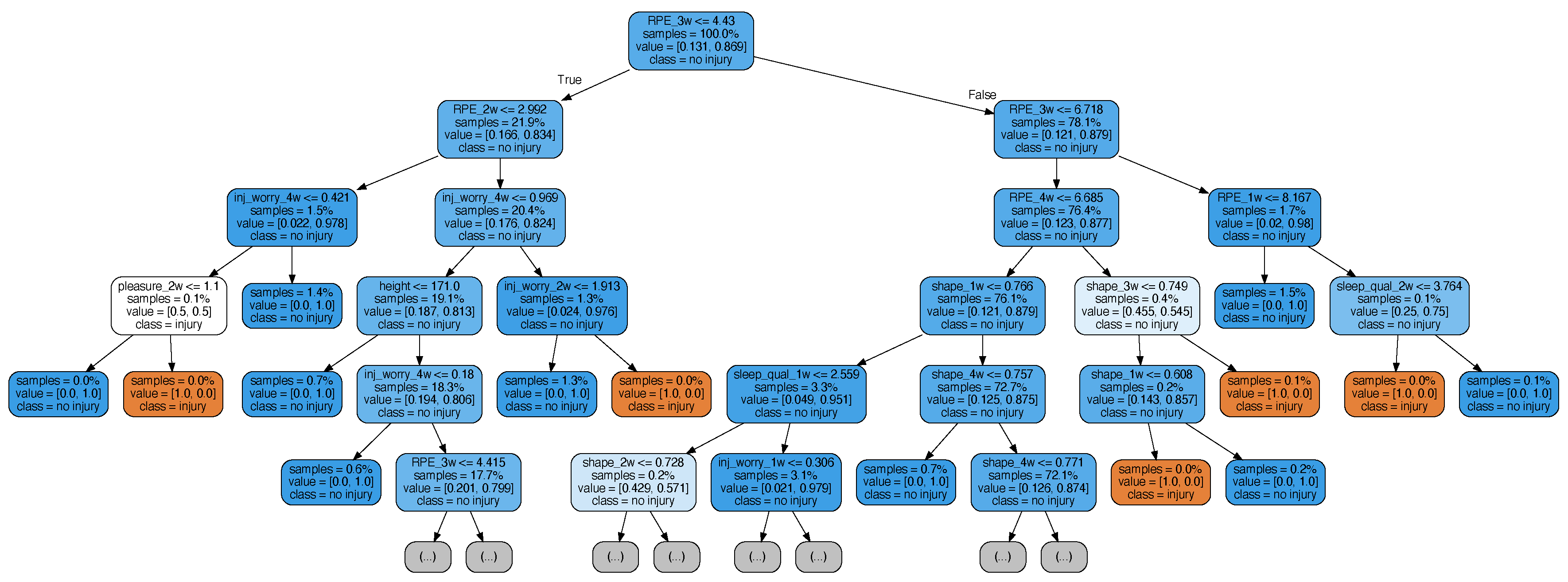
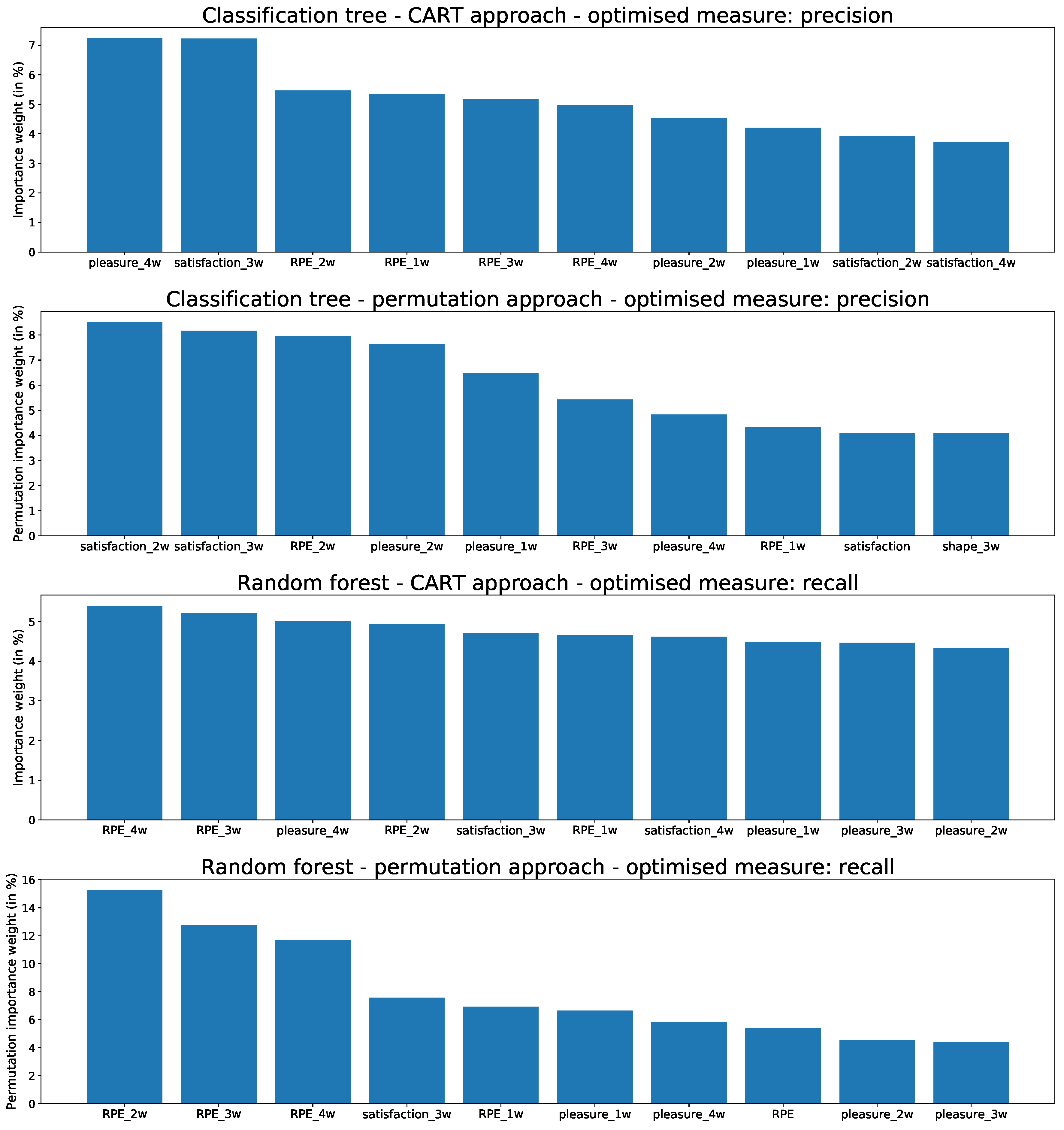
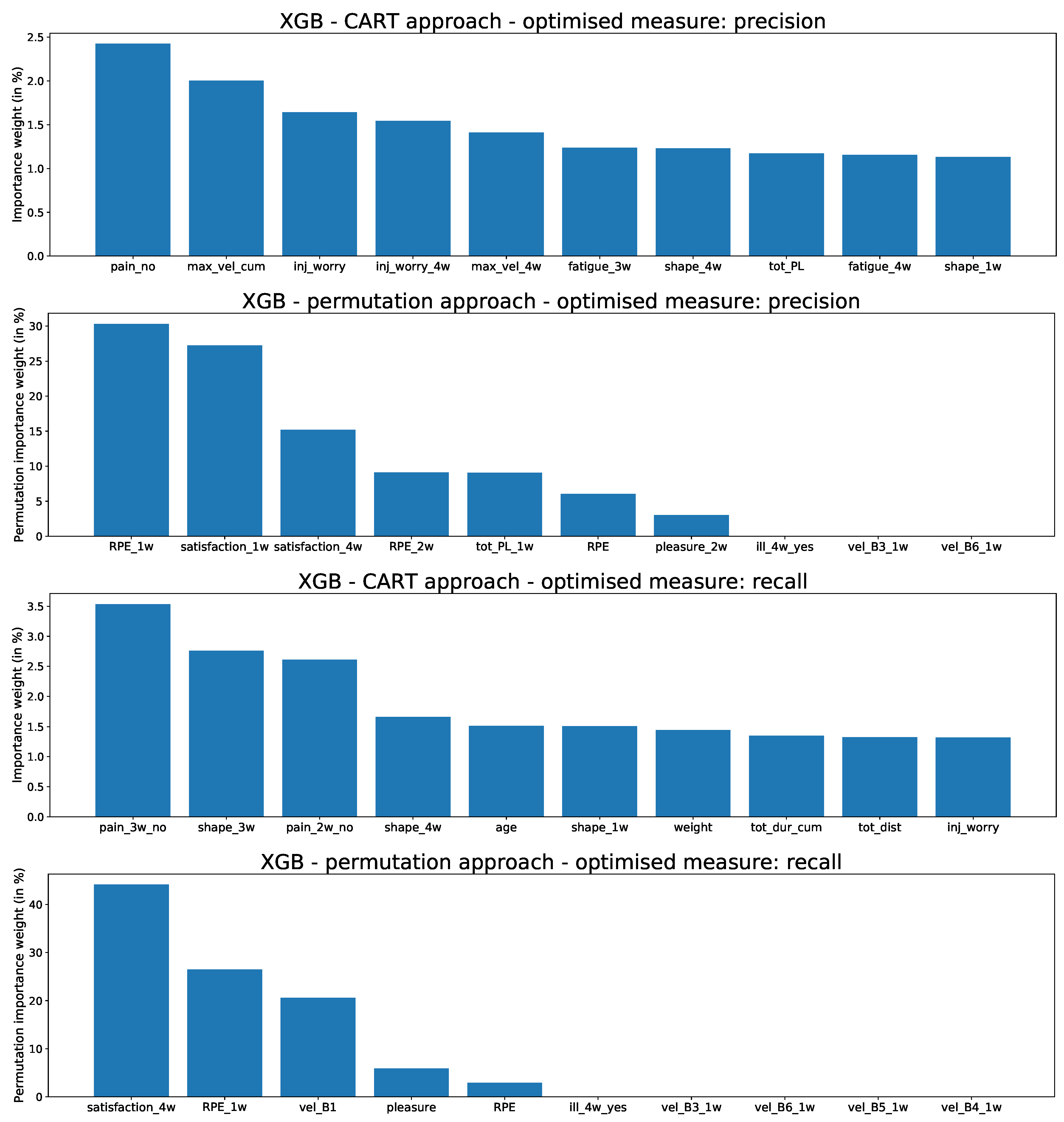
3.2. Predictive Explanation
- graphs corresponding to decision trees for legitimate configuration (i.e., when decision tree performs well according to Section 3.1)
- the weights of predictive variables obtained from tree-based models
- a discriminative condition relatively to 1 feature (with a numerical threshold) that determines which is the next node to be considered given features values (e.g., for the initial node).
- the proportion of the learning dataset that falls into the node (e.g., 100% for the initial node).
- the labels proportions of the examples contained in the node (e.g., the initial node contains 13.1% of injured players and 86.9% of not injured ones).
- the label attached to the node which is the most frequent one in the subset of the learning examples it contains.
4. Discussion
Limitation and Future Directions
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Model | Parameter | Accuracy | Precision | Recall | AUC |
|---|---|---|---|---|---|
| KNN | K | 1 | 2 | 1 | 1 |
| LDA | tol | 1.30 | 9.87 | 1.75 | 1.65 |
| criterion | entropy | entropy | entropy | entropy | |
| tree | max depth | 8083 | 10,000 | 10,000 | 10,000 |
| min samples split | 2 | 2 | 2 | 12 | |
| min impurity decrease | 0 | 0 | 0 | 0.00332908 | |
| gaussianNB | var smoothing | 0.04 | 0.04 | 0.00 | 0.02 |
| n estimators | 10,000 | 10 | 8145 | 10,000 | |
| criterion | entropy | entropy | entropy | entropy | |
| forest | max depth | 63 | 100 | 93 | 10 |
| min samples split | 2 | 2 | 2 | 2 | |
| min impurity decrease | 0 | 0 | 0 | 0 | |
| max features | 0.5 | 0.01 | 0.5 | 0.5 | |
| C | 823,469 | 442,788 | 397,591 | 1,000,000 | |
| SVM | gamma | 2.9 | 2.8 | 2.6 | 0 |
| degree | 7 | 8 | 8 | 1 | |
| hidden layer sizes | (100, 100, 50) | (100, 50, 50) | (50, 100, 100) | (100, 100, 100) | |
| MLP | activation | tanh | relu | relu | relu |
| alpha | 1.00 | 0.0001 | 1 | 1 | |
| penalty | l2 | l2 | l2 | l2 | |
| logit | tol | 0.45 | 0.51 | 0.08 | 1 |
| C | 516,729 | 9658 | 270,370 | 1 | |
| l1 ratio | 0 | 1 | 0 | 1 | |
| penalty | l2 | none | l2 | l1 | |
| Elasticnet | tol | 0.48 | 0.00 | 1.00 | 0.00 |
| C | 250,061 | 1 | 0 | 227,702 | |
| l1 ratio | 0 | 1 | 0 | 1 | |
| max depth | 5 | 10 | 3 | 10 | |
| n estimators | 946 | 1 | 1 | 654 | |
| XGB | eta | 0.01 | 0.01 | 0.59 | 0.12 |
| gamma | 0 | 5 | 0 | 0 | |
| sampling method | gradient based | gradient based | gradient based | uniform | |
| Ridge | alpha | 6.39 | 0 | 0 | 6.83 |
| tol | 1 | 0 | 0 | 1 |
| Model | Parameter | Accuracy | Precision | Recall | AUC |
|---|---|---|---|---|---|
| KNN | K | 1 | 1 | 1 | 4 |
| LDA | tol | 5.12 | 0 | 0 | 0 |
| criterion | entropy | gini | entropy | entropy | |
| max depth | 50 | 1513 | 10,000 | 9529 | |
| tree | min samples split | 2 | 2 | 2 | 25 |
| min impurity decrease | 0 | 1.35 | 0 | 3.5 | |
| gaussianNB | var smoothing | 0.0325 | 0 | 1 | 0.13 |
| n estimators | 1 | 415 | 252 | 5269 | |
| criterion | entropy | gini | entropy | entropy | |
| forest | max depth | 87 | 29 | 92 | 75 |
| min samples split | 2 | 2 | 2 | 5 | |
| min impurity decrease | 0 | 0 | 0 | 0 | |
| max features | 0.5 | 0.195 | 0.5 | 0.3638 | |
| C | 176530 | 1 | 1 | 816,071 | |
| SVM | gamma | 1.11 | 1 | 1 | 1 |
| degree | 3 | 8 | 1 | 7 | |
| hidden layer sizes | (50. 100. 100) | (50. 50. 100) | (100. 100. 50) | (100. 100. 100) | |
| MLP | activation | relu | relu | relu | relu |
| alpha | 1 | 1 | 1 | 1 | |
| penalty | l2 | l2 | l2 | l2 | |
| logit | tol 0.98 | 0.01459 | 0.38 | 0.0028 | |
| C | 3125 | 2976 | 999,758 | 2275 | |
| l1 ratio | 0 | 0 | 0 | 1 | |
| penalty | elasticnet | l1 | elasticnet | l1 | |
| elasticnet | tol | 7 | 1 | 1 | 1 |
| C | 966341 | 1 | 1 | 683,586 | |
| l1 ratio | 0 | 1 | 0 | 1 | |
| max depth | 5 | 4 | 5 | 10 | |
| n estimators | 737 | 594 | 875 | 904 | |
| XGB | eta | 0.256 | 0.45327 | 0.4529 | 0.03162 |
| gamma | 0 | 0 | 0 | 0 | |
| sampling method | uniform | uniform | gradient based | uniform | |
| Ridge | alpha | 33 | 17.1 | 0 | 0 |
| tol | 1 | 0 | 1 | 0 |

References
- Della Villa, F.; Mandelbaum, B.R.; Lemak, L.J. The Effect of Playing Position on Injury Risk in Male Soccer Players: Systematic Review of the Literature and Risk Considerations for Each Playing Position. Am. J. Orthop. 2018, 47, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Jones, C.M.; Griffiths, P.C.; Mellalieu, S.D. Training Load and Fatigue Marker Associations with Injury and Illness: A Systematic Review of Longitudinal Studies; Springer International Publishing: Berlin/Heidelberg, Germany, 2017; Volume 47. [Google Scholar]
- Gómez-Piqueras, P.; Gonzalez-Villora, S.; Sainz de Baranda Andujar, M.; Contreras-Jordan, O. Functional Assessment and Injury Risk in a Professional Soccer Team. Sports 2017, 5, 9. [Google Scholar] [CrossRef] [PubMed]
- Gabbett, T.J. The development and application of an injury prediction model for noncontact, soft-tissue injuries in elite collision sport athletes. J. Strength Cond. Res. 2010, 24, 2593–2603. [Google Scholar] [CrossRef] [PubMed]
- Borresen, J.; Ian Lambert, M.; Lambert, M.I. The quantification of training load, the training response and the effect on performance. Sports Med. 2009, 39, 779–795. [Google Scholar] [CrossRef]
- Impellizzeri, F.M.; Rampinini, E.; Coutts, A.J.; Sassi, A.; Marcora, S.M. Use of RPE-based training load in soccer. Med. Sci. Sports Exerc. 2004, 36, 1042–1047. [Google Scholar] [CrossRef]
- Casamichana, D.; Castellano, J.; Calleja-Gonzalez, J.; RomaN, J.S.; Castagna, C. Relationship between indicators of training load in soccer players. J. Strength Cond. Res. 2013, 27, 369–374. [Google Scholar] [CrossRef]
- Randers, M.B.; Mujika, I.; Hewitt, A.; Santisteban, J.; Bischoff, R.; Solano, R.; Zubillaga, A.; Peltola, E.; Krustrup, P.; Mohr, M. Application of four different football match analysis systems: A comparative study. J. Sports Sci. 2010, 28, 171–182. [Google Scholar] [CrossRef]
- Vigne, G.; Gaudino, C.; Rogowski, I.; Alloatti, G.; Hautier, C. Activity profile in elite Italian soccer team. Int. J. Sports Med. 2010, 31, 304–310. [Google Scholar] [CrossRef]
- Di Salvo, V.; Baron, R.; Tschan, H.; Calderon Montero, F.J.; Bachl, N.; Pigozzi, F. Performance characteristics according to playing position in elite soccer. Int. J. Sports Med. 2007, 28, 222–227. [Google Scholar] [CrossRef]
- Carling, C.; Bloomfield, J.; Nelsen, L.; Reilly, T. The role of motion analysis in elite soccer: Contemporary performance measurement techniques and work rate data. Sports Med. 2008, 38, 839–862. [Google Scholar] [CrossRef]
- Colby, M.J.; Dawson, B.; Heasman, J.; Rogalski, B.; Gabbett, T.J. Accelerometer and GPS-derived running loads and injury risk in elite Australian footballers. J. Strength Cond. Res. 2014, 28, 2244–2252. [Google Scholar] [CrossRef] [PubMed]
- Akenhead, R.; Nassis, G.P. Training load and player monitoring in high-level football: Current practice and perceptions. Int. J. Sports Physiol. Perform. 2016, 11, 587–593. [Google Scholar] [CrossRef] [PubMed]
- Raya-Gonzalez, J.; Nakamura, F.Y.; Castillo, D.; Yanci, J.; Fanchini, M. Determining the relationship between internal load markers and noncontact injuries in young elite soccer players. Int. J. Sports Physiol. Perform. 2019, 14, 421–425. [Google Scholar] [CrossRef] [PubMed]
- Haddad, M.; Padulo, J.; Chamari, K. The usefulness of session rating of perceived exertion for monitoring training load despite several influences on perceived exertion. Int. J. Sports Physiol. Perform. 2014, 9, 882–883. [Google Scholar] [CrossRef] [PubMed]
- Malone, S.; Roe, M.; Doran, D.A.; Gabbett, T.J.; Collins, K. High chronic training loads and exposure to bouts of maximal velocity running reduce injury risk in elite Gaelic football. J. Sci. Med. Sport 2017, 20, 250–254. [Google Scholar] [CrossRef] [PubMed]
- Bartlett, J.D.; O’Connor, F.; Pitchford, N.; Torres-Ronda, L.; Robertson, S.J. Relationships between internal and external training load in team-sport athletes: Evidence for an individualized approach. Int. J. Sports Physiol. Perform. 2017, 12, 230–234. [Google Scholar] [CrossRef]
- Claudino, J.G.; de Capanema, D.O.; de Souza, T.V.; Serrao, J.C.; Machado Pereira, A.C.; Nassis, G.P. Current Approaches to the Use of Artificial Intelligence for Injury Risk Assessment and Performance Prediction in Team Sports: A Systematic Review. Sports Med. Open 2019, 5, 28. [Google Scholar] [CrossRef]
- Rossi, A.; Pappalardo, L.; Cintia, P.; Iaia, F.M.; Fernandez, J.; Medina, D. Effective injury forecasting in soccer with GPS training data and machine learning. PLoS ONE 2018, 13, e0201264. [Google Scholar] [CrossRef] [PubMed]
- Roe, G.; Darrall-Jones, J.; Black, C.; Shaw, W.; Till, K.; Jones, B. Validity of 10 Hz GPS and Timing Gates for Assessing Maximum Velocity in Professional Rugby Union Players. Int. J. Sports Physiol. Perform. 2017, 12, 836–839. [Google Scholar] [CrossRef]
- Rampinini, E.; Alberti, G.; Fiorenza, M.; Riggio, M.; Sassi, R.; Borges, T.O.; Coutts, A.J. Accuracy of GPS devices for measuring high-intensity running in field-based team sports. Int. J. Sports Med. 2015, 36, 49–53. [Google Scholar] [CrossRef]
- Rampinini, E.; Bishop, D.; Marcora, S.M.; Ferrari Bravo, D.; Sassi, R.; Impellizzeri, F.M. Validity of simple field tests as indicators of match-related physical performance in top-level professional soccer players. Int. J. Sports Med. 2007, 28, 228–235. [Google Scholar] [CrossRef] [PubMed]
- Di Salvo, V.; Gregson, W.; Atkinson, G.; Tordoff, P.; Drust, B. Analysis of high intensity activity in premier league soccer. Int. J. Sports Med. 2009, 30, 205–212. [Google Scholar] [CrossRef] [PubMed]
- Barrett, S.; Midgley, A.; Lovell, R. PlayerLoadTM: Reliability, convergent validity, and influence of unit position during treadmill running. Int. J. Sports Physiol. Perform. 2014, 9, 945–952. [Google Scholar] [CrossRef] [PubMed]
- Fisher, R.A. The Use of Multiple Measurements in Taxonomic Problems. Ann. Eugen. 1936, 7, 179–188. [Google Scholar] [CrossRef]
- McLachlan, G. Discriminant Analysis and Statistical Pattern Recognition; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Maron, M.E. Automatic Indexing: An Experimental Inquiry. J. ACM 1961, 8, 404–417. [Google Scholar] [CrossRef]
- Rish, I. An empirical study of the naive Bayes classifier. In Proceedings of the International Joint Conference Artificial Intelligence 2001 Work Empir Methods Artificial Intelligence, Seattle, WA, USA, 4–10 August 2001; pp. 41–46. [Google Scholar]
- Breiman, L.; Friedman, J.; Stone, C.J. Classification Algorithms and Regression Trees. Classif. Regres. Trees 1984, 246–280. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Boser, B.E.; Guyon, I.M.; Vapnik, V.N. A training algorithm for optimal margin classifiers. In Proceedings of the 5th Annual Workshop on Computational Learning Theory (COLT’92), Pittsburgh, PA, USA, 27–29 July 1992; pp. 144–152. [Google Scholar]
- Werbos, P. Beyond Regression: New Tools for Prediction and Analysis in the Behavioral Sciences. Ph.D. Thesis, Department of Applied Mathematics, Harvard University, Cambridge, MA, USA, 1974, unpublished. [Google Scholar]
- McCulloch, W.S.; Pitts, W.A. logical calculus nervous activity. Bull. Math. Biol. 1943, 52, 99–115. [Google Scholar] [CrossRef]
- Rosenblatt, F. Frosenblatt. Psychol. Rev. 1958, 65, 1–23. [Google Scholar]
- Jebara, T. Machine Learning: Discriminative and Generative; Kluwer Academic; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Jaspers, A.; De Beéck, T.O.; Brink, M.S.; Frencken, W.G.; Staes, F.; Davis, J.J.; Helsen, W.F. Relationships between the external and internal training load in professional soccer: What can we learn from machine learning? Int. J. Sport. Physiol. Perform. 2018, 13, 625–630. [Google Scholar] [CrossRef]
- Saw, A.E.; Main, L.C.; Gastin, P.B. Monitoring the athlete training response: Subjective self-reported measures trump commonly used objective measures: A systematic review. Br. J. Sport. Med. 2016, 50, 281–291. [Google Scholar] [CrossRef] [PubMed]
- Halson, S.L. Monitoring training load to understand fatigue in athletes. Sport. Med. 2014, 44, 139–147. [Google Scholar] [CrossRef] [PubMed]
- Clemente, F.M.; Mendes, B.; Nikolaidis, P.T.; Calvete, F.; Carrico, S.; Owen, A.L. Internal training load and its longitudinal relationship with seasonal player wellness in elite professional soccer. Physiol. Behav. 2017, 179, 262–267. [Google Scholar] [CrossRef] [PubMed]
| Type of Data | Name | Definition |
|---|---|---|
| personnal features | age | age at the beginning of the 2017 season |
| weight | weight at the beginning of the 2017 season | |
| height | height at the beginning of the 2017 season | |
| Body Mass Index | ||
| role | role | |
| tot_dur | total duration | |
| tot_dist | total distance covered | |
| tot_PL | total Player Load | |
| vel_B1 | distance covered between 0 and 1 km/h | |
| vel_B2 | distance covered between 0 and 6 km/h | |
| vel_B3 | distance covered between 6 and 15 km/h | |
| vel_B4 | distance covered between 15 and 20 km/h | |
| vel_B5 | distance covered between 20 and 25 km/h | |
| vel_B6 | distance covered at more than 25 km/h | |
| acc_B2 | number of accelerations above 2 m/ | |
| acc_B3 | number of decelerations above −2m/ | |
| max_vel | maximum speed in m/s | |
| pre-session questionnaire | sleep_qual (VAS10) | sleep quality |
| fatigue (VAS10) | fatigue state of the player | |
| shape (VAS10) | being in good shape | |
| mood (VAS10) | actual mood of the player | |
| pain (yes or no) | perceived pain | |
| inj_worry (if pain, VAS10) | worry in relation to pain | |
| ill | sick or not | |
| post-session questionnaire | (VAS10) | rating of perceived exertion of the session |
| satisfaction (VAS10) | satisfaction during his performance | |
| pleasure (VAS10) | pleasure during the session |
| accuracy | How many examples | |
| we correctly predicted | ||
| precision | How many of those | |
| predicted injury are actually injury | ||
| recall | Of all injury examples, | |
| how many of those we correctly predicted | ||
| Area Under the Curve () | = rate (TP/FP) |
| Set Name | Past Injuries | Personal Features | Data | Questionnaires Data |
|---|---|---|---|---|
| only injuries | x | |||
| personal features | x | x | ||
| x | x | x | ||
| questionnaires | x | x | x | |
| all | x | x | x | x |
| Horizon | Metric | Set Name | Classifier |
|---|---|---|---|
| 1 week | precision | questionnaires | tree |
| 1 week | recall | questionnaires | forest |
| 1 month | precision | all | XGB |
| 1 month | recall | all | XGB |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vallance, E.; Sutton-Charani, N.; Imoussaten, A.; Montmain, J.; Perrey, S. Combining Internal- and External-Training-Loads to Predict Non-Contact Injuries in Soccer. Appl. Sci. 2020, 10, 5261. https://doi.org/10.3390/app10155261
Vallance E, Sutton-Charani N, Imoussaten A, Montmain J, Perrey S. Combining Internal- and External-Training-Loads to Predict Non-Contact Injuries in Soccer. Applied Sciences. 2020; 10(15):5261. https://doi.org/10.3390/app10155261
Chicago/Turabian StyleVallance, Emmanuel, Nicolas Sutton-Charani, Abdelhak Imoussaten, Jacky Montmain, and Stéphane Perrey. 2020. "Combining Internal- and External-Training-Loads to Predict Non-Contact Injuries in Soccer" Applied Sciences 10, no. 15: 5261. https://doi.org/10.3390/app10155261
APA StyleVallance, E., Sutton-Charani, N., Imoussaten, A., Montmain, J., & Perrey, S. (2020). Combining Internal- and External-Training-Loads to Predict Non-Contact Injuries in Soccer. Applied Sciences, 10(15), 5261. https://doi.org/10.3390/app10155261







