Dynamic Response of Rock Containing Regular Sawteeth Joints under Various Loading Rates and Angles of Application
Abstract
1. Introduction
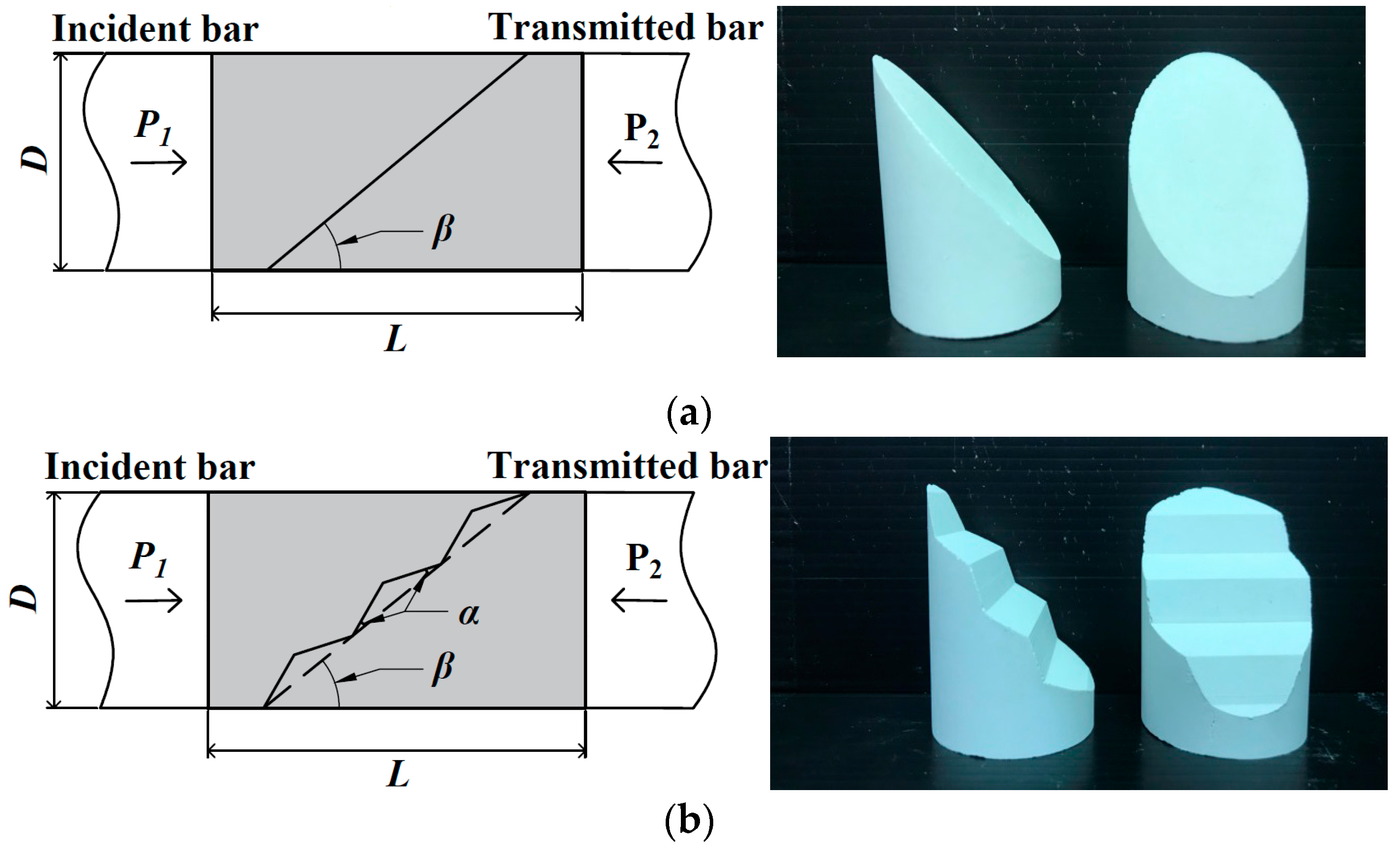
2. Experiments
2.1. Preparation of Specimens
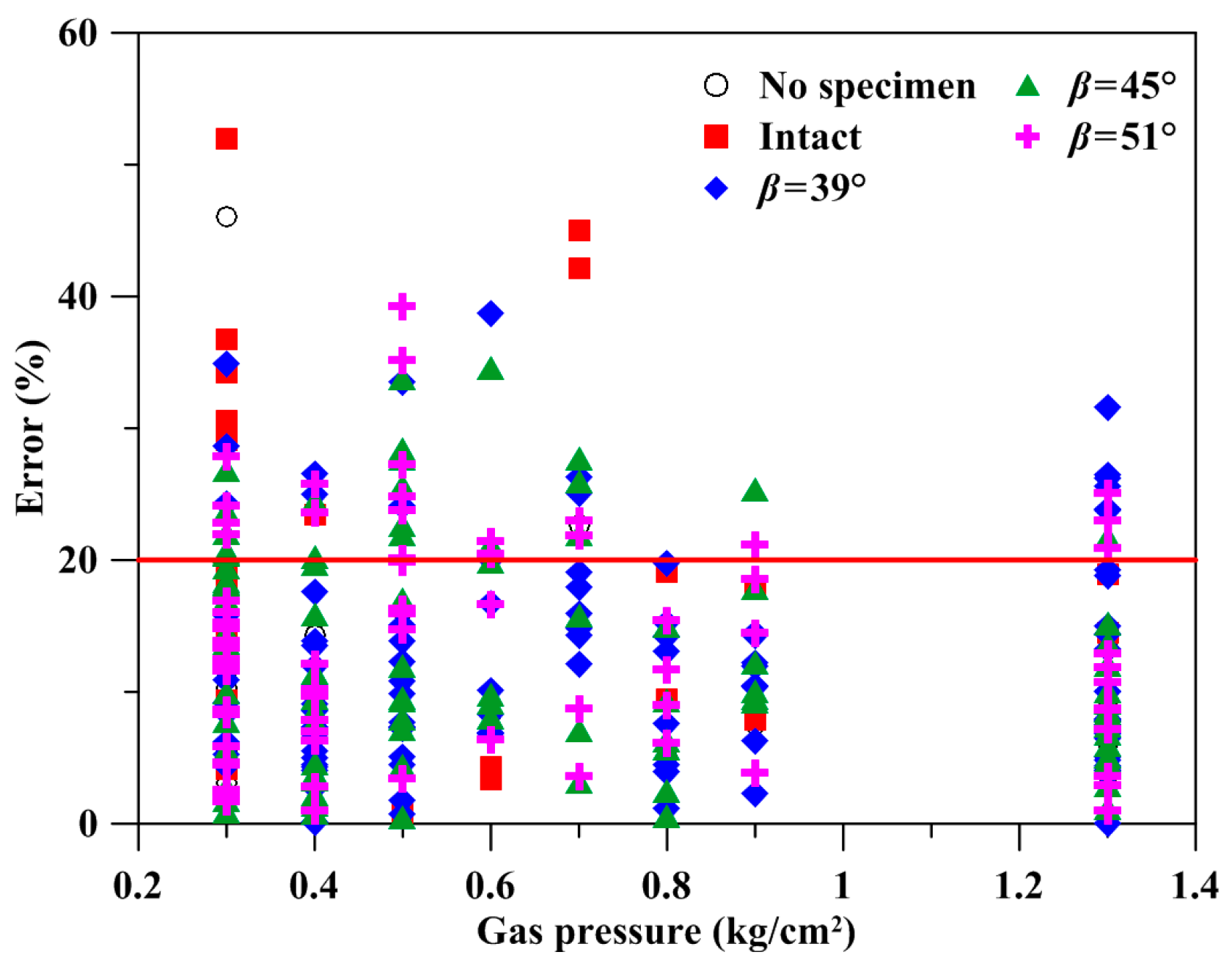
2.2. Experimental Apparatus
3. Results
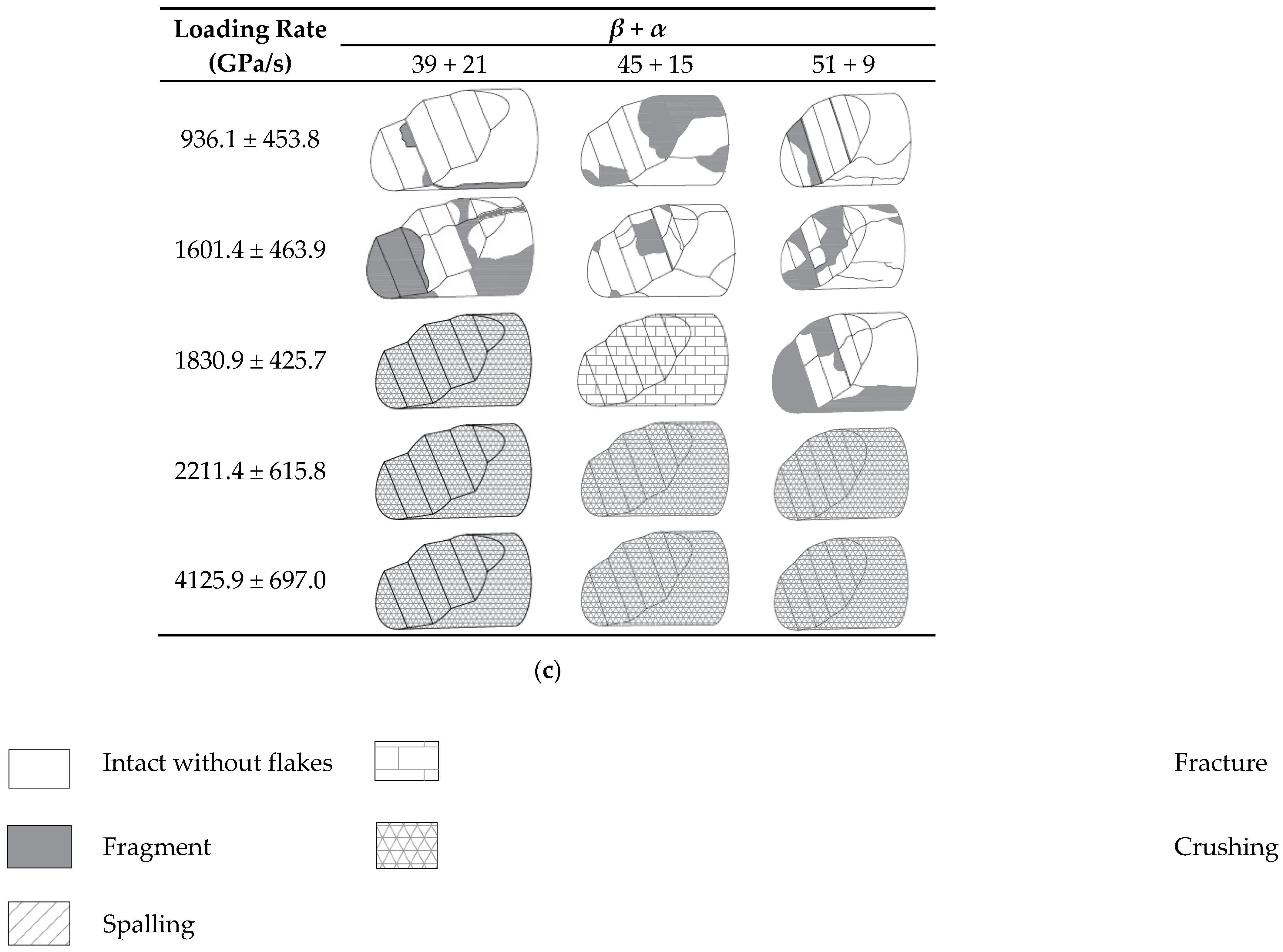
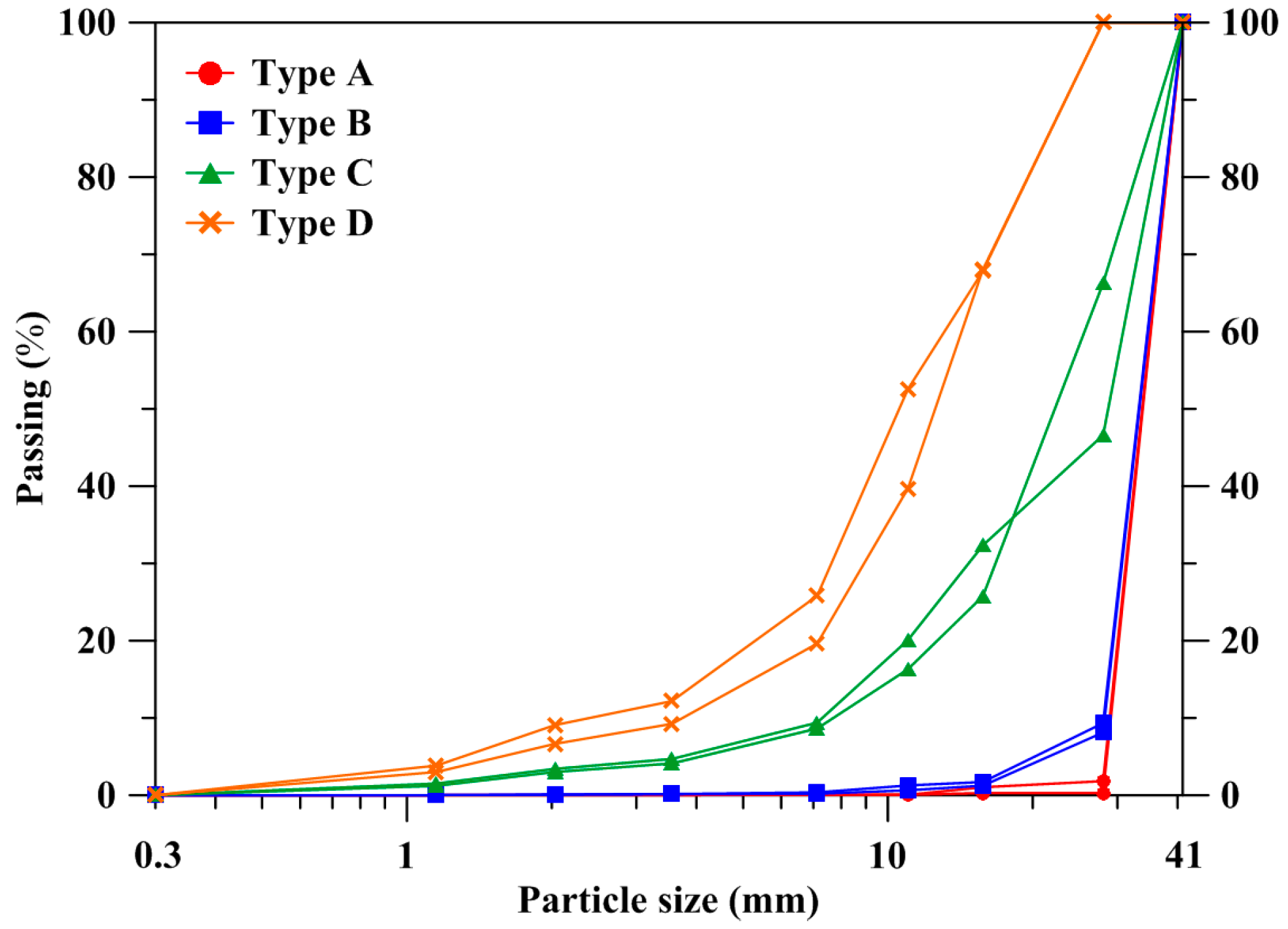
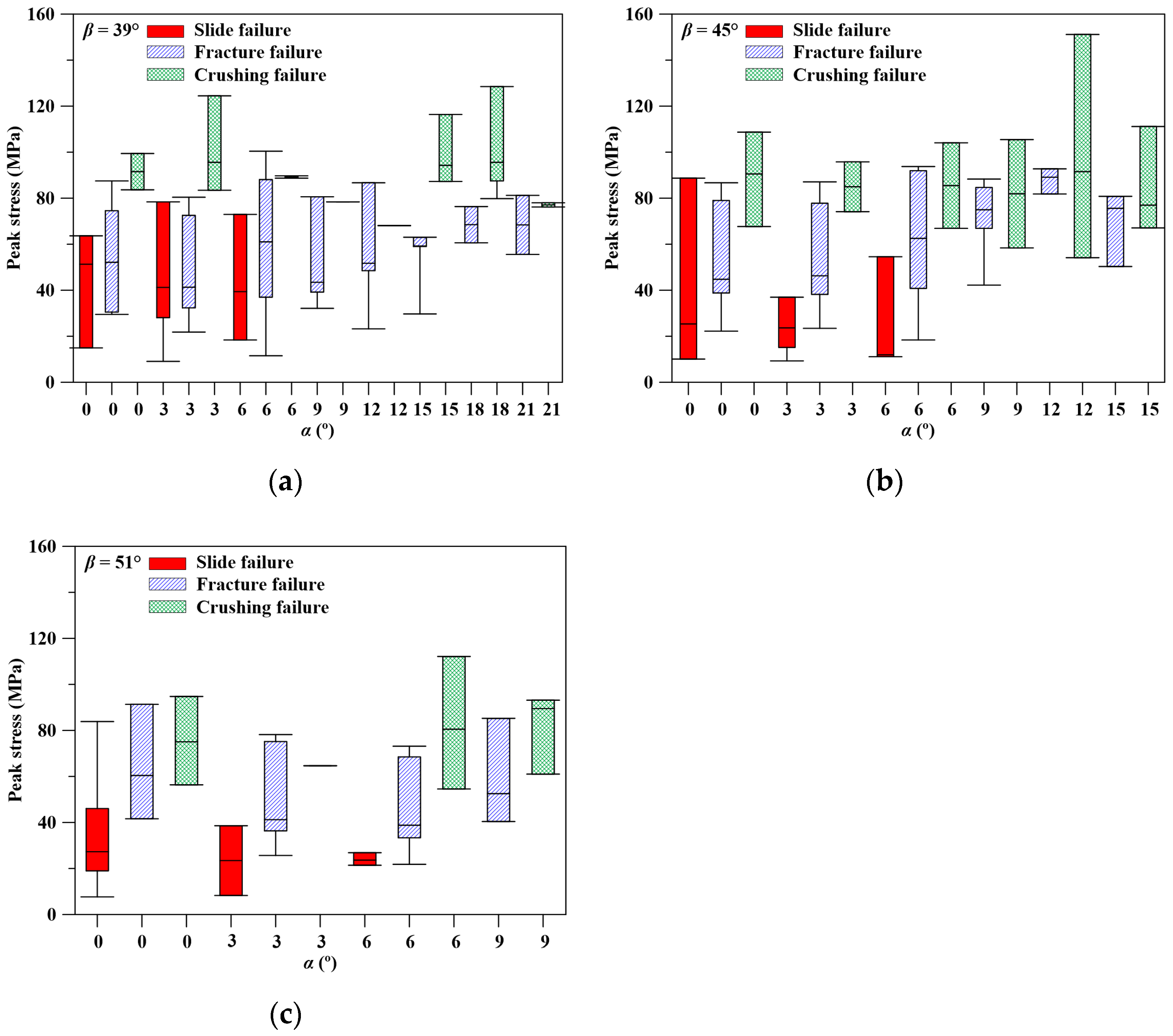
3.1. Failure Type
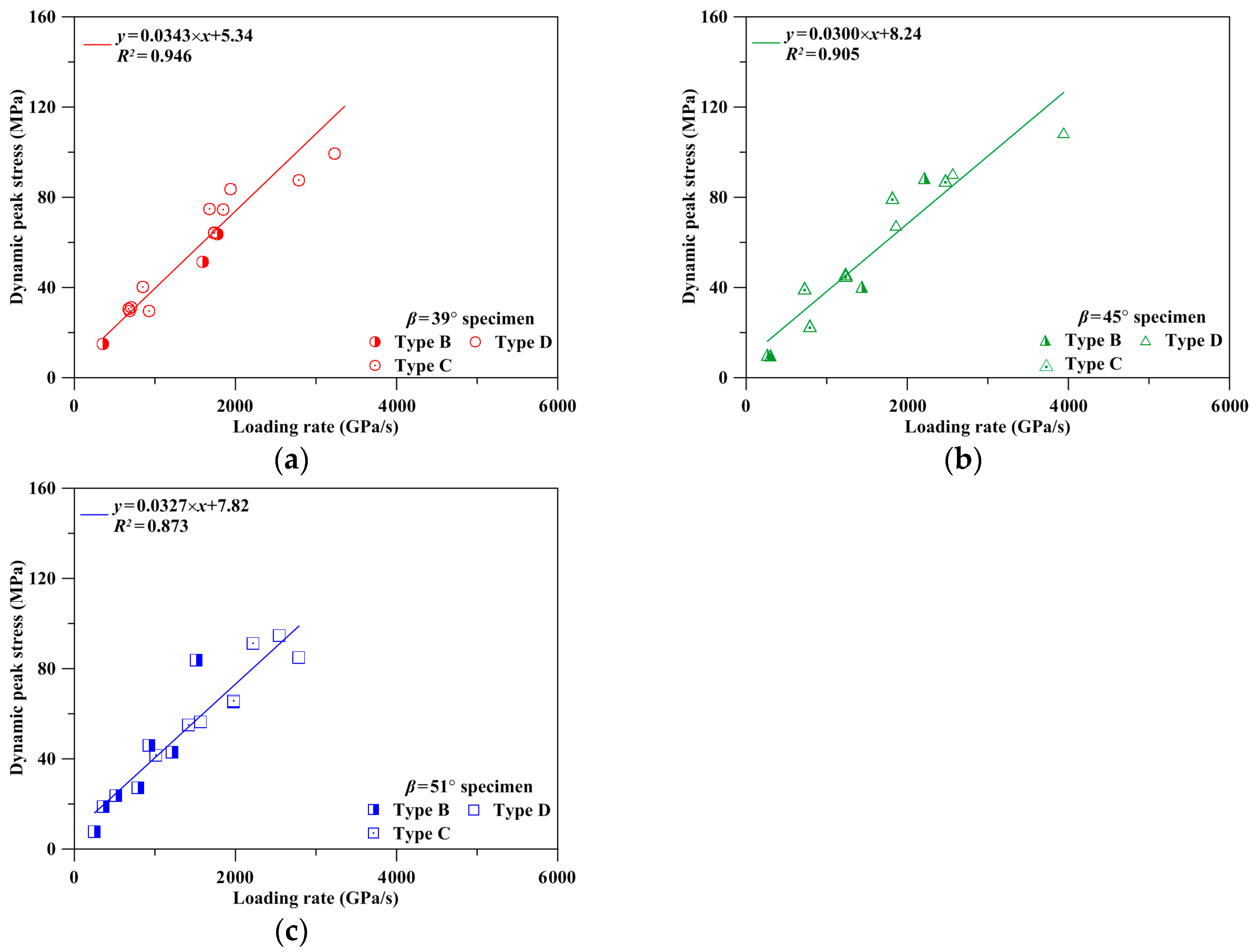
3.2. Dynamic Peak Stress
4. Discussion
4.1. Appearance of Joint
4.2. ANOVA on Factors that Affect Dynamic Peak Strength of Jointed Specimen
4.3. Pattern of Joints
4.4. Angle of Triangular Sawteeth
4.5. Loading Rate
5. Conclusions
- The appearance of a joint makes the outcomes for a specimen in an SHPB test more diverse. The failures of an intact specimen and a jointed specimen can be classified into the following four types: (A) intact with or without tiny flakes, (B) slide failure, (C) fracture failure, and (D) crushing failure. Therefore, the relationship between dynamic peak stress and loading rate varies greatly.
- The results of ANOVA indicate that the loading rate, the angle of the base plane (β), and asperity (α) all affect the dynamic peak stress of jointed specimens when fracture failure occurs. When slide failure occurs, the dynamic peak stress of the jointed specimen is affected by loading rate and β, when the specimen is crushed to failure, the loading rate is the sole factor that significantly influences its dynamic peak stress.
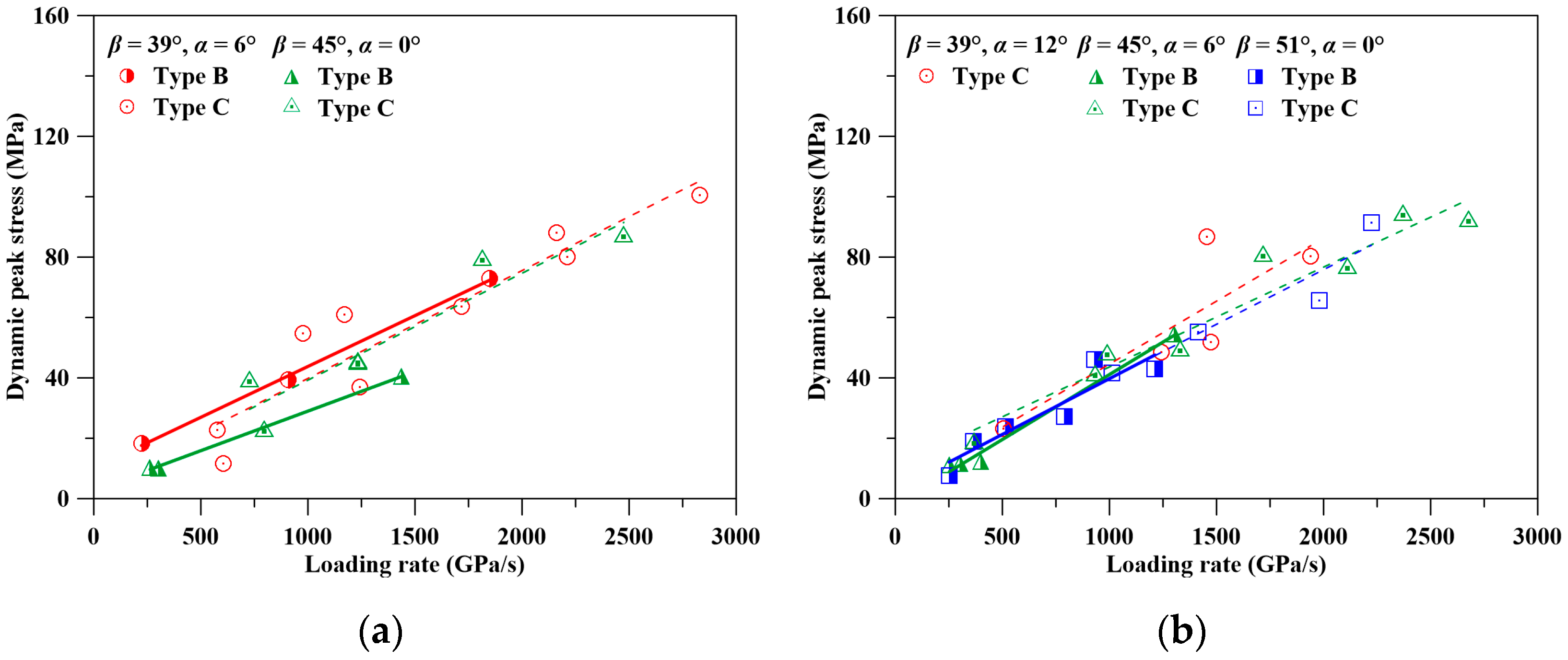
- The slope of the relationship between the dynamic peak stress and the loading rate, and the upper limit of the dynamic peak stress under slide failure of the planar joint specimen, are both smaller than those of the sawteeth joint specimen when the loads that are applied on joint surface have similar maximum angles. The slope of the relationship between the dynamic peak stress and the loading rate under fracture failure for the planar joint specimen is close to that for the sawteeth joint specimen. The small sawtooth with α ≤ 6° provides additional friction on the surface of jointed specimen under slide failure. No slide failure is observed for the specimen with α > 6°.
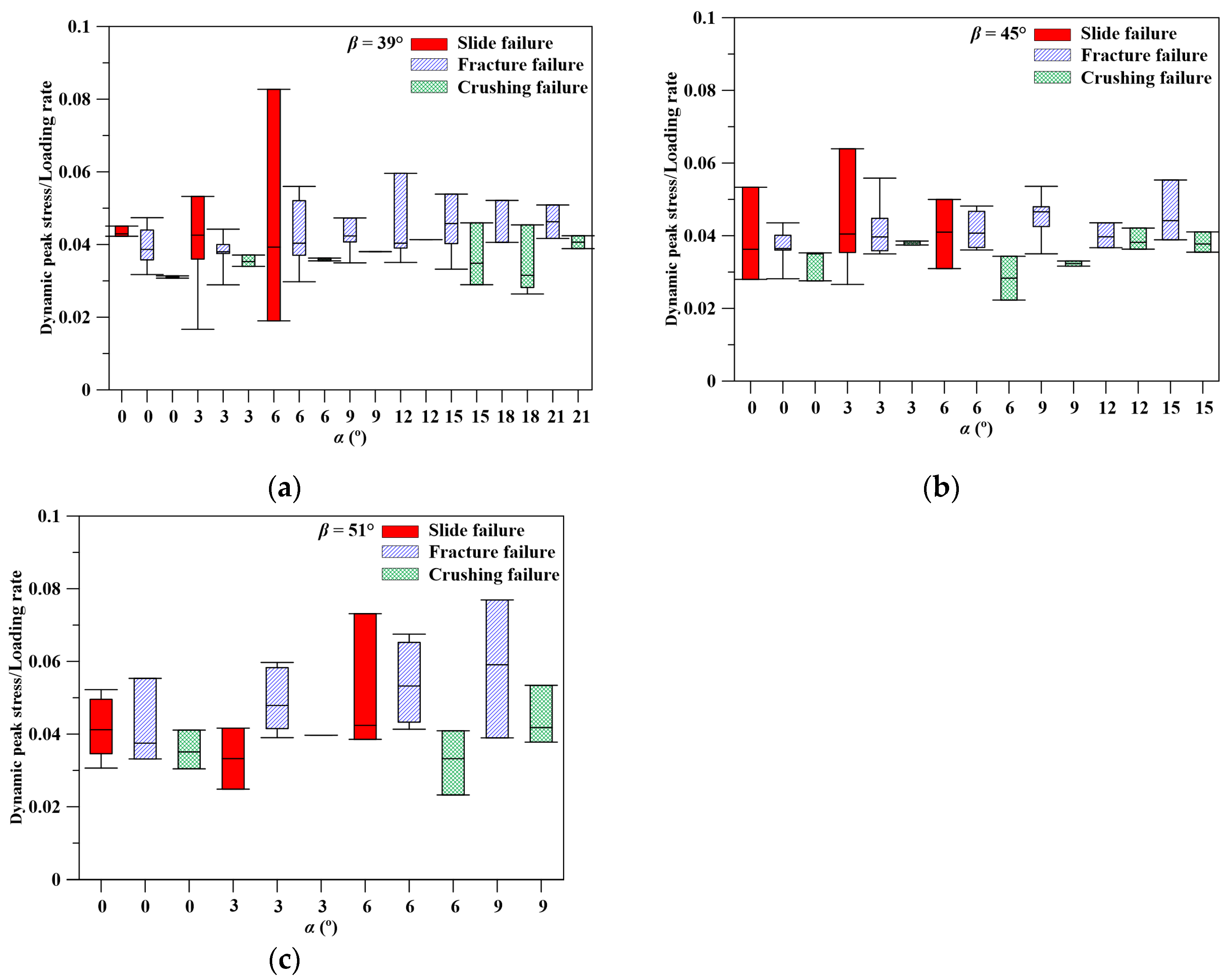
- Increasing angle α increases the DSLR of the jointed specimen at slide failure, and this effect is influenced by the angle β of the specimen and the associated failure type. The angle α insignificantly affects the DSLR when the jointed specimen is crushed to failure.
- The dynamic peak stress of a specimen increases with the loading rate at a gradually decreasing rate. The β and α of the jointed specimen affect the location of stress concentration during loading, further influencing the dynamic peak stress for specimens under slide failure and fracture failure. When the loading rate is high and the specimen is crushed to failure, the influences of β and α disappear. Increasing the loading rate reduces the efficiency of increase of dynamic peak stress.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rehbock-Sander, M.; Jesel, T. Fault induced rock bursts and micro-tremors-experiences from the Gotthard Base Tunnel. Tunn. Undergr. Space Technol. 2018, 81, 358–366. [Google Scholar] [CrossRef]
- Kung, C.L.; Wang, T.T.; Chen, C.H.; Huang, T.H. Response of a circular tunnel through rock to a harmonic Rayleigh wave. Rock Mech. Rock Eng. 2018, 51, 547–559. [Google Scholar] [CrossRef]
- Chao, W.A.; Wu, Y.M.; Zhao, L.; Chen, H.; Chen, Y.G.; Chang, J.M.; Lin, C.M. A first near real-time seismology based landquake monitoring system. Sci. Rep. 2017, 7, 1–12. [Google Scholar] [CrossRef]
- Ku, C.S.; Kuo, Y.T.; Chao, W.A.; You, S.H.; Huang, B.S.; Chen, Y.G.; Taylor, F.W.; Wu, Y.M. A first-layered crustal velocity model for the western Solomon Islands: Inversion of the measured group velocity of surface waves using ambient noise. Seismol. Res. Lett. 2018, 89, 2274–2283. [Google Scholar] [CrossRef]
- Pal, S.; Kaynia, A.M.; Bhasin, R.K.; Paul, D.K. Earthquake stability analysis of rock slopes: A case study. Rock Mech. Rock Eng. 2012, 45, 205–215. [Google Scholar] [CrossRef]
- Kumsar, H.; Aydan, Ö.; Ulusay, R. Dynamic and Static Stability Assessment of Rock Slopes Against Wedge Failures. Rock Mech. Rock Eng. 2000, 33, 31–51. [Google Scholar] [CrossRef]
- Wang, Z.; Tian, N.; Wang, J.; Liu, J.; Hong, L. Experimental Study on Damage Mechanical Characteristics of Heat-Treated Granite under Repeated Impact. J. Mater. Civ. Eng. 2018, 30, 04018274. [Google Scholar] [CrossRef]
- Mishra, S.; Chakraborty, T.; Matsagar, V.; Loukus, J.; Bekkala, B. High Strain-Rate Characterization of Deccan Trap Rocks Using SHPB Device. J. Mater. Civ. Eng. 2018, 30, 04018059. [Google Scholar] [CrossRef]
- Aydan, Ö. Rock Dynamics; ISRM Book Series; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Liu, S.; Xu, J.Y. Effect of strain rate on the dynamic compressive mechanical behaviors of rock material subjected to high temperatures. Mech. Mater. 2015, 82, 28–38. [Google Scholar] [CrossRef]
- Török, Á.; Ficsor, A.; Davarpanah, M.; Vásárhelyi, B. Comparison of Mechanical Properties of Dry, Saturated and Frozen Porous Rocks. In Proceedings of the IAEG/AEG Annual Meeting Proceedings, San Francisco, CA, USA, 17–21 September 2018. [Google Scholar]
- Mastrorocco, G.; Salvini, R.; Vanneschi, C. Fracture mapping in challenging environment: A 3D virtual reality approach combining terrestrial LiDAR and high definition images. Bull. Eng. Geol. Environ. 2018, 77, 691–707. [Google Scholar] [CrossRef]
- Zhan, S.S.; Wang, T.T.; Huang, T.H. Variations of hydraulic conductivity of fracture sets and fractured rock mass with test scale: Case study at Heshe well site in central Taiwan. Eng. Geol. 2016, 206, 94–106. [Google Scholar] [CrossRef]
- Liu, X.J.; Zheng, X.; Cheng, W.C.; Kong, Q.; Wang, J.J. The shear strength of the nature loess joint: A Case study in Shaanxi Province. J. Test. Eval. 2019, 47, 2297–2312. [Google Scholar] [CrossRef]
- Tian, Y.C.; Liu, Q.S.; Ma, H.; Liu, Q.; Deng, P.H. New peak shear strength model for cement filled rock joints. Eng. Geol. 2018, 233, 269–280. [Google Scholar] [CrossRef]
- He, S.Y. Experimental Study of Crack Propagation Law of Shale Containing Prefabricated Fractures. Adv. Civ. Eng. Mater. 2018, 7, 558–575. [Google Scholar] [CrossRef]
- Jiang, Y.F.; Wang, L.Q.; Wu, Q.; Sun, Z.; Elmo, D.; Zheng, L.B. An improved shear stress monitoring method in numerical direct shear tests by Particle Flow Code. J. Test. Eval. 2020, 48. [Google Scholar] [CrossRef]
- Chiu, C.C.; Weng, M.C.; Huang, T.H. Modeling rock joint behavior using a rough-joint model. Int. J. Rock Mech. Min. Sci. 2016, 89, 14–25. [Google Scholar] [CrossRef]
- Kazerani, T.; Yang, Z.Y.; Zhao, J. A discrete element model for predicting shear strength and degradation of rock joint by using compressive and tensile test data. Rock Mech. Rock Eng. 2012, 45, 695–709. [Google Scholar] [CrossRef]
- Wang, Z.L.; Li, H.R.; Wang, J.G.; Shi, H. Experimental study on mechanical and energy properties of granite under dynamic triaxial condition. Geotech. Test. J. 2018, 41, 1063–1075. [Google Scholar] [CrossRef]
- Xia, K.W.; Yao, W. Dynamic rock tests using split Hopkinson (Kolsky) bar system—A review. J. Rock Mech. Geotech. Eng. 2015, 7, 27–59. [Google Scholar] [CrossRef]
- Zhang, Q.B.; Zhao, J. A review of dynamic experimental techniques and mechanical behaviour of rock materials. Rock Mech. Rock Eng. 2014, 47, 1411–1478. [Google Scholar] [CrossRef]
- Pyrak-Nolte, L.J.; Myer, L.R.; Cook, N.G.W. Transmission of seismic waves across single natural fractures. J. Geophys. Res. 1990, 95, 8617–8638. [Google Scholar] [CrossRef]
- Zhao, J.; Cai, J.G. Transmission of elastic P-waves across single fractures with a nonlinear normal deformational behavior. Rock Mech. Rock Eng. 2001, 34, 3–22. [Google Scholar] [CrossRef]
- Li, M.; Qiao, L.; Li, Q.W. Energy dissipation of rock specimens under high strain rate with single joint in SHPB tensile tests. Chin. J. Geotech. Eng. 2017, 39, 1336–1343. [Google Scholar]
- Rong, L.; Li, J.; Li, H.; Li, Z.; Hong, S. Measurement of seismic quality factor of jointed rock based on stress wave energy. Chin. J. Rock Mech. Eng. 2017, 36, 2474–2483. [Google Scholar]
- Li, J.C.; Li, N.N.; Li, H.B.; Zhao, J. An SHPB test study on wave propagation across rock masses with different contact area ratios of joint. Int. J. Impact Eng. 2017, 105, 109–116. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, X.P.; Jiang, Y.J.; Wu, X.Z.; Wang, S.G. Rate-dependent mechanical behavior of rough rock joints. Int. J. Rock Mech. Min. Sci. 2016, 83, 231–240. [Google Scholar] [CrossRef]
- Atapour, H.; Moosavi, M. The influence of shearing velocity on shear behavior of artificial joints. Rock Mech. Rock Eng. 2014, 47, 1745–1761. [Google Scholar] [CrossRef]
- Yang, Z.Y.; Chiang, D.Y. An experimental study on the progressive shear behavior of rock joints with tooth-shaped asperities. Int. J. Rock Mech. Min. Sci. 2000, 37, 1247–1259. [Google Scholar] [CrossRef]
- Wu, W.; Li, J.C.; Zhao, J. Loading rate dependency of dynamic responses of rock joints at low loading rate. Rock Mech. Rock Eng. 2012, 45, 421–426. [Google Scholar] [CrossRef]
- Liu, X.R.; Kou, M.M.; Lu, Y.M.; Liu, Y.Q. An experimental investigation on the shear mechanism of fatigue damage in rock joints under pre-peak cyclic loading condition. Int. J. Fatigue 2018, 106, 175–184. [Google Scholar] [CrossRef]
- Li, H.H. Mechanical Responses of rock joints with regular asperities under various shear rates investigated by double shear test. J. Test. Eval. 2017, 45, 470–483. [Google Scholar] [CrossRef]
- Zhou, L.J.; Xu, S.L.; Shan, J.F.; Liu, Y.G.; Wang, P.F. Heterogeneity in deformation of granite under dynamic combined compression/shear loading. Mech. Mater. 2018, 123, 1–18. [Google Scholar] [CrossRef]
- Shu, P.Y.; Li, H.H.; Wang, T.T.; Ueng, T.H. Dynamic strength of rock with single planar joint under various loading rates at various angles of loads applied. J. Rock Mech. Geotech. Eng. 2018, 10, 545–554. [Google Scholar] [CrossRef]
- Deere, D.U. Geological considerations. In Rock Mechanics in Engineering Practice; Stagg, K.G., Zienkiewicz, O.C., Eds.; Wiley: New York, NY, USA, 1968; pp. 1–20. [Google Scholar]
- Song, B.; Chen, W. Dynamic stress equilibration in split Hopkinson pressure bar tests on soft materials. Exp. Mech. 2004, 44, 300–312. [Google Scholar] [CrossRef]





| Gas Pressure (kg/cm2) | No Specimen | Intact Specimen | Planar Joint Specimen | Sawteeth Joint Specimen | |||
|---|---|---|---|---|---|---|---|
| Front PMF | Rear PMF | Front PMF | Rear PMF | Front PMF | Rear PMF | ||
| 0.8–1.3 |  |  |  |  |  |  |  |
| 0.5–0.7 |  |  |  |  |  |  |  |
| 0.3–0.4 |  |  |  |  |  |  |  |
 |  |  |  |  |  |  | |
| Failure Type | Subtype | Grain Size Distribution Range | Color |
|---|---|---|---|
| A. Integrated with or without tiny flake-off | - | D10 > 28.0 mm | |
| B. Slide failure | - | 15.8 mm < D10 < 41.0 mm | |
| C. Fracture failure | break along the concave of the sawteeth (C1) | 7.1 mm < D20 < 15.8 mm 15.8 mm < D60 < 41.0 mm | |
| complete fracture (C2) | |||
| D. Crushing failure | - | D20 < 11.0 mm D60 < 15.8 mm |
| Loading Rate (GPa/s) | Intact | β + α | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 39 | 42 | 45 | 48 | 51 | 54 | 57 | 60 | ||
| 936.1 ± 453.8 | A | B(39°+ 0°) | B(39°+ 3°) | B(45°+ 0°) | B(45°+ 3°) | B(51°+ 0°) | B(51°+ 3°) | B(51°+ 6°) | C1(51°+ 9°) |
| B(45°+ 6°) | C1(45°+ 9°) | C1(45°+ 12°) | C1(45°+ 15°) | ||||||
| B(39°+ 6°) | C1(39°+ 9°) | C1(39°+ 12°) | C1(39°+ 15°) | C1(39°+ 18°) | C1(39°+ 21°) | ||||
| 1601.4 ± 463.9 | A | B(39°+ 0°) | B(39°+ 3°) | B(45°+ 0°) | B(45°+ 3°) | B(51°+ 0°) | C1(51°+ 3°) | C1(51°+ 6°) | C1(51°+ 9°) |
| B(51°+ 0°) | C1(51°+ 3°) | C1(51°+ 6°) | C2(51°+ 9°) | ||||||
| B(45°+ 0°) | C1(45°+ 3°) | C1(45°+ 6°) | C2(45°+ 9°) | C1(45°+ 12°) | C1(45°+ 15°) | ||||
| C2 | B(39°+ 0°) | B(39°+ 3°) | C1(45°+ 6°) | C2(45°+ 9°) | C2(45°+ 12°) | C2(45°+ 15°) | |||
| B(39°+ 6°) | C1(39°+ 9°) | C1(39°+ 12°) | C2(39°+ 15°) | C2(39°+ 18°) | C1(39°+ 21°) | ||||
| C1(39°+ 6°) | C2(39°+ 9°) | C1(39°+ 12°) | C2(39°+ 15°) | C2(39°+ 18°) | C2(39°+ 21°) | ||||
| 1830.9 ± 425.7 | C2 | C1(39°+ 0°) | C1(39°+ 3°) | C1(45°+ 0°) | C1(45°+ 3°) | C1(51°+ 0°) | C2(51°+ 3°) | C2(51°+ 6°) | C2(51°+ 9°) |
| C1(51°+ 0°) | C2(51°+ 3°) | C2(51°+ 6°) | C2(51°+ 9°) | ||||||
| C1(45°+ 0°) | C2(45°+ 3°) | C2(45°+ 6°) | C2(45°+ 9°) | C2(45°+ 12°) | C2(45°+ 15°) | ||||
| C2 | C2(39°+ 0°) | C1(39°+ 3°) | C2(45°+ 6°) | C2(45°+ 9°) | C2(45°+ 12°) | C2(45°+ 15°) | |||
| C1(39°+ 6°) | C2(39°+ 9°) | C2(39°+ 12°) | C2(39°+ 15°) | C2(39°+ 18°) | D(39°+ 21°) | ||||
| C2(39°+ 6°) | C2(39°+ 9°) | C2(39°+ 12°) | C2(39°+ 15°) | D(39°+ 18°) | D(39°+ 21°) | ||||
| 2211.4 ± 615.8 | D | C2(39°+ 0°) | C2(39°+ 3°) | C2(45°+ 0°) | C2(45°+ 3°) | C2(51°+ 0°) | C2(51°+ 3°) | D(51°+ 6°) | D(51°+ 9°) |
| C2(45°+ 6°) | D(45°+ 9°) | D(45°+ 12°) | D(45°+ 15°) | ||||||
| C2(39°+ 6°) | C2(39°+ 9°) | C2(39°+ 12°) | D(39°+ 15°) | D(39°+ 18°) | D(39°+ 21°) | ||||
| 4125.9 ± 697.0 | D | D(39°+ 0°) | D(39°+ 3°) | D(45°+ 0°) | D(45°+ 3°) | D(51°+ 0°) | D(51°+ 3°) | D(51°+ 6°) | D(51°+ 9°) |
| D(45°+ 6°) | D(45°+ 9°) | D(45°+ 12°) | D(45°+ 15°) | ||||||
| D(39°+ 6°) | D(39°+ 9°) | D(39°+ 12°) | D(39°+ 15°) | D(39°+ 18°) | D(39°+ 21°) | ||||
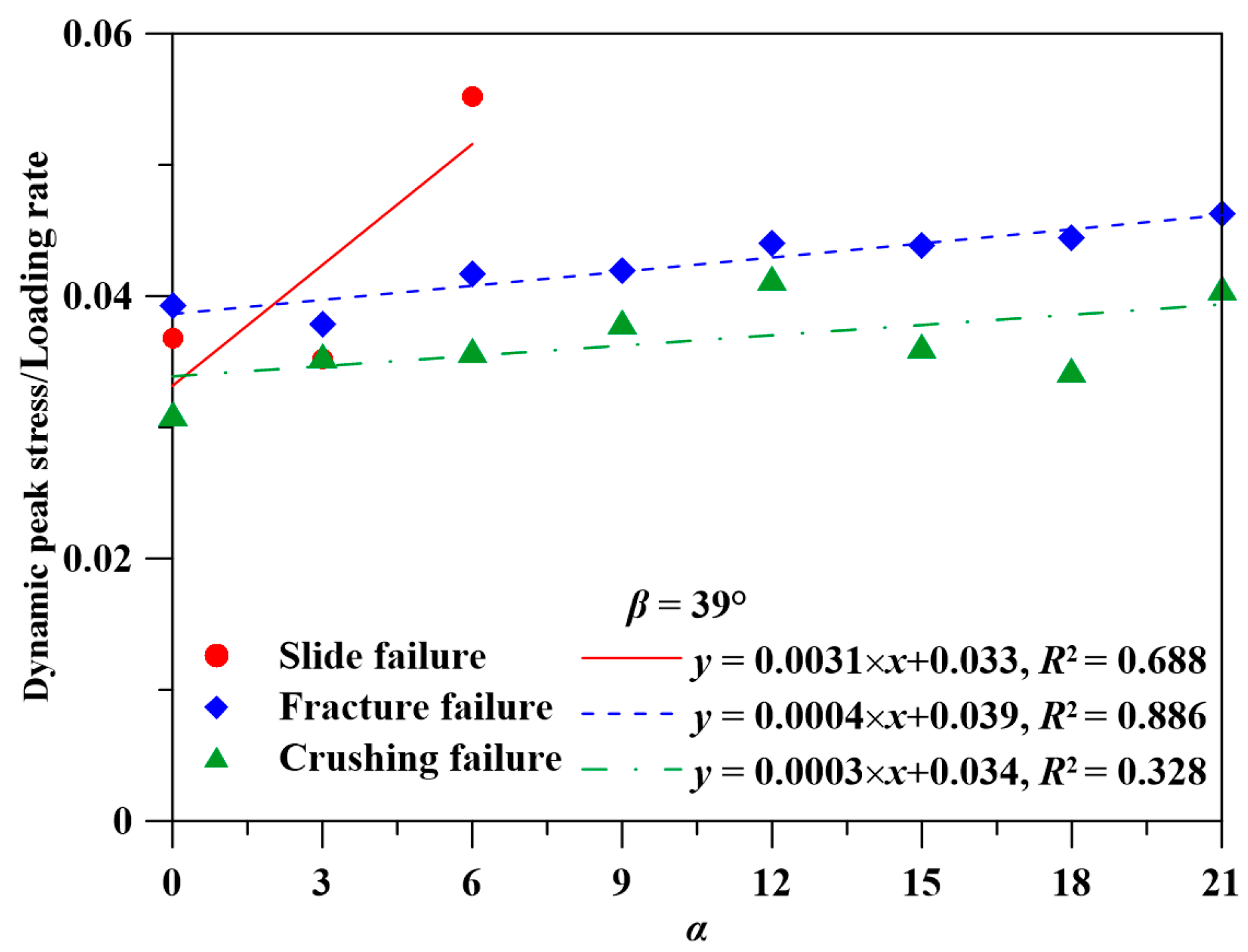
| Equation | Coefficient of Determination, R2 | Corresponding Figure |
|---|---|---|
| 0.630 | 8(a) | |
| 0.862 | 8(b) | |
| 0.868 | 8(c) | |
| 0.828 | 8(d) | |
| 0.946 | 9(a) | |
| 0.905 | 9(b) | |
| 0.873 | 9(c) | |
| 0.999 | 10(a) | |
| 0.998 | 10(a) | |
| 0.891 | 10(a) | |
| 0.873 | 10(a) | |
| 0.856 | 10(b) | |
| 0.990 | 10(b) | |
| 0.889 | 10(b) | |
| 0.937 | 10(b) | |
| 0.719 | 10(b) |
| DF | SS | MS | F | p | |
| Regression | 3 | 47,244.38 | 15,748.13 | 257.22 | 0.00 |
| Residual Error | 108 | 6612.20 | 61.22 | ||
| Total | 111 | 53,856.58 | |||
| Coef | SE Coef | T | p | 90% CI | |
| Intercept | 56.35 | 0.74 | 76.22 | 0.00 | (55.12, 57.58) |
| Loading rate | 20.30 | 0.75 | 27.00 | 0.00 | (19.06, 21.55) |
| Base plane angle | 2.40 | 0.77 | 3.13 | 0.00 | (1.13, 3.68) |
| Asperity angle | 3.09 | 0.77 | 4.03 | 0.00 | (1.82, 4.36) |
| Slide Failure | Fracture Failure | Crushing Failure | |
|---|---|---|---|
| Loading rate | ◎ | ◎ | ◎ |
| Base plane angle | ○ | ○ | X |
| Asperity angle | X | ○ | X |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shu, P.-Y.; Lin, C.-Y.; Li, H.-H.; Cheng, T.-W.; Ueng, T.-H.; Wang, T.-T. Dynamic Response of Rock Containing Regular Sawteeth Joints under Various Loading Rates and Angles of Application. Appl. Sci. 2020, 10, 5204. https://doi.org/10.3390/app10155204
Shu P-Y, Lin C-Y, Li H-H, Cheng T-W, Ueng T-H, Wang T-T. Dynamic Response of Rock Containing Regular Sawteeth Joints under Various Loading Rates and Angles of Application. Applied Sciences. 2020; 10(15):5204. https://doi.org/10.3390/app10155204
Chicago/Turabian StyleShu, Pei-Yun, Chen-Yu Lin, Hung-Hui Li, Ta-Wui Cheng, Tzuu-Hsing Ueng, and Tai-Tien Wang. 2020. "Dynamic Response of Rock Containing Regular Sawteeth Joints under Various Loading Rates and Angles of Application" Applied Sciences 10, no. 15: 5204. https://doi.org/10.3390/app10155204
APA StyleShu, P.-Y., Lin, C.-Y., Li, H.-H., Cheng, T.-W., Ueng, T.-H., & Wang, T.-T. (2020). Dynamic Response of Rock Containing Regular Sawteeth Joints under Various Loading Rates and Angles of Application. Applied Sciences, 10(15), 5204. https://doi.org/10.3390/app10155204






