An Enhanced Genetic Algorithm for Parameter Estimation of Sinusoidal Signals
Abstract
1. Introduction
- Validation through the results of a comparative analysis in terms of performance-monitoring metrics based on the mean, coefficients of determination (), and the sum of squared residuals value () of each algorithm;
- An intelligible concept with easy realization and a worry-free tradeoff between global and local search in comparison to general hybrid techniques.
2. Mathematical Ecological Theory Foundation
- When the birth rate is higher than the mortality rate, , the final population size for an infinite amount of time, t, can be simplified as:This means that a species can exist forever.
- When the birth rate is equal to the mortality rate, , the exponential terms in the numerator and denominator become 1, so Equation (3) is given as follows:Here, as time approaches infinity, the final population size will equal to the initial value. What if the initial population size equals to 1 or 2? Although this species can live for a long time, the problem of self-reproduction and inbreeding results in an extinction.
- When the birth rate is smaller than the mortality rate, , it is clear that 0 as ∞. Hence, one can get the following expression:Obviously, this equation represents an inevitable extinction of a species.
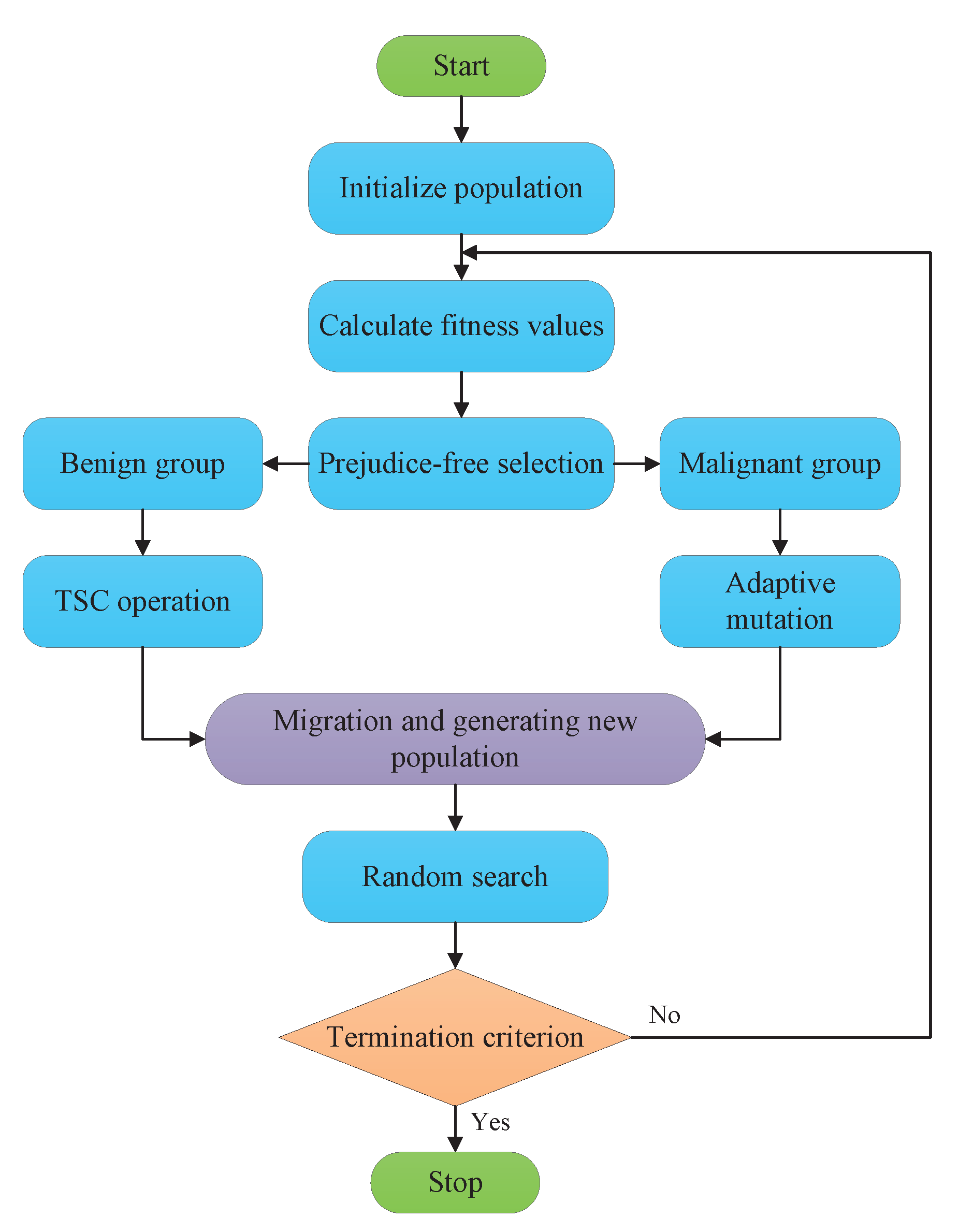
3. The Proposed EGA
3.1. Prejudice-Free Selection
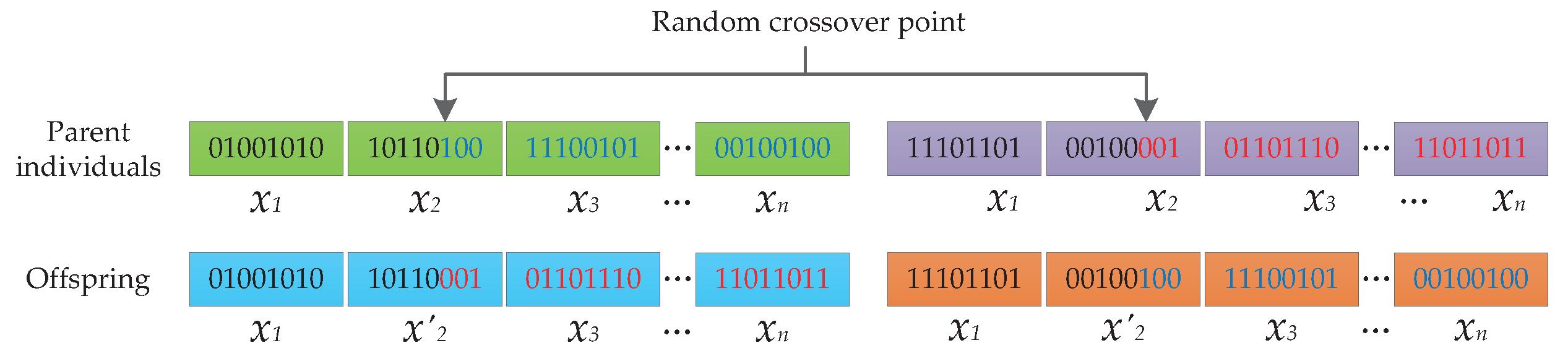
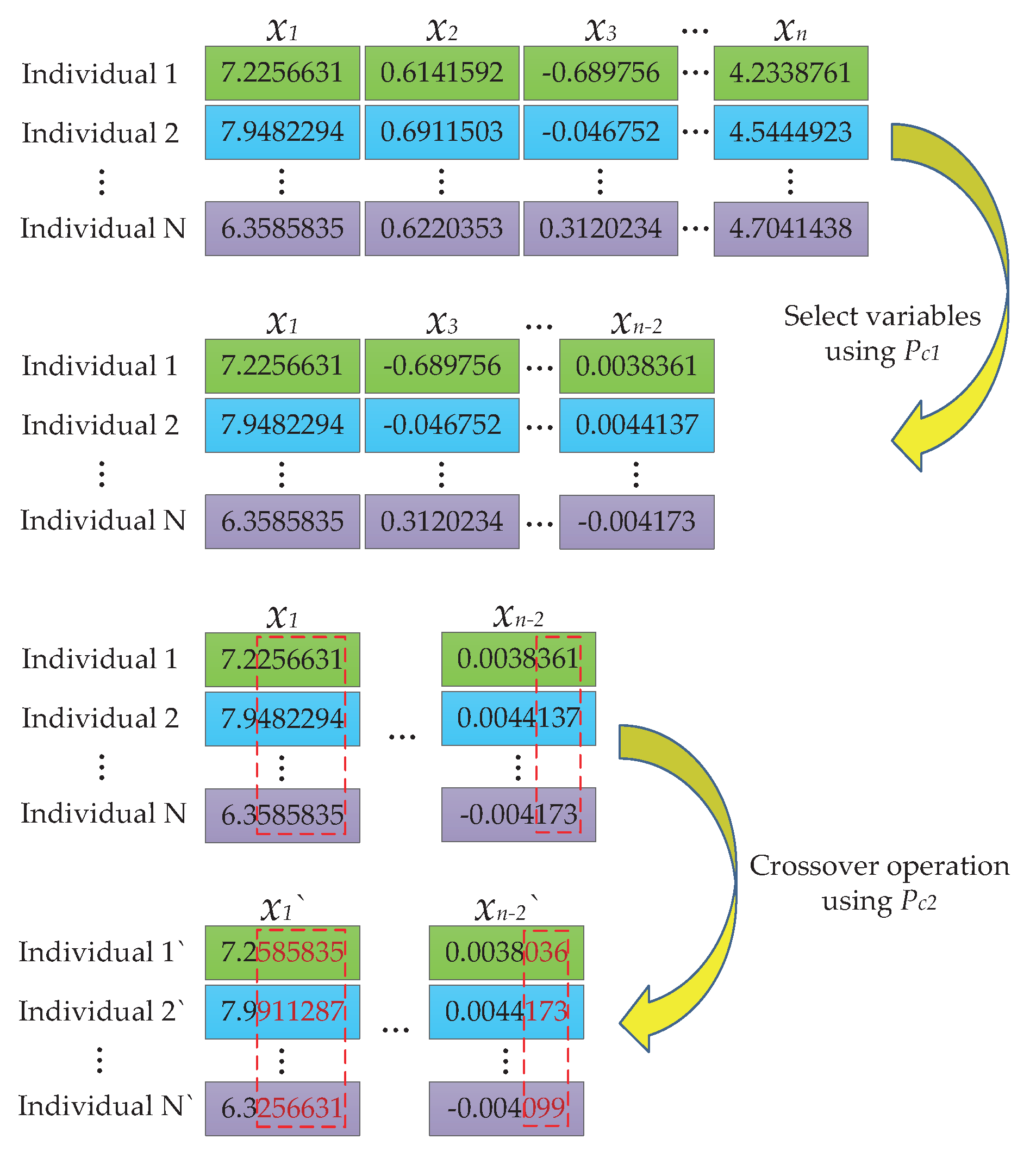
3.2. Two-Step Crossover (TSC) Operator
- Dividing each chromosome into segments based on the number of the variables to be solved, and gathering all the specific segments for a certain variable to form a variable set for the related variable;
- Randomly selecting some variable sets with a probability ;
- Implementing crossover operation on each elected set to update the variables with a probability ;
- Once the crossover is completed, reassembling the variable sets together to get the new individuals.
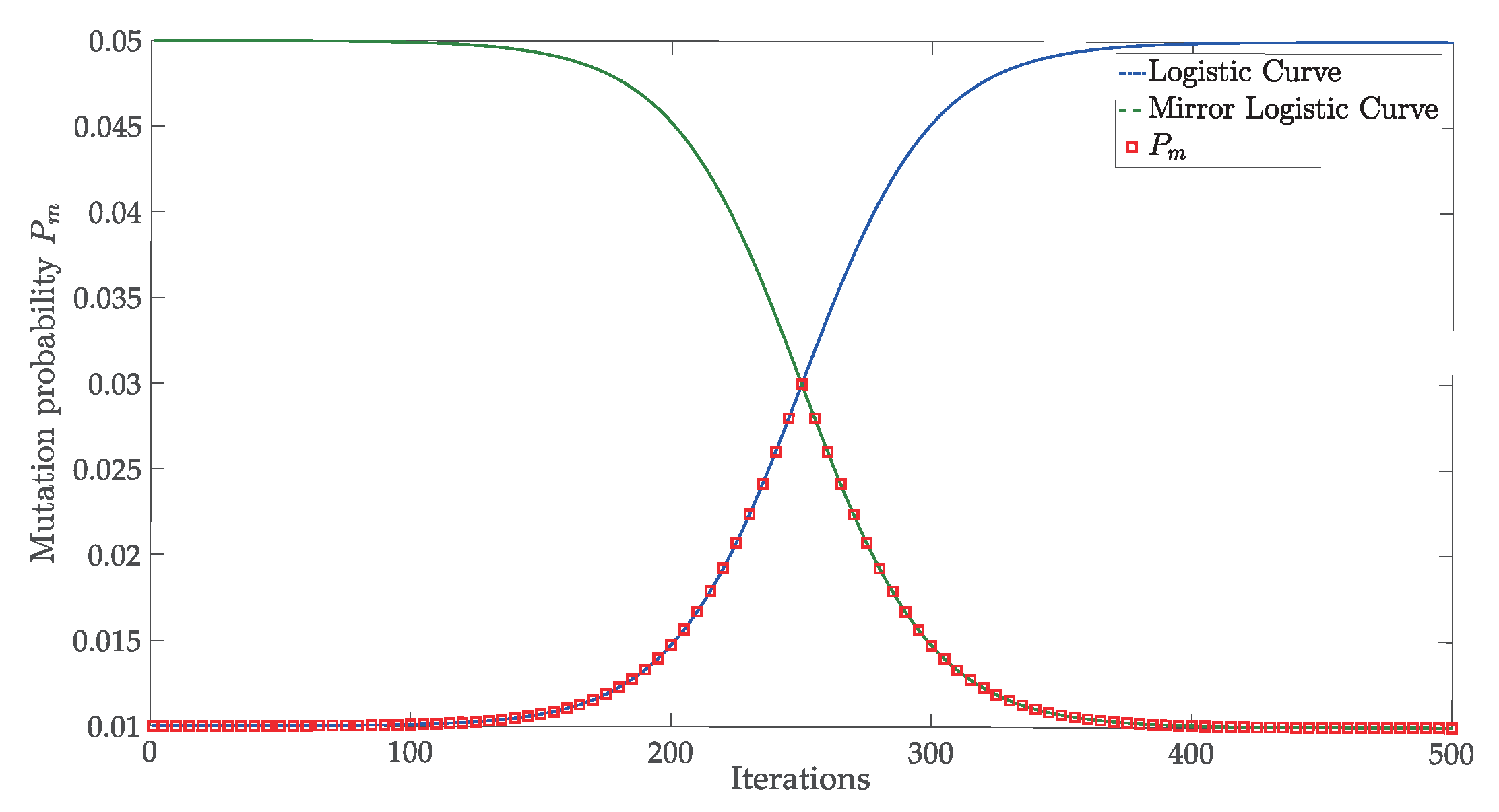
3.3. Adaptive Mutation Operator
3.4. EGA Procedures
| Algorithm 1 The pseudo-code of the enhanced genetic algorithm. |
| Input: size of initial population |
| maximum number of iteration |
| probabilities of the two-step crossover operation |
| probabilities of the initial and final adaptive mutation operation |
| number for generating new individuals around the best solution in each |
| iteration |
| objective function |
| Output: the best solution and corresponding objective value in each iteration |
| function () |
| for do |
| end for |
| while do |
| for do |
| end for |
| end while |
| end function |
4. Benchmark Function Study
5. Parameter Estimation of Sinusoidal Signals
5.1. The Voice Dataset
5.2. The Circadian Rhythms
6. Conclusions
- a prejudice-free selection mechanism for preserving population diversity;
- a TSC operation for enhancing information exchange among individuals and variables;
- An adaptive mutation strategy to avoid premature convergence and stagnation scenarios.
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Drugman, T.; Stylianou, Y. Maximum Voiced Frequency Estimation: Exploiting Amplitude and Phase Spectra. IEEE Signal Process. Lett. 2014, 21, 1230–1234. [Google Scholar] [CrossRef]
- Beltran-Carbajal, F.; Silva-Navarro, G. A fast parametric estimation approach of signals with multiple frequency harmonics. Electr. Power Syst. Res. 2017, 144, 157–162. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, C.; Ji, X.; Chen, J.; Han, T. An Improved Performance Frequency Estimation Algorithm for Passive Wireless SAW Resonant Sensors. Sensors 2014, 14, 22261–22273. [Google Scholar] [CrossRef] [PubMed]
- Stoica, P.; Li, H.; Li, J. Amplitude estimation of sinusoidal signals: Survey, new results, and an application. IEEE Trans. Signal Process. 2000, 48, 338–352. [Google Scholar] [CrossRef]
- Duda, K.; Barczentewicz, S. Interpolated DFT for sinα(x) Windows. IEEE Trans. Instrum. Meas. 2014, 63, 754–760. [Google Scholar] [CrossRef]
- Djukanović, S. An Accurate Method for Frequency Estimation of a Real Sinusoid. IEEE Signal Process. Lett. 2016, 23, 915–918. [Google Scholar] [CrossRef]
- Zhang, J.; Wen, H.; Teng, Z.; Martinek, R.; Bilik, P. Power system dynamic frequency measurement based on novel interpolated STFT algorithm. Adv. Electr. Electron. Eng. 2017, 15. [Google Scholar] [CrossRef]
- Ye, S.; Kocherry, D.L.; Aboutanios, E. A novel algorithm for the estimation of the parameters of a real sinusoid in noise. In Proceedings of the 23rd European Signal Processing Conference (EUSIPCO), Nice, France, 31 August–4 September 2015; pp. 2271–2275. [Google Scholar] [CrossRef]
- Karimi-Ghartemani, M.; Iravani, M.R. Robust and frequency-adaptive measurement of peak value. IEEE Trans. Power Deliv. 2004, 19, 481–489. [Google Scholar] [CrossRef]
- Samarah, A. A comparative study of single phase grid connected phase looked loop algorithms. Jordan J. Mech. Ind. Eng. 2017, 11, 185–194. [Google Scholar]
- Spavieri, G.; Ferreira, R.T.; Fernandes, R.A.; Lage, G.G.; Barbosa, D.; Oleskovicz, M. Particle Swarm Optimization-based approach for parameterization of power capacitor models fed by harmonic voltages. Appl. Soft Comput. 2017, 56, 55–64. [Google Scholar] [CrossRef]
- Martinez-Ayala, E.; Ayala-Ramirez, V.; Sanchez-Yanez, R.E. Noisy signal parameter identification using Particle Swarm Optimization. In Proceedings of the IEEE 21st International Conference on Electrical Communications and Computers (CONIELECOMP), San Andres Cholula, Mexico, 28 February–2 March 2011; pp. 142–146. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Z.; Zhao, B.; Xu, L. Parameters estimation of sinusoidal frequency modulation signal with application in synthetic aperture radar imaging. J. Appl. Remote Sens. 2016, 10, 020502. [Google Scholar] [CrossRef]
- Kiran, M.S. Particle swarm optimization with a new update mechanism. Appl. Soft Comput. 2017, 60, 670–678. [Google Scholar] [CrossRef]
- Xiao, X.; Lai, J.H.; Wang, C.D. Parameter estimation of the exponentially damped sinusoids signal using a specific neural network. Neurocomputing 2014, 143, 331–338. [Google Scholar] [CrossRef]
- Mitra, A.; Kundu, D.; Agrawal, G. Frequency estimation of undamped exponential signals using genetic algorithms. Comput. Stat. Data Anal. 2006, 51, 1965–1985. [Google Scholar] [CrossRef]
- Djurović, I.; Simeunović, M.; Lutovac, B. Are genetic algorithms useful for the parameter estimation of FM signals? Digit. Signal Process. 2012, 22, 1137–1144. [Google Scholar] [CrossRef]
- Silva, R.P.M.d.; Delbem, A.C.B.; Coury, D.V. Genetic algorithms applied to phasor estimation and frequency tracking in PMU development. Int. J. Electr. Power Energy Syst. 2013, 44, 921–929. [Google Scholar] [CrossRef]
- Mitra, S.; Mitra, A.; Kundu, D. Genetic algorithm and M-estimator based robust sequential estimation of parameters of nonlinear sinusoidal signals. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 2796–2809. [Google Scholar] [CrossRef]
- Coury, D.V.; Silva, R.P.M.d.; Delbem, A.C.B.; Casseb, M.V.G. Programmable logic design of a compact Genetic Algorithm for phasor estimation in real-time. Electr. Power Syst. Res. 2014, 107, 109–118. [Google Scholar] [CrossRef]
- Raja, M.A.Z.; Zameer, A.; Khan, A.U.; Wazwaz, A.M. A new numerical approach to solve Thomas–Fermi model of an atom using bio-inspired heuristics integrated with sequential quadratic programming. SpringerPlus 2016, 5, 1400. [Google Scholar] [CrossRef]
- Raja, M.A.Z.; Niazi, S.A.; Butt, S.A. An intelligent computing technique to analyze the vibrational dynamics of rotating electrical machine. Neurocomputing 2017, 219, 280–299. [Google Scholar] [CrossRef]
- Dong, H.; Li, T.; Ding, R.; Sun, J. A novel hybrid genetic algorithm with granular information for feature selection and optimization. Appl. Soft Comput. 2018, 65, 33–46. [Google Scholar] [CrossRef]
- Wang, J.; Ersoy, O.K.; He, M.; Wang, F. Multi-offspring genetic algorithm and its application to the traveling salesman problem. Appl. Soft Comput. 2016, 43, 415–423. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, N.; Bi, Y.; Srinivasan, D. Parameter identification of PEMFC model based on hybrid adaptive differential evolution algorithm. Energy 2015, 90, 1334–1341. [Google Scholar] [CrossRef]
- Renczes, B. Numerical Problems of Sine fitting Algorithms. Ph.D. Thesis, Budapest University of Technology and Economics, Budapest, Hungary, 2017. [Google Scholar]
- Draa, A.; Bouzoubia, S.; Boukhalfa, I. A sinusoidal differential evolution algorithm for numerical optimisation. Appl. Soft Comput. 2015, 27, 99–126. [Google Scholar] [CrossRef]
- Zhang, X.M. Parameter estimation of shallow wave equation via cuckoo search. Neural Comput. Appl. 2017, 28, 4047–4059. [Google Scholar] [CrossRef]
- Merkle, D.; Middendorf, M. Swarm intelligence and signal processing [DSP Exploratory]. IEEE Signal Process. Mag. 2008, 25, 152–158. [Google Scholar] [CrossRef]
- Zang, W.; Ren, L.; Zhang, W.; Liu, X. A cloud model based DNA genetic algorithm for numerical optimization problems. Future Gener. Comput. Syst. 2018, 81, 465–477. [Google Scholar] [CrossRef]
- Raja, M.A.Z.; Umar, M.; Sabir, Z.; Khan, J.A.; Baleanu, D. A new stochastic computing paradigm for the dynamics of nonlinear singular heat conduction model of the human head. Eur. Phys. J. Plus 2018, 133, 364. [Google Scholar] [CrossRef]
- Raja, M.A.Z.; Shah, Z.; Manzar, M.A.; Ahmad, I.; Awais, M.; Baleanu, D. A new stochastic computing paradigm for nonlinear Painlevé II systems in applications of random matrix theory. Eur. Phys. J. Plus 2018, 133, 254. [Google Scholar] [CrossRef]
- Sabir, Z.; Manzar, M.A.; Raja, M.A.Z.; Sheraz, M.; Wazwaz, A.M. Neuro-heuristics for nonlinear singular Thomas-Fermi systems. Appl. Soft Comput. 2018, 65, 152–169. [Google Scholar] [CrossRef]
- Ali, M.Z.; Awad, N.H.; Suganthan, P.N.; Shatnawi, A.M.; Reynolds, R.G. An improved class of real-coded Genetic Algorithms for numerical optimization. Neurocomputing 2018, 275, 155–166. [Google Scholar] [CrossRef]
- Zaman, F.; Qureshi, I.M. 5D parameter estimation of near-field sources using hybrid evolutionary computational techniques. Sci. World J. 2014, 2014. [Google Scholar] [CrossRef]
- Bacaër, N. A Short History of Mathematical Population Dynamics; Springer Science & Business Media: Berlin, Germany, 2011. [Google Scholar] [CrossRef]
- Sarmady, S. An investigation on genetic algorithm parameters. Sch. Comput. Sci. Univ. Sains Malays. 2007, 126. [Google Scholar]
- Sathya, S.S.; Kuppuswami, S. Analysing the migration effects in nomadic genetic algorithm. Int. J. Adapt. Innov. Syst. 2010, 1, 158–170. [Google Scholar] [CrossRef]
- Sathya, S.S.; Radhika, M. Convergence of nomadic genetic algorithm on benchmark mathematical functions. Appl. Soft Comput. 2013, 13, 2759–2766. [Google Scholar] [CrossRef]
- Umbarkar, A.; Sheth, P. Crossover operators in genetic algorithms: A review. ICTACT J. Soft Comput. 2015, 6. [Google Scholar] [CrossRef]
- Lim, S.M.; Sultan, A.B.M.; Sulaiman, M.N.; Mustapha, A.; Leong, K. Crossover and mutation operators of genetic algorithms. Int. J. Mach. Learn. Comput. 2017, 7, 9–12. [Google Scholar] [CrossRef]
- Wang, K.; Wang, N. A protein inspired RNA genetic algorithm for parameter estimation in hydrocracking of heavy oil. Chem. Eng. J. 2011, 167, 228–239. [Google Scholar] [CrossRef]
- Jamil, M.; Yang, X.S. A literature survey of benchmark functions for global optimisation problems. Int. J. Math. Model. Numer. Optim. 2013, 4, 150–194. [Google Scholar] [CrossRef]
- Nabaei, A.; Hamian, M.; Parsaei, M.R.; Safdari, R.; Samad-Soltani, T.; Zarrabi, H.; Ghassemi, A. Topologies and performance of intelligent algorithms: A comprehensive review. Artif. Intell. Rev. 2018, 49, 79–103. [Google Scholar] [CrossRef]
- Oliver, W.; Yu, J.; Metois, E. The Singing Tree:: Design of an Interactive Musical Interface. In Proceedings of the 2nd Conference on Designing Interactive Systems: Processes, Practices, Methods, and Techniques (DIS ’97), Amsterdam, The Netherlands, 18–20 August 1997; pp. 261–264. [Google Scholar] [CrossRef]
- Andrews, D.; Herzberg, A. A Collection of Problems from Many Fields for the Student and Research Worker; Springer: Berlin, Germany, 1985. [Google Scholar] [CrossRef]
- Smyth, G.K. Employing Symmetry Constraints for Improved Frequency Estimation by Eigenanalysis Methods. Technometrics 2000, 42, 277–289. [Google Scholar] [CrossRef]
- Smyth, G.K.; Hawkins, D.M. Robust Frequency Estimation Using Elemental Sets. J. Comput. Graph. Stat. 2000, 9, 196–214. [Google Scholar] [CrossRef][Green Version]
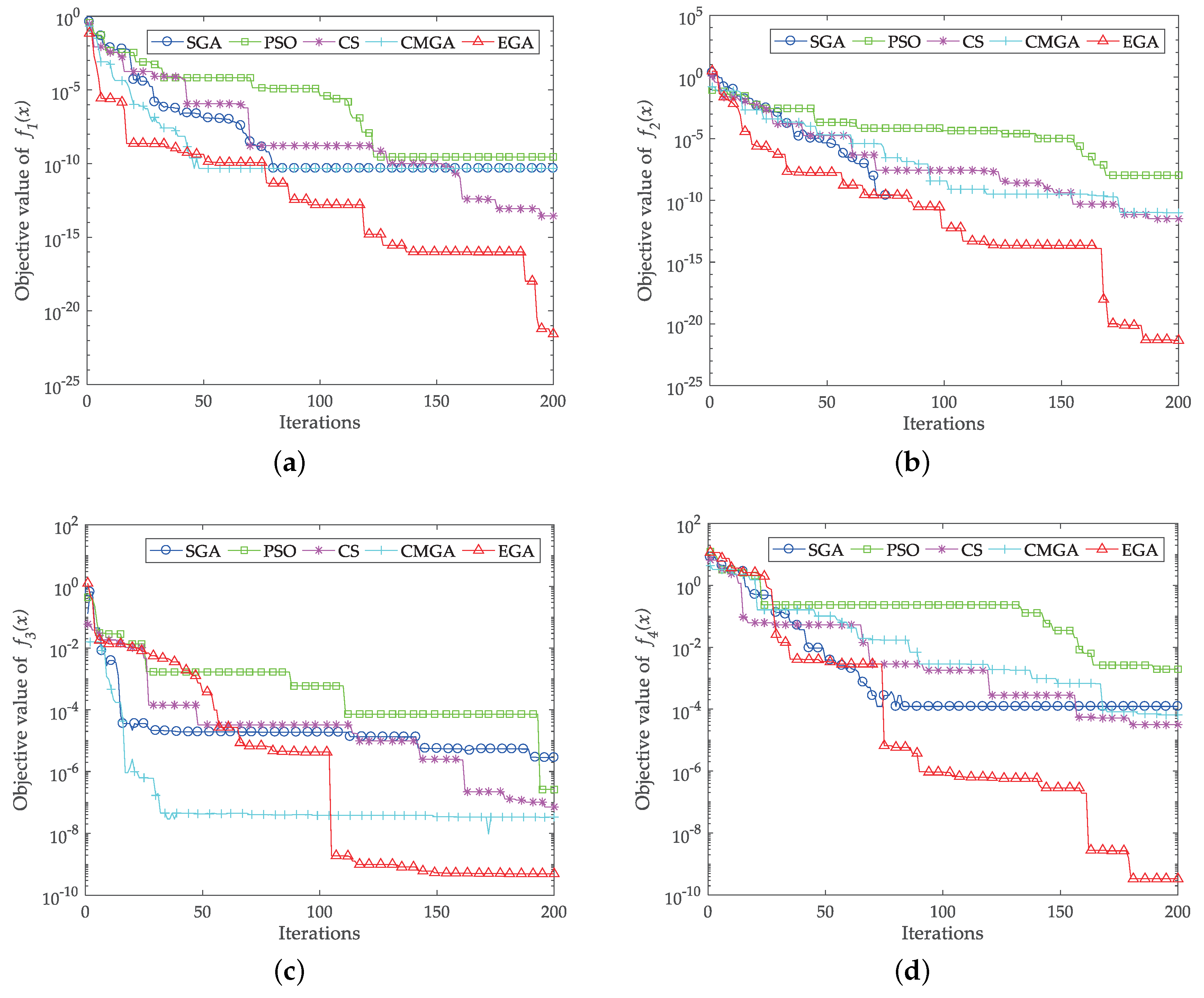

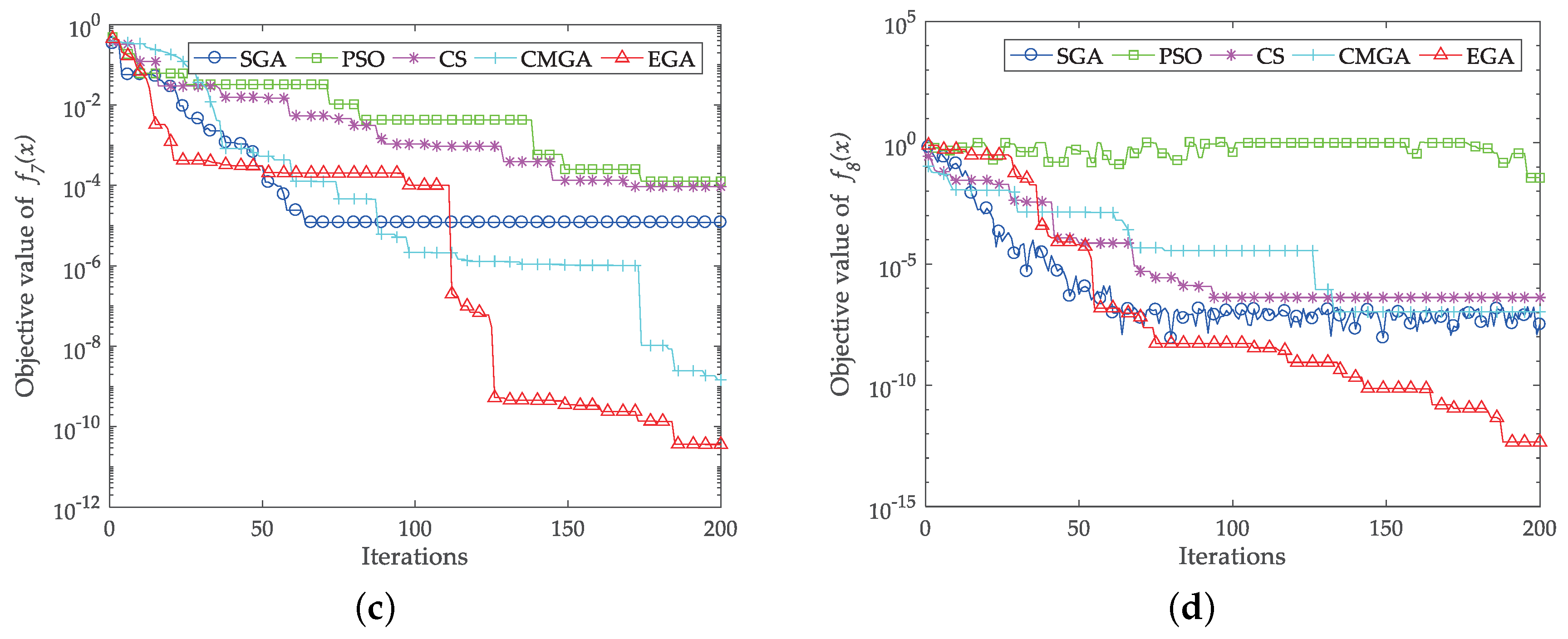
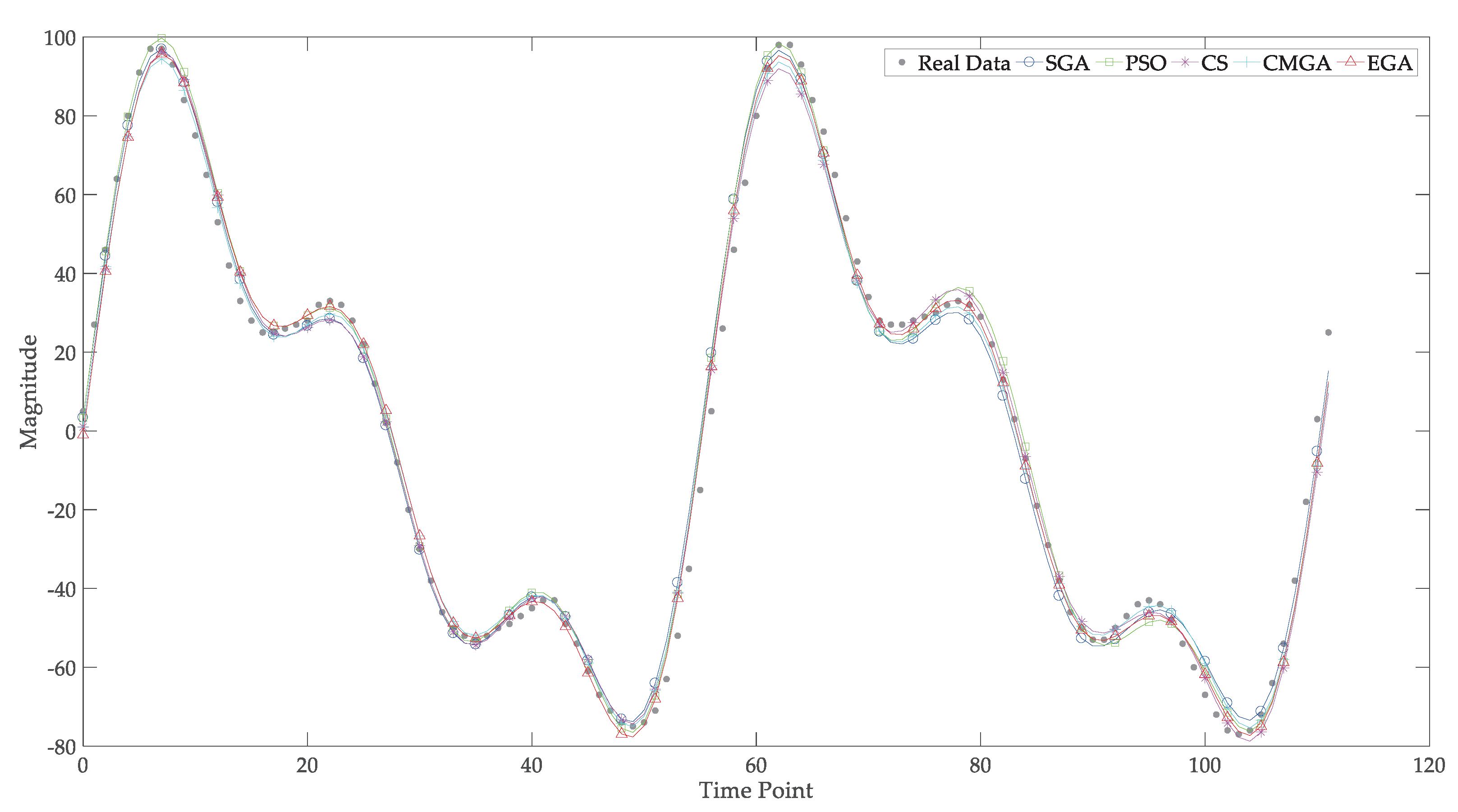

| SGA | PSO | CS | CMGA | EGA |
|---|---|---|---|---|
| − | ||||
| − | − | − | − |
| Function | Optimum | SGA | PSO | CS | CMGA | EGA |
|---|---|---|---|---|---|---|
| 0 | ||||||
| 0 | ||||||
| 0 | ||||||
| 0 | ||||||
| 0 | ||||||
| 0 | ||||||
| 0 |
| Function | Optimum | SGA | PSO | CS | CMGA | EGA |
|---|---|---|---|---|---|---|
| 0 | ||||||
| 0 | ||||||
| 0 | ||||||
| 0 | ||||||
| 0 | ||||||
| 0 | ||||||
| 0 |
| Function | SGA | PSO | CS | CMGA | EGA | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Parameter | SGA | PSO | CS | CMGA | EGA | |
|---|---|---|---|---|---|---|
| Offset | K | |||||
| Amplitude | ||||||
| Frequency | ||||||
| Phase | ||||||
| Parameter | SGA | PSO | CS | CMGA | EGA |
|---|---|---|---|---|---|
| Offset | |||||
| Amplitude | |||||
| Frequency | |||||
| Phase | |||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, C.; Serrao, P.; Liu, M.; Cho, C. An Enhanced Genetic Algorithm for Parameter Estimation of Sinusoidal Signals. Appl. Sci. 2020, 10, 5110. https://doi.org/10.3390/app10155110
Jiang C, Serrao P, Liu M, Cho C. An Enhanced Genetic Algorithm for Parameter Estimation of Sinusoidal Signals. Applied Sciences. 2020; 10(15):5110. https://doi.org/10.3390/app10155110
Chicago/Turabian StyleJiang, Chao, Pruthvi Serrao, Mingjie Liu, and Chongdu Cho. 2020. "An Enhanced Genetic Algorithm for Parameter Estimation of Sinusoidal Signals" Applied Sciences 10, no. 15: 5110. https://doi.org/10.3390/app10155110
APA StyleJiang, C., Serrao, P., Liu, M., & Cho, C. (2020). An Enhanced Genetic Algorithm for Parameter Estimation of Sinusoidal Signals. Applied Sciences, 10(15), 5110. https://doi.org/10.3390/app10155110





