Abstract
The Ritchey–Chrétien telescope has been the key optical module for remote sensing instruments (RSI), in which the root mean square (RMS) random surface wavefront error and the alignment error of the primary and the secondary mirror takes the highest weighting in the tolerance analysis for the fabrication and assembly of the telescope. Therefore, the higher tolerance of those items becomes preferable for higher efficiency of RSI manufacturing. In this paper, the correlation between those tolerance items and the f-number of the telescope has been investigated. Although the f-number is normally a system parameter well specified in the beginning of the design process, it is not very rigid in practice and has a certain amount of allowable range. The optimal f-number can then be chosen based on the consideration of those key tolerance items. The proposed concept can be generalized as a novel methodology of design for tolerance.
1. Introduction
With the advent of the space age, the demand of the remote sensing instrument (RSI) is becoming higher. Current technology has been developed to launch remote sensing satellite constellation within the same period of the launch window for multiple Earth observation purposes [1]. Therefore, efficiency of RSI fabrication is becoming essential in order to meet the schedule of the launch window with a large amount of satellites. The most time-consuming procedure in making remote sensing satellites would be the manufacturing and the alignment of optical components in the telescope [2,3,4]. Although computer-added engineering has been developed for reducing the effort of manual work, it is still highly desired that the tolerance of those precision optics can be increased, so as to reduce the time consumed in the fabrication and assembly, even with automated process [5,6].
For a Ritchey–Chrétien telescope, the major tolerance items would be a tilt and lateral shift, as well as the RMS random surface wavefront error (WFE) of the two mirror components [7,8,9]. Normally, tolerance is set based on the minimal requirement of image quality, for which the modulation transfer function (MTF) has been largely used as the major/reference index. It is possible to manipulate system layout for relaxing tolerance during the design phase, which in turn could benefit from the efficiency of fabrication and the cost of the product. However, the basic structure of the Ritchey–Chrétien telescope has a compact layout with only two mirror components, regardless of those corrector lens elements close to the image sensor for aberration correction, and therefore has not much of this kind degree of freedom to control systematic errors in telescope engineering [10]. In this paper, a new concept of design for tolerance is proposed, in which some specific system parameters could be chosen as the degree of freedom for trading the tolerance issue.
System parameters, such as focal length, f-number, etc., are normally fixed in the beginning of the design phase, and all the paraxial layout and optical analysis should stick to these basic requirements. However, in many cases, those system parameters might not be as rigid as they should be when tracing back to the optical functionality of the system. For some specific system parameters, there could be a certain amount of allowable range while keeping the required optical performance. In developing the remote sensing satellite where the Ritchey–Chrétien telescope architecture is adapted, the f-number of the telescope has been used as a tunable parameter in the tolerance analysis. The relationship between the f-number and the major tolerance items of two mirror components is investigated as the reference to choose the optimal f-number in favor of those tolerance items for the ease and efficiency of manufacturing and assembly process. Section 2 presents the procedure of finding the allowable range of f-number and nine design cases of the Ritchey–Chrétien telescope, which all meet the required optical specification but with a different f-number within the allowable range. Section 3 gives the tolerance analysis on RMS random surface WFE and the alignment error of the primary and the secondary mirror versus nine different f-numbers from the design cases in Section 2. Section 4 gives the conclusion.
2. Allowable Range of F-Numbers and Design Cases of the Telescope
The optical specifications of the Ritchey–Chrétien telescope is shown in Table 1.

Table 1.
Specifications of the optical system.
Considering the effect of central obstruction on small aberrations for the Ritchey–Chrétien telescope, Figure 1 shows the MTF versus normalized spatial frequency ξ/ξc (ξc is the cut-off frequency) for various obstruction ratios ε [11,12], in which only primary and secondary mirrors are involved. Based on the required specification of as-built MTF ≥ 0.25, the obstruction ratio ε should not be more than 0.5. The colored region between the curves of ε = 0.3 and ε = 0.4 in Figure 1 can be divided into three spatial frequency bands, marked as I, II and III in Figure 1. It is desired that the sensor’s Nyquist frequency 71.429 lp/mm used for specifying required MTF can be located in region II, because it tends to over design and induce higher cost than required if this spatial frequency is located in region I. In addition, the MTF started to drop quickly in region III and therefore the image performance tended to be poor if the spatial frequency was located in it. Similarly, the best obstruction ratio should be in the range between ε = 0.3 and ε = 0.4.
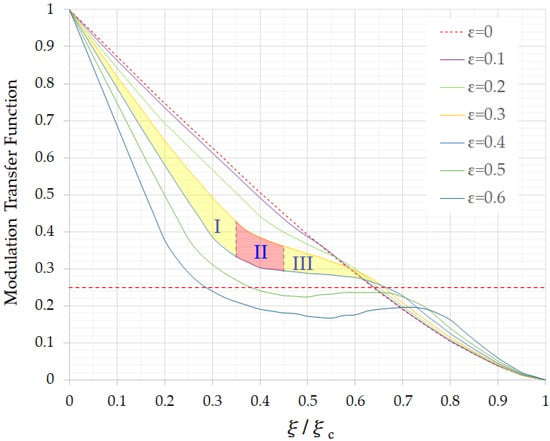
Figure 1.
Modulation transfer function (MTF) versus normalized spatial frequency for various central obstruction ratios ε [11,12].
Based on the above argument, normalized spatial frequency ξ/ξc was scanned from 0.35 to 0.45, which was in region II as shown in Figure 1, with a step of 0.01 to evaluate the allowable range of the f-number. Table 2 shows the f-numbers at various ξ/ξc, where ξ = 71.429 lp/mm, λ = 632.8 nm and the relationship between cut-off frequency ξc and f-number fn is shown in Equation (1) [13]

Table 2.
Corresponding f-number for various ξ/ξc between 0.35 and 0.45.
It indicates that the allowable range of f-number is around 7.7 to 10.0.
With the allowable range of the f-number, several cases were chosen for further optimization. Since the effective focal length was fixed with the required magnification ratio and the size of the image sensor, the parameter that can be changed became a pupil diameter only. The diameter was changed from 560 to 800 mm with a step of 30 mm, which led to a change of f-number from 7.5 to 10.7, and a total of 9 cases. The optical layout for further optimization is shown in Figure 2, in which M1 and M2 stand for primary mirror and secondary mirror respectively. A corrector lens was included for improving aberration and was composed of 4 lens elements, denoted with L1, L2, L3 and L4 in Figure 2. Focal plane assembly (FPA) is the final image position.

Figure 2.
Optical layout of Ritchey–Chrétien telescope for design cases.
The optical design program, Synopsys CODE V® (Synopsys Inc., Mountain View, CA, USA), was used for the optimization of 9 cases with a different f-number [14,15]. The merit functions used in the optimization process were similar in different cases, and the target was to achieve a minimal MTF of 0.3 at 71.429 lp/mm. The higher MTF than what is specified (0.25) must leave a sufficient error budget for tolerancing. Table 3 shows the optical performance and system parameter of those 9 design cases, including minimal MTF, distortion, chief ray angle and obstruction ratio. All the 9 cases meet the same system performance specification shown in Table 1 with same optical layout shown in Figure 2, including the lens material. The only difference made with a different f-number is the detail parameters, such as obstruction ratio, curvature and spacing/thickness. The lens data of the all 9 design cases are as listed in Appendix A, Table A1.

Table 3.
Optical performance of 9 design cases with optimization.
3. Tolerance of Mirror Elements Versus the F-Number
In the mounting of Ritchey–Chrétien telescope, an on-axis collimated beam was shone on the assembly of the primary and secondary mirror, and both mirrors were tilted and laterally shifted for alignment until the zero-coma condition was achieved, which was verified with an interferometer at the exit pupil of the telescope. A similar process was repeated for inserting corrector lens module. At the final stage, the FPA was put on and the MTF of the system at a different field angle was verified by tilting the whole telescope with respect to the collimated beam. At this stage, the secondary mirror was the only compensator for adjustment.
There were at least two key tolerance items in the manufacturing and assembly process of the optical telescope, namely optical surface tilt/shift errors, and the RMS random surface WFE. The tolerance analysis was also performed with CODE V® [2,8,15,16,17,18,19]. In the analysis, the minimum MTF of 0.25 at the spatial frequency of 71.429 lp/mm was set as the criteria.
The results of the inverse tolerance analysis for the optical surface de-center error, optical surface tilt error and system RMS random surface WFE of M1 and M2 surface with respect to each f-number in different design cases is shown in Table 4. The analysis did not include any compensator, i.e., the position of all the components locate at the position as designed, including FPA.

Table 4.
Tolerance of the optical surface de-center error, optical surface tilt error and system RMS random surface wavefront error (WFE) of the M1 and M2 surface versus the f-number.
It indicates from Table 4 that the surface de-center error and tilt error increased with the increase of the f-number, while the tolerance of RMS random surface WFE decreased with the increase of the f-number [20].
The relationship between all the tolerance items versus the f-number is plotted in Figure 3a,b for M1 and M2 respectively. Figure 3 can be viewed from two different ways. One is to determine the f-number first, and the budget of all the tolerance items of M1 and M2 can be drawn from the diagram. The other one is setting the budget [21] of tolerance items of M1 and M2 as the preferable value first, and then check from the diagram to find out the f-number that can meet all the requirements. The latter one is what was to be emphasized in this work, and the concept is equivalent to using the f-number as a compensator in tolerancing. As the f-number would have become fixed when the hardware is built, it cannot be used as a compensator in the assembly process. The only possibility to use it as a compensator is in the design process. Just like all the compensators that will be assigned with an allowable range for adjustment, there is also an allowable range of the f-number in this work evaluated from Figure 1.
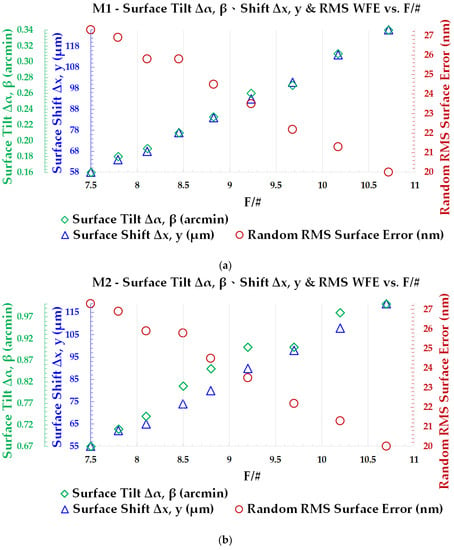
Figure 3.
Tolerance of de-center, tilt and RMS random surface WFE versus the f-number: (a) M1 and (b) M2.
As what can be seen from Figure 3, tuning the f-number in either direction within the allowable range will not be able to favorite all the tolerance items simultaneously. There is already a trade-off for even a single mirror component. Therefore, determination of the so called optimal f-number will depend on the capacity of the manufacturer on handling various tolerance items. Table 5 lists an example of specified tolerance for M1 and M2, and the f-number around 9.7 will be able to meet all the required tolerance.

Table 5.
Specified tolerance of M1 and M2.
4. Conclusions
For Ritchey–Chrétien telescope, it is found that the tolerance of the tilt and the de-center of both mirrors increased with the increase of the telescope f-number, while the tolerance of RMS random surface WFE of both mirrors decreased with the increase of the f-number. There was a trade-off between these two tolerance items in choosing the f-number within the allowable range, nevertheless, the room for fine-tuning the f-number is available, and the decision depends on the capacity of manufacturing and assembly process.
The proposed methodology can also be applied for other similar cases of optical design, and becomes a generic optimization process to fine tune specific system parameters within an allowable range based on the correlation between those system parameters and the key tolerance items.
Author Contributions
Conceptualization, C.-H.C. and S.-F.L.; methodology, S.-F.L.; software, S.-F.L.; validation, Y.-K.H.; formal analysis, S.-F.L.; investigation, S.-F.L.; resources, S.-F.L. and Y.-K.H.; data curation, S.-F.L. and Y.-K.H.; writing—original draft preparation, S.-F.L.; writing—review and editing, C.-H.C. and S.-F.L.; visualization, C.-H.C. and S.-F.L.; supervision, C.-H.C. and S.-F.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Lens data of the nine sets optical designs
Table A1.
Lens data of the nine sets optical designs
| Design Case | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pupil Diameter/fn | 800/7.5 | 770/7.8 | 740/8.1 | 710/8.5 | 680/8.8 | 650/9.2 | 620/9.7 | 590/10.2 | 560/10.7 | |||||||||||
| Surface | Type | Material | Radius | Thickness | Radius | Thickness | Radius | Thickness | Radius | Thickness | Radius | Thickness | Radius | Thickness | Radius | Thickness | Radius | Thickness | Radius | Thickness |
| M1 | Conic | ZERODUR | –2770.622 | –998.50 | –2772.368 | –999.27 | –2771.799 | –998.60 | –2771.040 | –998.23 | –2773.306 | –999.32 | –2772.677 | –999.11 | –2772.403 | –997.62 | –2772.582 | –997.58 | –2772.672 | –997.57 |
| Conic Constants | –1.158236204 | –1.158495625 | –1.161542256 | –1.162045757 | –1.1626831 | –1.165604029 | –1.165797514 | –1.169222324 | –1.17032774 | |||||||||||
| M2 | Conic | ZERODUR | –1067.075 | 1079.22 | –1067.331 | 1079.07 | –1068.899 | 1079.08 | –1068.980 | 1077.18 | –1069.105 | 1079.67 | –1068.500 | 1080.70 | –1074.296 | 1080.41 | –1074.880 | 1080.72 | –1075.137 | 1081.14 |
| Conic Constants | –4.662679579 | –4.665672011 | –4.70237211 | –4.709208378 | –4.716077121 | –4.742799171 | –4.766289194 | –4.802887116 | –4.815626274 | |||||||||||
| L1 | Sphere | SILICA | 173.075 | 35.60 | 172.000 | 35.19 | 169.666 | 34.88 | 169.204 | 34.18 | 168.708 | 33.90 | 166.027 | 33.77 | 166.276 | 32.90 | 164.703 | 32.58 | 163.660 | 32.22 |
| Sphere | –362.650 | 6.27 | –363.669 | 5.92 | –359.746 | 5.63 | –363.209 | 5.92 | –359.505 | 6.28 | –345.696 | 5.11 | –358.561 | 6.57 | –353.486 | 6.49 | –349.625 | 6.39 | ||
| L2 | Sphere | SILICA | –396.301 | 20.00 | –402.299 | 20.00 | –403.298 | 20.00 | –408.167 | 20.00 | –400.460 | 20.00 | –385.414 | 20.00 | –403.308 | 20.00 | –400.979 | 20.00 | –396.968 | 20.00 |
| Sphere | 214.798 | 26.42 | 216.256 | 26.97 | 215.456 | 26.41 | 219.428 | 25.24 | 218.517 | 23.58 | 214.096 | 26.50 | 216.042 | 22.06 | 216.187 | 21.00 | 215.816 | 20.80 | ||
| L3 | Sphere | SILICA | –235.739 | 6.00 | –236.312 | 6.00 | –231.928 | 6.00 | –236.334 | 6.00 | –235.304 | 6.00 | –228.056 | 6.00 | –230.529 | 6.00 | –226.726 | 6.00 | –224.828 | 6.00 |
| Sphere | 223.899 | 97.16 | 219.778 | 97.62 | 218.980 | 98.99 | 216.485 | 102.71 | 219.462 | 102.05 | 219.213 | 99.30 | 218.780 | 103.78 | 220.203 | 105.14 | 220.580 | 105.40 | ||
| L4 | Sphere | SILICA | 302.732 | 23.82 | 300.210 | 23.72 | 306.828 | 23.50 | 307.639 | 23.21 | 315.745 | 23.01 | 320.653 | 23.11 | 322.406 | 22.77 | 336.094 | 22.56 | 343.035 | 22.44 |
| Sphere | –1788.857 | 150.00 | –1947.817 | 150.00 | –1790.501 | 150.00 | –2144.501 | 150.00 | –1917.467 | 150.00 | –1473.205 | 150.00 | –1751.763 | 150.00 | –1531.474 | 150.00 | –1419.355 | 150.00 | ||
| Filter | Sphere | SILICA | Infinity | 1.10 | Infinity | 1.10 | Infinity | 1.10 | Infinity | 1.10 | Infinity | 1.10 | Infinity | 1.10 | Infinity | 1.10 | Infinity | 1.10 | Infinity | 1.10 |
| Sphere | Infinity | 2.96 | Infinity | 2.96 | Infinity | 2.96 | Infinity | 3.01 | Infinity | 2.96 | Infinity | 2.96 | Infinity | 2.96 | Infinity | 2.96 | Infinity | 2.97 | ||
| Cover | Sphere | D 263® T | Infinity | 0.70 | Infinity | 0.70 | Infinity | 0.70 | Infinity | 0.70 | Infinity | 0.70 | Infinity | 0.70 | Infinity | 0.70 | Infinity | 0.70 | Infinity | 0.70 |
| Sphere | Infinity | 0.75 | Infinity | 0.75 | Infinity | 0.75 | Infinity | 0.75 | Infinity | 0.75 | Infinity | 0.75 | Infinity | 0.75 | Infinity | 0.75 | Infinity | 0.75 | ||
| Image | FPA | Infinity | –– | Infinity | –– | Infinity | –– | Infinity | –– | Infinity | –– | Infinity | –– | Infinity | –– | Infinity | –– | Infinity | –– | |
References
- Bennett, D.A.; Bell, R.M.; Helmuth, D.B.; Cochrane, A.T.; Miller, T.N.; Lentz, C.A. Remote sensing satellite constellation for world–wide wild fire monitoring. In Proceedings of the Remote Sensing for Environmental Monitoring, GIS Applications, and Geology IX, SPIE Remote Sensing, Berlin, Germany, 7 October 2009; SPIE: Berlin, Germany, 2009; Volume 7478, p. 74780W. [Google Scholar]
- Shack, R.V.; Thompson, K. Influence of alignment errors of a telescope system on its aberration field. In Proceedings of the Optical Alignment I, 24th Annual Technical Symposium, San Diego, CA, USA, 31 December 1980; Shagam, R.M., Sweatt, W.C., Eds.; SPIE: San Diego, CA, USA, 1980; Volume 251, pp. 146–153. [Google Scholar]
- Wilson, R.N.; Delabre, B. Concerning the alignment of modern telescopes: Theory, practice, and tolerances illustrated by the ESO NTT. Publ. Astron. Soc. Pac. 1997, 109, 53–60. [Google Scholar] [CrossRef][Green Version]
- Schmid, T.; Thompson, K.P.; Rolland, J.P. A unique astigmatic nodal property in misaligned Ritchey–Chrétien telescopes with misalignment coma removed. Opt. Express 2010, 18, 5282–5288. [Google Scholar] [CrossRef]
- Yang, H.S.; Lee, Y.W.; Kim, E.D.; Choi, Y.W.; Rasheed, A.A.A. Alignment methods for Cassegrain and RC telescope with wide field of view. In Proceedings of the Space Systems Engineering and Optical Alignment Mechanisms, Optical Science and Technology, the SPIE 49th Annual Meeting, Denver, CO, USA, 30 September 2004; Peterson, L.D., Guyer, R.C., Eds.; SPIE: Denver, CO, USA, 2004; Volume 5528, pp. 334–341. [Google Scholar]
- Hampson, K.M.; Gooding, D.; Cole, R.; Booth, M.J. High precision automated alignment procedure for two–mirror telescopes. Appl. Opt. 2019, 58, 7388–7391. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Yang, H.S.; Lee, Y.W.; Kim, S.W. Merit function regression method for efficient alignment control of two–mirror optical systems. Opt. Express 2007, 15, 5059–5068. [Google Scholar] [CrossRef]
- Lee, H.; Dalton, G.B.; Tosh, I.A.; Kim, S.W. Computer–guided alignment II: Optical system alignment using differential wavefront sampling. Opt. Express 2007, 15, 15424–15437. [Google Scholar] [CrossRef]
- Oh, E.; Ahn, K.B.; Kim, S.W. Experimental sensitivity table method for precision alignment of Amon–Ra instrument. J. Astron. Space Sci. 2014, 31, 241–246. [Google Scholar] [CrossRef][Green Version]
- Abitbol, M.H.; Ahmed, Z.; Barron, D.; Basu Thakur, R.; Bender, A.N.; Benson, B.A.; Bischoff, C.A.; Bryan, S.A.; Carlstrom, J.E.; Chang, C.L.; et al. Telescope engineering to control systematic errors. In CMB–S4 Technology Book, 1st ed.; ArXiv: Ithaca, NY, USA, 2017; pp. 14–16. [Google Scholar]
- O’Neill, E.L. Transfer function for an annular aperture. J. Opt. Soc. Am. 1956, 46, 285–288. [Google Scholar] [CrossRef]
- Wilson, R.N. Reflecting Telescope Optics I Basic Design Theory and its Historical Development, 2nd ed.; Springer: New York, NY, USA, 2007; pp. 319–320. [Google Scholar]
- Smith, W.J. Modern Optical Engineering, 4th ed.; McGraw–Hill Education: New York, NY, USA, 2008; pp. 392–397. [Google Scholar]
- King, W.B. Use of the modulation–transfer function (MTF) as an aberration–balancing merit function in automatic lens design. J. Opt. Soc. Am. 1969, 59, 1155–1158. [Google Scholar] [CrossRef]
- Synopsys. CODE V®, Synopsys: Mountain View, CA, USA, 2019.
- Hopkins, H.H.; Tiziani, H.J. A theoretical and experimental study of lens centring errors and their influence on optical image quality. Br. J. Appl. Phys. 1966, 17, 33–54. [Google Scholar] [CrossRef]
- Rimmer, M. Analysis of perturbed lens systems. Appl. Opt. 1970, 9, 533–538. [Google Scholar] [CrossRef] [PubMed]
- Rimmer, M. A tolerancing procedure based on modulation transfer function (MTF). In Proceedings of the Computer–Aided Optical Design, 22nd Annual Technical Symposium, San Diego, CO, USA, 1 December 1978; SPIE: San Diego, CA, USA, 1978; Volume 147, pp. 66–70. [Google Scholar]
- Koch, D.G. A statistical approach to lens tolerancing. In Proceedings of the Computer–Aided Optical Design, the 22nd Annual Technical Symposium, San Diego, CA, USA, 1 December 1978; SPIE: San Diego, CA, USA, 1978; Volume 147, pp. 71–82. [Google Scholar]
- Bely, P.Y. The Design and Construction of Large Optical Telescopes, 1st ed.; Springer: New York, NY, USA, 2002; pp. 9–18. [Google Scholar]
- Ginsberg, R.H. Outline of tolerancing (from performance specification to toleranced drawings). Opt. Eng. 1981, 20, 175–180. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).