Simultaneous Smoothing and Untangling of 2D Meshes Based on Explicit Element Geometric Transformation and Element Stitching
Abstract
1. Introduction
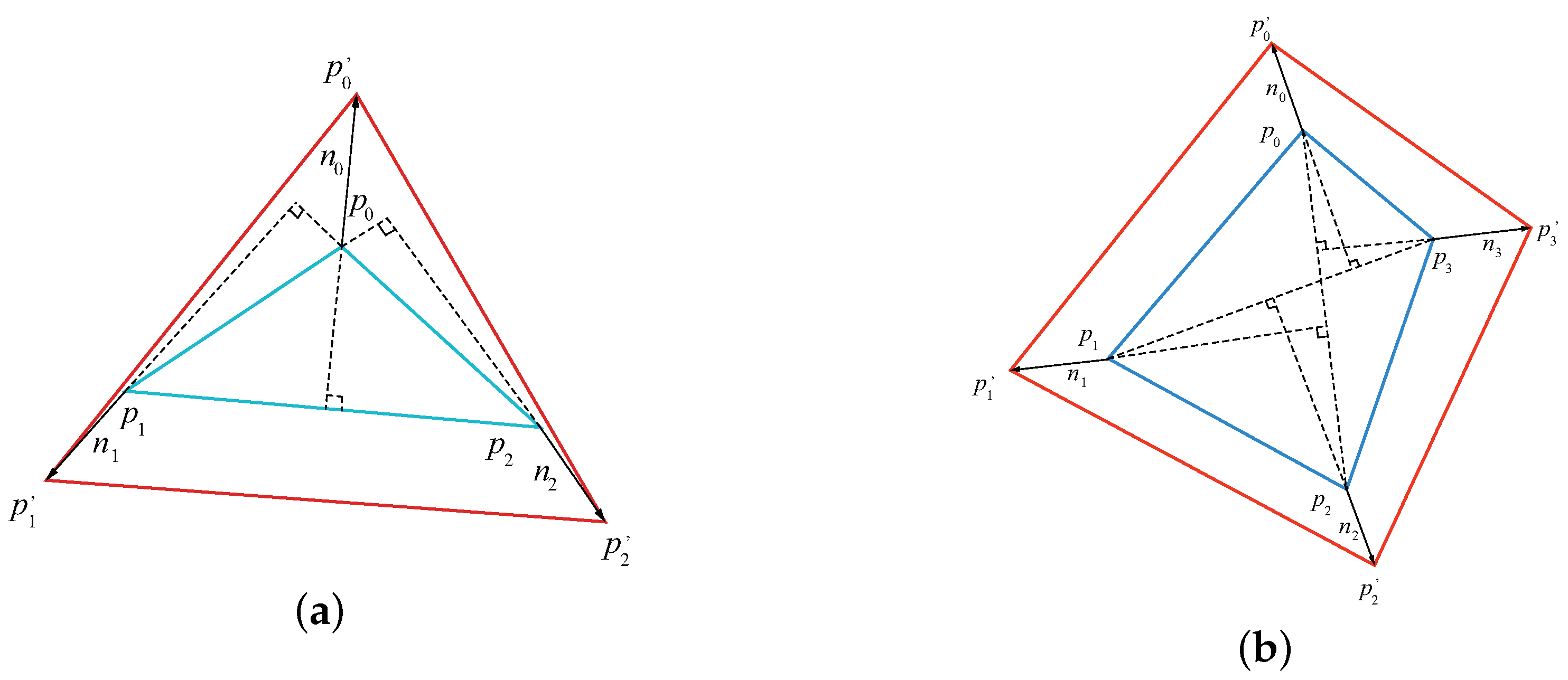
2. Explicit Element Geometric Transformation
2.1. Basic Geometric Transformation
2.2. Analysis of the Transformation
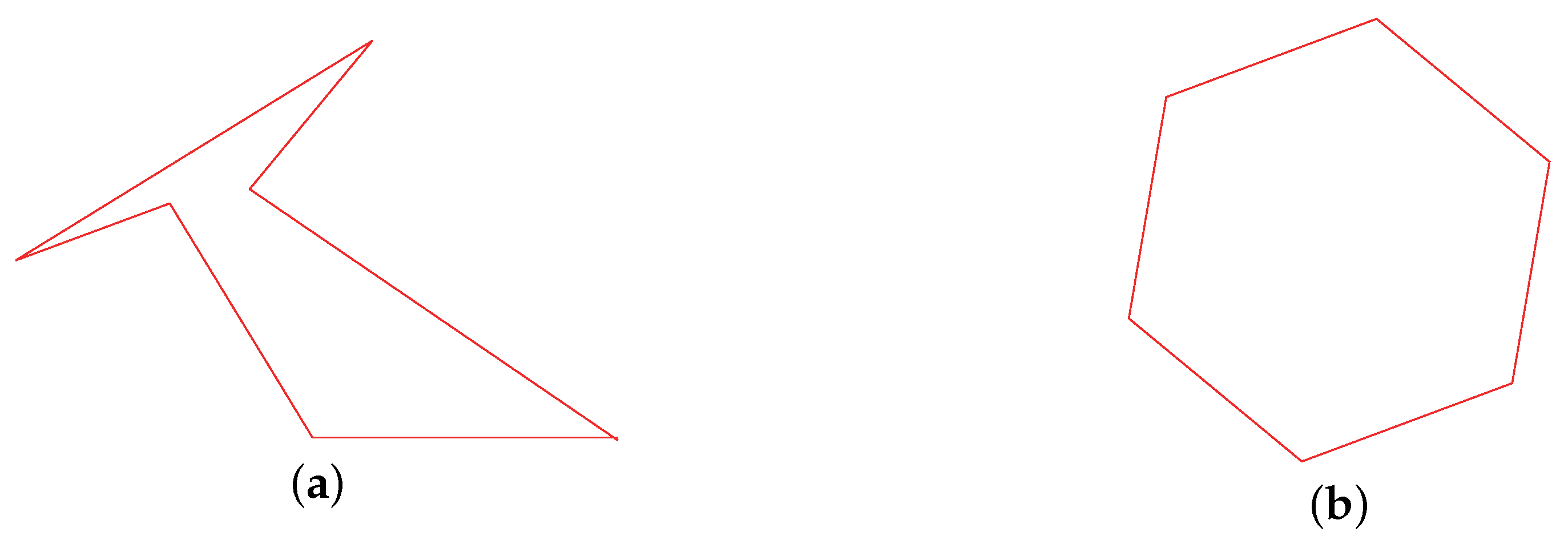
3. Smoothing and Untangling Approach
3.1. Shape Metrics
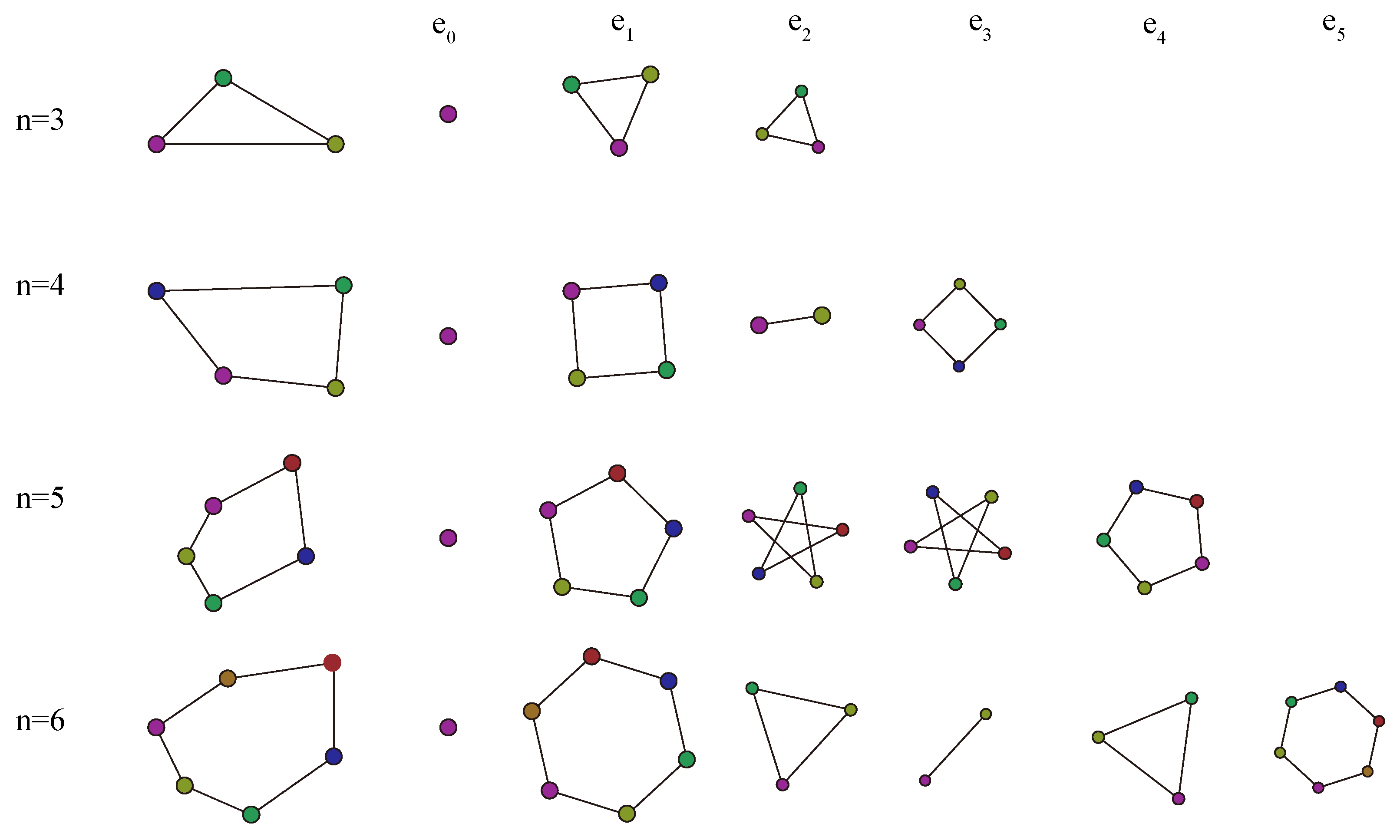
3.2. Element Stitching Operation
3.3. Untangling and Smoothing Pipeline
| Algorithm 1 EEGT-based simultaneous untangling and smoothing of 2D meshes. |
|
4. Examples
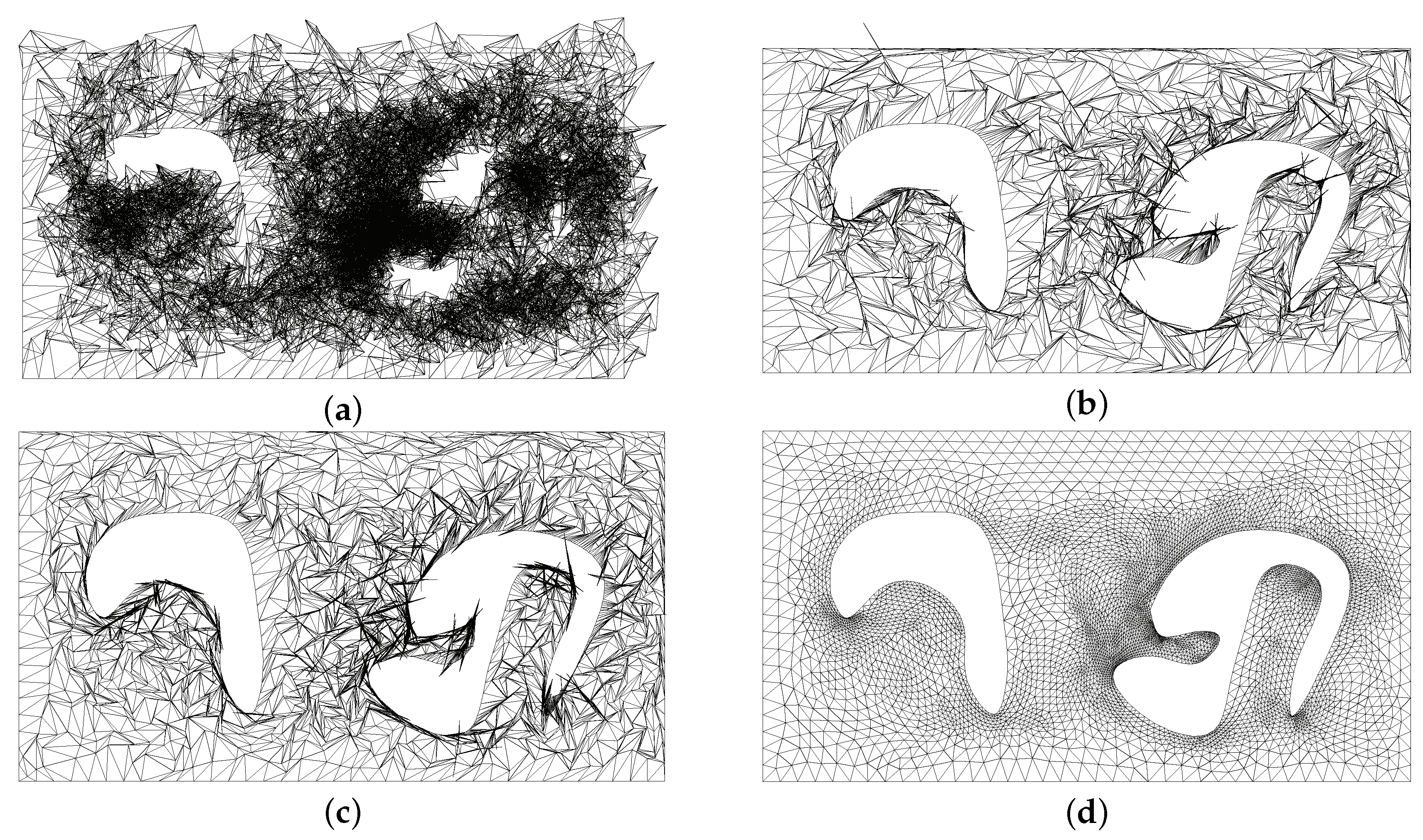
4.1. Quadrilateral Mesh Example
4.2. Mesh Deformation Example
4.3. Triangular Mesh Example
4.4. Implementation on Gpu
5. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| MR | Mean ratio |
| EEGT | Explicit element geometric transformation |
| Mesquite | Mesh quality improvement toolkit |
| GPU | Graphics processing unit |
| PDEs | Partial differential equations |
References
- Berzins, M. Solution-based mesh quality indicators for triangular and tetrahedral meshes. Int. J. Comput. Geom. Appl. 2000, 10, 333–346. [Google Scholar] [CrossRef]
- Berzins, M. Mesh quality: A function of geometry, error estimates or both? Eng. Comput. 1999, 15, 236–247. [Google Scholar] [CrossRef]
- Batdorf, M.; Freitag, L.; Ollivier-Gooch, C.; Batdorf, M.; Freitag, L.; Ollivier-Gooch, C. Computational study of the effect of unstructured mesh quality on solution efficiency. In Proceedings of the 13th Annual AIAA Computational Fluid Dynamics Conference, Snowmass Village, CO, USA, 29 June–2 July 1997; pp. 1–11. [Google Scholar]
- Shewchuk, J.R. Delaunay refinement algorithms for triangular mesh generation. Comput. Geom. 2002, 22, 21–74. [Google Scholar] [CrossRef]
- Cheng, S.W.; Dey, T.K.; Shewchuk, J. Delaunay Mesh Generation; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Huang, W.; Russell, R.D. Adaptive Moving Mesh Methods; Springer Science & Business Media: Berlin, Germany, 2010; Volume 174. [Google Scholar]
- Chandru, M.; Das, P.; Ramos, H. Numerical treatment of two-parameter singularly perturbed parabolic convection diffusion problems with non-smooth data. Math. Methods Appl. Sci. 2018, 41, 5359–5387. [Google Scholar] [CrossRef]
- Chandru, M.; Prabha, T.; Das, P.; Shanthi, V. A numerical method for solving boundary and interior layers dominated parabolic problems with discontinuous convection coefficient and source terms. Differ. Equ. Dyn. Syst. 2019, 27, 91–112. [Google Scholar] [CrossRef]
- Das, P. An a posteriori based convergence analysis for a nonlinear singularly perturbed system of delay differential equations on an adaptive mesh. Numer. Algorithms 2019, 81, 465–487. [Google Scholar] [CrossRef]
- Das, P.; Rana, S.; Vigo-Aguiar, J. Higher order accurate approximations on equidistributed meshes for boundary layer originated mixed type reaction diffusion systems with multiple scale nature. Appl. Numer. Math. 2020, 148, 79–97. [Google Scholar] [CrossRef]
- Das, P. Comparison of a priori and a posteriori meshes for singularly perturbed nonlinear parameterized problems. J. Comput. Appl. Math. 2015, 290, 16–25. [Google Scholar] [CrossRef]
- Das, P. A higher order difference method for singularly perturbed parabolic partial differential equations. J. Differ. Equ. Appl. 2018, 24, 452–477. [Google Scholar] [CrossRef]
- Das, P.; Mehrmann, V. Numerical solution of singularly perturbed convection-diffusion-reaction problems with two small parameters. BIT Numer. Math. 2016, 56, 51–76. [Google Scholar] [CrossRef]
- Danczyk, J.; Suresh, K. Finite element analysis over tangled simplicial meshes: Theory and implementation. Finite Elem. Anal. Des. 2013, 70, 57–67. [Google Scholar] [CrossRef]
- Peraire, J.; Vahdati, M.; Morgan, K.; Zienkiewicz, O.C. Adaptive remeshing for compressible flow computations. J. Comput. Phys. 1987, 72, 449–466. [Google Scholar] [CrossRef]
- Kossaczkỳ, I. A recursive approach to local mesh refinement in two and three dimensions. J. Comput. Appl. Math. 1994, 55, 275–288. [Google Scholar] [CrossRef]
- Kim, J. An Iterative Mesh Untangling Algorithm Using Edge Flip. Math. Probl. Eng. 2017, 2017, 2953736. [Google Scholar] [CrossRef]
- Field, D.A. Laplacian smoothing and Delaunay triangulations. Commun. Appl. Numer. Methods 1988, 4, 709–712. [Google Scholar] [CrossRef]
- Freitag, L.A.; Plassmann, P. Local optimization-based simplicial mesh untangling and improvement. Int. J. Numer. Methods Eng. 2000, 49, 109–125. [Google Scholar] [CrossRef]
- Knupp, P.M. Hexahedral and tetrahedral mesh untangling. Eng. Comput. 2001, 17, 261–268. [Google Scholar] [CrossRef]
- Franks, J.W.; Knupp, P.M. A new strategy for untangling 2D meshes via node-movement. In CSRI Summer Proceedings; Sandia National Laboratories: Albuquerque, NM, USA, 2010; pp. 152–165. [Google Scholar]
- Brewer, M.L.; Diachin, L.F.; Knupp, P.M.; Leurent, T.; Melander, D.J. The Mesquite Mesh Quality Improvement Toolkit. In Proceedings of the 12th International Meshing Roundtable, Santa Fe, NM, USA, 14–17 September 2003; pp. 239–250. [Google Scholar]
- Kim, J.; Panitanarak, T.; Shontz, S.M. A multiobjective mesh optimization framework for mesh quality improvement and mesh untangling. Int. J. Numer. Methods Eng. 2013, 94, 20–42. [Google Scholar] [CrossRef]
- Escobar, J.M.; Rodrıguez, E.; Montenegro, R.; Montero, G.; González-Yuste, J.M. Simultaneous untangling and smoothing of tetrahedral meshes. Comput. Methods Appl. Mech. Eng. 2003, 192, 2775–2787. [Google Scholar] [CrossRef]
- Escobar, J.; Montero, G.; Montenegro, R.; Rodríguez, E. An algebraic method for smoothing surface triangulations on a local parametric space. Int. J. Numer. Methods Eng. 2006, 66, 740–760. [Google Scholar] [CrossRef]
- Gargallo-Peiró, A.; Roca, X.; Sarrate, J. A surface mesh smoothing and untangling method independent of the CAD parameterization. Comput. Mech. 2014, 53, 587–609. [Google Scholar] [CrossRef]
- Kim, J.; Choi, J.; Kang, W. A Data-Driven Approach for Simultaneous Mesh Untangling and Smoothing Using Pointer Networks. IEEE Access 2020, 8, 70329–70342. [Google Scholar] [CrossRef]
- Vartziotis, D.; Wipper, J. The geometric element transformation method for mixed mesh smoothing. Eng. Comput. 2009, 25, 287–301. [Google Scholar] [CrossRef]
- Vartziotis, D.; Wipper, J. Fast smoothing of mixed volume meshes based on the effective geometric element transformation method. Comput. Methods Appl. Mech. Eng. 2012, 201, 65–81. [Google Scholar] [CrossRef]
- Sun, S.; Zhang, M.; Gou, Z. Smoothing algorithm for planar and surface mesh based on element geometric deformation. Math. Probl. Eng. 2015, 2015, 435648. [Google Scholar] [CrossRef]
- Davis, P.J. Circulant Matrices; American Mathematical Soc.: Providence, RI, USA, 2013. [Google Scholar]
- Knupp, P.M. Algebraic mesh quality metrics. SIAM J. Sci. Comput. 2001, 23, 193–218. [Google Scholar] [CrossRef]
- Sun, S.; Lv, S.; Yuan, Y.; Yuan, M. Mesh deformation method based on mean value coordinates interpolation. Acta Mech. Solida Sin. 2016, 29, 1–12. [Google Scholar] [CrossRef]


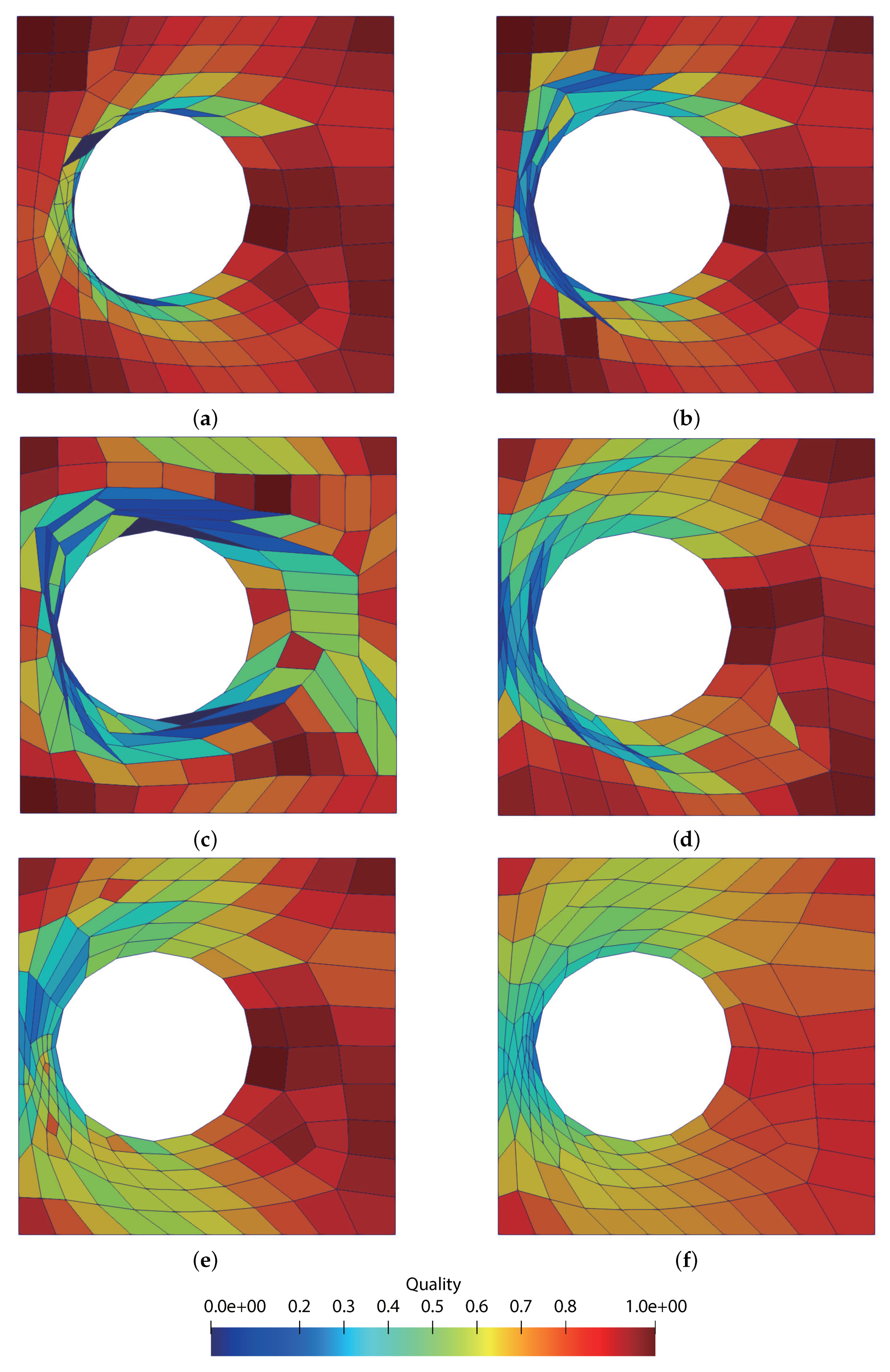

| Methods | Time(s) | Number of Inverted Elements | ||
|---|---|---|---|---|
| Initial mesh | − | 0.6347 | 0 | 23 |
| Untangle-Beta | 0.09 | 0.6003 | 0.0207 | 0 |
| Size | 0.41 | 0.5073 | 0 | 4 |
| Shape-Size | 0.239 | 0.5634 | 0.0953 | 0 |
| Untangle-Beta + Shape Improve Wrapper | 0.525 | 0.6312 | 0.2297 | 0 |
| EEGT | 0.006 | 0.5844 | 0.2502 | 0 |
| Methods | Time(s) | Number of Inverted Elements | ||
|---|---|---|---|---|
| Initial mesh | − | 0.3243 | 0 | 459 |
| Untangle-Beta | 5.402 | 0.1766 | 0 | 5533 |
| Size | 900.233 | 0.1355 | 0 | 1637 |
| Shape-Size | 54.494 | 0.2829 | 0 | 3833 |
| EEGT | 29.849 | 0.8102 | 0.4157 | 0 |
| EEGT + Shape Improve Wrapper | 108.089 | 0.9006 | 0.2963 | 0 |
| Methods | Time(s) | Number of Inverted Elements | ||
|---|---|---|---|---|
| Initial mesh | − | 0.2566 | 0 | 4914 |
| Size | 4.927 | 0.2043 | 0 | 1825 |
| Shape-Size | 32.472 | 0.1729 | 0 | 2636 |
| EEGT | 37.488 | 0.9130 | 0.6461 | 0 |
| Compute Capability | 5.0 |
| Number of stream multiprocessor | 5 |
| Cores per stream multiprocessor | 128 |
| Warp Size | 32 |
| Clock Rate | 1.12 GHz |
| Global Memory | 4 GB |
| Peak FP32 Performance | 1.3Tflops |
| Meshes | Platform | Number of Elements | Number of Inverted Elements | Time(s) |
|---|---|---|---|---|
| Quadrilateral mesh example | CPU GPU | 140 | 23 | 0.006 4.184 |
| Mesh deformation example | CPU GPU | 11,363 | 459 | 29.849 0.817 |
| Triangular mesh example | CPU GPU | 10,085 | 4914 | 37.488 1.199 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, S.; Gou, Z.; Geng, M. Simultaneous Smoothing and Untangling of 2D Meshes Based on Explicit Element Geometric Transformation and Element Stitching. Appl. Sci. 2020, 10, 5019. https://doi.org/10.3390/app10145019
Sun S, Gou Z, Geng M. Simultaneous Smoothing and Untangling of 2D Meshes Based on Explicit Element Geometric Transformation and Element Stitching. Applied Sciences. 2020; 10(14):5019. https://doi.org/10.3390/app10145019
Chicago/Turabian StyleSun, Shuli, Zhihong Gou, and Mingguang Geng. 2020. "Simultaneous Smoothing and Untangling of 2D Meshes Based on Explicit Element Geometric Transformation and Element Stitching" Applied Sciences 10, no. 14: 5019. https://doi.org/10.3390/app10145019
APA StyleSun, S., Gou, Z., & Geng, M. (2020). Simultaneous Smoothing and Untangling of 2D Meshes Based on Explicit Element Geometric Transformation and Element Stitching. Applied Sciences, 10(14), 5019. https://doi.org/10.3390/app10145019




