A Discrete Hidden Markov Model for SMS Spam Detection

Abstract

Many machine learning methods have been applied for short messaging service (SMS) spam detection, including traditional methods such as naïve Bayes (NB), vector space model (VSM), and support vector machine (SVM), and novel methods such as long short-term memory (LSTM) and the convolutional neural network (CNN). These methods are based on the well-known bag of words (BoW) model, which assumes documents are unordered collection of words. This assumption overlooks an important piece of information, i.e., word order. Moreover, the term frequency, which counts the number of occurrences of each word in SMS, is unable to distinguish the importance of words, due to the length limitation of SMS. This paper proposes a new method based on the discrete hidden Markov model (HMM) to use the word order information and to solve the low term frequency issue in SMS spam detection. The popularly adopted SMS spam dataset from the UCI machine learning repository is used for performance analysis of the proposed HMM method. The overall performance is compatible with deep learning by employing CNN and LSTM models. A Chinese SMS spam dataset with 2000 messages is used for further performance evaluation. Experiments show that the proposed HMM method is not language-sensitive and can identify spam with high accuracy on both datasets.

1. Introduction

Nowadays, one of the most popular and common communication services is the short message service, known as SMS. SMS traffic volumes have risen from 1.46 billion in 2000 to 7.9 trillion in 2012 [1]. SMS-capable mobile phone users had reached 6.1 billion users by the year 2015 [2]. The growth of mobile users has generated a great deal of revenue [1]. Based on the latest statistics [3], global SMS revenue is predicted to hit 83.2 billion dollars in 2022 even though the revenue has continued to decrease after 2017. In addition, about half (43 billion dollars) of the global SMS revenue belongs to the global P2P (person-to-person) SMS messages market and the other half (40.2 billion dollars) belongs to A2P (application-to-person). A2P messages are sent by companies, such as bulksmsonline.com and bulksms.com, who provide bulk SMS sending services for commercial needs, e.g., verification codes, e-commercial notifications, express delivery notifications.

While enjoying the convenience of communication via electronic devices, unexpected advertising or even malicious information has flooded our email and phone message boxes. This spam information is usually unwanted or unsolicited electronic messages sent in bulk to a group of recipients [4]. It is being sent by spammers or even criminals who are driven by these most profitable spamming businesses. Spam first spread explosively but mainly in emails in the first decade of the 21th century, indicated by the statistical results provided in [5]. As SMS is low-cost, bulk-sending, and reliably reaches the receiver, spam began moving to this most popular and globally used SMS service. The companies hosting the bulk SMS sending service have to continuously improve their spam filtering technology to combat against spam SMS. However, it is a challenging task as SMS contains limited words including abbreviations, etc. In addition, SMS spammers tend to use legitimate words to increase its rank in spam filters and use obfuscated words to confuse the spam filters.

Antispam techniques have been developed for decades. Many methods for antispam emails have been applied in the antispam SMS field. Traditional machine learning methods for spam detection including naïve Bayes (NB) [6,7], vector space model (VSM) [8], and support vector machine (SVM) [9], and novel methods such as long short-term memory (LSTM) [10] and the convolutional neural network (CNN) [11] all stand on the well-known bag of words (BoW) model, which assumes documents are an unordered collection of words. Based on this assumption, word or term occurrences are the only concern but the order of words in the document is ignored. Based on the BoW assumption, many feature extraction algorithms [12,13,14] were invented to make use of term frequency, such as TF.IDF (stands for term frequency and inversed document frequency) and word distribution. However, these algorithms do not work well in SMS spam detection, because of the strict length limitation of SMS. Most of the terms (words) occur only once in a single SMS. Human language is actually sequential data. Word order is critical information for SMS spam detection.

Motivated to address the aforementioned issues, we propose a new method based on the discrete hidden Markov model (HMM) for spam SMS detection in this paper. An HMM is a statistical model with two stochastic processes [15]. The underlying stochastic process that has the Markov property is a sequence of hidden states, and the observable stochastic process is a sequence of observation states that reflect the hidden states through some probabilistic distribution. HMMs are a formal foundation for building probabilistic models of linear sequence labeling problems [16]. In this paper, the SMS messages are preprocessed by removing the recommended stop words (e.g., #&gt, &lt, \\, &amp, that, shall, is) and punctuation to form the observation sequence with original word order. The HMM is trained by the labeled observation sequence. Then, the SMS classification is a typical decoding problem in HMM by using the Viterbi algorithm. To the best of our knowledge, this is the first research on applying HMM for SMS spam detection based on word order.

The main contributions of this research are threefold:

• We first propose to use a hidden Markov model for spam SMS detection based on word order. This method uses the word order information that consists of the key importance for human language, but it has been ignored by many traditional methods based on the BoW model.
• This research solves the issue where the TF.IDF algorithm for word weighting does not work well in SMS spam detection, due to the extremely low term frequency.
• The proposed method can be applied to alphabetic text (e.g., English) and hieroglyphic text (e.g., Chinese). It is not language-sensitive.

The rest of the paper is organized as follows. Related work is discussed in Section 2. The problem formulation and the proposed SMS spam detection method based on the discrete HMM are presented in Section 3. The experimental results and performance comparisons with well-known models are outlined in Section 4. The conclusions are drawn and future work is discussed in Section 5.

2. Related Work

2.1. Rule-Based Filtering Technologies

The rule-based filtering techniques are popular in commercial business. SpamAssassin [17] is a successful forerunner of typical rule-based systems (RBSs). It has been adopted by antispam industry companies, such as Symantec and McAfee [18]. The next-generation RBS of Wirebrush4SPAM [19] was then developed to increase its throughput. Both SpamAssassin and Wirebrush4SPAM host a set of scored rules and run a score-based mechanism. A spam email is detected when the sum of scores from triggered rules is greater or equal to the value of a global threshold, which is called required score. However, throughput is a challenging issue of RBSs, and their time complexity of filtering algorithms could not be reduced to an acceptable level. To address the throughput issue, a constant time complexity spam detection algorithm was developed by Xia [20].

2.2. Content-Filtering Technologies

Content-filtering technologies have utilized machine learning technologies to combat spam. One of the most common technologies is the Bayesian classification filter [21]. Bayesian methods, such as naïve Bayes, worked efficiently and had become an important machine learning algorithm in information retrieval. It is based on Bayes theorem with a strong naïve independence assumption that treats each and every word as single, mutually exclusive, and independent. It is defined as a graphical probabilistic model for multivariate analysis. The nodes of the directed graph represent problem variables and the edges represent conditional dependencies between such variables. Jiang et al. [6] put forward a deep feature weighting (DFW) for naïve Bayes and applied it to text classification. Moreover, to enhance its accuracy, Bayesian methods are often hybrid with other algorithms. Sable et al. [7] introduced a hybrid system of SMS classification based on a naïve Bayes classifier and Apriori Algorithm. Ebadati and Ahmadzadeh [22] proposed a genetic algorithm (GA)-naïve Bayes for spam email detection with a genetic algorithm (GA) for feature extraction. Arifin at al. [23] focused on spam detection for SMS by a naïve Bayes classifier and frequent patterns (FP) tree mining, known as FP-Growth.

Vector space model is based on the BoW model. It represents documents as document vectors that are full of word weights and classify documents based on the cosine similarity value of the vectors. VSM is often used for text classification and information retrieval. Santos et al. [24] filtered spam by representing e-mails with the enhanced topic-based vector space model (eTVSM).

Support vector machine is a set of binary SVM classifiers. It trains a decision equation from an n-dimensional space representation of the data into two regions using a hyperplane, which leads to high accuracy. It is popular because it is robust for many circumstances with high classifying speed. In natural language processing (NLP) research, the SVM n-dimensional space is the same BoW vector space of VSM. Chan et al. [25] proposes a word attack strategy and a feature reweighting method toward the SMS scenario in SVM when the length of a message is limited. Tekerek [9] compared the result of NB, K-nearest neighborhood (KNN), SVM, random forest (RF), and random tree (RT), and found that SVM had the best result.

Entropy, as an information theory, is also used with co-training by Zhang et al. [26,27] to combat spam reviews, which promote sales or defame competitors by misleading consumers. Decision tree is also a method for combating spam. Gashti [28] proposed a hybrid of harmony search algorithm (HSA) and decision tree for selecting the best features and classification.

Deep learning has aroused extensive attention these years. Pumrapee et al. [10] proposed an SMS spam detection method based on long short-term memory (LSTM). Research by Roy et al. [11] used convolutional neural network (CNN) and LSTM models in spam SMS detection to achieve the highest accuracy so far.

In addition, researchers also investigated hybrid models for performance improvement. Uysal et al. [29] investigated the impact of feature extraction and selection of the BoW model and then used KNN and SVM for spam SMS filtering. Karthika et al. [30] applied a latent semantic indexing (LSI)-based SVM model for email spam classification. Arijit et al. [31] filtered SMS spam by a recurrent neural network and LSTM. Yang et al. [32] used a multi-modal fusion, which applied LSTM and CNN models to process the text. Zhao et al. [33] applied six classifiers in the basic module and a deep neural network in the combination module. There are also other models for SMS spam detection, such as the neural network [34], KNN [35], and negative selection algorithm (NSA) [36]. Recently, Shang [37] developed a score-based filtering mechanism in consensus of hybrid multi-agent systems with malicious nodes, which can also be applied for spam detection.

2.3. Hidden Markov Model for Spam Detecions

HMM and its variants have found a wide variety of applications. There was a hierarchical hidden Markov model (HHMM) for real-time finger motion synthesis [38], a hierarchical multivariate HMM with reactive interpolation functionality for full-body motion reconstruction [39], a combining speaker-specific Gaussian mixture model (GMM) with a syllable-based HMM for speaker recognition [40], and a Spherical-Self Organizing Map (S-SOM) with HMM for classifying sets of time series [41], to list just a few examples. HMMs have also laid a solid foundation for their applications in NLP, including part-of-speech tagging in many languages [42,43] and name entity recognition [44].

However, based on our literature review including the latest review papers about SMS spam detection techniques [4,45,46], there is no report on using HMM for SMS spam detection based on the word order. Rafique and Farooq [47] used HMM for SMS spam detection on byte-level, which is the low communication level of SMS delivery. Gordillo and Conde [48], as forerunners in this field, proposed a HMM for detecting spam mail in 2007. The paper focused on obfuscated words detection, such as the example in the paper, m0ney or mo.ney for the word money. Therefore, instead of words, they focused on spam detection at the language character level, such as letters in English. They treated characters in spam emails like a DNA chain and used a similar DNA chain classification method for spam emails. Ebrahimi et al. [49] built a HMM for detection and classification of duplicate bug reports (BRs) by focusing on the relation of current BRs and incoming BRs. Similarly, Washha et al. [50] put forward a topic-based HMM for spam tweet filtering and predicted the tweet sample classification based on an assumed high dependency among successive tweets. Vennila et al. [51] used HMM in spam detection over internet telephony in voice, which belongs to a far different research field from this study. The existing work focused on emails, bug reports, and tweets, etc. Unlike the existing work, we aim to use a hidden Markov model for spam SMS detection based on the word order, which is a new application of HMM.

3. The Discrete HMM for SMS Spam Detection

3.1. Problem Formulation and Notations

A typical SMS contains sequential words with punctuation. In English, as words are divided by blank spaces, English SMS is easy to be split, whereas in some other languages, e.g., Chinese, there are no blank spaces between words. These SMS messages have to first feed into a segmentation algorithm to extract words. In any case, each SMS text is first split or segmented into sequential words with punctuation at the very beginning.

Not all words are suitable for NLP. Punctuation and words only for positioning do not have much semantic information. Especially for SMS, many informal words, shortened and abbreviated words, social media acronyms, and some strange character sequences often appear in SMS. Part of them is also meaningless. They are called the stop words. Therefore, these stop words and punctuation are removed from the sequential words.

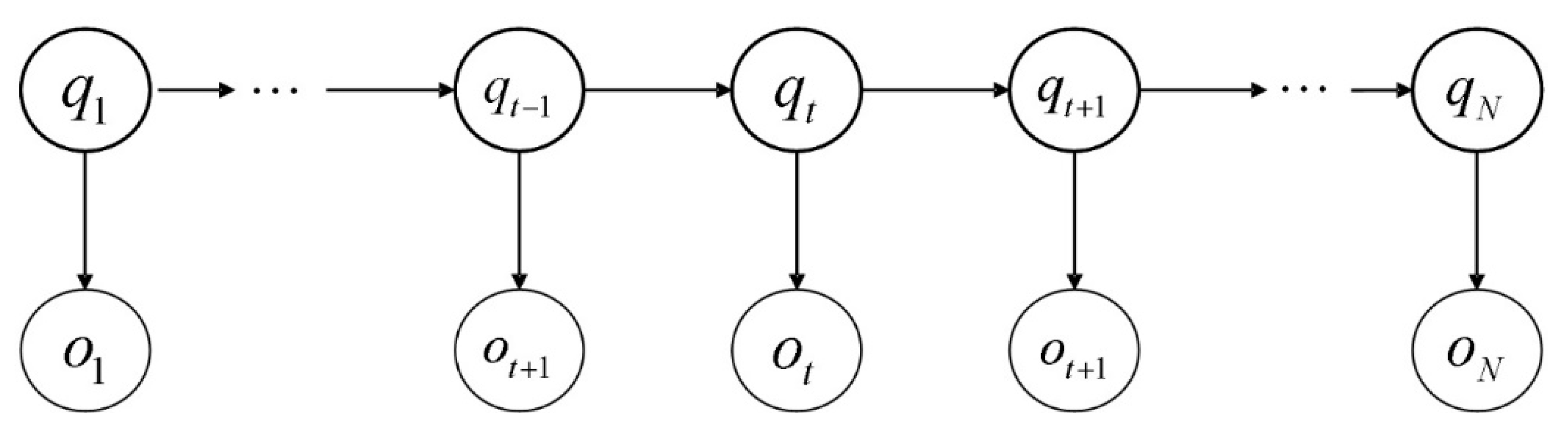
After these preprocesses, each SMS is refined to a word sequence, which is full of meaningful words. Let $N$ denote the total number of all rest meaningful words in SMS including the duplicated ones. This set with N sequential words is the observation sequence denoted as $\underset{\_}{X}=\{o_1, o_2, o_3, \cdots , o_N\}$. The corresponding hidden state sequence is denoted as $\underset{\_}{Y}=\{q_1, q_2, q_3, \cdots , q_N\}$, satisfying the Markov property. The structure of these two sequences is represented by the directed graph in Figure 1.

The HMM, denoted by λ, can be defined by a three-tuple:

$$\lambda = (\pi ,\hspace{0.17em}A,\hspace{0.17em}B)$$

(1)

where $\pi$ is the initial probability distribution, A is the state transition probability matrix, and B is the observation probability distribution matrix.

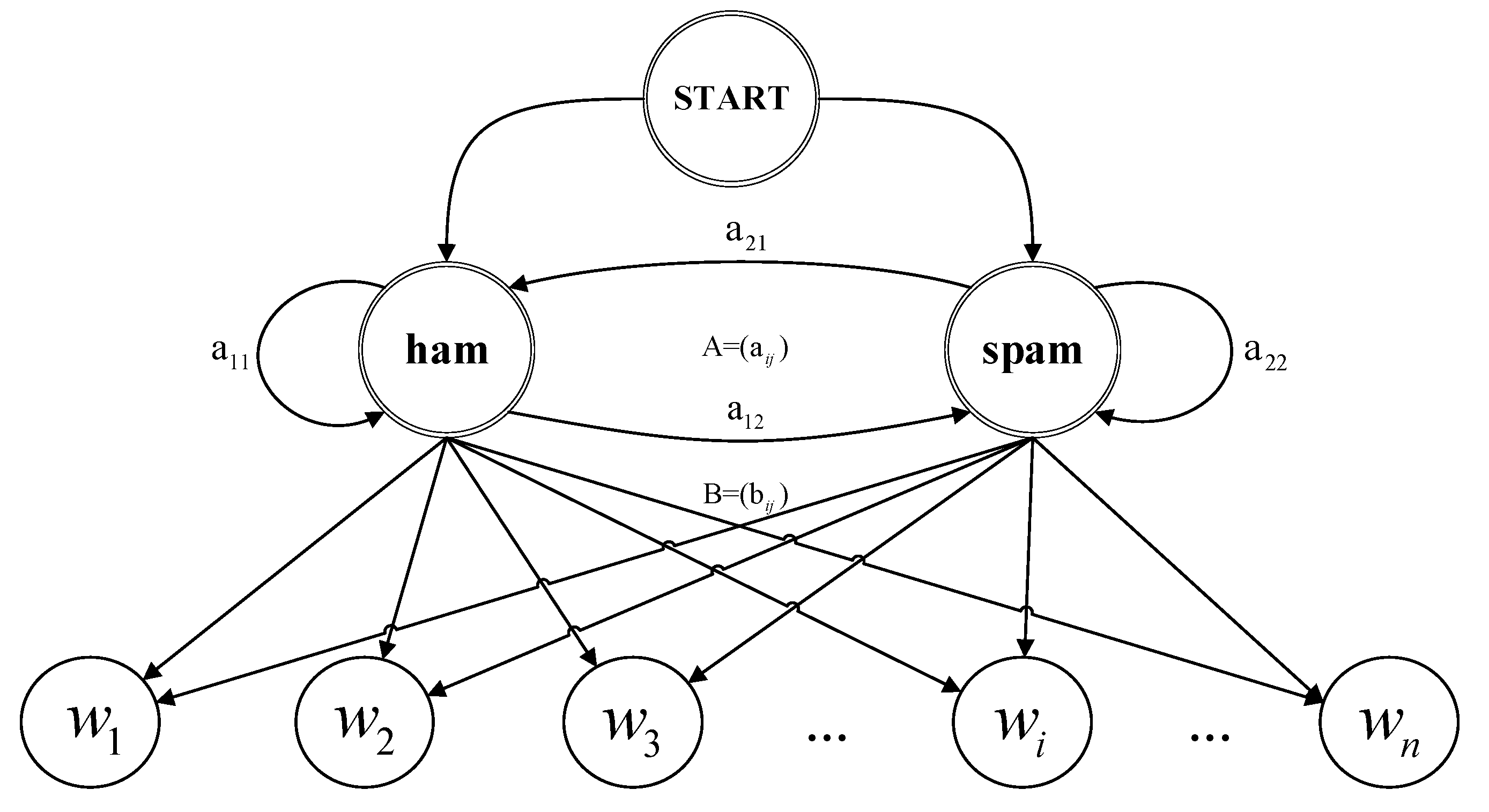
For SMS spam detection, the set of hidden states is $S=\left\{s_1, s_2\right\}=\left\{ham, spam\right\}$. Thus, $A={(a_{ij})}_{2\times 2}$, where $a_{ij}=P(q_{t+1}=s_j|q_t=s_i)$, for $i,j=1,\hspace{0.17em}2$ and ${\displaystyle \sum _{j=1}^2{a}_{ij}}=1$, for $\hspace{0.17em}i=1,\hspace{0.17em}2$.

Let $W=\{w_1, w_2, w_3, \cdots , w_n\}$ denote the set of observation states, which includes all different words in every spam and ham SMS. $n$ is the total number of different words in both sets. Thus, $B {=(\mathrm{b}}_{ij}{)}_{2\times n}$, where $b_{ij}=P(o_t=w_j|q_t=s_i)$, for $i=1,2,\hspace{0.17em}j=1,\cdots ,n$.

$\pi$ is a 2 × 1 initial probability distribution over the state, ${\pi }_1=P(q_1=s_1)$, ${\pi }_2=P(q_1=s_2)$, and ${\pi }_1+{\pi }_2=1$.

The proposed hidden Markov model for spam detection is shown in Figure 2.

3.2. Observation States and Observation Sequence

The $i^{th}$ SMS can be represented as the rest meaningful sequential words in the set of observation states $W$: $SM{S}_i=\{w_1^{SM{S}_i}, w_2^{SM{S}_i}, w_3^{SM{S}_i}, \cdots , w_{LengthofSM{S}_i}^{SM{S}_i}\}$, ($0<i\le M$). $M$ is the total number of SMS. $w_i^{SM{S}_i}$ is one of the meaningful words in the $i^{th}$ SMS.

For example, take the following two SMS messages from the UCI repository dataset, which can be downloaded from http://www.dt.fee.unicamp.br/~tiago/smsspamcollection. The same dataset has been used in [2,4,8,9,10,11,13,21,23,25,31,46,52,53,54,55,56,57] for performance evaluations.

ham: What you thinked about me. First time you saw me in class.

spam: Are you unique enough? Find out from 30th August. www.areyouunique.co.uk.

Please note that the example dataset only contains 2 SMS messages and words you and me are duplicated in the two SMS messages.

The two SMS messages can be segmented as word and punctuation sequences with the original order: [What, you, thinked, about, me, ., First, time, you, saw, me, in, class, .] and [Are, you, unique, enough, ?, Find, out, from, 30th, August, ., www, ., areyouunique, ., co, ., uk]. After removing stop words and punctuation, the word sequences also keep its order and become refined ones: [What, you, thought, me, First, time, you, saw, me, class] and [Are, you, unique, enough, Find, 30th, August, www, areyouunique, co, uk].

Then, the observation states set $W$ is generated, i.e., $W$ = {What, you, thought, me, First, time, saw, class, Are, unique, enough, Find, 30th, August, www, areyouunique, co, uk}. Each word in $W$ appears in ham and spam SMS sets with a certain frequency. These occurrence frequencies will be used to obtain the observation probability distribution.

In addition, the refined two-word sequences combine together to form the observation sequence $\underset{\_}{X}=\{o_1, o_2, o_3, \cdots , o_N\}$. In this example, $\underset{\_}{X}$ = {What, you, thinked, me, First, time, you, saw, me, class, Are, you, unique, enough, Find, 30th, August, www, areyouunique, co, uk}. It is obvious that the original word order is kept.

Therefore, the observation sequence $\underset{\_}{X}=\{o_1, o_2, o_3, \cdots , o_N\}$ can be represented as

$$\begin{array}{c}\begin{array}{c}\underset{\_}{X}=\{w_1^{SM{S}_1}, w_2^{SM{S}_1}, w_3^{SM{S}_1}, \cdots , w_{LengthofSM{S}_1}^{SM{S}_1},\\ \cdots ,\end{array}\\ \begin{array}{c}{w}_1^{SM{S}_i}, w_2^{SM{S}_i}, w_3^{SM{S}_i}, \cdots , w_{LengthofSM{S}_i}^{SM{S}_i},\\ \cdots ,\end{array}\\ w_1^{SM{S}_M}, w_2^{SM{S}_M}, w_3^{SM{S}_M}, \cdots , w_{LengthofSM{S}_M}^{SM{S}_i}\}\end{array}$$

(2)

Please note that different SMSs may have different lengths. All sequential words in each SMS combine together to form the final observation sequence $\underset{\_}{X}$.

3.3. Label Each Word in Observation Sequence for HMM Learning

Among these training SMS from the UCI repository dataset, some of them are labeled as spam and the others are labeled as ham. The labeled SMS dataset can be described as:

$$\begin{array}{ccc}SM{S}_1& w_1^{SM{S}_1}, w_2^{SM{S}_1}, w_3^{SM{S}_1}, \cdots , w_{LengthofSM{S}_1}^{SM{S}_1}& ham\\ SM{S}_2& w_1^{SM{S}_2}, w_2^{SM{S}_2}, w_3^{SM{S}_2}, \cdots , w_{LengthofSM{S}_2}^{SM{S}_2}& spam\\ \cdots & \cdots & \cdots \\ SM{S}_i& w_1^{SM{S}_i}, w_2^{SM{S}_i} , w_3^{SM{S}_i} , \cdots , w_{LengthofSM{S}_i}^{SM{S}_i}& ham\\ \cdots & \cdots & \cdots \\ SM{S}_M& w_1^{SM{S}_M}, w_2^{SM{S}_M}, w_3^{SM{S}_M}, \cdots , w_{LengthofSM{S}_M}^{SM{S}_i}& spam\end{array}$$

(3)

Take a look at the instances above again. The SMS, What you thinked about me. First time you saw me in class., is labeled as ham and the other one, Are you unique enough? Find out from 30th August. www.areyouunique.co.uk, is labeled as spam. Thus, it is represented as [What, you, thinked, me, First, time, you, saw, me, class] with the label ham and [Are, you, unique, enough, Find, 30th, August, www, areyouunique, co, uk] with the label spam.

However, each word in the observation sequence should be marked as ham or spam for the HMM learning. As the UCI repository dataset only has a label for each SMS, we use a compromised method to label all words in the observation sequence, i.e., labeling the words in the SMS based on the label of the SMS. The labels for the observation sequence can be represented as:

$$\begin{array}{c}\begin{array}{c}\{ham, ham, ham, \cdots , ham,\\ \cdots ,\end{array}\\ \begin{array}{c}ham, ham, ham, \cdots , ham,\\ \cdots ,\end{array}\\ spam, spam, spam, \cdots , spam\}\end{array}$$

(4)

For the instances above, as the first SMS is a ham one, each word in the refined sequence is labeled as ham. As the second SMS is a spam one, each word in the sequence is labeled as spam. That is, the part of observation sequence [What, you, thought, me, First, time, you, saw, me, class] is labeled as [ham, ham, ham, ham, ham, ham, ham, ham, ham, ham] and [Are, you, unique, enough, Find, 30th, August, www, areyouunique, co, uk] is labeled as [spam, spam, spam, spam, spam, spam, spam, spam, spam, spam, spam].

3.4. Observation Probability Distribution

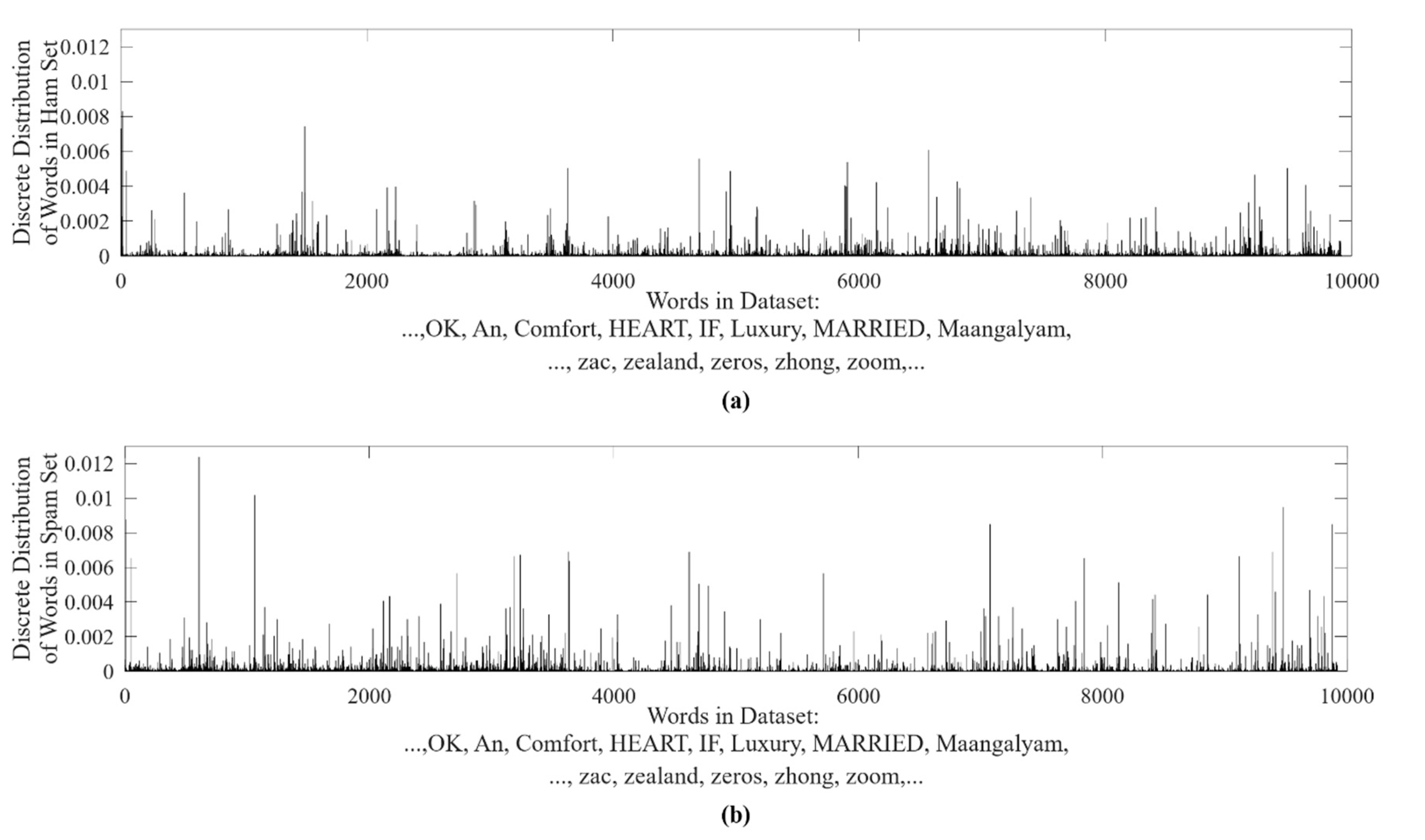
We calculate the probability of each observation state, i.e., each word in W, appearing in ham and spam SMS sets. The probability distribution is depicted in Figure 3. The word order in W is fixed for easy comparison, as shown in Figure 3.

The higher the frequency of a certain word, the higher the probability in the distribution. As the word order in W is fixed in Figure 3, we can compare the probability of each word in ham and spam sets visibly. It is found that:

• As some words only have probability in a single dataset and their probability is equal to zero in another dataset, this indicates that these words only appear in the spam messages set or ham messages set;
• As the probabilities of many words are quite different in different datasets, it is referred that these words appear in both sets with much different word frequencies;
• Only a very small portion of them appear in both sets evenly.

It is true that the BoW also took advantage of this information to design term weights algorithms. However, the TF algorithm does not work well in the SMS scenario, because of the shortage of term occurrence.

In this paper, we first calculate two observation state distributions in spam and ham subsets. The two distributions are combined together to form the initial value of the HMM observation probability distribution matrix, $B={(b_{ij})}_{2\times n}$.

3.5. HMM Learning

The Baum–Welch algorithm [15] is typically used for finding HMM parameters $\lambda = (\pi ,A,B)$. That is, given HMM with initial parameters

$${\lambda }_0=\left({\pi }_0, A_0, B_0\right)$$

(5)

and observation sequence

$$\underset{\_}{X}={\left\{o_t\right\}}_{t=1}^N$$

(6)

to update $\lambda =\left(\pi , A, B\right)$ iteratively and find parameters that maximize the likelihood of observed data, i.e.,

$$\underset{\lambda }{\arg \max }p\left({\left\{o_t\right\}}_{t=1}^N|\lambda \right)$$

(7)

The initial parameters ${\lambda }_0=\left({\pi }_0, A_0, B_0\right)$ are initialized as:

${\pi }_0=\left[0.5, 0.5\right]$ indicates that the state can start from ham or spam with the same probability.

$A_0=\left[\begin{array}{cc}0.5& 0.5\\ 0.5& 0.5\end{array}\right]$ means each state transmission has the same probability.

$B_0={(b_{ij})}_{2\times n}$ infers the initial observation probability distribution calculated in Section 3.4.

The Baum–Welch algorithm starts with initial parameters and then repeatedly takes two steps: Expectation step (E-step) and maximization step (M-step) until convergence (i.e., the difference of log-likelihood is less than small number d), as shown in Figure 4.

3.6. SMS Property Prediction

Given the observation sequence and the trained hidden Markov model to find the optimal hidden state sequence, this is a typical decoding problem in HMM. The Viterbi algorithm [15] is applied to find the most likely hidden state sequence based on the input of each word sequence of the testing SMS. In formalization, we are given the testing observation sequence ${\left\{o_t\right\}}_{t=1}^N$ and trained HMM with parameters $\lambda =(\pi , A, B)$ to find the most likely state sequence. That is,

$$\underset{{\left\{q_t\right\}}_{t=1}^N}{{\displaystyle \arg \max }}\hspace{0.17em}p\left({\left\{q_t\right\}}_{t=1}^N|{\left\{o_t\right\}}_{t=1}^N\right)$$

(8)

Via the Viterbi decoding algorithm, for each word sequence of the testing SMS, the optimal hidden state sequence is produced. The state sequence is the combination of ham and spam. The prediction of the SMS property is based on the majority role, i.e., an SMS will be labeled as ham if the optimal hidden state sequence has more hams than spams. Otherwise, the SMS will be labeled as spam.

3.7. The Workflow of the Discrete HMM for SMS Spam Detection

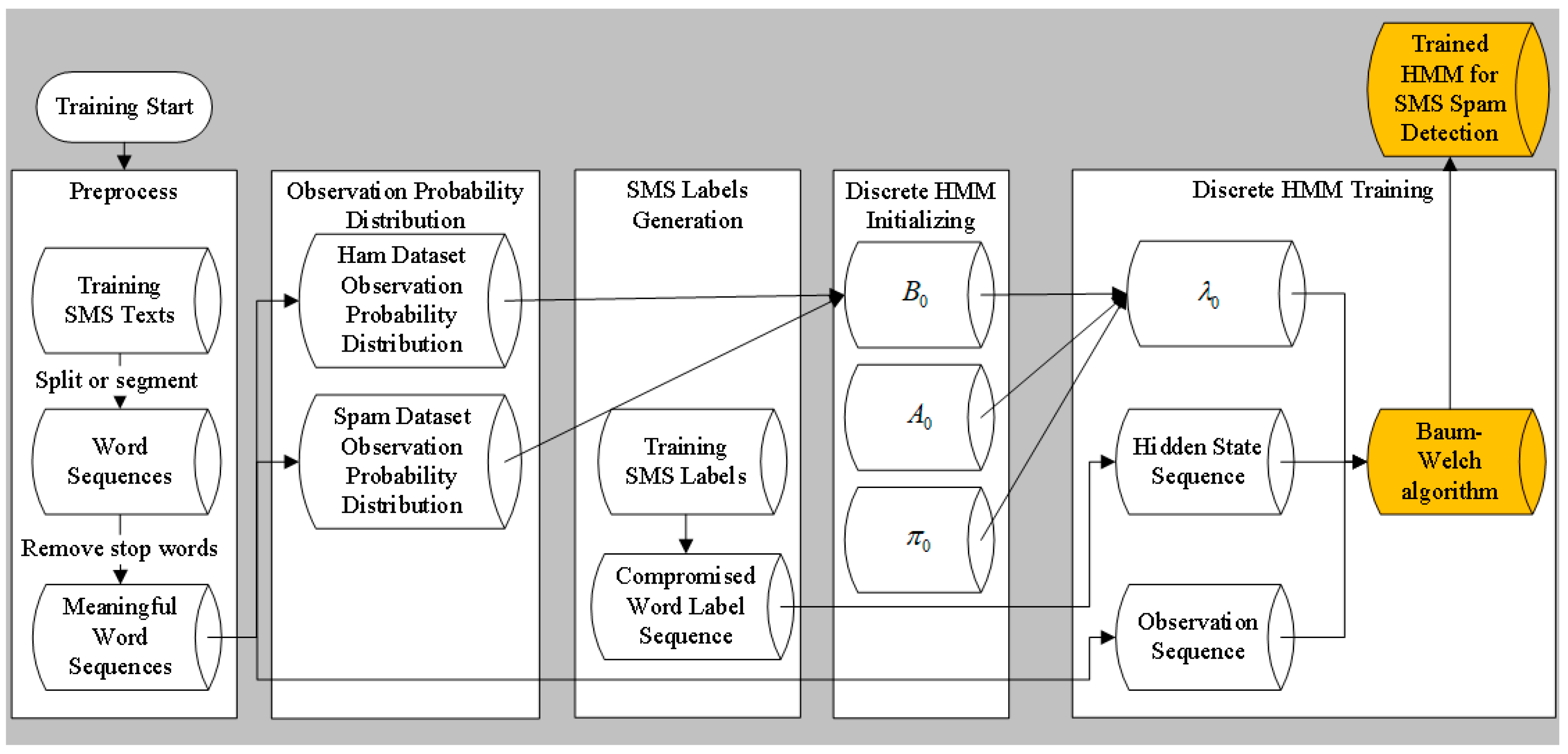
3.7.1. Data Preparation and HMM Learning

Step 1: Training an SMS dataset by first splitting or segmenting it into word sequences to keep their original order. Then, stop words are removed from the sequence and rest meaningful words form the observation sequence.

Step 2: Observation state probability distributions in ham and spam datasets are statistically analyzed and obtained.

Step 3: The compromised word label sequences are generated based on the labeled training SMS messages.

Step 4: The discrete HMM model is initialized as ${\lambda }_0=\left({\pi }_0, A_0, B_0\right)$. The initial parameters are given in Section 3.5.

Step 5: The hidden state sequence and the observation sequence feed the discrete HMM. The discrete HMM is optimized by the Baum–Welch algorithm until convergence.

The training process workflow is shown in Figure 5.

3.7.2. SMS Classification

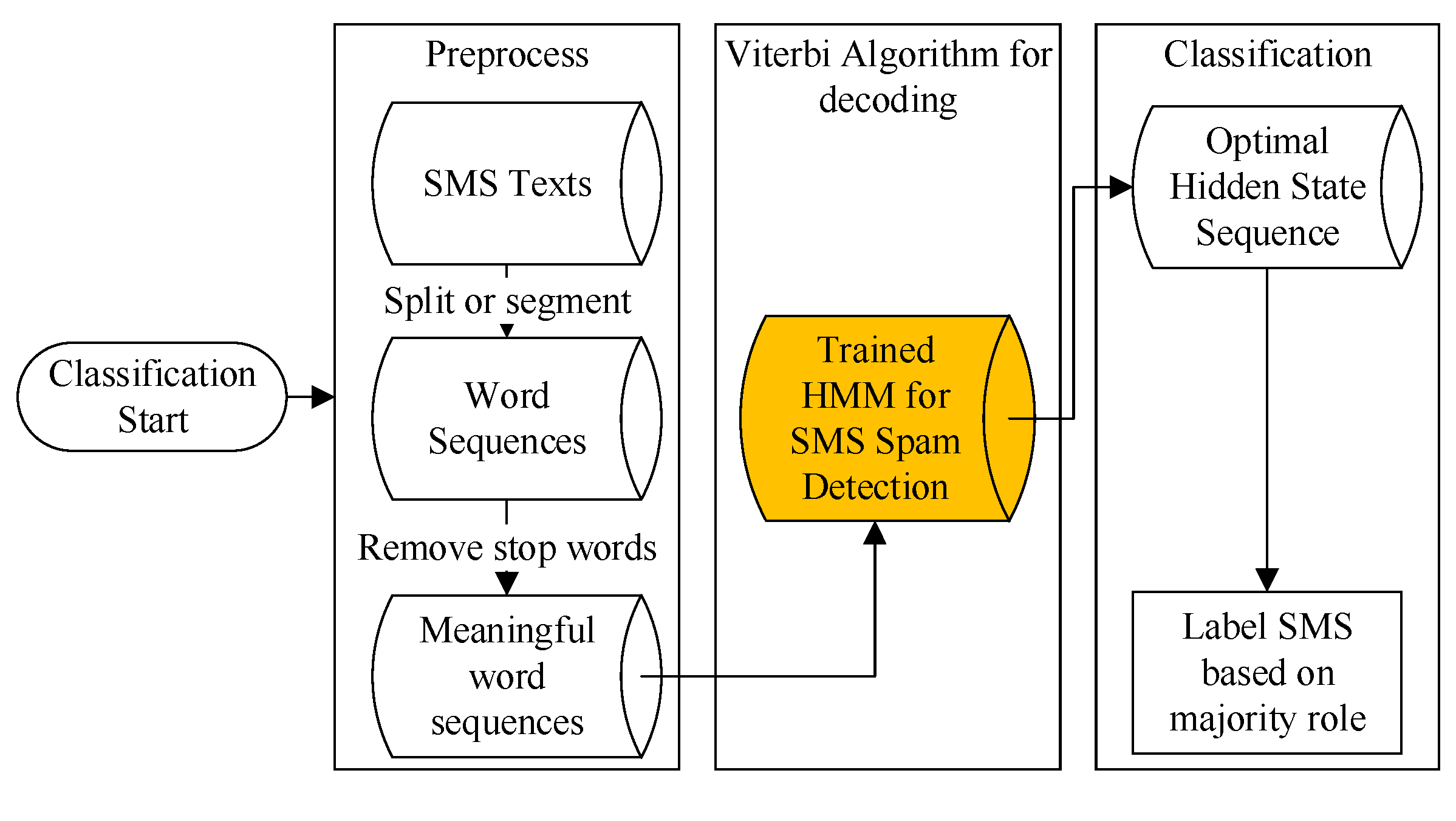
Given the trained HMM and observation sequence, the classification process involved finding out the optimal hidden state sequence and making a prediction of the SMS property based on the majority role. The SMS classification workflow is shown in Figure 6.

Step 1: Like the preprocess in the training workflow, the SMS dataset for classification is also first split or segmented into word sequences to keep their original word order. Then, stop words are removed from the sequence and the observation sequence is formed.

Step 2: Use the Viterbi decoding algorithm to find the optimal hidden state sequence for each SMS.

Step 3: Predict the SMS property based on the majority role.

4. Experiment Results and Discussion

4.1. Dataset and Analysis

This research uses the widely adopted UCI repository dataset for performance evaluations. This unbalanced dataset contains a total of 5574 English SMS messages, in which 747 SMS messages are spam and 4827 are ham, as shown in

Table 1. UCI dataset statistics.

	Number of SMS	Percentage of SMS
Spam	747	13.4%
Ham	4827	86.6%
Total	5574	100%

. These messages were collected from Grumbletext—a UK public forum (www.grumbletext.co.uk), the SMS corpus from the National University of Singapore, and Caroline Tagg’s Ph.D. thesis [58].

The experimental code is developed with Python 3.7 and Python packages including pyhanlp, pomegranate, and collections. The code runs on a MacBook with an Intel Core i7-7820 CPU and 16 GB of memory.

We first split the SMS, extract words, and remove the stop words. This resulted in 9955 meaningful words being extracted in total to form the set of observation states $W$. Then, we calculate the term frequency of each word in each SMS. The summary of the statistical results is shown in

Table 2. Term frequency in spam and ham SMS set.

Term Frequency	Number of Words with the Same Term Frequency
1	9272
2	580
3	77
4	15
5	5
6	3
7	1
8–9	0
10	1
11–13	0
14	1

. We find that:

• 9272 words appear only once in a single SMS and accounts for 93.13%.
• The words that appear three times and above only account for 1.03% in total.

Apparently, most of the words only occur once in a single SMS. Therefore, the feature extraction algorithms, like TF.IDF, does not work well for SMS spam detection.

4.2. Evaluation Metrics

The well-known and persuasive evaluation metrics for classification are precision (P), recall (R), F-measure (F1), and accuracy (A) [59]. Their parameters for metrics calculation are shown in

Table 3. Metrics parameters.

Actual	Predicted
	Negative	Positive
Negative	true negative (TN)	false negative (FN)
Positive	false positive (FP)	true positive (TP)

. Among these metrics, accuracy is the most important item [28].

Precision (P) is the fraction of relevant instances among all retrieved instances.

$$\mathrm{Precision} \left(\mathrm{P}\right)=\frac{TP}{TP+FP}$$

(9)

Recall (R), called Sensitivity, is the fraction of the total amount of relevant instances that are actually retrieved.

$$\mathrm{Recall} \left(\mathrm{R}\right)=\frac{TP}{TP+FN}$$

(10)

F-measure (F1) is the harmonic mean of the precision and recall. It is a balance between precision and recall.

$$\mathrm{F}-\mathrm{Measure} \left(\mathrm{F}1\right)= 2\times \frac{P\times R}{P+R}$$

(11)

Accuracy (A) is the fraction of spam SMS messages that are correctly predicted among all SMS.

$$\mathrm{Accuracy} \left(\mathrm{A}\right)=\frac{TN+TP}{TN+TP+FN+FP}$$

(12)

Area under the curve (AUC) is also a well-known criterion for classification. It is the average of the true positive rate (TPR) and false positive rate (FPR). The greater the AUC value, the more accurate the model.

$$\mathrm{AUC}=\left(\left(\frac{TP}{TP+FN}\right)+\left(\frac{TN}{TN+FP}\right)\right)/2$$

(13)

4.3. Result of the Discrete HMM on the UCI Repository Dataset

To evaluate the performance of the proposed HMM method, we split the UCI repository dataset into two datasets. One is the training dataset containing 66% (about 2/3) spam and 66% ham SMS, and the other one is the testing dataset containing the rest 34% SMS, as shown in

Table 4. Training and testing dataset statistics.

	Training Dataset	Testing Dataset	Total Number of SMS
Spam	493	254	747
Ham	3186	1641	4827
Percentage	66%	34%	100%

.

The reason we divide the dataset in this way is that we want to compare the performance of the proposed HMM method with the best performance achieved by the CNN method in [11]. Roy et al. [11] used the same UCI dataset and divided the database as 2/3 for training and 1/3 for testing in their experiment.

Following the procedures described in Section 3.7, the confusion matrix is shown in

Table 5. Confusion matrix of the results.

Dataset	Actual	Predicted		Prediction %
The proposed HMM		Spam	Ham	Spam	Ham	AUC
	Spam	222	50	0.892	0.031	0.900
	Ham	27	1559	0.108	0.969

.

The evaluation results are shown in

Table 6. Evaluation results.

Dataset	Class	Accuracy (A)	Precision (P)	Recall (R)	F-Measure (F1)
The proposed HMM	Spam	0.959	0.892	0.816	0.852
	Ham		0.969	0.983	0.976

.

To illustrate the performance of the proposed HMM method, we compare the results with those obtained by other machine learning models, including naïve Bayes (NB), support vector machine (SVM), non-negative matrix factorization (NMF), latent Dirichlet allocation (LDA), long short-term memory (LSTM), and convolutional neural network (CNN). The result comparison is shown in

Table 7. Summary of the experimental results with different models.

Model	Class	Accuracy (A)	Precision (P)	Recall (R)	F-Measure (F1)
NB [56]	overall	0.842	0.95	0.972	0.87
SVM [56]	overall	0.936	0.97	0.977	0.94
NMF [56]	overall	0.917	0.96	0.976	0.92
LDA [56]	overall	0.904	0.96	0.976	0.92
LSTM [11]	Spam	0.953	0.849	0.777	0.811
	Ham		0.972	0.976	0.973
CNN [11]	Spam	0.979	0.988	0.858	0.922
	Ham		0.982	0.996	0.988
The proposed HMM	Spam	0.959	0.892	0.816	0.852
	Ham		0.969	0.983	0.976

. As we pointed out before, all methods listed in Table 7 are evaluated by the same UCI dataset. Results of NB, SVM, NMF, and LDA methods were presented by Nagwani and Sharaff [56]. The results of LSTM and CNN were presented by Roy et al. [11]. The highest accuracy is achieved by the CNN method. The proposed HMM method has slightly better accuracy than LSTM. It is compatible with the CNN method.

4.4. Result of the Discrete HMM on Other SMS Dataset in Chinese

The HMM presented in this paper can be applied to other languages. In order to evaluate its performance in different languages, we apply the proposed HMM method on a Chinese SMS dataset containing 2000 SMS messages. The dataset is derived from the production environment of our cooperated SMS service company that provides the SMS service in the East China area.

We choose 700 spam SMS and 700 ham SMS from the Chinese SMS dataset as the training set and the rest 300 spam SMS and 300 ham as the testing set. The statistics of the training and testing datasets are shown in

Table 8. Training and testing dataset statistics.

	Training Dataset	Testing Dataset	Total Number of SMS
Spam	700	300	1000
Ham	700	300	1000
Percentage	70%	30%	100%

.

The confusion matrix turned out to be that shown in

Table 9. Confusion matrix of the results.

Dataset	Actual	Predicted		Prediction %
The proposed HMM		Spam	Ham	Spam	Ham	AUC
	Spam	293	7	0.977	0.023	0.985
	Ham	2	298	0.007	0.993

.

The evaluation results of the proposed HMM are shown in

Table 10. Evaluation results.

Dataset	Class	Accuracy (A)	Precision (P)	Recall (R)	F-Measure (F1)
The proposed HMM	Spam	0.985	0.977	0.993	0.985
	Ham		0.993	0.977	0.985

.

4.5. Result Discussions

4.5.1. UCI Repository Dataset Results

We use 2/3 dataset for training and 1/3 dataset for testing, which has the same division ratio of the paper [11]. The model classified spam and ham SMS with an excellent accuracy of 0.959, which is better than those of NB, SVM, NMF, LDA, and LSTM. In addition, the model performs even better in ham classification with precision 0.969, recall 0.983, and F1 0.976. Although the spam performance is a little under expectation with precision 0.892, recall 0.816, and 0.852, it still performs better than that of LSTM.

The performance could be better if the HMM model is trained enough. English words have many different forms. For verbs, they have past tense, present tense, future tense, and third-person singular forms. A similar situation happens in nouns and adjectives. Therefore, compared to the many English words, the total of 9955 words are not sufficient for observation states in the experiment, and words in the training dataset are less likely to reappear in the testing dataset. As a result, the spam classification performance is affected as the model does not know how to label the untrained words.

In addition, LSTM and CNN are very complex models that consume computer resources greatly. The HMM model proposed in this paper is relatively simple, which has fast training and predicting speed. Thus, our model is easy to implement in commercial applications to process other languages.

4.5.2. Chinese SMS Dataset Results and Its Non-Language-Sensitivity

Apparently, based on the experimental results, the proposed HMM works better in classifying Chinese SMS messages. Especially, it performed the best by securing a remarkable accuracy of 98.5% to classify spam and ham SMS. Compared to the experimental results on English SMS messages, the division ratio of training and testing SMS is similar, but the results are obviously much better.

The reason lies in English and Chinese languages themselves. In English, many words have different forms. As these synonyms have not merged in this research, the different forms of words are treated as different observation states. On the contrary, Chinese words never change. Compared to English, the words in the Chinese SMS training dataset are more likely to reappear in the testing dataset. Therefore, the HMM introduced in this paper works better in Chinese SMS spam detection.

Furthermore, the LSTM and CNN models presented in the paper [11] were dependent on SMS written in English only. However, the HMM present in this paper may be implemented widely in the future because it is not language-sensitive.

5. Conclusions and Future Work

This paper proposed a discrete hidden Markov model for SMS spam detection, and it is the first research taking advantage of word order information to detect spam SMS. Compared to other traditional and even novel machine learning models, the proposed HMM method scored excellent results among them. In addition, HMM is a relatively simple machine learning model. It can be implemented into the spam filtering industry to meet the huge throughput requirement. In addition, this paper resolved the issue in which the traditional feature extraction algorithm, like TF.IDF, does not work well for SMS spam detection, due to the extremely low term frequency. The proposed HMM is not language-sensitive, which was also validated on Chinese SMS spam detection. The overall performance of the proposed HMM is better on the Chinese dataset than the English dataset.

The proposed HMM still has limitations. The accuracy depends highly on the size of the training set. The bigger the training set, the more likely SMS words will reoccur in the testing dataset and the better the achieved accuracy. In our future research, we will provide an improved HMM model to make it suitable to a small training set scenario. In addition, as there is no training dataset that has a label for each word of the SMS, each word was labeled based on the property of the SMS in this research. This compromised word labeling method also affected the spam classification accuracy. We will tackle this issue by applying artificial neural networks. Furthermore, the other HMM variants will be explored for SMS spam detection.