Abstract
This study studies the problem of on-orbit maintenance task planning for space-robot clusters. Aiming at the problem of low maintenance efficiency of space-robot cluster task-planning, this study proposes a cluster-task-planning method based on energy and path optimization. First, by introducing the penalty-function method, the task planning problem of the space-robot cluster under limited energy is analyzed, and the optimal-path model for task planning with comprehensive optimization of revenue and energy consumption are constructed; then, the maintenance task points are clustered to reduce the scale of the problem, thus reducing the difficulty of solving the problem; finally, a modified differential evolution algorithm is proposed to solve the problem of space-robot cluster task-planning, improve the performance of space-robot cluster task-assignment and path planning. Simulation results show that the proposed optimal-path model of space-robot cluster and the modified differential evolution algorithm can effectively solve the task-planning problem of spatial robot clusters.
1. Introduction
With the continuous consumption of earth’s energy, human vision has turned to space, and large-scale space solar-power stations (SSPS) have entered the vision of various space powers. On–orbit services, such as the assembly and maintenance of large space equipment [1,2] such as SSPS, are hot topics in current research. The mission planning of space robots plays an important role in on–orbit services. In recent years, research on space robot mission planning has made considerable progress [3,4], which has laid a solid foundation for the on-orbit assembly and maintenance of large space agencies.
Due to the limited efficiency of a single space robot, the collaborative operation of a cluster composed of multiple space robots is an effective way to complete large space tasks. Space-robot cluster task allocation and path planning are one of the core problems of multirobot system research [5,6,7]. Whether the task planning is reasonable is directly related to the final performance of the entire multirobot system. As the complexity and scale of the tasks performed increase, the effectiveness and efficiency of the task-planning method becomes increasingly important.
Aiming at the problem of collaborative task planning for robot clusters, many documents have proposed a series of models and algorithms [8,9,10,11,12,13,14], mainly including behavior-based allocation methods, market-mechanism methods, swarm-intelligence methods and idle chain-based methods. Zhen and Xing et al. [15] proposed an intelligent self-organizing algorithm to solve the problem of collaborative search attack tasks of multiple agents. The architecture divides the global optimization problem into several local optimization problems. Each agent can solve its own local optimization problem, and then make the best decision for the multiagent system through the information exchange between the agents. Han and Li et al. [16] proposed a task planning algorithm based on the correlation between robot capabilities and team collaboration, under which an initialized associative array R was used to group the robots so that the robots in the group had better collaboration capabilities when performing tasks. Yao and Qi et al. [17] proposed an iterative strategy with an improved mission planning framework. By improving the onboard computing and communication resource management of agents, based on this strategy, each agent will reevaluate unreasonable planning results. Schwarzrock et al. [18] solved the task planning problem of multirobot systems by using group intelligence technology and proposed three complementary algorithms, forming a new method of increasing the amount of tasks executed. Gerkey and Mataric [19] developed a task-independent and system-independent classification method based on optimization theory, which is used to study task allocation problems. Moreover, its goal is to allocate limited resources in a way that effectively accomplishes certain tasks.
The problem of multirobot task assignment is a challenging research topic in the field of robotics [20,21,22,23,24]. The task assignment problem of the spacer-robot cluster can be transformed into an optimization problem, and then some intelligent-optimization methods can be used to solve the optimization problem. Hussein and Marinplaza et al. [25] proposed a general method to solve the problem of multirobot task assignment (MRTA). This method combines simulated annealing and genetic algorithm and can appropriately use all available resources to optimize the allocation, thereby improving the overall system performance and reducing costs. Zheng and Li [26] proposed an optimized multirobot task-allocation and scheduling method based on fish swarm algorithm. Chen and Zhang et al. [27] proposed a memetic algorithm based on ant colony optimization. At the same time, the problem of the maximum travel distance and total travel distance of multiple robots is optimized.
Due to the strong similarity between the MRTA problem and the multiple traveling salesman problem, some researchers regard the MRTA problem as an example of the multiple traveling salesman problem. The traveling salesman problem is one of the standard combined discrete optimization problems. There are two methods for solving the TSP: Exact method and heuristic method. Khan and Maiti [28] adopted multiple update rules and K-opt operations to improve the artificial bee colony algorithm, they used the characteristics of the exchange sequence to exchange the urban sequence (solution/path) of the problem, and created update rules of different solutions (path) for the algorithm to solve the travel agent problem. Trigui and Cheikhrouhou et al. [29] proposed a centralized solution based on fuzzy logic algebra and combined with two goals: taking the minimum total travel distance of the traveling salesman and the maximum travel distance of any robot as the goal. Mahi et al. [30] combined the characteristics of particle swarm optimization, ant colony algorithm and 3-opt algorithm, and proposed a hybrid algorithm PSO-ACO-3-opt for solving standard TSPs.
The task-planning method of the spacer-robot cluster will directly affect the efficiency of the entire system. Therefore, choosing the optimal robot cluster task-planning method becomes the key to effectively solve the task planning problem of the robot cluster system. The existing methods usually consider the task planning problem of robot clusters as a multiple traveling salesman problem and establish the shortest-path model of robot cluster task-planning. When using the shortest-path model to solve space maintenance tasks, there exist the following problems: (1) no modeling analysis of space-robot cluster task-planning problems under resource constraints; (2) no consideration of the maximum benefit of space maintenance when space resources are limited; (3) no considering the difficulty of solving large-scale planning problems.
Based on the analysis of the current research situation, this study proposes a new space-robot cluster task-planning scheme for the maintenance of SSPS. First, the task planning of the space-robot cluster under limited energy is analyzed, and a task planning model of space-robot clusters is proposed with penalty function added, which is comprehensively optimal for the consideration of income and energy consumption. Then, the task-clustering method is used to cluster the maintenance tasks to reduce the problem size and reduce the problem solving time; finally, a modified differential evolution algorithm including multiple neighborhood operations, roulette, de-crossover, multiple groups and other strategies is proposed to solve the problem of task allocation and path planning of multi-robots, complete the mission planning of the space-robot cluster, and improve the maintenance efficiency.
The rest of the paper is organized as follows: Section 2 introduces the background of basic space maintenance tasks and the theoretical basis of modeling. Section 3 proposes the modeling theory of space-robot cluster task-planning. In Section 4, a modified differential evolution algorithm is proposed, and the algorithm is described in detail. In Section 5, the accuracy and effectiveness of the proposed model and algorithm are verified by experiments, and the results are discussed. Section 6 presents the conclusion.
2. Theory Background
2.1. Space Solar Power Station Model
SSPS [31,32] is based on space solar-power generation technology, which can provide constant and pollution-free energy. The SSPS mainly consists of three parts: solar power generation device, energy conversion and transmission device, ground receiving and conversion device. The space above the atmosphere is not affected by the weather, nor is it absorbed or scattered by the atmosphere. The solar energy received is far more than the ground, and the solar-power station can track the sun at any time on the orbit, and keep it in working condition.
The array of solar cells that convert energy into electricity at a SSPS consists of thousands of solar cells. Solar cells are made of pure silicon element blocks. Due to the long service cycle of the SSPS, it is easy to cause damage to parts under the condition of high radiation and large temperature variation in space. Aiming at the maintenance problem of large SSPS, this paper proposes the task planning scheme of space-robot cluster.
2.2. Basic Differential Evolution Algorithm
The differential evolution algorithm (DE) is an efficient evolutionary optimization technology, first proposed by Storn and Price [33]. DE is a direct-search method based on population. In this section, we will briefly explain the working process of DE.
Step 1: Initialization
DE algorithm has a population composed of individual vectors with dimensions of , where each individual is represented as: , , expressed evolutionary algebra. Set the lower limit of the parameter variable is and the upper limit is .
Among them, represents the generation of uniform random Numbers between .
Step 2: Variation
According to several different mutation strategies commonly used in the literature, the following operations are performed for each target vector :
- DE/rand/1
- DE/rand/2
- DE/best/1
- DE/best/2
- DE/current-to-best/1
In the formula: represents the individual in the population obtained after mutation, the randomly selected sequence and the target vector sequence are different from each other, is the best performing individual in the generation. is the mutation operator, which controls the amplification of the deviation vector.
Step 3: Cross
In order to increase the diversity of interference vectors, crossover operation is introduced, and the test vector is:
Among them, is the random number between , is the crossover factor, which is a constant within the range of ; the larger the value of , the greater the possibility of crossover; is an integer randomly selected within the range of , which can ensure that the experimental individual obtains at least one element from the mutant individual .
Step 4: Select
By calculating the fitness of the experimental vector, and then through the selection mechanism of greedy thought, the original population and the experimental population are compared one-to-one, and the next generation is selected to ensure that the next generation is better than the previous generation.
2.3. Clustering Algorithm
Due to the large scale of space solar-power stations, there are many nodes to be repaired, which greatly increases the difficulty of space-robot cluster to perform maintenance tasks. The current task planning algorithm is not very effective for planning large-scale problems, and as the number of tasks increases, the planning time increases significantly. Therefore, how to reduce the scale of the problem is one of the elements to solve the task planning problem. This study uses clustering algorithm to reduce the scale of the problem and reduce the difficulty of solving the planning problem.
Clustering has been extensively studied for many years, and researchers have proposed many clustering algorithms [34,35,36,37]. For large-scale space problems, space task segmentation can be effectively divided into disjoint subsets, and only allow each space robot to select from subsets of the whole task set. According to the target of space maintenance task, a group of data points is divided into several clusters by cluster analysis, and then the task planning of space-robot cluster is carried out for the maintenance points after clustering, so as to reasonably arrange and organize space robots.
The movement of the space robot is divided into the movement of the space robot base and the movement of the mechanical arm. For space maintenance operations, the movement of the satellite base moves between the clustering centers points, and the space robot only needs to operate the mechanical arm to complete the maintenance task within the clustering scope, without moving the base of the space robot. According to the results after clustering, the task planning of space robots is carried out. This hierarchical planning idea can effectively reduce the planning complexity and shorten the planning time.
If point is taken as the center of the clustering, when the distance between point and point is less than , then point is put into set , as shown in Equation (9), and the rest points are followed in turn.
Among them: represents the clustering radius, and represents the number of layers of clustering, which can be set according to the requirements.
Repeat the above process to obtain other clustering sets. The set of regional maintenance targets clustered by point targets is , and is the total number of clusters.
3. Task Planning Model of Space-Robot Cluster
Energy in space is a scarce resource. For space robots, it is necessary to consider that the task completed is optimal when the energy is constant. In this paper, the optimal-path model of a space-robot cluster under resource constraints is proposed, which can easily solve the task planning model of spatial robot cluster. In this paper, each space robot is regarded as an independent task executor, which has the basic characteristics of an intelligent agent. The space-robot cluster is expressed as , in which represents the total number of space robots. The space maintenance task cluster is expressed as , where represents the total number of spatial clustering task sets; , where represents the total number of tasks in each cluster.
3.1. Constraints
The problem of collaborative task allocation of space-robot clusters aims at designing charging piles for space robots at specific locations in accordance with the principle of sustainable work during the execution of tasks. Therefore, the path of space robot should be a closed path starting from the charging pile position. The space robot needs to satisfy some constraints to complete the maintenance task: reserve energy, number of space robots, closed path and so on.
Defining variables
The energy consumed by the robot performing the task can be expressed as
where in:
where represents the number of cluster nodes on the space robot path, represents the energy consumption per unit distance of the robot, represents the path length of the space robot from the node to the node on the path, represents the distance between node and node , represents the starting position of the robot, is the energy consumption of the robot repairing a single maintenance node, represents the number of maintenance nodes in the cluster node on the path of the space robot. Constraint (12) ensures that each maintenance point has at most one space robot for maintenance; constraint (13) ensures that each node in the maintenance path has only one starting point; constraint (14) ensures that the node in each maintenance path has only one end point. In general, these constraints can ensure that each maintenance point is assigned to at most one space robot, and the space robot passes all the assigned nodes and walks a closed loop.
In order to ensure that the robot can safely return to the starting point, the energy of the space robot is greater than that of the charging pile at the last maintenance point. Each robot should return to the charging pile position before the safe energy of the battery is exhausted, namely:
In which is the total energy of the robot, is the safety factor.
3.2. Objective Function
The task planning of space-robot cluster mainly considers the benefits and costs of completing the tasks of each node with limited energy. For simplicity, we only consider the moving distance of space robots and the cost of repairing solar panels. Assuming that the damage degree of solar panel is divided into three levels, with damage level I for 10–40%, II for 40–70% and III for 70–100% and the maintenance benefit increases with the increase of damage degree.
The goal of space-robot cluster task-planning is to maximize the overall benefit
subject to
where and respectively represent the weight coefficients of maintenance revenue and maintenance cost, is the maintenance revenue in the cluster node of the robot, is the damage level and is the profit coefficient.
In this model, the objective function (16) aims to maximize the value of the profit and the maximum revenue and the minimum energy consumption of completing the task must be considered. Moreover, the energy consumption includes the maintenance path consumption and the maintenance node consumption; constraint (18) represents the energy limit of each space robot.
According to the research on constraint-processing methods, constraint-processing methods are mainly divided into three categories: penalty-function methods, feasible-rule methods and multi-objective methods. The penalty-function method is to add a penalty function to the objective function. Because of its simple principle and easy implementation, it is one of the most widely used constraint-processing methods. In this paper, by analyzing the task planning model of space robot, the concept of penalty function is introduced to transform the constraint problem into an unconstrained problem.
By introducing the penalty function, the objective function is
In which
In which: , respectively represent the maintenance revenue and the maintenance cost, represents the penalty coefficient.
4. Modified Differential Evolution Algorithm
Since the emergence of differential evolution algorithm, scholars have done much research work and achieved many results [38,39,40,41,42]. DE algorithm is an evolutionary algorithm based on population optimization, which mainly searches by differential variation, crossover and selection operations and can be used to solve global optimization problems. This paper proposes some improvements for the difference algorithm to solve the problem of space-robot cluster collaborative task planning.
4.1. Adaptive Control Parameter Strategy
In the search process of the basic differential evolution algorithm, the mutation operator takes a constant, but in practice, the value of the mutation operator is difficult to determine, if the value of the mutation operator is too large, the search efficiency of the algorithm is reduced, and the accuracy of the global optimal solution is low; if the mutation operator is too small, the diversity of the population is prone to premature convergence. This paper uses a strategy with an adaptive mutation operator.
Among them, is the initial mutation operator, is the maximum evolutionary algebra, is the current evolutionary algebra. In the early stage of the algorithm, the adaptive mutation operator has a large value, which keeps the diversity of individuals. In the later stage of the algorithm, the mutation operator decreases gradually, retains good information and increases the probability of searching the global optimal solution.
4.2. Roulette Selection Strategy
In order to increase the probability of excellent individuals being selected, roulette selection is used to maintain the principle that the higher the fitness is, the higher the probability of being selected. The roulette method completely relies on random numbers for selection each time, which increases the uncertainty of selection. The basic idea of roulette selection is that the probability of each individual being selected is proportional to its fitness, so the probability of each individual being selected can be obtained by calculating the fitness ratio.
Among them, is the probability that individual is selected in the next generation evolution and is the fitness function value corresponding to individual .
Then calculate the cumulative probability of each individual, that is, the sum of the selection probabilities of all individuals.
Moreover, then randomly generate , if , then select individuals .
In this study, the roulette operation is performed on the population after mutation and crossover and the optimal individual generated by the roulette selection is used to participate in the next generation of group evolution, which can improve the convergence efficiency of the algorithm.
4.3. Multi-Neighbor Operation Strategy
In the early stage of the DE algorithm iteration, the individual differences in the population are large, and the mutation operation will make the algorithm have a strong global search ability; by the middle of the iteration, its optimal values tend to be consistent. In order to improve the diversity of DE algorithm individuals and avoid the premature convergence of DE algorithm and the problem of local extremes, this study proposes a multi-neighbor operation strategy. For individuals in the population, the multiple pairs of positions are exchanged randomly and the value at each position of the exchange is the node on the exchange path.
where, is the neighborhood factor, .
4.4. De-Crossover Strategy
In the planning process, in order to increase the convergence speed, it is necessary to design a de-crossover strategy to reduce cross paths. First of all, it is necessary to judge whether the two line segments and cross, , , , and the two lines are:
Set, when , two line segments and are parallel or coincide; when, the calculation formula of and are:
When and , the paths and have an intersection, otherwise none.
Five nodes are used to illustrate the crossover strategy, as shown in Figure 1. The specific process is as follows, starting from node , walk a closed loop along , where and cross, then replace with and and chain node to node in reverse order, so the loop is formed. The specific operation is shown in the pseudocode Algorithm 1.
| Algorithm 1. The pseudo-code of uncrossed strategy. |
| Input: path (A, B, C, D, E, A) Output: path_uncross (A, D, C, B, E, A) 1. for i←1:length(path) 2. j←i + 1 3. While j<length(path) 4. ab←path(i,i+1) 5. cd←path(j,j+1) 6. flag←Cross_judgement (ab, cd) % Judge whether cross 7. if flag=1 8. path(i+1:j)←path(j:-1:i+1) 9. end if 10. j←j+1 11. end While 12. end for 13. path_uncross←path 14. return path_uncross |
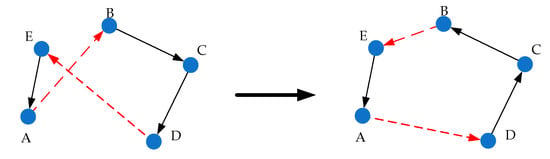
Figure 1.
Schematic diagram of uncrossed strategy.
4.5. Multi-Population Integration Strategy
In order to solve the problem that differential evolution algorithm is prone to local optimal solution and premature maturity, this study proposes a multi-population differential evolution algorithm. The algorithm splits the initial large population into multiple subpopulations, and each subpopulation is assigned to a mutation strategy, so as to realize parallel exploration among subpopulations, thereby enhancing the global exploration ability of the algorithm. With iteration, the reward subpopulations are assigned to the best performing mutation strategies in previous generations in order to obtain more computing resources and gradually enhance the algorithm’s ability to locally explore excellent solutions.
For population 1, population 2 and population 3, we adopted different strategies, our principle is to select well-researched mutation strategies, and each strategy has its own advantages. The three mutation strategies selected in this paper include “DE/Rand-to-pbest/1”, “DE/current-to-RAND/1” and “DE/pbad-to-pbest/1”. Among them, “DE/current-to-pbest/1” uses multiple excellent individual information to make the algorithm not converge prematurely, and the base vector is randomly selected, so its global search ability is relatively strong; “DE/current-to-rand/1” is an arithmetic crossover, which has the characteristics of constant rotation and has advantages in solving the rotation problem; “DE/pbad-to-pbest/1” can make use of good solution information and it can utilize the information of the bad solution (pbad) toward the good solution to balance exploration and exploitation. In this paper, the global and local exploration ability of the algorithm is effectively guaranteed by this mechanism. The pseudocode for the multi-population integration strategy is shown in Algorithm 2.
| Algorithm 2. Pseudo-code of multi-population integration strategy. |
| 1. Set up the each 2. Initialize the , (Change the reward population per generation) 3. Randomly initialize to randomly distribute it in the search space 4. Initialize the and set up the 5. Set up the and 6. while do 7. ; 8. if 9. 10. 11. end if 12. According to is randomly divided into 13. Set up the and 14. for to 15. for to 16. switch 17. case 1: %Perform the first mutation strategy DE/rand-to-pbest/1 in 18. 19. case 2: %Perform the second mutation strategy DE/current-to-rand/1 in 20. 21. case 3: %Perform the third mutation strategy DE/pbad-to-pbest/1 in 22. 23. end switch 24. Perform crossover operations and boundary condition processing 25. if 26. 27. else 28. 29. end if 30. end for 31. 32. end while |
4.6. Algorithm Flow
For task planning of space-robot cluster, the overall planning process is shown in Figure 2.
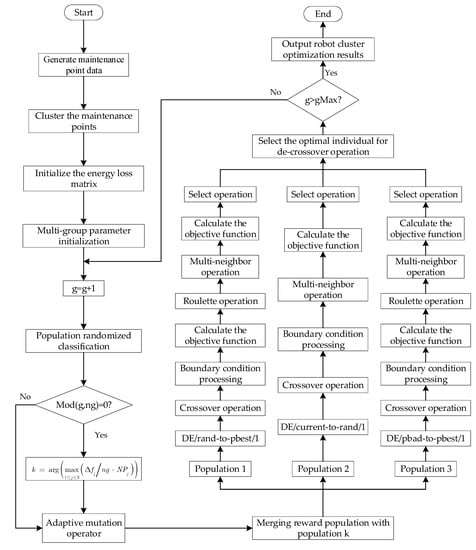
Figure 2.
Flow chart of the algorithm.
- First, generating the coordinates of the maintenance node, the maintenance level and the revenue and determine the number of space robots and the origin coordinates;
- Cluster the maintenance nodes to obtain the coordinates of the cluster center point, the revenue within the cluster and the number of target points within the cluster;
- Generate the energy loss matrix between clusters and the distance energy loss matrix from the space robot to each cluster center;
- Modified differential evolution algorithm.
- (1)
- Initialize the multi-population parameters;
- (2)
- Randomized population;
- (3)
- Adaptive differential evolution operator ;
- (4)
- The reward subpopulation is assigned to the population, set and , where ;
- (5)
- carry out their respective strategy differential evolution operations;
- (6)
- Population combination, judge whether the end condition is satisfied and output the robot cluster optimization result if it is satisfied, otherwise repeat steps (3)–(5).
5. Experimental Results
The effectiveness of the algorithm is verified by computer simulation. The simulation was implemented in Matlab 2016a, and the computer parameters were Intel Core i7-8750 processor, 2.20 GHz CPU and 8 GB RAM memory configuration. The basic parameters of the simulated SSPS are as follows: the size of the maintenance area is 180 m × 60 m, the size of the solar panel is 0.5 m × 0.6 m and the damage rate of the solar panel is between 2%–2.5%.
5.1. Space Maintenance Point Clustering
Due to the different degrees of damage to the solar panels in the space solar-power station, their maintenance priorities are also different. For the degree of each solar panel damage Class I, Class II and Class III, the benefits increase as the degree of damage increases. This paper takes the maintenance of solar array as an example, and performs task clustering on 800 maintenance point targets, so as to test the performance of the algorithm. The target coordinates of maintenance points are input into the clustering algorithm, and the maintenance points are clustered into regional target clusters and single maintenance point clusters by the clustering algorithm. The results of the clustering algorithm are shown in Table 1, (x, y) represents the position coordinates of each cluster center, Number of points in the cluster (NPC) is the number of points that need to be repaired in each cluster area, and the Income within cluster (IC) represents the sum of the income of all maintenance points within the cluster. As shown in Equation (17), this paper sets the profit coefficient to 10. According to Equation (9), we set (half of the robotic arm length), .

Table 1.
Information after clustering of space tasks.
When the maintenance point in the cluster is greater than or equal to 3, it is the regional target clustering—and when it is less than 3—it is the noise point in the clustering algorithm, namely, the single target clustering. As can be seen from Table 1, the clustering results include 92 regional target clustering and 8 single target clustering, and the total income of 800 maintenance points is 15,870. The clustering algorithm is used to reduce 800 maintenance nodes to 100 clustering centers, which effectively reduces the scale of planning problems and reduces the difficulty of solving the planning problems.
5.2. Comparison Experiment of Optimal-Path Model Optimization
5.2.1. Experimental Comparison
In the process of task planning, it is necessary to reasonably consider the relationship between the paths between clusters and the number of points within the clusters—and then to complete the optimization of the robot clusters revenue and energy consumption under a certain energy. In this experiment, under the condition of certain energy, the newly proposed optimal-path model of space-robot cluster and the shortest-path model of space-robot cluster are compared. The optimal path is solved by the modified differential evolution algorithm, and the total number, revenue and completion rate of the maintenance tasks under the condition of certain energy are compared.
In order to simplify problem solving, it is assumed that each space robot’s movement consumption and maintenance failure point consumption a are the same, set . In this experiment, the corresponding parameters are set as: The clustering results of 800 maintenance points are taken as the target node to be planned in this experiment. The charging piles in each space are the starting point of each space robot. The space robots are required to return to the starting position after repairing each target node according to the design path. The initial positions of the five space robots are, respectively (0, 0), (−90, 30), (−90, −30), (90, 30), (90, −30).
In this experiment, the total battery capacity of the space-robot cluster is set to 5000, 6000 and 7000, respectively. The energy of each robot is shown in Table 2. Considering the optimal-path model and the shortest-path model of the robot cluster, the maximum number, the maximum revenue and the task completion rate of the space-robot cluster maintenance solar array are calculated. The maintenance path and completed tasks are shown in Table 3, Table 4 and Table 5, respectively. In this experiment, the safety factor, maintenance revenue weight, maintenance cost weight and penalty function coefficients are set as Consumption is the energy consumption of each space robot. Income is the total income of repair points on the repair path. Number of tasks is the number of tasks completed by the space-robot cluster at a given energy. Income rate is the ratio of the income completed by the space-robot cluster and the total task income.

Table 2.
Space-robot capacity information.

Table 3.
Comparison of task-planning paths for a space-robot cluster with a total energy of 5000.

Table 4.
Comparison of task-planning paths for a space-robot cluster with a total energy of 6000.

Table 5.
Comparison of task-planning paths for a space-robot cluster with a total energy of 7000.
As can be seen from Table 3, the energy consumption of each space robot are basically close to its maximum of available energy, it has made full use of energy, but under the model of optimal path space-robot clustering task earnings significantly higher than that of the shortest-path model, which is about 1.38 times of the shortest-path model, the benefits of maintenance were obvious ascension; it can also be seen that the number of maintenance nodes in the optimal-path model is much higher than that in the shortest-path model, which is about 1.36 times that of the shortest-path model, by comparing the Income rate, it can be seen that the task return rate of the optimal path is also much higher than the shortest-path model. In conclusion, under the same energy constraints, the planning effect of the optimal-path model is better than that of the shortest-path model. Similarly, Table 4 and Table 5 show the optimization results of the optimal path and the shortest path under the other two energies. By comparing Table 3, Table 4 and Table 5, the planning effect of the optimal-path model is better than that of the shortest-path model at different energy levels, which shows the superiority of the optimal-path model proposed in this paper.
In space, resource constraint is one of the main factors that affect the space robot, and they must maximize efficiency with limited resources. It can be clearly seen from Table 3, Table 4 and Table 5 that under certain resource conditions, the number of tasks completed by the optimal path, the total revenue and the task completion rate are obviously better than the shortest path. The total revenue of the optimal path is 42.33% more than the total revenue of the shortest path, and the number of tasks completed by the optimal path is 40.67% more than the average number of tasks completed by the shortest path. Therefore, the optimal-path model has obvious advantages in dealing with the task allocation problem of space-robot clusters with limited resources.
The specific maintenance routes of the space-robot cluster with energies of 5000, 6000 and 7000 are, respectively shown in Figure 3, Figure 4 and Figure 5, the starting point of the optimized path is the location of each space charging pile. Figure 3, Figure 4 and Figure 5 correspond to the paths in Table 3, Table 4 and Table 5, wherein star points represent the starting positions of the space robot, solid line loop in the optimal-path model represents the maintenance path of the space robot, and the path consumption of each robot corresponds to the corresponding table. The solid line and stippling line in the shortest path represent the maintenance path of the space robot, while the dotted line represents the position in the shortest path that the space robot cannot complete under the condition of limited energy. The stippling line is the route that the space robot can return to the charging pile position within a safe energy range. However, in some cases, because the points in the cluster are too scattered, the different results of the cluster will have a certain impact on the number of completed tasks. This experiment proves the feasibility of the optimal path.
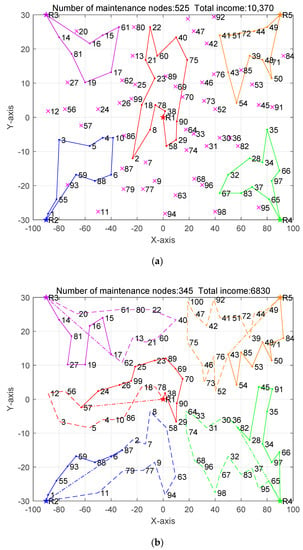
Figure 3.
Comparison of maintenance routes when the space-robot cluster energy is 5000. (a) Optimal-path model; (b) shortest-path model.
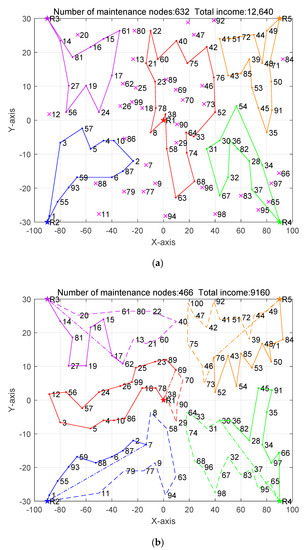
Figure 4.
Comparison of maintenance routes when the space-robot cluster energy is 6000. (a) Optimal-path model; (b) shortest-path model.
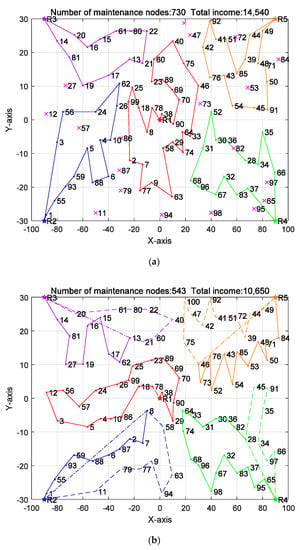
Figure 5.
Comparison of maintenance routes when the space-robot cluster energy is 7000. (a) Optimal-path model; (b) shortest-path model.
5.2.2. Parameter Analysis
Since the modified differential evolution algorithm is very sensitive to parameters, different parameters will lead to different programming results for the same calculation. Taking the space-robot cluster at 6000 energy as an example, the optimization parameters are analyzed. The population number is selected according to experience, the commonly used range of . In this paper, an adaptive mutation operator F is adopted, whose value can be adjusted adaptively. The crossover operator selects an appropriate value according to experience. In the modified differential evolution algorithm, the proportion of subpopulations (as ) and have a great influence on the final optimization results. In order to obtain the optimal solution, this paper conducts a separate analysis on the influence of these two parameters, as shown in Table 6.

Table 6.
The influence of and on the modified differential evolution algorithm.
We obtained by comparing multiple groups of experiments that when , , the effect of this experiment is the best. Different parameters may need to be set for different space maintenance problems. This paper provides a feasible parameter selection scheme.
5.3. Comparison Experiment of Modified Differential Evolution Algorithm
In order to verify the superiority of the algorithm in this experiment, taking the total energy of the space-robot cluster is 6000 as an example, the basic differential evolution algorithm (DE), the adaptive differential evolution algorithm (JDE), the multi-population integrated differential evolution algorithm (MPEDE) and the modified differential evolution algorithm (modified DE) are used, respectively to solve the optimal path of the maintenance task of the large SSPS. The test results are shown in Table 7.

Table 7.
Comparison of different types of algorithms.
Some conclusions can be drawn by comparing the different types of algorithms in Table 7. The modified differential evolution algorithm is more effective than DE, JDE and MPEDE in the objective function value, the maximum profit and the number of maintenance points of the space-robot cluster. In terms of the total maintenance revenue of space-robot clusters, the modified differential evolution algorithm is 2.45 times that of DE, 1.32 times that of JDE and 1.28 times that of MPEDE. In the total maintenance points of space-robot cluster, the modified differential evolution algorithm is 2.52 times of DE, 1.35 times of JDE and 1.26 times of MPEDE. This shows that the modified difference algorithm proposed in this paper is better than the existing methods in solving the optimal-path model of spatial robot clusters.
Figure 6 shows the comparison of the maximum income of the space-robot cluster, Figure 7 shows the comparison of the maximum maintenance points. Figure 8 shows the comparison of the objective function value. At the beginning, due to the existence of the penalty coefficient, the objective function is negative, and it will be very large, which makes the graph display not obvious. In order to make it clear, we have truncated the vertical coordinate of Figure 8.
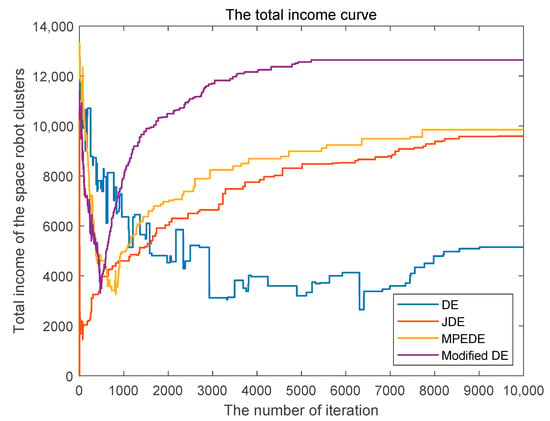
Figure 6.
Total income when the space-robot cluster energy is 6000.
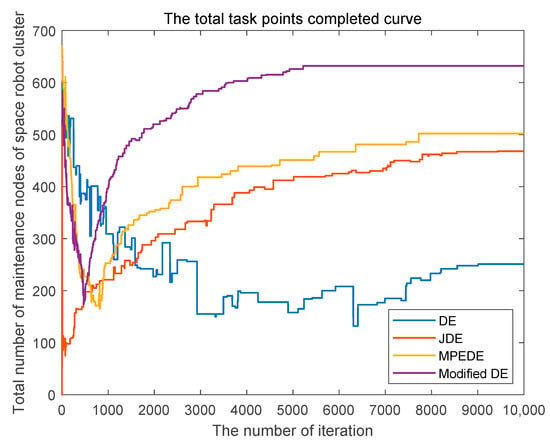
Figure 7.
Total task points completed when the space-robot cluster energy is 6000.
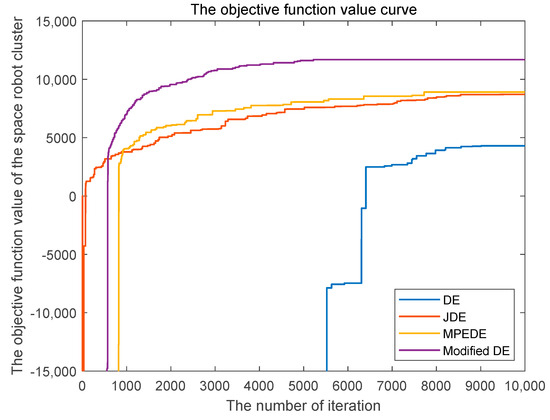
Figure 8.
Value of the objective function when the space-robot cluster energy is 6000.
It can be seen from Figure 6, Figure 7 and Figure 8 that the number of iterations of the modified differential evolution algorithm is significantly less than that of DE, JDE and MPEDE in solving the optimal solution of the maximum benefit, the number of maintenance points and the objective function value of the space-robot cluster. The convergence effect of the modified differential evolution algorithm is better than that of other algorithms.
In this paper, the variation factor of differential evolution algorithm is improved, the diversity of individuals is maintained in the early stage, the mutation operator is reduced in the later stage and the probability of searching the global optimal solution is increased. The combination of roulette and multi-neighborhood operations is used to ensure the optimal value of the population and avoid falling into the local optimal; the convergence of the model is accelerated by the de-crossing strategy; the multi-population strategy-integration method is used to obtain more computational resources in the evolution of better mutation strategies. Therefore, the modified differential evolution algorithm proposed in this paper has the advantages of global optimality and fast convergence speed, which improves the convergence speed and convergence effect of the algorithm, and the overall performance is better than other existing algorithms.
For the optimal path problem of space robots for maintenance tasks of large space solar-power stations, in order to better prove the performance of the modified DE proposed in this paper, we take the space-robot cluster with a total energy of 6000 as an example, the genetic algorithm (GA), ant colony optimization algorithm (ACO), artificial bee colony algorithm (ABC) and modified DE are, respectively used to solve the optimal path of maintenance task of large space solar-power station. The test results are shown in Table 8.

Table 8.
Comparison of other algorithms.
By comparing the different optimization algorithms in Table 8, we can see that in the space maintenance task, the modified differential evolution algorithm is better than the GA, ACO and ABC in solving the optimal solution of the maximum benefit, the number of maintenance points and the objective function value of the space-robot cluster. Therefore, this paper chooses to use the modified DE for the optimal path planning of the space robot, so that it can better complete the space maintenance task.
6. Conclusions
The on-orbit maintenance task planning of large SSPS is an important research hotspot and the use of space-robot clusters to complete space maintenance operations is a development trend. Energy in space is one of the important factors to be considered. In order to solve this problem, we have modeled and analyzed the space-robot cluster problem. The optimal-path model of the space-robot cluster proposed in this paper improves the task planning effect of the space-robot cluster. The superiority of modeling is verified by comparing with the shortest-path model. Clustering operations on target maintenance nodes can greatly reduce the difficulty and time loss of task planning for space-robot clusters and effectively improve the efficiency of space robot task allocation. Aiming at the defects of slow convergence speed and easy to fall into the local optimum in the later stage of differential evolution algorithm, this paper improves the convergence speed and convergence effect of the algorithm through a series of improvement measures and proves that the modified DE can solve the optimal path problem of space-robot cluster more effectively through simulation experiments. This article provides an efficient algorithm to solve the problem of space-robot cluster task-planning for space maintenance operations; it will also have very good benefits for the maintenance problem of larger space agencies in the future.
Future research can integrate other realistic constraints in the space robot task model, such as considering the space robot’s time window, battery life, network communication, attitude orbit control, etc. On the other hand, in the process of task planning for the space-robot cluster, the space environment and the actual situation of the space robot are considered, dynamic task assignment is performed and the problem of secondary assignment of tasks is considered.
Author Contributions
P.X. and Q.L. provided conceptualization and resources. P.X. did the investigation, methodology and the validation, wrote the software. Q.L. established the computational model, discussed the results and wrote the study. H.J. and F.C. did the formal analysis and reviewed and edited the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, Grant Number 61673010.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Glaser, P.E. Power from the Sun: Its Future. Science 1968, 162, 857–861. [Google Scholar] [CrossRef] [PubMed]
- Oegerle, W.R.; Purves, L.; Budinoff, J.; Moe, R.V.; Carnahan, T.M.; Evans, D.C.; Kim, C.K. Concept for a large scalable space telescope: In-space assembly. Proc. SPIE 2006, 6265, 62652C. [Google Scholar]
- Yoshida, K.; Hashizume, K.; Abiko, S. Zero reaction maneuver: Flight validation with ETS-VII space robot and extension to kinematically redundant arm. In Proceedings of the 2001 ICRA. IEEE International Conference on Robotics and Automation (Cat. No. 01CH37164), Seoul, Korea, 21–26 May 2001; pp. 441–446. [Google Scholar]
- Zemlyakov, S.D.; Rutkovskii, V.Y.; Sukhanov, V.M.O. Some questions of control of the robotized in-orbit assembly of large space structures. Autom. Remote Control 2006, 67, 1215–1227. [Google Scholar] [CrossRef]
- Lee, D. Resource-based task allocation for multi-robot systems. Robot. Auton. Syst. 2018, 103, 151–161. [Google Scholar] [CrossRef]
- Kanakia, A.; Touri, B.; Correll, N. Modeling multi-robot task allocation with limited information as global game. Swarm Intell. 2016, 10, 147–160. [Google Scholar] [CrossRef]
- Yan, Z.; Jouandeau, N.; Cherif, A.A. A Survey and Analysis of Multi-Robot Coordination. Int. J. Adv. Robot. Syst. 2013, 10, 399. [Google Scholar] [CrossRef]
- Badreldin, M.; Hussein, A.; Khamis, A. A comparative study between optimization and market-based approaches to multi-robot task allocation. Adv. Artif. Intell. 2013, 2013, 12. [Google Scholar] [CrossRef]
- Vig, L.; Adams, J.A. Market-Based Multi-robot Coalition Formation. In Proceedings of the Distributed Autonomous Robotic Systems; Springer: Tokyo, Japan, 2006; pp. 227–236. [Google Scholar]
- Yin, P.; Yu, S.; Wang, P.; Wang, Y. Multi-objective task allocation in distributed computing systems by hybrid particle swarm optimization. Appl. Math. Comput. 2007, 184, 407–420. [Google Scholar] [CrossRef]
- Carter, A.E.; Ragsdale, C.T. A new approach to solving the multiple traveling salesperson problem using genetic algorithms. Eur. J. Oper. Res. 2006, 175, 246–257. [Google Scholar] [CrossRef]
- Tan, Y.; Zheng, Z. Research Advance in Swarm Robotics. Def. Technol. 2013, 9, 18–39. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, Q.; Ma, L.; Zhang, Z.; Liu, Y. A hybrid ant colony optimization algorithm for a multi-objective vehicle routing problem with flexible time windows. Inf. Sci. 2019, 490, 166–190. [Google Scholar] [CrossRef]
- Moisiadis, V.; Tsolakis, N.; Katikaridis, D.; Sørensen, C.G.; Bochtis, D. Mobile Robotics in Agricultural Operations: A Narrative Review on Planning Aspects. Appl. Sci. 2020, 10, 3453. [Google Scholar] [CrossRef]
- Zhen, Z.; Xing, D.; Gao, C. Cooperative search-attack mission planning for multi-UAV based on intelligent self-organized algorithm. Aerosp. Sci. Technol. 2018, 76, 402–411. [Google Scholar] [CrossRef]
- Han, Y.; Li, D.; Chen, J.; Yang, X.; Hu, Y.; Zhang, G. A Multi-Robots Task Allocation Algorithm Based on Relevance and Ability with Group Collaboration. Int. J. Intell. Eng. Syst. 2010, 3, 33–41. [Google Scholar] [CrossRef]
- Yao, W.; Qi, N.; Wan, N.; Liu, Y. An iterative strategy for task assignment and path planning of distributed multiple unmanned aerial vehicles. Aerosp. Sci. Technol. 2019, 86, 455–464. [Google Scholar] [CrossRef]
- Schwarzrock, J.; Zacarias, I.; Bazzan, A.L.C.; Fernandes, R.Q.D.A.; Moreira, L.H.; De Freitas, E.P. Solving task allocation problem in multi Unmanned Aerial Vehicles systems using Swarm intelligence. Eng. Appl. Artif. Intell. 2018, 72, 10–20. [Google Scholar] [CrossRef]
- Gerkey, B.P.; Mataric, M.J. A Formal Analysis and Taxonomy of Task Allocation in Multi-Robot Systems. Int. J. Robot. Res. 2004, 23, 939–954. [Google Scholar] [CrossRef]
- Edison, E.; Shima, T. Integrated task assignment and path optimization for cooperating uninhabited aerial vehicles using genetic algorithms. Comput. Oper. Res. 2011, 38, 340–356. [Google Scholar] [CrossRef]
- Lee, M.; Chen, B.; Lu, W. Failure-Robot Path Complementation for Robot Swarm Mission Planning. Appl. Sci. 2019, 9, 3756. [Google Scholar] [CrossRef]
- Ye, F.; Chen, J.; Tian, Y.; Jiang, T. Cooperative Multiple Task Assignment of Heterogeneous UAVs Using a Modified Genetic Algorithm with Multi-type-gene Chromosome Encoding Strategy. J. Intell. Robot. Syst. 2020, 1–13. [Google Scholar] [CrossRef]
- Deng, Q.; Yu, J.; Wang, N. Cooperative task assignment of multiple heterogeneous unmanned aerial vehicles using a modified genetic algorithm with multi-type genes. Chin. J. Aeronaut. 2013, 26, 1238–1250. [Google Scholar] [CrossRef]
- Kitjacharoenchai, P.; Ventresca, M.; Moshref-Javadi, M.; Lee, S.; Tanchoco, J.M.A.; Brunese, P.A. Multiple traveling salesman problem with drones: Mathematical model and heuristic approach. Comput. Ind. Eng. 2019, 129, 14–30. [Google Scholar] [CrossRef]
- Hussein, A.; Marinplaza, P.; Garcia, F.; Armingol, J.M. Hybrid Optimization-Based Approach for Multiple Intelligent Vehicles Requests Allocation. J. Adv. Transp. 2018, 2018, 2493401. [Google Scholar] [CrossRef]
- Zheng, T.; Li, J. Multi-robot task allocation and scheduling based on fish swarm algorithm. In Proceedings of the 2010 8th World Congress on Intelligent Control and Automation, Jinan, China, 7–9 July 2010; pp. 6681–6685. [Google Scholar]
- Chen, X.; Zhang, P.; Du, G.; Li, F. Ant Colony Optimization Based Memetic Algorithm to Solve Bi-Objective Multiple Traveling Salesmen Problem for Multi-Robot Systems. IEEE Access 2018, 6, 21745–21757. [Google Scholar] [CrossRef]
- Khan, I.; Maiti, M.K. A swap sequence based Artificial Bee Colony algorithm for Traveling Salesman Problem. Swarm Evol. Comput. 2019, 44, 428–438. [Google Scholar] [CrossRef]
- Trigui, S.; Cheikhrouhou, O.; Koubaa, A.; Baroudi, U.; Youssef, H. FL-MTSP: A fuzzy logic approach to solve the multi-objective multiple traveling salesman problem for multi-robot systems. Soft Comput. 2017, 21, 7351–7362. [Google Scholar] [CrossRef]
- Mahi, M.; Baykan, O.K.; Kodaz, H. A new hybrid method based on Particle Swarm Optimization, Ant Colony Optimization and 3-Opt algorithms for Traveling Salesman Problem. Appl. Soft Comput. 2015, 30, 484–490. [Google Scholar] [CrossRef]
- Cheng, Z.; Hou, X.; Zhang, X.; Zhou, L.; Guo, J.; Song, C. In-orbit assembly mission for the Space Solar Power Station. Acta Astronaut. 2016, 129, 299–308. [Google Scholar] [CrossRef]
- Li, X.; Duan, B.; Song, L.; Yang, Y.; Zhang, Y.; Wang, D. A new concept of space solar power satellite. Acta Astronaut. 2017, 136, 182–189. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Rodriguez, A.; Laio, A. Clustering by fast search and find of density peaks. Science 2014, 344, 1492–1496. [Google Scholar] [CrossRef]
- Hartigan, J.A.; Wong, M.A. A K-Means Clustering Algorithm. J. R. Stat. Soc. Ser. C Appl. Stat. 1979, 28, 100–108. [Google Scholar]
- Xiao, P.; Ju, H.; Li, Q.; Xu, H.; Lu, C. Task Planning of Space Maintenance Robot Using Modified Clustering Method. IEEE Access 2020, 8, 45618–45626. [Google Scholar] [CrossRef]
- Fraley, C.; Raftery, A.E. Model-Based Clustering, Discriminant Analysis, and Density Estimation. J. Am. Stat. Assoc. 2002, 97, 611–631. [Google Scholar] [CrossRef]
- Rahnamayan, S.; Tizhoosh, H.R.; Salama, M.M.A. A novel population initialization method for accelerating evolutionary algorithms. Comput. Math. Appl. 2007, 53, 1605–1614. [Google Scholar] [CrossRef]
- Zhang, J.; Sanderson, A.C. JADE: Adaptive Differential Evolution with Optional External Archive. IEEE Trans. Evol. Comput. 2009, 13, 945–958. [Google Scholar] [CrossRef]
- Brest, J.; Greiner, S.; Boskovic, B.; Mernik, M.; Zumer, V. Self-Adapting Control Parameters in Differential Evolution: A Comparative Study on Numerical Benchmark Problems. IEEE Trans. Evol. Comput. 2006, 10, 646–657. [Google Scholar] [CrossRef]
- Wu, G.; Mallipeddi, R.; Suganthan, P.N.; Wang, R.; Chen, H. Differential evolution with multi-population based ensemble of mutation strategies. Inf. Sci. 2016, 329, 329–345. [Google Scholar] [CrossRef]
- Tong, L.; Dong, M.; Jing, C. An improved multi-population ensemble differential evolution. Neurocomputing 2018, 290, 130–147. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).