Learning Congruent Triangles through Ethnomathematics: The Case of Students with Difficulties in Mathematics
Abstract
1. Introduction
2. Theoretical Background
2.1. Ethnomathematics
2.2. Islamic Geometric Ornamentation
2.3. Congruent Triangles
2.4. Research Aim and Questions
- What characterizes students’ definitions of congruence and congruent triangles?
- What characterizes students’ learning processes when they are taught about congruent triangles based on Islamic ornamentation?
- To what extent does ethnomathematical learning of congruent triangles based on Islamic ornamentation affect students’ knowledge of congruent triangles?
3. Method
3.1. Participants
3.2. Data Sources and Procedure
3.2.1. Video Recording
3.2.2. Questionnaires
3.3. Data Analyses
3.3.1. Video Recordings
3.3.2. Questionnaires
3.4. Ethnomathematics Activities
3.4.1. The First Meeting
- Exhibition and discussion of the different types of Islamic ornamentation, such as animal, plant, and geometric ornamentation.
- Finding geometric shapes in the ornamentation.
- Cutting out different shapes and discussing their congruence.
- Discussing the meaning of congruence.
- Using different transformations as a mathematical process to enable movement from one shape to another in the ornamentation.
- Analyzing the geometrical properties of ornaments, as well as constructing them.
3.4.2. The Second Meeting
- Cutting out triangles and discussing which of them are congruent.
- Examining the congruence between a concrete triangle and the triangles used in ornamentation.
- Cutting out triangles and discussing which of them are congruent.
- Examining the congruence between a concrete triangle and the triangles used in ornamentation.
- Discussing the reasons why triangles are congruent.
- Drawing congruent triangles.
- Presenting the congruent notion and trying to record the properties of congruent triangles.
3.4.3. The Third Meeting
- Inquiry about incongruent triangles in the ornamentation, e.g., Which triangles are equal in one side; equal in one side and one angle; or equal in three angles.
- Inquiry through drawing the ornamentation, measuring its angles, then cutting out its triangles and making comparisons between them.
- Distinguishing congruent triangles in ornamentation based on (S, A, S).
- Writing the proof processes for congruent triangles based on (S, A, S).
3.4.4. The Fourth Meeting
- Inquiry about congruent triangles according to (A, S, A), through drawing triangles in the ornamentation.
- Inquiry about congruent triangles according to (A, S, A), through cutting out and pasting triangles.
- Distinguishing congruent triangles based on (A, S, A) in ornamentation.
- Writing the proof phases of congruent triangles based on (A, S, A).
3.4.5. The Fifth Meeting
- Drawing ornaments that include equal-side triangles.
- Drawing ornaments that include triangles with unequal sides.
- Inquiry about congruent triangles according to (S, S, S) through cutting out and pasting triangles.
- Distinguishing congruent triangles based on (S, S, S) in the ornamentation.
- Writing the proof processes for congruent triangles based on (S, S, S).
3.4.6. The Sixth Meeting
- Completing different processes in a given proof.
- Distinguishing data about triangles from the figure and expressing them as conditions for congruence/incongruence.
- Solving questions based on the three congruence theorems.
4. Findings
4.1. Defining Congruence in General and the Congruence of Triangles in Particular
4.1.1. Defining Congruence in General
| (2) | Marah: | Congruence is that one shape covers another. |
| (3) | Taqwa: | That means that the two shapes are equal. |
| (8) | Abed | These rhombuses [pointing to the rhombuses in the ornamentation] are congruent. |
| (9) | Doa’a | Yes, because they have the same area. |
| (16) | Reem: | Look at the squares [cutting out some squares in the ornamentation]. |
| (19) | Taqwa: | Put the squares here. |
| (21) | Saja: | They are the same, they are congruent [pointing at two squares with a minor difference]. |
| (22) | Nagam: | Why? These squares are not congruent. |
| (23) | Saja: | Because they do not cover each other exactly. |
| (24) | Taqwa: | Congruence is when the two shapes cover each other exactly. |
| (26) | Saja: | The two shapes have the same length of sides. |
| (29) | Reem: | When we compare between the two rhombuses, do we have to do direct coverage? (Pointing at two opposite rhombuses.) |
| (36) | Nagam: | You can translate… |
| (37) | Saja: | Ahh, we can rotate this rhombus to get this rhombus. |
4.1.2. Defining the Congruence of Triangles
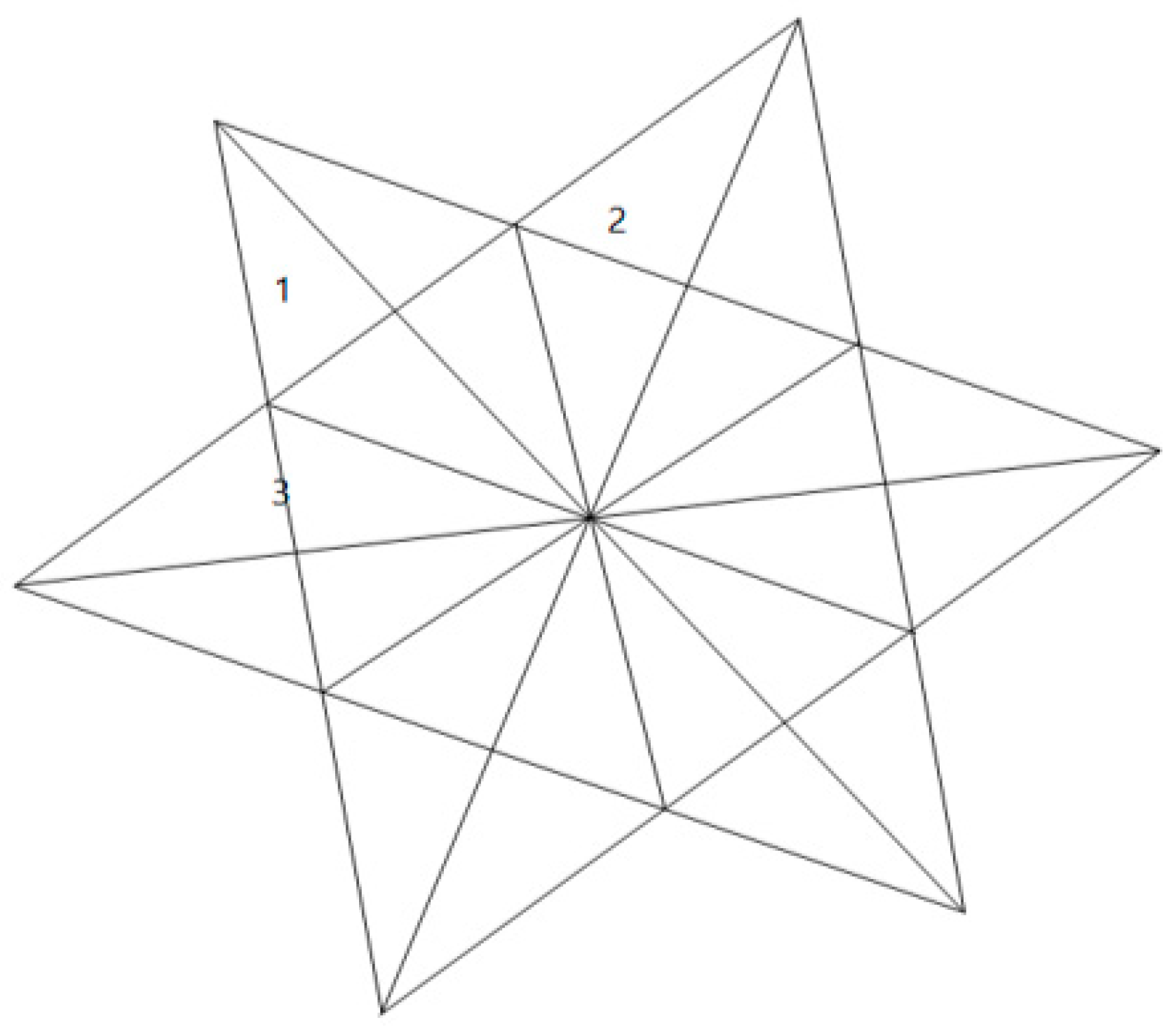
| (54) | Nagam: | Triangles 1 and 2 (see Figure 1) are congruent, because they cover each other completely. |
| (After cutting out the numbered triangles in the ornamentation.) | ||
| (68) | Saja: | There are other congruent triangles in the ornamentation. |
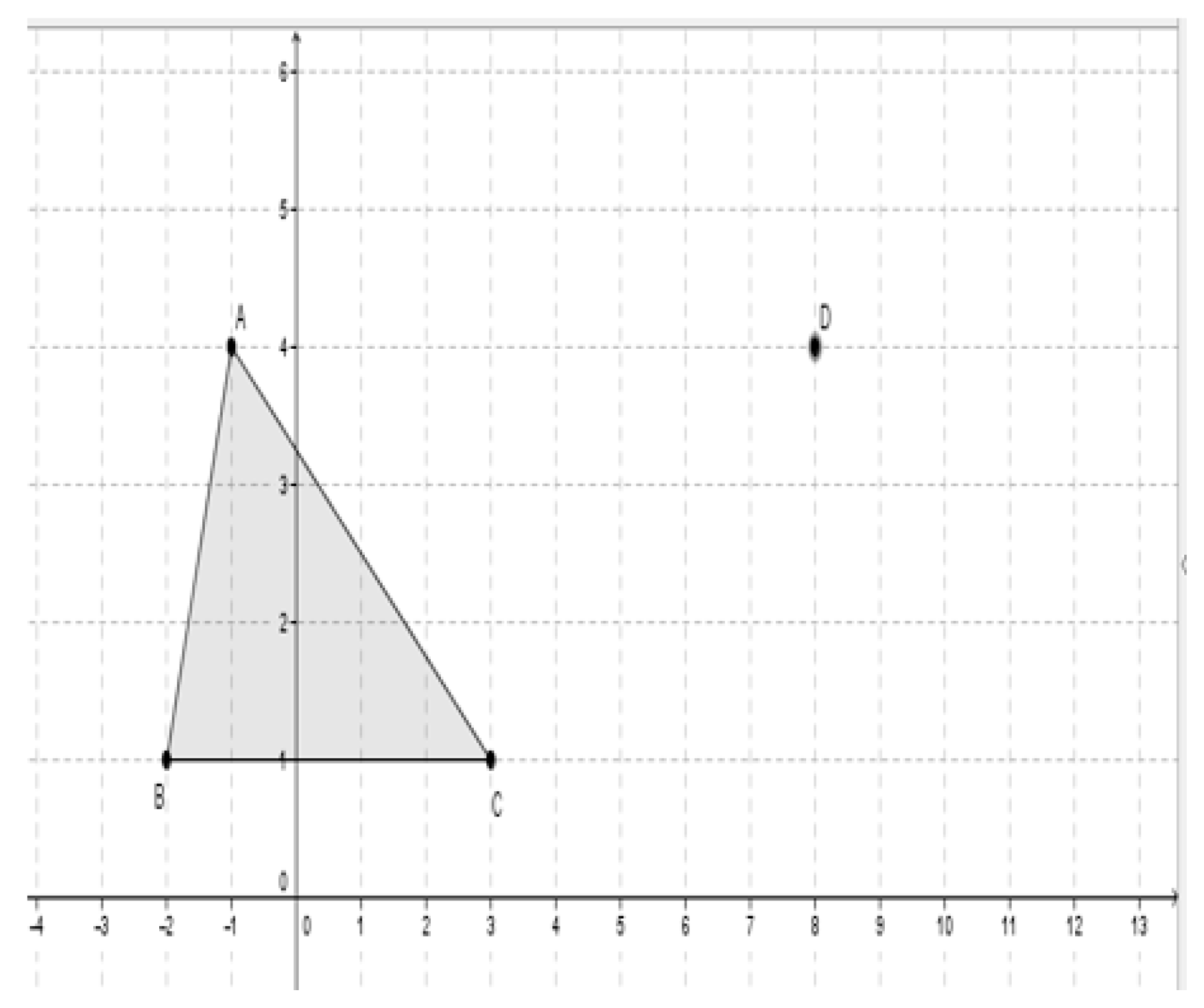
| (74) | Marah: | The vertex of the triangle must be D. (Drawing a triangle that is congruent to triangle ABC; see Figure 2) |
| (82) | Nagam: | I drew a triangle in the opposite position to the ABC triangle. |
| (83) | Teacher: | You can check if they are congruent. |
| (84) | Nagam: | I can do reflection. |
| (91) | Saja: | All these triangles are congruent. |
| (94) | Saja: | All these triangles are equal in their sides and angles. |
4.2. Investigating the Sufficient Conditions for Congruent Triangles by Using Islamic Ornamentation
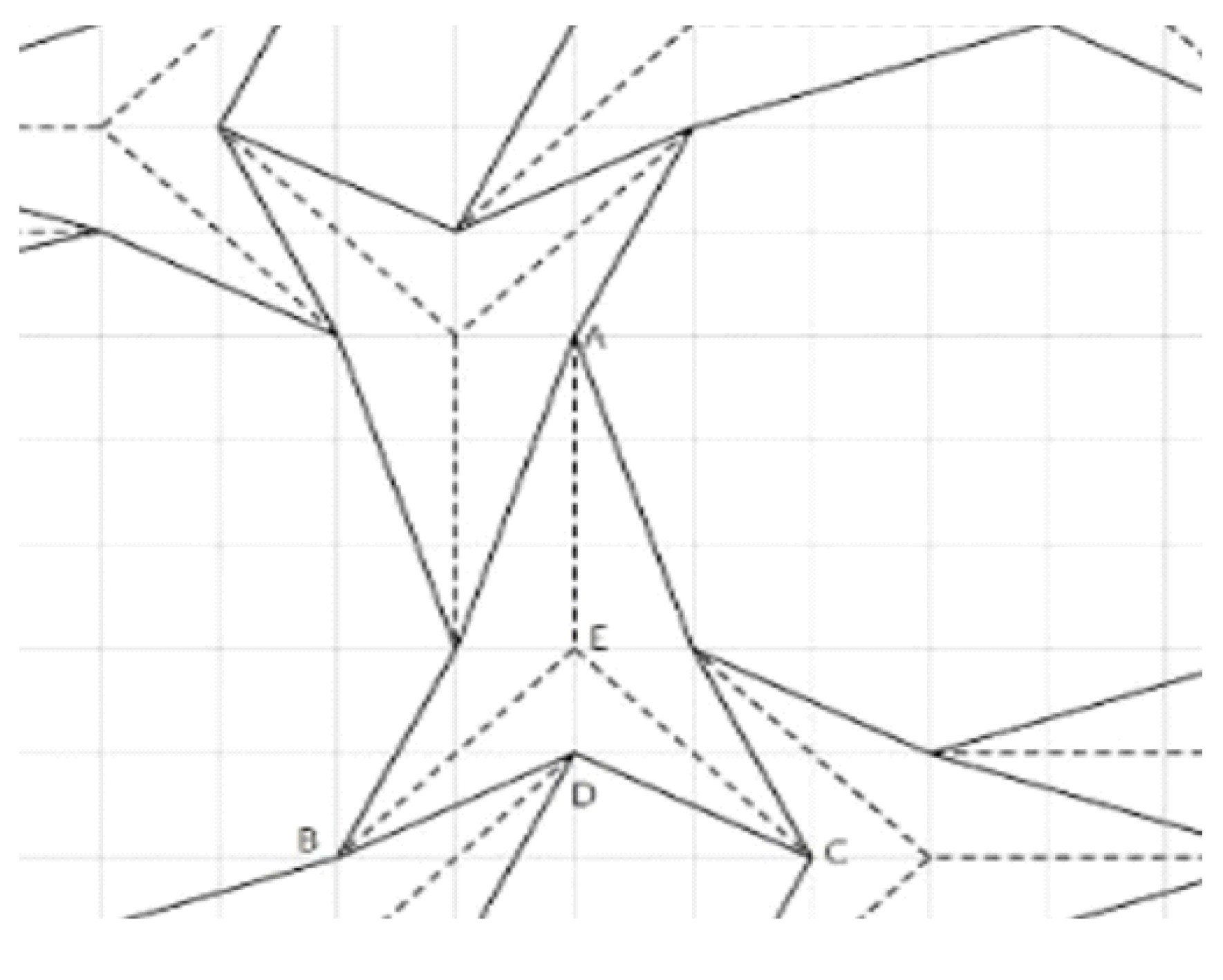
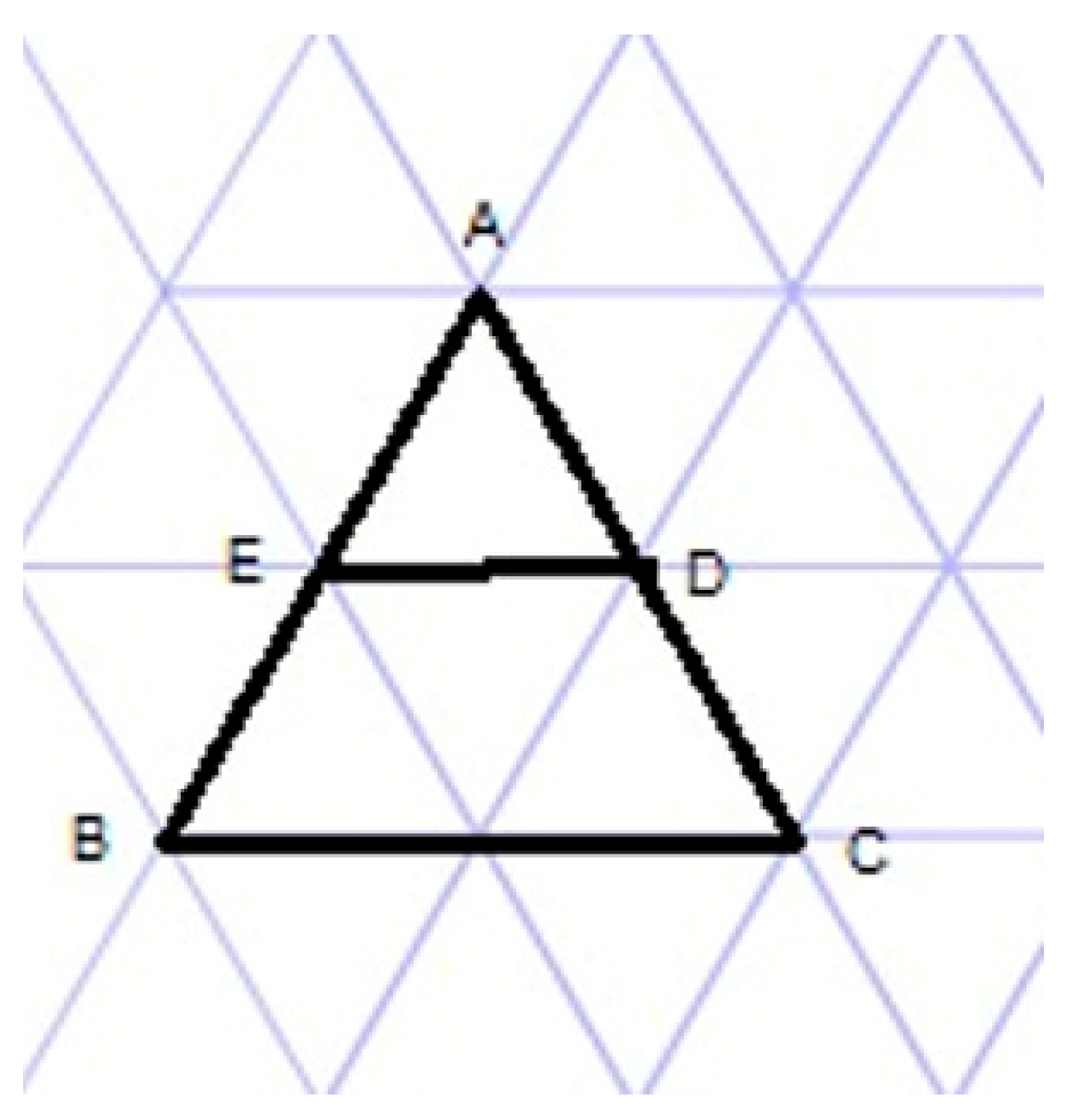
| (102) | Reem: | There are corresponding sides that are equal in triangles BDE and BDA (see Figure 3). |
| (105) | Nagam: | ED. |
| (107) | Saja: | No, it is BD. |
| (111) | Reem: | In this ornamentation the triangles are not congruent; one is a big ornament, and one is a small ornament. |
| (116) | Reem: | Two equal corresponding sides in two triangles is not a sufficient condition for congruence. |
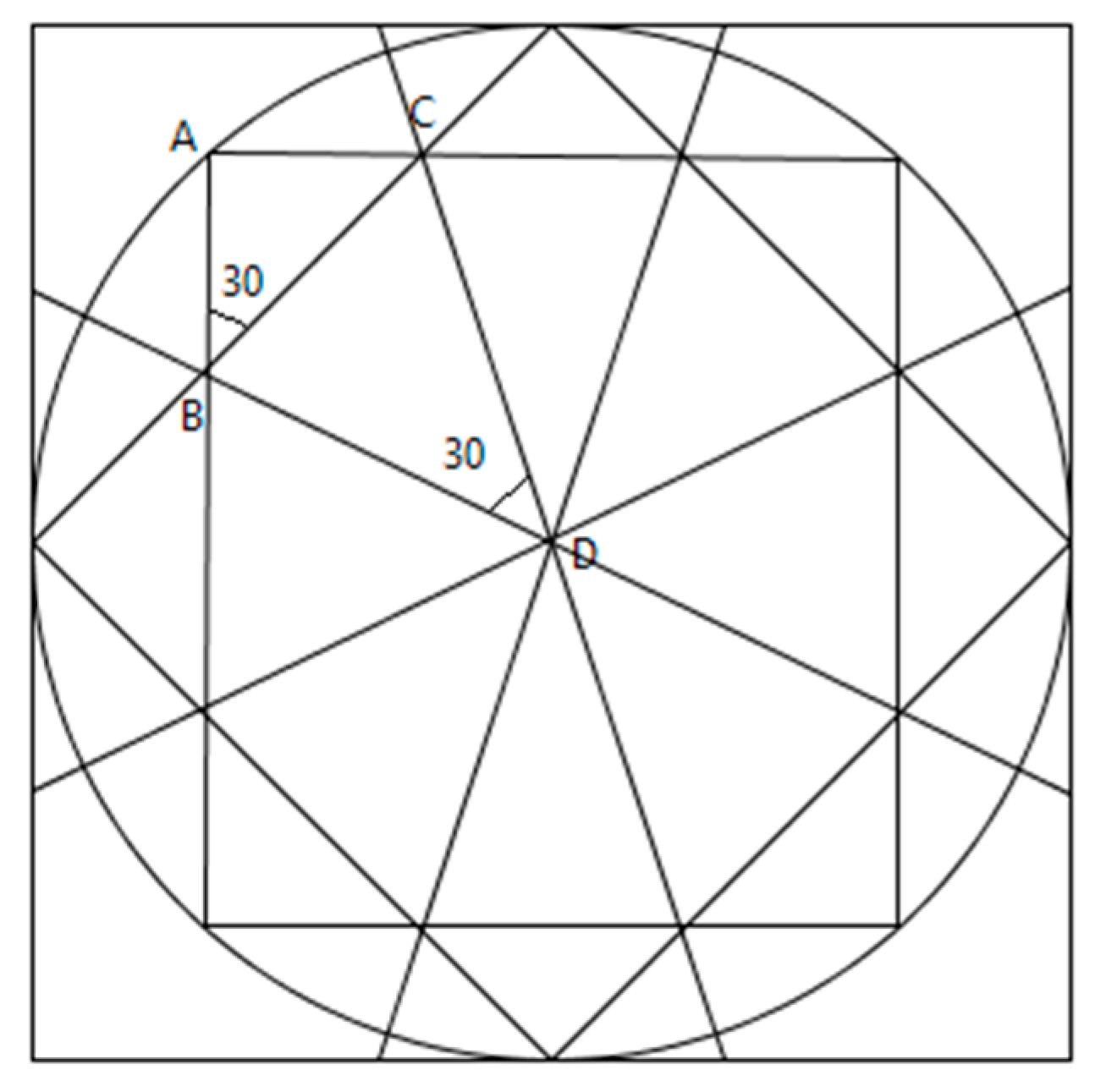
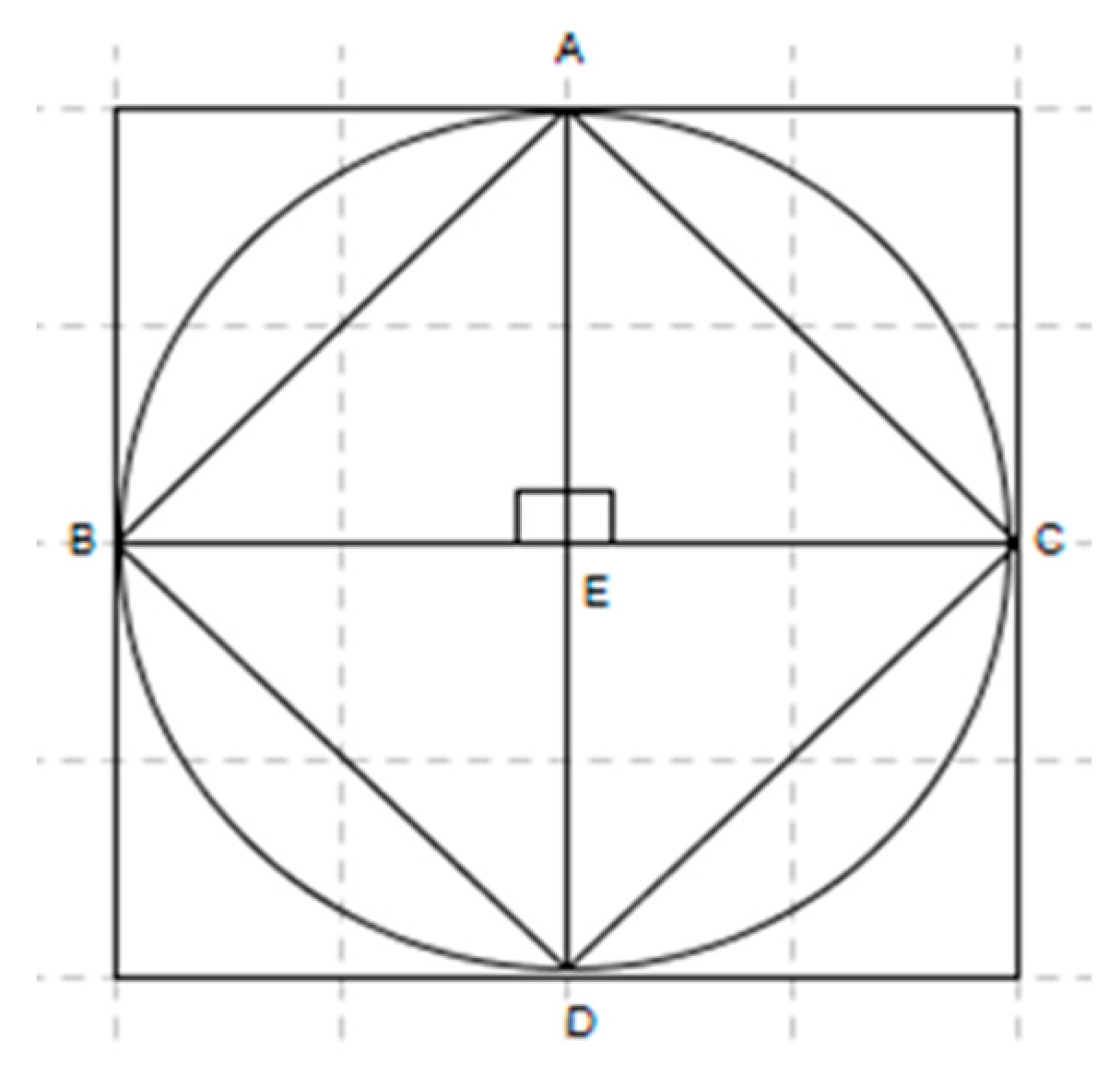
| (117) | Marah: | Look at this ornamentation (see Figure 4), we need to find out if all the corresponding angles and sides are equal in triangles ABC and BDC. |
| (119) | Saja: | The side BC. |
| (123) | Nagam: | The angles B and D. |
| (126) | Saja: | One side and one angle are sufficient for congruence. |
| (127) | Marah: | No, not enough—one is big, and one is small. |
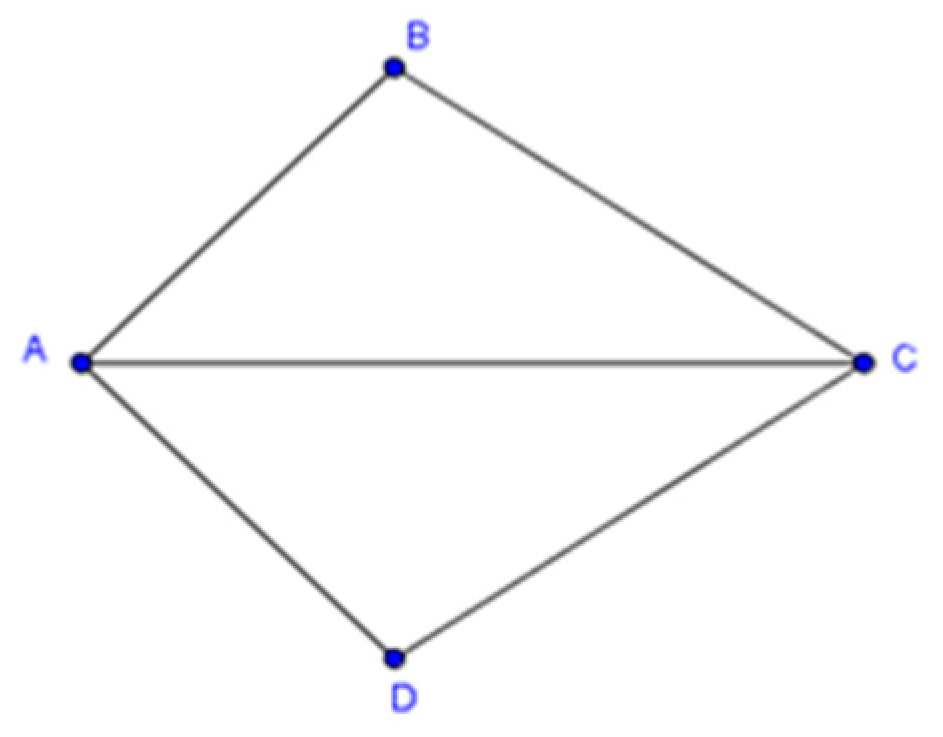
| (130) | Saja: | Now, the third ornamentation (see Figure 5). We need to check if the angles in triangles ABC and AED are equal. |
| (132) | Saja: | We have two parallel lines here, so the corresponding angles are equal. |
| (133) | Marah: | All the corresponding angles are equal. |
| (135) | Nagam: | But the triangles are not congruent; one is big, and the other is small. |
| (137) | Saja: | That means, three equal angles are not sufficient for congruent triangles. |
4.2.1. The First Theorem of Triangle Congruence: (S, A, S)
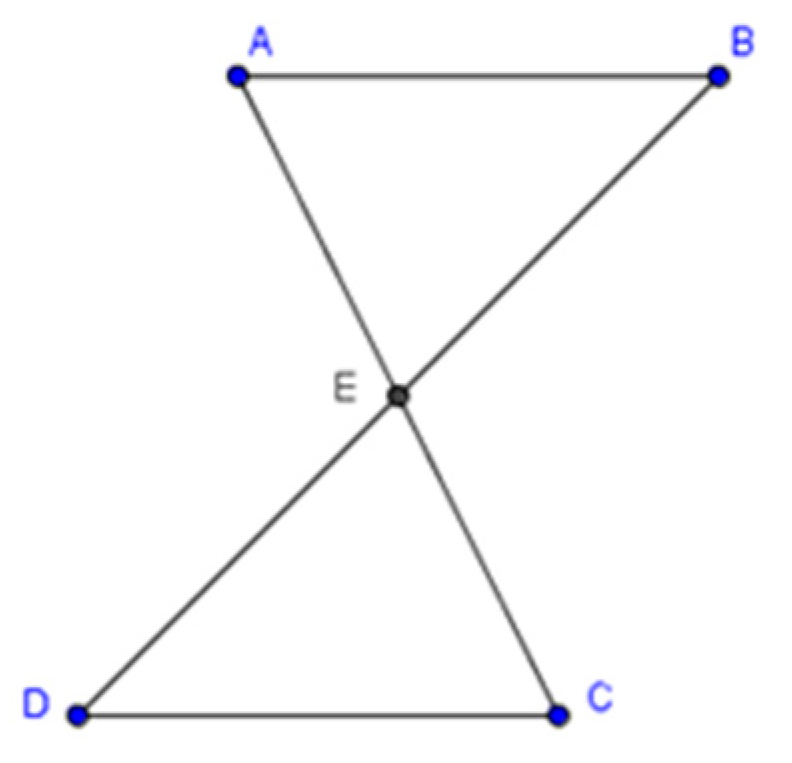
| (139) | Reem: | There are equal corresponding angles and sides in triangles AEB and AEC in the ornamentation (see Figure 6). |
| (140) | Saja: | EC and BE. |
| (142) | Reem | According to the ornamentation, the length of each one of their lengths is half the big square’s side. |
| (143) | Nagam: | AE and AE; AE is mutual. |
| (145) | Saja: | The angle, E, is equal to 90. |
| (147) | Taqwa: | So that means we have two sides and their included angle, which are equal. |
| (148) | Teacher | What about the congruence? |
| (149) | Saja: | Yes. |
| (150) | Taqwa: | They are congruent. What can we say about the conditions? |
| (151) | Saja: | Two equal sides. |
| (153) | Taqwa: | And angle? |
| (154) | Saja: | The angle must be in the middle. |
| (157) | Nagam: | Three elements, two sides, and one angle between the sides. |
4.2.2. The Second Theorem of Triangle Congruence: (A, S, A)
| (160) | Saja: | We need to draw triangles with angles 50° and 60°, and sides with a 5 cm length between them. |
| (161) | Taqwa: | How can we do it? |
| (162) | Teacher: | You must use the protractor to draw the angles. |
| (163) | Nagam: | Does it measure the sides? |
| (164) | Taqwa: | No, it is only for angles. |
| (165) | Teacher: | This point is the zero point, and the rays assign any angle we want… |
| (167) | Nagam: | First, we draw a segment 5 cm long. |
| (177) | Saja: | So, we need to put the protractor on the end point of the segment [she draws while talking] and here, 50° [using the protractor]. We assign a mark, and we assign an angle of 60° on the other side of the segment [again, using the protractor]. Now we draw the lines that connect these two points. |
| (178) | Marah: | We want to cut out one triangle. |
| Students draw several triangles using the same method. | ||
| (181) | Reem: | They are congruent. |
| (186) | Teacher: | What is the condition for congruence? |
| (187) | Nagam: | That they [the triangles] have the same angles. |
| (189) | Saja: | Two angles. |
| (191) | Marah: | And one side between the angles. |
| (195) | Taqwa: | We can conclude that, with the three conditions present—two angles, and one side between them—we have triangle congruence. |
4.2.3. The Third Theorem of Triangle Congruence: (S, S, S)
| (306) | Doa’a: | Draw a triangle, each side is 3 cm. |
| (The students draw and cut out different equilateral triangles) | ||
| (309) | Abed: | All these triangles [he puts the triangles on top of one another] are congruent. |
| (314) | Aya: | We need to write down the corresponding sides. |
| (318) | Noor: | DE=AB; DF=AC; EF=BC. |
| (321) | Aya: | Now we need to draw triangles with sides 4,3,4 |
| [The students draw and cut out different isosceles triangles] | ||
| (329) | Doa’a: | The triangles are congruent. |
| (339) | Doa’a: | It is sufficient that three sides in two triangles are equal, to have congruence. |
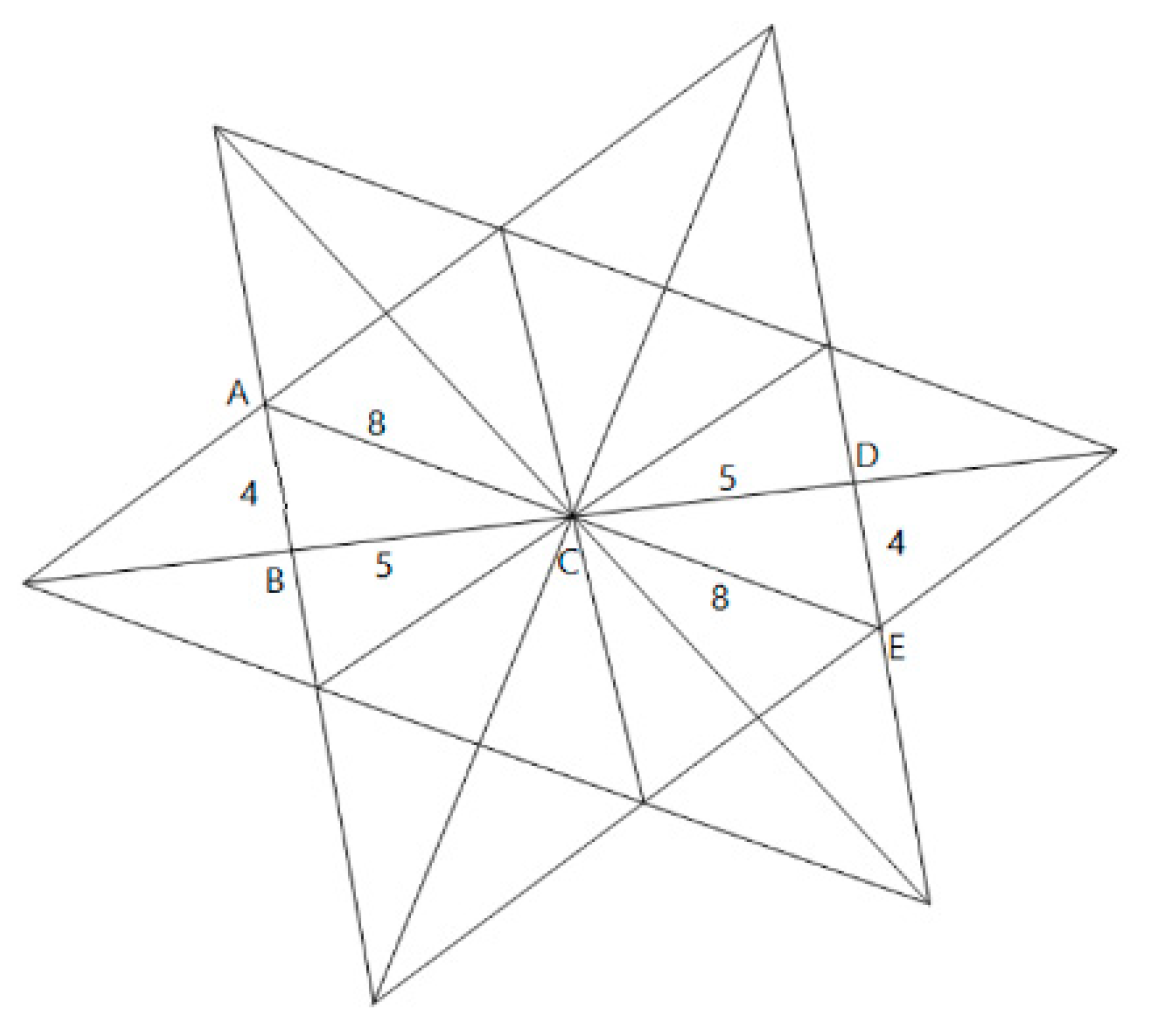
| (200) | Marah: | This triangle (she draws a triangle in the ornamentation; see Figure 7). |
| (201) | Nagam: | See these triangles [she cuts out and covers one triangle with another]. |
| (207) | Teacher: | Try to name the triangles in the ornamentation and write down the corresponding sides. |
| (208) | Nagam: | [Pointing at two triangles in the ornamentation] This is DEF, and this is ABC. |
| (211) | Marah: | AB=DE |
| (212) | Taqwa: | DF=AC |
| (213) | Saja: | EF=BC |
| (215) | Marah: | These triangles, DEF and ABC, have different lengths. |
| (218) | Reem: | They are congruent. |
| (223) | Marah: | When three corresponding sides are equal in two triangles, the triangles are congruent. |
4.3. The Impact of Working with Ornamentation on Students’ Proving Processes
- Writing the claim without an explanation: Student’s text indicates that the proof did not include explanations regarding the properties of the triangle. An example on students’ writing a claim without an explanation is shown in Figure 10.
- Writing the congruent theory only—writing the congruent theory only, without writing the phases of the proof. As an example, students wrote (A, S, A) only in their explanation of Task 1.
- Additional data: Students added data through their proofing, such as the equalities between the sides (BC=DC; AB=AD) in Task 1, where these equalities were not given in the question.
- The congruent theory is not mentioned—students write the qualities in the two triangles but did not wrote the appropriate congruent theory. An example is shown in Figure 11.
- One of the conditions is missing—students wrote only two conditions. An example is shown in Figure 12.
- Writing the wrong explanation—an explanation is shown in Figure 13.
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- D’Ambrosio, U. Ethnomathematics and its place in the history and pedagogy of mathematics. Learn. Math. 1985, 5, 44–48. [Google Scholar]
- D’Ambrosio, U. Ethnomathematics: An Overview. In Proceedings of the Second International Conference on Ethnomathematics, Ouro Preto, Brazil, 5–7 August 2002; de Monteiro, M., Ed.; Lyrium Comunacacao Ltda: Belo Horizonte, Brazil, 2002; pp. 3–5. [Google Scholar]
- Rosa, M.; Orey, D.C. Culturally relevant pedagogy: An ethnomathematical approach. Rev. Horizontes 2010, 28, 19–31. [Google Scholar]
- Orey, D.C. The ethnomathematics of the Sioux tipi and cone. In Mathematics across Cultures; Springer: Dordrecht, The Netherlands, 2000; pp. 239–252. [Google Scholar]
- Irwin, K.C. Using everyday knowledge of decimals to enhance understanding. J. Res. Math. Educ. 2001, 32, 399–420. [Google Scholar] [CrossRef]
- Massarwe, K.; Verner, I.; Bshouty, D. Ethnomathematics and multi-cultural education: Analysis and construction of geometric ornaments. J. Math. Cult. 2012, 6, 344–360. [Google Scholar]
- Massarwe, K.; Verner, I.; Bshouty, D. Fostering creativity through geometrical and cultural inquiry into ornaments. In The Elements of Creativity and Giftedness in Mathematics; Brill Sense: Leiden, The Netherlands, 2011; pp. 217–231. [Google Scholar]
- Widada, W.; Herawaty, D.; Lubis, A.N.M.T. Realistic mathematics learning based on the ethnomathematics in Bengkulu to improve students’ cognitive level. J. Phys. Conf. Ser. 2018, 1088, 012028. [Google Scholar] [CrossRef]
- Adam, S. Ethnomathematical ideas in the curriculum. Math. Educ. Res. J. 2004, 16, 49–68. [Google Scholar] [CrossRef]
- Ogunkunle, R.A.; George, N.R. Integrating ethnomathematics into secondary school mathematics Curriculum for effective artisan creative skill development. Eur. Sci. J. 2015, 11, 386–395. [Google Scholar]
- Gerdes, P. Ethnomathematics, geometry and educational experiences in Africa. Afr. Dev. 2005, 30, 48–65. [Google Scholar] [CrossRef]
- Snipes, V.; Moses, P. Linking mathematics and culture to teach geometry concepts. LTM J. La. Assoc. Teach. Math. 2001, 1, 1–17. [Google Scholar]
- Hickman, R.; Huckstep, P. Art and mathematics in education. J. Aesthet. Educ. 2003, 37, 1–12. [Google Scholar]
- Fukushima, C. Islamic Art and Geometric Design, Activities for Learning; Metropolitan: New York, NY, USA, 2004. [Google Scholar]
- Laudano, F.; Vincenzi, G. Congruence theorems for quadrilaterals. J. Geom. Gr. 2017, 21, 45–59. [Google Scholar]
- Wu, H.S. Key Mathematical Ideas in Grades 5–8. In Proceedings of the Annual Meeting of the NCTM, Anaheim, CA, USA, 12 September 2005; Available online: http://math.berkeley.edu/~wu/NCTM2005a.pdf (accessed on 6 April 2005).
- Jones, K.; Fujita, T.; Miyazaki, M. Learning congruency-based proofs in geometry via a web-based learning system. Proc. Br. Soc. Res. Learn. Math. 2013, 33, 31–36. [Google Scholar]
- Wang, Z.; Wang, Z.; An, S. Error Analysis of 8th Graders’ Reasoning and Proof of Congruent Triangles in China. J. Math. Educ. 2018, 11, 85–120. [Google Scholar]
- Real-Fernández, A.; Molina-Carmona, R.; Llorens-Largo, F. Computational characterization of activities and learners in a learning system. Appl. Sci. 2020, 10, 2208. [Google Scholar] [CrossRef]
- D’Ambrosio, U. The role of mathematics education in building a democratic and just society. Learn. Math. 1990, 10, 20–23. [Google Scholar]
- Sugianto, A.; Abdullah, W.; Widodo, S.T. Reyog Ponorogo art exploration as mathematics learning resources: An ethnomathematics study. J. Phys. Conf. Ser. 2019, 1188, 012095. [Google Scholar] [CrossRef]
- Wager, A.A. Incorporating out-of-school mathematics: From cultural context to embedded practice. J. Math. Teach. Educ. 2012, 15, 9–23. [Google Scholar] [CrossRef]
- Ditasona, C. Ethnomathematics Exploration of the Toba Community: Elements of Geometry Transformation Contained in Gorga (Ornament on Bataks House). IOP Conf. Ser. Mat. Sci. Eng. 2018, 335, 012042. [Google Scholar] [CrossRef]
- Amit, M.; Abu Qouder, F. Bedouin Ethnomathematics-how integrating cultural elements into mathematics classrooms impacts motivation, self-esteem and achievement. International Congress on mathematical education. Proc. PME 2015, 39, 24–31. [Google Scholar]
- Rosa, M.; Orey, D.C. Ethno mathematics: The cultural aspects of mathematics. Rev. Latinoam. Etnomat. 2011, 4, 32–54. [Google Scholar]
- Abiam, P.O.; Abonyi, O.S.; Ugama, J.O.; Okafor, G. Effects of ethnomathematics-based instructional approach on primary school pupils’ achievement in geometry. J. Sci. Res. Rep. 2016, 1–15. [Google Scholar] [CrossRef]
- Widada, W.; Herawaty, D.; Nugroho, K.U.Z.; Anggoro, A.F.D. The ability to Understanding of the Concept of Derivative Functions for Inter-Level Students During Ethnomathematics Learning. J. Phys. Conf. Ser. 2019, 1179, 012056. [Google Scholar] [CrossRef]
- Nursyahidah, F.; Saputro, B.A.; Rubowo, M.R. Supporting second grade lower secondary school students’ understanding of linear equation system in two variables using ethnomathematics. J. Phys. Conf. Ser. 2018, 983, 012119. [Google Scholar] [CrossRef]
- Gustami, S. NukilanSeni Ornamen Indonesia; ASRI: Yogyakarta, Indonesia, 1980. [Google Scholar]
- Fyhn, A.B. Sámi culture and algebra in the curriculum. In Proceedings of the Sixth Congress of the European Society for Research in Mathematics Education, Lyon, France, 28 January–1 February 2009; Institut National de Recherche Pédagogique: Lyon, France, 2010; pp. 489–498. [Google Scholar]
- Ahmad, M.; Rashid, K.; Naz, N. Study of the ornamentation of Bhong Mosque for the survival of decorative patterns in Islamic architecture. Front. Arch. Res. 2018, 7, 122–134. [Google Scholar] [CrossRef]
- Shafiq, J. Architectural Elements in Islamic Ornamentation: New Vision in Contemporary Islamic Art. Arts Des. Stud. 2014, 21, 11–21. [Google Scholar]
- Cenani, S.; Cagdas, G. Shape grammar of geometric Islamic ornaments. In Proceedings of the 24th eCAADe, Volos, Greece, 6–9 September 2006; p. 292. [Google Scholar]
- Burkhart, T. Art of Islam: Language and Meaning; World Wisdom: London, UK, 1976. [Google Scholar]
- Robson, E.; Stedall, J. The Oxford Handbook of the History of Mathematics; OUP: Oxford, UK, 2008. [Google Scholar]
- Moraová, H.; Novotná, J. Ornaments in teaching symmetry. Multicult. Migr. Math. Educ. Lang. 2015, 55, 253–283. [Google Scholar]
- Clapham, C.; Nicholson, J. The Concise Oxford Dictionary of Mathematics; OUP: Oxford, UK, 2009. [Google Scholar]
- Shatnawi, F.S. The foundations of mathematics: And basic engineering concepts; Dar Al-Masirah: Amman, Jordan, 2008. (In Arabic) [Google Scholar]
- Jones, R.T.; Peterson, B.B. Almost congruent triangles. Math. Mag. 1974, 47, 180–189. [Google Scholar] [CrossRef]
- Leung, K.C.I.; Ding, L.; Leung, A.Y.L.; Wong, N.Y. Prospective Teachers’ Competency in Teaching How to Compare Geometric Figures: The Concept of Congruent Triangles as an Example. In Proceedings of the KSME 2014 Spring Conference on Mathematics Education, Seoul, Korea, 4–5 April 2014; Hankuk University of Foreign Studies: Seoul, Korea; pp. 130–791. [Google Scholar]
- Patkin, D.; Plaksin, O. Congruent Triangles Sufficient and Insufficient Conditions Suggested Milestones for Inquiry and Discussion. Kor. Soc. Math. Educ. 2011, 15, 327–340. [Google Scholar]
- González, G.; Herbst, P. Students’ conceptions of congruency through the use of dynamic geometry software. Int. J. Comp. Math. Learn. 2009, 14, 153–182. [Google Scholar]
- Thompson, P.W. Conceptual analysis of mathematical ideas: Some spadework at the foundations of mathematics education. In Proceedings of the Annual Meeting of the International Group for the Psychology of Mathematics Education, Bergen, Norway, 14–18 July 2004; PME: Morelia, Mexico, 2004; Volume 1, pp. 31–49. [Google Scholar]
- Thompson, P.W.; Saldanha, L.A. Fractions and multiplicative reasoning. In Research Companion to the Principles and Standards for School Mathematics; National Council of Teachers of Mathematics: Reston, VI, USA, 2003; pp. 95–113. [Google Scholar]
- Glaser, B.G.; Strauss, A.L. Discovery of Grounded Theory: Strategies for Qualitative Research; Aldine: Chicago, IL, USA, 1967. [Google Scholar]
- Le, N.Q.K.; Yapp, E.K.Y.; Yeh, H.Y. ET-GRU: Using multi-layer gated recurrent units to identify electron transport proteins. BMC Bioinform. 2019, 20, 377. [Google Scholar] [CrossRef]
- Pham, T.V.; Jimenez, C.R. An accurate paired sample test for count data. Bioinformatics 2012, 28, i596–i602. [Google Scholar] [CrossRef]
- Gravemeijer, K. RME theory and mathematics teacher education. In The Handbook of Mathematics Teacher Education; Brill Sense: Leiden, The Netherlands, 2008; Volume 2, pp. 283–302. [Google Scholar]
- Sankaran, S.; Sampath, H.; Sivaswamy, J. Learning Fractions by Making Patterns—An Ethnomathematics Based Approach. In Proceedings of the 17th International Conference on Computers in Education, Hong Kong, China, 12–14 October 2009. [Google Scholar]
- Widada, W.; Herawaty, D.; Anggoro, A.F.D.; Yudha, A.; Hayati, M.K. Ethnomathematics and outdoor learning to improve problem solving ability. In Proceedings of the International Conference on Educational Sciences and Teacher Profession (ICETeP 2018), Bengkulu, Indonesia, 26–28 October 2018; Atlantis Press: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Massarwe, K.; Verner, I.; Bshouty, D. An ethnomathematics exercise in analyzing and constructing ornaments in a geometry class. J. Math. Cult. 2010, 5, 1–20. [Google Scholar]
- Pekrun, R.; Goetz, T.; Titz, W.; Perry, R.P. Academic emotions in students’ self-regulated learning and achievement: A program of qualitative and quantitative research. Educ. Psychol. 2002, 37, 91–105. [Google Scholar] [CrossRef]
- Carbonneu, K.J.; Marley, S.C. Activity-Based Learning Strategies; International Guide to Student Achievement; Routledge: Abingdon, UK, 2012; p. 282. [Google Scholar]
- Fan, L.; Qi, C.; Liu, X.; Wang, Y.; Lin, M. Does a transformation approach improve students’ ability in constructing auxiliary lines for solving geometric problems? An intervention-based study with two Chinese classrooms. Educ. Stud. Math. 2017, 96, 229–248. [Google Scholar] [CrossRef]
- Shahbari, J.A.; Tabach, M. Making sense of the average concept through engagement in model-eliciting activities. Int. J. Math. Educ. Sci. Technol. 2020, 1–18. [Google Scholar] [CrossRef]
- Daher, W.M. Grade 10 Students’ Technology-based Exploration Processes of Narratives Associated with the sine Function. EURASIA J. Math. Sci. Technol. Educ. 2020, 16, 1852. [Google Scholar] [CrossRef][Green Version]
- Carlotta Olivetti, E.; Violante, M.G.; Vezzetti, E.; Marcolin, F.; Eynard, B. Engagement evaluation in a virtual learning environment via facial expression recognition and self-reports: A Preliminary Approach. Appl. Sci. 2020, 10, 314. [Google Scholar] [CrossRef]
- Shin, D.H.; Chung, K.; Park, R.C. Detection of Emotion Using Multi-Block Deep Learning in a Self-Management Interview App. Appl. Sci. 2019, 9, 4830. [Google Scholar] [CrossRef]



| Category | Before Learning | After Learning |
|---|---|---|
| Equal sides: When the sides of the triangles are equal, they are congruent. | 6.6% | 0 |
| Equal angles: When the angles of the triangles are equal, they are congruent. | 13.3% | 6.6% |
| Similarities: When there is a similarity between the triangles, they are congruent. | 20% | 10% |
| Coverage of sides and angles: When the sides and angles of two triangles cover each other, the two triangles are congruent. | 10% | 33.3% |
| Complete cover: Triangles are congruent when one covers the other precisely. | 6.6% | 50% |
| No answer. | 43.3% | 0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shahbari, J.A.; Daher, W. Learning Congruent Triangles through Ethnomathematics: The Case of Students with Difficulties in Mathematics. Appl. Sci. 2020, 10, 4950. https://doi.org/10.3390/app10144950
Shahbari JA, Daher W. Learning Congruent Triangles through Ethnomathematics: The Case of Students with Difficulties in Mathematics. Applied Sciences. 2020; 10(14):4950. https://doi.org/10.3390/app10144950
Chicago/Turabian StyleShahbari, Juhaina Awawdeh, and Wajeeh Daher. 2020. "Learning Congruent Triangles through Ethnomathematics: The Case of Students with Difficulties in Mathematics" Applied Sciences 10, no. 14: 4950. https://doi.org/10.3390/app10144950
APA StyleShahbari, J. A., & Daher, W. (2020). Learning Congruent Triangles through Ethnomathematics: The Case of Students with Difficulties in Mathematics. Applied Sciences, 10(14), 4950. https://doi.org/10.3390/app10144950






