Next Article in Journal
Industry 4.0 and World Class Manufacturing Integration: 100 Technologies for a WCM-I4.0 Matrix
Previous Article in Journal
Phase Transformation, Optical and Emission Performance of Zinc Silicate Glass-Ceramics Phosphor Derived from the ZnO–B2O3–SLS Glass System
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Sciences
Volume 10
Issue 14
10.3390/app10144941
applsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Influence of the Screw Positioning on the Stability of Locking Plate for Proximal Tibial Fractures: A Numerical Approach

by
Tommaso Ingrassia
1,*,
Vincenzo Nigrelli
1,
Daniele Pecorella
1,
Laura Bragonzoni
2 and
Vito Ricotta
1
1
Department of Engineering, Università degli Studi di Palermo, 90128 Palermo, Italy
2
Department for Life Quality Studies, University of Bologna, Campus Rimini, 47921 Rimini, Italy
*
Author to whom correspondence should be addressed.
Appl. Sci. 2020, 10(14), 4941; https://doi.org/10.3390/app10144941
Submission received: 25 May 2020 / Revised: 2 July 2020 / Accepted: 15 July 2020 / Published: 18 July 2020
(This article belongs to the Section Applied Biosciences and Bioengineering)
Browse Figures
Versions Notes

Abstract

:
Tibial fractures are common injuries in people. The proper treatment of these fractures is important in order to recover complete mobility. The aim of this work was to investigate if screw positioning in plates for proximal tibial fractures can affect the stability of the system, and if it can consequently influence the patient healing time. In fact, a more stable construct could allow the reduction of the non-weight-bearing period and consequently speed up the healing process. For that purpose, virtual models of fractured bone/plate assemblies were created, and numerical simulations were performed to evaluate the reaction forces and the maximum value of the contact pressure at the screw/bone interface. A Schatzker type I tibial fracture was considered, and four different screw configurations were investigated. The obtained results demonstrated that, for this specific case study, screw orientation affected the pressure distribution at the screw/bone interface. The proposed approach could be used effectively to investigate different fracture types in order to give orthopaedists useful guidelines for the treatment of proximal tibial fractures.

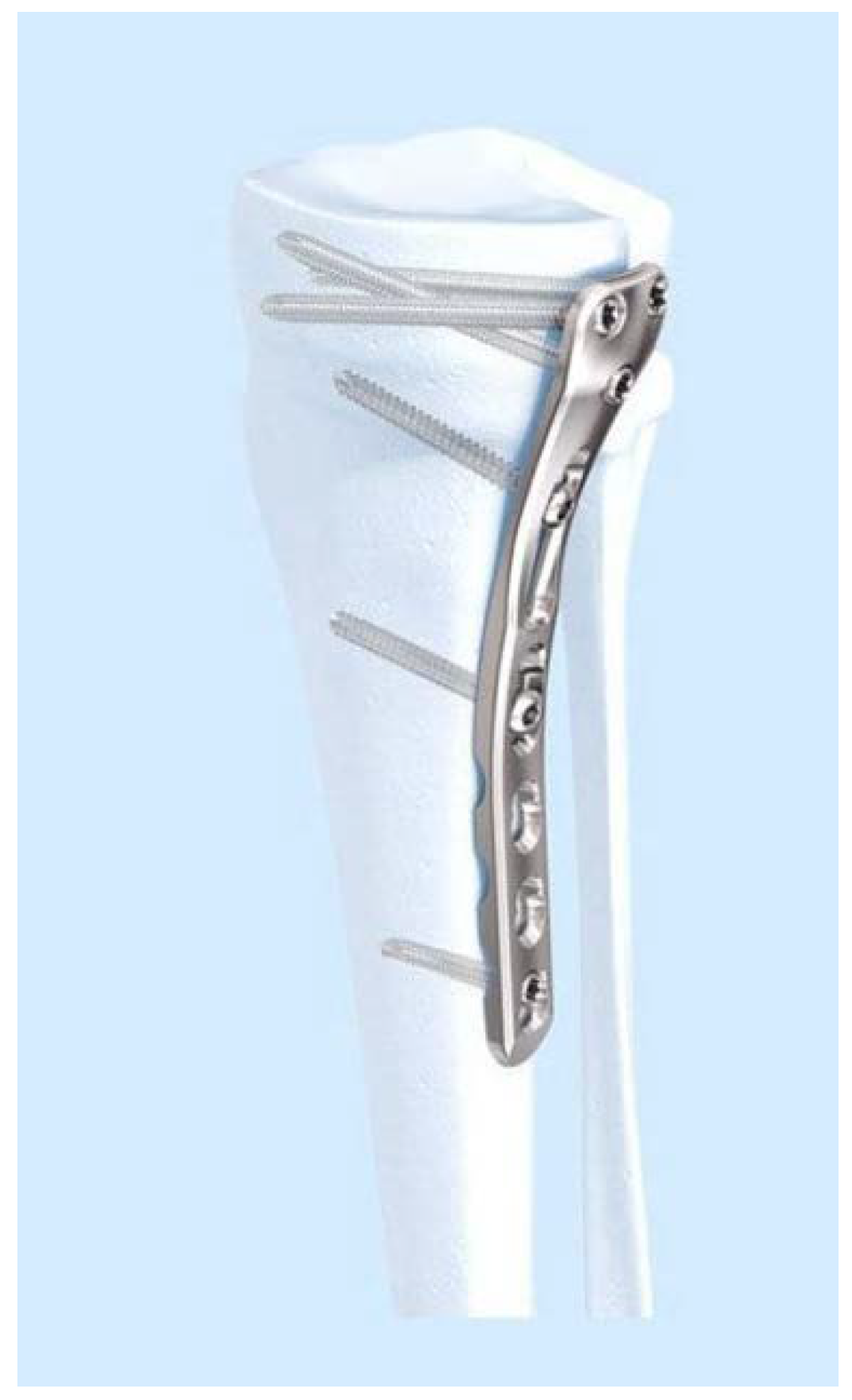
1. Introduction

Tibial plateau fracture treatment remains a difficult surgical problem, even though important advances have been made in the care of intra-articular fractures [1,2]. This surgical challenge is mostly related to the complex anatomy of the articular surface of the proximal tibia, which includes large cartilaginous surfaces, insertions of ligaments, meniscal structures and a high level of force transmission on the tibial joint in axial loading [3]. The treatment goal is anatomic reduction and stable fixation leading to an early mobilization and a minimization of the surgical trauma [1,2]. So far, no single treatment method has been widely established as gold standard for all types of tibial fractures [4,5]. The most common surgical treatments include interlocking intramedullary nailing [4,6], locking compression plates [7,8] and external fixation systems [9]. Treatment failures are common and generally related to residual pain, stiffness, deformity, instability and a decrease in range of motion [1,8]. Moreover, residual articular incongruity, axial malalignment and instability often result in post-traumatic osteoarthritis [1,3,10]. The full understanding of these fractures is the key element in the decision-making process when choosing the best possible treatment [11].
Open reduction and internal fixation with a locking compression plate (LCP), as shown in Figure 1 [12], is currently one of the most common methods of treatment.
Recently, fixation methods and expected outcomes for tibial plateau fractures have become a topic of great interest [3,11]. A great deal of work has been done in developing modern locking plate systems that provide fracture fixation based on completely different mechanical principles than those of conventional plate systems [14,15]. It is not an overstatement to say that the introduction of the locking plate was a revolution in tibial plateau fracture treatment [16]. State-of-the-art locking plates provide an increased angular stability and an improved design, matching the periarticular bone surface. Furthermore, these plates are compatible with minimally invasive percutaneous osteosynthesis [12]. Unlike conventional plates, locking plates allow secondary bone healing (the strain is kept between 2% and 10%) and the enhancement of fracture fixation—even in unfavourable configurations or poor bone quality [14]—since they operate as fixed-angle devices. By using this type of locking, it is possible to obtain:
  • Maintenance of the primary reduction, as the implant blocks the bone segments in their respective positions regardless of the reduction degree;
  • Stability under load which entails a lower risk of a secondary loss of the intraoperative reduction;
  • Greater blood supply to the cortical bone.
In recent years, many studies have examined the finite element method (FEM) analysis of locking plates in order to better understand which parameters can affect the performance of this type of fixation system. They typically investigate how number, length, type, or shape of the screws and the shape of the plates affect the implant stability [4,8,17,18,19,20,21]. Some authors [22] have demonstrated the influence of the screw configuration on the stability of tibial tubercle osteotomy (without plates), but as far as we know, the influence of the screw configuration on the stability of tibial locking plates has not yet been adequately analysed. Therefore, in our study, attention is focused on investigating the influence of the screw orientation on LCP stability. In order to do that, FEM analyses have been performed on the 3D assembly of a locking plate and fractured tibia in four different geometrical configurations.

2. Materials and Methods

The medical literature reports several classifications of plateau tibial fractures. Currently the classification of Schatzker [1] is the one most adopted. This classification is based on a two-dimensional representation of the fracture, and divides tibial plateau fractures into six different groups according to pure shearing, pure compression and their combination (Figure 2) [1,2]. Other aspects considered are the age of the patient, the bone quality, the morphologic architecture of the fracture and the energy of the trauma. The first three groups (Types I, II, III) are fractures of the lateral tibial plateau and are generally associated with a low-energy mechanism and no fracture comminution. Types IV to VI are high-energy injuries associated with knee joint instability. Ranging from subluxation to dislocation, these types of fracture are therefore more serious and related to considerable damage of the soft tissue.
In this work, we decided to study the Schatzker type I fracture (Figure 2), which is a cleavage fracture of the lateral column. This kind of fracture is quite common in younger people [5], who have a denser cancellous bone that better withstands impact. In particular, we studied a fractured right tibia equipped with a plate fixed to the bone with locking screws.
The research activity was articulated into three main steps. The first step consisted of the 3D acquisition and CAD modelling of the tibial bone and the locking plate. In the second step, all the 3D reconstructed models were imported and assembled through a CAD system and a common fracture of the tibia was virtually simulated. Finally, FEM analyses were performed to evaluate the stability of the system at different fixing screw orientations.

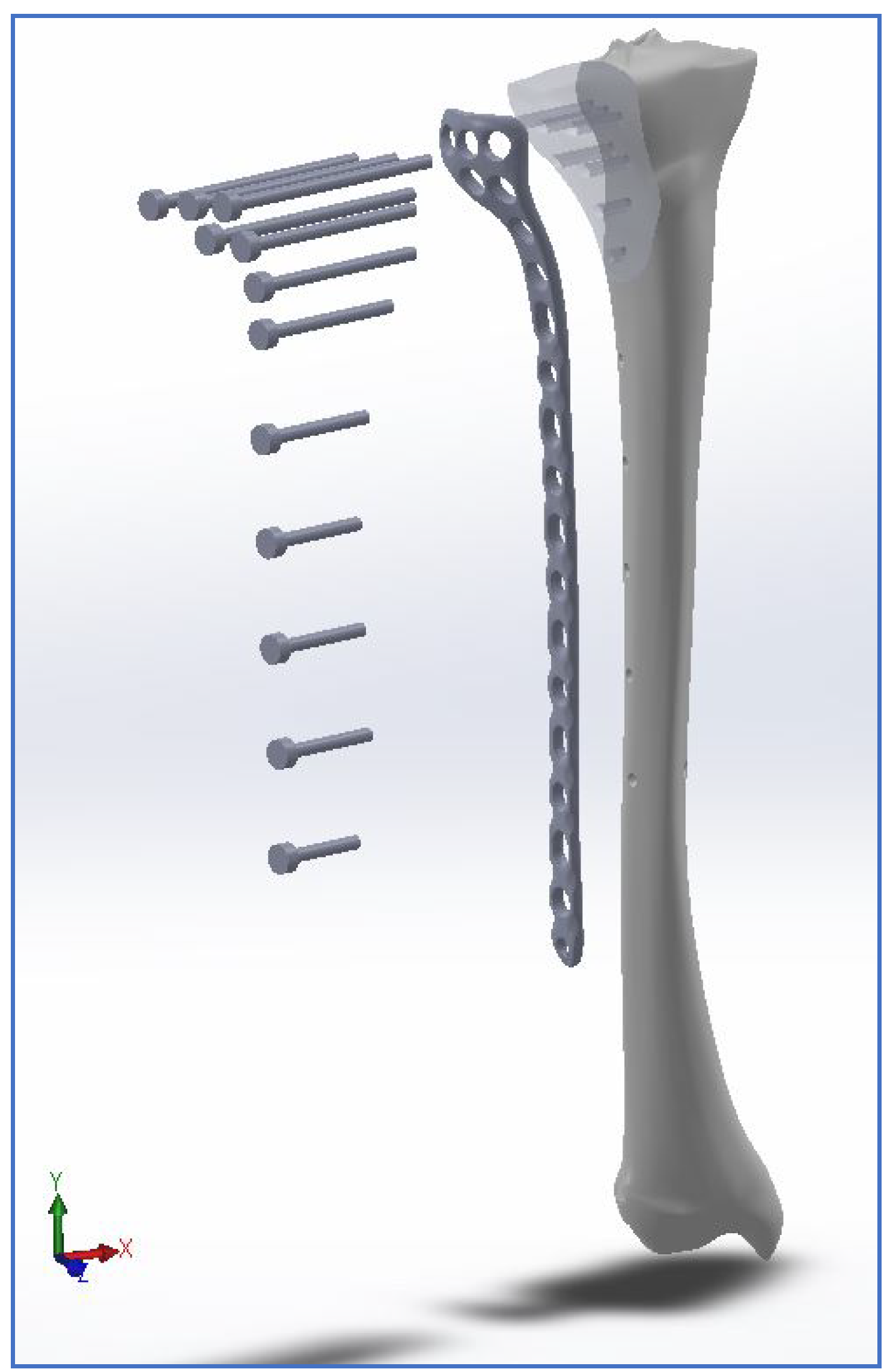
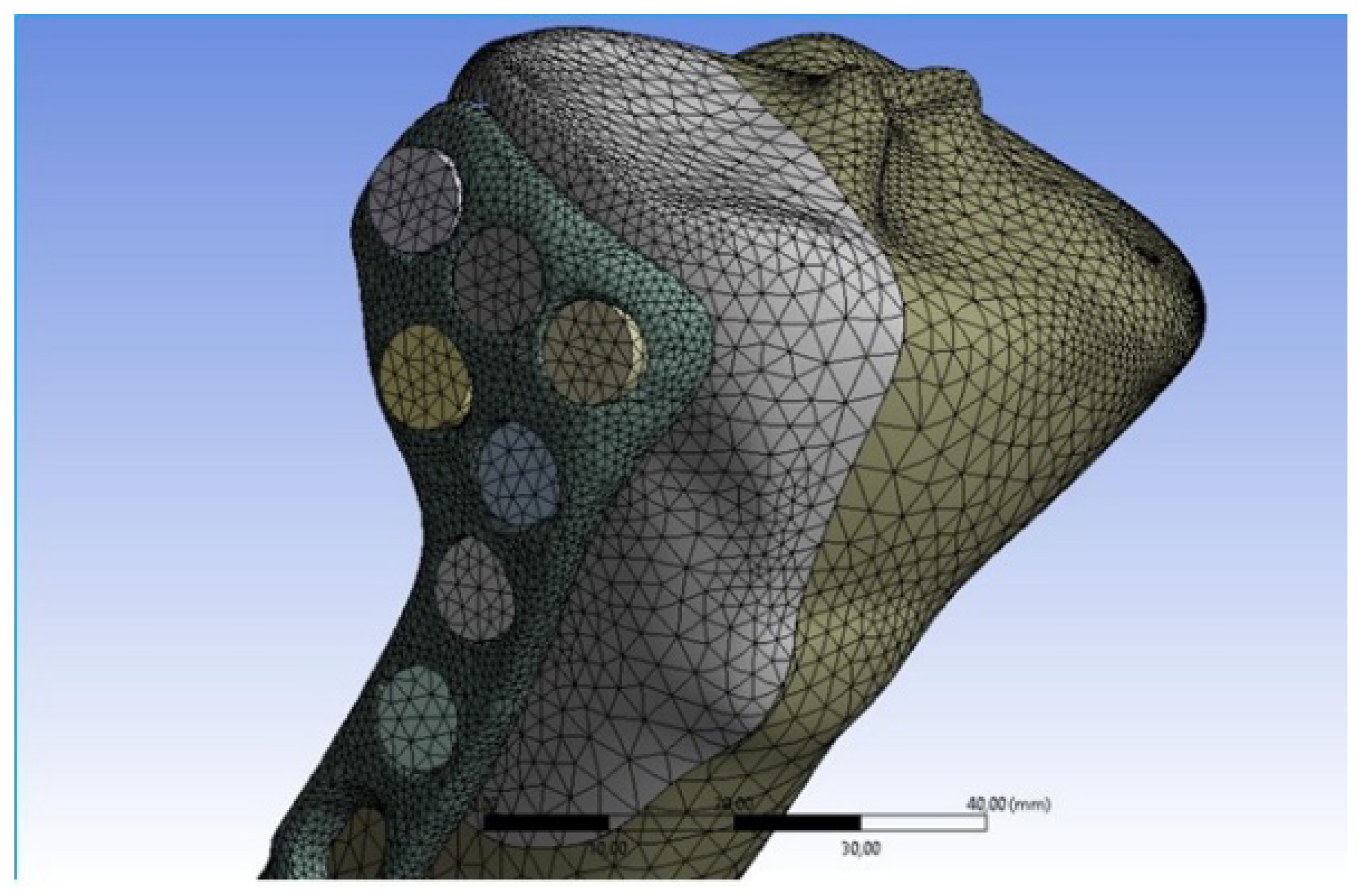
2.1. 3D Acquisition and CAD Modelling

A classic reverse-engineering approach [23,24,25] was used to digitalize the locking plate and the tibia. The length and thickness of the plate were 237 mm and 3.5 mm, respectively. The diameter of screws was 3.5 mm and their length ranged from 30 to 65 mm. The plate and the screws were digitally acquired (Figure 3) through a triangulation-based 3D laser scanner by Hexagon metrology (Hexagon Manufacturing Intelligence, Cobham, Great Britain). This scanner has a high level of accuracy (0.013 mm) which allows it to acquire point clouds at high speed (150,000 points/second). The acquired plate and screw point clouds were post-processed and converted into NURBS surfaces using Polyworks 2015 software (InnovMetric, Québec, Canada, 2015). Finally, the NURBS surfaces were converted into CAD solid models (Figure 3). The reconstructed CAD models differ by less than 0.035 mm from the point clouds.
The CAD model of the tibia, in contrast, was reconstructed from DICOM images of a medium-sized 1.76-m-tall man. To simulate the fracture on the 3D model, reference was made to similar clinical cases. All parts were assembled using 3D parametric CAD software (Figure 4).
To better understand if the screw positioning affects the stability of proximal tibial fractures treated with LCP, the orientation of four screws was changed, keeping the remaining ones fixed. Four different configurations were investigated by modifying the angle of screws 4–7 (Figure 5).
After analysing some commercial tibial plates, it emerged that the angle of the screws mainly varied from about −7° to 10°. For this reason, the authors decided to study different configurations by varying the angle of the screws from −5° to 10°. Considering that the main goal of the study was to investigate if the screw orientation affects the implant stability, this assumption did not affect the reliability of the results. Figure 6 shows the values of the angles for each configuration analysed.

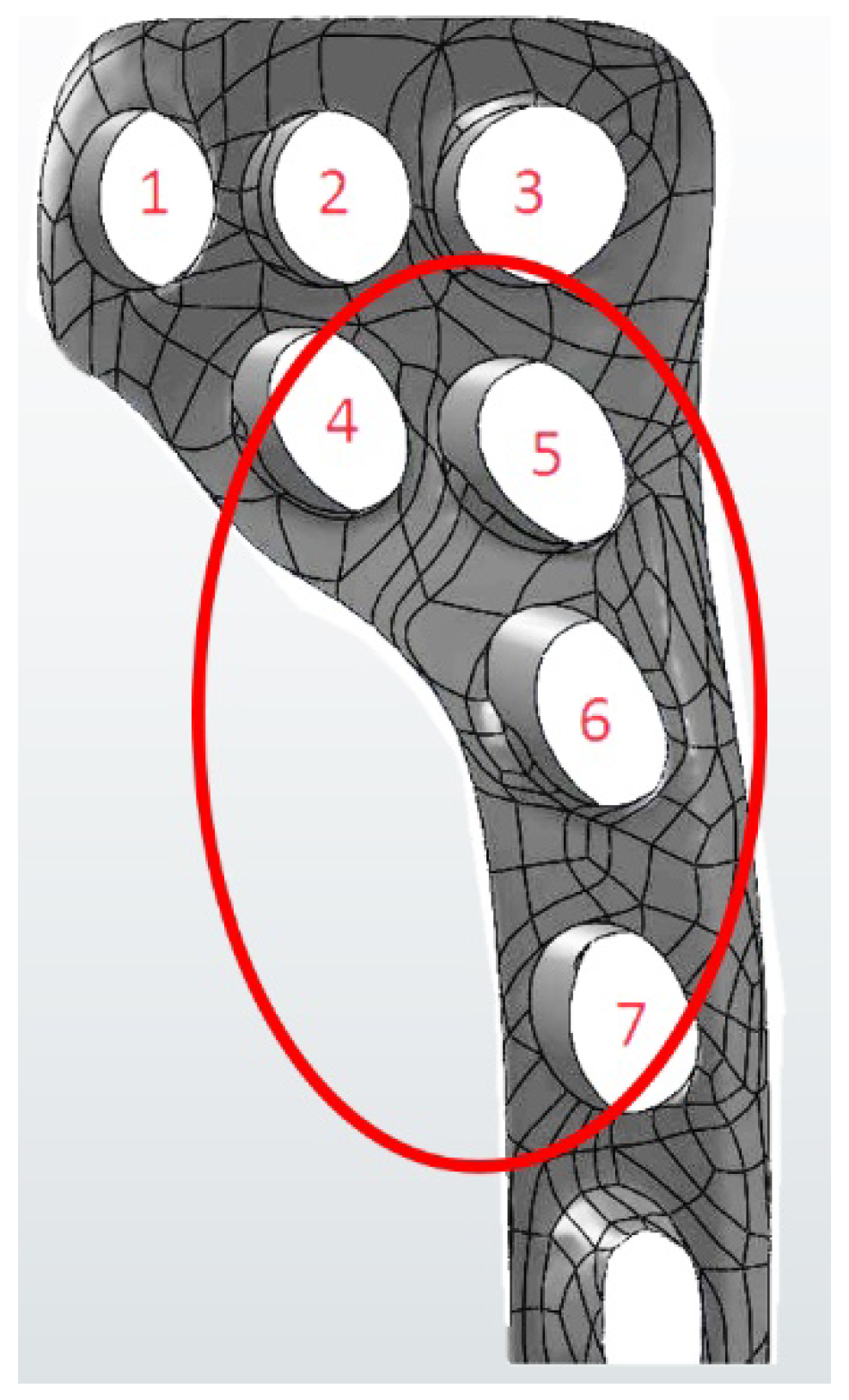
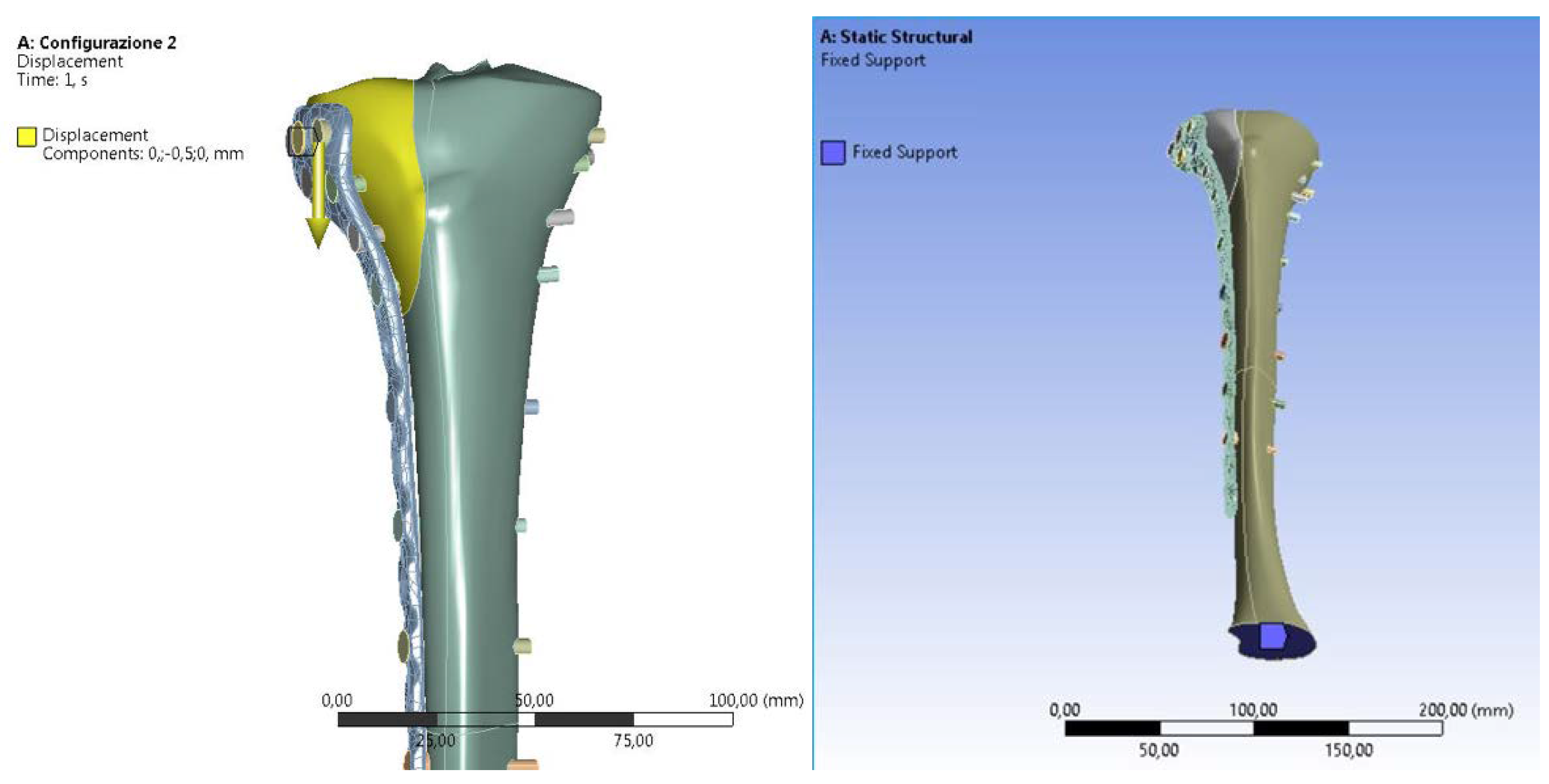
2.2. FEM Analyses

Finite element method analysis is an important assisting tool used largely to evaluate the behaviour of orthopaedic implants [4,8,9,26]. Such analyses can be used to estimate the displacement and load distribution of bones and implants [8,26,27]. Moreover, it has been shown that FE models can be used to predict fracture healing [26,28,29]. For these reasons, in this work, an FEM-based approach was used and virtual simulations [30,31] performed using the commercial software Ansys Workbench R.18 (Ansys Inc., Canonsburg, PA, USA, 2018). All finite element analyses were performed using a Dell Precision T7810 workstation with a 24-core Intel Xeon E5-2670 processor and 128 GB of RAM.
Regarding the mechanical properties of the materials, the bone was considered as an orthotropic material, with the principal direction aligned along the long axis of the bone [32], while both screws and plate (Ti6Al4V alloy) were considered as isotropic. The bone and the titanium alloy were considered as elastic linear hardening materials.
Table 1 and Table 2 report, respectively, the mechanical properties of the bone and of the titanium alloy Ti6Al4V. In Table 1, E1, E2, E3, G12, G13, G23, n12, n13 and n23 respectively represent the Young’s moduli (Ei), the shear moduli (Gij) and the Poisson ratios (nij) along the radial (1), transverse (2) and longitudinal (3) directions of the cortical bone [32]. In Table 2, E and n represent the Young’s modulus and the Poisson’s ratio of the titanium alloy.
To avoid unrealistic high stress concentrations due to sharp discontinuities, mid-side node elements were used to model the curved boundaries. Moreover, to ensure a high accuracy of the results, aspect ratios were also checked during meshing to maintain all elements within acceptable distortion limits. Ten-node tetrahedral elements were used to mesh the implant-bone assembly, and eight-node surface-to-surface contact elements were used to mesh the bone/bone and bone/plate interfaces (Figure 7). A preliminary convergence analysis (convergence threshold value: 5%) [33] was performed to set the most suitable element dimension. The final mesh consisted of about 405,000 elements and 600,000 nodes.
According to previous studies [17,34,35], a bonded contact was imposed at the screw/bone interface and a frictional surface-to-surface contact was used at the bone/plate and bone/bone interfaces. The friction coefficients of the bone/bone and bone/plate interfaces were 0.45 and 0.3 respectively [17,34,35]. As for the contact algorithm, the augmented Lagrangian method was used [36]. According to similar studies on the stability of fixation implants [34,37], the following boundary conditions were imposed to the FEM models: the tibia was locked at its lower end, and a displacement along its main longitudinal axle was imposed on top of the fractured part of the tibia (Figure 8). In particular, a 0.5 mm displacement was imposed. This value represents a threshold beyond which the implant may no longer be considered stable [37,38].

3. Results

The reaction force (F) at the lower end of the tibia and the maximum value of pressure (pmax) at the screw/tibia interfaces were calculated for each configuration in order to evaluate the stability of the locking system. The reaction force (F) and the maximum pressure (pmax) at the bone/screw interface can in fact give useful information on implant stability. The greater the force required to cause the 0.5 mm displacement of the fractured fragment, the higher the reaction force at the distal tibia, thereby ensuring a high stability of the fixation system. As for the pressure at the screw/tibia interface, values that are too high can lead to bone damage and, consequently, to screw-loosening and therefore implant instability. Accordingly, it can be deduced that the configuration (Figure 9) with a higher value of the reaction force (F) is more stable, and the one with a lower pressure (pmax) ensures reduced damage of the bone and, consequently, a higher stability of the implant.
To obtain highly reliable numerical models, we set up the FEM models following a largely validated protocol [19,37,39]. Table 3 summarizes the main results obtained for each configuration analysed.
Figure 10 reports, for each screw configuration, the calculated values of the reaction force (F).
The difference between the highest and lowest force reaction values, in the first and third configurations respectively, is quite small. This small difference indicates, for the analysed configurations, a limited influence of the screw orientation on the calculated reaction force.
Figure 11 shows the pressure maps at the screw/tibia interfaces.
In this case, for the configurations analysed, it can be seen that the difference between the highest value of pmax (563.48 MPa for configuration N.4) and the lowest value (384.05 MPa for configuration N.2) is about 180 MPa, showing a remarkable influence of the screw orientation. Moreover, it can be seen that the maximum value always occurs at the interface between the fragmented part of the bone (yellow area in Figure 12) and screw n.7. This may be attributed to the position of screw n.7, which is subjected to a greater load given that it is the last screw that keeps the fragmented part in contact with the remaining bone.

4. Discussion

Fractures of the tibia are common injuries of the lower extremities occurring both in young and old age people. In particular, proximal fractures are approximately 11% of all fractures of the tibia [40] and, among these, plateau fractures are the most common representing about 9% of all tibial fractures [4,41]. If these fractures are not suitably treated to restore the articular surface or the limb alignment, and to allow early knee motion, both a marked decrease in the range of motion and joint instability can occur [8]. To avoid the above-mentioned complications, a surgical approach is needed to reduce the fracture, restore joint anatomy and mobility, as well as axial alignment of the limb and to allow early mobilization [42,43,44]. Thus far, the clinical treatment of complex tibial plateau fractures is still a challenge. Regarding Schatzker type I fractures, one of the most common surgical approaches is plate fixation with locking screws to achieve a very stable construct [2], thereby ensuring a good osteosynthesis. Locking compression plates in fact minimize local damage to soft tissue and blood supply of the periosteum, and show a low incidence of non-union and infection, hence giving very good results in terms of functional rehabilitation and clinical therapeutic effects [41,45,46]. Unfortunately, this kind of fixation technique requires, post-operatively, a non-weight-bearing period of up to eight weeks [2]. This long period of inactivity can impair the patient’s functionality and can also affect the articular cartilage [27]. For this reason, it would be very interesting to understand how various design parameters (e.g., screw orientation, plate positioning, etc.) affect the stability of the construct. A more stable fixation system could in fact allow reduction of the non-weight-bearing time, thus reducing the negative effects on a patient’s functionality and speeding up the healing process. Several studies have been performed on this topic, focusing mainly on how the stability of the construct is influenced by the type and number of screws [17,47], or by the shape or positioning of the plate [8,18,39,48,49].
This study investigates how the position of the screws affects the stability of proximal tibial fractures treated with locking compression plates. A numerical approach was used and four different screw configurations were analysed. The stability of the different configurations was measured in terms of the reaction force, which is directly proportional to the force necessary to cause the mobilization of the fractured bone fragment, and to the maximum value of pressure at the screw/tibia interfaces which can cause bone damage and consequently screw-loosening and implant instability. Therefore, more stable configurations can be characterised as having a high reaction force and a low pressure at the screw/tibia interface. From the analysis of the obtained results it emerged that the orientation of the screws does not affect the reaction force. As a matter of fact, the reaction force variation was almost negligible for all configurations.
Instead, when it comes to the maximum contact pressure at the screw/bone interfaces (Figure 13), a remarkable influence of the orientation of the screws was detected. Configuration N.2 has the lowest value, equal to 384.05 MPa, which is about 38% less than the highest value (563.48 MPa) calculated for configuration N.4. This means that for the specific type of fracture analysed (Schatzker type I), configuration N.2, among those analysed, ensures the highest level of stability of the construct.
Of course, even if the obtained result is valid only for the specific case analysed, the adopted approach can be used to study other different types of fractures in order to find the best configuration on a case-by-case basis. Moreover, the proposed methodology could be effectively used to plan a personalized surgical approach, depending on the individual characteristics of each patient, and using optimization methods. Additionally, taking future developments into account, in order to reduce the computational cost and processing time, a large number of case studies could be preventively investigated and collected to create a database. Surgeons could use such a database, comparing specific cases under examination with those already analysed to obtain useful information and guidelines.

5. Conclusions

Many studies have demonstrated that several parameters can affect the construct stability and healing time of different fixation systems used for the treatment of proximal tibial fractures. As far as is known, there is not a large amount of information about the influence of screw orientation on tibial locking plate stability. In this study, a numerical approach was developed in order to investigate whether different screw configurations can affect the stability of a specific type of tibial plateau fracture treated with a locking compression plate. The obtained results demonstrate that the screw orientation affects the pressure distribution at the bone/screw interface. The proposed approach can be effectively used, coupled with an optimization module, to investigate any type of fracture-and-fixation system to obtain useful surgical guidelines. Moreover, by using the proposed methodology, personalized treatments could be planned before surgery for each patient, depending on the specific type of fracture and bone characteristics.

Author Contributions

Conceptualization, T.I., V.N. and V.R.; Data curation, D.P.; Methodology, T.I., V.N. and V.R.; Software, T.I., D.P. and V.R.; Validation, T.I., L.B. and D.P.; Supervision, T.I. and V.N.; Writing—original draft, T.I. and V.R.; Writing—review and editing, T.I., L.B., D.P. and V.R. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Schatzker, J.; Tile, M. The Rationale of Operative Fracture Care, 3rd ed.; Springer: Heidelberg, Germany, 2005; Chapter 19; pp. 447–469. [Google Scholar]
  2. Burdin, G. Arthroscopic management of tibial plateau fractures: Surgical technique. Orthop. Traumatol. Surg. Res. 2013, 99, 208–218. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  3. Märdian, S.; Landmann, F.; Wichlas, F.; Haas, N.P.; Schaser, K.-D.; Schwabe, P. Outcome of angular stable locking plate fixation of tibial plateau fractures Midterm results in 101 patients. Indian. J. Orthop. 2015, 49, 620–629. [Google Scholar] [CrossRef]
  4. Chen, F.; Huang, X.; Ya, Y.; Ma, F.; Qian, Z.; Shi, J.; Guo, S.; Yu, B. Finite element analysis of intramedullary nailing and double locking plate for treating extra-articular proximal tibial fractures. J. Orthop. Surg. Res. 2018, 13, 12. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  5. Chen, F.; Zhao, Z.; Liu, J.; Cui, X.; Zhang, D.; Su, X.; Zhao, J.; Tang, P.; Liao, H. Automatic estimation of morphological characteristics of proximal tibia for precise plate treatment using model matching. Comput. Med. Imaging Graph. 2020, 81, 101714. [Google Scholar] [CrossRef] [PubMed]
  6. Ingrassia, T.; Mancuso, A. Virtual prototyping of a new intramedullary nail for tibial fractures. Int. J. Interact. Des. Manuf. 2013, 7, 159–169. [Google Scholar] [CrossRef] [Green Version]
  7. Hasenboehler, E.; Rikli, D.; Babst, R. Locking compression plate with minimally invasive plate osteosynthesis in diaphyseal and distal tibial fracture: A retrospective study of 32 patients. Inj. Int. J. Care Inj. 2007, 38, 365–370. [Google Scholar] [CrossRef] [PubMed]
  8. Chen, P.; Lu, H.; Shen, H.; Wang, W.; Ni, B.; Chen, J. Newly designed anterolateral and posterolateral locking anatomic plates for lateral tibial plateau fractures: A finite element study. J. Orthop. Surg. Res. 2017, 12, 35. [Google Scholar] [CrossRef] [Green Version]
  9. Ma, C.H.; Wu, C.H.; Tu, Y.K.; Lin, T.S. Metaphyseal locking plate as a definitive external fixator for treating open tibial fractures—Clinical outcome and a finite element study. Inj. Int. J. Care Inj. 2013, 44, 1097–1101. [Google Scholar] [CrossRef]
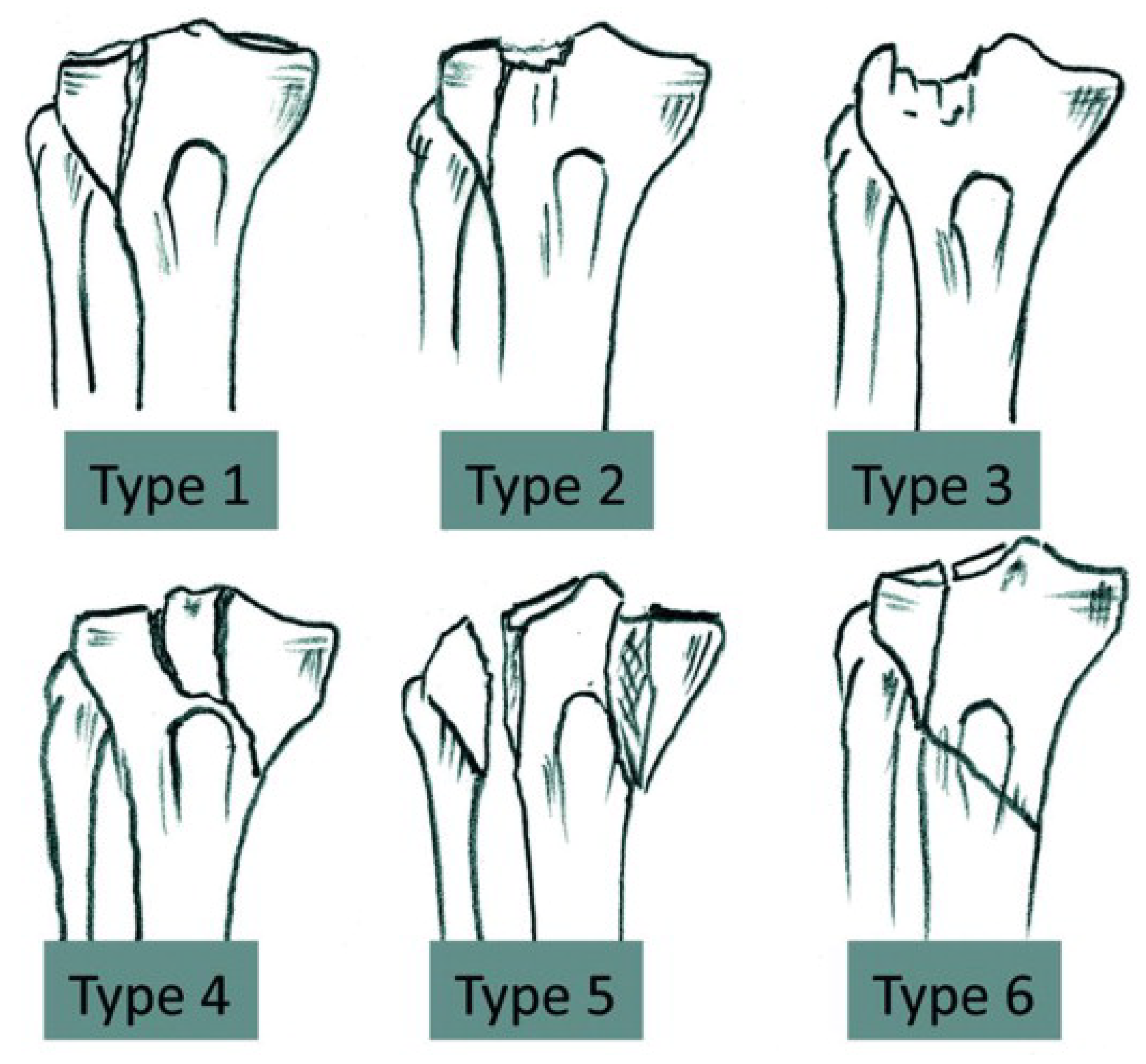
  10. Kfuri Júnior, M.; Fogagnolo, F.; Carneiro Bitar, R.; Lara Freitas, R.; Salim, R.; Jansen Paccola, C.A. Tibial Plateau Fractures. Rev. Bras. Orthop. 2009, 44, 468–474. [Google Scholar] [CrossRef] [Green Version]
  11. Kfuri, M.; Schatzker, J. Revisiting the Schatzker classification of tibial plateau fractures. Inj. Int. J. Care Inj. 2018, 49, 2252–2263. [Google Scholar] [CrossRef] [Green Version]
  12. Biggi, F.; Di Fabio, S.; D’Antimo, C.; Trevisani, S. Tibial plateau fractures: Internal fixation with locking plates and the MIPO technique. Inj. Int. J. Care Inj. 2010, 41, 1178–1182. [Google Scholar] [CrossRef] [PubMed]
  13. Available online: https://gha.health/produkt/loqteq-proximal-lateral-tibia-plate-3-5-4-5/ (accessed on 22 June 2020).
  14. Egol, K.A.; Kubiak, E.N.; Fulkerson, E.; Kummer, F.J.; Koval, K.J. Biomechanics of Locked Plates and Screws. J. Orthop. Trauma. 2004, 18, 488–493. [Google Scholar] [CrossRef]
  15. Cordey, J.; Borgeaud, M.; Perren, S.M. Force Transfer between the Plate and the Bone: Relative Importance of the Bending Stiffness of the Screws Friction Between Plate and Bone. Inj. Int. J. Care Inj. 2000, 3, C21–C28. [Google Scholar] [CrossRef]
  16. Cronier, P.; Pietu, G.; Dujardin, C.; Bigorre, N.; Ducellier, F.; Gerard, R. The concept of locking plates. Orthop. Traumatol. Surg. Res. 2010, 96, S17–S36. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  17. Chen, Y.; Chang, C.; Li, C.; Chen, C.; Chung, C.; Chang, C.; Peng, Y. Biomechanical investigation of the type and configuration of screws used in high tibial osteotomy with titanium locking plate and screw fixation. J. Orthop. Surg. Res. 2019, 14, 35. [Google Scholar] [CrossRef]
  18. Ren, D.; Liu, Y.; Lu, J.; Xu, R.; Wang, P. A Novel Design of a Plate for Posterolateral Tibial Plateau Fractures through Traditional Anterolateral Approach. Sci. Rep. 2018, 8, 16418. [Google Scholar] [CrossRef] [PubMed]
  19. Jacquet, C.; Marret, A.; Myon, R.; Ehlinger, M.; Bahlouli, N.; Wilson, A.; Kley, K.; Rossi, J.-M.; Parratte, S.; Ollivier, M. Adding a protective screw improves hinge′s axial and torsional stability in High Tibial Osteotomy. Clin. Biomech. 2020, 74, 96–102. [Google Scholar] [CrossRef] [PubMed]
  20. Chieh-Szu Yang, J.; Chen, C.-F.; Lee, O.K. Benefits of opposite screw insertion technique in medial open-wedge high tibial osteotomy: A virtual biomechanical study. J. Orthop. Transl. 2020, 20, 31–36. [Google Scholar] [CrossRef]
  21. Ghimire, S.; Miramini, S.; Richardson, M.; Mendis, P.; Zhang, L. Effects of dynamic loading on fracture healing under different locking compression plate configurations: A finite element study. J. Mech. Behav. Biomed. Mater. 2019, 94, 74–85. [Google Scholar] [CrossRef]
  22. Chang, C.; Chen, Y.; Li, C.; Chung, C.; Tseng, C.; Chang, C.; Peng, T. Biomechanical investigation of tibial tubercle osteotomy fixed with various screw configurations. Inj. Int. J. Care Inj. 2019, 50, 263–271. [Google Scholar] [CrossRef]
  23. Ingrassia, T.; Nalbone, L.; Nigrelli, V.; Pisciotta, D.; Ricotta, V. Influence of the Metaphysis Positioning in a New Reverse Shoulder Prosthesis; AG Advances on Mechanics, Design Engineering and Manufacturing, Lecture Notes in Mechanical Engineering; Springer International Publishing: Cham, Switzerland, 2017; pp. 469–478. [Google Scholar]
  24. Ingrassia, T.; Nigrelli, V.; Ricotta, V.; Nalbone, L.; D’Arienzo, A.; D’Arienzo, M.; Porcellini, G. A new method to evaluate the influence of the glenosphere positioning on stability and range of motion of a reverse shoulder prosthesis. Inj. Int. J. Care Inj. 2019, 50, S12–S17. [Google Scholar] [CrossRef] [PubMed]
  25. Ingrassia, T.; Nalbone, L.; Nigrelli, V.; Ricotta, V.; Pisciotta, D. Biomechanical analysis of the humeral tray positioning in reverse shoulder arthroplasty design. Int. J. Interact. Des. Manuf. 2018, 12, 651–661. [Google Scholar] [CrossRef]
  26. Inzana, J.A.; Varga, P.; Windolf, M. Implicit modeling of screw threads for efficient finite element analysis of complex bone-implant systems. J. Biomech 2016, 49, 1836–1844. [Google Scholar] [CrossRef] [PubMed]
  27. Carrera, I.; Gelber, P.E.; Chary, G.; Gonzalez-Ballester, M.A.; Monllau, J.C.; Noailly, J. Fixation of a split fracture of the lateral tibial plateau with a locking screw plate instead of cannulated screws would allow early weight bearing: A computational exploration. Int. Orthop. 2016, 40, 2163–2169. [Google Scholar] [CrossRef]
  28. Anderson, D.D.; Thomas, T.P.; Marin, A.C.; Elkins, J.M.; Lack, W.D.; Lacroix, D. Computational Techniques for the Assessment of Fracture Repair. Inj. Int. J. Care Inj. 2014, 45, S23–S31. [Google Scholar] [CrossRef] [Green Version]
  29. Byrne, D.P.; Lacroix, D.; Prendergast, P.J. Simulation of Fracture Healing in the Tibia: Mechanoregulation of Cell Activity Using a Lattice Modeling Approach. J. Orthop. Res. 2011, 29, 1496–1503. [Google Scholar] [CrossRef]
  30. Tumino, D.; Ingrassia, T.; Nigrelli, V.; Pitarresi, G.; Urso Miano, V. Mechanical behavior of a sandwich with corrugated GRP core: Numerical modeling and experimental validation. Frat. ed Integrità Strutt. 2014, 30, 317–326. [Google Scholar] [CrossRef] [Green Version]
  31. Mirulla, A.I.; Bragonzoni, L.; Zaffagnini, S.; Bontempi, M.; Nigrelli, V.; Ingrassia, T. Virtual simulation of an osseointegrated trans-humeral prosthesis: A falling scenario. Inj. Int. J. Care Inj. 2018, 49, 784–791. [Google Scholar] [CrossRef]
  32. Perez, A.; Mahar, A.; Negus, C.; Newton, P.; Impelluso, T. A computational evaluation of the effect of intramedullary nail material properties on the stabilization of simulated femoral shaft fractures. Med. Eng. Phys. 2008, 30, 755–760. [Google Scholar] [CrossRef]
  33. Cerniglia, D.; Ingrassia, T.; D’Acquisto, L.; Saporito, M.; Tumino, D. Contact between the components of a knee prosthesis: Numerical and experimental study. Fract. Struct. Integr. 2012, 22, 56–68. [Google Scholar] [CrossRef] [Green Version]
  34. Anwar, A.; Lv, D.; Zhao, Z.; Zhang, Z.; Lu, M.; Nazir, M.U.; Qasim, W. Finite element analysis of the three different posterior malleolus fixation strategies in relation to different fracture sizes. Inj. Int. J. Care Inj. 2017, 48, 825–832. [Google Scholar] [CrossRef] [PubMed]
  35. Knežević, J.; Kodvanj, J.; Čukelj, F.; Pamuković, F.; Pavić, A. A biomechanical comparison of four fixed-angle dorsal plates in a finite element model of dorsally-unstable radius fracture. Inj. Int. J. Care Inj. 2017, 48, S41–S46. [Google Scholar] [CrossRef]
  36. Simo, J.C.; Laursen, T.A. An Augmented Lagrangian Treatment of Contact Problems Involving Friction. Comput. Struct. 1992, 42, 97–116. [Google Scholar] [CrossRef]
  37. Ji, W.; Luo, C.; Zhan, S.; Zhan, Y.; Xie, X.; Zhang, B. Combined proximal tibial osteotomy for varus osteoarthritis of the knee: Biomechanical tests and finite-element analyses. Knee 2020, 27, 863–870. [Google Scholar] [CrossRef] [PubMed]
  38. Götz, R.; Gebhard, F.; Duerselen, L.; Ignatius, A.; Claes, L. Delayed bone healing following high tibial osteotomy related to increased implant stiffness in locked plating. Inj. Int. J. Care Inj. 2014, 45, 1648–1652. [Google Scholar]
  39. Luo, C.-A.; Hwa, S.-Y.; Lin, S.-C.; Chen, C.-M.; Tseng, C.-S. Placement-induced effects on high tibial osteotomized construct—Biomechanical tests and finite-element analyses. BMC Musculoskelet. Disord. 2015, 16, 1–10. [Google Scholar] [CrossRef] [Green Version]
  40. Kandemir, U.; Herfat, S.; Herzog, M.; Viscogliosi, P.; Pekmezci, M. Fatigue failure in extra-articular proximal tibia fractures: Locking Intramedullary nail versus double locking plates—A biomechanical study. J. Orthop. Trauma. 2017, 31, 49–54. [Google Scholar] [CrossRef]
  41. Huang, X.; Zhi, Z.; Yu, B.; Chen, F. Stress and stability of plate-screw fixation and screw fixation in the treatment of Schatzker type IV medial tibial plateau fracture: A comparative finite element study. J. Orthop. Surg. Res. 2015, 10, 182. [Google Scholar] [CrossRef] [Green Version]
  42. Prat-Fabregat, S.; Camacho-Carrasco, P. Treatment strategy for tibial plateau fractures: An update. EFORT Open Rev. 2016, 1, 225–232. [Google Scholar] [CrossRef]
  43. Ingrassia, T.; Lombardo, B.; Nigrelli, V.; Ricotta, V.; Nalbone, L.; D’Arienzo, A.; D’Arienzo, M.; Porcellini, G. Influence of sutures configuration on the strength of tendon-patch joints for rotator cuff tears treatment. Inj. Int. J. Care Inj. 2019, 50, S18–S23. [Google Scholar] [CrossRef]
  44. Feng, W.; Fu, L.; Liu, J.; Qi, X.; Li, D.; Yang, C. Biomechanical evaluation of various fixation methods for proximal extra-articular tibial fractures. J. Surg. Res. 2012, 178, 722–727. [Google Scholar] [CrossRef] [PubMed]
  45. Farouk, O.; Krettek, C.; Miclau, T.; Schandelmaier, P.; Guy, P.; Tscherne, H. Minimally invasive plate osteosynthesis: Does percutaneous plating disrupt femoral blood supply less than the traditional technique? J. Orthop. Trauma. 1999, 13, 401–406. [Google Scholar] [CrossRef] [PubMed]
  46. Hu, X.J.; Wang, H. Biomechanical assessment and 3D finite element analysis of the treatment of tibial fractures using minimally invasive percutaneous plates. Exp. Ther. Med. 2017, 14, 1692–1698. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  47. Sun, H.; He, Q.; Zhang, B.; Zhu, Y.; Zhang, W.; Chai, Y. A biomechanical evaluation of different fixation strategies for posterolateral fragments in tibial plateau fractures and introduction of the ‘magic screw’. Knee 2018, 25, 417–426. [Google Scholar] [CrossRef]
  48. MacLeod, A.R.; Serrancoli, G.; Fregly, B.J.; Toms, A.D.; Gill, H.S. The effect of plate design, bridging span, and fracture healing on the performance of high tibial osteotomy plates: An experimental and finite element study. Bone Jt. Res. 2019, 7, 639–649. [Google Scholar] [CrossRef]
  49. Kaze, A.D.; Maas, S.; Waldmann, D.; Zilian, A.; Dueck, K.; Pape, D. Biomechanical properties of five different currently used implants for open-wedge high tibial osteotomy. J. Exp. Orthop. 2015, 2, 14. [Google Scholar] [CrossRef] [Green Version]
Applsci 10 04941 g001 550
Figure 1. A common tibial locking compression plate (LCP) [13].
Figure 1. A common tibial locking compression plate (LCP) [13].
Applsci 10 04941 g001
Applsci 10 04941 g002 550
Figure 2. Schatzker classification for tibial plateau fractures [2].
Figure 2. Schatzker classification for tibial plateau fractures [2].
Applsci 10 04941 g002
Applsci 10 04941 g003 550
Figure 3. Hexagon metrology 3D laser scanner HP-L-20.8 (left) and reconstructed CAD model of the plate (right).
Figure 3. Hexagon metrology 3D laser scanner HP-L-20.8 (left) and reconstructed CAD model of the plate (right).
Applsci 10 04941 g003
Applsci 10 04941 g004 550
Figure 4. The exploded view of bone, plate and screws.
Figure 4. The exploded view of bone, plate and screws.
Applsci 10 04941 g004
Applsci 10 04941 g005 550
Figure 5. CAD model of the superior part of the plate and numbering of the screw holes.
Figure 5. CAD model of the superior part of the plate and numbering of the screw holes.
Applsci 10 04941 g005
Applsci 10 04941 g006 550
Figure 6. Schemes of the different configurations analysed (the screw angle is measured).
Figure 6. Schemes of the different configurations analysed (the screw angle is measured).
Applsci 10 04941 g006
Applsci 10 04941 g007 550
Figure 7. Particulars of the mesh of the proximal tibia.
Figure 7. Particulars of the mesh of the proximal tibia.
Applsci 10 04941 g007
Applsci 10 04941 g008 550
Figure 8. Boundary conditions: imposed displacement (left) and fully constrained surface (right).
Figure 8. Boundary conditions: imposed displacement (left) and fully constrained surface (right).
Applsci 10 04941 g008
Applsci 10 04941 g009 550
Figure 9. Scheme of the reaction force F.
Figure 9. Scheme of the reaction force F.
Applsci 10 04941 g009
Applsci 10 04941 g010 550
Figure 10. Calculated reaction forces (F) at the distal tibia for the analysed configurations.
Figure 10. Calculated reaction forces (F) at the distal tibia for the analysed configurations.
Applsci 10 04941 g010
Applsci 10 04941 g011 550
Figure 11. FEM analysis results: pressure maps at the screw/tibia interfaces.
Figure 11. FEM analysis results: pressure maps at the screw/tibia interfaces.
Applsci 10 04941 g011
Applsci 10 04941 g012 550
Figure 12. Position of screw n.7.
Figure 12. Position of screw n.7.
Applsci 10 04941 g012
Applsci 10 04941 g013 550
Figure 13. Calculated max pressure values for all configurations.
Figure 13. Calculated max pressure values for all configurations.
Applsci 10 04941 g013
Table
Table 1. Main mechanical properties of the cortical bone.
Table 1. Main mechanical properties of the cortical bone.
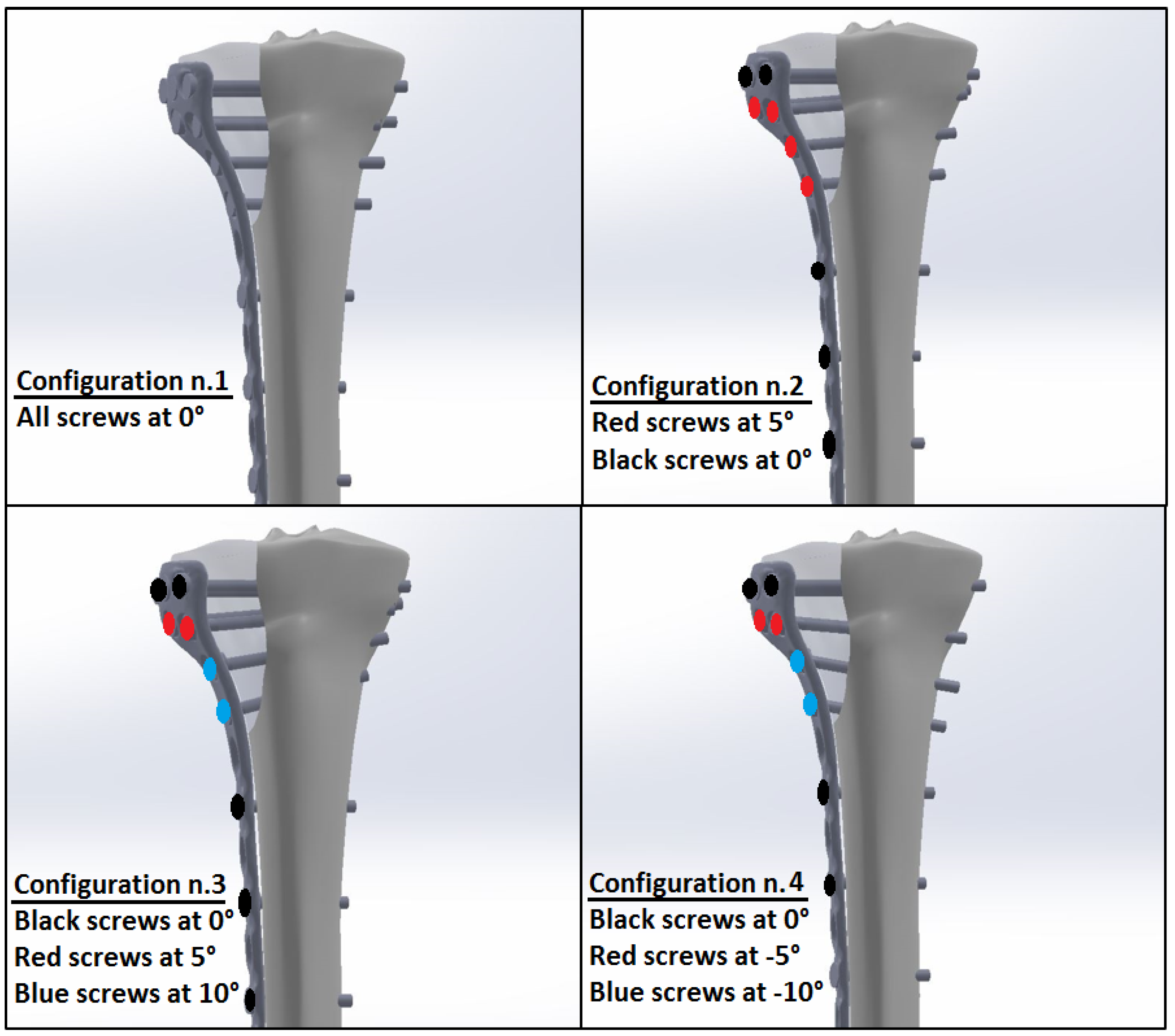
E1 (GPa)E2 (GPa)E3 (GPa)G12 (GPa)G13 (GPa)G23 (GPa)n12n13n23
6.918.5118.42.413.564.910.490.120.14
Table
Table 2. Main mechanical properties of the titanium alloy Ti6Al4V.
Table 2. Main mechanical properties of the titanium alloy Ti6Al4V.
MaterialE (GPa)n
Ti6Al4V1150.33
Table
Table 3. FEM results.
Table 3. FEM results.
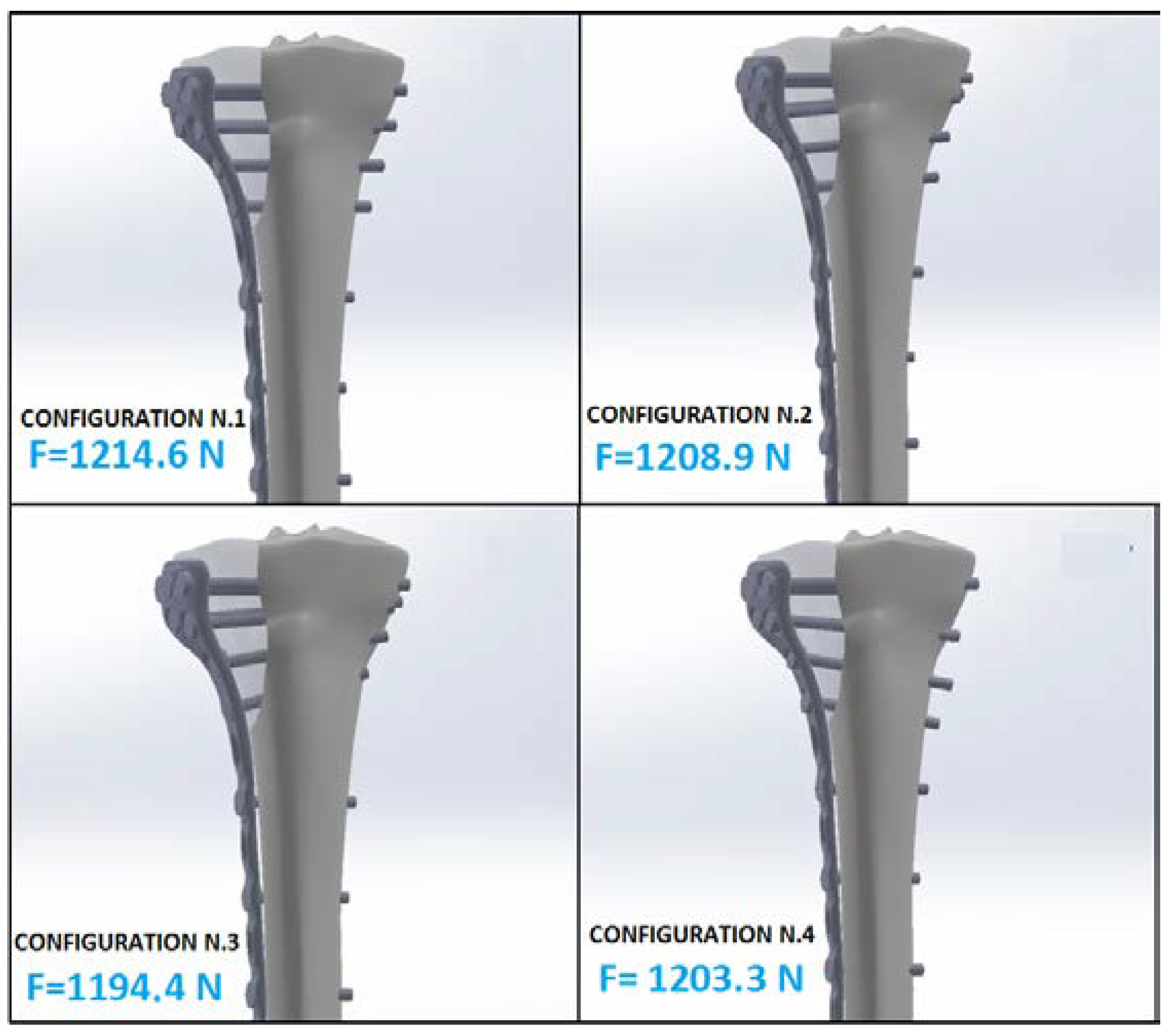
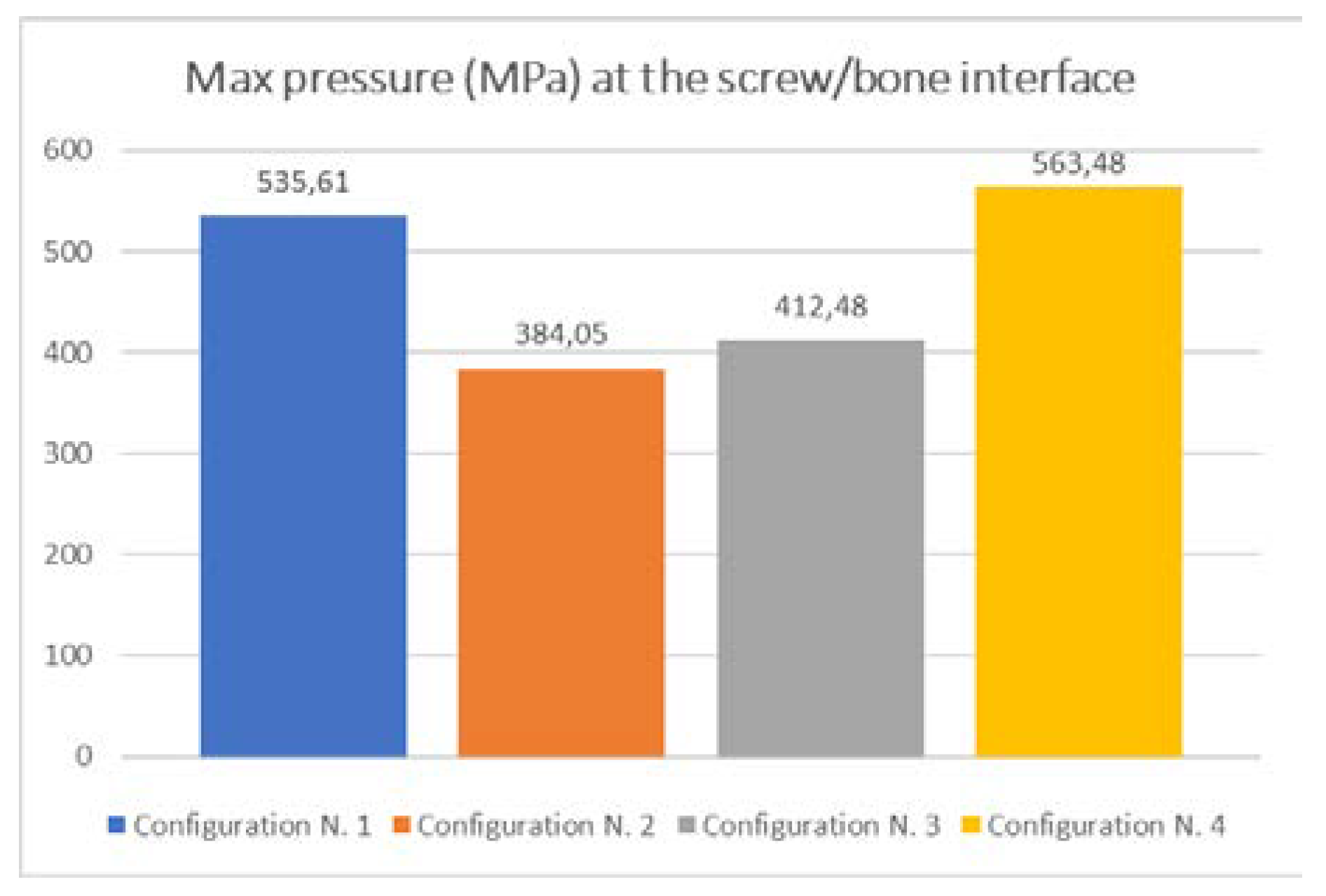
Configuration NumberReaction Force F (N)Pressure Max pmax (MPa)
11214.6535.61
21208.9384.05
31194.4412.48
41203.3563.48

Share and Cite

MDPI and ACS Style

Ingrassia, T.; Nigrelli, V.; Pecorella, D.; Bragonzoni, L.; Ricotta, V. Influence of the Screw Positioning on the Stability of Locking Plate for Proximal Tibial Fractures: A Numerical Approach. Appl. Sci. 2020, 10, 4941. https://doi.org/10.3390/app10144941

AMA Style

Ingrassia T, Nigrelli V, Pecorella D, Bragonzoni L, Ricotta V. Influence of the Screw Positioning on the Stability of Locking Plate for Proximal Tibial Fractures: A Numerical Approach. Applied Sciences. 2020; 10(14):4941. https://doi.org/10.3390/app10144941

Chicago/Turabian Style

Ingrassia, Tommaso, Vincenzo Nigrelli, Daniele Pecorella, Laura Bragonzoni, and Vito Ricotta. 2020. "Influence of the Screw Positioning on the Stability of Locking Plate for Proximal Tibial Fractures: A Numerical Approach" Applied Sciences 10, no. 14: 4941. https://doi.org/10.3390/app10144941

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop