3.1. Problem Formulation
In the general case, the teacher allocation problem boils down to allocating resources (teachers) to activities (courses). A well-prepared allocation must guarantee the satisfaction of constraints related to the specific contact hour limits, minimum academic staff complement, courses taught by instructors with an appropriate academic degree or title, etc. In the analysis presented below, the formal definition of the Teacher Allocation Problem (TAP) is adopted. It accentuates the role of the competency framework of the available teaching staff.
Given is a set of courses to teach in a given academic year. The courses are conducted in the winter or the summer semester. There are various course formats (lectures, tutorials, labs, workshops, seminars) and each course (taught in a specific format) has a fixed number of course sections or classes. Students in each course section are obliged to attend a fixed number of course meetings (colloquially called classes). Each course meeting has an assigned number of teaching credits.
Also given is a set of teachers. Each teacher (lecturer) has a set of competencies (skills, qualifications) to teach specific courses/course meetings. The set is described in a binary way (can/cannot teach a specific course). The competencies of individual teachers make up the competency framework of the entire staff (a set of teachers).
The staff members’ competencies can change. The resulting change in the framework is understood as an acquisition, by at least one staff member, of new competencies, allowing them to teach a specific course (a group of courses).
In addition, each teacher has an academic/professional degree/title (professor, doctor, master, engineer) and is assigned a specific number of teaching credits (teaching load, credit hours) per academic year.
A permissible teacher allocation is understood as an allocation of teachers to course meetings which satisfies the following constraints:
Each course meeting can be conducted by only one competent teacher,
The set of all course meetings for a specific course section (group) can be run by no more than three teachers,
Lectures and seminars can only be delivered by professors and doctors,
Each teacher should have a guaranteed teaching quota,
All course meetings must be assigned to teachers,
Others (following from various disruptions and/or individual needs of a university/organisational unit).
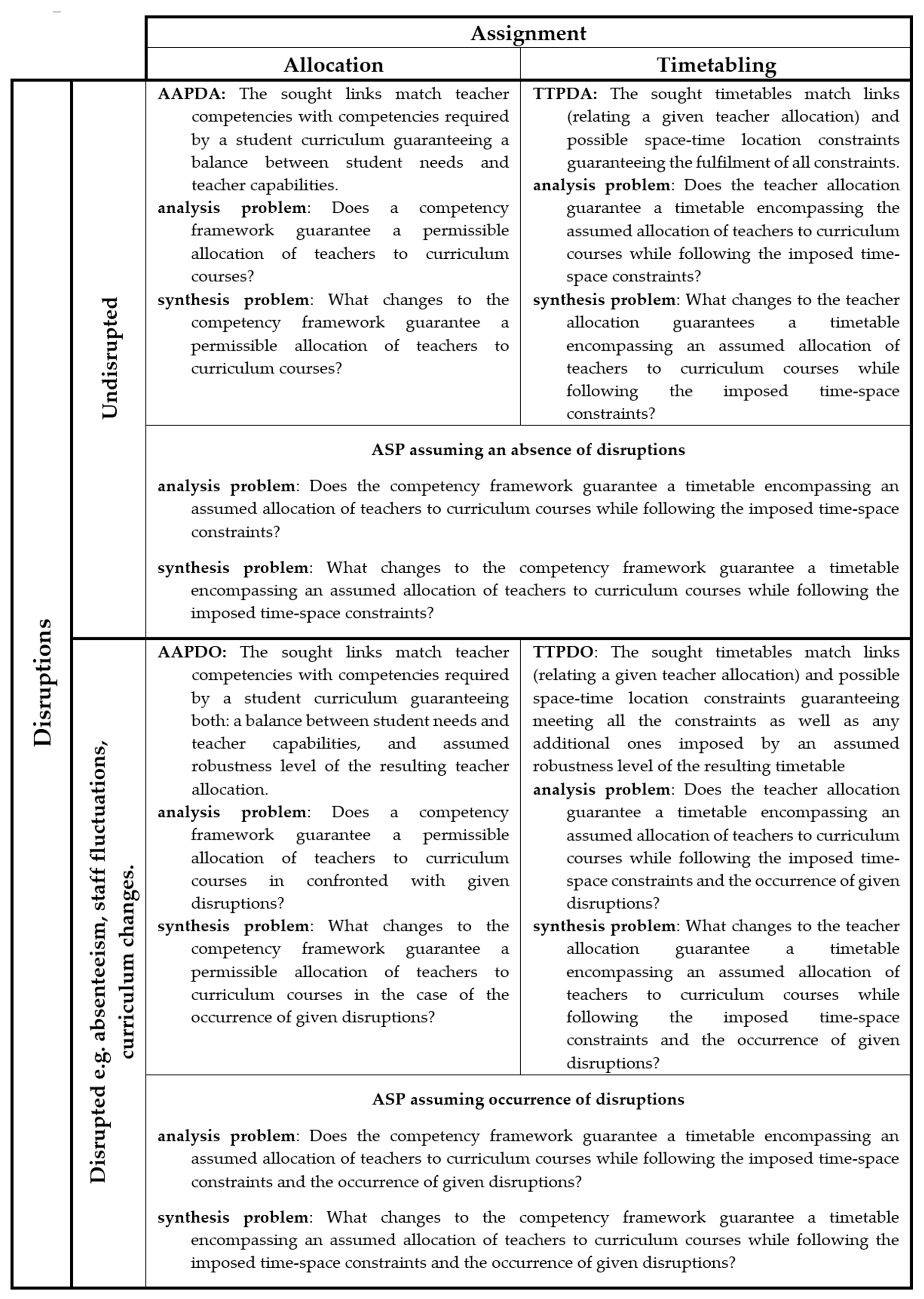
The presented assumptions constitute the verbal model of the ASP problem, in which detailed sub-problems are formulated in accordance with the adopted taxonomy, see
Figure 1. Indeed, focusing on AAPDO, the problem of synthesis can be considered in the context of searching for the competency framework,
, robust to disruptions that affect the possibility of carrying out the ordered activities.
This situation is illustrated by the following simplified example. Given is the set of courses containing three courses:
. Each course,
has a number of tasks assigned to it. Consequently, courses
and
require unit tasks, whereas course
requires 2 tasks. A staff of three teachers from set
is planned for the execution of the courses. The competencies of the individual teachers comprise the personnel competency framework presented in
Table 1. The framework is represented by a competency matrix,
in which values “1” and “0” stand for having or not having a specific competency, respectively.
The organisation observes the following course completion rules (constraints):
- (a)
A task of a course can only be carried out by a competent teacher,
- (b)
Each teacher must perform no less than 1 task and no more than 2 tasks,
- (c)
All tasks of courses must be assigned to teachers.
The competency framework enables the completion of tasks in a process that satisfies the constraints above, in accordance with teacher allocation,
, presented in
Table 2. In a permissible teacher allocation.
, teacher
carries out a task of course
, teacher
carries out a task of course
, and teacher
carries out two tasks of course
.
Let us consider a situation in which teacher
is absent from the execution of tasks (teacher absence). In this situation, it is necessary to modify teacher allocation,
(
Table 2), by substituting the teacher allotted to performing tasks of course
. As competency framework
(
Table 1) shows, none of the remaining teachers has the competencies to complete tasks of course
. The absence of teacher
requires that two tasks of course
should be delegated to other teachers. It is not possible to delegate both tasks to them because they lack competencies enabling the execution of course
. In this case, the following question should be considered: Does there exist a competency framework,
that guarantees a permissible allocation,
despite the absence of teacher
? This competency framework,
is presented in
Table 3. Permissible teacher allocation,
where one task of course
is allocated to teacher
and one to teacher
is presented in
Table 4. In this situation, constraints (b) and (c) are satisfied (
Table 4).
It is easy to note that the obtained competency framework,
, presented in
Table 3, ensures that tasks are completed despite the absence of teacher
, which means the framework is robust to the type of disruption under consideration.
In the example considered above, competency framework,
(
Table 3), guarantees permissible teacher allocation,
regardless of which teacher is absent. In other words, the competency framework,
is fully robust to the absence of a single teacher. This situation is not always possible. Typically, the given competency framework will secure only certain variants of teacher absence. The number of scenarios for a given disruption for which a given competency framework guarantees an acceptable allocation of teachers to courses is determined by what is known as the robustness of a competency framework function.
Describing the robustness of competency framework,
of a given staff of teachers,
, who perform tasks of set
(a set of courses), to the absence of
teachers requires the concept of Robustness of a Competency Framework, that is defined as a function
:
where:
, a domain of variable
describing the number of absent teachers. Therefore, the function of the competency framework robustness is determined from the equation:
where:
| is a family of -number of simultaneous teacher absences: , for example, for the case of an absence of two teachers in the example above (Table 3 and Table 4 contains 3 absence scenarios. |
| is a subset of set () which contains absence scenarios for which competency framework, guarantees permissible teacher allocation to courses in the event of absences of teachers. In a special case, subset can be an empty set, i.e., , which corresponds to a situation in which no suitable replacement enabling the execution of all the courses from set can be found for any of the 28 absence scenarios. |
The adopted measure of robustness, , which is a ratio between the number of absences for which there are appropriate replacements || to the number of all possible cases of absence ||, takes values from the range , where:
stands for lifelessness (robustlessness), i.e., there is no suitable replacement enabling the execution of all tasks from set for any of the possible cases of absence (-number of simultaneous teacher absences).
stands for full robustness, i.e., for each of the possible cases of absence (-number of simultaneous teacher absences) there is at least one replacement guaranteeing the execution of all the tasks from set .
In the context of the proposed measure of robustness,
, the problem of synthesis of the robust competency framework,
boils down to the question: Does there exist, for a given set of tasks,
executed by
teachers, a competency framework,
, which guarantees robustness,
(to the absence of
teachers), greater than or equal to arbitrarily adopted values,
? The search for competency frameworks, that guarantee a specific level of robustness,
is a combinatorial optimisation NP-hard problem belonging to the class of synthesis problems [
12].
In general, the synthesis problem of competency frameworks robust to a selected set of disruptions, AAPDO, can be formulated as follows: Given is a university employing academic staff described by the competency framework provided. The organisation’s objectives and the set of tasks it carries out are known. The goal is to find an answer to the question: Does there exist a model and a method of constructing competency frameworks robust to selected disruptions caused by teacher absenteeism, loss of qualifications, etc.?
3.2. Model
The declarative framework-driven reference model of AAPDO presented below allows, in a natural way, for the formulation of a constraint satisfaction problem to generate competency frameworks robust to disruptions caused by teacher absenteeism.
A university potential and the student curricula requirements can be represented as a model linking two main elements: set of jobs, (courses), and competency framework, , representing the competencies possessed by the university teachers.
Set of courses
: The courses determined by student curricula are represented by set
where
is the
-th course. It is generally assumed that lectures on a given subject (course
) are conducted for a number of student groups. The implementation of course
is, therefore, related to the implementation of a certain number of tasks (
) of given durations (sizes) (
). Tasks of
can have different sizes
, however, for simplicity, let us assume that each task of
is of the same size, i.e.,
. In that context, course
is described by two elements: the number of tasks (
) and their duration (
):
where:
is the number of tasks of course
, and
is the duration (size) of each task of course
.
It is assumed that courses are conducted by a competent teacher.
University teaching staff: A staff of teachers,
employed by the university is allocated to perform the planned tasks. Set
defines a staff of teachers, where
is a pair:
where:
is the minimum working hours of the
-th teacher (
)
is the maximum working hours of the
-th teacher (
).
University teaching staff,
corresponds to the competency framework defined as a function
that assigns to each pair
a value from the set
:
—when teacher
does not have the competence to execute tasks from course
, and
—when teacher
has the competence to execute tasks from course
. To simplify the notation, it is assumed that
. As a result, the matrix representation of the competency framework of a staff of teachers,
takes the form:
where:
,
.
Teacher allocation,
specifies which tasks are assigned to each member of staff,
in the execution of tasks from course
. The allocation is a function
that assigns to each pair
a value from set
:
—when teacher
does not execute tasks of course
, and
—when teacher
executes tasks of course
. For simplicity considerations, it is assumed that
, and the resulting matrix representation of allocation takes the form:
where:
represents the number of tasks from course
executed by teacher
.
It is further assumed that:
Tasks can only be executed by a competent teacher, i.e., .
Teacher working time limits may not be exceeded, i.e., and .
Disruptions and the measure of robustness of the competency framework: Let us discuss one type of disruption, namely teacher absences. This disruption is characterised by a family of combinations of set . In other words, the family consists of scenarios parametrised by —the number of simultaneous teacher absences. The occurrence of this type of disruptions spurs the search for allocation, that allows a set of courses, Z, to be executed without interruptions. How this should be interpreted is that when one teacher is absent, their responsibilities can be transferred to another currently available teacher. It is not always possible to implement such an allocation, , however, to assess the chances of implementing an allocation, we use the concept of robustness of a competency framework (1).
To put this type of problems into formal terms, the following reference model is introduced:
Sets:
| : | Set of courses: |
| : | Set of teachers: |
| Family of scenarios parametrised by the number of simultaneous teacher absences: . |
| : | A single scenario of absence of teachers, |
| : | Subset (), which contains absence scenarios for which competency framework, guarantees a permissible teacher allocation, to courses in the event of absences of teachers. |
Parameters:
| Number of courses () |
| : | Number of tasks from course |
| Number of teachers () |
| Number of absent teachers, (), |
| : | Duration of the task from course (in hours) |
| : | Minimum working hours of teacher ) |
| : | Maximum working hours of teacher ) |
| : | Predicted robustness of the competency framework () |
Decision variables:
| : | Competency framework given by matrix where: : Robustness of competency framework, for the absence of teachers is described by function (1). |
| : | Competency framework which takes into account absences of teachers defined in set : where: |
| Teacher allocation, , where: means the number of tasks from course executed by teacher . |
| : | Allocation in situations when teachers defined in set are absent from work: , where: represents the number of tasks from course executed by teacher . |
| : | A variable that specifies whether there exists allocation ensuring execution of tasks from courses, . The value of variable depends on ancillary sub-variables: , , , which specify whether constraints (6)–(13) are satisfied. |
Constraints:
The element
of matrix
that characterises the absence of teacher
(
) takes the value 0:
Tasks are only executed by teachers who have the appropriate competence:
All tasks,
from course
should be executed:
Workload of teacher
is equal to or greater than the minimum number of working hours,
:
Workload of teacher
is not greater than the maximum number of working hours,
:
Robustness,
is calculated as a ratio of the number of absence scenarios
for which the competency framework is robust to the absence of
teachers to all possible disruption scenarios (
):
To summarise, the model proposed above comprises a set of decision variables (describing competency framework, the measure of its robustness and teacher allocation), discrete domains of decision variables and a set of constraints (relationships connecting the decision variables) which specify the requirements for the competency framework and the execution of planned courses.
The concepts of the competency framework and teacher allocation, are represented by decision variables , and . Allocation, , in the event of teacher absence defined in set , which meets constraints (6)–(13), is hereafter referred to as a permissible allocation. Given the assumptions presented above, the model is deterministic.
From how the model is specified, that is being limited to defining the decision variables, variable domains and the constraints on subsets of variables, the problem under consideration belongs to the class of Constraint Satisfaction Problems (CSP).
3.3. Method
The structure of the proposed model that includes a set of decision variables and a set of constraints that relate those variables to one another in a natural way allows to formulate the problem in hand as a CSP and implement it in a constraint programming environment:
where:
| —a set of decision variables which includes: robustness of competency framework , competency framework , competency frameworks for cases when the teachers from set are absent, corresponding task allocations . |
| —a finite set of decision variable domains |
| —a set of constraints specifying the relationships between the competency framework and its robustness (constraints 1–10). |
To solve
(14), it is enough to find the values of decision variables
(competency framework),
(teacher allocation) and
(robustness of a competency framework), determined by domains
for which all the constraints of set
are satisfied. In other words, what is sought is a solution that guarantees a given level of robustness,
in the case of simultaneous absences of
teachers. In general, a CSP defined in this way can be treated as an optimisation problem. In such cases, the investigation focuses on determining the minimum competency framework,
(e.g., one that meets the criterion of the minimum number of competence changes). In the general case, a CS (14) can be treated as an optimisation problem whose goal is to determine the minimum competency framework,
(e.g., one that requires a minimum number of changes to be made to the baseline competency framework). CSP converted into a Constraint Optimisation Problem (COP) is given by the formula:
where:
are defined as in (11), and
is the objective function:
To solve (15), determine such values of decision variable for which all constraints given in the set are satisfied and for which function has a minimum value (a minimum number of changes have to be made to the original competency framework, ) or, to put it differently, returns a minimum competency framework. In general, (15) synthesises minimal competency frameworks robust to simultaneous absences of teachers.
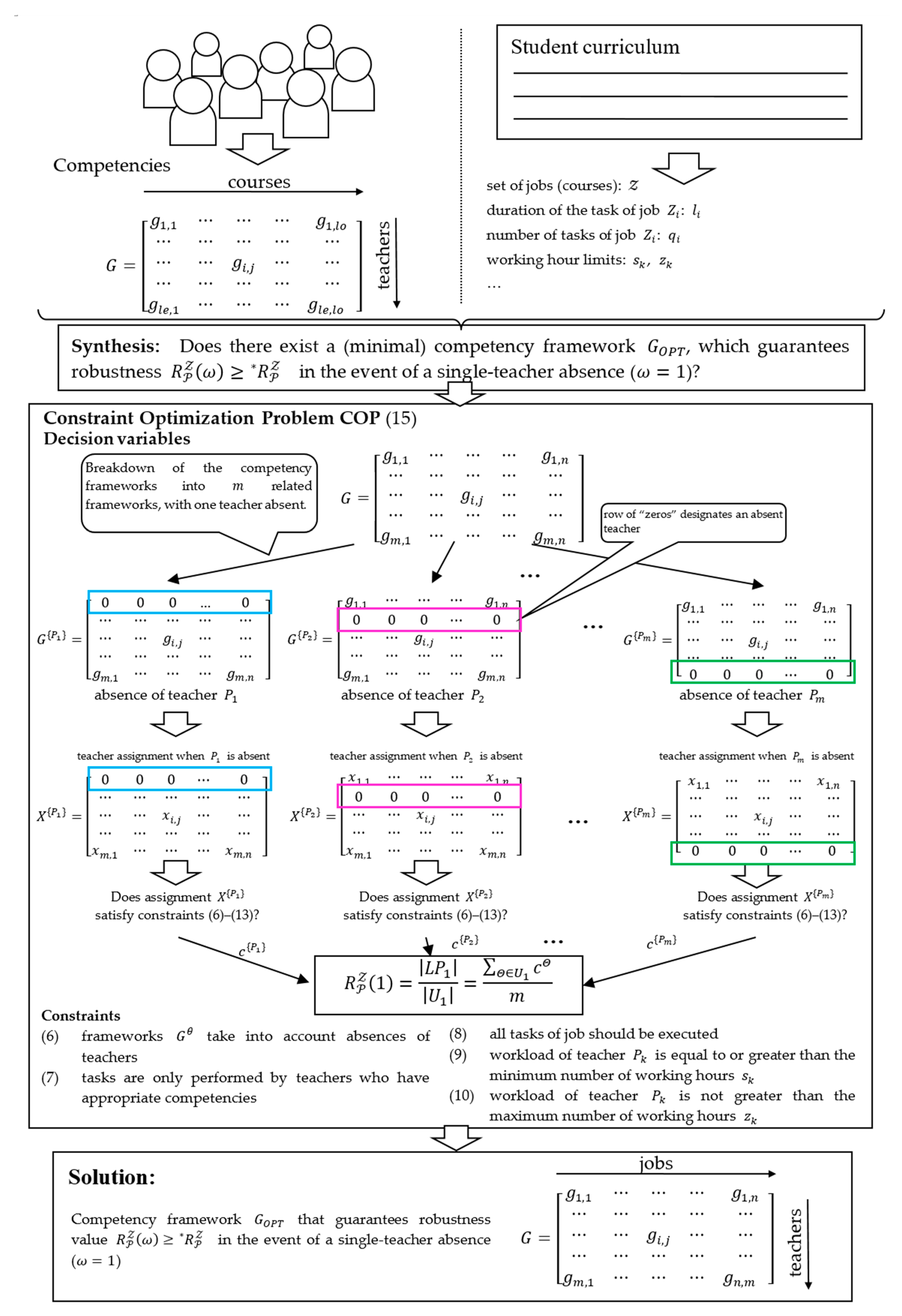
The model of the synthesis problem
presented in
Figure 2 illustrates the procedure of finding a competency framework,
with a given level of robustness (
) for the case of individual teacher absence (
). A specific level of robustness can be obtained from the introduction of decision variables
which represent the competency frameworks for the cases of individual teacher absences:
. Full robustness (
) is reached when there exists a framework,
, for which each
guarantees teacher allocation
that meets constraints (6)–(13) (
). In other words, the solution to problem
(15) is a minimal competency framework,
that guarantees completion of all tasks for all cases of single-teacher absences.
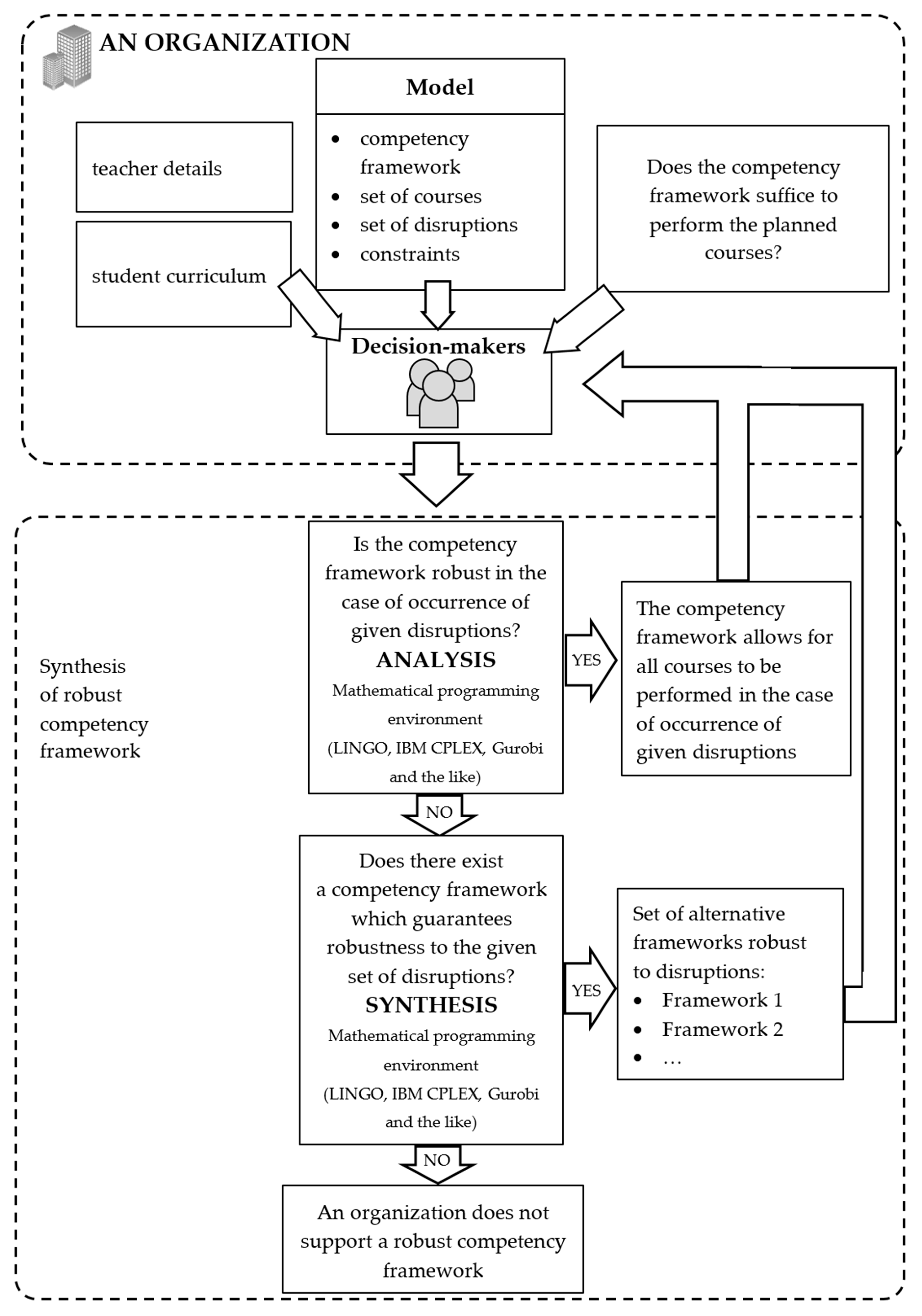
The method shown in
Figure 3 was developed for the synthesis of a minimal competency framework robust to disruptions resulting from various factors, including simultaneous absences of
teachers or loss of qualifications (competencies). Decision-makers are aware of the possible occurrence of a specific set of disruptions. Our decision support tool is designed to answer the question regarding the analysis (evaluation) of the robustness of the competency framework to a selected set of disruptions. When the answer is positive (the competency framework is sufficiently flexible to allow the available personnel to complete all courses), the university can proceed to execute the tasks without fear of disruption. When the answer is negative (the competency framework is insufficiently flexible to allow the available teachers to complete all courses), the decision-maker may then implement the method proposed in this paper to look for an answer to the question regarding the synthesis of the competency framework (solution to
(15)), i.e., to search available data (in this case, the competency framework) to find a teacher allocation that meets specific expectations (e.g., robustness of the competency framework to the selected set of disruptions). When the answer is positive, the decision-maker obtains a set of alternative competency frameworks that guarantee the organisation’s robustness to a selected set of disruptions. It is on the basis of this set of admissible alternative frameworks, that substantiated decisions regarding issues such as further development of the staff can be made. It is the decision-maker’s responsibility to choose the most favourable variant (one that meets a criterion of the choice). A negative answer informs the decision-maker that it is impossible in the given organisation to build a competency framework robust to the selected set of disruptions and consider changing (increasing) working time limits, employing new staff, outsourcing to temporary workers, etc.
Implemented in LINGO programming environments with a hybrid approach proposed by Wikarek and Sitek [
62], the method was used in a series of computational experiments testing the synthesis competency framework of teaching staff in a real university environment. Preliminary results have confirmed the benefits of the adopted declarative approach that allow designing an open structure model, as well as an implementation of the method derived from this model and used in interactive decision support systems (DSS) dedicated to online solving of staff planning problems [
63].