Seismic Vulnerability of Cabinet Facility with Tuned Mass Dampers Subjected to High- and Low-Frequency Earthquakes
Abstract
1. Introduction
2. Numeric Modeling of NPP Equipment
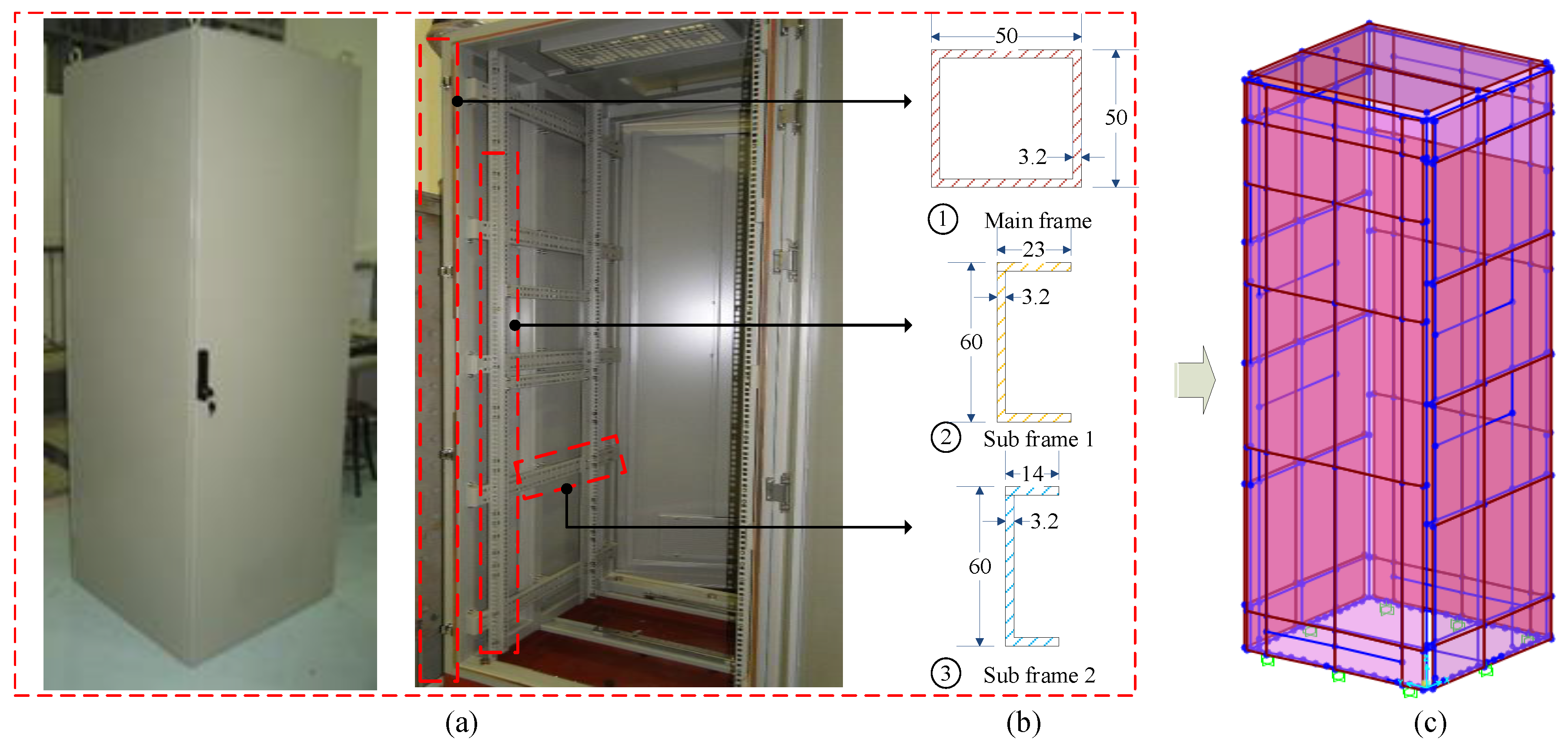
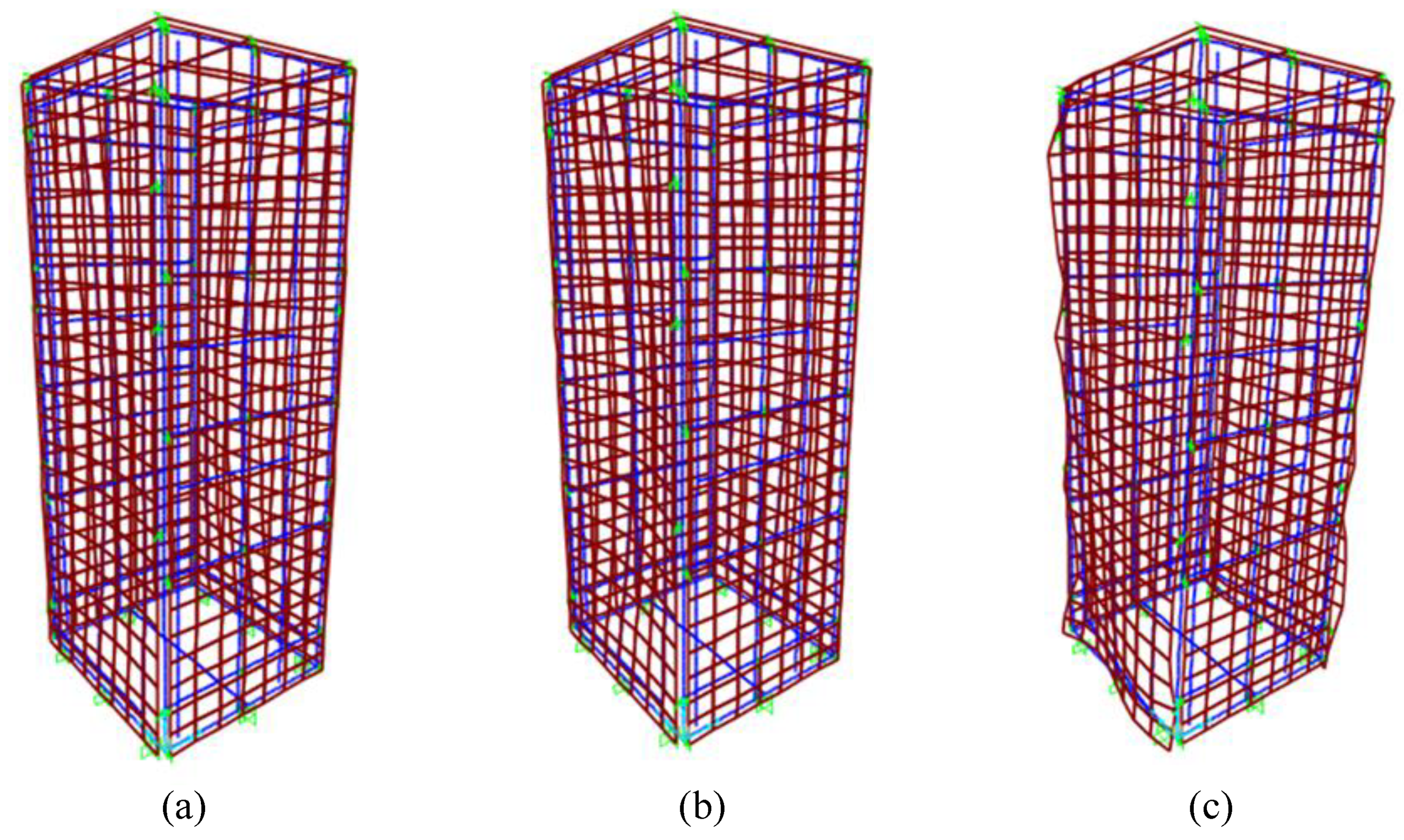
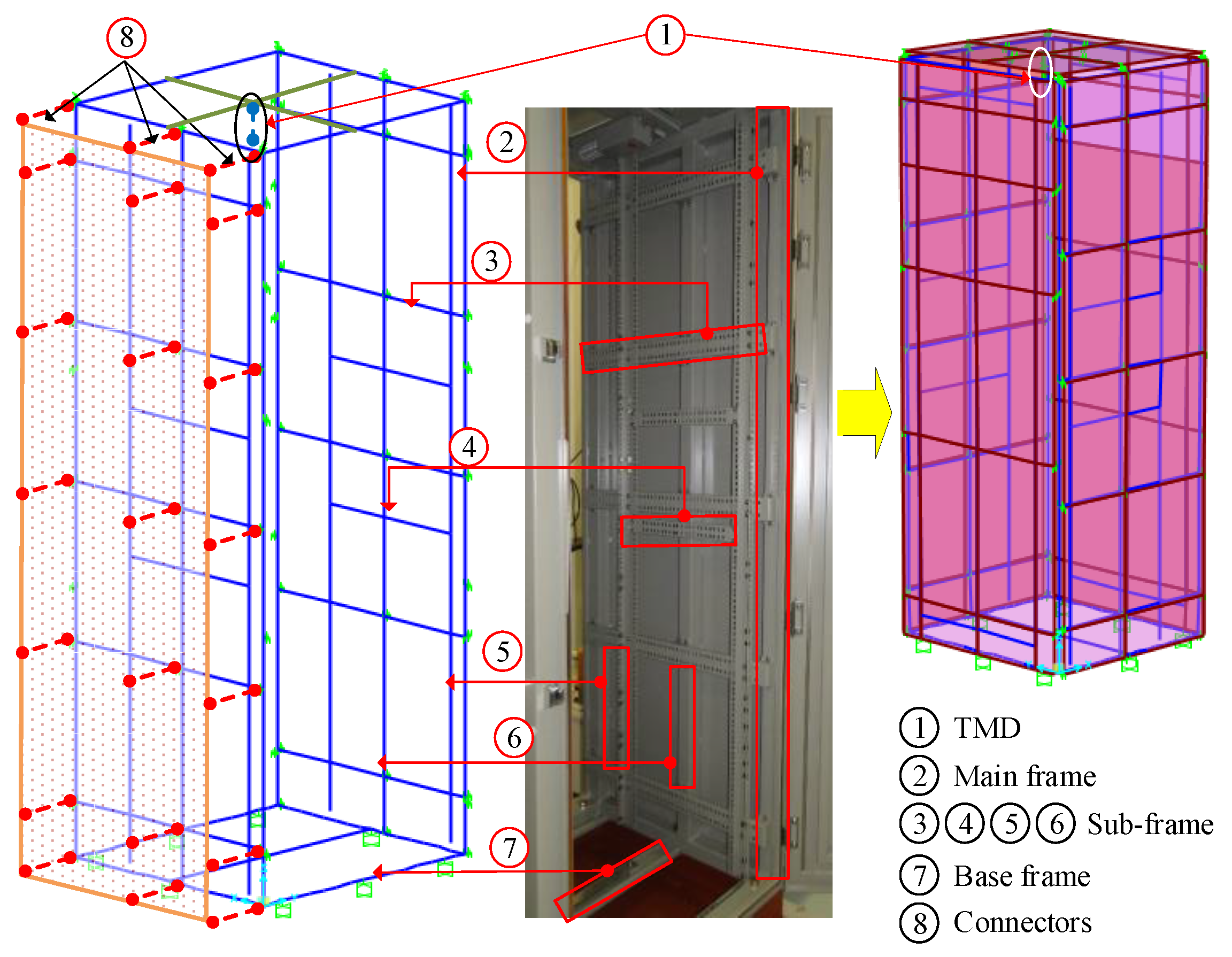
2.1. Structural Configurations
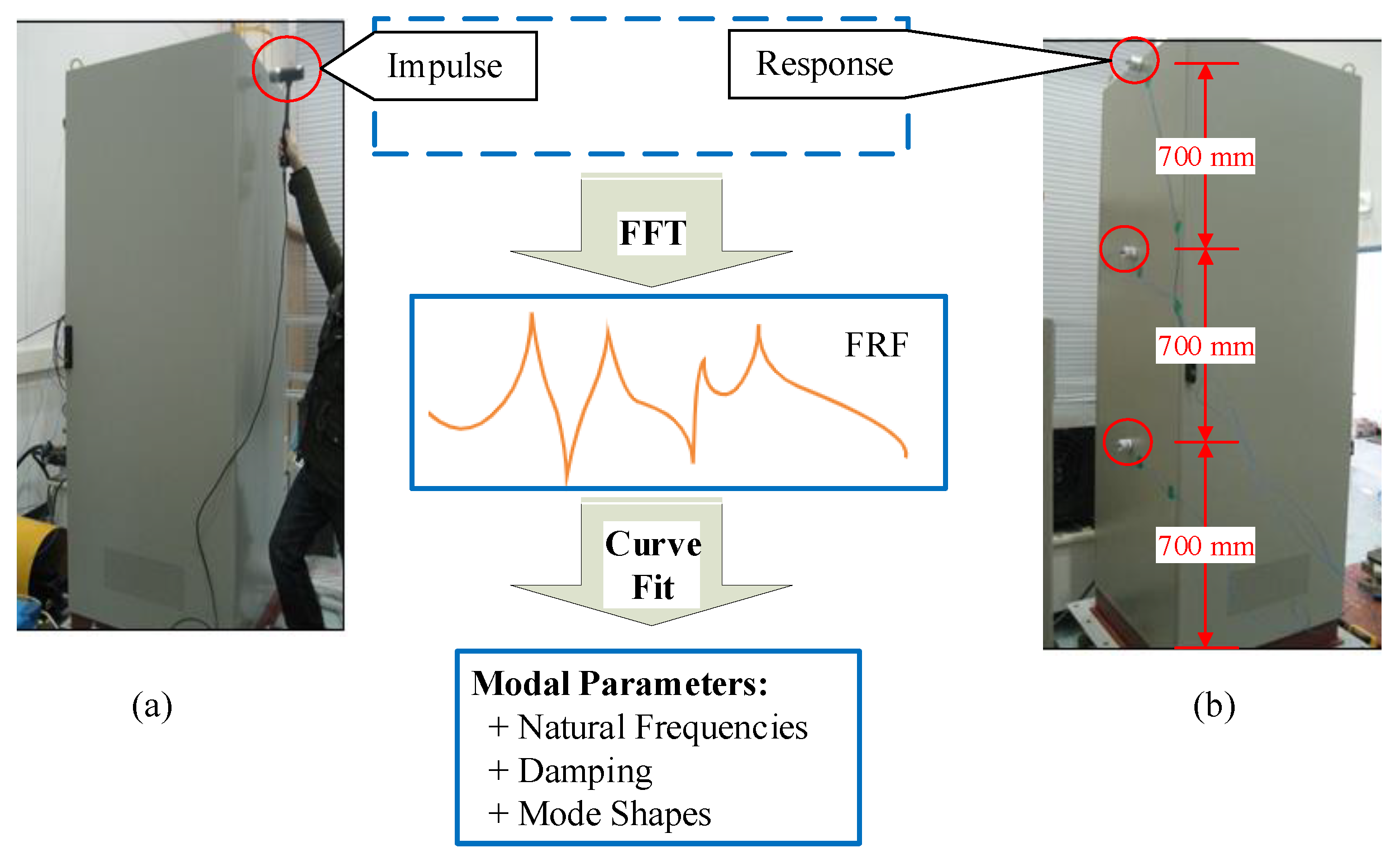
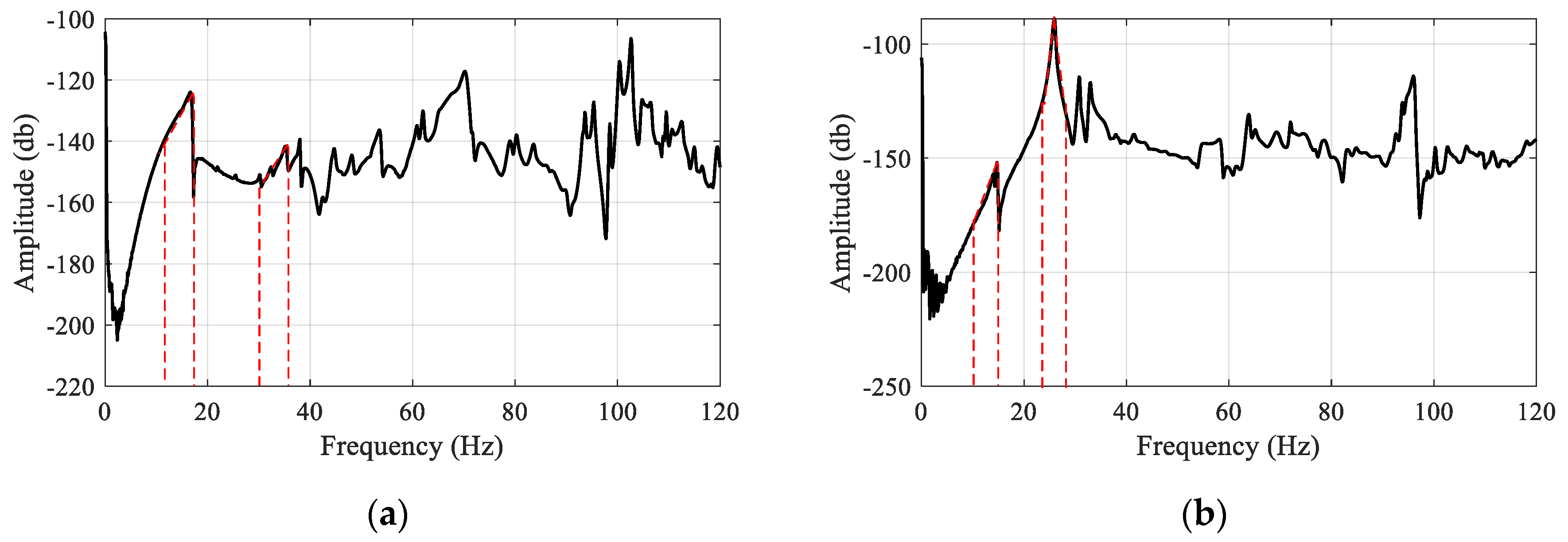
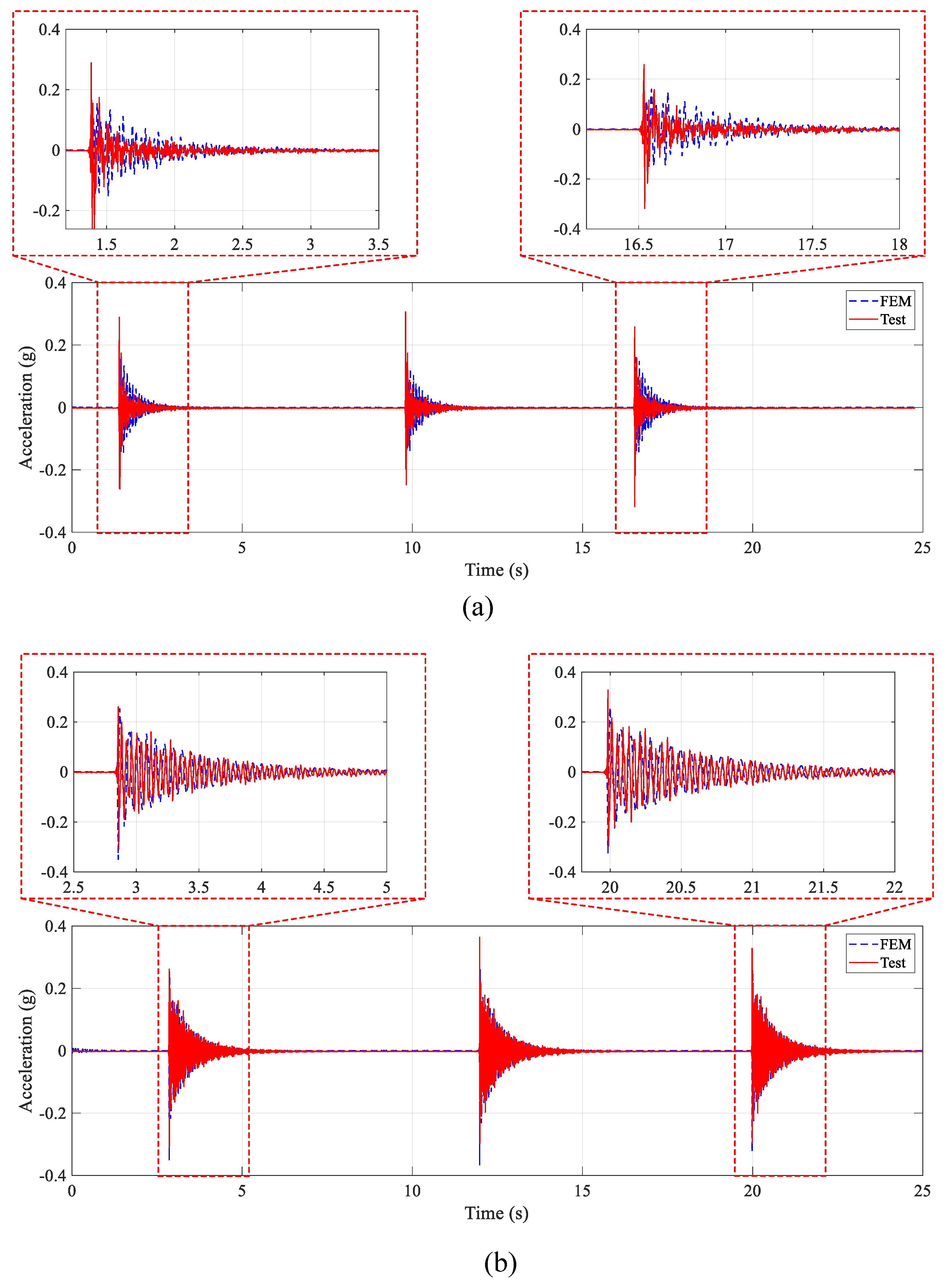
2.2. Validation of the Numeric Model
2.3. Modal Analysis
2.4. Modeling with Tuned Mass Damper (TMD)
2.4.1. Mathematical Modeling of the TMD System
2.4.2. Optimum TMD Parameters
2.4.3. Structural Modeling with TMD System
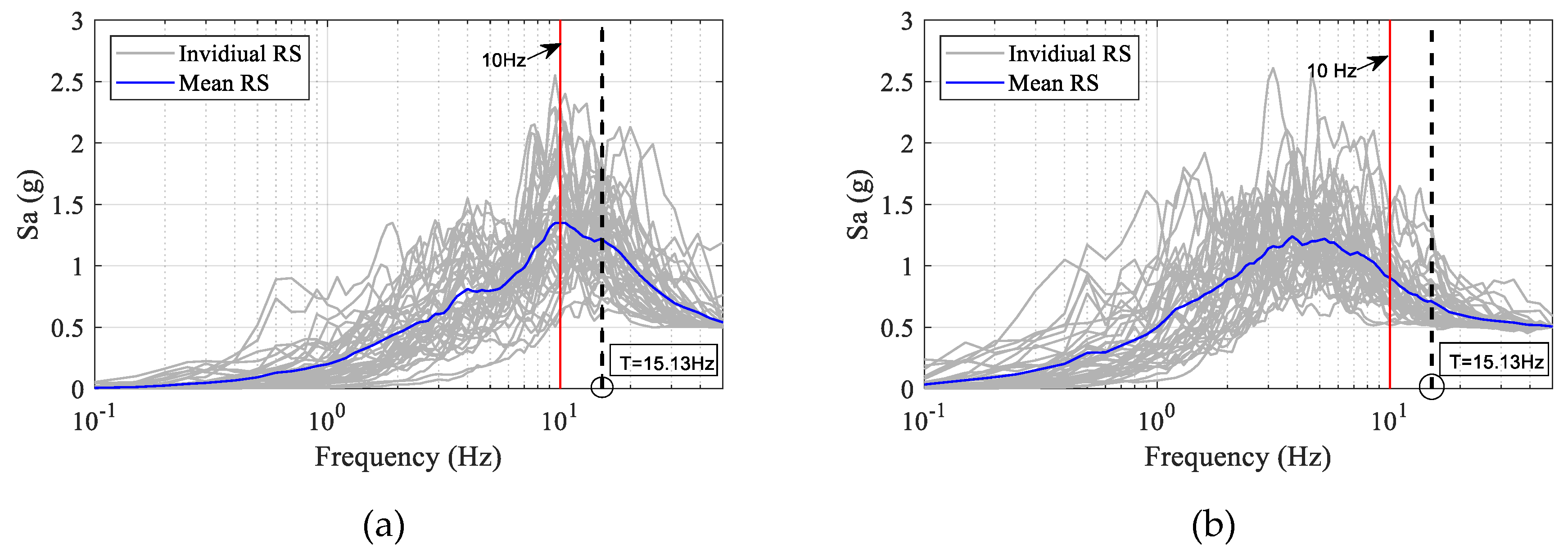
3. Ground Motion Selection
4. Results and Discussions
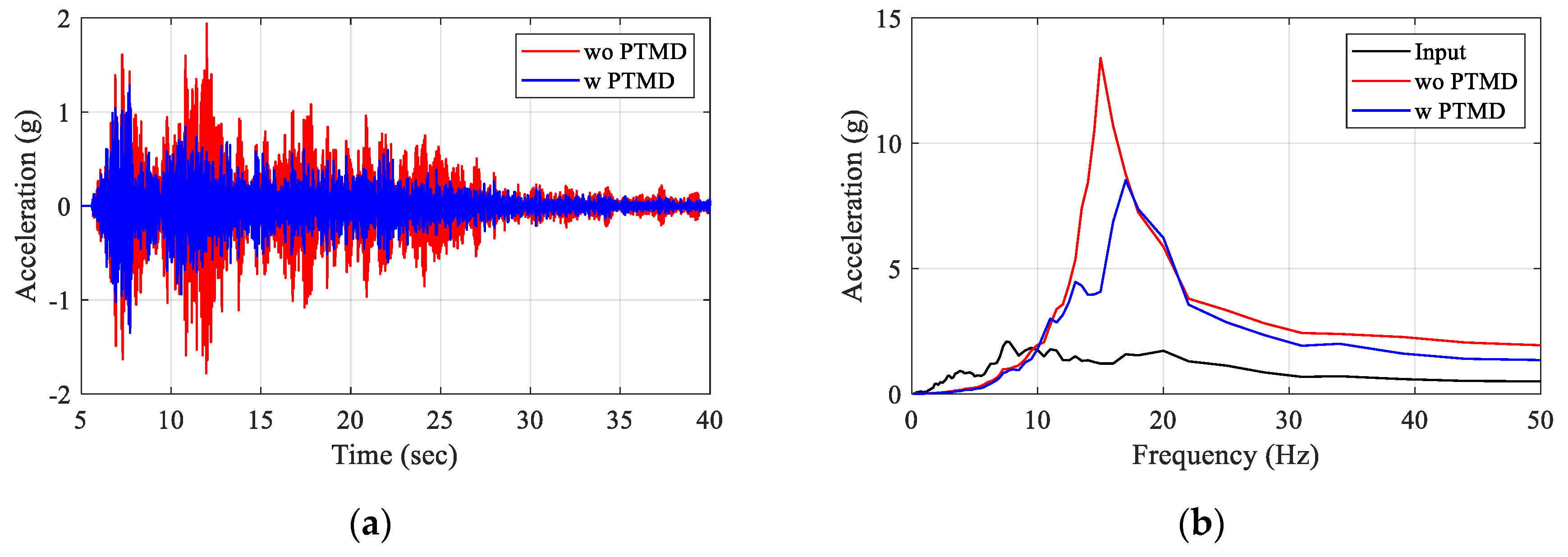
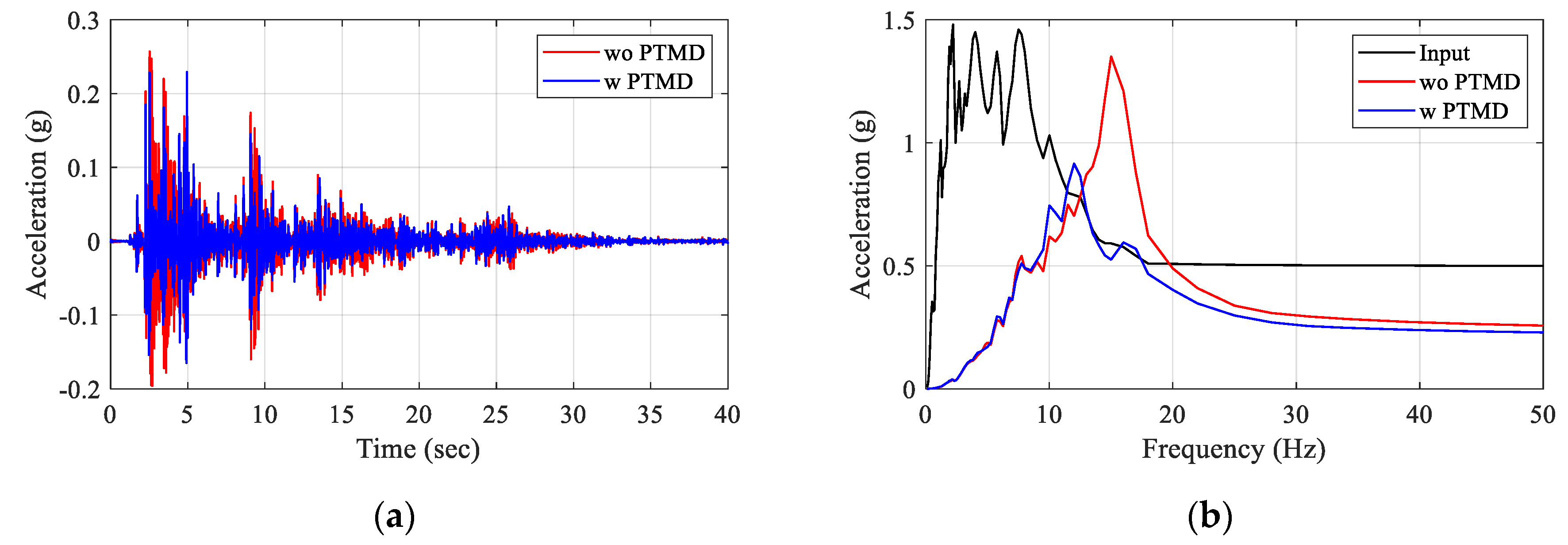
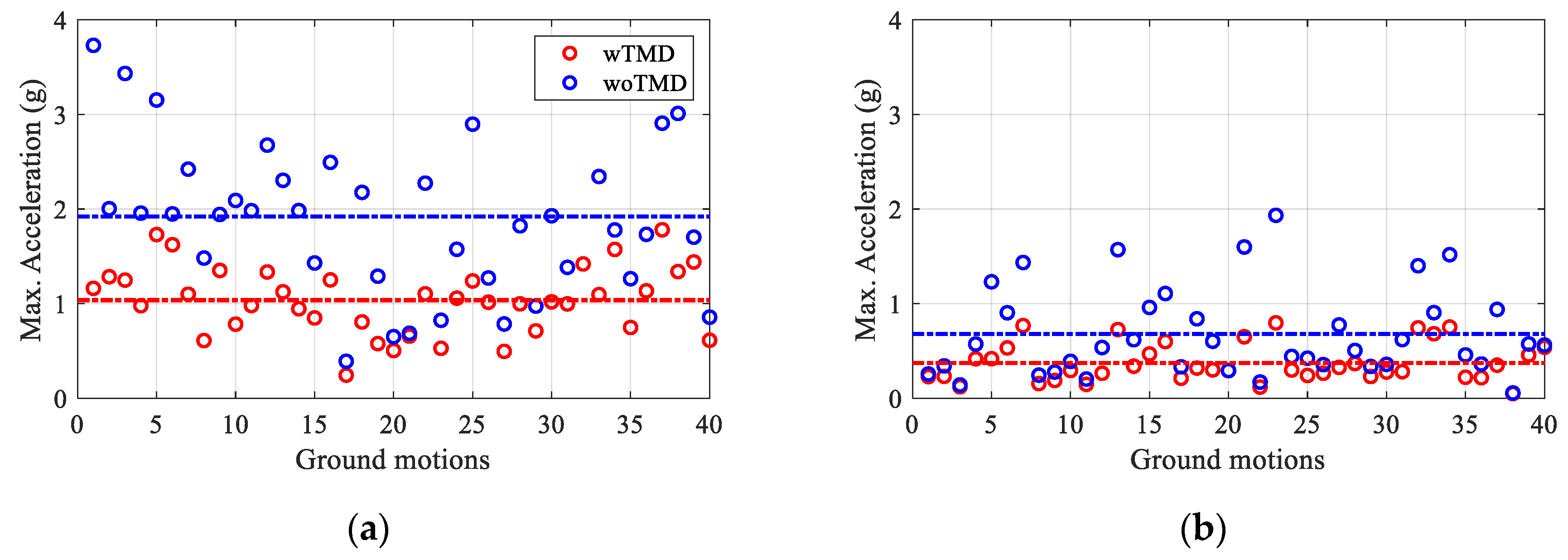
4.1. Comparison of Uncontrolled and Controlled Responses
4.2. Effect of Frequency Contents on the Seismic Responses
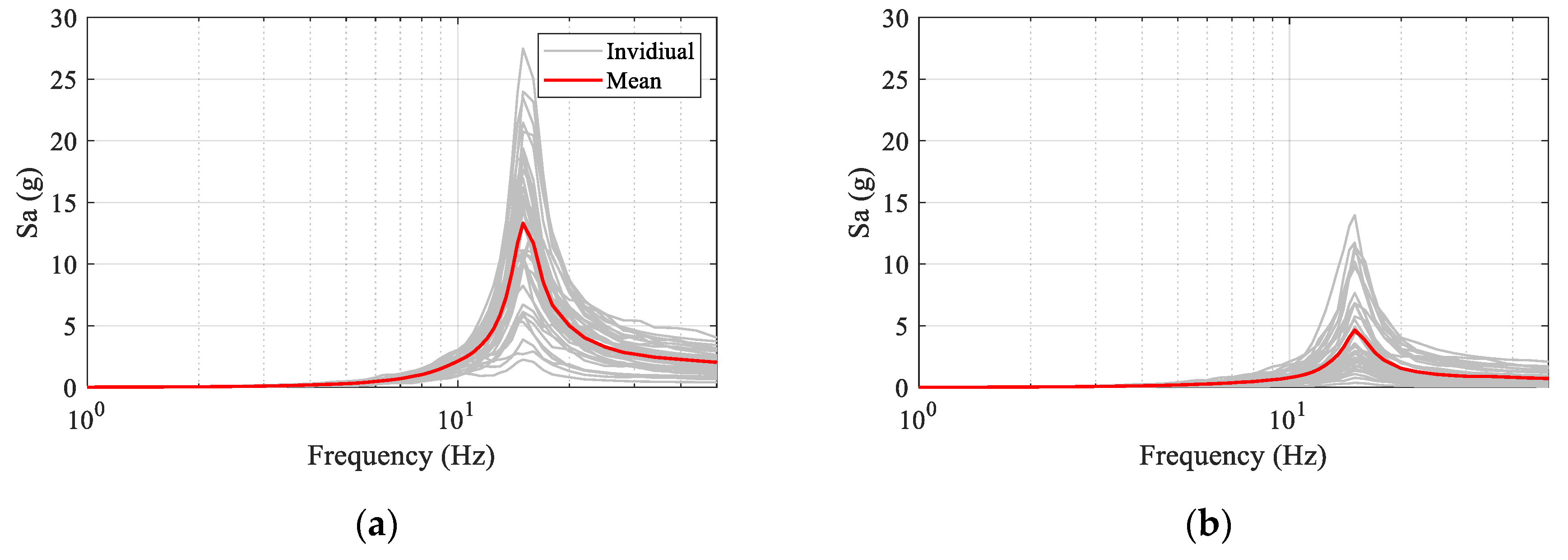
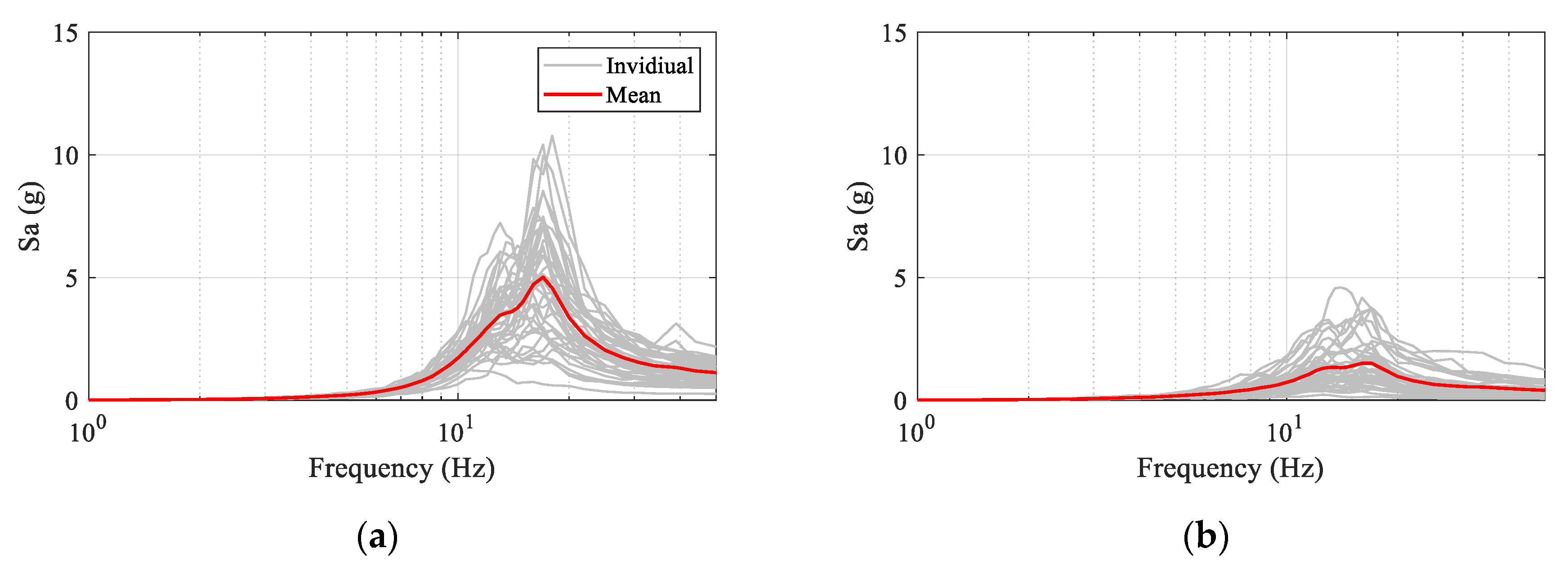
4.3. Fragility Analysis
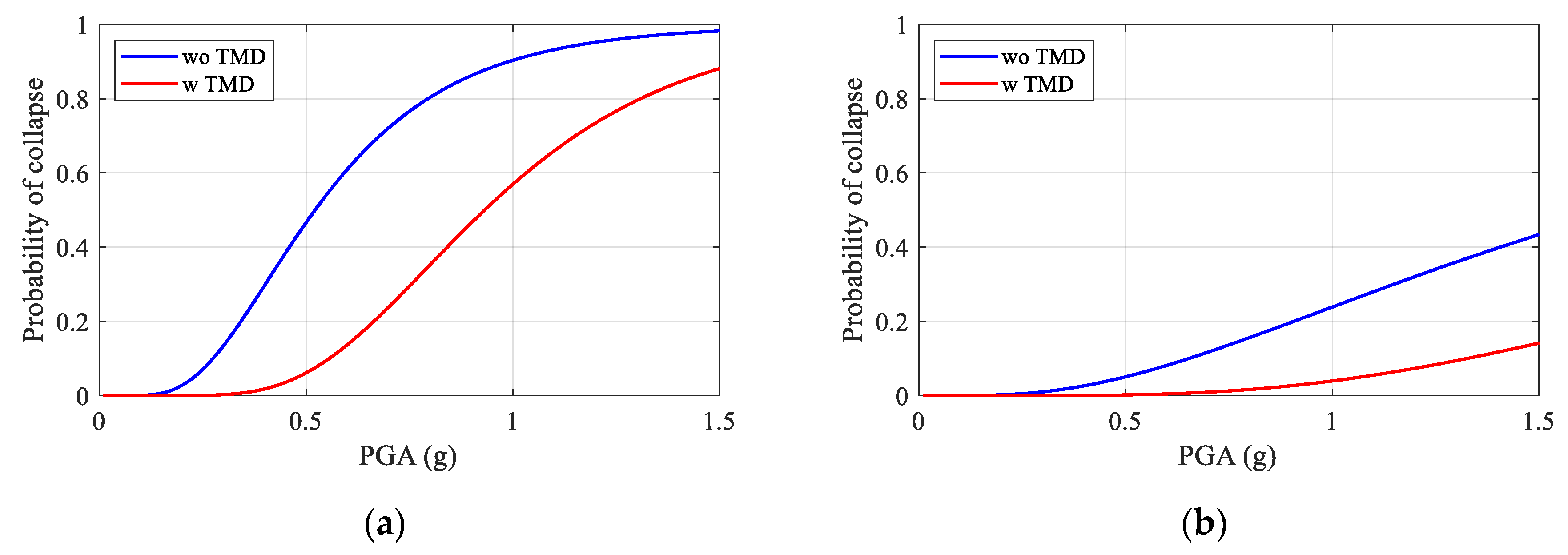
4.3.1. Effects of the Vibration Control System on the Seismic Vulnerability of the Cabinet
4.3.2. Effects of Frequency Contents on the Seismic Vulnerability of the Cabinet
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Anajafi, H.; Medina, R.A. Damping modification factor for elastic floor spectra. Bull. Earthq. Eng. 2019, 17, 6079–6108. [Google Scholar] [CrossRef]
- Sullivan, T.J.; Calvi, P.M.; Nascimbene, R. Towards improved floor spectra estimates for seismic design. Earthq. Struct. 2013, 4, 109–132. [Google Scholar] [CrossRef]
- Filiatrault, A.; Sullivan, T. Performance-based seismic design of nonstructural building components: The next frontier of earthquake engineering. Earthq. Eng. Eng. Vib. 2014, 13, 17–46. [Google Scholar] [CrossRef]
- Rodriguez, M.E.; Restrepo, J.I.; Carr, A.J. Earthquake-induced floor horizontal accelerations in buildings. Earthq. Eng. Struct. Dyn. 2002, 31, 693–718. [Google Scholar] [CrossRef]
- Singh, M.P.; Moreschi, L.M.; Suárez, L.E.; Matheu, E.E. Seismic Design Forces. II: Flexible Nonstructural Components. J. Struct. Eng. 2006, 132, 1533–1542. [Google Scholar] [CrossRef]
- Adam, C.; Furtmüller, T. Response of nonstructural components in ductile load-bearing structures subjected to ordinary ground motions. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008. [Google Scholar]
- Adam, C.; Furtmüller, T.; Moschen, L. Floor response spectra for moderately heavy nonstructural elements attached to ductile frame structures. In Computational Methods in Applied Sciences; Springer: New York, NY, USA, 2013; Volume 30, pp. 69–89. [Google Scholar]
- Anajafi, H.; Medina, R.A. Lessons Learned from Evaluating the Responses of Instrumented Buildings in the United States: The Effects of Supporting Building Characteristics on Floor Response Spectra. Earthq. Spectra 2019, 35, 159–191. [Google Scholar] [CrossRef]
- Di Sarno, L.; Magliulo, G.; D’Angela, D.; Cosenza, E. Experimental assessment of the seismic performance of hospital cabinets using shake table testing. Earthq. Eng. Struct. Dyn. 2019, 48, 103–123. [Google Scholar] [CrossRef]
- Filiatrault, A.; Matt, H. Seismic response of high voltage electrical transformer-bushing systems. J. Struct. Eng. 2006, 132, 287–295. [Google Scholar] [CrossRef]
- Tran, T.-T.; Kim, D. Uncertainty quantification for nonlinear seismic analysis of cabinet facility in nuclear power plants. Nucl. Eng. Des. 2019, 355, 110309. [Google Scholar] [CrossRef]
- Nguyen, P.C.; Doan, N.T.N.; Ngo-Huu, C.; Kim, S.E. Nonlinear inelastic response history analysis of steel frame structures using plastic-zone method. Thin Walled Struct. 2014, 85, 220–233. [Google Scholar] [CrossRef]
- Cao, A.T.; Tran, T.T.; Nguyen, T.H.X.; Kim, D. Simplified Approach for Seismic Risk Assessment of Cabinet Facility in Nuclear Power Plants Based on Cumulative Absolute Velocity. Nucl. Technol. 2019, 206, 1–15. [Google Scholar] [CrossRef]
- Suehiro, S.; Sugimoto, J.; Hidaka, A.; Okada, H.; Mizokami, S.; Okamoto, K. Development of the source term PIRT based on findings during Fukushima Daiichi NPPs accident. Nucl. Eng. Des. 2015, 286, 163–174. [Google Scholar] [CrossRef]
- Gupta, A.; Cho, S.G.; Hong, K.J.; Han, M. Current state of in-cabinet response spectra for seismic qualification of equipment in nuclear power plants. Nucl. Eng. Des. 2019, 343, 269–275. [Google Scholar] [CrossRef]
- Li, Y.; Manoly, K. GI 199 and 2011 Mineral, VA Earthquake Impact to North Anna Nuclear Power Plant. In Proceedings of the 15th World Conference on Earthquake Engineering, Lisbon, Portugal, 24–28 September 2012. [Google Scholar]
- Nguyen, D.D.; Thusa, B.; Han, T.S.; Lee, T.H. Identifying significant earthquake intensity measures for evaluating seismic damage and fragility of nuclear power plant structures. Nucl. Eng. Technol. 2019, 52, 192–205. [Google Scholar] [CrossRef]
- Goodno, B.J.; Gould, N.C.; Caldwell, P.; Gould, P.L. Effects of the January 2010 haitian earthquake on selected electrical equipment. Earthq. Spectra 2011, 27, 251–276. [Google Scholar] [CrossRef]
- Tran, T.T.; Cao, A.T.; Nguyen, T.H.X.; Kim, D. Fragility assessment for electric cabinet in nuclear power plant using response surface methodology. Nucl. Eng. Technol. 2019, 51, 894–903. [Google Scholar] [CrossRef]
- Tran, T.T. Modelling and Simualtion of Uncertianties for Nuclear Facilities and Soil Deposits; Kunsan National University: Gunsan, Korea, 2020. [Google Scholar]
- Salman, K.; Tran, T.T.; Kim, D. Grouping effect on the seismic response of cabinet facility considering primary-secondary structure interaction. Nucl. Eng. Technol. 2019, 52, 1318–1326. [Google Scholar] [CrossRef]
- Salman, K.; Tran, T.T.; Kim, D. Seismic capacity evaluation of NPP electrical cabinet facility considering grouping effects. J. Nucl. Sci. Technol. 2020, 57, 1–13. [Google Scholar] [CrossRef]
- Gupta, A.; Rustogi, S.; Gupta, A. Ritz vector approach for evaluating incabinet response spectra. Nucl. Eng. Des. 1999, 190, 255–272. [Google Scholar] [CrossRef]
- HAZUS. Earthquake Loss Estimation Methodology: Hazus-MH 2.1, Advanced Engineering Building Module (AEBM): Technical and User’s Manual; Federal Emergency Management Agency: Washington, DC, USA, 1969. [Google Scholar]
- Bancfyopadhyay, K.K.; Hofmayer, C.H.; Kassir, K.M.; Shteyngart, S. Seismic Fragility of Nuclear Power Plant Components [PHASE II]; Brookhaven National Laboratory: Upton, NY, USA, 1991. [Google Scholar]
- Ormondroyd, J.; Den Hartog, J.P. The theory of the dynamic vibration absorber. Trans. ASME Appl. Mech. 1928, 50, 9–22. [Google Scholar]
- Wirsching, P.H.; Yao, J.T.P. Safety design concepts for seismic structures. Comput. Struct. 1973, 3, 809–826. [Google Scholar] [CrossRef]
- Wirsching, P.H.; Campbell, G.W. Minimal structural response under random excitation using the vibration absorber. Earthq. Eng. Struct. Dyn. 1973, 2, 303–312. [Google Scholar] [CrossRef]
- Rahman, M.S.; Chang, S.; Kim, D. Multiple wall dampers for multi-mode vibration control of building structures under earthquake excitation. Struct. Eng. Mech. 2017, 63, 537–549. [Google Scholar]
- Anajafi, H.; Medina, R.A. Comparison of the seismic performance of a partial mass isolation technique with conventional TMD and base-isolation systems under broad-band and narrow-band excitations. Eng. Struct. 2018, 158, 110–123. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Cox, J.A.; Lombardi, D.; Muir Wood, D. Dynamics of offshore wind turbines supported on two foundations. Proc. Inst. Civ. Eng. Geotech. Eng. 2013, 166, 159–169. [Google Scholar] [CrossRef]
- Sgobba, S.; Marano, G.C. Optimum design of linear tuned mass dampers for structures with nonlinear behavior. Mech. Syst. Signal Process. 2010, 24, 1739–1755. [Google Scholar] [CrossRef]
- Cho, S.G.; Chang, S.; Sung, D. Application of Tuned Mass Damper to Mitigation of the Seismic Responses of Electrical Equipment in Nuclear Power Plants. Energies 2020, 13, 427. [Google Scholar] [CrossRef]
- Kwag, S.; Kwak, J.; Lee, H.; Oh, J.; Koo, G.-H. Enhancement in the Seismic Performance of a Nuclear Piping System using Multiple Tuned Mass Dampers. Energies 2019, 12, 2077. [Google Scholar] [CrossRef]
- Chang, S.; Sun, W.; Cho, S.G.; Kim, D. Vibration Control of Nuclear Power Plant Piping System Using Stockbridge Damper under Earthquakes. Sci. Technol. Nucl. Install. 2016, 2016, 1–12. [Google Scholar] [CrossRef]
- Chang, S.; Sung, D. Modal-Energy-Based Neuro-Controller for Seismic Response Reduction of a Nonlinear Building Structure. Appl. Sci. 2019, 9, 4443. [Google Scholar] [CrossRef]
- Kwag, S.; Ryu, Y.; Ju, B.-S. Efficient Seismic Fragility Analysis for Large-Scale Piping System Utilizing Bayesian Approach. Appl. Sci. 2020, 10, 1515. [Google Scholar] [CrossRef]
- Anajafi, H. Improved Seismic Design of Non-Structural Components (NSCs) and Development of Innovative Control Approaches to Enhance The Seismic Performance of Buildings and NSCs; University of New Hampshire: Durham, NH, USA, 2018. [Google Scholar]
- Tan, J.; Ho, S.C.M.; Zhang, P.; Jiang, J. Experimental study on vibration control of suspended piping system by single-sided pounding tuned mass damper. Appl. Sci. 2019, 9, 285. [Google Scholar] [CrossRef]
- Nguyen, P.C.; Kim, S.E. A new improved fiber plastic hinge method accounting for lateral-torsional buckling of 3D steel frames. Thin Walled Struct. 2018, 127, 666–675. [Google Scholar] [CrossRef]
- Watkins, D.A.; Chiu, L.; Hutchinson, T.C.; Hoehler, M. Survey and Characterization of Floor and Wall Mounted Mechanical and Electrical Equipment in Buildings; University of California: San Diego, CA, USA, 2009. [Google Scholar]
- Archila, M.; Ventura, C.; Figueira, A.; Yang, Y. Modal testing of non-structural components for seismic risk assessment. In Proceedings of the Society for Experimental Mechanics Series; Springer: New York, NY, USA, 2012; Volume 1, pp. 239–246. [Google Scholar]
- NIST. NIST GCR 18-917-43 Recommendations for Improved Seismic Performance of Nonstructural Components; NEHRP: Washington, DC, USA, 2018. [Google Scholar]
- Adam, C.; Fotiu, P.A. Dynamic analysis of inelastic primary-secondary systems. Eng. Struct. 2000, 22, 58–71. [Google Scholar] [CrossRef]
- Obando, J.C.; Lopez-Garcia, D. Inelastic Displacement Ratios for Nonstructural Components Subjected to Floor Accelerations. J. Earthq. Eng. 2018, 22, 569–594. [Google Scholar] [CrossRef]
- Anajafi, H.; Medina, R.A.; Santini-Bell, E. Inelastic floor spectra for designing anchored acceleration-sensitive nonstructural components. Bull. Earthq. Eng. 2020, 18, 2115–2147. [Google Scholar] [CrossRef]
- Brincker, R.; Zhang, L.; Andersen, P. Modal identification of output-only systems using frequency domain decomposition. Smart Mater. Struct. 2001, 10, 441–445. [Google Scholar] [CrossRef]
- Tran, T.-T.; Nguyen, P.-C.; So, G.; Kim, D. Seismic behavior of steel cabinets considering nonlinear connections and site-response effects. Steel Compos. Struct. 2020, 36, 17–29. [Google Scholar]
- Paz, M.; Kim, Y.H. Structural Dynamics Theory and Computation; Springer: New York, NY, USA, 2019. [Google Scholar]
- Yue, Q.; Zhang, L.; Zhang, W.; Kärnä, T. Mitigating ice-induced jacket platform vibrations utilizing a TMD system. Cold Reg. Sci. Technol. 2009, 56, 84–89. [Google Scholar] [CrossRef]
- Gaur, S.; Elias, S.; Höbbel, T.; Matsagar, V.A.; Thiele, K. Tuned mass dampers in wind response control of wind turbine with soil-structure interaction. Soil Dyn. Earthq. Eng. 2020, 132, 106071. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, K.; Mercan, O.; Chen, H.; Tan, P. Experimental and numerical studies on the optimal design of tuned mass dampers for vibration control of high-rise structures. Eng. Struct. 2020, 211, 110486. [Google Scholar] [CrossRef]
- Ghassempour, M.; Failla, G.; Arena, F. Vibration mitigation in offshore wind turbines via tuned mass damper. Eng. Struct. 2019, 183, 610–636. [Google Scholar] [CrossRef]
- Jia, F.; Jianwen, L. Performance degradation of tuned-mass-dampers arising from ignoring soil-structure interaction effects. Soil Dyn. Earthq. Eng. 2019, 125, 105701. [Google Scholar] [CrossRef]
- Amir, M.K.; Biggs, J.M.; Veneziano, D. Seismic Effectiveness of Tuned Mass Dampers. J. Struct. Div. 1981, 107, 1465–1484. [Google Scholar]
- Den Hartog, J.P. Mechanical Vibrations; McGraw-Hill: New York, NY, USA, 1956. [Google Scholar]
- Pisharady, A.S.; Basu, P.C. Methods to derive seismic fragility of NPP components: A summary. Nucl. Eng. Des. 2010, 240, 3878–3887. [Google Scholar] [CrossRef]
- Vamvatsikos, D.; Cornell, C.A. Incremental dynamic analysis. Earthq. Eng. Struct. Dyn. 2002, 31, 491–514. [Google Scholar] [CrossRef]
- Zhang, H.; Li, C.; Jiang, S.-M.; Liu, P.-F.; Gao, Q.-M. Fragility Analysis of Concrete-Filled Steel Tubular Frame Structures with BRBs under Multiple Earthquakes Considering Strain Rate Effects. Appl. Sci. 2019, 10, 165. [Google Scholar] [CrossRef]
- Tran, T.-T.; Nguyen, T.-H.; Kim, D. Seismic incidence on base-isolated nuclear power plants considering uni- and bi-directional ground motions. J. Struct. Integr. Maint. 2018, 3, 86–94. [Google Scholar] [CrossRef]
- Pujari, N.N.; Mandal, T.K.; Ghosh, S.; Lala, S. Optimisation of IDA-based fragility curves. In Safety, Reliability, Risk and Life-Cycle Performance of Structures and Infrastructures, Proceedings of the 11th International Conference on Structural Safety and Reliability, New York, NY, USA, 16–20 June 2013; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Baker, J.W. Efficient analytical fragility function fitting using dynamic structural analysis. Earthq. Spectra 2015, 31, 579–599. [Google Scholar] [CrossRef]


| Parameters | Unit | Value |
|---|---|---|
| Mass | kg | 10 |
| Mass ratio | – | 0.099 |
| Frequency ratio | – | 0.910 |
| Damping ratio | % | 0.184 |
| Stiffness | N/m | 74.899 |
| Case | wo TMD | w TMD | ||
|---|---|---|---|---|
| HF | LF | HF | LF | |
| AFF | 3.84 | 1.36 | 2.07 | 0.74 |
| θ | β | |||
|---|---|---|---|---|
| HF | LF | HF | LF | |
| Wo | 0.521 | 1.699 | 0.500 | 0.746 |
| W | 0.932 | 2.833 | 0.403 | 0.592 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tran, T.-T.; Cao, A.-T.; Kim, D.; Chang, S. Seismic Vulnerability of Cabinet Facility with Tuned Mass Dampers Subjected to High- and Low-Frequency Earthquakes. Appl. Sci. 2020, 10, 4850. https://doi.org/10.3390/app10144850
Tran T-T, Cao A-T, Kim D, Chang S. Seismic Vulnerability of Cabinet Facility with Tuned Mass Dampers Subjected to High- and Low-Frequency Earthquakes. Applied Sciences. 2020; 10(14):4850. https://doi.org/10.3390/app10144850
Chicago/Turabian StyleTran, Thanh-Tuan, Anh-Tuan Cao, Dookie Kim, and Seongkyu Chang. 2020. "Seismic Vulnerability of Cabinet Facility with Tuned Mass Dampers Subjected to High- and Low-Frequency Earthquakes" Applied Sciences 10, no. 14: 4850. https://doi.org/10.3390/app10144850
APA StyleTran, T.-T., Cao, A.-T., Kim, D., & Chang, S. (2020). Seismic Vulnerability of Cabinet Facility with Tuned Mass Dampers Subjected to High- and Low-Frequency Earthquakes. Applied Sciences, 10(14), 4850. https://doi.org/10.3390/app10144850






