Featured Application
Lattice fracture analysis for various loading and boundary conditions, calibration and validation approaches for numerical modeling.
Abstract
The lattice fracture model is a discrete model that can simulate the fracture process of cementitious materials. In this work, the Delft lattice fracture model is reviewed and utilized for fracture analysis. First, a systematic calibration procedure that relies on the combination of two uniaxial tensile tests is proposed to determine the input parameters of lattice elements—tensile strength, compressive strength and elastic modulus. The procedure is then validated by simulating concrete fracture under complex loading and boundary conditions: Uniaxial compression, three-point bending, tensile splitting, and double-edge-notch beam shear. Simulation results are compared to experimental findings in all cases. The focus of this publication is therefore not only on summarizing existing knowledge and showing the capabilities of the lattice fracture model; but also to fill in an important gap in the field of lattice modeling of concrete fracture; namely, to provide a recommendation for a systematic model calibration using experimental data. Through this research, numerical analyses are performed to fully understand the failure mechanisms of cementitious materials under various loading and boundary conditions. While the model presented herein does not aim to completely reproduce the load-displacement curves, and due to its simplicity results in relatively brittle post-peak behavior, possible solutions for this issue are also discussed in this work.
1. Introduction
Understanding the fracture behavior of cementitious composites is important when assessing material properties and ensuring structural safety [1,2]. In the past decades, a growing number of robust and reliable models, focused on fracture analysis, have been used in the literature [3,4]. These models can be briefly grouped as the continuum, piece-wise continuum, and discrete models [5]. Continuum models, such as finite element models, usually regard the displacement field as continuous and differentiable and simulate cracks in an average or smeared sense [6]. Limited by a small number of discontinuities assumption, this numerical method cannot encompass the entire fracturing process, i.e., crack initiation and propagation [7,8]. Based on the linear elastic fracture mechanics, piece-wise continuum models are proposed to simulate the crack propagation process through a pre-existing stress-free crack. However, in such models, the cracks are always aligned with the inter-element lines. Also, both the continuum and piece-wise continuum models have difficulties in the singularity-related issue since fracture patterns comprise various cracks, including the main crack with different branches, secondary cracks, and micro-cracks.
As an alternative method, discrete models with full discontinuity have emerged for fracture analysis of cementitious materials [7]. Lattice model is one of such discrete models in which both heterogeneity and discontinuity in cementitious materials can be incorporated [9] as well as avoidance of singularity-related issues [10]. The lattice numerical method dates back to the work of Hrennikoff [11]. Successive developments for this method can be found in the literature [12,13,14,15,16,17,18,19,20]. In general, three categories of the lattice model can be distinguished [14,15,16,17,18,21,22,23,24,25,26,27]:
(1) The lattice beam network model (LBM), also known as Delft lattice fracture model, was proposed by Schlangen and van Mier [18] to overcome the drawbacks of discrete and smeared crack finite element models and explain the fracture mechanism for cementitious materials.
(2) The lattice discrete particle model (LDPM), developed by Cusatis et al. [14,15,22], is a synthesis of the confinement shear model and discrete particle model. This model simulates the fracture process by modeling the mechanical interaction of adjacent coarse aggregate pieces; it can explicitly represent a coarser fraction of aggregate in large structural applications.
(3) The lattice spring model (LSM), which is based on the concept of a rigid-body-spring model [28], simulates the interaction between pairs of particles, or the motion of the particles by springs. The LSM has been applied to modeling three-dimensional cementitious materials and structural systems [29,30,31] under static, fatigue, and dynamic loadings.
After the pioneering work by Schlangen [32], a series of 2D numerical analyses were performed for fracture analysis of cementitious materials using LBM, including the uniaxial tensile test, uniaxial compressive test [32,33], three-point bending test [34], four-point shear test [32], Nooru-Mohamed test and Pull-out test [18,32]. Owing to the wide application of LBM for fracture analysis, a comprehensive summary work on the lattice model is necessary. Recently, two literature studies [35,36] reviewed the different types of lattice model with regards to theory, development, application and perspective, clearly showing that some coefficients in LBM are user-defined and inconsistent under different numerical analysis. It is therefore not surprising that numerical analyses through the use of consistent input parameters are still necessary.
With the development of computational techniques, the LBM has also been extended to 3D [37,38], thereby providing a more realistic representation of the fracture analysis. Producing realistic crack patterns is crucial to analyze the material physical and mechanical properties over the service life. In this research, 3D numerical analyses were conducted to simulate realistic fracture processes. Specifically, a systematic calibration procedure using experimental data was conducted for parameter determination in LBM and the corresponding validations were then performed to simulate fracture of cementitious materials subjected to various loading and boundary conditions.
This study firstly reviews model discretization, element type and failure criterion of LBM. Next, a systematic calibration procedure using two uniaxial tensile experiments is utilized for parameter determination. Then, the procedure is validated by simulating concrete fracture under complex loading and boundary conditions: uniaxial compression, three-point bending, tensile splitting, and double-edge-notch (DEN) beam shear. For simplicity of the calibration and the validation process, two assumptions are made: The material is regarded as homogeneous and brittle-linear constitutive relationship is utilized.
2. Modeling
In the LBM used herein, the continuum is first discretized by a network of Timoshenko beam elements. Timoshenko beam was utilized to account for shear deformation, considering the ratio between length and cross-section of the beam element to be low. Specifically, the domain was divided into several cubic cells. Then, a sub-cell was defined within each cell and the lattice nodes were randomly placed in each sub-cell using a random number generator. A parameter, defined as the ratio between the length of sub-cell and cell, was used to represent the randomness of the mesh. In order to avoid large variations in element length and introduce geometry disorder of material texture, randomness of 0.2 was adopted in the following analyses in this paper. The final lattice network was generated through Delaunay triangulation, see Figure 1.
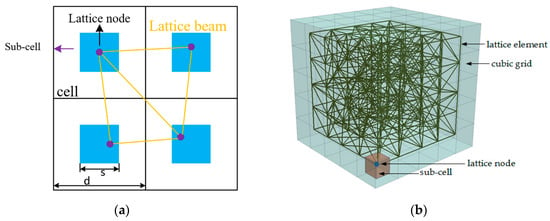
Figure 1.
(a) Schematic view of LBM (lattice beam network model) generation; (b) node and mesh generation procedure using Delaunay triangulation. Reproduced from [20]. Copyright 2018, Elsevier.
Then, a series of linear elastic calculations were conducted for the stress distribution among lattice elements under prescribed loading and boundary conditions. Normal force and bending moment were taken into account for the element stress calculation.
where is the normal force for the lattice beam element, A is the element cross-sectional area, and W is the cross-sectional factor for bending resistance, as indicated in Equation (2) ( is the diameter of the lattice element). The coefficients and are the normal force factor and the bending influence factor, determining the final failure mode in which either normal force or bending moment play a dominant role.
The is commonly adopted as 1.0 [21,39,40]. However, publications on bending influence factor determination are scarce. Several researchers use the aforementioned fracture criterion but the value varies from the material type and experimental conditions in their publications [19,32,38,39,41]. Because of the inconsistency of , the value was determined through a systematic calibration approach in this work.
In LBM, for each step of the analysis, loading was increased until exactly one element reached a stress equivalent to the assigned compressive/tensile strength. This element was defined as the critical element and removed from the system. The removed element determined crack initiation and propagation as well as load-displacement response. Then, the lattice network was updated and relaxed and the loading procedure was repeated until the system reached the pre-determined failure criterion (e.g., load or displacement).
In terms of computational effort, parallel computing technique, operating on multicore computer or clusters was integrated into the LBM, which significantly decreased computation efforts, making its application to model large-scale structures and/or when a considerable number of elements is needed possible.
More details on the lattice fracture model are available in the literature [41]. Building upon this literature, the 3D lattice fracture model was revisited here and relevant fracture analyses can then be implemented by using the input parameters proposed in this study.
3. Calibration
In order to simulate the crack initiation and propagation during fracture of cementitious materials, attention should be paid to the determination of input parameters. Recently, research concerning the calibration and validation in LDPM [42,43] shows great success in lattice modeling. LBM input parameters necessary for fracture simulation are described below, together with their effect on the macroscopic model response.
- Elastic modulus, E, and shear modulus, G, govern the response in the elastic regime. In LBM, the Poisson’s ratio is determined by the randomness. Based on the 0.2 randomness, the Poisson’s ratio of 0.18 is derived in the study.
- Tensile strength, ft, and compressive strength, fc, of lattice elements govern the macroscopic strength of the model. In this paper, the compressive strength of the lattice element is assumed as 10 times higher than the tensile strength, considering the fact that cementitious materials have a higher resistance to the compressive loading than tensile loading [3].
- Normal force factor, , and bending influence factor, , govern the crack pattern. The macroscopic model response, including the elastic regime and softening part, is also influenced by these two factors. In this paper, the is set to 1, which is in line with the literature [18,32,44]. The is determined through the calibration procedure that follows.
A calibration procedure that relies on a combination of two uniaxial tensile tests is proposed to determine input parameters of lattice elements—tensile strength, compressive strength, elastic modulus, and . The calibration procedure proposed in Figure 2 was used for determining these input parameters. Herein, the uniaxial tensile test performed by van Vliet and co-authors [45] was used for parameter calibration. In their experiments, uniaxial tensile tests of dog-bone specimens of different sizes with rotating boundaries were performed. A special hinge construction was developed to ensure the free rotations of specimens in two orthogonal directions and the point of rotation is situated exactly at the glue layer between the specimen and the loading platen. To model this loading boundary, the displacement in the vertical direction was fixed and applied as prescribed displacement in the simulation. Detailed information about the sample size can be found in Figure 3a and Table 1. In the experiment, linear variable displacement transducers (LVDTs) with a measuring length of 60 mm were placed on both the front and the back sides of the two specimens specified in Table 1. In the numerical analysis, the measured displacement can be obtained by recording the vertical displacements of node A and node B (see Figure 3b).
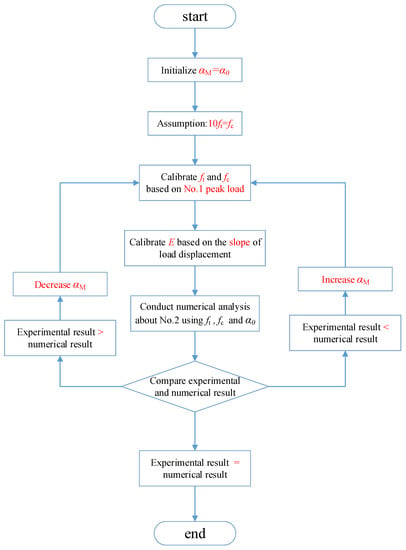
Figure 2.
Flowchart of the calibration process.
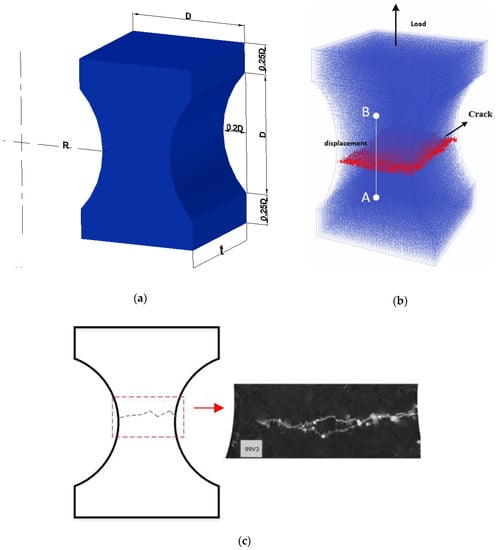
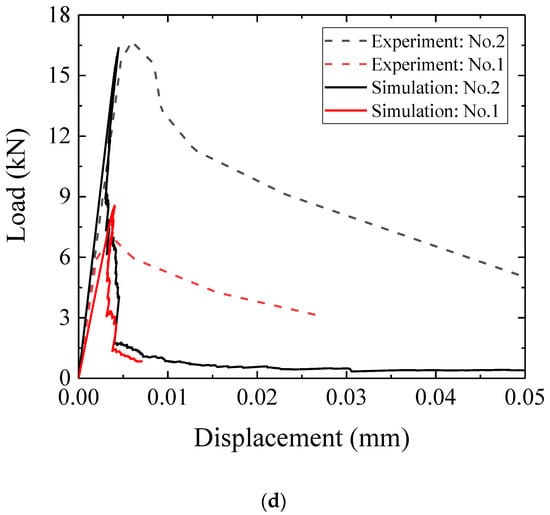
Figure 3.
(a) Setup for uniaxial tensile test, (b) failure mode for uniaxial tensile test (red-cracked element), (c) failure mode for uniaxial tension test in the experiment [46]. Reproduced from [46]. Copyright 2003, Elsevier. (d) typical load-displacement curve for direct tensile tests.

Table 1.
Detailed information about the specimens.
Following the calibration flowchart, the local mechanical property E, fc, ft and can be calibrated by fitting the load-displacement curve for these two models. The best-fitting results are shown in Table 2. Figure 3b,c show the numerical and experimental crack patterns for the final failure mode with regards to the uniaxial tensile test in dog-bone shape and Figure 3d shows a comparison between the experimental and numerical results. The numerical results agree well with the experimental results before the peak load. After the peak load, the numerical results show more brittle behavior compared to the experimental data. Concerning the crack patterns, a typical failure mode can be found and the main crack occurs in the middle of the specimen, which agrees well with the experimental results [45].

Table 2.
Values of input parameters in the numerical analyses.
After calibration, the value of the bending influence factor ( = 0.05) was derived based on two computational uniaxial tensile tests. This calibrated value for is the same as the frequently utilized value in the previous research [32,39,44]. In the next section, validation was performed to verify whether this value can provide correct crack patterns and load-displacement response under different loading and boundary conditions [46].
4. Validation
In this section, other loading configurations namely, uniaxial compressive test [47], splitting tensile test [48], three-point bending test [49], and DEN beam shear test [32] are simulated to validate the obtained and evaluate the LBM performance for fracture analysis.
4.1. Uniaxial Compression Test
Uniaxial compressive test conducted by Shafieifar et al. [47] was used for the validation of fracture analysis under compressive loading. In the experiment, cubic samples with size 50 mm × 50 mm × 50 mm were subjected to compressive loads actuated by two steel plates at opposite faces of the cube. To model this loading boundary, x and y displacement were restrained and the prescribed displacement was applied along with z-direction (Figure 4a,b). The element mechanical properties E, fc, and ft can also be calibrated by fitting the experimental stress-strain curve, as shown in Table 3.
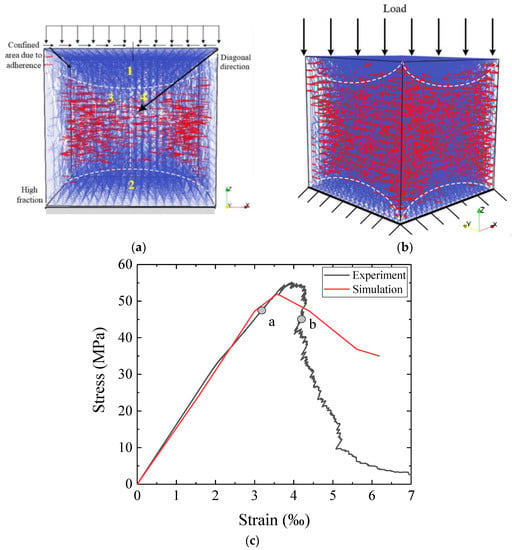
Figure 4.
Uniaxial compressive test (a) crack pattern at a point, (b) crack pattern at b point (red-cracked element), (c) stress-strain response.

Table 3.
Values of input parameters in the numerical simulation of the uniaxial compressive test.
Figure 4a,b show the crack patterns under uniaxial compressive loading in different stages and Figure 4c shows a comparison between the experimental and numerical results. Due to the local confinement near the boundaries provided by friction of the loading platens (zones 1 and 2 in Figure 4a), the cone-shaped inner part of the specimen remained uncracked. A majority of cracks initiated from areas marked as 3 and 4. This numerical result shows the same tendency as experiments [47].
According to previous research [4,50], the slenderness and boundary conditions significantly influence the crack pattern and load-displacement curve of concrete subjected to uniaxial compressive loading. To understand their influence, the relevant numerical analyses were performed. The input parameters used are listed in Table 3 and Table 4. Figure 5 shows the typical crack patterns for the specimens under uniaxial compressive loading from the experimental and numerical perspectives. For the high friction boundary condition, the cone shape inner parts of the specimens remained uncracked. For taller specimens, the boundary restraint influenced less. As a result, the cracks mainly occured in the middle zone of the specimen and less cracking occured in the area close to the top and the bottom surface. This explains the fact that simulations of samples with decreasing slenderness show higher load-carrying capacity.

Table 4.
Values of input parameters in the numerical analyses about slenderness and boundary conditions.
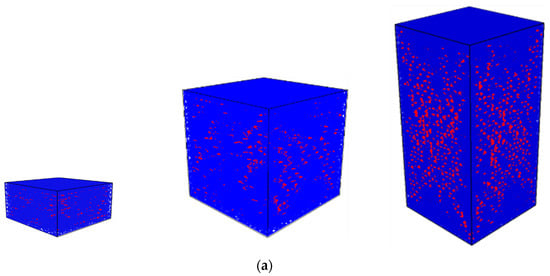
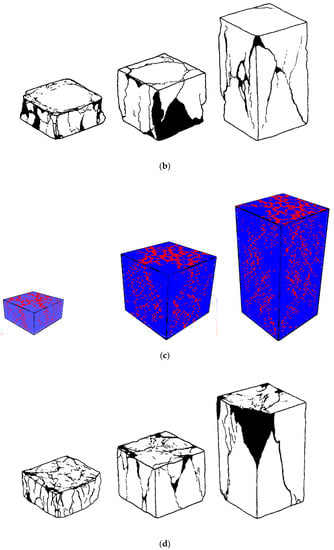
Figure 5.
Crack patterns for (a) high friction boundary condition in numerical analysis, (b) high friction boundary condition from the literature [51]. Reproduced from [51]. Copyright 1996, Wiley Online Library. (c) low friction boundary condition in numerical analysis, (d) low friction boundary condition from the literature [51] (red-cracked element). Reproduced from [51]. Copyright 1996, Wiley Online Library.
For the low friction boundary condition, the failure mode was characterized by localized cracks which were almost parallel to the applied load. Specifically, a large number of elements in the upper and lower surfaces were broken. In contrast, for the high friction boundary condition, the failure mode was characterized by inclined cracks that left the simulated sample ends almost undamaged. Furthermore, for low friction boundary conditions, many micro-cracks occured on the top and bottom area during the fracture process. This is in agreement with experimental observations [4].
In Figure 6a,b, the stress-strain curves with different slenderness and boundary conditions are plotted. For the high friction boundary condition, the slenderness significantly influenced the peak load. Specifically, increasing slenderness resulted in lower strength and lead to more brittle softening behavior. For the low friction boundary condition, increasing slenderness showed less influence on the peak load but resulted in a more brittle softening part behavior. According to the numerical results, high friction boundary condition provided a higher bearing capacity than the low friction boundary. This can be explained by the cohesion in the boundary which constrains the lateral deformation and improved the load-bearing capacity. The numerical results are in accordance with the literature [4].
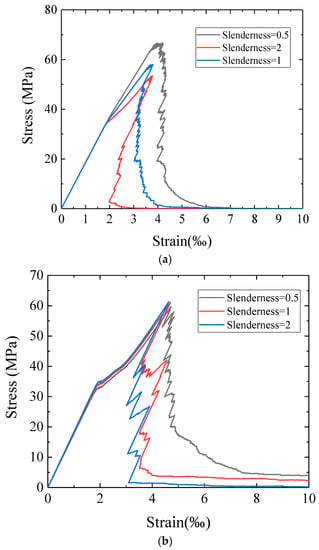
Figure 6.
(a) Stress-strain curve for high friction boundary condition, (b) stress-strain curve for low friction boundary condition.
4.2. Tensile Splitting Test
Brazilian splitting tests conducted by Bažant et al. [48] were simulated in this section. In their experiments, cylindrical specimens with different diameters D (19 mm, 38 mm, 76 mm, 152 mm) are tested. The thickness of the specimens was kept constant (B = 51 mm), as shown in Figure 7a. Since the loading condition is not specified in this publication, an assumption that the specimens are loaded through steel loading platens is made herein. In the numerical analysis, the prescribed displacement was applied to the vertical direction and the displacements in other directions were set to 0 to model the experimental loading condition, as shown in Figure 7b. In this section, the input parameters in Table 5 were calibrated by fitting the peak load of the experimental sample with a diameter of 38 mm. Specimens of other sizes were utilized to evaluate the LBM ability on tensile splitting fracture analysis. Furthermore, since the publication only provides tensile splitting strength rather than the whole stress displacement curve, the elastic modulus was assigned as 25 GPa without calibration.
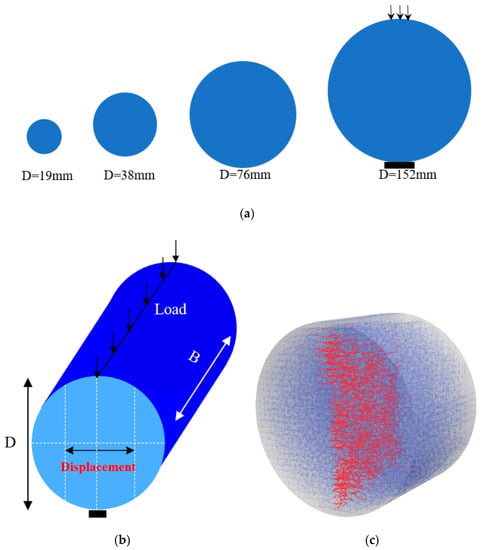
Figure 7.
(a) Setup for tensile splitting test, (b) failure mode for splitting tensile test, (c) crack patterns for splitting tensile test (red-cracked element).

Table 5.
Values of input parameters in the numerical analyses about the tensile splitting test.
Figure 8a reports the nominal stress, defined as 2P/(πBD), versus displacement curves obtained by the numerical analyses. The peak load of the nominal stress was the tensile splitting strength. The peak nominal stress for splitting tensile test decreased as the size increased. It can be observed from Figure 8b that the numerical results agree well with experimental results for specimens with diameters ranging from 19 to 152 mm. Note that the numerical result for the digital specimen with a diameter of 19 mm showed lower strength than the experiment, which is attributed to the relatively large element size compared to specimen size and boundary condition. Specifically, the cell size (2.5 mm) was utilized to avoid size effect, nevertheless mesh size was not enough to produce accurate calculations. To model the loading condition of the experiments, a displacement was prescribed in the vertical direction at the nodes belonging to the loading area in the simulation. Due to the influence of cell size, for the smallest digital sample, with diameter of 19 mm, it was difficult to apply the load with the same width as others. Therefore, stress concentration may have occurred in the smallest modeled sample, resulting in a lower simulated strength. For the specimen with a diameter equal to 152 mm, LBM overestimated the experimental strength, which was induced by the different failure mechanisms. Specifically, in the experimental campaign, most samples failed due to a splitting crack initiating in the center of the specimen, while for the specimen with a size of 152 mm, there was significant damage underneath the loading platen [48]. For the numerical procedure, all models followed a comparable crack pattern. Yet accurately, some micro-cracks occured within the loading area, and then a splitting crack initiated in the center of the model and propagated to the top and bottom boundaries. Finally, the modeled sample gradually lost the capacity to bear the load. Thus, the deviation for the largest model can be well explained by the different types of dominant cracking modalities.
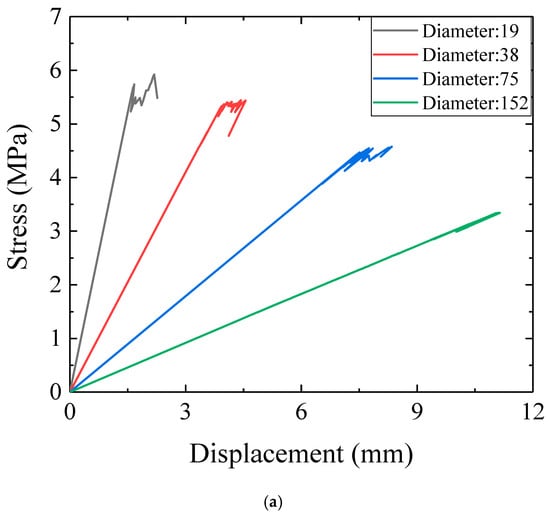
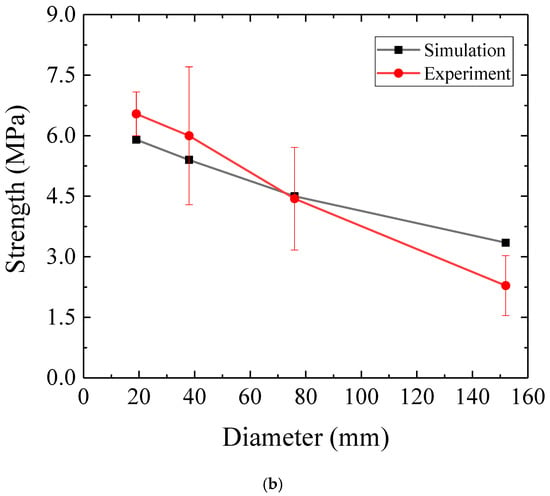
Figure 8.
(a) Comparison between numerical results and experimental results, (b) typical stress-displacement curve for tensile splitting tests.
4.3. Three-Point Bending Test
4.3.1. Size Effect
Three-point bending tests performed by Xu et al. [49] are simulated in this section to evaluate the LBM ability on flexural fracture analysis. Their research examines the size effect on the fracture response of concrete. These experimental samples, defined as large, medium, and small, are characterized by the span equal to 160 mm, 280 mm, and 400 mm, respectively, and the height equal to 40 mm, 70 mm, and 100 mm, respectively. All specimens have the same thickness and notch length to beam depth ratio equal to 0.4. During the experiment, the crack mouth opening displacement (CMOD) was measured to record the crack width. The mesh used in LBM is given in Figure 9a.
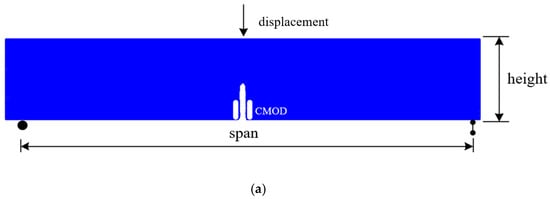
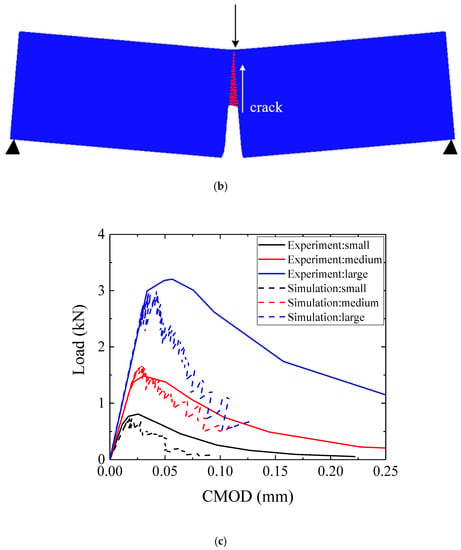
Figure 9.
(a) Geometry of three-point bending test specimen, (b) the comparison between experimental results with numerical results for three-point bending test, (c) crack pattern for the three-point bending test (red-cracked element; deformations have been scaled for clarity).
The input parameters including E, fc, and ft were calibrated by the best fitting of the Load-CMOD curve for the medium specimen and can be found in Table 6. Regarding crack patterns, a typical failure mode for a three-point bending test can be found in Figure 9b. A single localized crack started from the notch and propagated to the upper surface, which is the same as the crack pattern observed in the literature [49]. The crack pattern for the three model sizes was almost identical. This is in agreement with the experiments performed by Nallathambi et al. [52]. Also, Figure 9c shows that the numerical results agree well with the experimental ones before the peak load and are less satisfactory during the softening part. This deviation together with potential approaches are discussed in Section 5.

Table 6.
Values of input parameters in the numerical analyses about three-point bending test.
4.3.2. The Influence of Notch Ratio
Three-point bending tests investigating the effect of notch length to beam depth ratio [52] are simulated to evaluate the LBM ability to predict the flexural fracture behavior with respect to the final crack patterns and load-displacement curve. The mechanical properties of lattice elements are calibrated using the sample with the notch equal to 0.1 (Table 7). These specimens are characterized by a span of 400 mm, height of 100 mm, and depth of 100 mm, respectively. The models with different notch ratios used in their experiments are 0.05, 0.1, 0.3, and 0.5, respectively. The load is applied in the middle of the top side and the vertical displacement is measured (see Figure 10a).

Table 7.
Values of input parameters in the numerical analyses about notch ratio on three-point bending test.
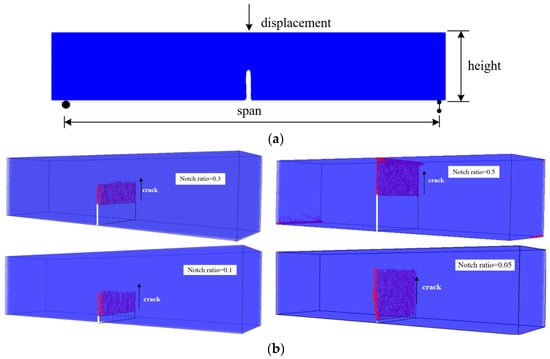
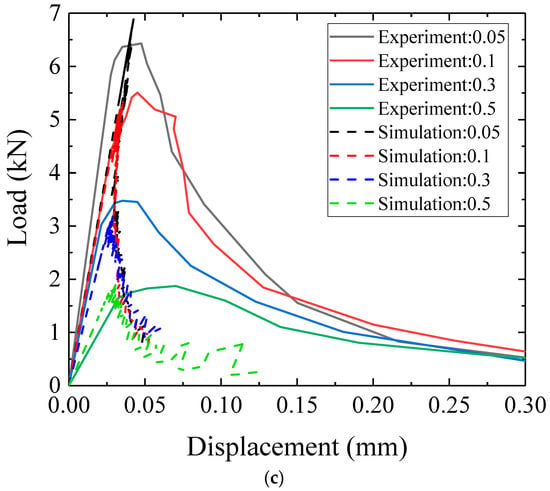
Figure 10.
(a) Crack patterns for the smallest notch ratio, (b) crack patterns for the model with different notch ratio (red-cracked element) (c) load and displacement curve for the models with different notch ratio.
Figure 10b shows the final crack patterns for the numerical models with different notch ratios. Regardless of the notch ratio, the same fracture behavior can be found, in which the initial crack occurs from the top of the notch and propagates throughout the ligament until the system loses the bearing capacity. A good agreement, in terms of the load-displacement curve before the peak load, was found between the experimental and numerical results in Figure 10c. A clear deviation during the post-peak still exists, with the model showing much more brittle behavior compared to the experiments.
It is also worth mentioning that for models with different notch ratios, the crack patterns and the corresponding displacement for the peak load did not change significantly, which is in accordance with the experimental data [52].
4.4. Double-Edge-Notched Beam Shear Test
The DEN beam shear tests performed by Schlangen [32] were analyzed to simulate the pure shear zone and produce a shear crack. An experimental sample with span of 400 mm, depth of 37.5 mm, and height of 150 mm was simulated. The experiments were performed under two different boundary conditions (fixed-supported and freely-rotating), which was achieved by mounting diagonal bars to the loading frame in the experiments. The value of crack mouth opening displacement (CMOD) and the crack mouth sliding displacement (CMSD) at the top and the bottom notch on the front of the specimen was used as a feedback signal for displacement in the experiment (see Figure 11a,b). In numerical analyses, the fixed-support was modeled with a constrain in x, y and z directions for nodes on the lower surface, and in z-direction for the nodes on the upper surface while in x and y, a prescribed load was applied with the ratio of 1:15 (Figure 11a). For freely-rotating supports, nodes in the left support were constrained with respect to x, y and x directions, and nodes in the right support were fixed in z-direction. Furthermore, the prescribed load was applied to the nodes on the upper surface without any other constraints (Figure 11b). Furthermore, the loading area was utilized in the numerical analyses to avoid stress concentrations below the loading points.
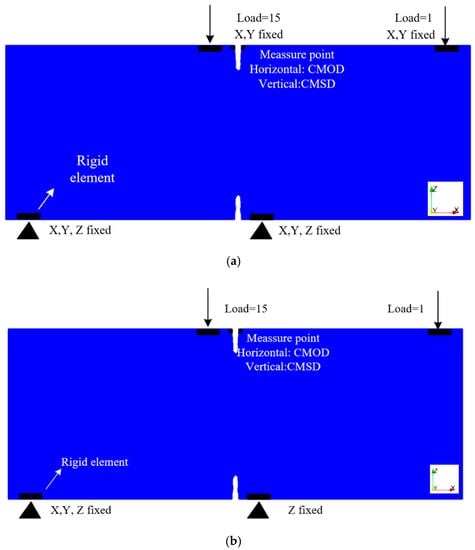
Figure 11.
Setup for DEN (double-edge-notch) beam shear test (a) fixed supports, (b) freely rotating.
Local mechanical properties of lattice elements were calibrated by the experiment with fixed supports; the properties are given in Table 8. For fixed supports, both cracks continued to propagate until they were arrested in the compression zone. Due to the limitation of horizontal support, the double-curved cracks were arrested due to the new configuration of the horizontal forces in the model and stop from propagating further; then a splitting crack arose at the center of the beam and the system eventually failed, in which the final crack pattern in Figure 12a is the same as that observed in the experiment (see Figure 12b). Figure 12c shows the final crack patterns for the sample with free rotating supports. At the beginning, two cracks occurred and grew at both notches and propagated towards the respective opposite specimen sides. Then, one crack stopped propagating and the other one became dominant and continued until reaching the lower surface. The formed crack was a typically curved crack that grew outside the shear zone and ended at the outer side of the middle support (see Figure 12c), which is close to the experimental results (see Figure 12d).

Table 8.
Values of input parameters in the numerical analyses about DEN beam shear test.
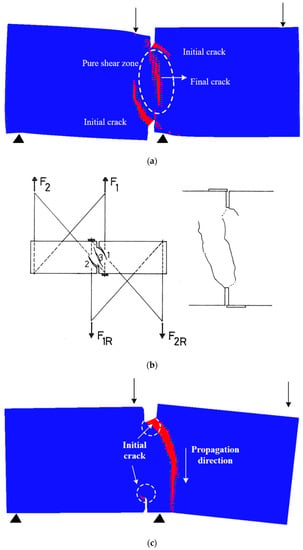
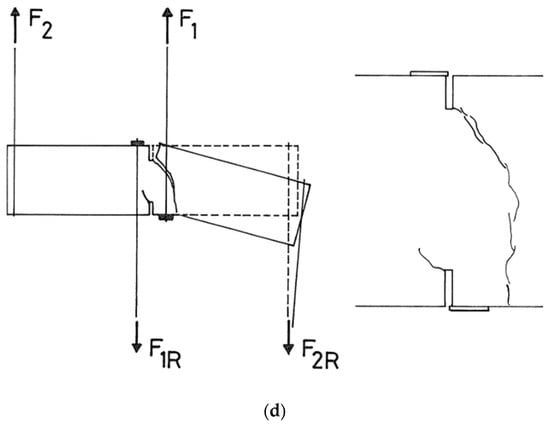
Figure 12.
(a) Crack pattern for fixed supports in numerical analysis, the deformation is enlarged for better observation, (b) crack pattern for fixed supports in the experiment [32]. Reproduced from [32]. Copyright 1993, Delft University of Technology. (c) crack pattern for freely rotating in numerical analysis, the deformation is enlarged for better observation (red-cracked element; deformations have been scaled for clarity), (d) crack pattern for freely rotating in the experiment [32]. Reproduced from [32]. Copyright 1993, Delft University of Technology.
A comparison between the numerical and experimental load-displacement curve is plotted in Figure 13 with high and low friction. The agreement between experimental and numerical results is good up to the peak load. For the post-peak branch in the numerical analysis, the load increased with the increased displacement, opposite to the experimental result for fixed boundary condition. This can be explained by the fact that ideal (i.e., high friction) boundary conditions cannot be achieved in the real experiments so that the load-displacement curve shows the decreasing tendency for the softening part.
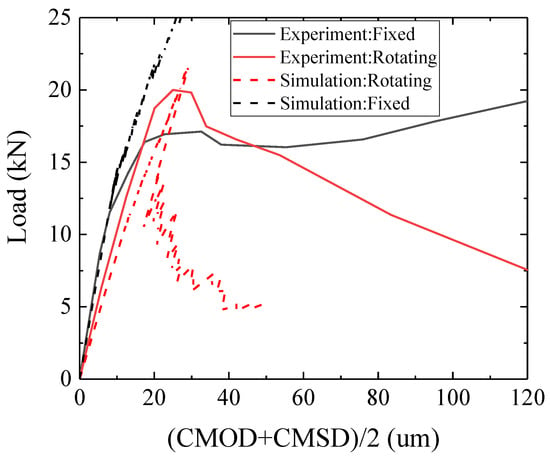
Figure 13.
The comparison between the experimental results and numerical results.
5. Discussion
While the LBM is capable of simulating the fracture process of cementitious materials under various loading and boundary conditions, relatively brittle post-peak behavior exists. Several potential approaches for overcoming the post-peak brittleness have been proposed in the past [3]: (1) Considering the material mesostructured explicitly in the simulations, as shown in Figure 14a; (2) using a multi-linear constitutive relationship (instead of the typical elastic-brittle one), essentially considering material softening at the elemental level, as shown in Figure 14b; (3) changing the removal mechanism of “failed” lattice beams (i.e., not removing the element altogether in a single step, but first removing its bending stiffness, essentially making it a truss element, and then the axial stiffness), as shown in Figure 14c.
Figure 14.
(a) Mesostructured model, (b) multi-linear constitutive relationship, (c) schematic view of the element degradation at the first step [53]. Reproduced from [53]. Copyright 2019, Elsevier.
Herein, these potential methods quantitively reflect the influence on post-peak behavior through numerical analyses and the detailed input parameters can be found in Table 9. The model No.1 is regarded as the reference model; in the model No.2, one element is removed by two steps as explained before. Accurately, in the first step, the critical element degrading from a Timoshenko beam element into a truss element loses the capacity to bear the torque and bending; in the second step, the truss element is thoroughly removed and a crack path is recorded. The second step can simulate the friction of crack faces in a way; the model No.3 investigates the effect of a multi-linear constitutive relation. To be specific, a multi-linear curve (in black) with five segments is utilized standing for the constitutive relation and capturing its characteristics. The points are taken at: (1) Peak load; (2) point for which stress is 70% peak load; (3) point for which strain is 0.5%; (4) point which the strain reaches 1.25%; and (5) point for which the stress is 10% peak load. After the last point, the element is removed from the system, representative for the crack in the system; model No.4 includes the mesostructured procedure, in which coarse aggregate and interface elements are introduced for a realistic sample. The corresponding material properties for different phases are listed in Table 9. The high friction boundary condition is applied to all simulations.

Table 9.
The input parameters for the numerical analysis.
Figure 15 showcases the influence of material heterogeneity, multi-linear constitutive relationship, and removal mechanism, clearly showing that their influence can contribute to the ductility and completely reproduce the load-displacement curve of the experiments [3,54,55,56]. However, since these factors significantly complicate the calibration process, the brittle-linear mechanical properties and homogeneous material are utilized during the calibration and validation process. For completely reproducing the load-displacement curves, an experimentally validated multi-scale modeling scheme has recently been proposed by Zhang [57]. In his work, the constitutive relation of lattice elements is derived from lower-scale (i.e., micro-scale) simulations or measurements. Based on the experimental measurements of micro-scale sized specimens, micromechanical models for both the bulk cement paste and the interfacial transition zone have been calibrated and validated under various loading conditions [39,44,53,58]. This can offer reliable constitutive relations of local elements for mesoscale models [40,59]. Together with the current work, it is possible to extend the multi-scale modeling scheme.
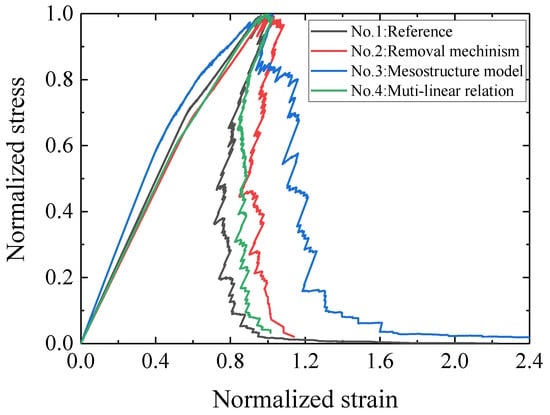
Figure 15.
Normalized stress and normalized strain curve with different influence factors.
6. Conclusions
In this paper, a systematic calibration procedure that relies on a combination of two uniaxial tensile tests is proposed to determine input parameters of lattice elements—tensile strength, elastic modulus, and . The procedure is then validated by simulating concrete fracture under different complex loading and boundary conditions: Uniaxial compression, three-point bending, tensile splitting, and double-edge-notch (DEN) beam shear. Simulation results are compared to experimental findings in all cases and show the LBM capacity to simulate the fracture process of cementitious materials under various loading and boundary conditions. While the post-peak behavior is brittle due to the simplicity of the model used, potential solutions have been provided for a complete load and displacement curve. Based on this calibration and validation work, parametric analyses including the size effect, slenderness, notch ratio, and boundary condition are performed to give further explanations on the fracture mechanisms in cementitious materials.
Based on the results obtained in this study, the following conclusions can be formulated.
- The calibration method with a combination of two uniaxial tensile tests is utilized to get the value of the bending influence factor ( = 0.05), which can be used to simulate the fracture process of cementitious materials under different boundary conditions.
- The LBM can simulate the fracture process of concrete under uniaxial compression and tension. The model captures the effect of high friction boundary and low friction boundary conditions on compressive strength well. Also, the LBM can reproduce the differences in crack patterns and the load-displacement curve for different boundary conditions and slenderness.
- The LBM can reproduce the fracture process accurately and analyze the size effect on the load-displacement curve for concrete subjected to a three-point bending test. Furthermore, the LBM is also able to capture the influence of the notch size and the size effect on the load-displacement response.
- The LBM can simulate the fracture process in the Brazilian splitting test. Furthermore, it predicts the size effect on the splitting test and produces the same crack patterns observed in the experiments.
- The LBM can simulate the fracture process during a DEN beam shear experiment. It does not only predict the crack nucleation and propagation accurately but also shows the influence of different boundary conditions.
At present, the LBM has been extensively developed as an efficient numerical model to simulate the fracture process of cementitious materials. Based on this summary, systematic calibration and validation as guides for the determination of input parameters is proposed for future research. Also, the multiscale research suggestion provides a promising choice for further research about mechanical properties and fracture processes for cementitious materials.
Author Contributions
Formal analysis, Z.C.; investigation, Z.C.; methodology, Z.C. and H.Z.; supervision, E.S. and B.Š.; validation, Z.C. and H.Z.; writing—original draft, Z.C.; writing—review and editing, H.Z.; E.S., and B.Š. All authors have read and agreed to the published version of the manuscript.
Funding
Ze Chang and Hongzhi Zhang would like to acknowledge the funding supported by China Scholarship Council under grant number 201806060129 and 201506120067, respectively.
Acknowledgments
The authors gratefully thank Claudia Romero Rodriguez for her linguistic assistance during the revision of this manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bao, J.; Wang, L. Combined effect of water and sustained compressive loading on chloride penetration into concrete. Constr. Build. Mater. 2017, 156, 708–718. [Google Scholar] [CrossRef]
- Nitka, M.; Tejchman, J. Modelling of concrete behaviour in uniaxial compression and tension with DEM. Granul. Matter 2015, 17, 145–164. [Google Scholar] [CrossRef]
- Van Mier, J.G.M. Concrete Fracture: A Multiscale Approach; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Van Mier, J.G.M. Fracture Processes of Concrete; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Lilliu, G. 3D Analysis of Fracture Processes in Concrete; Eburon Uitgeverij BV: Utrecht, The Netherlands, 2007. [Google Scholar]
- De Borst, R. Some recent developments in computational modelling of concrete fracture. Int. J. Fract. 1997, 86, 5–36. [Google Scholar] [CrossRef]
- D’Addetta, G.A.; Kun, F.; Ramm, E. On the application of a discrete model to the fracture process of cohesive granular materials. Granul. Matter 2002, 4, 77–90. [Google Scholar] [CrossRef]
- Kwan, A.; Wang, Z.; Chan, H. Mesoscopic study of concrete II: Nonlinear finite element analysis. Comput. Struct. 1999, 70, 545–556. [Google Scholar] [CrossRef]
- Sagar, R.V.; Prasad, B.R.; Nazreen, S.; Singh, R. Modeling mode-I fracture process in concrete at meso-scale: Computational aspects of lattice model and a comparison between results of two dimensional lattice simulation and acoustic emission measurements. Eng. Fract. Mech. 2019, 210, 257–278. [Google Scholar] [CrossRef]
- Chen, H.; Jiao, Y.; Liu, Y. A nonlocal lattice particle model for fracture simulation of anisotropic materials. Compos. Part B Eng. 2016, 90, 141–151. [Google Scholar] [CrossRef]
- Hrennikoff, A. Solution of problems of elasticity by the framework method. Appl. Mech. 1941, 12, 169–175. [Google Scholar]
- Šavija, B.; Pacheco, J.; Polder, R. Lattice model as a tool for modelling transport phenomena in cement based composites. In Proceedings of the Numerical Modeling Strategies for Sustainable Concrete Structures, Aix en Provence, France, 29 May–1 June 2012; pp. 1–8. [Google Scholar]
- Bolander, J.E.; Sukumar, N. Irregular lattice model for quasistatic crack propagation. Phys. Rev. B 2005, 71, 094106. [Google Scholar] [CrossRef]
- Cusatis, G.; Mencarelli, A.; Pelessone, D.; Baylot, J. Lattice Discrete Particle Model (LDPM) for failure behavior of concrete. II: Calibration and validation. Cem. Concr. Compos. 2011, 33, 891–905. [Google Scholar] [CrossRef]
- Cusatis, G.; Pelessone, D.; Mencarelli, A. Lattice Discrete Particle Model (LDPM) for failure behavior of concrete. I: Theory. Cem. Concr. Compos. 2011, 33, 881–890. [Google Scholar] [CrossRef]
- Luković, M.; Šavija, B.; Schlangen, E.; Ye, G.; van Breugel, K. A 3D Lattice Modelling Study of Drying Shrinkage Damage in Concrete Repair Systems. Materials 2016, 9, 575. [Google Scholar] [CrossRef] [PubMed]
- Schlangen, E.; Garboczi, E. New method for simulating fracture using an elastically uniform random geometry lattice. Int. J. Eng. Sci. 1996, 34, 1131–1144. [Google Scholar] [CrossRef]
- Schlangen, E.; van Mier, J.G.M. Simple lattice model for numerical simulation of fracture of concrete materials and structures. Mater. Struct. 1992, 25, 534–542. [Google Scholar] [CrossRef]
- Vassaux, M.; Ragueneau, F.; Richard, B.; Millard, A. Compressive behavior of a lattice discrete element model for quasi-brittle materials. Comput. Modell. Concr. Struct. 2014, 1, 335–344. [Google Scholar] [CrossRef]
- Zhang, H.; Šavija, B.; Schlangen, E. Towards understanding stochastic fracture performance of cement paste at micro length scale based on numerical simulation. Constr. Build. Mater. 2018, 183, 189–201. [Google Scholar] [CrossRef]
- Schlangen, E.; Garboczi, E. Fracture simulations of concrete using lattice models: Computational aspects. Eng. Fract. Mech. 1997, 57, 319–332. [Google Scholar] [CrossRef]
- Fascetti, A.; Bolander, J.E.; Nistico’, N. Lattice Discrete Particle Modeling of Concrete under Compressive Loading: Multiscale Experimental Approach for Parameter Determination. J. Eng. Mech. 2018, 144, 04018058. [Google Scholar] [CrossRef]
- Herrmann, H.J.; Hansen, A.; Roux, S. Fracture of disordered, elastic lattices in two dimensions. Phys. Rev. B 1989, 39, 637–648. [Google Scholar] [CrossRef]
- Ince, R.; Arslan, A.; Karihaloo, B. Lattice modelling of size effect in concrete strength. Eng. Fract. Mech. 2003, 70, 2307–2320. [Google Scholar] [CrossRef]
- Luković, M.; Yang, Y.; Schlangen, E.; Hordijk, D. On the Potential of Lattice Type Model for Predicting Shear Capacity of Reinforced Concrete and SHCC Structures. In High Tech Concrete: Where Technology and Engineering Meet; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2017; pp. 804–813. [Google Scholar]
- Šavija, B.; Luković, M.; Schlangen, E. Modeling the rapid chloride migration test for concrete using the lattice model and characteristic Galerkin approach. In Computational Modelling of Concrete Structures; Informa UK Limited: Colchester, UK, 2014; pp. 629–638. [Google Scholar]
- De Barros-Leite, J.; Slowik, V. Simulation of concrete fracture by using mesolevel truss and particle models. In Proceedings of the Fifth International Conference on Fracture Mechanics of Concrete and Concrete Structures, Vail, CO, USA, 12–16 April 2004; pp. 12–16. [Google Scholar]
- Kawai, T. New discrete models and their application to seismic response analysis of structures. Nucl. Eng. Des. 1978, 48, 207–229. [Google Scholar] [CrossRef]
- Bolander, J.; Saito, S. Fracture analyses using spring networks with random geometry. Eng. Fract. Mech. 1998, 61, 569–591. [Google Scholar] [CrossRef]
- Bolander, J.E.; Hong, G.S. Rigid-body-spring network modeling of prestressed concrete members. Struct. J. 2002, 99, 595–604. [Google Scholar]
- Yip, M.; Mohle, J.; Bolander, J.E. Automated Modeling of Three-Dimensional Structural Components Using Irregular Lattices. Comput. Civ. Infrastruct. Eng. 2005, 20, 393–407. [Google Scholar] [CrossRef]
- Schlangen, E. Experimental and Numerical Analysis of Fracture Processes in Concrete; Delft University of Technology: Delft, The Netherlands, 1993. [Google Scholar]
- Abreu, M.; Lemos, J.; Carmeliet, J.; Schlangen, E.J.F. Modelling Compressive Cracking in Concrete Using a Modified Lattice Model; Taylor & Francis Group: London, UK, 2007. [Google Scholar]
- Liu, J.; Zhao, Z.; Deng, S.; Liang, N. Modified generalized beam lattice model associated with fracture of reinforced fiber/particle composites. Theor. Appl. Fract. Mech. 2008, 50, 132–141. [Google Scholar] [CrossRef]
- Pan, Z.-C.; Ma, R.; Wang, D.; Chen, A.-R. A review of lattice type model in fracture mechanics: Theory, applications, and perspectives. Eng. Fract. Mech. 2018, 190, 382–409. [Google Scholar] [CrossRef]
- Nikolic, M.; Karavelić, E.; Ibrahimbegovic, A.; Miščević, P. Lattice Element Models and Their Peculiarities. Arch. Comput. Methods Eng. 2017, 25, 753–784. [Google Scholar] [CrossRef]
- Lilliu, G.; van Mier, J. 3D lattice type fracture model for concrete. Eng. Fract. Mech. 2003, 70, 927–941. [Google Scholar] [CrossRef]
- Qian, Z.; Schlangen, E.; Ye, G.; van Breugel, K. Modeling Framework for Fracture in Multiscale Cement-Based Material Structures. Materials 2017, 10, 587. [Google Scholar] [CrossRef]
- Zhang, H.; Šavija, B.; Figueiredo, S.C.; Luković, M.; Schlangen, E. Microscale Testing and Modelling of Cement Paste as Basis for Multi-Scale Modelling. Materials 2016, 9, 907. [Google Scholar] [CrossRef]
- Zhang, H.; Šavija, B.; Figueiredo, S.C.; Schlangen, E. Experimentally validated multi-scale modelling scheme of deformation and fracture of cement paste. Cem. Concr. Res. 2017, 102, 175–186. [Google Scholar] [CrossRef]
- Qian, Z. Multiscale Modeling of Fracture Processes in Cementitious Materials; Delft University of Technology: Delft, The Netherlands, 2012. [Google Scholar]
- Abdellatef, M.; Boumakis, I.; Wan-Wendner, R.; Alnaggar, M. Lattice Discrete Particle Modeling of concrete coupled creep and shrinkage behavior: A comprehensive calibration and validation study. Constr. Build. Mater. 2019, 211, 629–645. [Google Scholar] [CrossRef]
- Alnaggar, M.; Bhanot, N. A machine learning approach for the identification of the Lattice Discrete Particle Model parameters. Eng. Fract. Mech. 2018, 197, 160–175. [Google Scholar] [CrossRef]
- Zhang, H.; Šavija, B.; Schlangen, E. Combined experimental and numerical study on micro-cube indentation splitting test of cement paste. Eng. Fract. Mech. 2018, 199, 773–786. [Google Scholar] [CrossRef]
- Van Vliet, M.R.; van Mier, J.G. Experimental investigation of size effect in concrete and sandstone under uniaxial tension. Eng. Fract. Mech. 2000, 65, 165–188. [Google Scholar] [CrossRef]
- Van Mier, J.; van Vliet, M. Influence of microstructure of concrete on size/scale effects in tensile fracture. Eng. Fract. Mech. 2003, 70, 2281–2306. [Google Scholar] [CrossRef]
- Shafieifar, M.; Farzad, M.; Azizinamini, A. Experimental and numerical study on mechanical properties of Ultra High Performance Concrete (UHPC). Constr. Build. Mater. 2017, 156, 402–411. [Google Scholar] [CrossRef]
- Bazant, Z.P.; Kazemi, M.T.; Hasegawa, T.; Mazars, J. Size effect in Brazilian split-cylinder tests: Measurements and fracture analysis. ACI Mat. J. 1991, 88, 325–332. [Google Scholar]
- Xu, S.; Zhu, Y. Experimental determination of fracture parameters for crack propagation in hardening cement paste and mortar. Int. J. Fract. 2009, 157, 33–43. [Google Scholar] [CrossRef]
- Van Mier, J.G.M.; Shah, S.P.; Arnaud, M.; Balayssac, J.P.; Bascoul, A.; Choi, S.; Dasenbrock, D.; Ferrara, G.; French, C.; Gobbi, M.E.; et al. Strain-softening of concrete in uniaxial compression. Mater. Struct. 1997, 30, 195–209. [Google Scholar] [CrossRef]
- Van Vliet, M.A.; van Mier, J.M. Experimental Investigation of Concrete Fracture under Uniaxial Compression; Wiley: Hoboken, NJ, USA, 1996; pp. 115–127. [Google Scholar]
- Nallathambi, P.; Karihaloo, B.; Heaton, B. Various size effects in fracture of concrete. Cem. Concr. Res. 1985, 15, 117–126. [Google Scholar] [CrossRef]
- Zhang, H.; Xu, Y.; Gan, Y.; Chang, Z.; Schlangen, E.; Šavija, B. Combined experimental and numerical study of uniaxial compression failure of hardened cement paste at micrometre length scale. Cem. Concr. Res. 2019, 126, 105925. [Google Scholar] [CrossRef]
- Hillerborg, A.; Modéer, M.; Petersson, P.-E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cem. Concr. Res. 1976, 6, 773–781. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Oh, B.H. Crack band theory for fracture of concrete. Mater. Struct. 1983, 16, 155–177. [Google Scholar] [CrossRef]
- Roelfstra, P.; Wittmann, F. Numerical method to link strain softening with failure of concrete, Fracture toughness and fracture energy of concrete. In Fracture Toughness and Fracture Energy in Concrete; Elsevier Science: Amsterdam, The Netherlands, 1986; pp. 163–175. [Google Scholar]
- Zhang, H. Experimentally Validated Multi-Scale Fracture Modelling Scheme of Cementitious Materials; Delft University of Technology: Delft, The Netherlands, 2019. [Google Scholar]
- Zhang, H.; Gan, Y.; Xu, Y.; Zhang, S.; Schlangen, E.; Šavija, B. Experimentally informed fracture modelling of interfacial transition zone at micro-scale. Cem. Concr. Compos. 2019, 104, 103383. [Google Scholar] [CrossRef]
- Zhang, H.; Šavija, B.; Xu, Y.; Schlangen, E. Size effect on splitting strength of hardened cement paste: Experimental and numerical study. Cem. Concr. Compos. 2018, 94, 264–276. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).