Vibration Analysis and Empirical Law Definition for Different Equipment in a Civil Construction
Abstract
1. Introduction
1.1. Objectives of the Study
1.2. Literature Review
2. Materials and Methods
2.1. Case Study
2.2. Equipment for Data Adquisition
- Several tests were done in situ to determine the attenuation vibration law for the specific ground of the case study and for each piece of equipment, described in Section 2, in the real location and carrying out a regular operation;
- Recording of the vibration transmission in the historical site foundations during 48 work days, 24 h a day.
2.3. Vibration Fundamentals
2.4. Set Up
- (a)
- Mechanical excavation using a Hitachi 500 with a V-type bucket for rock. Installation of 4 seismographs and 2 seismic stations;
- (b)
- Ripping operation using a Komatsu PC 450 LC6K equipped with a ripper. Installation of 3 seismographs and 2 seismic stations;
- (c)
- Fragmentation using a Hitachi ZX240 equipped with a hydraulic breaker hammer Furukawa F45. Installation of 4 seismographs and 2 seismic stations;
- (d)
- Earth moving and compacting roller. The first operation was done with a Bulldozer Cat D6N, while the second one using a Bomag BD211D. In both cases 4 seismographs and 2 seismic stations were used.
2.5. Maximum Allowable Velocity
3. Results and Discussion
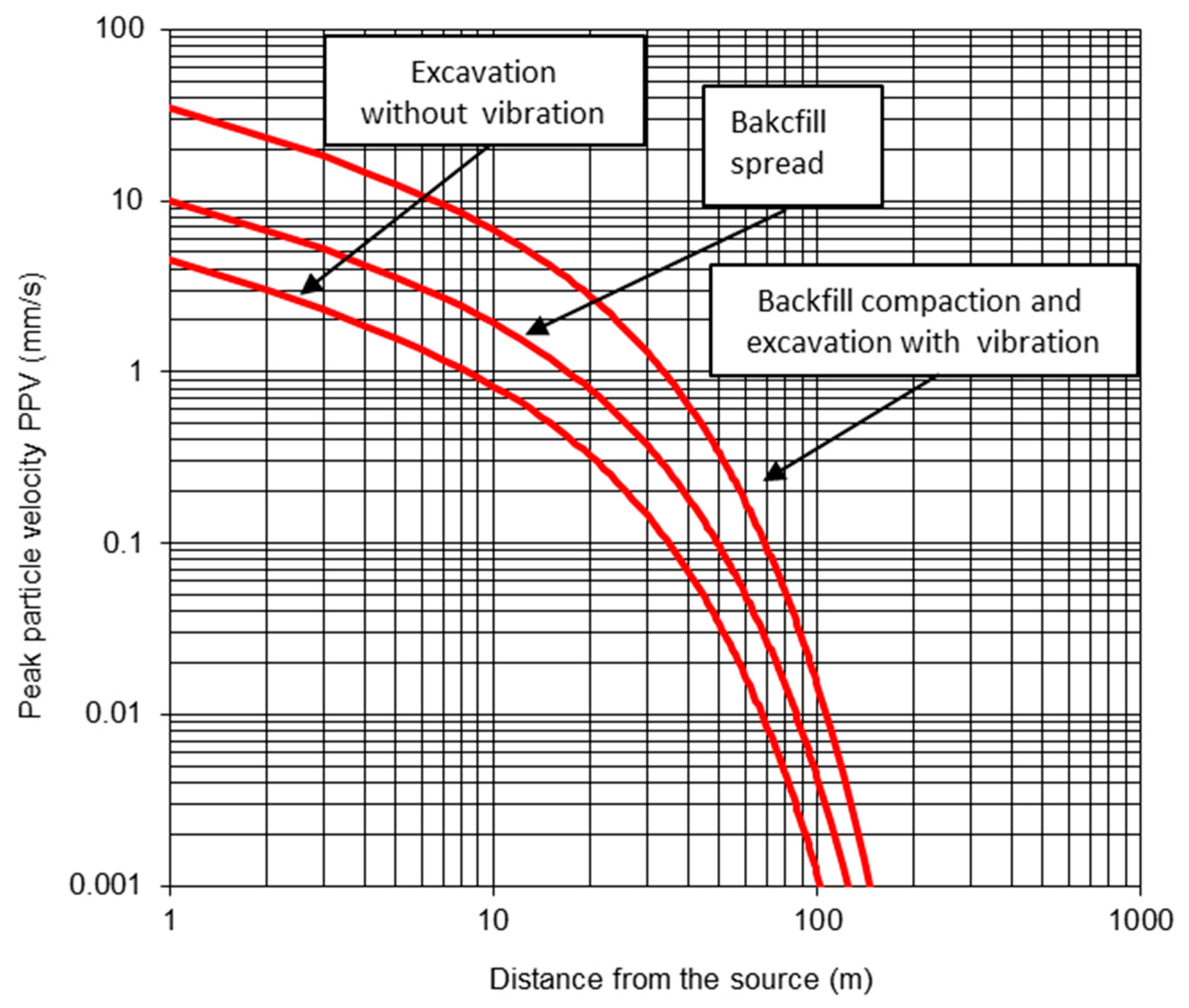
3.1. Anlalysis of the Equipment
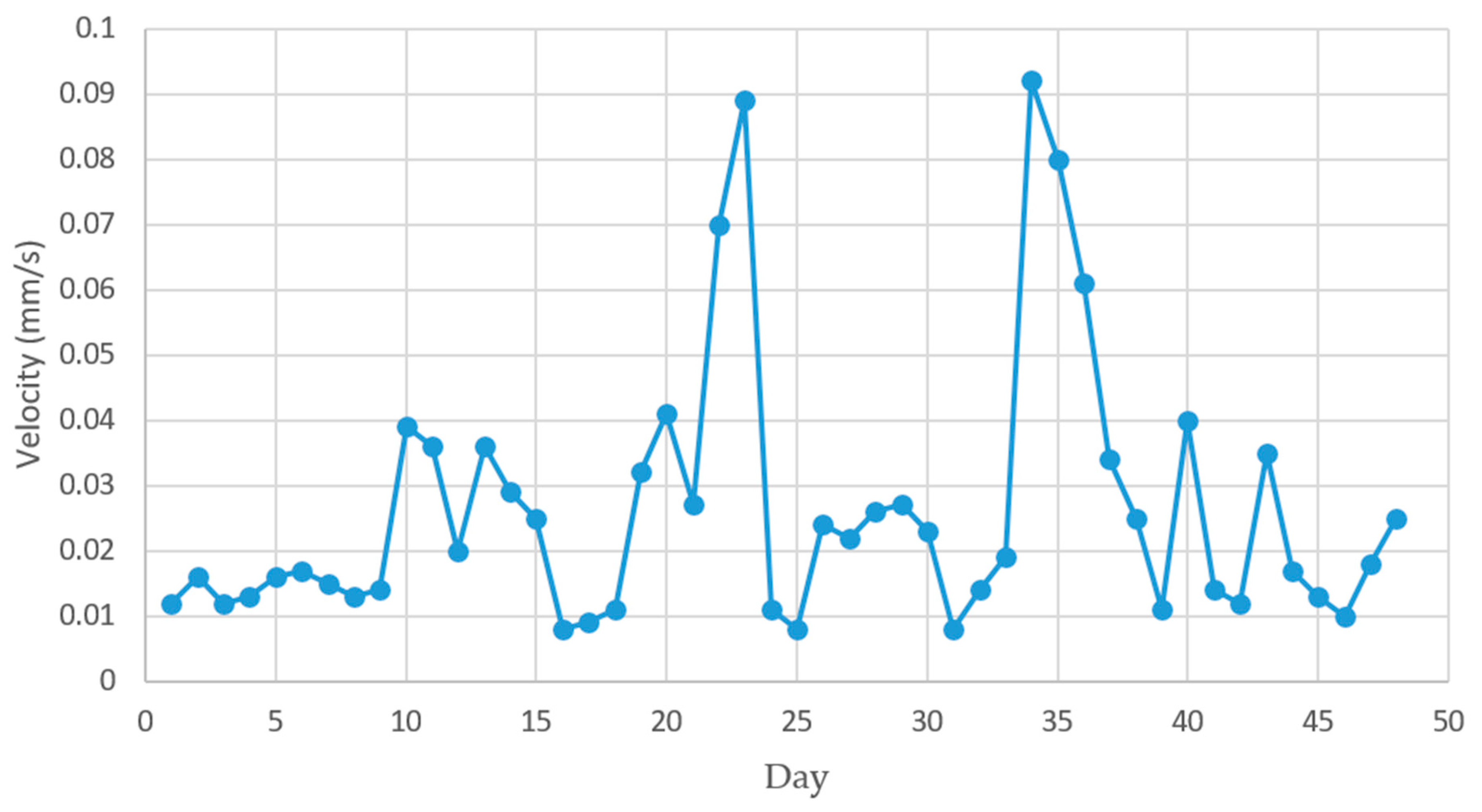
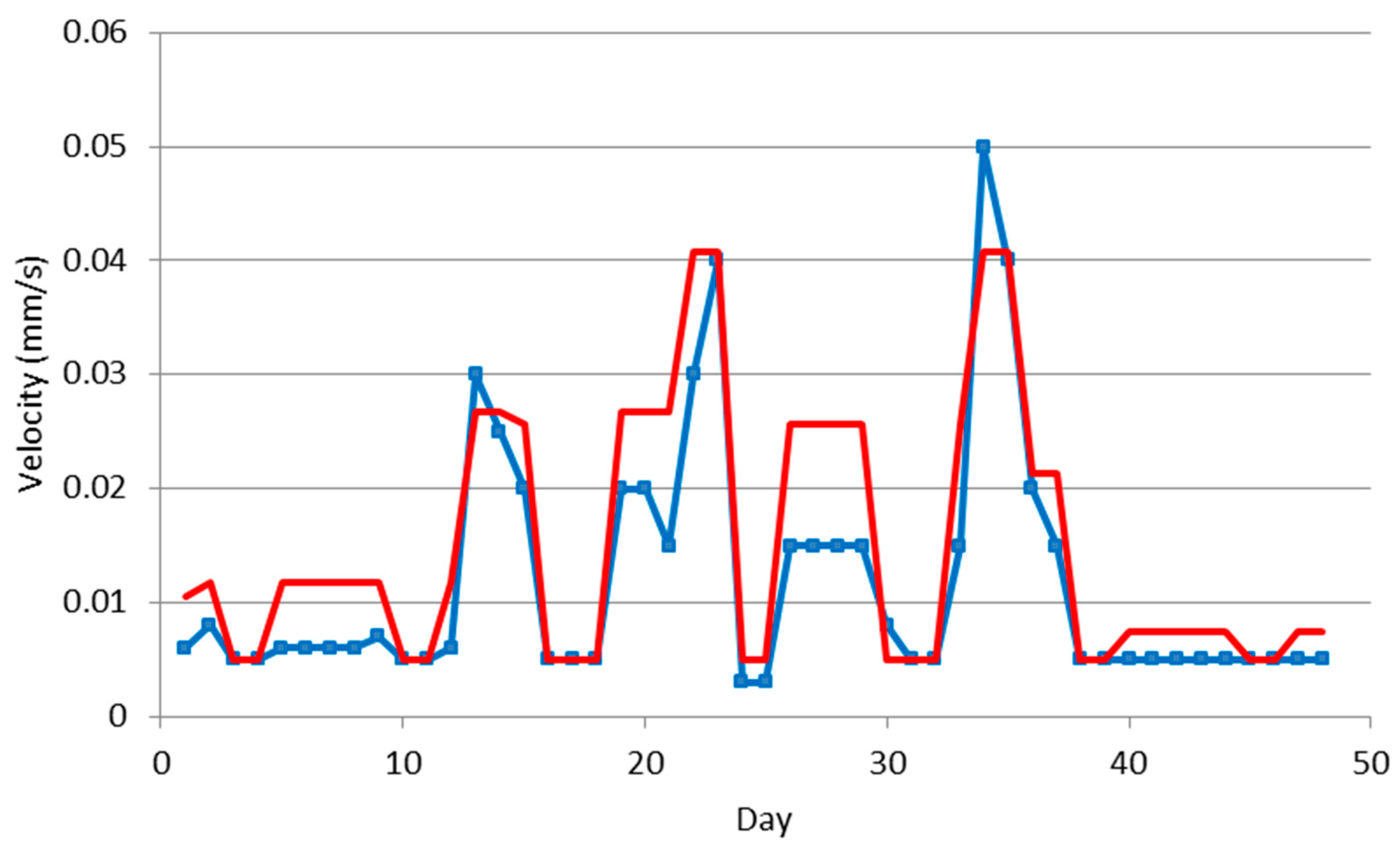
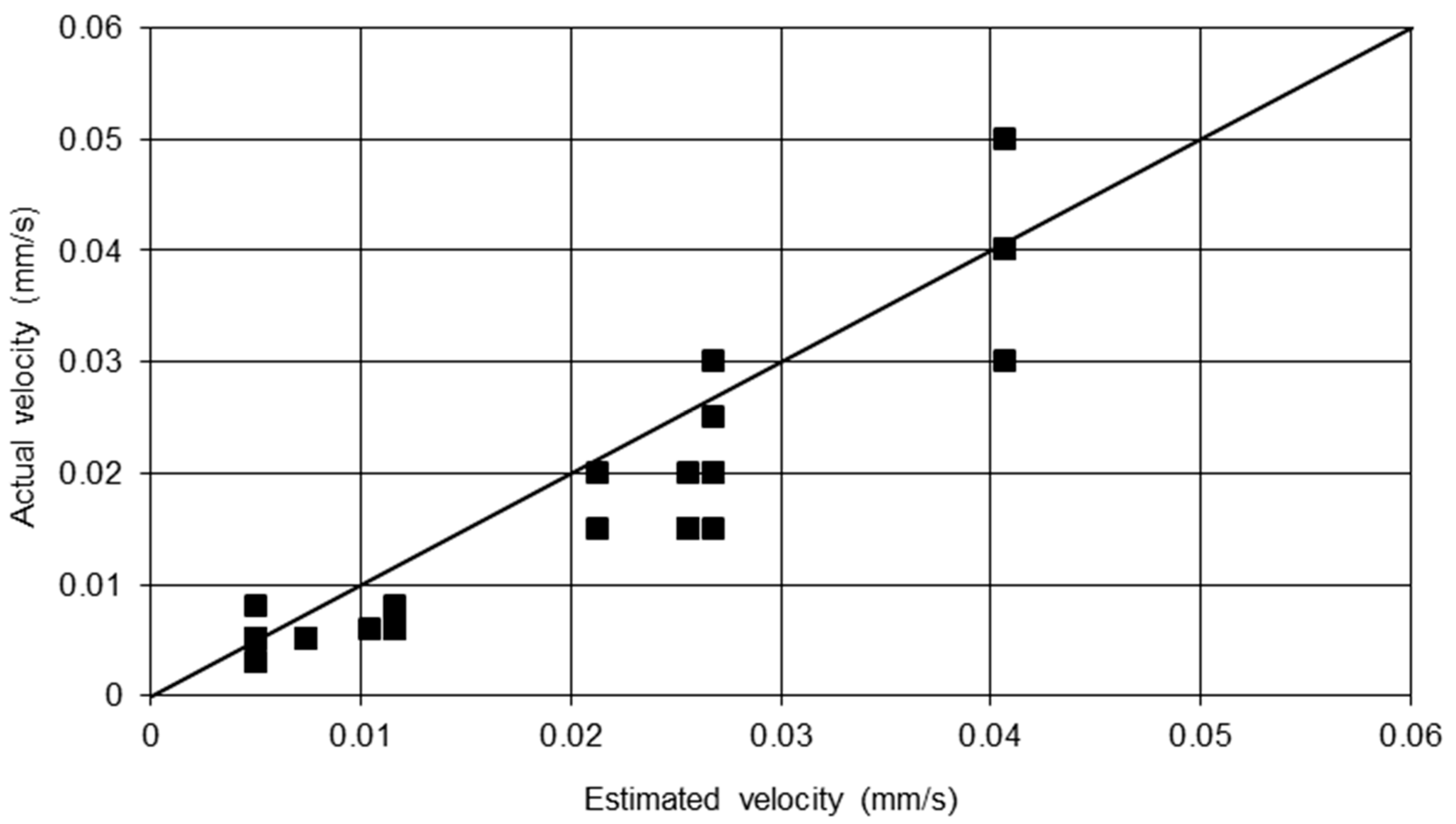
3.2. Historical Site Analysis
- VBmax: background maximum velocity;
- VExmax: excavator maximum velocity;
- VRmax: ripper maximum velocity;
- VVRmax: vibrating ripper maximum velocity;
- VBDmax: bulldozer maximum velocity;
- VCRmax: vibrating roller maximum velocity;
- n: number of equipment.
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gordon, C.G.; Amick, C.H. Groundborne vibration thoughts on control by foundation design and other techniques. Prcocedings Internoise 1989, 1, 547–550. [Google Scholar]
- Dowding, C.H. Construction Vibrations; Prentice-Hall: Englewood Cliffs, NJ, USA, 1996; ISBN 9780132991087. [Google Scholar]
- Toraño, J.; Rodriguez, R.; Diego, I.; Menéndez, M. Environmental impact of rock excavation in urban areas: Comparison between blasting and hydraulic breaker hammer. Civ. Eng. Environ. Syst. 2006, 23, 117–126. [Google Scholar] [CrossRef]
- Rodriguez, R.; Diaz-Aguado, M.B.; Garcia, M. Impact of new tunnels on those from the industrial era in Spain. Proc. Inst. Civ. Eng.-Eng. Hist. Heritage 2012, 165, 241–255. [Google Scholar] [CrossRef]
- Brady, B.H.G.; Brown, E.T. Rock Mechanics for Underground Mining, 3rd ed.; Springer Science: Berlin/Heidelberg, Germany, 2004; ISBN 1-4020-2064-3. [Google Scholar]
- Ramos, L.F.; Marques, L.; Lourenço, P.B.; De Roeck, G.; Campos-Costa, A.; Roque, J. Monitoring historical masonry structures with operational modal analysis: Two case studies. Mech. Syst. Signal Process. 2010, 24, 1291–1305. [Google Scholar] [CrossRef]
- García-Macías, E.; Ubertini, F. Automated operational modal analysis and ambient noise deconvolution interferometry for the full structural identification of historic towers: A case study of the Sciri Tower in Perugia, Italy. Eng. Struct. 2020, 215, 110615. [Google Scholar] [CrossRef]
- Kong, X.; Cai, C.S.; Hu, J. The state-of-the-art on framework of vibration-based structural damage identification for decision making. Appl. Sci. 2017, 7, 497. [Google Scholar] [CrossRef]
- Burgemeister, K.; Fisher, K.; Franklin, K. Measurement and prediction of construction vibration affecting sensitive laboratories. Proc. Acoust. 2011, 33, 20–26. [Google Scholar]
- Amick, H.; Gendreau, M.; Busch, T.; Gordon, C. Evolving criteria for research facilities: Vibration. Build. Nanoscale Res. Beyond 2005, 5933. [Google Scholar] [CrossRef]
- Lane, R.; Pelham, K. Ground Vibrations Emanating from Construction Equipment; New Hampshire Department of Transportation Bureau of Materials & Research: Concord, NH, USA, 2012. [Google Scholar] [CrossRef]
- Yan, Y.; Hou, X.; Fei, H. Review of predicting the blast-induced ground vibrations to reduce impacts on ambient urban communities. J. Clean. Prod. 2020, 260, 121135. [Google Scholar] [CrossRef]
- Department of Environment and Conservation. Assessing Vibration: A Technical Guideline; Department of Environment and Conservation: Sydney, Australia, 2006; ISBN 1741378125.
- Cenek, P.D.; Sutherland, A.J.; McIver, I.R. Ground Vibration from Road Construction; NZ Transport Agency: Queenstown, New Zealand, 2012. [Google Scholar]
- Andrews, J.; Buehler, D.; Gill, H.; Bender, W.L. Transportation and Construction-Induced Vibration Guidance Manual 2013; California Department of Transportation: Sacramento, CA, USA, 2013.
- Ungar, E.E.; Sturz, D.H.; Amick, H. Vibration Control Design of High Technology Facilities. Sound Vib. 1990, 24, 20–27. [Google Scholar]
- Amick, H.; Gendreau, M. Construction vibrations and their impact on vibration-sensitive facilities. Proc. Constr. Congr. VI 2000, 278, 758–767. [Google Scholar] [CrossRef]
- Kowalska-Koczwara, A.; Stypula, K. Assessment of the vibration influence on humans in buildings in the Standards of different countries. Procedia Eng. 2016, 161, 970–974. [Google Scholar] [CrossRef]
- California Department of Transportation. Transportation-Related Earthborne Vibrations; Technical Advisory TAV-02-01-R9601; California Department of Transportation: Sacramento, CA, USA, 2002.
- Nelson, P.M. Transportation Noise Reference; Butterworths: London, UK, 1987. [Google Scholar]
- Hendriks, R. Transportation Related Earthborne Vibrations; California Department of Transportation: Sacramento, CA, USA, 2002.
- Richart, F.E. Vibrations of Soil and Foundations; Prentice-Hall: Englewood Cliffs, NJ, USA, 1970. [Google Scholar]
- Telford, W.M.; Geldart, L.P.; Sheriff, R.E. Applied Geophysics; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Jones & Stokes Associates. Transportation and Construction Induced Vibration Guidance Manual; California Department of Transportation, Noise, Vibration and Hazardous Waste Management Office: Sacramento, CA, USA, 2004.
- Sambuelli, L. Theoretical Derivation of a Peak Particle Velocity–Distance Law for the Prediction of Vibrations from Blasting. Rock Mech. Rock Engeering 2009, 42, 547–556. [Google Scholar] [CrossRef]
- Jackson, N.M.; Hammons, M.I.; Walker, R.; Von Quintus, H. Use of Nondestructive Techniques to Estimate the Allowable Vibratory Compaction Level during Construction; State of Florida Department of Transportation: Tallahassee, FL, USA, 2007.
- Amick, H. Construction Vibrations and Their Impact on Vibration-Sensitive Facilities; Colin Gordin & Associates: San Mateo, CA, USA, 2000. [Google Scholar]
- Santamarina, J.C.; Klein, K.A.; Fam, M.A. Soils and Waves; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Murmu, S.; Maheshwari, P.; Verma, H.K. Empirical and probabilistic analysis of blast-induced ground vibrations. Int. J. Rock Mech. Min. Sci. 2018, 103, 267–274. [Google Scholar] [CrossRef]
- Kadiri, I.; Tahir, Y.; Iken, O.; Fertahi, S.; Agounoun, R. Experimental and statistical analysis of blast induced ground vibrations (BIGV) prediction in Senegal’s quarry. Studia Geotech. et Mech. 2019, 41, 231–246. [Google Scholar] [CrossRef]
- Chae, Y.S. Design of excavation blasts to prevent damage. Civ. Eng.—Am. Soc. Civ. Eng. 1978, 48, 77–79. [Google Scholar]
- Konon, W. Vibration criteria for historic buildings. J. Constr. Eng. Manag. 1985, 111, 208–215. [Google Scholar] [CrossRef]
- Crabb, G.I.; Hiller, D.M. Prediction of groundborne vibration from vibrating rollers. Proc. Inst. Civ. Eng. Transp. 2002, 153, 131–140. [Google Scholar] [CrossRef]
- Hanson, C.E.; Towers, D.A.; Meister, L.D. Transit Noise and Vibration Impact Assessment; Office of Planning and Environment, Federal Transit Administration: Washington, DC, USA, 2006.
- Woods, R.D. Dynamic Effects of Pile Installations on Adjacent Structures; Synthesis of Highway Practice 253; National Academy Press: Washington, DC, USA, 1997. [Google Scholar]
- Schexnayder, C.J.; Ernzen, J.E. Mitigation of Nighttime Construction Noise, Vibration, and Other Nuisances; National Academy Press: Washington, DC, USA, 1999. [Google Scholar]
- Hiller, D.M.; Crabb, G.I. Groundborne Vibrations Caused by Mechanised Construction Works; TRL report 429; Highways Agency: Crowthorne, Berkshire, UK; Transport Research Laboratory: Crowthorne, Berkshire, UK, 2000. [Google Scholar]
- Jackson, N.M.; Choubane, D.; Lee, H.S.; Holzschuher, C.; Hammons, M.I.; Walker, R. Recommended practice for identifying vibration-sensitive work zones based on falling weight deflectometer data. J. Transp. Res. Board 2008, 2081, 139–149. [Google Scholar] [CrossRef]
- American Association of State Highway and Transportation Officials. Standard Recommended Practice for Evaluation of Transportation-Related Earthborne Vibrations; American Association of State Highway and Transportation Officials: Washington, DC, USA, 1990. [Google Scholar]
- Schiappa de Azevedo, F.; Patricio, J. Annoyance and damage in buildings caused by vibrations. Considerations for a vibration control good practice. In Proceedings of the 4th Iberian Congress of acoustics, Acustica, Guimaraes, Portugal, 2004; pp. 1–14. [Google Scholar]
- Tsiambaos, G.; Saroglou, H. Excavatability assessment of rock masses using the Geological Strength Index (GSI). Bull. Eng. Geol. Environ. 2010, 69, 13–27. [Google Scholar] [CrossRef]
- Bell, F.G. Engineering in Rock Masses; Butterworth-Heinemann Limited: Ann Arbor, MI, USA, 1992; ISBN 9780750610636. [Google Scholar]
- Nichols, H.R.; Johnson, C.R.; Duvall, W.I. Blasting Vibrations and Their Effects on Structures; Bureau of Mines Bulletin: Denver, CO, USA, 1971; p. 656. [Google Scholar]
- Amick, H. Frecuency-dependent soil propagation model. Proc. SPIE Int. Soc. Opt. Eng. 1999, 9, 72–80. [Google Scholar] [CrossRef]
- Studer, J.; Suesstrunk, A. Swiss Standard for Vibration Damage to Buildings. In Proceedings of the Tenth International Conference on Soil Mechanics and Foundation Engineering, Stockholm, Sweden, 15–19 June 1981; International Federation for Structural Concrete: Stockholm, Sweden, 1981. [Google Scholar]
- Forsblad, I. Vibratory Soil and Rock Fill Compaction. In Dynapac Maskin AB; International Federation for Structural Concrete: Solna, Stockholm, Sweden.
- Wiss, J.F. Construction Vibrations: State of the Art. J. Geotech. Div. 1981, 107, 167–181. [Google Scholar]
- Pistrol, J.; Kopf, F.; Adam, D.; Villwock, S.; Völkel, W. Ambient vibration of oscillating and vibrating rollers. In Proceedings of the Vienna Congress on Recent Advances in Earthquake Engineering and Structural Dynamics 2013, Viena, Austria, 28–30 August 2013. [Google Scholar]




| Source | Threshold Value (mm/s) |
|---|---|
| Studer and Suesstrunk [45] | 1.8–3 |
| Forsblad [46] | 2 |
| Swiss Standard | 3 |
| Standard DIN 4150 | 2.5–10 |
| Schiappa de Azevedo and Patricio [37] | 1.75–10 |
| V Bucket | Ripper | ||
|---|---|---|---|
| Distance (m) | Velocity (mm/s) | Distance (m) | Velocity (mm/s) |
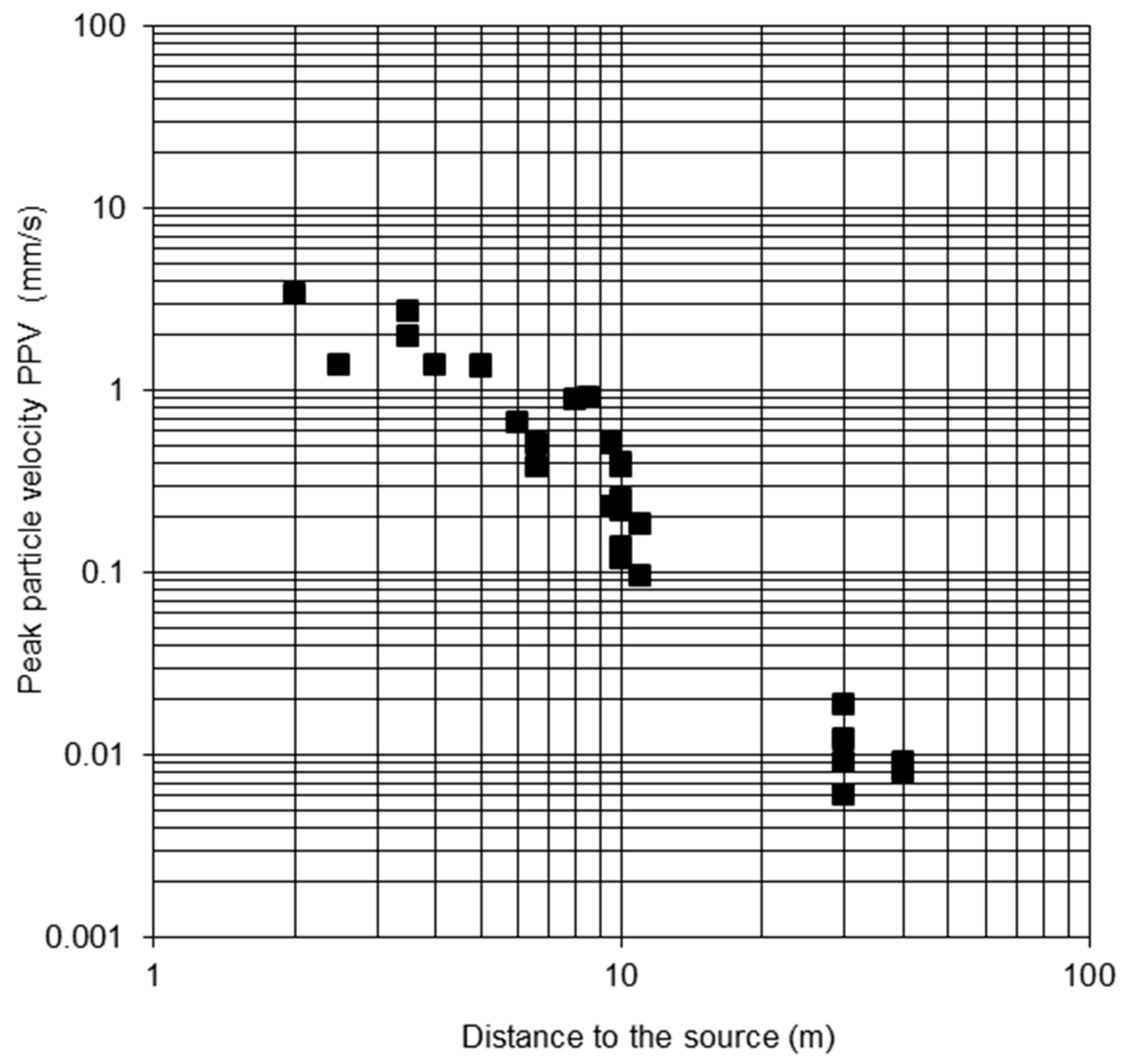
| 2.5 | 1.36 | 4 | 1.36 |
| 5 | 1.33 | 10 | 0.38 |
| 6 | 0.66 | 10 | 0.25 |
| 6.6 | 0.38 | 11 | 0.095 |
| 6.6 | 0.51 | 11 | 0.183 |
| 9.5 | 0.23 | 30 | 0.009 |
| 10 | 0.215 | 30 | 0.019 |
| 40 | 0.008 | ||
| 40 | 0.009 | ||
| Vibrating Ripper | Hydraulic Hammer | ||
|---|---|---|---|
| Distance (m) | Velocity (mm/s) | Distance (m) | Velocity (mm/s) |
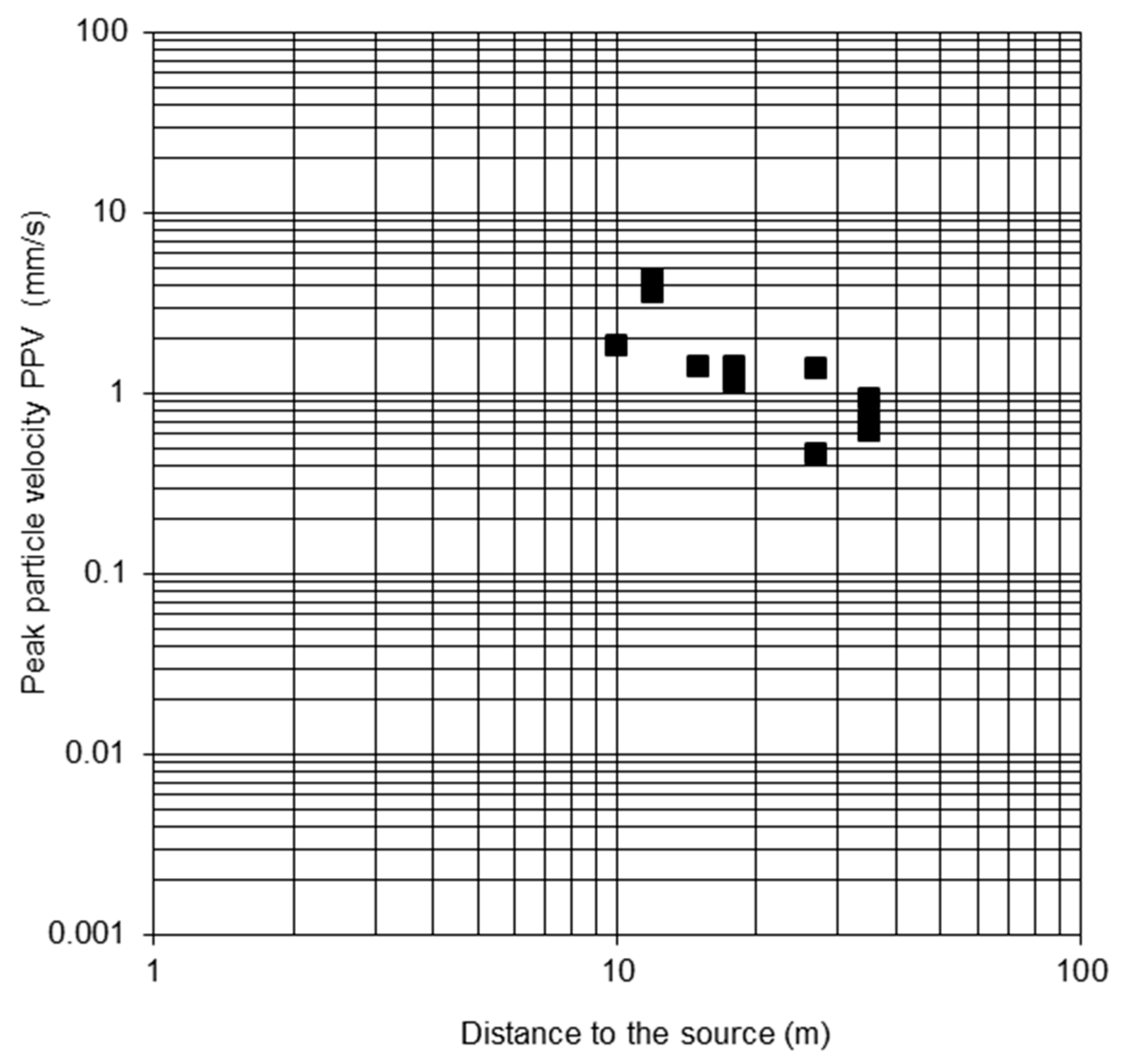
| 2 | 4.31 | 2 | 3.33 |
| 2 | 3.63 | 3.5 | 1.99 |
| 10 | 1.85 | 3.5 | 2.72 |
| 15 | 1.39 | 5 | 1.36 |
| 18 | 1.16 | 8 | 0.88 |
| 18 | 1.39 | 8.5 | 0.90 |
| 27 | 1.38 | 9.5 | 0.51 |
| 27 | 0.46 | 10 | 0.40 |
| 35 | 0.92 | 10 | 0.119 |
| 35 | 0.69 | 10 | 0.137 |
| 35 | 0.62 | 30 | 0.012 |
| 30 | 0.006 | ||
| Bulldozer | Vibrating Roller | ||
|---|---|---|---|
| Distance (m) | Velocity (mm/s) | Distance (m) | Velocity (mm/s) |
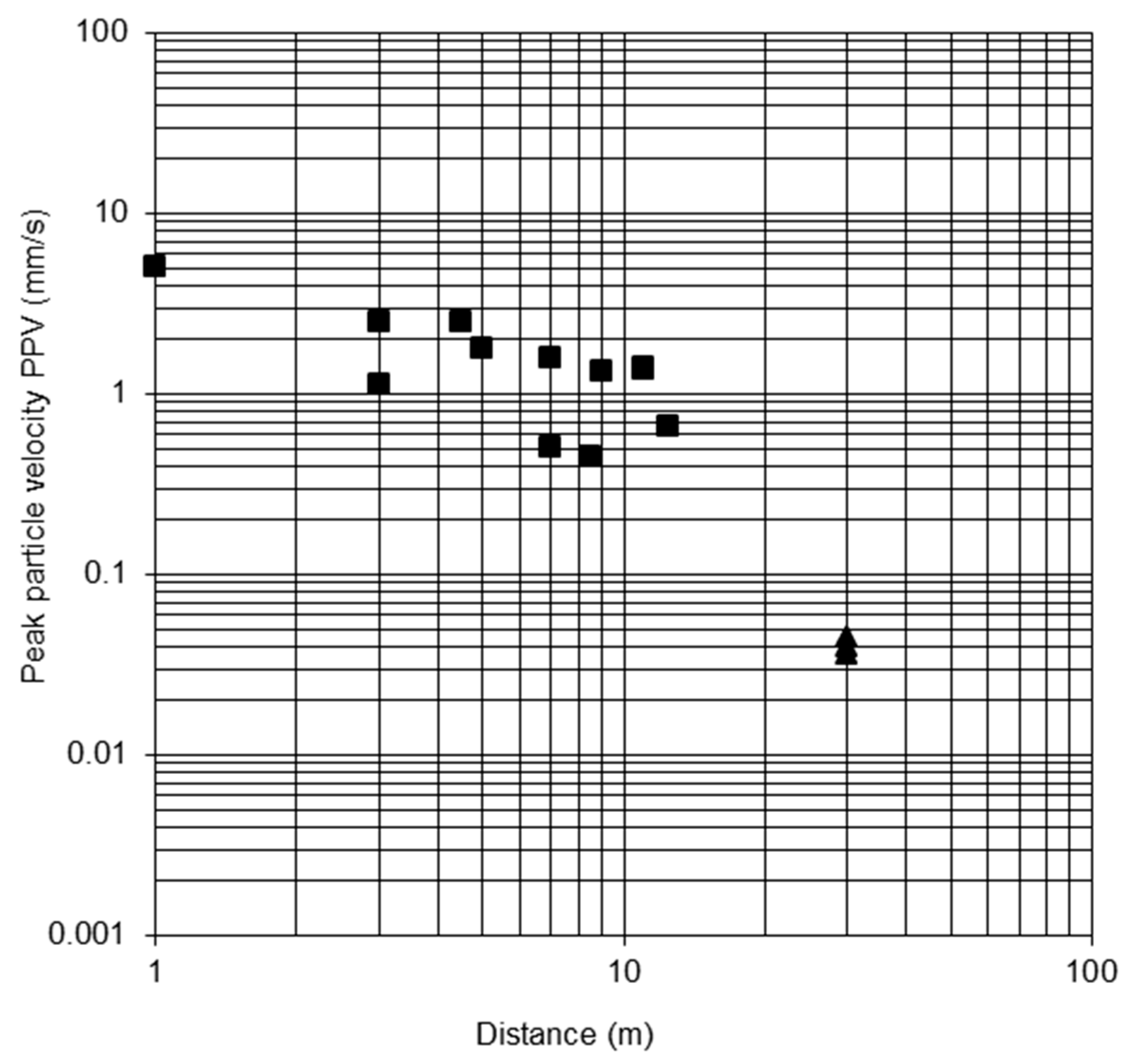
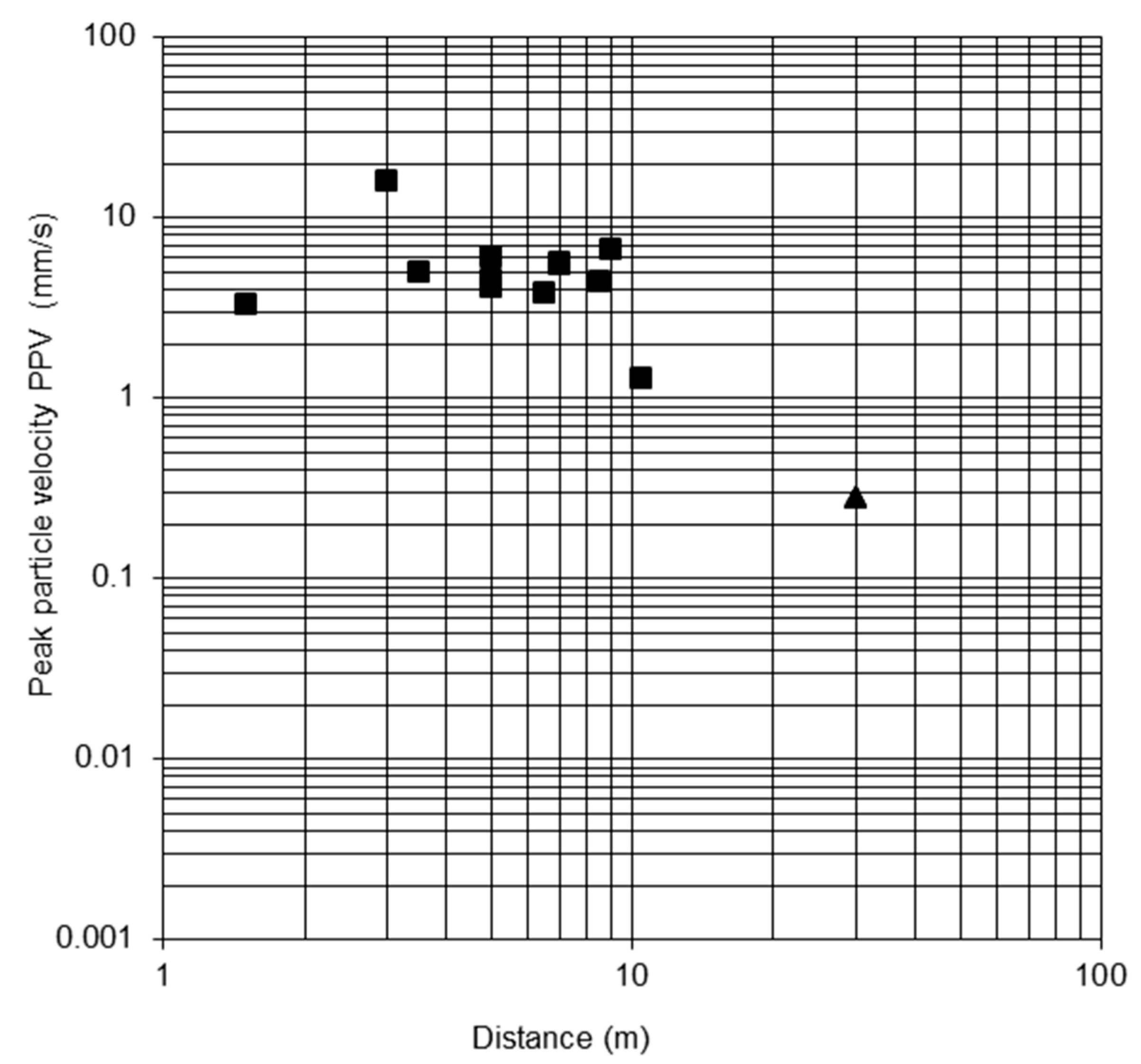
| 1 | 5.1 | 1.5 | 3.33 |
| 3 | 2.5 | 3 | 15.76 |
| 3 | 1.14 | 3.5 | 4.99 |
| 4.5 | 2.5 | 5 | 4.54 |
| 5 | 1.77 | 5 | 6.12 |
| 7 | 1.58 | 5 | 3.99 |
| 7 | 0.51 | 6.5 | 3.85 |
| 8.5 | 0.45 | 7 | 5.44 |
| 9 | 1.33 | 7 | 5.33 |
| 11 | 1.4 | 8.5 | 4.31 |
| 11 | 1.36 | 9 | 6.6 |
| 12.5 | 0.66 | 10.5 | 1.27 |
| 30 | 0.044 | 30 | 0.27 |
| 30 | 0.035 | 30 | 0.27 |
| 30 | 0.039 | 30 | 0.27 |
| V Bucket | Ripper | Vibration Ripper | Bulldozer | Vibrating Roller | Velocity |
|---|---|---|---|---|---|
| 1 | 0 | 0 | 1 | 0 | 0.006 |
| 1 | 1 | 0 | 1 | 0 | 0.008 |
| 0 | 0 | 0 | 0 | 0 | 0.005 |
| 0 | 0 | 0 | 0 | 0 | 0.005 |
| 1 | 1 | 0 | 1 | 0 | 0.006 |
| 1 | 1 | 0 | 1 | 0 | 0.006 |
| 1 | 1 | 0 | 1 | 0 | 0.006 |
| 1 | 1 | 0 | 1 | 0 | 0.006 |
| 1 | 1 | 0 | 1 | 0 | 0.007 |
| 0 | 0 | 0 | 0 | 0 | 0.005 |
| 0 | 0 | 0 | 0 | 0 | 0.005 |
| 1 | 1 | 0 | 1 | 0 | 0.006 |
| 1 | 1 | 1 | 1 | 0 | 0.030 |
| 1 | 1 | 1 | 1 | 0 | 0.025 |
| 1 | 0 | 1 | 1 | 0 | 0.020 |
| 0 | 0 | 0 | 0 | 0 | 0.005 |
| 0 | 0 | 0 | 0 | 0 | 0.005 |
| 0 | 0 | 0 | 0 | 0 | 0.005 |
| 1 | 1 | 1 | 1 | 0 | 0.020 |
| 1 | 1 | 1 | 1 | 0 | 0.020 |
| 1 | 1 | 1 | 1 | 0 | 0.015 |
| 1 | 0 | 1 | 1 | 1 | 0.030 |
| 1 | 0 | 1 | 1 | 1 | 0.040 |
| 0 | 0 | 0 | 0 | 0 | 0.003 |
| 0 | 0 | 0 | 0 | 0 | 0.003 |
| 1 | 0 | 1 | 1 | 0 | 0.015 |
| 1 | 0 | 1 | 1 | 0 | 0.015 |
| 1 | 0 | 1 | 1 | 0 | 0.015 |
| 1 | 0 | 1 | 1 | 0 | 0.015 |
| 0 | 0 | 0 | 0 | 0 | 0.008 |
| 0 | 0 | 0 | 0 | 0 | 0.005 |
| 0 | 0 | 0 | 0 | 0 | 0.005 |
| 1 | 0 | 1 | 1 | 0 | 0.015 |
| 1 | 0 | 1 | 1 | 1 | 0.050 |
| 1 | 0 | 1 | 1 | 1 | 0.040 |
| 1 | 0 | 1 | 0 | 0 | 0.020 |
| 1 | 0 | 1 | 0 | 0 | 0.015 |
| 0 | 0 | 0 | 0 | 0 | 0.005 |
| 0 | 0 | 0 | 0 | 0 | 0.005 |
| 1 | 1 | 0 | 0 | 0 | 0.005 |
| 1 | 1 | 0 | 0 | 0 | 0.005 |
| 1 | 1 | 0 | 0 | 0 | 0.005 |
| 1 | 1 | 0 | 0 | 0 | 0.005 |
| 1 | 1 | 0 | 0 | 0 | 0.005 |
| 0 | 0 | 0 | 0 | 0 | 0.005 |
| 0 | 0 | 0 | 0 | 0 | 0.005 |
| 1 | 1 | 0 | 0 | 0 | 0.005 |
| 1 | 1 | 0 | 0 | 0 | 0.005 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodríguez, R.; Bascompta, M. Vibration Analysis and Empirical Law Definition for Different Equipment in a Civil Construction. Appl. Sci. 2020, 10, 4689. https://doi.org/10.3390/app10144689
Rodríguez R, Bascompta M. Vibration Analysis and Empirical Law Definition for Different Equipment in a Civil Construction. Applied Sciences. 2020; 10(14):4689. https://doi.org/10.3390/app10144689
Chicago/Turabian StyleRodríguez, Rafael, and Marc Bascompta. 2020. "Vibration Analysis and Empirical Law Definition for Different Equipment in a Civil Construction" Applied Sciences 10, no. 14: 4689. https://doi.org/10.3390/app10144689
APA StyleRodríguez, R., & Bascompta, M. (2020). Vibration Analysis and Empirical Law Definition for Different Equipment in a Civil Construction. Applied Sciences, 10(14), 4689. https://doi.org/10.3390/app10144689






