Optimization of Phase-Only Computer-Generated Holograms Based on the Gradient Descent Method
Abstract
:1. Introduction
2. Theory
2.1. Gradient Descent Method for Optimizing Phase-Only CGHs
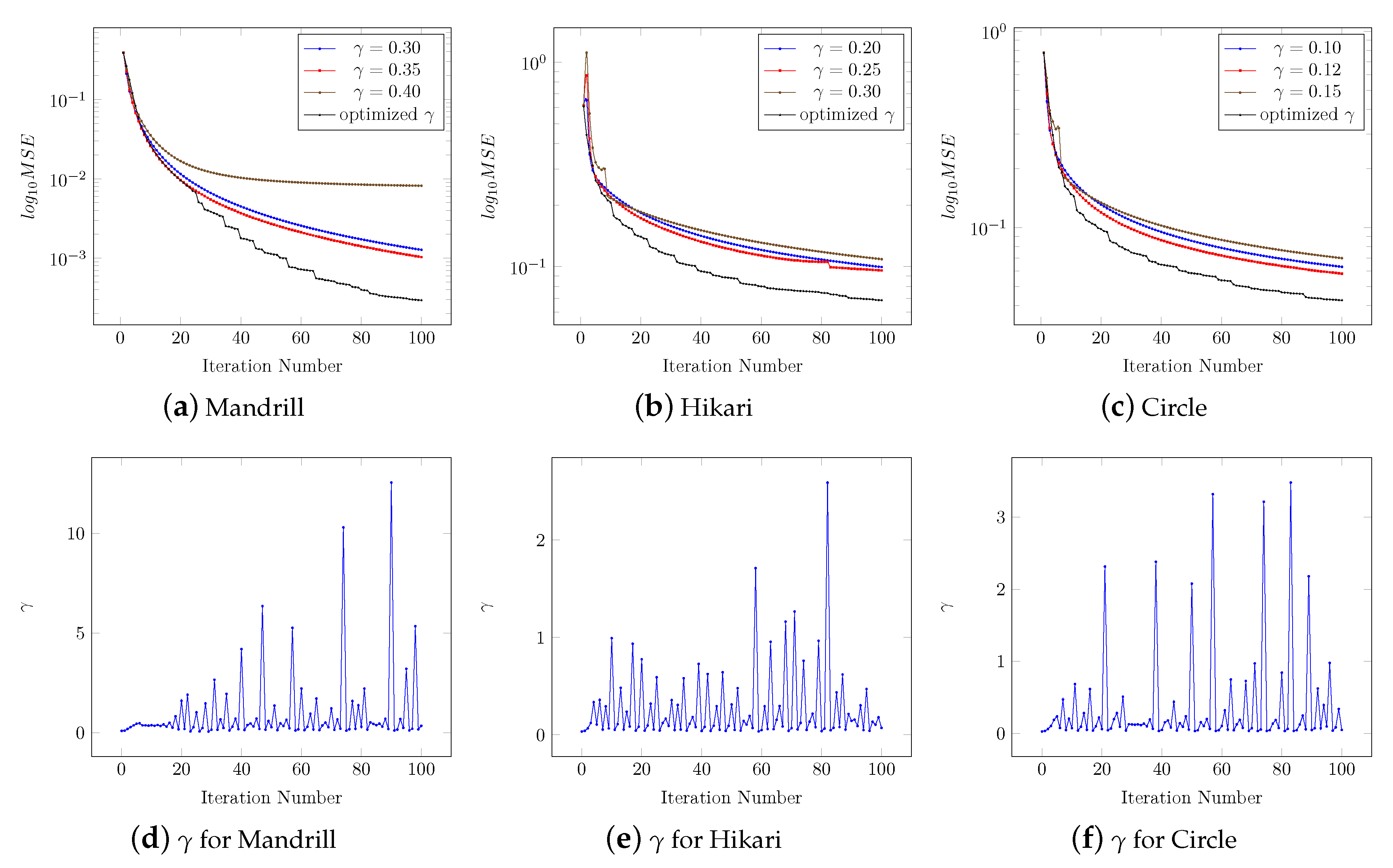
2.2. Determination of Step Length Coefficient
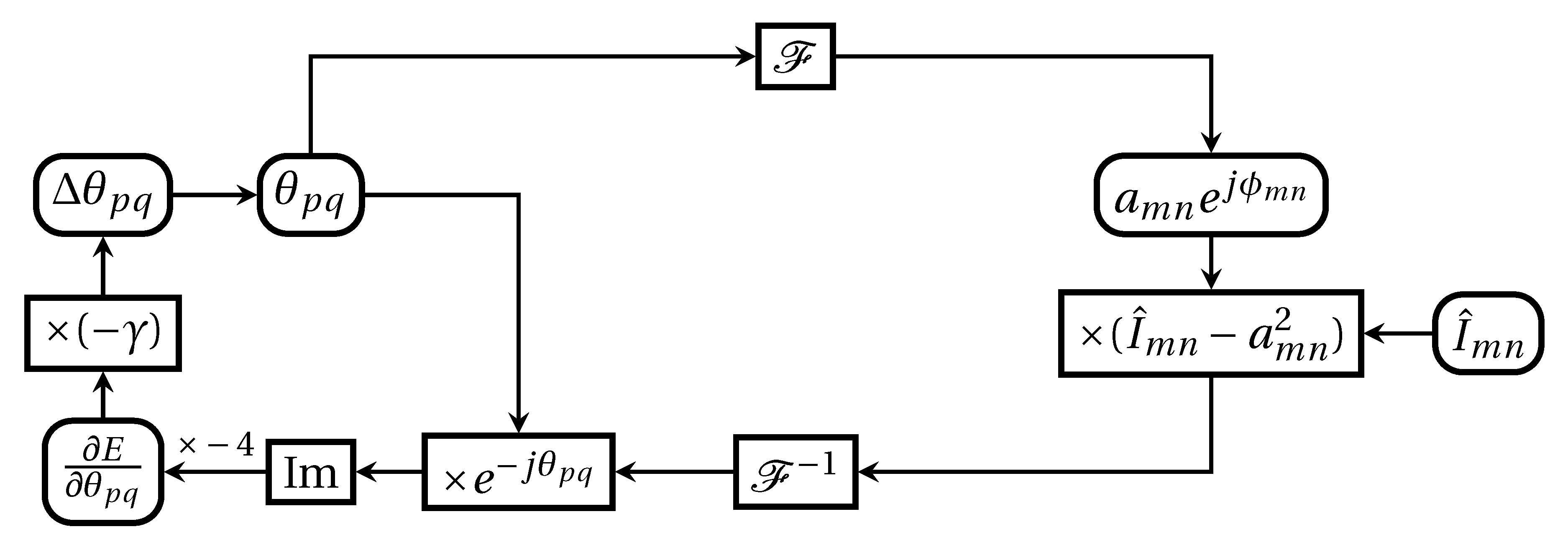
3. Proposed Calculation Process
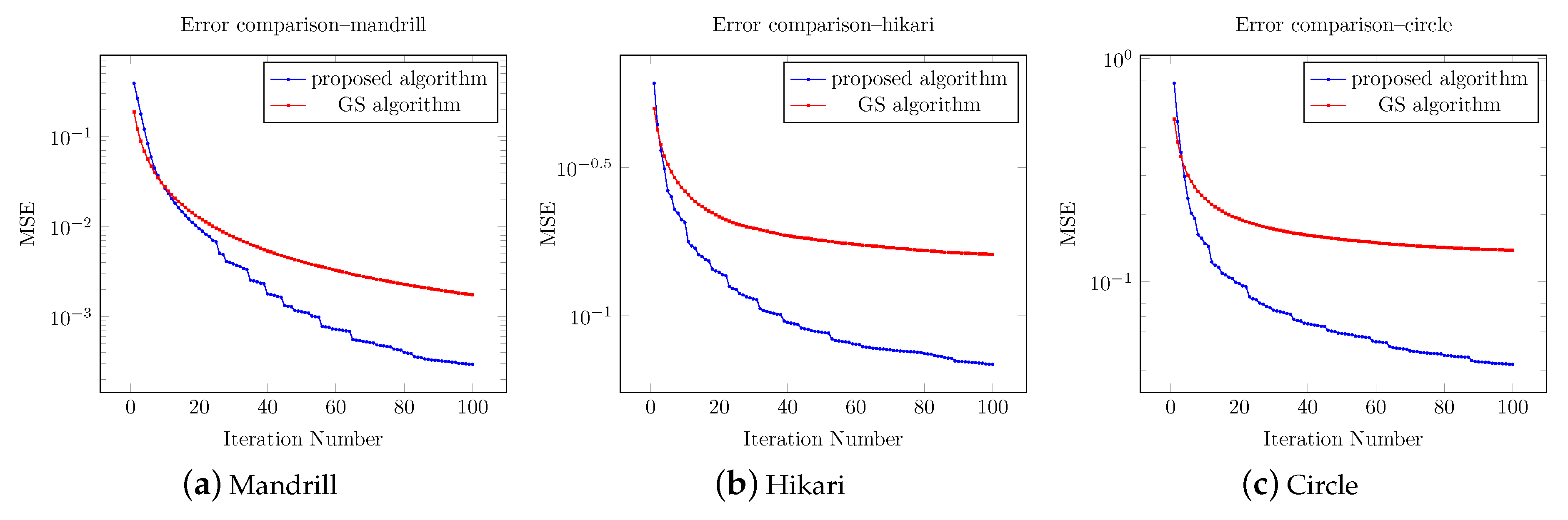
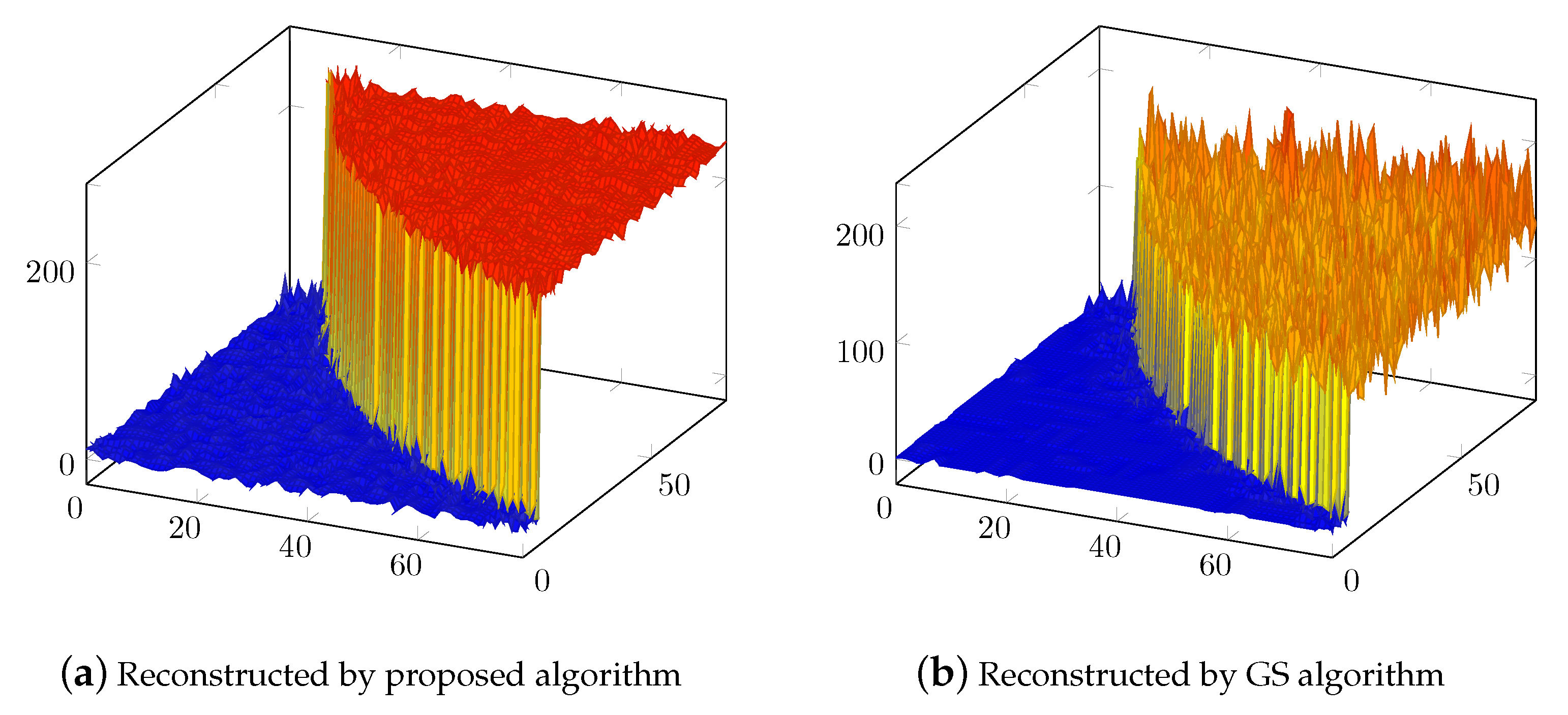
4. Verification of Proposed Technique
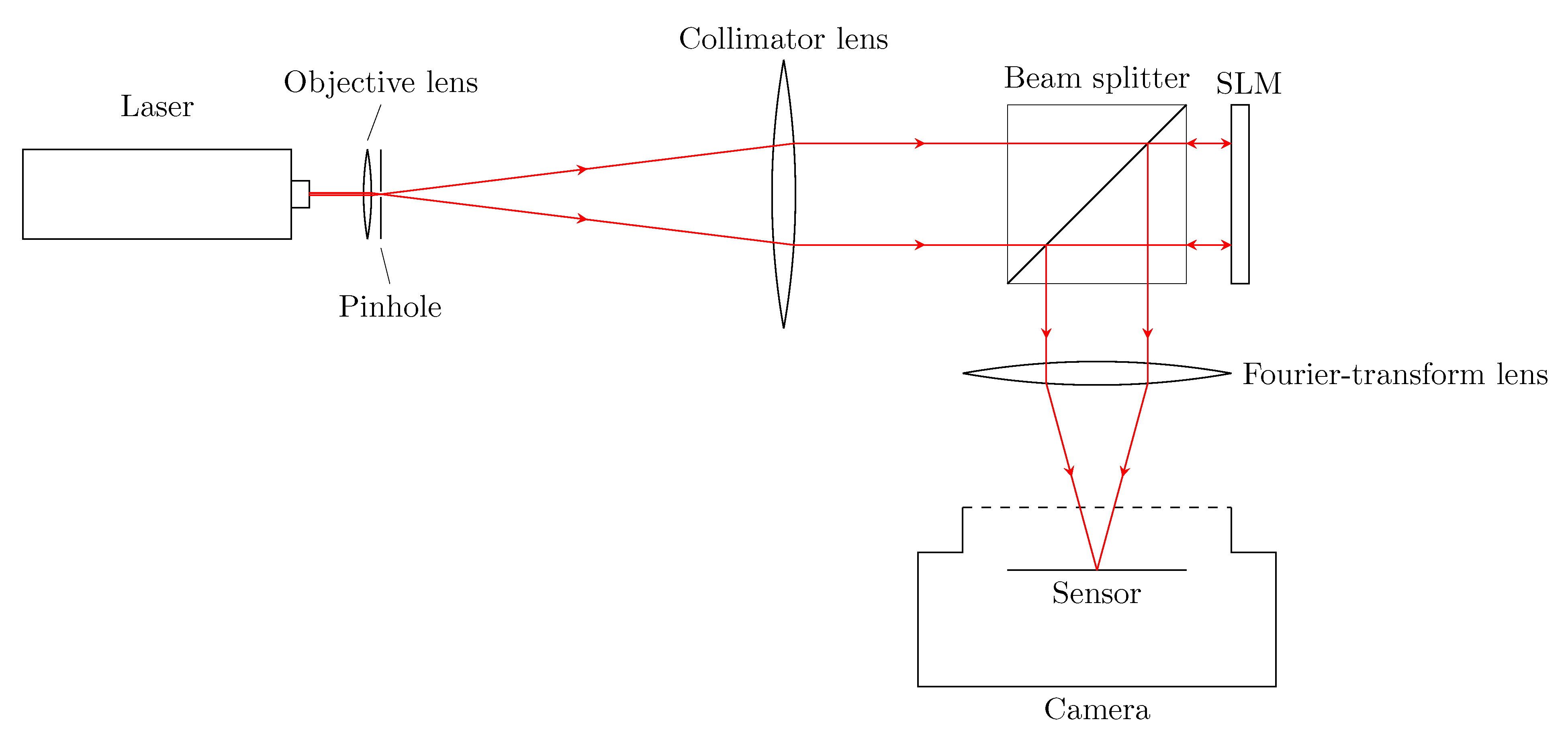
5. Experiments
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gabor, D. A New Microscopic Principle. Nature 1948, 181, 777–778. [Google Scholar] [CrossRef]
- Gabor, D. Microscopy by reconstructed wavefronts. Proc. R. Soc. 1949, 197, 454–487. [Google Scholar]
- Brown, B.R.; Lohmann, A. Complex spatial filtering with binary masks. Appl. Opt. 1966, 5, 967–969. [Google Scholar] [CrossRef]
- Brown, B.R.; Lohmann, A. Computer generated binary holograms. IMB J. Res. Dev. 1969, 13, 160–168. [Google Scholar] [CrossRef]
- Kronrod, M.A.; Merzlyakov, N.S.; Yaroslavsky, L.P. Computer Synthesis of Transparency Holograms. Sov. Phys.-Tech. Phys. 1972, 13, 414–418. [Google Scholar]
- Yaroslavskii, L.; Merzlyakov, N. Methods of Digital Holography. Consultance Bureau; Springer: Berlin/Heidelberg, Germany, 1980. [Google Scholar]
- Chen, C.Y.; Li, W.C.; Chang, H.T.; Chuang, C.H.; Chang, T.J. 3-D modified Gerchberg-Saxton algorithm developed for panoramic computer-generated phase-only holographic display. JOSA B 2017, 34, B42–B48. [Google Scholar] [CrossRef]
- Tsang, P.W.M.; Chow, Y.T.; Poon, T.-C. Generation of patterned-phase-only holograms (PPOHs). Opt. Express 2017, 25, 9088–9093. [Google Scholar] [CrossRef] [PubMed]
- Mullins, B.; Greenhalgh, P.; Chistmas, J. The Holographic Future of Head Up Displays. SID Symp. Dig. Tech. Pap. 2017, 48, 886–889. [Google Scholar] [CrossRef]
- Dufresne, E.R.; Spalding, G.C.; Dearing, M.T.; Sheets, S.A.; Grier, D.G. Computer-Generated Holographic Optical Tweezer Arrays. Rev. Sci. Instrum. 2001, 72, 1810. [Google Scholar] [CrossRef] [Green Version]
- Yeh, J.H.; Kostuk, R.K. Free-space holographic optical interconnects for board-to-board and chip-to-chip interconnections. Opt. Lett. 1996, 21, 1274–1277. [Google Scholar] [CrossRef] [PubMed]
- Farah, N.; Levinsky, A.; Brosh, I.; Kahn, I.; Shoham, S. Holographic fiber bundle system for patterned optogenetic activation of large-scale neuronal networks. Neurophotonics 2015, 2, 045002. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kirk, A.G.; Hall, T.J. Design of Binary Computer Generated Holograms by Simulated Annealing—Coding Density and Reconstruction Error. Opt. Commun. 1992, 94, 491–496. [Google Scholar] [CrossRef]
- Wen, M.; Yao, J.; Wong, W.K.; Chen, G.C.K. Holographic diffuser design using a modified genetic algorithm. Opt. Eng. 2005, 44, 085801. [Google Scholar] [CrossRef]
- Nguyen, T.-A.; An, J.W.; Choi, J.K.; Kim, N.; Jeon, S.H.; Kwon, Y.S. Hybrid algorithm to reduce the computation time of genetic algorithm for designing binary phase holograms. Opt. Eng. 2004, 43. [Google Scholar] [CrossRef]
- Gillet, J.N.; Sheng, Y. Multiplexed computer-generated holograms with polygonal-aperture layouts optimized by genetic algorithm. Appl. Opt. 2003, 42, 4156–4165. [Google Scholar] [CrossRef]
- Seldowitz, M.A.; Allebach, J.P.; Sweeney, D.W. Synthesis of digital holograms by direct binary search. Appl. Opt. 1987, 26, 2788–2798. [Google Scholar] [CrossRef]
- Leportier, T.; Park, M.C.; Kim, Y.S.; Kim, T. Converting optical scanning holograms of real objects to binary Fourier holograms using an iterative direct binary search algorithm. Opt. Express 2015, 23, 3403–3411. [Google Scholar] [CrossRef]
- Leportier, T.; Park, M.C. Advanced DBS (Direct-Binary Search) Method for Compensating Spatial Chromatic Errors on RGB Digital Holograms in a Wide-Depth Range with Binary Holograms. IEICE Trans. Fundament. Electron. Commun. Comput. Sci. 2018, E101A, 848–849. [Google Scholar] [CrossRef]
- Gerchberg, R.W.; Saxton, W.O. Practical Algorithm for Determination of Phase from Image and Diffraction Plane Pictures. Optik 1972, 35, 237–246. [Google Scholar]
- Pasienski, M.; DeMarco, B. A high-accuracy algorithm for designing arbitrary holographic atom traps. Opt. Express 2008, 16, 2176–2190. [Google Scholar] [CrossRef] [Green Version]
- Gaunt, A.; Hadzibabic, Z. Robust Digital Holography For Ultracold Atom Trapping. Sci. Rep. 2012, 2, 721. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, H.; Yue, W.; Song, Q.; Liu, J.; Situ, G. A hybrid Gerchberg-Saxton-like algorithm for DOE and CGH calculation. Opt. Lasers Eng. 2017, 89, 109–115. [Google Scholar] [CrossRef] [Green Version]
- Hwang, H.-E.; Chang, H.T.; Lai, W.-N. Fast double-phase retrieval in Fresnel domain using modified Gerchberg-Saxton algorithm for lensless optical security systems. Opt. Express 2009, 17, 13700–13710. [Google Scholar] [CrossRef] [PubMed]
- Wen, C. 3D Gerchberg-Saxton Optical Correlation. IEEE Photonics J. 2018, 10. [Google Scholar] [CrossRef]
- Fienup, J.R. Phase retrieval algorithms: A comparison. Appl. Opt. 1982, 21, 2758–2769. [Google Scholar] [CrossRef] [Green Version]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]







© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Takaki, Y. Optimization of Phase-Only Computer-Generated Holograms Based on the Gradient Descent Method. Appl. Sci. 2020, 10, 4283. https://doi.org/10.3390/app10124283
Liu S, Takaki Y. Optimization of Phase-Only Computer-Generated Holograms Based on the Gradient Descent Method. Applied Sciences. 2020; 10(12):4283. https://doi.org/10.3390/app10124283
Chicago/Turabian StyleLiu, Shujian, and Yasuhiro Takaki. 2020. "Optimization of Phase-Only Computer-Generated Holograms Based on the Gradient Descent Method" Applied Sciences 10, no. 12: 4283. https://doi.org/10.3390/app10124283
APA StyleLiu, S., & Takaki, Y. (2020). Optimization of Phase-Only Computer-Generated Holograms Based on the Gradient Descent Method. Applied Sciences, 10(12), 4283. https://doi.org/10.3390/app10124283




