Integral Aircraft Wing Panels with Penetration Cracks: The Influence of Structural Parameters on the Stress Intensity Factor
Abstract
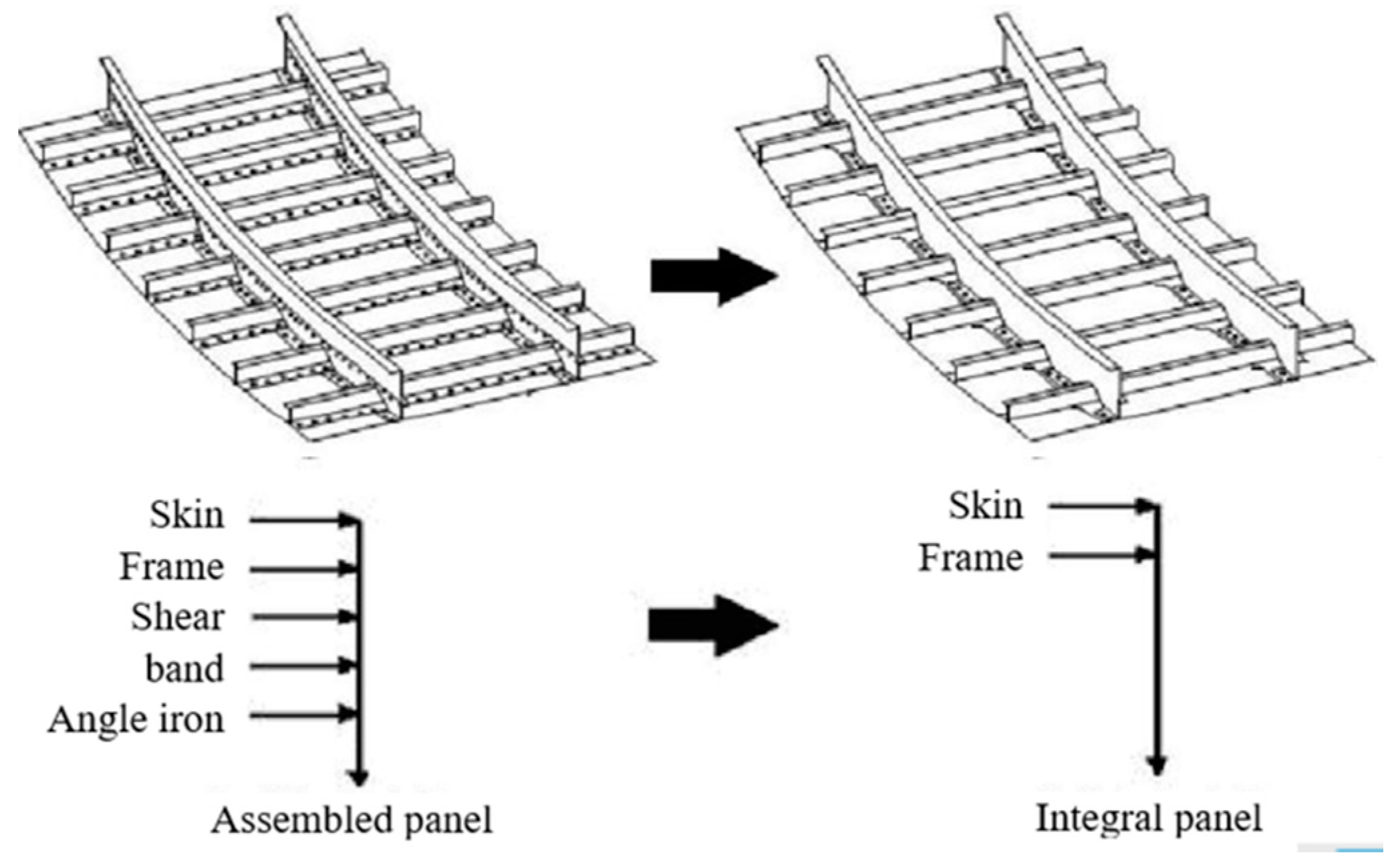
:1. Introduction
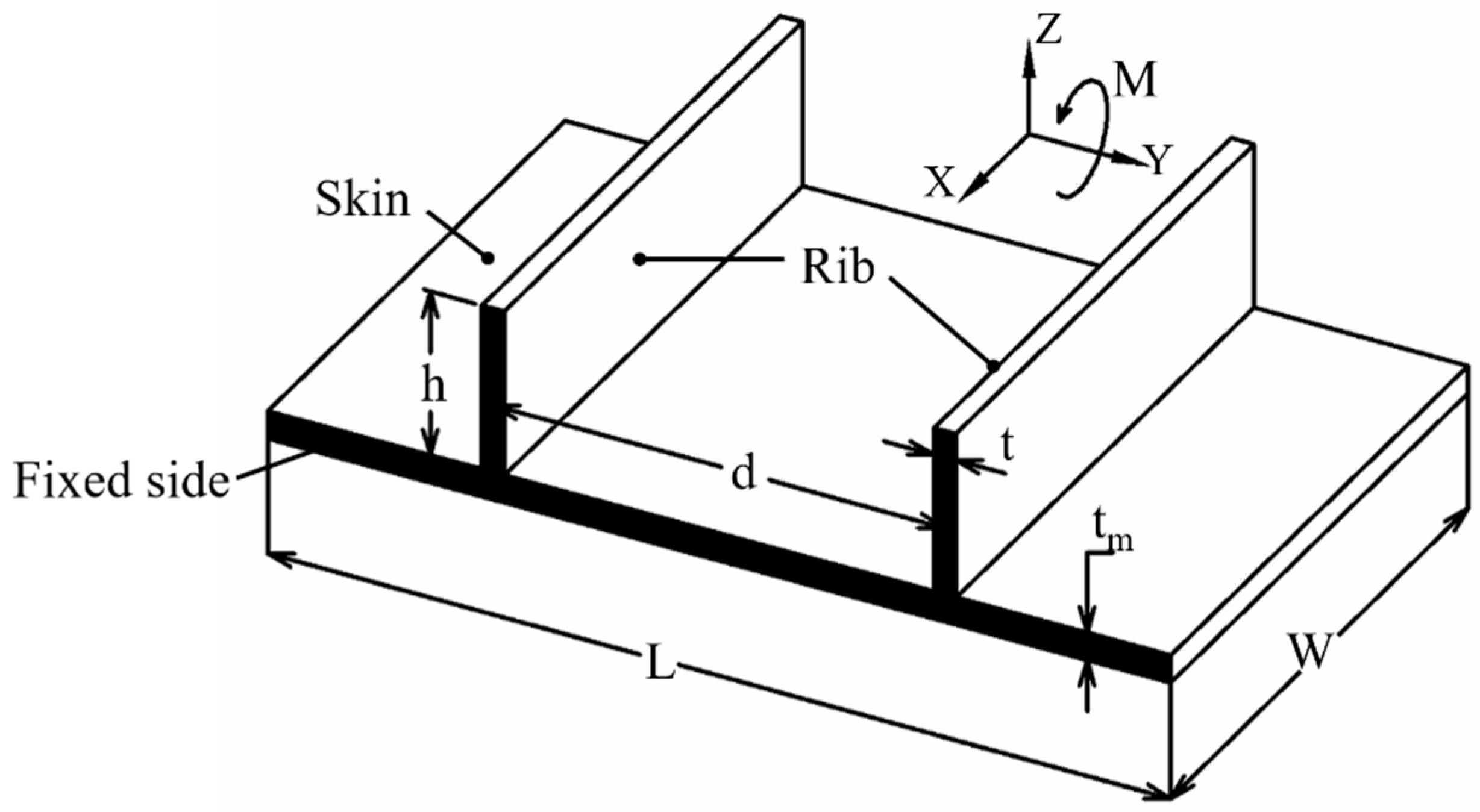
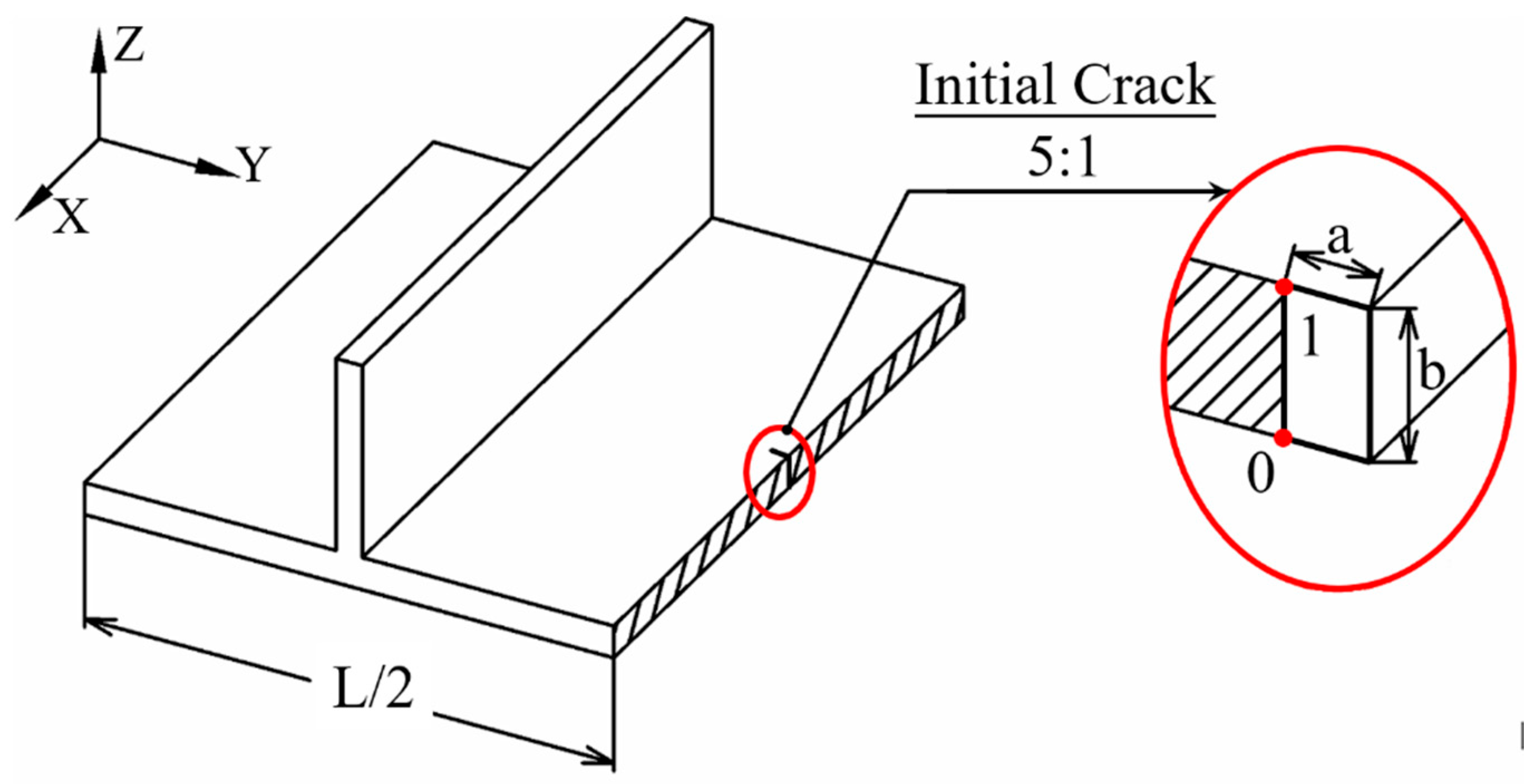
2. Finite Element Model
2.1. Damage Tolerance and Stress Intensity Factor
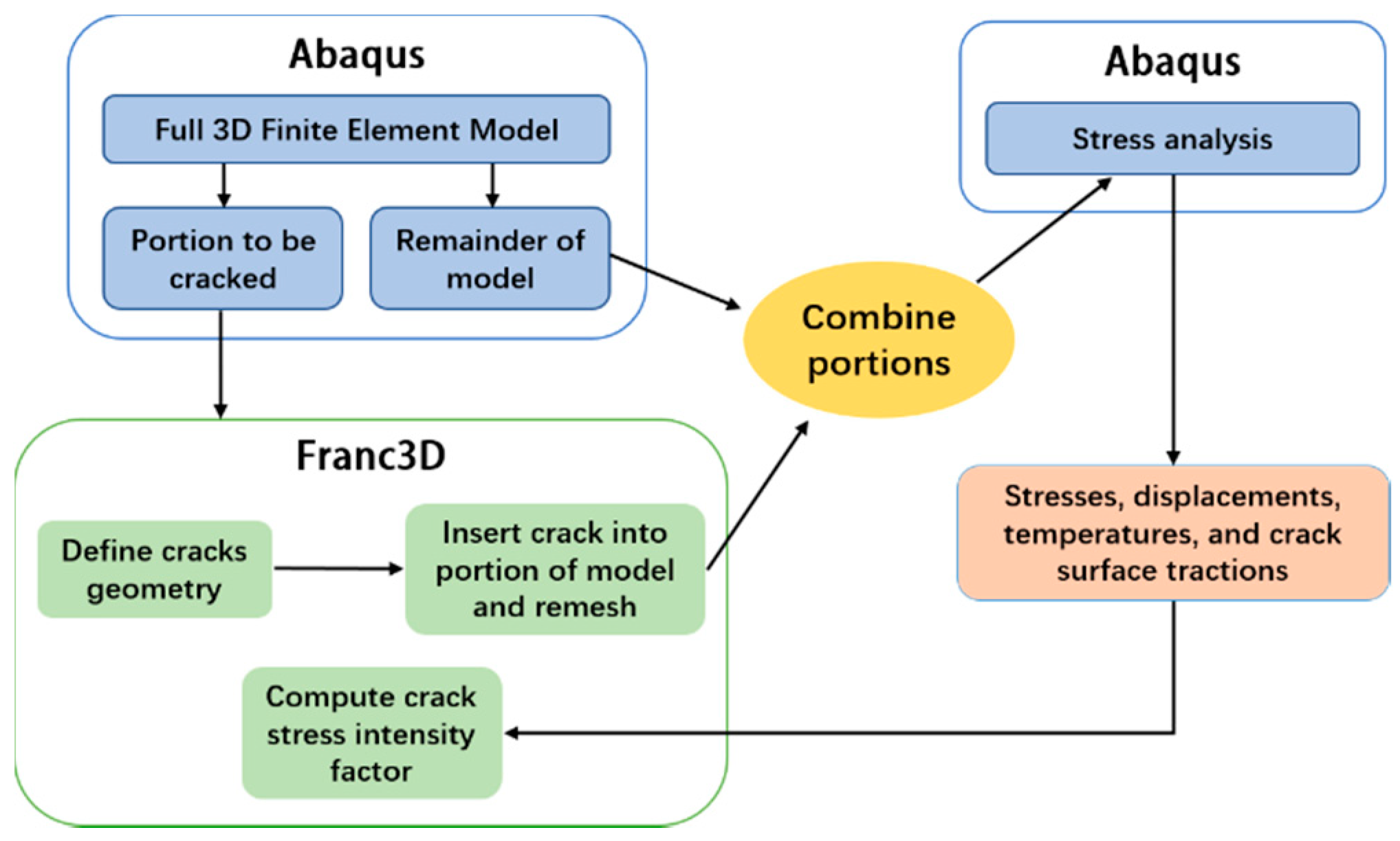
2.2. ABAQUS-FRANC3D Co-Modeling
- Build the finite element model in ABAQUS, and define the corresponding model size, material properties, assembly form and grid division;
- In ABAQUS, the model is divided into the regions to implant cracks and the complementary remaining regions;
- In FRANC3D, the area to implant the crack is imported, and the corresponding crack is implanted at the predetermined position. The appropriate mesh refinement parameters are selected.
- Import the splicing new model into ABAQUS, define contact properties, apply bending load and boundary conditions, create a calculation file, add necessary keywords and submit the calculation;
- The calculation results were extracted in ABAQUS to obtain the stress-strain field of the finite element model, and the fracture parameter report of the crack tip could be obtained in FRANC3D.
3. Results and Discussion
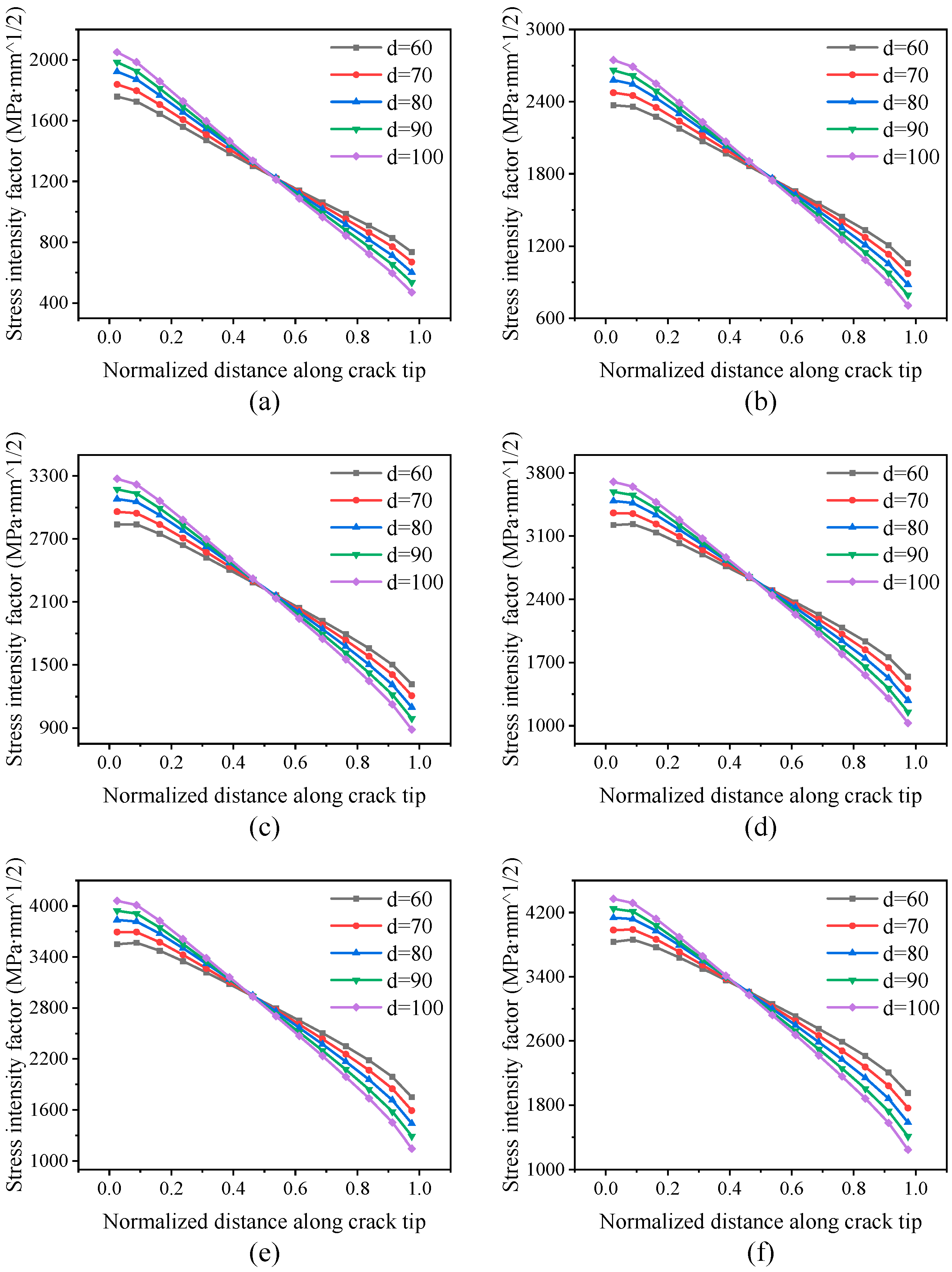
3.1. Influence of Rib Spacing on SIF of Crack Tip
3.2. Influence of Rib Height on SIF of Crack Tip
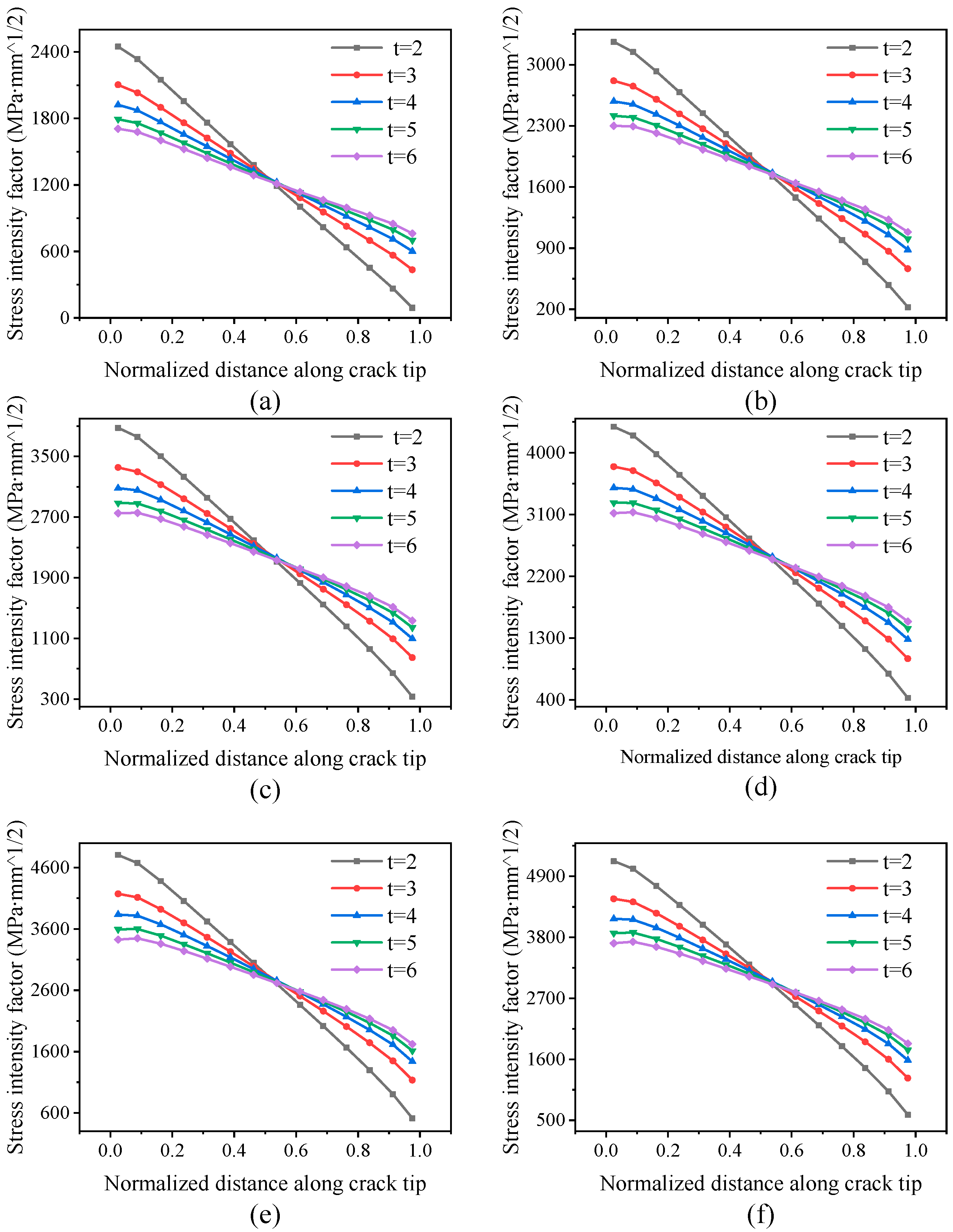
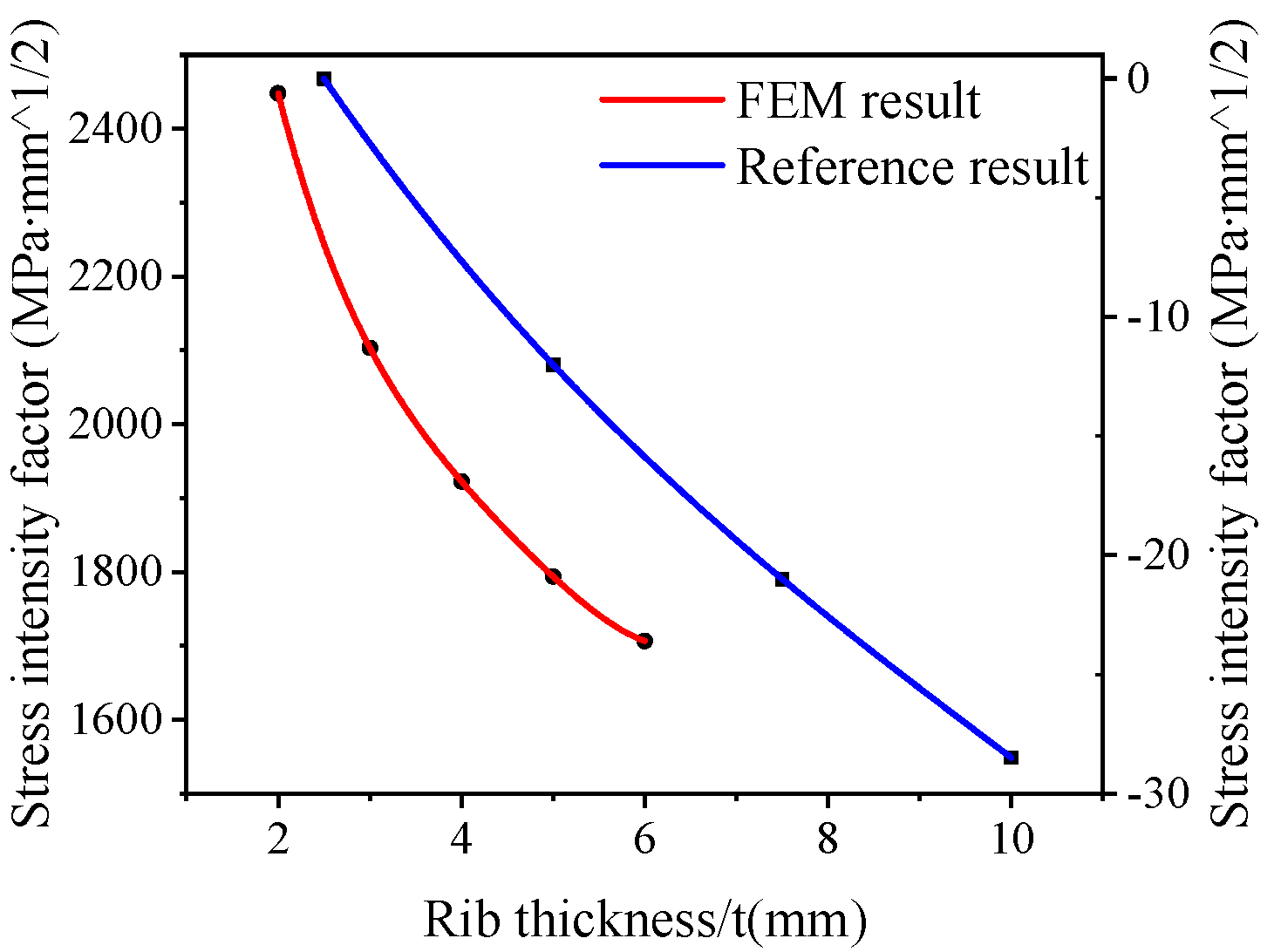
3.3. Influence of Rib Thickness on SIF of Crack Tip
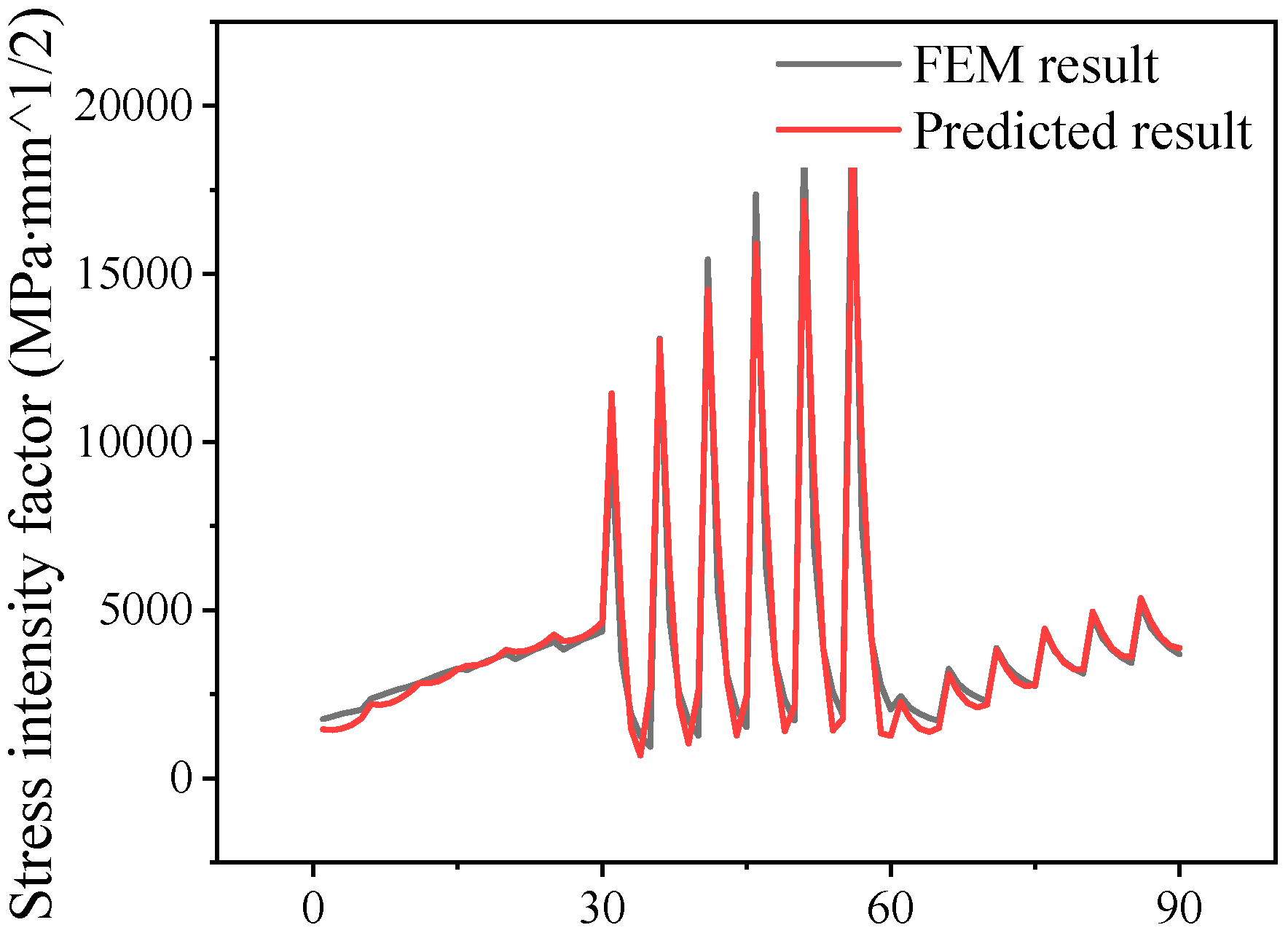
3.4. Prediction Model of SIF at Crack Tip of Integral Panel
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Munroe, J.; Wilkins, K.; Gruber, M.; Domack, M. Integral Airframe Structures (IAS): Validated Feasibility Study of Integrally Stiffened Metallic Fuselage Panels for Reducing Manufacturing Costs. Available online: https://dl.acm.org/doi/book/10.5555/888417 (accessed on 16 June 2020).
- Zhang, X.; Boscolo, M.; Figueroa-Gordon, D.; Allegri, G.; Irving, P.E. Fail-Safe Design of Integral Metallic Aircraft Structures Reinforced by Bonded Crack Retarders. Eng. Fract. Mech. 2009, 76, 114–133. [Google Scholar] [CrossRef] [Green Version]
- Grbović, A.; Sedmak, A.; Kastratović, G.; Petrašinović, D.; Vidanović, N.; Sghayer, A. Effect of laser beam welded reinforcement on integral skin panel fatigue life. Eng. Fail. Anal. 2019, 101, 383–393. [Google Scholar] [CrossRef]
- Moreira, P.; Castro, P. Fractographic analysis of fatigue crack growth in lightweight integral stiffened panels. Int. J. of Struct. Integr. 2010, 1, 233–258. [Google Scholar] [CrossRef]
- Arrieta, A.J.; Striz, A.G. Optimal design of aircraft structures with damage tolerance requirements. Struct. Multidiscip. Optim. 2005, 30, 155–163. [Google Scholar] [CrossRef]
- Qi-qing, H.; Liu, J.; Yin, Z. Fracture Characteristics Analysis Method and Study of Wing-Beam Integrated structure. Aeronaut. Comput. Tech. 2006, 36, 114–116. [Google Scholar]
- Yan, X.; Wang, S.; Yi, S. Research and Analysis on Methods of Three-dimensional Crack Stress Intensity Factor for Integral Panel. Adv. Aeronaut. Sci. Eng. 2011, 2, 205–209. [Google Scholar]
- Šedek, J.; Růžek, R.; Raška, J.; Běhal, J. Comparative Study of Prediction Methods for Fatigue Life Evaluation of an Integral Skin-Stringer Panel under Variable Amplitude Loading. Procedia Eng. 2015, 114, 124–131. [Google Scholar] [CrossRef] [Green Version]
- Fossati, M.; Colombo, D.; Manes, A.; Giglio, M. Numerical modelling of crack growth profiles in integral skin-stringer panels. Eng. Fract. Mech. 2011, 78, 1341–1352. [Google Scholar] [CrossRef]
- Boscolo, M.; Allegri, G.; Zhang, X. Design and Modelling of Selective Reinforcements for Integral Aircraft Structures. Aiaa J. 2008, 46, 2323–2331. [Google Scholar] [CrossRef] [Green Version]
- Hoang-Ngoc, C.-T.; Paroissien, E. Simulation of single-lap bonded and hybrid (bolted/bonded) joints with flexible adhesive. Int. J. Adhes. Adhes. 2010, 30, 117–129. [Google Scholar] [CrossRef] [Green Version]
- Liao, Y.; Li, Y.; Pan, Q.; Huang, M.; Zhou, C. Residual fatigue life analysis and comparison of an aluminum lithium alloy structural repair for aviation applications. Eng. Fract. Mech. 2018, 194, 262–280. [Google Scholar] [CrossRef]
- Liao, Y.; Li, Y.; Huang, M.; Wang, B.; Yang, Y.; Pei, S. Effect of hole relative size and position on crack deflection angle of repaired structure. Theor. Appl. Fract. Mech. 2019, 101, 92–102. [Google Scholar] [CrossRef]
- Sun, Z.; Huang, M. Fatigue crack propagation of new aluminum lithium alloy bonded with titanium alloy strap. Chin. J. Aeronaut. 2013, 26, 601–605. [Google Scholar] [CrossRef] [Green Version]
- Heidari Shabestari, S.S.; Kayran, A. Development of a regression model for the life assessment of open-hole specimens with double through cracks utilizing stress intensity factor calculations via XFEM. Procedia Struct. Integr. 2019, 21, 154–165. [Google Scholar] [CrossRef]
- Narasimhachary, S.B.; Bhachu, K.S.; Shinde, S.R.; Gravett, P.W.; Newman, J.C. A single edge notch specimen for fatigue, creep-fatigue and thermo-mechanical fatigue crack growth testing. Eng. Fract. Mech. 2018, 199, 760–772. [Google Scholar] [CrossRef]
- Siegl, J.; Nedbal, I.; Kunz, J. Fatigue crack growth history in damage tolerance design of aircraft structures. Int. J. Fatigue 2009, 31, 1062–1067. [Google Scholar] [CrossRef]
- Bang, D.J.; Ince, A.; Noban, M. Modeling approach for a unified crack growth model in short and long fatigue crack regimes. Int. J. Fatigue 2019, 128, 105182. [Google Scholar] [CrossRef]
- Atroshchenko, E.; Potapenko, S.; Glinka, G. Stress intensity factor for a semi-elliptical crack subjected to an arbitrary mode I loading. Math. Mech. Solids 2014, 3. [Google Scholar] [CrossRef]
- Warzynek, P.A.; Carter, B.J.; Banks-Sills, L. The M-Integral for Computing Stress Intensity Factors in Generally Anisotropic Materials; NASA Technical Report Server: Ithaca, NY, USA, 2005.
- Newman, J.C.; Raju, I.S. An empirical stress-intensity factor equation for the surface crack. Eng. Fract. Mech. 1981, 15, 185–192. [Google Scholar] [CrossRef]
- Lv, F.; Zhou, C.-Y.; Cheng, R.-J.; Miao, X.-T.; He, X.-H. A numerical analysis based on M-integral about the interaction of parallel surface cracks in an infinite plate. Theor. Appl. Fract. Mech. 2018, 96, 370–379. [Google Scholar] [CrossRef]
- Sukumar, N.; Moes, N.; Moran, B.; Belytschko, T. Extended Finite Element Method for three-dimensional crack modelling. Int. J. Numer. Methods Eng. 2000, 48, 1549–1570. [Google Scholar] [CrossRef]
- Dhia, H.B.; Jamond, O. On the use of XFEM within the Arlequin framework for the simulation of crack propagation. Comput. Methods Appl. Mech. Eng. 2010, 199, 1403–1414. [Google Scholar] [CrossRef] [Green Version]
- Patil, V.; Chouhan, V.; Pandya, Y. Geometrical complexity and crack trajectory based fatigue life prediction for a spur gear having tooth root crack. Eng. Fail. Anal. 2019, 105, 444–465. [Google Scholar] [CrossRef]
- Lin, G.; Lin, H.; Zhao, Y. Aluminium Alloy Application Manual; China Machine Press: Beijing, China, 2006. [Google Scholar]
- Niu, C.; Feng, Z.; Cheng, X.; Zhang, J. Structural Stress Analysis and Dimension Design of Practical Aircraft; Aviation industry press: Beijing, China, 2009. [Google Scholar]
- Lima, M.M.; Godoy, C.; Avelar-Batista, J.C.; Modenesi, P.J. Toughness evaluation of HVOF WC–Co coatings using non-linear regression analysis. Mater. Sci. Eng. A 2003, 357, 337–345. [Google Scholar] [CrossRef]
- Geng, J.; Xu, J.; Nie, W.; Peng, S.; Zhang, C.; Luo, X. Regression analysis of major parameters affecting the intensity of coal and gas outbursts in laboratory. Int. J. Min. Sci. Technol. 2017, 27, 327–332. [Google Scholar] [CrossRef]


| Material Type | Tensile Strength σb/MPa | Yield Strength σ0.2/MPa | Elongation % | Young’s Modulus E/GPa | Poisson’s Ratio ν | Fracture Toughness Kc/MPa·mm1/2 |
|---|---|---|---|---|---|---|
| 2024 | 470 | 325 | 20 | 72 | 0.33 | 4017 |
| Groups | Model Length L(mm) | Model Width W(mm) | Skin Thickness tm(mm) | Rib Spacing d(mm) | Rib Height h(mm) | Rib Thickness t(mm) |
|---|---|---|---|---|---|---|
| 1 | 120 | 100 | 5 | 60 | 30 | 4 |
| 2 | 140 | 100 | 5 | 70 | 30 | 4 |
| 3 | 160 | 100 | 5 | 80 | 30 | 4 |
| 4 | 180 | 100 | 5 | 90 | 30 | 4 |
| 5 | 200 | 100 | 5 | 100 | 30 | 4 |
| Model Length L (mm) | 120 | 140 | 160 | 180 | 200 |
| Bending load M (N·mm) | 5.86 × 106 | 6.83 × 106 | 7.81 × 106 | 8.78 × 106 | 9.76 × 106 |
| Groups | Model Length L(mm) | Model Width W(mm) | Skin Thickness tm(mm) | Rib Spacing d(mm) | Rib Height h(mm) | Rib Thickness t(mm) |
|---|---|---|---|---|---|---|
| 1 | 160 | 100 | 5 | 80 | 10 | 4 |
| 2 | 160 | 100 | 5 | 80 | 20 | 4 |
| 3 | 160 | 100 | 5 | 80 | 30 | 4 |
| 4 | 160 | 100 | 5 | 80 | 40 | 4 |
| 5 | 160 | 100 | 5 | 80 | 50 | 4 |
| Groups | Model Length L(mm) | Model Width W(mm) | Skin Thickness tm(mm) | Rib Spacing d(mm) | Rib Height h(mm) | Rib Thickness t(mm) |
|---|---|---|---|---|---|---|
| 1 | 160 | 100 | 5 | 80 | 30 | 2 |
| 2 | 160 | 100 | 5 | 80 | 30 | 3 |
| 3 | 160 | 100 | 5 | 80 | 30 | 4 |
| 4 | 160 | 100 | 5 | 80 | 30 | 5 |
| 5 | 160 | 100 | 5 | 80 | 30 | 6 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hai, G.; Bin, Y.; Yunxin, W.; Zhiqi, L.; Yaoqiong, L.; Fei, D. Integral Aircraft Wing Panels with Penetration Cracks: The Influence of Structural Parameters on the Stress Intensity Factor. Appl. Sci. 2020, 10, 4142. https://doi.org/10.3390/app10124142
Hai G, Bin Y, Yunxin W, Zhiqi L, Yaoqiong L, Fei D. Integral Aircraft Wing Panels with Penetration Cracks: The Influence of Structural Parameters on the Stress Intensity Factor. Applied Sciences. 2020; 10(12):4142. https://doi.org/10.3390/app10124142
Chicago/Turabian StyleHai, Gong, Yi Bin, Wu Yunxin, Liao Zhiqi, Liu Yaoqiong, and Du Fei. 2020. "Integral Aircraft Wing Panels with Penetration Cracks: The Influence of Structural Parameters on the Stress Intensity Factor" Applied Sciences 10, no. 12: 4142. https://doi.org/10.3390/app10124142
APA StyleHai, G., Bin, Y., Yunxin, W., Zhiqi, L., Yaoqiong, L., & Fei, D. (2020). Integral Aircraft Wing Panels with Penetration Cracks: The Influence of Structural Parameters on the Stress Intensity Factor. Applied Sciences, 10(12), 4142. https://doi.org/10.3390/app10124142






