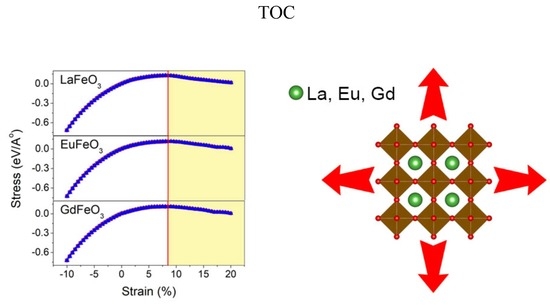
First-Principles Study of the Stabilization and Mechanical Properties of Rare-Earth Ferritic Perovskites (RFeO3, R = La, Eu, Gd)
Abstract
1. Introduction
2. Computational Methods
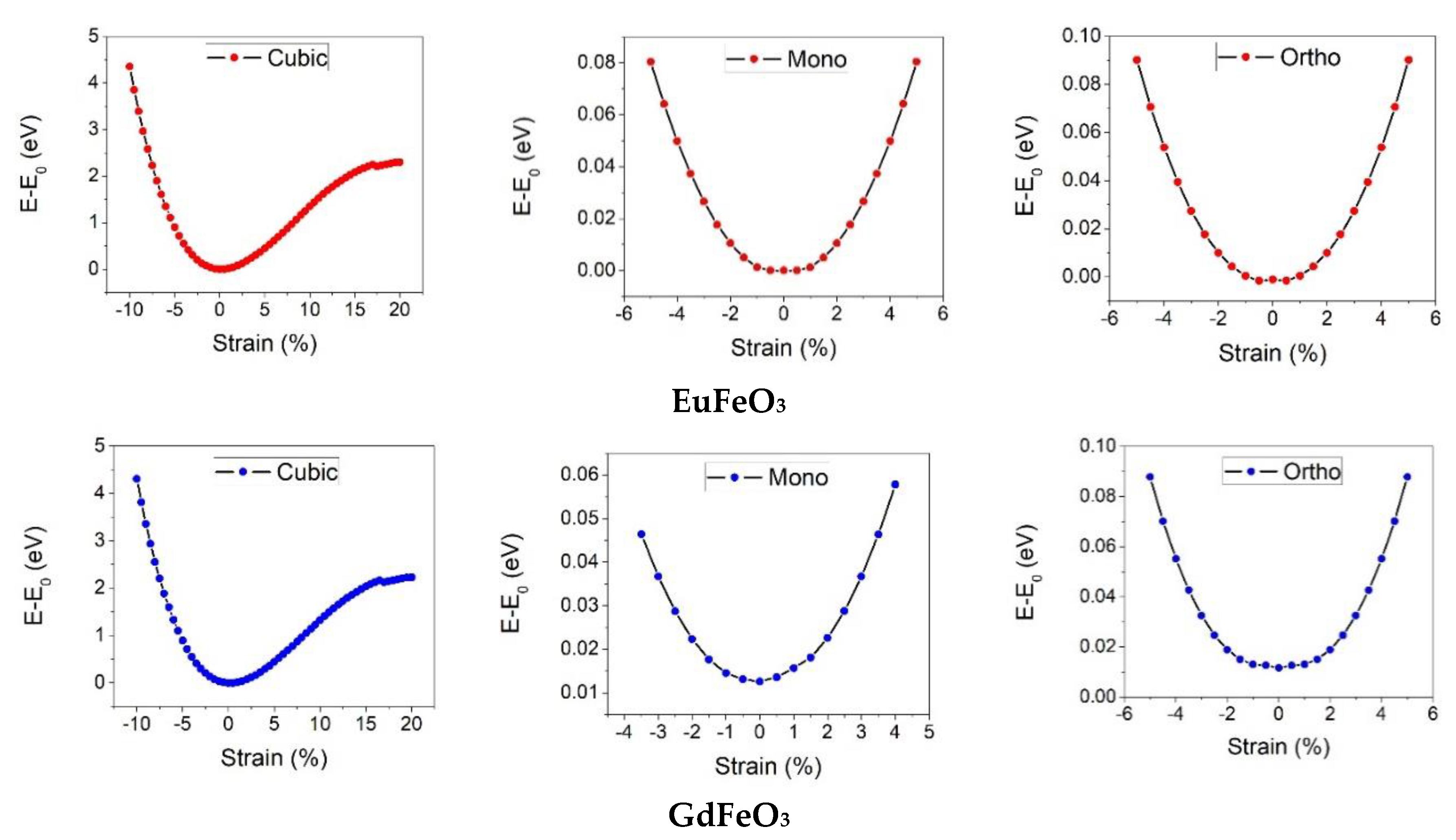
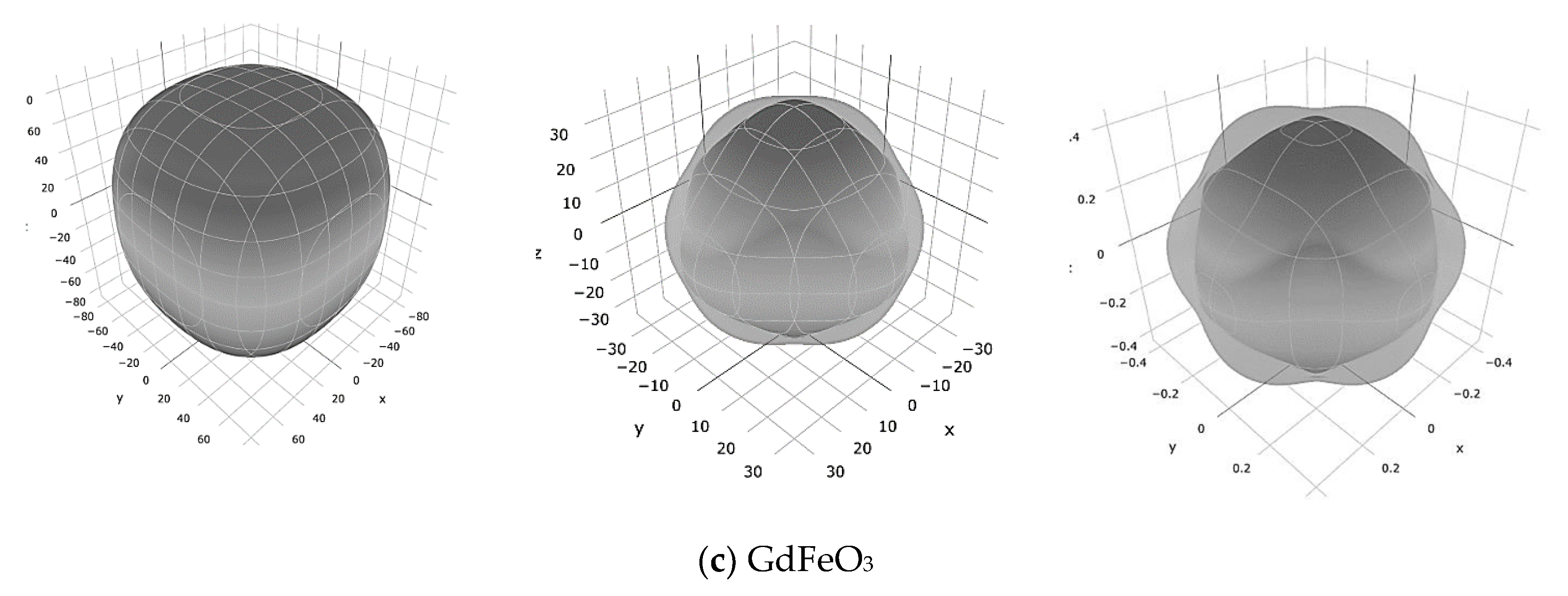
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shah, J.; Bhatt, P.; Dayas, K.D.D.; Kotnala, R.K.; Dayas, K.D.D. Significant role of antiferromagnetic GdFeO3 on multiferroism of bilayer thin films. Mater. Res. Express 2018, 5, 026416. [Google Scholar] [CrossRef]
- Tang, P.; Tong, Y.; Chen, H.; Cao, F.; Pan, G. Microwave-assisted synthesis of nanoparticulate perovskite LaFeO3 as a high active visible-light photocatalyst. Curr. Appl. Phys. 2013, 13, 340–343. [Google Scholar] [CrossRef]
- Zhao, J.Y.; Zhao, Z.Y.; Wu, J.C.; Xu, H.S.; Liu, X.G.; Zhao, X.; Sun, X.F. A comparative study of ultra-low-temperature thermal conductivity of multiferroic orthoferrites R FeO3 (R = Gd and Dy). AIP Adv. 2017, 7, 055806. [Google Scholar] [CrossRef]
- Sultan, K.; Ikram, M.; Asokan, K.; Asokan, K. Effect of Mn doping on structural, morphological and dielectric properties of EuFeO3 ceramics. RSC Adv. 2015, 5, 93867–93876. [Google Scholar] [CrossRef]
- Verma, A.S.; Kumar, A. Bulk modulus of cubic perovskites. J. Alloy. Compd. 2012, 541, 210–214. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Physics Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef] [PubMed]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Choquette, A.K.; Colby, R.; Moon, E.J.; Schlepütz, C.M.; Scafetta, M.D.; Keavney, D.J.; May, S.J. Synthesis, structure, and spectroscopy of epitaxial EuFeO3 thin films. Cryst. Growth Des. 2015, 15, 1105–1111. [Google Scholar] [CrossRef]
- Mihai, O.; Raaen, S.; Chen, D.; Holmen, A. Preparation of stable cubic LaFeO 3 nanoparticles using carbon nanotubes as templates. J. Mater. Chem. A 2013, 1, 7006–7011. [Google Scholar] [CrossRef]
- Gosavi, P.V.; Biniwale, R.B. Pure phase LaFeO3 perovskite with improved surface area synthesized using different routes and its characterization. Mater. Chem. Phys. 2010, 119, 324–329. [Google Scholar] [CrossRef]
- Persson, K. Materials Data on LaFeO3 (SG:221) by Materials Project; U.S. Department of Energy Office of Scientific and Technical Information: Oak Ridge, TN, USA, 2014.
- Ansari, R.; Malakpour, S. Structural and elastic properties characterization of Be and Mg doped boron nitride nanotubes using DFT calculations. Superlattices Microstruct. 2015, 82, 113–123. [Google Scholar] [CrossRef]
- Voigt, W. Lehrbuch der Kristallphysik (Mit Ausschluss der Kristalloptik); Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Prager, W.; Hodge, P.G. Theory of Perfectly Plastic Solids; J. Wiley & Sons, Inc.: New York, NY, USA, 1951. [Google Scholar]
- Hill, R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. Sect. A 1952, 65, 349. [Google Scholar] [CrossRef]
- Bannikov, V. Elastic, electronic and magnetic properties of new oxide perovskite BaVO3: A first-principles study. Mater. Chem. Phys. 2016, 171, 119–125. [Google Scholar] [CrossRef]
- Shein, I.; Kozhevnikov, V.L.; Ivanovskii, A.L. First-principles calculations of the elastic and electronic properties of the cubic perovskites SrMO3 (M = Ti, V, Zr and Nb) in comparison with SrSnO3. Solid State Sci. 2008, 10, 217–225. [Google Scholar] [CrossRef]
- Born, M.; Huang, K. Dynamical Theory of Crystal Lattices; Clarendon Press: Oxford, UK, 1954. [Google Scholar]
- Gaillac, R.; Pullumbi, P.; Coudert, F.-X. ELATE: An open-source online application for analysis and visualization of elastic tensors. J. Phys. Condens. Matter 2016, 28, 275201. [Google Scholar] [CrossRef] [PubMed]
- Bader, R.F.W. A quantum theory of molecular structure and its applications. Chem. Rev. 1991, 91, 893–928. [Google Scholar] [CrossRef]
- Bader, R.F.W. Atoms in molecules. Acc. Chem. Res. 1985, 18, 9–15. [Google Scholar] [CrossRef]
- Koritsanszky, T.S.; Coppens, P. Chemical applications of X-ray charge-density analysis. Chem. Rev. 2001, 101, 1583–1628. [Google Scholar] [CrossRef] [PubMed]
- Otero-de-la-Roza, A.; Blanco, M.A.; Pendás, A.M.; Luaña, V. Critic: A new program for the topological analysis of solid-state electron densities. Comput. Phys. Commun. 2009, 180, 157–166. [Google Scholar] [CrossRef]
- Otero-de-la-Roza, E.; Johnson, E.R.; Luaña, V. Critic2: A program for real-space analysis of quantum chemical interactions in solids. Comput. Phys. Commun. 2014, 185, 1007–1018. [Google Scholar] [CrossRef]
- Morales-García, A.; Soares, A.L., Jr.; Dos Santos, E.C.; de Abreu, H.A.; Duarte, H.L.A. First-principles calculations and electron density topological analysis of covellite (CuS). J. Phys. Chem. A 2014, 118, 5823–5831. [Google Scholar] [CrossRef] [PubMed]
- Zhurova, E.A.; Tsirelson, V.G. Electron density and energy density view on the atomic interactions in SrTiO3. Acta Crystallogr. Sect. B Struct. Sci. 2002, 58, 567–575. [Google Scholar] [CrossRef] [PubMed]
- Conroy, M.W.; Oleynik, I.I.; Zybin, S.V.; White, C.T. First-principles anisotropic constitutive relationships in ββ-cyclotetramethylene tetranitramine (β-HMX). J. Appl. Phys. 2008, 104, 053506. [Google Scholar] [CrossRef]
- Birch, F. Finite Elastic Strain of Cubic Crystals. Phys. Rev. 1947, 71, 809–824. [Google Scholar] [CrossRef]
- Peng, Q.; Ji, W.; De, S. Mechanical properties of the hexagonal boron nitride monolayer: Ab initio study. Comput. Mater. Sci. 2012, 56, 11–17. [Google Scholar] [CrossRef]
- Yu, M.; Trinkle, D.R. Accurate and Efficient Algorithm for Bader Charge Integration. J. Chem. Phys. 2011, 134, 064111. [Google Scholar] [CrossRef] [PubMed]
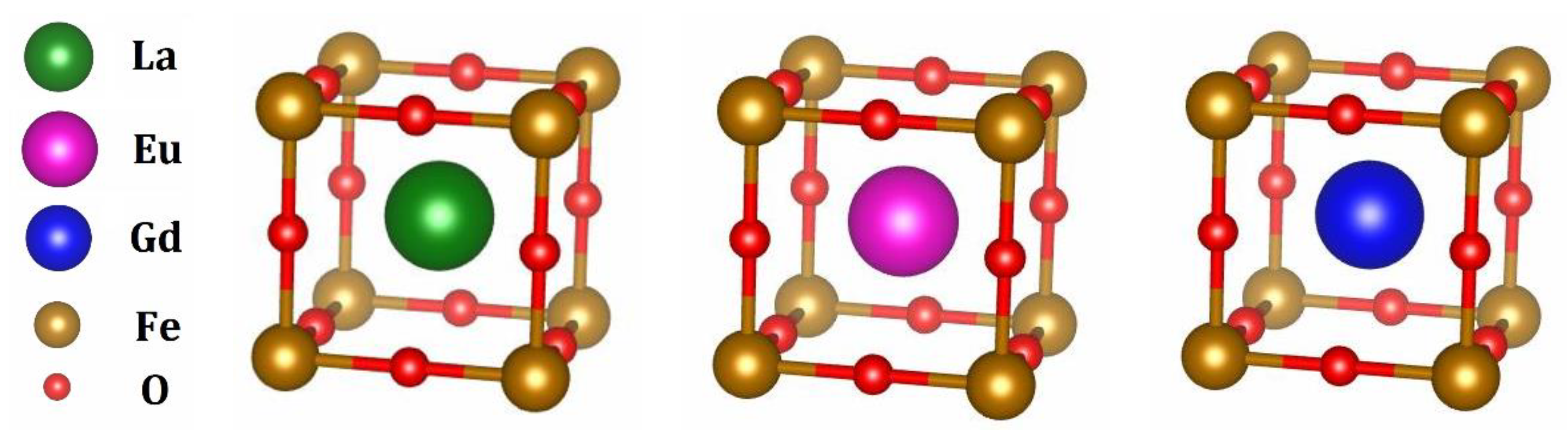


| Experiment Data | Theoretical Data | |
|---|---|---|
| LaFeO3 | 3.89 [10] | 3.82 |
| 3.92 [11] | 3.92 [5] | |
| 3.93 * [9] | 3.95 [12] | |
| EuFeO3 | 3.75 | |
| 3.68 * [9] | 3.83 [5] | |
| GdFeO3 | 3.74 | |
| - | 3.82 [5] |
| C11 (GP) | C12 (GP) | C44(GP) | |
|---|---|---|---|
| LaFeO3 | 278.06 | 154.63 | 92.92 |
| EuFeO3 | 242.64 | 148.81 | 45.34 |
| GdFeO3 | 215.56 | 156.80 | 34.77 |
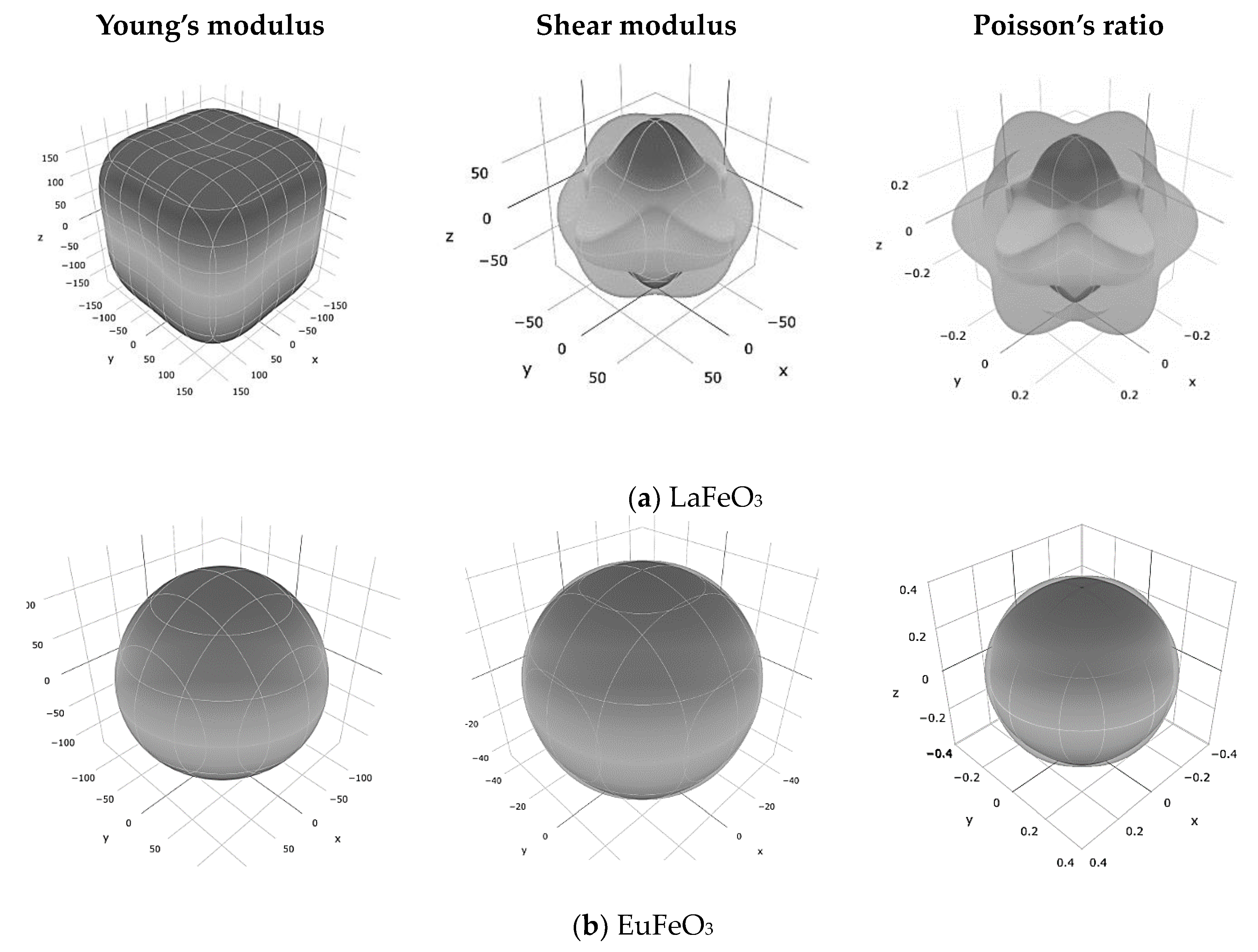
| Averaging Scheme | Bulk Modulus (B) (GPa) | Young’s (E) Modulus (GPa) | Shear Modulus (G) (GPa) | Poisson’s Ratio | |
|---|---|---|---|---|---|
| LaFeO3 | Voigt (V) | 195.77 | 212.24 | 80.44 | 0.32 |
| Reuss (R) | 195.77 | 204.9 | 77.29 | 0.32 | |
| Hill (H) | 195.77 | 208.58 | 78.86 | 0.32 | |
| Other Work | 186.5 [5] | ||||
| EuFeO3 | Voigt (V) | 180.09 | 127.1 | 45.97 | 0.38 |
| Reuss (R) | 180.09 | 127.06 | 45.957 | 0.38 | |
| Hill (H) | 180.09 | 127.08 | 45.963 | 0.38 | |
| Other Work | 201.2 [5] | ||||
| GdFeO3 | Voigt (V) | 176.39 | 92.17 | 32.62 | 0.41 |
| Reuss (R) | 176.39 | 91.58 | 32.40 | 0.41 | |
| Hill (H) | 176.39 | 91.88 | 32.51 | 0.41 | |
| Other Work | 204.2 [5] |
| Sample | Vt | Vl | Vm | θD |
|---|---|---|---|---|
| LaFeO3 | 3333.8 | 6470.7 | 4435.9 | 792.0 |
| EuFeO3 | 2384.1 | 5463.2 | 3266.7 | 594.8 |
| GdFeO3 | 1983.0 | 5148.7 | 2758.7 | 503.1 |
| Number and Type of Cps | ρ(rc) | ∇2ρ(rc) | λ1 | λ2 | λ3 | ||
|---|---|---|---|---|---|---|---|
| (e.A−3) | (e.A−5) | (e.A−5) | (e.A−5) | (e.A−5) | |||
| LaFeO3 | Bond | 6 | 0.66 | 13.33 | −2.19 | −2.19 | 17.73 |
| Bond | 12 | 0.22 | 2.59 | −0.73 | −0.68 | 4.01 | |
| Ring | 24 | 0.12 | 1.71 | −0.20 | 0.93 | 0.98 | |
| Cage | 8 | 0.11 | 1.72 | 0.29 | 0.29 | 1.34 | |
| Cage | 3 | 0.06 | 0.85 | 0.24 | 0.24 | 0.37 | |
| EuFeO3 | Bond | 6 | 0.73 | 13.34 | −3.07 | −3.07 | 19.49 |
| Bond | 12 | 0.21 | 2.75 | −0.65 | −0.61 | 4.02 | |
| Ring | 24 | 0.12 | 1.77 | −0.16 | 0.86 | 1.08 | |
| Cage | 8 | 0.12 | 1.82 | 0.30 | 0.30 | 1.22 | |
| Cage | 3 | 0.06 | 0.80 | 0.26 | 0.26 | 0.26 | |
| GdFeO3 | Bond | 6 | 0.74 | 13.57 | −2.88 | −2.88 | 18.46 |
| Bond | 12 | 0.2 | 2.56 | −0.69 | −0.63 | 4.02 | |
| Ring | 24 | 0.12 | 1.75 | −0.17 | 0.85 | 1.03 | |
| Cage | 8 | 0.12 | 1.83 | 0.31 | 0.31 | 1.32 | |
| Cage | 3 | 0.06 | 0.83 | 0.25 | 0.25 | 0.27 | |
| V | f (Ω) | B(Ω) | Q(Ω) | OS(Ω) | ||
|---|---|---|---|---|---|---|
| LaFeO3 | La | 17.18 | 0.308 | 268.83 | 2.071 | +3 |
| Fe | 7.16 | 0.128 | 221.59 | +1.475 | +3 | |
| O | 10.45 × 3 | 0.188 × 3 | 176.37 | −1.182 × 3 | −2 × 3 | |
| Total | 55.70 | 1.00 | 210.66 | 0 | 0 | |
| EuFeO3 | Eu | 15.08 | 0.287 | 256.59 | +1.896 | +3 |
| Fe | 6.83 | 0.130 | 191.23 | +1.527 | +3 | |
| O | 10.19 × 3 | 0.194 × 3 | 169.23 | −1.141 × 3 | −2 × 3 | |
| Total | 52.54 | 1.00 | 196.99 | 0 | 0 | |
| GdFeO3 | Gd | 14.80 | 0.283 | 249.64 | +1.882 | +3 |
| Fe | 6.78 | 0.130 | 185.91 | +1.537 | +3 | |
| O | 10.23 × 3 | 0.196 × 3 | 167.25 | −1.139 × 3 | −2 × 3 | |
| Total | 52.29 | 1.00 | 193.04 | 0 | 0 | |
| LaFeO3 | EuFeO3 | GdFeO3 | |
|---|---|---|---|
| 0.126 | 0.115 | 0.111 | |
| 8.5% | 8.5% | 8.5% | |
| 0.126 | 0.115 | 0.111 | |
| 8.5% | 8.5% | 8.5% | |
| 0.126 | 0.115 | 0.111 | |
| 8.5% | 8.5% | 8.5% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Faghihnasiri, M.; Najafi, V.; Shayeganfar, F.; Ramazani, A. First-Principles Study of the Stabilization and Mechanical Properties of Rare-Earth Ferritic Perovskites (RFeO3, R = La, Eu, Gd). Appl. Sci. 2020, 10, 4008. https://doi.org/10.3390/app10114008
Faghihnasiri M, Najafi V, Shayeganfar F, Ramazani A. First-Principles Study of the Stabilization and Mechanical Properties of Rare-Earth Ferritic Perovskites (RFeO3, R = La, Eu, Gd). Applied Sciences. 2020; 10(11):4008. https://doi.org/10.3390/app10114008
Chicago/Turabian StyleFaghihnasiri, Mahdi, Vahid Najafi, Farzaneh Shayeganfar, and Ali Ramazani. 2020. "First-Principles Study of the Stabilization and Mechanical Properties of Rare-Earth Ferritic Perovskites (RFeO3, R = La, Eu, Gd)" Applied Sciences 10, no. 11: 4008. https://doi.org/10.3390/app10114008
APA StyleFaghihnasiri, M., Najafi, V., Shayeganfar, F., & Ramazani, A. (2020). First-Principles Study of the Stabilization and Mechanical Properties of Rare-Earth Ferritic Perovskites (RFeO3, R = La, Eu, Gd). Applied Sciences, 10(11), 4008. https://doi.org/10.3390/app10114008