Abstract
Fiber-reinforced polymers (FRP) are commonly used as internal reinforcement in RC structures in aggressive environments. The design of concrete elements reinforced with FRP bars is usually ruled by serviceability criteria rather than the ultimate limit state. Six continuous concrete beams over two spans with longitudinal and transverse glass FRP (GFRP) reinforcement were investigated until failure to estimate the effects of different reinforcement arrangements on the limit states of continuous beams. The ratio of longitudinal reinforcement between the midspan and middle support sections (i.e., the design moment redistribution) and the type of GFRP reinforcement were the main parameters. The experimental results were compared to prediction models and other code formulations under serviceability and ultimate limit states. The bond-dependent coefficient kb was investigated to assess adhesion conditions for GFRP reinforcement and concrete. The results showed that moment redistribution in continuous beams with GFRP reinforcement happens with slippage between the reinforcement and concrete in the middle support without the load capacity being reduced. A modified model was suggested for better deflection prediction of continuous beams reinforced with GFRP bars. Based on deformability factors, the tested continuous beams, although containing GFRP reinforcement that has brittle behavior, showed a certain kind of ductile behavior.
1. Introduction
Continuous concrete beams are often used within RC structures that are exposed to aggressive environmental conditions, such as garages, bridges, overpasses, reservoirs, marine structures, and retaining walls. In these environments, a reduction of concrete alkalinity occurs, which often results in steel reinforcement corrosion, endangering the serviceability and functionality of the RC structures. In order to overcome this problem, fiber-reinforced polymer (FRP) bars and stirrups have lately been used as alternative solutions in RC structures, especially in aggressive conditions. The use of FRP reinforcement can provide significant savings related to the maintenance, strengthening and recovery of structures, in particular when they are exposed to various destructive influences during their service life, certainly leading to economic benefits. Additionally, FRP bars are successfully used to improve the mechanical performance of others structural elements, for example laminated glass beams [1] or structural timber elements [2].
Numerous studies have been conducted on simple beams reinforced with FRP bars to estimate the flexural behavior regarding deflection and cracks [3,4,5,6,7,8,9,10,11,12,13,14,15,16]. Several authors have proposed modification of Branson’s equation for calculation of the effective moment of inertia (Toutanji and Saafi [4], Yost et al. [5], Rafi and Nadjai [6], Mousavi and Esfahani [7], Adam et al. [8], Ju et al. [9]), while Bischoff [10,11] calculated the effective moment of inertia derived from curvatures in order to predict the load–deflection response. For cracking behavior, prediction models are generally based on design equations for members with steel reinforcement. Extensive analysis was conducted to determine values of the bond coefficient kb, which depends on the characteristics of the FRP bars and the surrounding concrete [12,13,14,15,16], of which the crack width in the member is significantly dependent.
A modest number of research works on the FRP-reinforced continuously supported beams [17,18,19,20,21,22,23,24,25,26] show that moment redistribution between the cross-sections in the critical sections is possible. The possibility of this phenomenon occurring depends most on the arrangement of the reinforcement along a beam [17,18,19,20,21,26]. Increasing the bottom FRP reinforcement at the midspan of a continuous beam with reduction of the top FRP reinforcement in the middle support leads to increase in the load capacity of the beam, reducing deformation and postponing crack propagation in the beam midspan [18,20,21,23,24]. On the other hand, the increase of the top reinforcement over the middle support with identical reinforcement in the midspan does not contribute to increasing the load capacity or to reduction of deformation [23]. There is an indication that continuous beams with FRP bars show some warnings before failure regarding large deformations and wide cracks [18,19,21,26]. Additionally, due to the low modulus of elasticity of the FRP reinforcement, moment redistribution from the middle support, compared to the elastic analysis, starts at low load levels [18,19]. All of the above stated points represent a good basis to introduce internal force redistribution to improve the behavior of continuous beams with FRP reinforcement, in turn improving the serviceability and ultimate limit state. Due to the low modulus of elasticity, FRP elements exhibit significant deformations and wide cracks, meaning their design is often governed by the serviceability limit state, especially when GFRP bars are used.
This study is part of the conducted research on continuous beams with GFRP reinforcement, with aim of investigating a number of parameters to assess flexural behavior [27]. Some preliminary results from this experimental program have been published in a previous study [26], which are repeated in this paper because they are the basis for the analysis in this work. This paper is an extension of the study of six continuous previously reported beams reinforced with ribbed and wrapped GFRP bars [26]. The experimental results are compared to code predictions regarding the serviceability and ultimate limit states. The load-carrying capacity obtained in the experiments is evaluated for the ultimate limit state and compared with code-predicted equations. Additionally, the adequacy of the prediction models for estimating cracking and deflection is investigated, as well as the service load at which serviceability criteria are fulfilled in terms of the limitation of maximal crack widths, deflections, and stresses in the FRP reinforcement. The values of bond coefficient kb are determined for different critical sections of the beam. The ductility behavior of the beams with GFRP bars is presented and discussed.
2. Experimental Program
Six GFRP-reinforced concrete beams continuously supported over two spans were tested up to failure. The beams had two spans measuring 1850 mm in length each, with a 150 × 250 mm rectangular cross-sections. All beams were loaded with point midspan forces in both spans, reinforced with GFRP bars in the longitudinal and transverse direction. For all tested beams, longitudinal GFRP reinforcement was continuously placed along the beam. The geometry is given in Figure 1, along with reinforcement details for tested beams and load disposition.
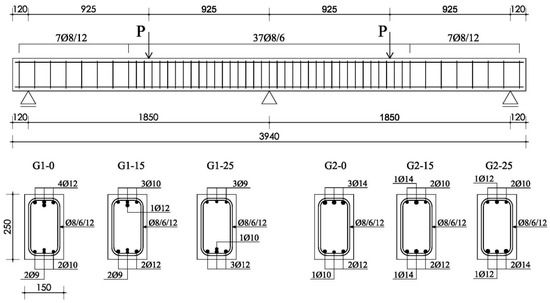
Figure 1.
Geometry and section details for continuous tested beams (all dimensions in mm).
The beams were divided into two series (series 1—mark G1, and series 2—mark G2) with different longitudinal GFRP reinforcement. In the beam G1-0, longitudinal reinforcement was adopted based on elastic bending moment analysis. Beams G1-15 and G1-25 were dimensioned with assumed moment redistribution of 15% and 25% from the middle support to the midspan, respectively. In this way, all beams within the same series were designed to have an identical failure load. After the moment redistribution was implemented, all beams experienced concrete compression failure, as recommended by the actual codes for FRP-reinforced beams. Beams series 2 were modeled similarly as beams series 1. GFRP-wrapped stirrups with a diameter of 8 mm at a distance of 60 mm for interior shear span and at a distance of 120 mm for exterior shear span were adopted for all beams to ensure flexural mode of failure. Characteristics of the experimental beams are given in Table 1.

Table 1.
Reinforcement details and concrete compressive strength for tested beams.
2.1. Materials
For the longitudinal reinforcement, ribbed GFRP bars were used for the beams series 1(mark G1) with an epoxy matrix and wrapped GFRP bars were used for the beams series 2(mark G2) with a polyester matrix (Figure 2). The real material properties of GFRP bars were examined by tensioning five samples for each bar diameter until failure, according to ACI 440.3R-12 [28]. The test results are given in Table 2. The experimental beams were cast using two concrete batches for each series of beams. Concrete compressive strength 28 days after casting was obtained by analyzing 8 cubes with 150 mm edges, 8 cubes with 200 mm edges, and 17 cylinders with dimensions of 150/300 mm. Test results for concrete cylinders measuring 150/300 mm are shown in Table 1.

Figure 2.
GFRP longitudinal and transverse bars (dimensions in mm).

Table 2.
Mechanical and deformation properties of GFRP bars.
2.2. Experimental Setup and Instrumentation
The tested continuously supported beams comprised two equal spans with two horizontally moveable end supports and one hinged support at the middle of the beam. Two hydraulic presses with a capacity of 200 kN were used to load the beams. Strain gauges were used to measure actual strains in the critical sections of the beams. Electrical strain gauges were attached to areas of tension and compression longitudinal reinforcement in both bottom and upper zones of the beams (Figure 3). Six strain gauges were attached on the concrete compression zone of the continuous beams in critical sections. Three linear variable differential transducers (LVDT) were placed on each span to measure deflections at three different locations of each beam span. Crack widths were measured in critical sections by a Zeiss microscopic magnifier. Two load cells with a capacity of 100 kN were used to measure the end support reactions. The experimental beams were loaded monotonically in appropriate increments to the failure, with a speed for each increment of approximately 5 kN/min. All data were electronically recorded in the computer using a data logger. The equipped continuous beam before testing is shown in Figure 3.
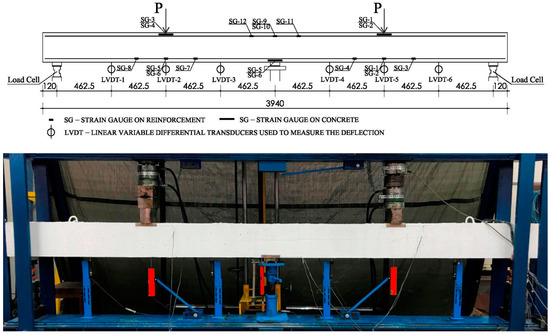
Figure 3.
Equipped continuous beam before testing (dimensions in mm).
3. Results and Discussion
3.1. Crack Propagation and Modes of Failure
During loading of the beams, the first vertical cracks in the critical sections occur at similar loads. Generally, new cracks in the midspan can occur until failure, while new cracks in the middle support area stop appearing at a load corresponding to 50% of the failure load. The crack formation for the two series of beams with different longitudinal GFRP reinforcement differed significantly. The small number of wide cracks in beams series 2 in both the midspan and the middle support areas indicates poor adhesion conditions between the GFRP reinforcement and concrete. The main reason for this occurrence is probably the different surface treatments used on the ribbed GFRP bars in the beams series 1 and on the wrapped GFRP bars for beams series 2. Regarding beams series 1, the highest number of cracks in the middle support area appeared in beam G1-0, while the highest number of cracks in the midspan appeared in beam G1-25. A number of short, slightly sloping, and horizontal cracks were particularly pronounced in the beam midspan, indicating large deformations of beam G1-25. Characteristically for beam G1-25, just before failure, cracks appeared in the immediate vicinity of the end supports, resulting from the adopted reinforcement, which was significantly larger in the midspan compared to the support, as a consequence of designed redistribution of internal forces. Because of this, the beam G1-25 provided the highest load-carrying capacity out of the beams series 1. Shear cracks occurred at a load level above 60% of the failure load, at the hogging moment region in the beam G1-0, due to high reinforcement axial stiffness. The crack patterns at failure for all beams are shown in the Figure 4.
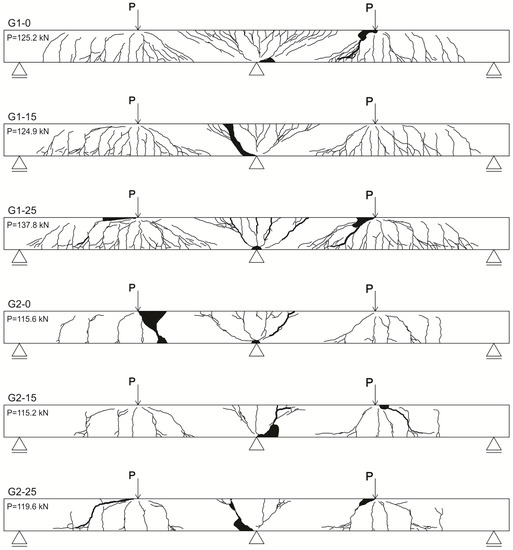
Figure 4.
Crack patterns of experimental beams at failure (P—load at failure).
The mode of failure for all beams was concrete crushing in compression in combination with the shear. In beams G1-0, G1-25, and G2-0, failure took place in the midspan, in beams G1-15 and G2-15 in the middle support, while in the beams G2-25 failure appeared simultaneously in the midspan and at the middle support. It was characteristic that failure in beams G1-15 and G2-0 was destructive, followed by rupture of compressed and tensioned bars by the dowel effect. The modes of failure of all tested beams are shown in the Figure 5. A detailed description of modes of failure and crack propagation of the beams was given in previous work [26].


Figure 5.
Modes of failure of experimental beams.
3.2. Load Capacity and Moment Redistribution
Measured applied loads in the middle of both spans and end reactions were used to determine internal forces along the length of the beam and to calculate the moment redistribution (Figure 6).
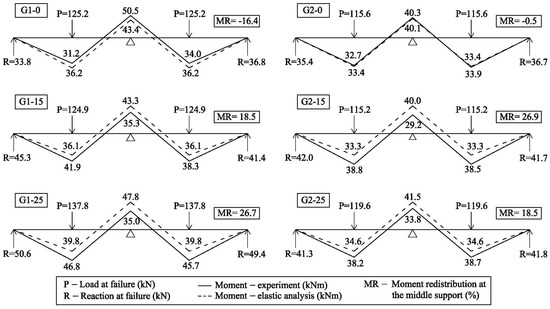
Figure 6.
Experimental versus elastic bending moments at failure.
Figure 7 shows the relationship between the percentage of moment redistribution in the middle support and the applied load. Beams G1-0 and G2-0 achieved negative moment redistribution at failure of 16.4% and 0.5%, respectively. However, the beams had completely different behavior. At first, beam G1-0 had a positive moment redistribution and beam G2-0 had a negative moment redistribution. With the further development of cracks, the trend of the moment redistribution changed in both beams. For beam G1-0, the negative moment redistribution appeared and increased with further loading, while for beam G2-0 the negative moment redistribution decreased. Beams G1-15, G1-25, G2-15, and G2-25 reached high percentages of moment redistribution at failure of 18.5%, 26.7%, 26.9%, and 18.5%, respectively. Positive moment redistribution started soon after cracking and stabilized as the propagation of cracks stabilized. This was a consequence of the “setup” of the tested beams due to the ratios of axial stiffness of reinforcement between the midspan and middle support sections. At failure, an increase of moment redistribution was observed as a result of the slippage between GFRP bars and surrounding concrete, especially for beams series 1. It can be concluded that moment redistribution in continuous beams with GFRP reinforcement occurs with a great influence from the ratio of reinforcement axial stiffness between critical sections. Further details of the results for moment redistribution can be found in previously published work [26].
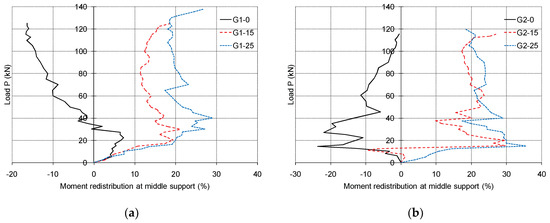
Figure 7.
Load–moment redistribution relationship in the middle support section for experimental beams: (a) series 1; (b) series 2.
All tested continuous beams were designed according to ACI-15 [29], while CSA-12 [30] and EC2-13 [31] were used as controls. As the moment redistribution is not allowed by actual codes for FRP-reinforced beams, for adopted reinforcement, failure loads are calculated by use of elastic analysis, i.e., based on bending moments, which are obtained as 0.156 Pl for the moment at the midspan and 0.188 Pl for the moment in the middle support section for continuous beams. The failure load was calculated as a lower load at which one of the critical sections (in the midspan or the middle support) reached flexural strength, using actual material properties. It should be noted that the bending behavior of the tested beams can be successfully described with simple equivalent-section-based analytical approaches, which can be used for different structural elements and materials with FRP bars [32]. In Figure 8, calculated failure loads according to ACI-15 [29], CSA-12 [30], and EC2-13 [31] are given in comparison to experimental failure loads. The ultimate bending moment Mn is calculated by the following equations when the reinforcement ratio ρf is greater than the balanced reinforcement ratio ρfb:
where ff is the stress in the tension FRP reinforcement; Ef is the modulus of elasticity of the FRP reinforcement; εcu is the ultimate strain of concrete; fc is concrete compressive strength; b and d are the width and effective depth of the beam, respectively; α1 and β1 are the strength reduction factors for concrete:
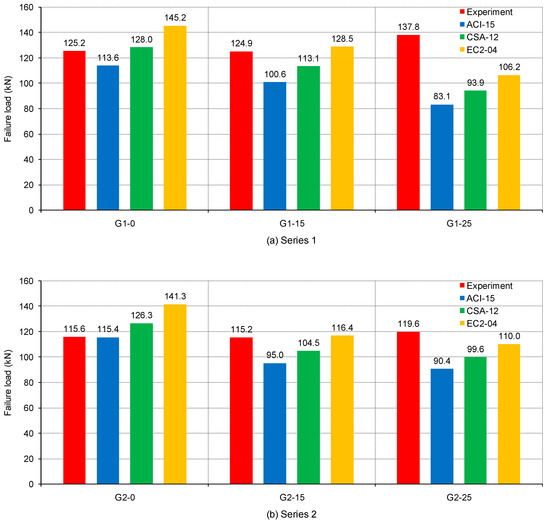
Figure 8.
Experimental and calculated failure loads for tested beams: (a) series 1; (b) series 2.
In Figure 8 it can be seen that load capacities in accordance with code predictions are the smallest for the beams that are designed to achieve the highest moment redistribution (G1-25 and G2-25), and the largest for the beams for which moment redistribution is not designed (G1-0 and G2-0). This is because the moment redistribution assumes a decrease of reinforcement at the support, which leads to capacity being reached for the section in the middle support area before the section in the beam midspan, as measured by assessing internal forces along beams obtained by elastic analysis. Consequently, for the moment redistribution, lower failure load values are obtained. This certainly does not coincide with the obtained experimental results, since the internal force redistribution in continuous beams occurs in relation to elastic analysis, as can be seen in Figure 8. It can be concluded that internal forces along the continuous beam depend on the arrangement of the reinforcement along the beam, which is a consequence of the elastic redistribution present in the continuous beams with GFRP reinforcement.
3.3. Load–Crack Width Relationship
In this section, the obtained experimental maximal crack widths are compared to the provisions for calculation of crack widths with the chosen codes. EC2-13 [31] calculates the crack width wk as the product of the maximal spacing of the cracks sr,max and the average strain, which represents the difference in the average strain in the reinforcement, including the tension stiffening of the concrete εfm and the average strain in the concrete between the cracks εcm:
where c is concrete cover; k1 is a coefficient taking into account the bond properties (0.8 for high bond bars and 1.6 for smooth bars); k2 is a coefficient taking into account the distribution of the strain (0.5 for bending and 1 for pure tension); Ø is the bar diameter, σf is the stress in the tension reinforcement; Ef is the modulus of elasticity of the FRP reinforcement; αe is the modular ratio Ef/Ec; kt is a coefficient taking into account the load duration (0.6 for short term loads and 0.4 for long term loads); ρp,eff is the effective reinforcement ratio; Af is the area of reinforcement; b, h, and d are the width, height, and effective depth of the beam, respectively; and x is the neutral axis depth.
The Italian guideline CNR-DT-203/06 [33] for elements with FRP reinforcement calculates the crack width wk as the product of the average distance between cracks srm and the average strain accounting for tension stiffening εfm:
where k1 is a coefficient taking into account the bond properties (1.6 for the FRP bars), σf is the stress in the tension reinforcement of the cracked cross-section, σfr is the stress in the tension reinforcement of the cracked cross-section when the first crack is observed, β is a coefficient relating the average crack width to the characteristic value (1.7 for cracking due to loads), β1 is a coefficient taking into account the bond properties (0.5 for the FRP bars), and β2 is a coefficient taking into account the load duration (1.0 for short-term loads and 0.5 for long-term loads).
The maximal crack width w for an element with a FRP reinforcement according to ACI-06 [34] and CSA-12 [30], Annex S, can be obtained from:
where ff is the stress in the tension reinforcement, Ef is the modulus of elasticity of the FRP reinforcement, β = (h − x)/(d − x), dc is the concrete cover from the center of the reinforcing bar, and s is the bar spacing.
ISIS-07 [35] suggests a similar equation to calculate the maximal crack width w for FRP-reinforced sections:
where A is an effective tension area of concrete surrounding the flexural tension reinforcement and having the same centroid as that reinforcement, divided by the number of the bars.
Equations (14) and (15) consider a coefficient kb for the bond between the concrete and FRP reinforcement. For different types of FRP reinforcement, resin formulations, and surface treatments, ACI represents the values of the coefficient kb, ranging from 0.6 to 1.72, with an average of 1.10. ACI-06 [34] and ACI-15 [29] suggest a conservative kb value of 1.4, an ISIS-07 [35] value of 1.2, and a CSA-12 [30] value of 1.0 for deformed FRP bars. For FRP bars with similar adhesion conditions using concrete containing steel bars, a kb value of 1.0 is considered.
Experimental crack widths in the critical sections during loading are compared with the predictions obtained according to ACI-06 [34], ISIS-07 [35], CSA-12 [30], EC2-13 [31], and CNR-06 [33] in Figure 9a,b. For the beams series 1 with ribbed bars, the experimental maximal crack widths in the midspan are less than those calculated by the current codes during the entire loading process. This provides evidence of the good bond strength between GFRP bars and concrete. For the middle support, significant deviations occur. In the beams G1-0 and G1-15, the measured maximal crack widths are the closest to the values obtained by CSA-12 [30], while in the beam G1-25 the maximal crack widths are higher than those predicted by CSA-12 [30]. The best-suited predictions for the beam G1-25 are by ISIS-07 [35] and EC2-13 [31], indicating slippage between GFRP bars and concrete in the middle support. This was expected because beam G1-25 had the smallest amount of reinforcement om the support out of the beams series 1 as a consequence of the designed moment redistribution of 25%.
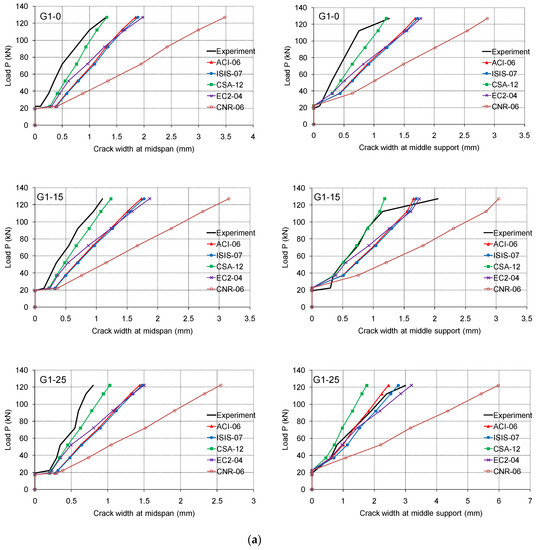
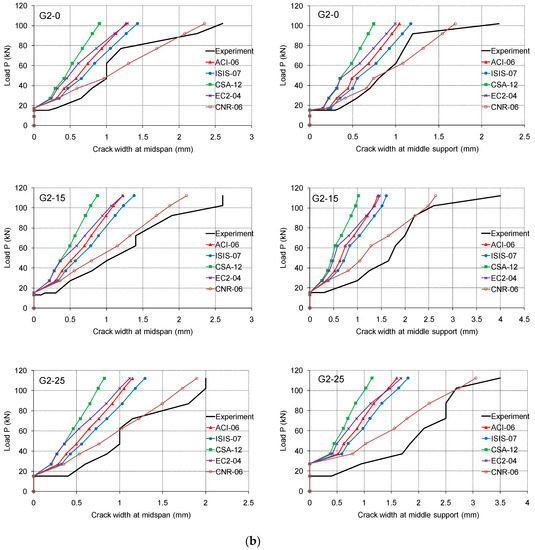
Figure 9.
(a) Experimental and predicted load–crack width relationships for tested beams series 1. (b) Experimental and predicted load–crack width relationships for tested beams series 2.
For the beams series 2, for the appropriate load level, the maximum crack widths obtained experimentally in both the midspan and the middle support section are greater than the calculated values. The best match to the experimental results is shown by CNR-06 [33], which also gives the highest values for the maximum crack width. The main reason for this occurrence is probably the small number of cracks formed in the critical sections, which consequently had large widths. It is evident that different surface treatments for GFRP bars directly affect the values of maximal crack widths for beams series 1 and 2. It is also noticeable that the deviations from the experimental values for the maximum crack widths in the middle support area compared to the prescribed regulations are larger for the cases of beams that are designed to redistribute moments (G2-15 and G2-25). It can be concluded that the axial stiffness of the GFRP reinforcement is clearly expressed on the maximal crack width in middle support section.
3.4. Bond-Dependent Coefficient kb Prediction
The experimental results of the measured crack widths for different load levels for tested beams were used to determine the coefficient kb. The coefficient kb was calculated for the beams at the midspan and middle support for 35 kN, 50 kN, 70 kN, and 90 kN loads for beams series 1; and 25 kN, 35 kN, 45 kN, 60 kN, and 75 kN loads for beams series 2 using Equations (14) and (15), in accordance with ACI-06 [34] and ISIS-07 [35], respectively. These load levels included a wide range of service loads, ranging from 22–72% of the failure load, or 2–6 times the first crack load. Table 3 gives the maximal values of coefficient kb for different load levels for the measured widths of three cracks in every critical section, in both the midspan and middle support sections. Additionally, Figure 10 shows the average values of the coefficient kb for the measured widths of three cracks in every critical section for different load levels of each beam, using Equation (14) in accordance with ACI-06 [34].

Table 3.
Coefficient kb for GFRP bars in the tested beams.
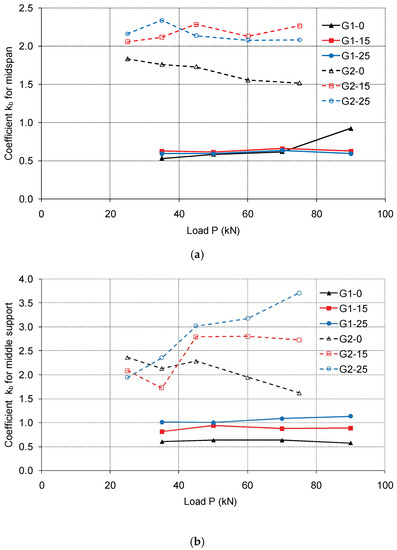
Figure 10.
Bond-dependent coefficient kb for different load levels of tested beams: (a) midspan; (b) middle support.
From Table 3, it can be seen that similar maximum values for the coefficients kb are obtained for the midspan for all beams series 1 using the applied codes. The values for coefficients kb are significantly less than the recommended values for the chosen codes. Additionally, these values are less than 1.0, the recommended value for the steel reinforcement, which indicates very good adhesion conditions between ribbed GFRP bars and the surrounding concrete. In Figure 10, uniform average coefficient values for different load levels can also be observed, except for beam G1-0, where the coefficient value increased with the 90 kN load. It can be concluded that for beams series 1, the designed internal force redistribution did not affect the variation of coefficient kb in the midspan. As expected, higher kb values were obtained for beams series 2, which also indicates poor adhesion conditions between wrapped GFRP bars and concrete. These values are greater than those recommended by the codes. Additionally, it can be observed that these coefficients are higher for beams G2-15 and G2-25, which were designed to achieve internal force redistribution, compared to beam G2-0.
For the middle support, the kb values are significantly different for the tested beams series 1. The highest values were obtained for the beam G1-25 (1.01 and 1.33), which had the smallest amount of reinforcement in the middle support section, while the smallest values were obtained for the beam G1-0 (0.55 and 0.65), which had the highest amount of reinforcement. For the beam G1-0, coefficient kb gave similar values in the midspan and middle support sections. For beams G1-15 and G1-25, the kb values increase in the support section, indicating that the internal force redistribution in the continuous GFRP-reinforced beams occurs with the slippage between bars and concrete in the middle support section. Additionally, in these beams, the slippage of the reinforcement practically started after the cracks occurred in the middle support area, as the kb values were uniform for different load levels (Figure 10). Considering beams series 2, similar conclusions can be drawn for the coefficients kb values for the middle support section, but with significantly higher values. Additionally, uneven values for average coefficients for different load levels are observed in Figure 10. For beam G2-0, these values decrease, while for beam G2-25 coefficient kb values increase as the load increases.
Generally, it can be concluded that the beams with GFRP reinforcement, which are designed for internal force redistribution, reach the designed load capacity with slippage of the reinforcement in the middle support area, with sufficient warning before failure. This phenomenon can be identified by the yielding of steel reinforcement in the section, where a considerable expansion of crack widths and internal force redistribution from that part of the beam occur. These occurrences are considered as desirable behavior before failure. The disadvantage for the beams with GFRP reinforcement is that the slippage of the reinforcement occurs very early at service loads (Figure 10), so special attention should be paid to crack width limitations.
3.5. Load–Deflection Relationship
The deflection Δ of continuously supported beams loaded with point midspan forces P could be calculated as:
where L is the span length, Ec is the modulus of elasticity of concrete, and Ie represents the effective moment of inertia.
ACI-06 [34] suggests an equation to calculate the effective moment of inertia Ie based on Branson’s pattern:
where Mcr is the cracking moment, Ma is the applied moment, Ig is the moment of inertia of the gross concrete section, and Icr is the moment of inertia of the cracked section. Factor βd is represented as:
where ρf is the FRP reinforcement ratio and ρfb is the balanced FRP reinforcement ratio.
According to ISIS-07 [35], the effective moment of inertia can be expressed as:
which is very similar to the approach proposed in EC2-13 [31] when the coefficients for long-term durations are included.
ACI-15 [29] suggests an equation to determine the effective moment of inertia based on research studies by Bischoff and Gross [11]:
where γ is integration factor, which considering beams loaded with midspan point forces, could be calculated as follows:
Based on the obtained experimental results, Habeeb and Ashour [23] suggested modification of the effective moment of inertia given in ACI-06 [34] for continuously supported GFRP-reinforced beams:
where γG = 0.6 is a reduction factor for the state after the cracks occur.
In Figure 11, the deflections for experimental beams are compared to the calculated ones proposed by ACI-06 [34], ACI-15 [29], ISIS-07 [35], and Habeeb and Ashour [23]. The experimental values for the cracking moment Mcr were used for all models. The specific load level deflections obtained through experiment are significantly higher than calculated values. Surely, the main reason for the mismatched diagrams is the fact that models used to calculate deflection are mainly based on research studies that were enforced on simple beams, which are calculated by the elastic analysis for uniform stiffness along the beam. The only match is for experimental and calculated deflections for the lower loads levels. The suggested model by Habeeb and Ashour [23] shows much better fitting of deflection with experimental results, with slightly higher values. Within load levels close to failure, exceptions occur when the experimental deflection curve falls further. Similar observations and comparisons regarding deflection values for tested beams were also made El-Moggy in his experimental research [19]. Considering the experimental beams of a single series, deflections are fairly uniform, even for the different reinforcement axial stiffness in the middle of the beam span. This is a consequence of internal force redistribution, which occurs in the critical sections after formation of cracks.
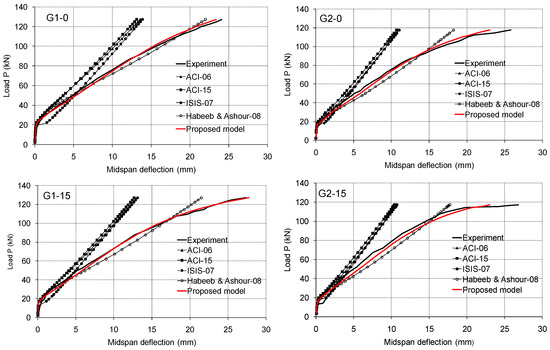
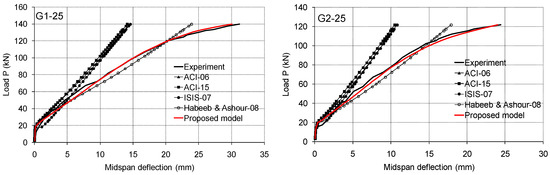
Figure 11.
Experimental and predicted load–deflection relationships for tested beams.
Since FRP-reinforced beams, due to the low modulus of elasticity of the FRP reinforcement, already show considerable deflection at service loads, eventual overload beyond these limits can cause damage to the structural members associated with these elements. For this reason, it is important to know the deflection response of the structural member during the entire loading process, not only at service loads. Hence, a modified model for calculation of deflection for continuously supported GFRP-reinforced beams for each load level is proposed. The model is based on the expression given in ACI-15 [29], with a modification factor value of 0.7, in accordance with the previous study by Baša et al. [26] and as shown in Equation (23), to reduce the moment of inertia after cracking. Additionally, in Equation (24) a non-linear parameter P is used in accordance with Ju et al. [9] for higher load levels:
The U.S. standard ACI-318-14 [36] for concrete structures with steel reinforcement suggests that the effective moment of inertia Ie for continuous beams should be calculated by the expression:
where Iem and Iec are the effective moment of inertia in the midspan and middle support sections, respectively.
In this way, the effects of internal force redistribution are introduced into the calculation of the effective moment of inertia. Considering the significant contribution of elastic moment redistribution in GFRP-reinforced continuous beams [26], the stiffness ratio between the critical cross-sections depends mainly on the stiffness ratio of the GFRP reinforcement in these cross-sections. Therefore, the influence of the cross-section stiffness in the middle support area on the deflection in the midspan for continuously supported GFRP-reinforced beams is more significant than for beams with steel reinforcement. For this reason, the authors applied a more appropriate expression for the calculation of the effective moment of inertia for these beams, with a more significant contribution of the cross-section stiffness in the middle support area:
The very good prediction of the experimental results with the proposed model is shown in Figure 11 over the entire loading process, where the effective moment of inertia Ie is less than the cracked moment of inertia Icr. Using the coefficient P, the proposed model shows a good development of deflection for higher load levels. Immediately after cracks occur, a large increase in deflections in accordance with ISIS-07 [35] is noticed. This sudden reduction in stiffness was not observed during testing of the beams series 1, as can be seen in Figure 11, which again indicates very good adhesion conditions between ribbed GFRP bars and concrete. Further experimental results would better confirm the proposed model.
3.6. Experimental Service Load
Often the required amount of reinforcement in a section is a consequence of fulfilling the serviceability criteria, which consider the limitations of maximal crack widths, deflection, and stresses in the FRP reinforcement. In ACI-15 [29], the beam deflection is limited to L/360 in the case where the observed structural element is not in contact with non-constructive elements, and is limited to L/240 in the case where the observed structural element is in contact with non-constructive elements. In the elements with FRP reinforcement, which is not susceptible to corrosion, larger crack widths may be allowed than in elements with steel reinforcement. Generally, the crack width is limited for aesthetic reasons. Thus, ACI-15 [29] and CSA-12 [30] limit the crack width to 0.5 mm for a very aggressive environment or to 0.7 mm for other conditions. Additionally, in order to prevent failure of FRP reinforcement from constant and cyclic loads due to the appearance of creep and fatigue, the stresses in the FRP reinforcement for service loads are limited. ACI-15 [29] limits the stress in GFRP reinforcement for service loads at 20% of tensile strength, while CSA-12 [30] limits this at 25%, in order to prevent failure due to creep rupture and fatigue. In Table 4, Table 5 and Table 6, the experimental loads at which midspan deflection of the beam reaches L/240, the maximal crack width reaches 0.7 mm, and the stresses in the GFRP reinforcement reach 20% of the tensile strength are given. Additionally, the percentage of service loads when the serviceability criteria are satisfied against the ultimate load for the midspan and for the middle support are also given.

Table 4.
Experimental service load for tested beams at which midspan deflection reaches L/240.

Table 5.
Experimental service load for the tested beams at which the maximal crack width reaches 0.7 mm.

Table 6.
Experimental service load for tested beams at which stress in the GFRP reinforcement reaches 20% of tensile strength.
The results in Table 4 show that for the criterion of limiting the deflection at L/240, the service loads are similar for beams series 1 (46.9–50.5%) and series 2 (53.0–57.0%). It can be concluded that the poor bond strength between the GFRP reinforcement and concrete in beams series 2 does not affect the level of service load obtained by limiting the deflection. For the criterion of limiting the maximal crack widths to 0.7 mm (Table 5), the service loads differ significantly for beams series 1 (31.2–62.3%) and series 2 (16.7–24.2%). The difference in results is a direct consequence of the very good bond strength between the ribbed GFRP reinforcement and concrete for beams series 1 and the poor adhesion conditions between the wrapped GFRP reinforcement and concrete for beams series 2. For the criterion of limiting stress in the reinforcement, the results are also similar. The service loads range from 22.1% to 33.3% of the ultimate load for beams series 1 and from 28.9% to 35.6% for beams series 2 (Table 6). For all limitation criteria, with the increase of the designed moment redistribution, the level of service load decreases in relation to the ultimate load, especially for beams series 1 with ribbed bars. For the criterion of limitation of crack widths, this is primarily a consequence of the reduction in the amount of reinforcement in the middle support section due to the designed moment redistribution, which causes greater crack widths in these sections. With this finding, it is noted that for the beam G1-25, the level of service load, as a criterion for crack width limitation, is significantly different for the midspan (79.8%) and for the support (31.2%). Considering beams series 1 with ribbed bars, the level of the service load is the smallest in the case of stress limitation in the GFRP reinforcement, as presented in Table 4, Table 5 and Table 6.
3.7. Ductility and Deformability
Ductility is a non-linear structural behavior that causes significant deformations before failure and creates the conditions for the redistribution of internal forces in the critical sections of the continuous beams. For structures with steel reinforcement, the ductility is defined by the ductility coefficient, which represents the ratio of total elastoplastic deformation and deformation at yielding. As FRP reinforcement shows linear elastic behavior until failure, this method of estimating ductility is not applicable to elements reinforced with FRP bars.
For sections with FRP reinforcement, the concept of deformability is used to determine the development of deformation before failure of the structure. Jaeger et al. [37] and Newhook et al. [38] proposed the deformability factor (J), as the product of the strength factor and deflection or curvature factor, for ultimate and service states:
where Mult, φult, and Δult are the moment, curvature, and deflection under the ultimate limit state, respectively; and Mser, φser, and Δser are the moment, curvature, and deflection under the serviceability limit state, respectively.
For the service state, the values for the moment and deflection or curvature correspond to a maximum concrete compressive strain of 1‰. The strain of 1‰ is considered as the beginning of inelastic deformation of the concrete. Applying this approach, ISIS-07 [35] suggests that the deformability factor for sections with FRP reinforcement should be greater than 4 for rectangular sections and greater than 6 for T-sections. As a criterion for determining the deformability factor in this research, the criterion of deflection is selected rather than the criterion of curvature. Moments and deflections for the ultimate limit state are obtained as the maximum values measured during the test. As can be seen in Table 7, the deformability factors (J) were higher than the minimum values in 4, as recommended by ISIS-07 [35]. This means that the tested continuous beams showed a certain kind of ductile behavior, although they contained GFRP reinforcement, which exhibits brittle behavior. The higher deflection factors (Δult/Δser) compared to strength factors (Mult/Mser) indicate that this ductile behavior of the beams is mainly a consequence of the high deformation capacity, which provides sufficient warning before failure.

Table 7.
Deformability factors for sections in the midspan for the tested beams.
The deformability factor, as an important criterion for describing the quality response of structures, is the ratio between the ultimate limit state and the serviceability limit state with respect to load capacity and deformation. Thus, the serviceability criteria defined in Section 3.6 served as baselines for calculating deformability factors (also known as robustness indices) based on Equation (27), where (Mult/Mser) is the strength factor and (Δult/Δser) is the deflection factor. In Figure 12, Figure 13 and Figure 14, the strength, deflection, and deformability factors are given, respectively, where moment and midspan deflection values under the serviceability limit state are defined for the serviceability criteria limitations given in Section 3.6.
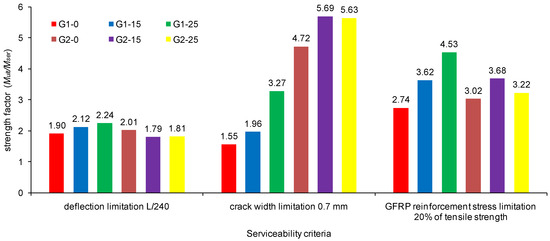
Figure 12.
Strength factors for serviceability criteria limitations for the tested beams.
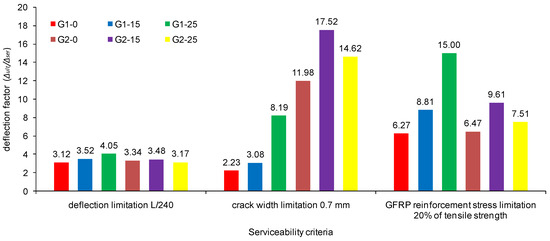
Figure 13.
Deflection factors for serviceability criteria limitations for the tested beams.
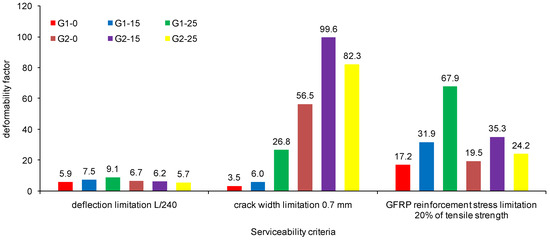
Figure 14.
Deformability factors for serviceability criteria limitations for the tested beams.
As constituents of the deformability factors, it is noticeable that the deflection factors are significantly greater than the strength factors for all criteria for all tested beams, which is desirable for achieving better beam behavior. Due to the low levels of service loads, as a consequence of limiting the crack width to 0.7 mm, high values of deformability factors for beams series 2 are obtained. For the beams series 1, the deformability factors are the highest for the GFRP reinforcement stress limitation. Additionally, an increase of the deformability factors (along with the strength and deflection factors) with an increase of the designed moment redistribution is evident for the beams series 1 for all criteria, showing good bond strength between the ribbed GFRP bars and concrete.
Generally, for service loads, the low modulus of elasticity of the GFRP reinforcement causes considerable deflections and wide cracks in continuous beams, which can be characterized as negative phenomena. However, with further loading, such a low modulus of elasticity with a high GFRP reinforcement tensile strength and with large deflections and wide cracks enables high safety coefficients and deformability factors to be reached. This provides sufficient warning of continuous beam failure, which is significant for prevention purposes. Thus, after overcoming the service loads, the low modulus of elasticity can be represented as a positive characteristic of the GFRP reinforcement. This especially refers to the continuous beams that achieved the designed moment redistribution.
4. Conclusions
The results of experiment performed on six GFRP-reinforced continuous beams are compared to the provisions of current codes regarding load capacity, cracking and deflection behavior, and ductility. Based on the described investigation, the following conclusions were drawn:
- For beams with ribbed GFRP bars with epoxy, the values of the maximal crack widths were less than those predicted by actual codes, while for beams with wrapped GFRP reinforcement with polyester they were higher than predicted. As the crack width largely depends on the degree of adhesion between the GFRP reinforcement and the concrete, the reliability of the chosen code in calculating the crack width depends on the prescribed coefficient kb.
- The bond dependent coefficient kb determined for the ribbed GFRP bars for crack widths in the midspan of the beams indicated very good bond strength between GFRP bars and concrete. With the reduction of the reinforcement over the middle support, the kb increased, indicating that the internal force redistribution in the GFRP-reinforced continuous beams occurred with the slippage between bars and concrete in the middle support section, without decreasing the load-carrying capacity.
- Actual codes for elements with FRP reinforcement underestimate the deflection of continuous beams with GFRP reinforcement. Therefore, a modified model for effective moment of inertia Ie for deflection prediction of GFRP-reinforced continuous beams was suggested, using non-linear parameter P for higher load levels. The proposed model for deflection calculation, when the effective moment of inertia Ie is less than the cracked moment of inertia Icr, gives very good prediction of the obtained experimental results for all load levels.
- The design of continuous concrete structures with GFRP reinforcement is governed by different criteria imposed for the serviceability limit state, as a low percentage of the service load is obtained in relation to the ultimate load. For service criteria limitations, with the increase of the designed moment redistribution, the level of service load decreases in relation to the ultimate load.
- Although the FRP reinforcement showed linear elastic behavior and the beams experienced concrete compression failure, obtaining deformability factors higher than 4, as recommended, indicated that continuously supported GFRP-reinforced beams showed a certain kind of ductile behavior, giving sufficient warning before failure.
- Continuous beams that reached the designed moment redistribution showed greater deformability factors, meaning that they exhibited a greater degree of ductile behavior compared to the beams that were designed based on elastic analysis.
Author Contributions
Conceptualization, N.B. and M.U.; methodology, N.B. and M.U.; validation, N.B., M.U. and N.K.V.; formal analysis, N.B. and M.M.; investigation, N.B. and M.M.; resources, N.B.; data curation, N.B. and M.M.; writing—original draft preparation, N.B.; writing—review and editing, M.U. and N.K.V.; visualization, N.B. and N.K.V.; supervision, M.U.; project administration, N.B. and M.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors would like to express their gratitude to the Engineering Chamber of Montenegro for the financial support and a local company from Montenegro for the donation of concrete admixtures. Additionally, the first author is grateful to the Laboratory of the Faculty of Civil Engineering at the University of Montenegro for technical help.
Conflicts of Interest
The authors declare that there is no conflict of interest regarding the publication of this paper.
References
- Bedon, C.; Louter, C. Numerical investigation on structural glass beams with GFRP-embedded rods, including effects of pre-stress. Compos. Struct. 2018, 184, 650–661. [Google Scholar] [CrossRef]
- Raftery, G.M.; Kelly, F. Basalt FRP rods for reinforcement and repair for timber. Compos. Part B 2015, 70, 9–19. [Google Scholar] [CrossRef]
- Barris, C.; Torres, L.; Turon, A.; Baena, M.; Catalan, A. An experimental study of the flexural behaviour of GFRP RC beams and comparison with prediction models. Compos. Struct. 2009, 91, 286–295. [Google Scholar] [CrossRef]
- Toutanji, H.A.; Saafi, M. Flexural behaviour of concrete beams reinforced with glass fiber-reinforced polymer GFRP bars. ACI Struct. J. 2000, 97, 712–719. [Google Scholar]
- Yost, J.R.; Gross, S.P.; Dinehart, D.W. Effective moment of inertia for glass fiber-reinforced polymer-reinforced concrete beams. ACI Struct. J. 2003, 100, 732–739. [Google Scholar]
- Rafi, M.M.; Nadjai, A. Evaluation of ACI 440 deflection model for fiber-reinforced polymer reinforced concrete beams and suggested modification. ACI Struct. J. 2009, 106, 762–771. [Google Scholar]
- Mousavi, S.R.; Esfahani, M.R. Effective moment of inertia prediction of FRP-reinforced concrete beams based on experimental results. J. Compos. Constr. 2012, 16, 490–498. [Google Scholar] [CrossRef]
- Adam, M.A.; Said, M.; Mahmoud, A.A.; Ali Shanour, S. Analytical and experimental flexural behavior of concrete beams reinforced with glass fiber reinforced polymers bars. Constr. Build. Mater. 2015, 84, 354–366. [Google Scholar] [CrossRef]
- Ju, M.; Oh, H.; Lim, J.; Sim, J. A modified model for deflection calculation of reinforced concrete beam with deformed GFRP rebar. Int. J. Polym. Sci. 2016, 2016, 2485825. [Google Scholar] [CrossRef]
- Bischoff, P.H. Reevaluation of deflection prediction for concrete beams reinforced with steel and fiber reinforced polymer bars. J. Struct. Eng. 2005, 131, 752–762. [Google Scholar] [CrossRef]
- Bischoff, P.H.; Gross, S.P. Equivalent moment of inertia based on integration of curvature. J. Compos. Constr. 2011, 15, 263–273. [Google Scholar] [CrossRef]
- Barris, C.; Torres, L.; Comas, J.; Mias, C. Cracking and deflections in GFRP RC beams: An experimental study. Compos. Part B 2013, 55, 580–590. [Google Scholar] [CrossRef]
- Elgabbas, F.; Vincent, P.; Ahmed, E.A.; Benmokrane, B. Experimental testing of basalt-fiber-reinforced polymer bars in concrete beams. Compos. Part B 2016, 91, 205–218. [Google Scholar] [CrossRef]
- Kassem, C.; Farghaly, A.S.; Benmokrane, B. Evaluation of flexural behavior and serviceability performance of concrete beams reinforced with FRP bars. J. Compos. Constr. 2011, 15, 682–695. [Google Scholar] [CrossRef]
- El-Nemr, A.; Ahmed, E.; Benmokrane, B. Flexural behavior and serviceability of normal- and high-strength concrete beams reinforced with glass fiber-reinforced polymer bars. ACI Struct. J. 2013, 110, 1077–1088. [Google Scholar]
- El-Nemr, A.; Ahmed, E.; Barris, C.; Benmokrane, B. Bond-dependent coefficient of glass- and carbon-FRP bars in normal- and high-strength concretes. Constr. Build. Mater. 2016, 113, 77–89. [Google Scholar] [CrossRef]
- Mostofinejad, D. Ductility and Moment Redistribution in Continuous FRP Reinforced Concrete Beams. Ph.D. Thesis, Department of Civil and Environmental Engineering, Carleton University, Ottawa, ON, Canada, 1997. [Google Scholar]
- El-Mogy, M.; El-Ragaby, A.; El-Salakawy, E. Effect of transverse reinforcement on the flexural behavior of continuous concrete beams reinforced with FRP. J. Compos. Constr. 2011, 15, 672–681. [Google Scholar] [CrossRef]
- El-Mogy, M.; El-Ragaby, A.; El-Salakawy, E. Flexural behavior of continuous FRP-reinforced concrete beams. J. Compos. Constr. 2010, 14, 669–680. [Google Scholar] [CrossRef]
- Matos, B.; Correia, J.R.; Castro, L.M.S.; França, P. Structural response of hyperstatic concrete beams reinforced with GFRP bars: Effect of increasing concrete confinement. Compos. Struct. 2012, 94, 1200–1210. [Google Scholar] [CrossRef]
- Santos, P.; Laranja, G.; Franca, P.M.; Correia, J.R. Ductility and moment redistribution capacity of multi-span T-section concrete beams reinforced with GFRP bars. Constr. Build. Mater. 2013, 49, 949–961. [Google Scholar] [CrossRef]
- Grace, N.F.; Soliman, A.K.; Abdel-Sayed, G.; Saleh, K.R. Behavior and ductility of simple and continuous FRP reinforced beams. J. Compos. Constr. 1998, 2, 186–194. [Google Scholar] [CrossRef]
- Habeeb, M.N.; Ashour, A.F. Flexural behavior of continuous GFRP reinforced concrete beams. J. Compos. Constr. 2008, 12, 115–124. [Google Scholar] [CrossRef]
- Ashour, A.F.; Habeeb, M.N. Continuous concrete beams reinforced with CFRP bars. Proc. ICE Struct. Build. 2008, 161, 349–357. [Google Scholar] [CrossRef]
- Kara, I.F.; Ashour, A.F. Moment redistribution in continuous FRP reinforced concrete beams. Constr. Build. Mater. 2013, 49, 939–948. [Google Scholar] [CrossRef]
- Baša, N.; Ulićević, M.; Zejak, R. Experimental research of continuous concrete beams with GFRP reinforcement. Adv. Civ. Eng. 2018, 2018, 6532723. [Google Scholar] [CrossRef]
- Baša, N. Effects of Redistribution of Internal Forces on Limit States of Continuous Beams Reinforced with FRP Reinforcement. Ph.D. Thesis, Faculty of Civil Engineering, Dissertation-University of Montenegro, Podgorica, Montenegro, 2019. [Google Scholar]
- ACI Committee 440. Guide Test Methods for Fiber-Reinforced Polymers (FRPs) for Reinforcing or Strengthening Concrete Structures (ACI 440.3R-12); American Concrete Institute: Farmington Hills, MI, USA, 2012. [Google Scholar]
- ACI Committee 440. Guide for the Design and Construction of Structural Concrete Reinforced with Fiber-Reinforced Polymer (FRP) Bars (ACI 440.1R-15); American Concrete Institute: Farmington Hills, MI, USA, 2015. [Google Scholar]
- Canadian Standards Association (CSA). Design and Construction of Buildings Components with Fiber-Reinforced Polymers; CSA S806-12; Canadian Standards Association (CSA): Toronto, ON, Canada, 2012. [Google Scholar]
- European Committee for Standardization CEN. Eurocode 2. In Design of Concrete Structures: General Rules and Rules for Buildings, Part 1-1; EN 1992-1-1; European Committee for Standardization CEN: Brussels, Belgium, 2013. [Google Scholar]
- Bedon, C.; Louter, C. Structural glass beams with embedded GFRP, CFRP or steel reinforcement rods: Comparative experimental, analytical and numerical investigations. J. Build. Eng. 2019, 22, 227–241. [Google Scholar] [CrossRef]
- CNR-DT 203/2006. Guide for the Design and Construction of Concrete Structures Reinforced with Fiber-Reinforced Polymer Bars; National Research Council: Rome, Italy, 2006. [Google Scholar]
- ACI Committee 440. Guide for the Design and Construction of Structural Concrete Reinforced with FRP Bars (ACI 440.1R-06); American Concrete Institute: Farmington Hills, MI, USA, 2006. [Google Scholar]
- ISIS Canada. Reinforcing Concrete Structures with Fiber Reinforced Polymers; ISIS-M03-07; Canadian Network of Centers of Excellence on Intelligent Sensing for Innovative Structures, University of Winnipeg: Winnipeg, MB, Canada, 2007. [Google Scholar]
- ACI Committee 318. Building Code Requirements for Structural Concrete (ACI 318-14), Commentary on Building Code Requirements for Structural Concrete; ACI 318R-14; American Concrete Institute: Farmington Hills, MI, USA, 2014. [Google Scholar]
- Jaeger, L.G.; Tadros, G.; Mufti, A. Balanced Section, Ductility and Deformability in Concrete with FRP Reinforcement, Industry’s Centre for Computer-Aided Engineering, CAS CAM; Techical University of Nova Scotia: Halifax, NS, Canada, 1995. [Google Scholar]
- Newhook, J.; Ghali, A.; Tadros, G. Concrete flexural members reinforced with fiber reinforced polymer: Design for cracking and deformability. Can. J. Civ. Eng. 2002, 29, 125–134. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).