Process Monitoring of Antisolvent Based Crystallization in Low Conductivity Solutions Using Electrical Impedance Spectroscopy and 2-D Electrical Resistance Tomography
Abstract
1. Introduction
2. Application of 1-D EIS and 2-D ERT as a PAT in Crystallization Processes
2.1. Application of Electrical Impedance Spectroscopy to the Crystallization Process
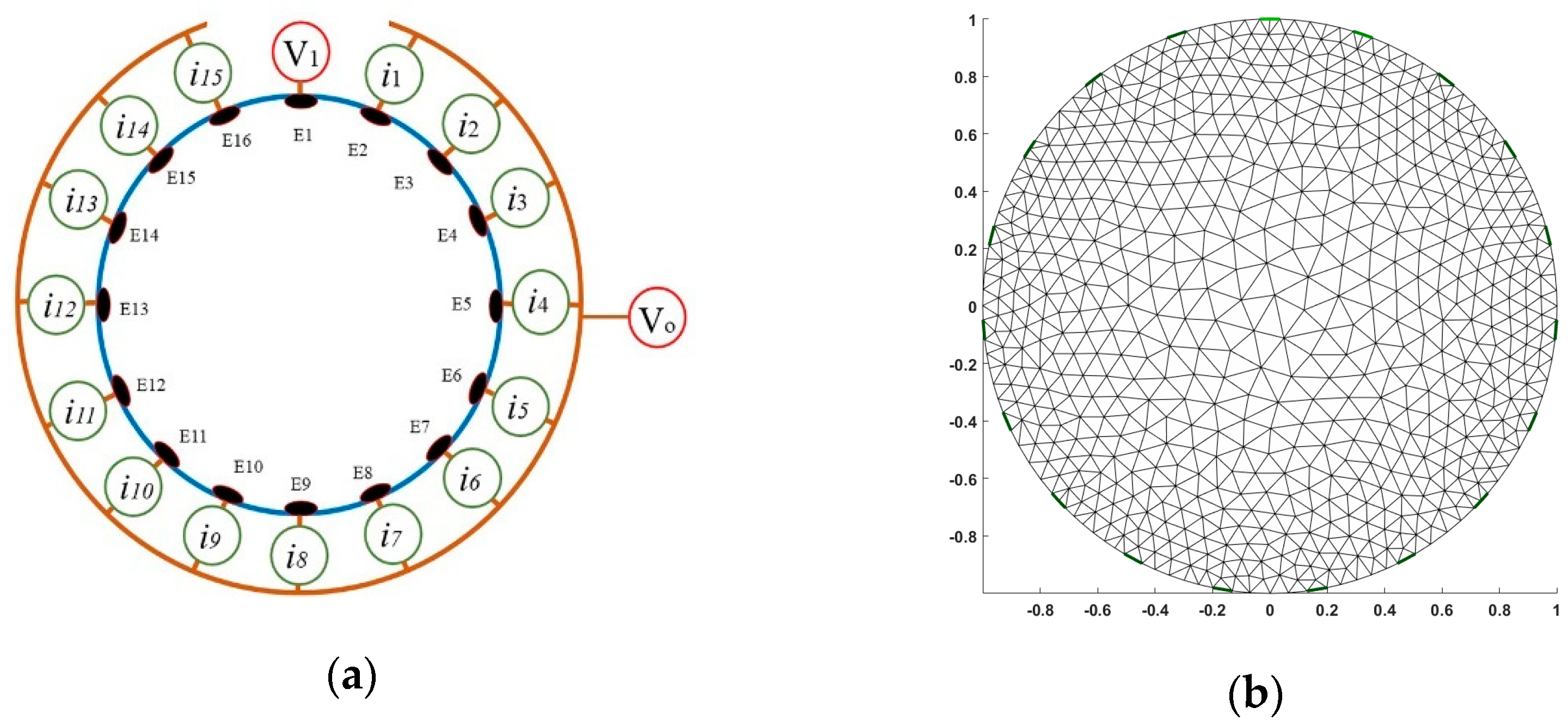
2.2. Application of a Voltage Injected–Current Detected (V–C) Based Low Conductivity Sensitive Electrical Resistance Tomography (ERT)
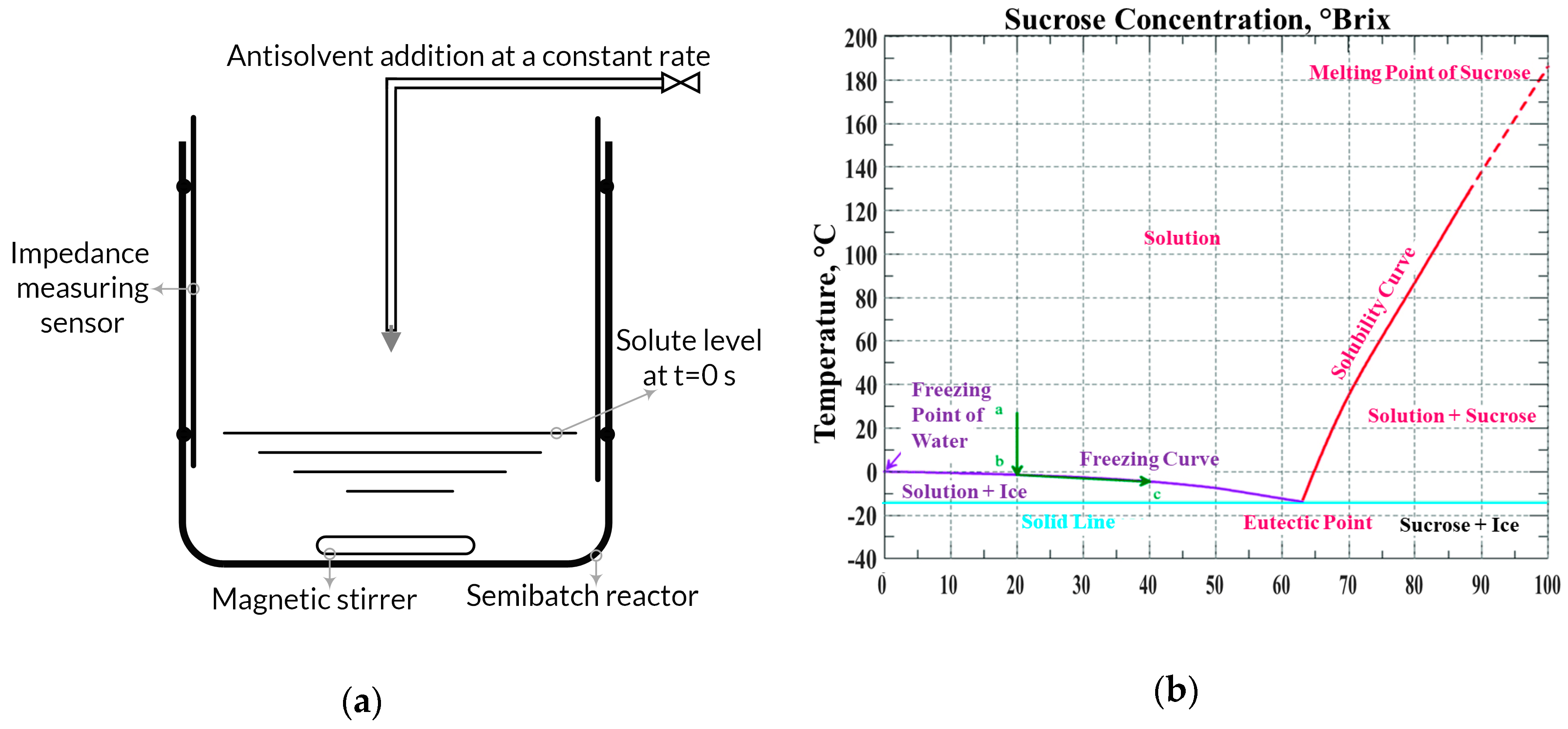
3. Experimental Setup, Materials, and Procedure
3.1. Experimental Apparatus Setup for EIS (Electrical Impedance Spectroscopy)
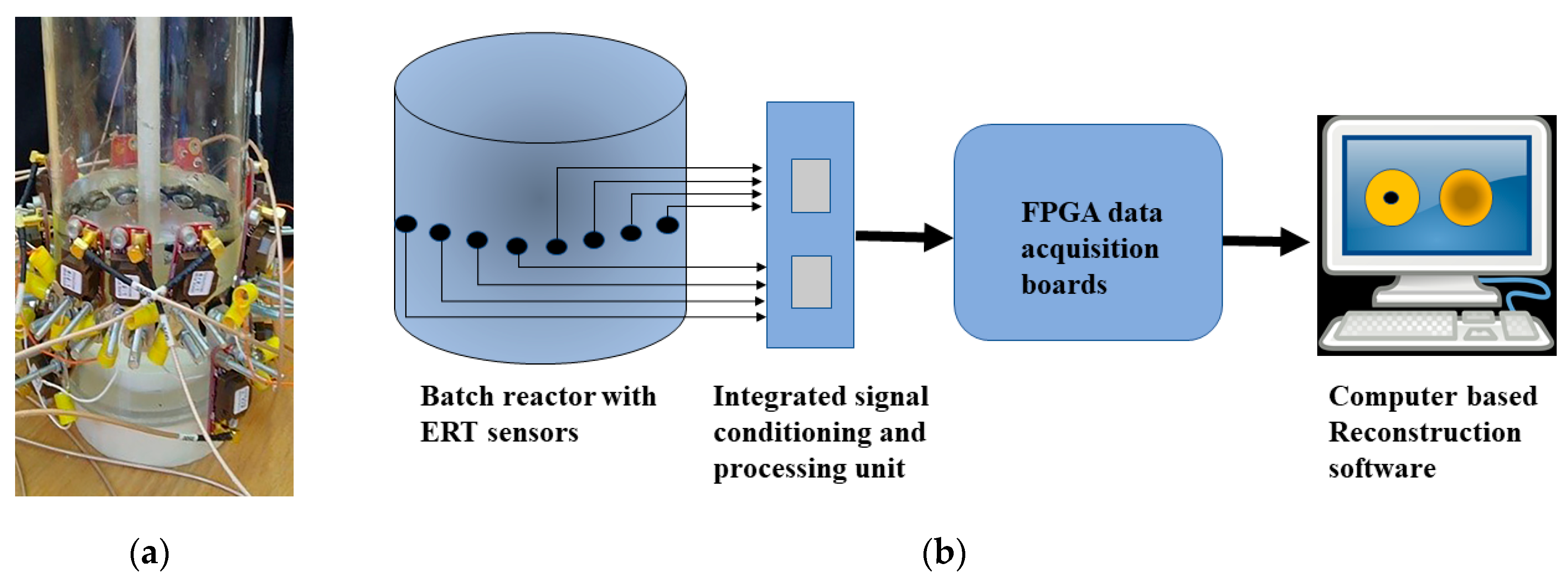
3.2. Experimental Apparatus Setup for ERT (Electrical Resistance Tomography)
4. Results and Discussion
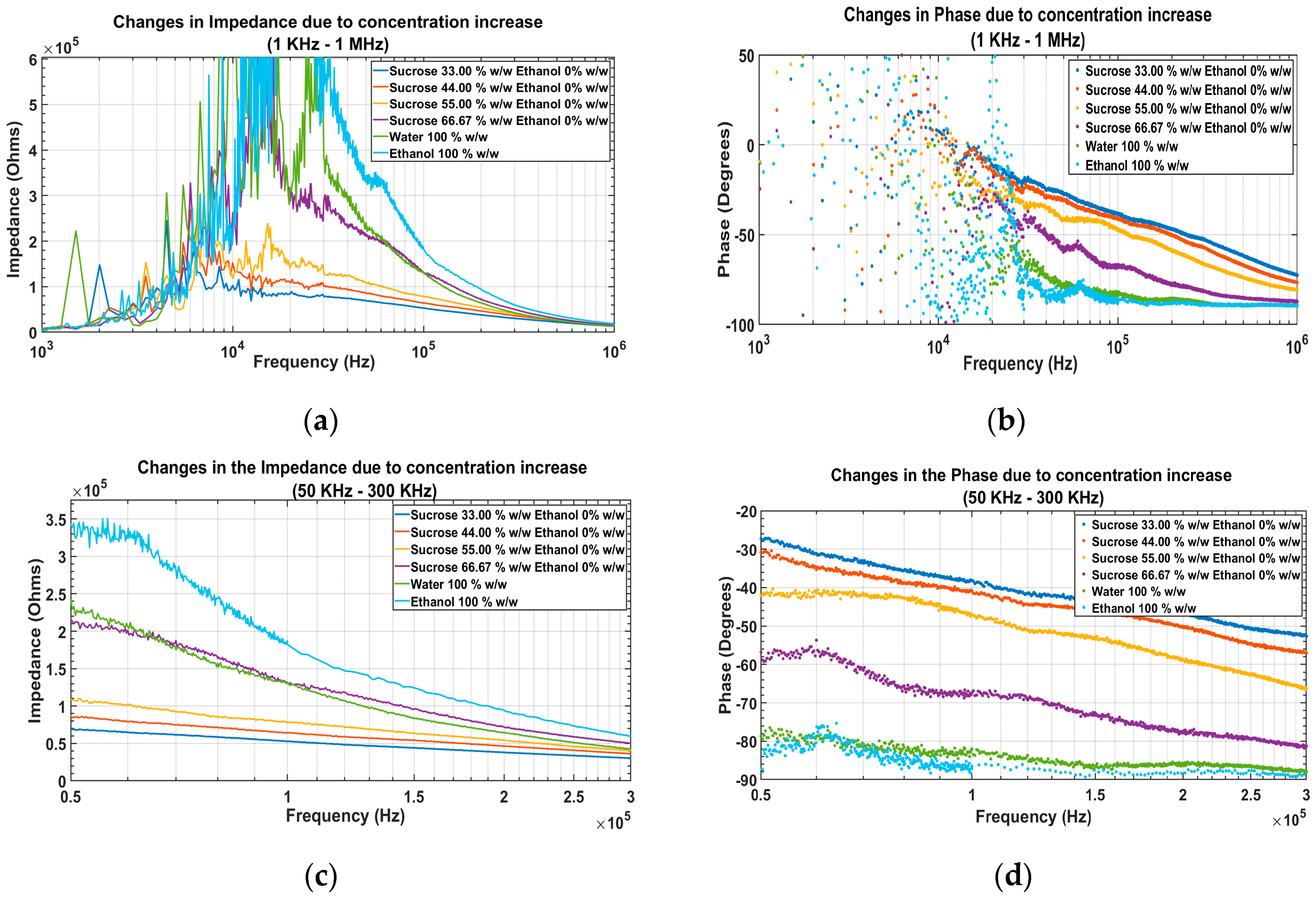
4.1. Results for EIS
4.1.1. EIS of the Solutions before Adding Ethanol
4.1.2. EIS of Solutions after Addition of Ethanol
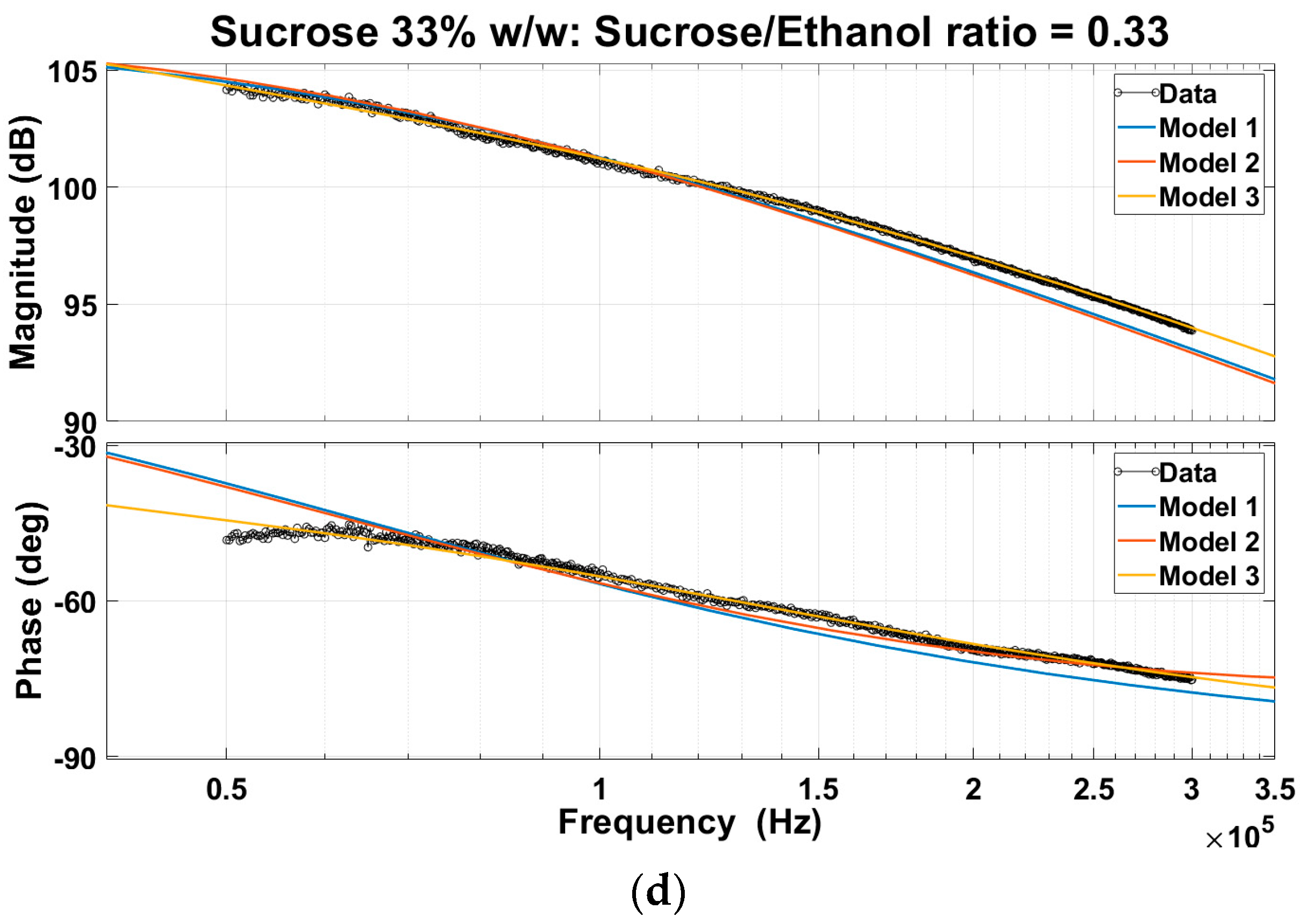
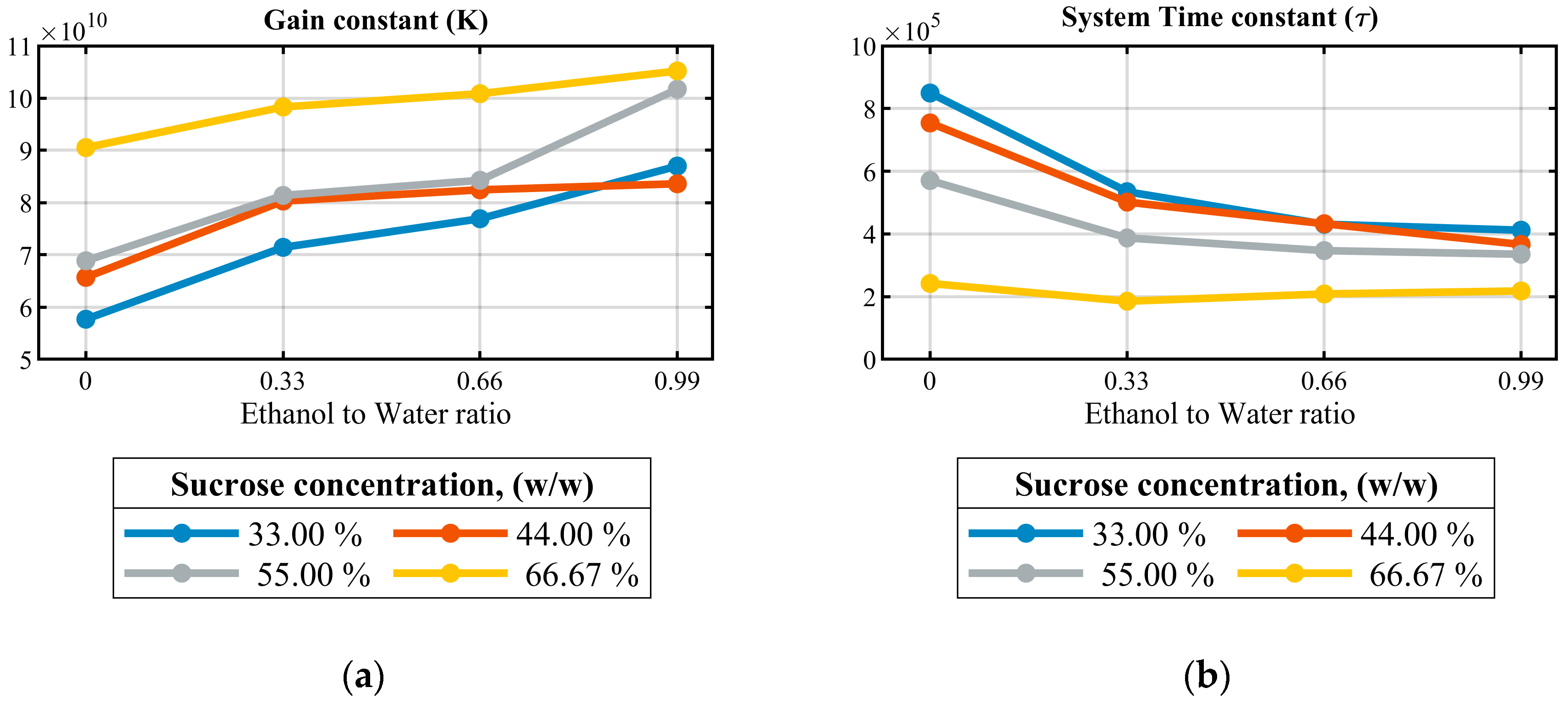
4.1.3. Creating Transfer Function Models from EIS Data and Comparative Analysis
4.2. Results for Electrical Resistance Tomography Experiments
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| PAT | Process analytical technology |
| ERT | Electrical resistance tomography |
| ECT | Electrical capacitance tomography |
| EIS | Electrical impedance spectroscopy |
| FEM | Finite element method |
| Hz | Hertz (measure of frequency) |
| w/w % | Weight to weight ratio in percentage |
| K | Steady-state gain constant |
| Time constant | |
| V–C based ERT | Voltage injected and current detected ERT |
| C–V based ERT | Current injected and voltage detected ERT |
| V | Voltage |
| I | Current |
| A | Amperes |
| 1-D | One dimensional |
| 2-D | Two dimensional |
| 3-D | Three dimensional |
| g | Grams |
| g/s | Grams per second |
| L | Litres |
| Impedance in phasor form with ω as the angular frequency | |
| z1, z2 …, zm | Zeroes |
| p1, p2…, pn | Poles |
| Correlation Matrix of random vector x | |
| Mean or Expected value | |
| Cross covariance of x and y | |
| ΔσNormalized | Normalized changes in conductivity |
References
- Simon, L.L.; Simone, E.; Oucherif, K.A. Crystallization process monitoring and control using process analytical technology. In Software Architectures and Tools for Computer Aided Process Engineering; Elsevier BV: Amsterdam, The Netherlands, 2018; Volume 41, pp. 215–242. [Google Scholar]
- Claßen, J.; Aupert, F.; Reardon, K.F.; Solle, D.; Scheper, T. Spectroscopic sensors for in-line bioprocess monitoring in research and pharmaceutical industrial application. Anal. Bioanal. Chem. 2016, 409, 651–666. [Google Scholar] [CrossRef]
- Simone, E.; Saleemi, A.N.; Nagy, Z.K. In Situ Monitoring of Polymorphic Transformations Using a Composite Sensor Array of Raman, NIR, and ATR-UV/vis Spectroscopy, FBRM, and PVM for an Intelligent Decision Support System. Org. Process. Res. Dev. 2014, 19, 167–177. [Google Scholar] [CrossRef]
- Sankowski, D.; Sikora, J. Electrical Capacitance Tomography: Theoretical Basis and Applications; Wydawnictwo Książkowe Instytutu Elektrotechniki: Warszawa, Poland, 2010. [Google Scholar]
- Grudzien, K.; Chaniecki, Z.; Romanowski, A.; Niedostatkiewicz, M.; Sankowski, D. ECT Image Analysis Methods for Shear Zone Measurements during Silo Discharging Process. Chin. J. Chem. Eng. 2012, 20, 337–345. [Google Scholar] [CrossRef]
- Ricard, F.; Brechtelsbauer, C.; Xu, Y.; Lawrence, C.; Thompson, D. Development of an Electrical Resistance Tomography Reactor for Pharmaceutical Processes. Can. J. Chem. Eng. 2008, 83, 11–18. [Google Scholar] [CrossRef]
- Koulountzios, P.; Rymarczyk, T.; Soleimani, M. A Quantitative Ultrasonic Travel-Time Tomography to Investigate Liquid Elaborations in Industrial Processes. Sensors 2019, 19, 5117. [Google Scholar] [CrossRef]
- Rymarczyk, T.; Polakowski, K.; Sikora, J. A new concept of discretisation model for imaging improving in ultrasound transmission tomography. Inform. Autom. Pomiary Gospod. Ochr. Środowiska 2019, 49, 48–51. [Google Scholar]
- Majchrowicz, M.; Kapusta, P.; Jackowska-Strumiłło, L.; Banasiak, R.; Sankowski, D. Multi-GPU, Multi-Node Algorithms for Acceleration of Image Reconstruction in 3D Electrical Capacitance Tomography in Heterogeneous Distributed System. Sensors 2020, 20, 391. [Google Scholar] [CrossRef]
- Garbaa, H.; Jackowska-Strumiłło, L.; Grudzien, K.; Romanowski, A. Application of electrical capacitance tomography and artificial neural networks to rapid estimation of cylindrical shape parameters of industrial flow structure. Arch. Electr. Eng. 2016, 65, 657–669. [Google Scholar] [CrossRef]
- Rymarczyk, T.; Kłosowski, G.; Kozłowski, E.; Tchórzewski, P. Comparison of Selected Machine Learning Algorithms for Industrial Electrical Tomography. Sensors 2019, 19, 1521. [Google Scholar] [CrossRef]
- Nagy, Z.K.; Fujiwara, M.; Braatz, R.D.; Myerson, A.S.; Erdemir, D.; Lee, A.Y. Monitoring and Advanced Control of Crystallization Processes. Handb. Ind. Cryst. 2019, 313–345. [Google Scholar] [CrossRef]
- Lewis, A.; Seckler, M.M.; Kramer, H.; Van Rosmalen, G. Industrial Crystallization; Cambridge University Press (CUP): Cambridge, UK, 2015. [Google Scholar]
- Nagy, Z.K.; Braatz, R.D. Advances and New Directions in Crystallization Control. Annu. Rev. Chem. Biomol. Eng. 2012, 3, 55–75. [Google Scholar] [CrossRef] [PubMed]
- Yu, Z.-Q.; Chow, P.S.; Tan, R.B.H. Application of Attenuated Total Reflectance−Fourier Transform Infrared (ATR−FTIR) Technique in the Monitoring and Control of Anti-solvent Crystallization. Ind. Eng. Chem. Res. 2006, 45, 438–444. [Google Scholar] [CrossRef]
- Nowee, S.M.; Abbas, A.; Romagnoli, J.A. Antisolvent crystallization: Model identification, experimental validation and dynamic simulation. Chem. Eng. Sci. 2008, 63, 5457–5467. [Google Scholar] [CrossRef]
- Bhangu, S.K.; AshokKumar, M.; Lee, J. Ultrasound Assisted Crystallization of Paracetamol: Crystal Size Distribution and Polymorph Control. Cryst. Growth Des. 2016, 16, 1934–1941. [Google Scholar] [CrossRef]
- Lee, J.; AshokKumar, M.; Kentish, S. Influence of mixing and ultrasound frequency on antisolvent crystallisation of sodium chloride. Ultrason. Sonochemistry 2014, 21, 60–68. [Google Scholar] [CrossRef]
- El Bazi, W.; Porte, C.; Mabille, I.; Havet, J.-L. Antisolvent crystallization: Effect of ethanol on batch crystallization of α glycine. J. Cryst. Growth 2017, 475, 232–238. [Google Scholar] [CrossRef]
- Lindenberg, C.; Krattli, M.; Cornel, J.; Mazzotti, M.; Brozio, J. Design and Optimization of a Combined Cooling/Antisolvent Crystallization Process. Cryst. Growth Des. 2009, 9, 1124–1136. [Google Scholar] [CrossRef]
- Howard, K.S.; Nagy, Z.K.; Saha, B.; Robertson, A.L.; Steele, G.; Martin, D. A Process Analytical Technology Based Investigation of the Polymorphic Transformations during the Antisolvent Crystallization of Sodium Benzoate from IPA/Water Mixture. Cryst. Growth Des. 2009, 9, 3964–3975. [Google Scholar] [CrossRef]
- Boukamp, B.; Denisov, D.; Hassanizadeh, M.; Hessling, D.; Huinink, H.; Karadimitriou, N.; Kuijpers, K.; Ravensbergen, J.; Sabater, C.; Schoemaker, F. Analyzing liquid penetration in paper by electrical impedance spectroscopy (EIS). Proc. Phys. Ind. 2013, 4, 25–44. [Google Scholar]
- Randviir, E.P.; Banks, C.E. Electrochemical impedance spectroscopy: An overview of bioanalytical applications. Anal. Methods 2013, 5, 1098. [Google Scholar] [CrossRef]
- Jiang, Z.; Yao, J.; Wang, L.; Wu, H.; Huang, J.; Zhao, T.; Takei, M. Development of a Portable Electrochemical Impedance Spectroscopy System for Bio-Detection. IEEE Sens. J. 2019, 19, 5979–5987. [Google Scholar] [CrossRef]
- Santoso, D.R.; Pitaloka, B.; Widodo, C.S.; Juswono, U.P. Low-Cost, Compact, and Rapid Bio-Impedance Spectrometer with Real-Time Bode and Nyquist Plots. Appl. Sci. 2020, 10, 878. [Google Scholar] [CrossRef]
- Conesa, C.; Garcia-Breijo, E.; Loeff, E.; Segui, L.; Fito, P.J.; Miró, N.L. An Electrochemical Impedance Spectroscopy-Based Technique to Identify and Quantify Fermentable Sugars in Pineapple Waste Valorization for Bioethanol Production. Sensors 2015, 15, 22941–22955. [Google Scholar] [CrossRef] [PubMed]
- Grossi, M.; Riccò, B. Electrical impedance spectroscopy (EIS) for biological analysis and food characterization: A review. J. Sens. Sens. Syst. 2017, 6, 303–325. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, M.; Hammond, R.B. Characterization of crystallisation processes with electrical impedance spectroscopy. Nucl. Eng. Des. 2011, 241, 1938–1944. [Google Scholar] [CrossRef]
- Zhao, Y.; Yao, J.; Wang, M. On-line monitoring of the crystallization process: Relationship between crystal size and electrical impedance spectra. Meas. Sci. Technol. 2016, 27, 074007. [Google Scholar] [CrossRef]
- Chakraborty, S.; Das, C.; Bera, N.K.; Chattopadhyay, S.; Karmakar, A.; Chattopadhyay, S. Analytical modelling of electrical impedance based adulterant sensor for aqueous sucrose solutions. J. Electroanal. Chem. 2017, 784, 133–139. [Google Scholar] [CrossRef]
- Eder, C.; Briesen, H. Impedance spectroscopy as a process analytical technology (PAT) tool for online monitoring of sucrose crystallization. Food Control. 2019, 101, 251–260. [Google Scholar] [CrossRef]
- Villanueva, D.; Posada, R.; Gonzalez, I.; García, Á.; Martinez-Sibaja, A. Monitoring of a Sugar Crystallization Process with Fuzzy Logic and Digital Image Processing. J. Food Process Eng. 2014, 38, 19–30. [Google Scholar] [CrossRef]
- Subbiah, B.; Morison, K.R. Electrical conductivity of viscous liquid foods. J. Food Eng. 2018, 237, 177–182. [Google Scholar] [CrossRef]
- Rao, G.; Sattar, M.A.; Wajman, R.; Jackowska-Strumillo, L. Application of the 2D-ERT to evaluate phantom circumscribed regions in various sucrose solution concentrations. In Proceedings of the 2019 International Interdisciplinary PhD Workshop (IIPhDW), Wismar, Germany, 15–17 May 2019; pp. 34–38. [Google Scholar]
- Yang, Z.J.; Yan, G. Detection of Impact Damage for Composite Structure by Electrical Impedance Tomography. In ACMSM25; Springer: Berlin/Heidelberg, Germany, 2019; pp. 519–527. [Google Scholar]
- Clausi, M.; Toto, E.; Botti, S.; Laurenzi, S.; La Saponara, V.; Santonicola, M.G. Direct effects of UV irradiation on graphene-based nanocomposite films revealed by electrical resistance tomography. Compos. Sci. Technol. 2019, 183, 107823. [Google Scholar] [CrossRef]
- Ghaednia, H.; Owens, C.; Roberts, R.; Tallman, T.N.; Hart, A.J.; Varadarajan, K.M. Interfacial load monitoring and failure detection in total joint replacements via piezoresistive bone cement and electrical impedance tomography. Smart Mater. Struct. 2020. [Google Scholar] [CrossRef]
- Salazar, A.J.; Bravo, R.J.; Murrugara, C.; Osberth, O.C.; Farkas, E.; Gravis, K.; Gavidia, L. Proposal for a real-time multi-frequency impedance tomography system. In Proceedings of the 3rd European Medical and Biological Engineering Conference, Prague, Czech Republic, 20–25 November 2005; Volume 11, pp. 1727–1983. [Google Scholar]
- Yang, Y.; Jia, J. A multi-frequency electrical impedance tomography system for real-time 2D and 3D imaging. Rev. Sci. Instrum. 2017, 88, 85110. [Google Scholar] [CrossRef]
- Hampel, U.; Wondrak, T.; Bieberle, M.; Lecrivain, G.; Schubert, M.; Eckert, K.; Reinecke, S.F. Smart Tomographic Sensors for Advanced Industrial Process Control TOMOCON. Chem. Ing. Tech. 2018, 90, 1238–1239. [Google Scholar] [CrossRef]
- Schiefelbein, S.L.; Fried, N.A.; Rhoads, K.G.; Sadoway, D.R. A high-accuracy, calibration-free technique for measuring the electrical conductivity of liquids. Rev. Sci. Instrum. 1998, 69, 3308–3313. [Google Scholar] [CrossRef]
- Barsukov, E.; Macdonald Ross, J. Impedance Spectroscopy. In Theory, Experiment and Applications; Wiley-Interscience: New York, NY, USA, 2005. [Google Scholar]
- Orazem, M.E.; Tribollet, B. Electrochemical Impedance Spectroscopy; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Nahvi, M.; Hoyle, B.S. Electrical Impedance Spectroscopy Sensing for Industrial Processes. IEEE Sens. J. 2009, 9, 1808–1816. [Google Scholar] [CrossRef]
- Ramos, P.M. How signal processing is changing impedance spectroscopy. In Proceedings of the 2018 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Houston, TX, USA, 14–17 May 2017; IEEE: New York, NY, USA, 2018; pp. 1–6. [Google Scholar]
- Wu, J.; Stark, J.P.W. A high accuracy technique to measure the electrical conductivity of liquids using small test samples. J. Appl. Phys. 2007, 101, 054520. [Google Scholar] [CrossRef]
- Becchi, M.; Avendaño, C.; Strigazzi, A.; Barbero, G. Impedance Spectroscopy of Water Solutions: The Role of Ions at the Liquid−Electrode Interface. J. Phys. Chem. B 2005, 109, 23444–23449. [Google Scholar] [CrossRef]
- Longo, J.P.N.; Galvão, J.R.; da Silva, J.C.C.; Martelli, C.; Morales, R.E.M.; da Silva, M.J. Dual sensor for simultaneous measurement of electrical impedance and temperature during ice formation process. In Proceedings of the 2nd International Symposium on Instrumentation Systems, Circuits and Transducers (INSCIT), Ceara, Brazil, 28 August–1 September 2017; IEEE: New York, NY, USA, 2017; pp. 1–4. [Google Scholar]
- Juansah, J.; Yulianti, W. Studies on Electrical behavior of Glucose using Impedance Spectroscopy. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2016; Volume 31, p. 012039. [Google Scholar]
- Rane, M.V.; Uphade, D.B. Energy Efficient Jaggery Making Using Freeze Pre-concentration of Sugarcane Juice. Energy Procedia 2016, 90, 370–381. [Google Scholar] [CrossRef]
- Liu, Q.; Han, Y.; Zhang, X. An image reconstruction algorithm based on Bayesian theorem for electrical resistance tomography. Optik 2014, 125, 6090–6097. [Google Scholar] [CrossRef]
- Rymarczyk, T.; Tchórzewski, P.; Sikora, J. Coupling boundary element method with level set method to solve inverse problem. Inform. Autom. Pomiary Gospod. Ochr. Środowiska 2017, 7, 80–83. [Google Scholar] [CrossRef]
- Kim, B.S.; Khambampati, A.K.; Jang, Y.J.; Kim, K.-Y.; Kim, S. Image reconstruction using voltage–current system in electrical impedance tomography. Nucl. Eng. Des. 2014, 278, 134–140. [Google Scholar] [CrossRef]
- Vaukonen, M. Electrical Impedance Tomography and Prior Information. Ph.D. Thesis, University of Kuopio, Kuopio, Finland, 1997. [Google Scholar]
- Cui, Z.; Wang, Q.; Xue, Q.; Fan, W.; Zhang, L.; Cao, Z.; Sun, B.; Wang, H.; Yang, W. A review on image reconstruction algorithms for electrical capacitance/resistance tomography. Sens. Rev. 2016, 36, 429–445. [Google Scholar] [CrossRef]
- Lionheart, W.R.B. EIT reconstruction algorithms: Pitfalls, challenges and recent developments. Physiol. Meas. 2004, 25, 125–142. [Google Scholar] [CrossRef]
- Adler, A.; Lionheart, W.R.B. Uses and abuses of EIDORS: An extensible software base for EIT. Physiol. Meas. 2006, 27, S25–S42. [Google Scholar] [CrossRef]
- Persson, P.-O.; Strang, G. A Simple Mesh Generator in MATLAB. SIAM Rev. 2004, 46, 329–345. [Google Scholar] [CrossRef]
- Marć, M.; Bystrzanowska, M.; Tobiszewski, M. Exploratory analysis and ranking of analytical procedures for short-chain chlorinated paraffins determination in environmental solid samples. Sci. Total. Environ. 2020, 711, 134665. [Google Scholar] [CrossRef]
- Olarte, O.; Barbé, K.; Van Moer, W.; Van Ingelgem, Y.; Hubin, A. Measurement and characterization of glucose in NaCl aqueous solutions by electrochemical impedance spectroscopy. Biomed. Signal Process. Control. 2014, 14, 9–18. [Google Scholar] [CrossRef]
- Sardeshpande, M.V.; Gupta, S.; Ranade, V.V. Electrical resistance tomography for gas holdup in a gas-liquid stirred tank reactor. Chem. Eng. Sci. 2017, 170, 476–490. [Google Scholar] [CrossRef]

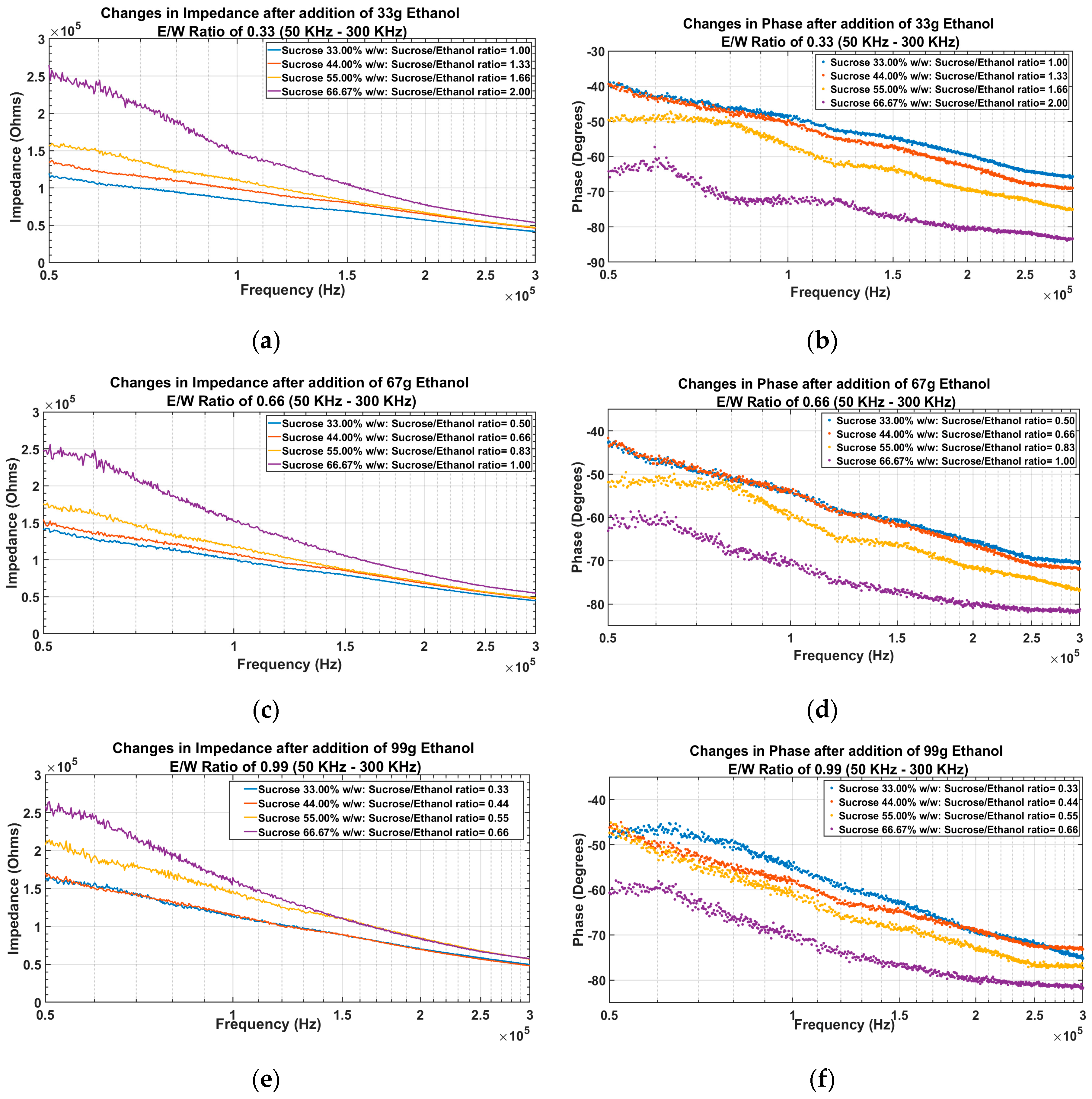
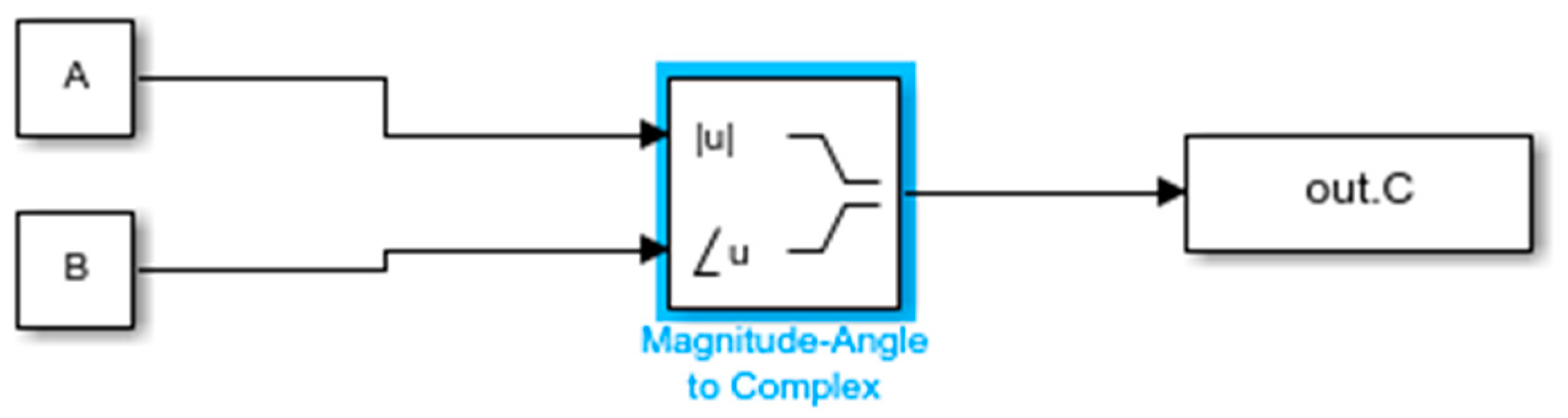


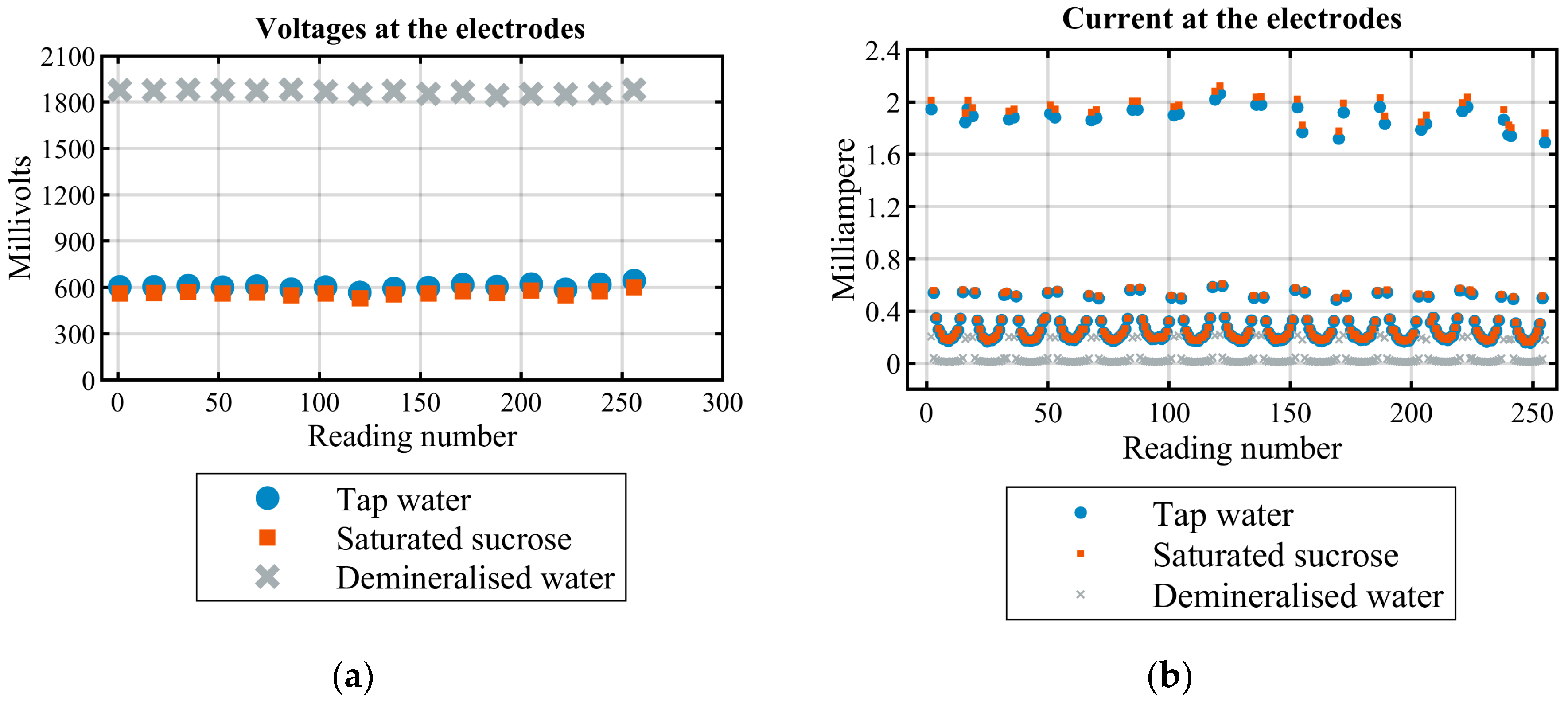
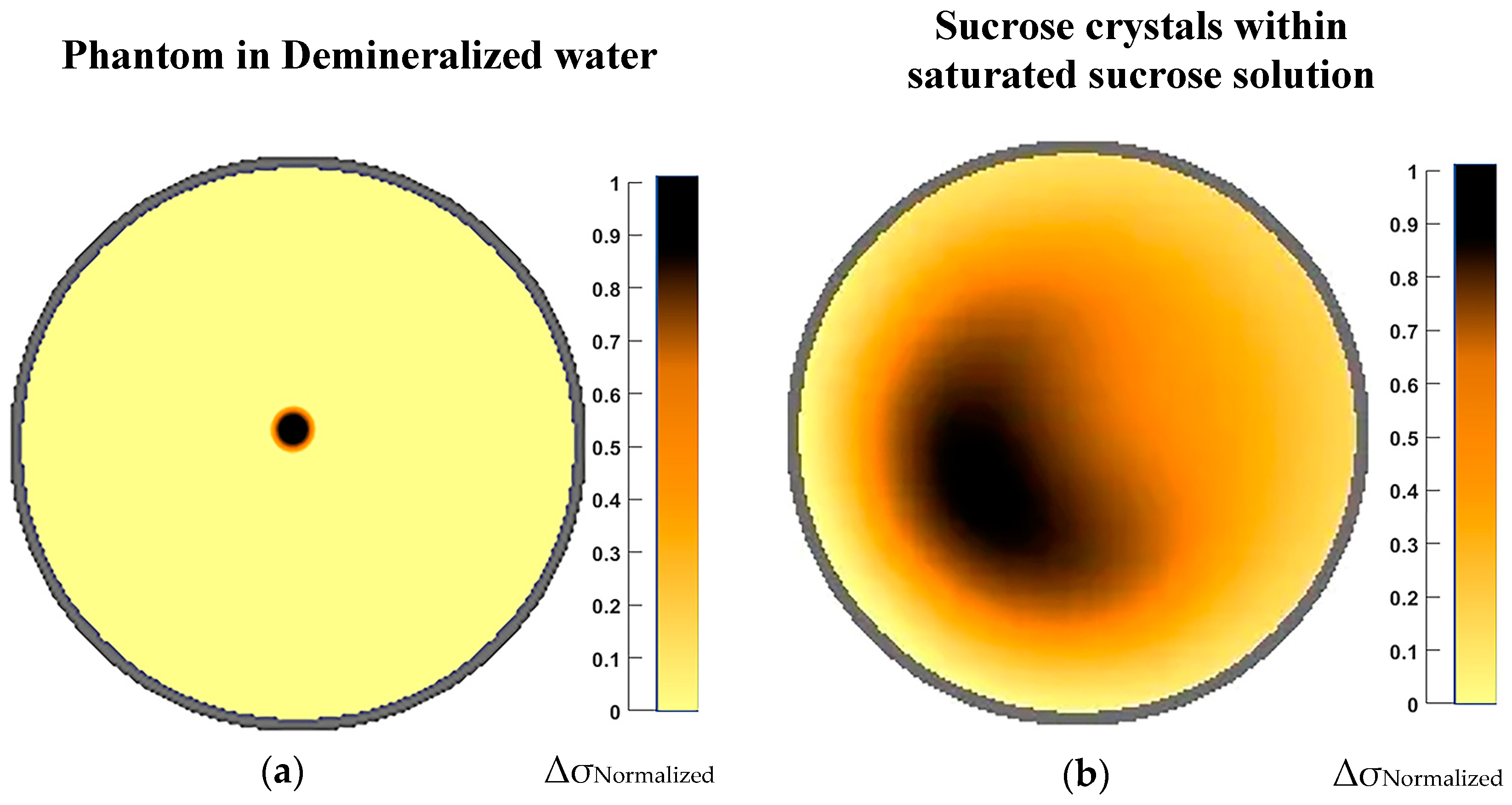
| Solution Index | Effective Ethanol to Water Ratio | Different Concentrations of Sucrose Solutions (% w/w) | Sucrose Weight Percentage in 100 mL | Effective Sucrose/Ethanol Ratio in 100 mL Solution |
|---|---|---|---|---|
| 1 | 0 | 33 | 33 | - |
| 2 | 44 | 44 | - | |
| 3 | 55 | 55 | - | |
| 4 | 66.67 | 66.67 | - | |
| 5 | 0.33 | 33 | 19.87 | 1 |
| 6 | 4 | 24.85 | 1.33 | |
| 7 | 55 | 29.25 | 1.66 | |
| 8 | 66.67 | 33.16 | 2 | |
| 9 | 0.66 | 33 | 16.58 | 0.5 |
| 10 | 44 | 20.95 | 0.66 | |
| 11 | 55 | 24.88 | 0.83 | |
| 12 | 66.67 | 28.44 | 1 | |
| 13 | 0.99 | 33 | 14.22 | 0.33 |
| 14 | 44 | 18.10 | 0.44 | |
| 15 | 55 | 21.65 | 0.55 | |
| 16 | 66.67 | 24.90 | 0.66 |
| Model | Number of Poles | Number of Zeroes | Order of the Model |
|---|---|---|---|
| Model 1 | 1 | 0 | First-order |
| Model 2 | 2 | 0 | Second-order |
| Model 3 | 2 | 1 | Second-order with a zero |
| Solution Index | Effective Ethanol to Water Ratio | Different Concentrations of Sucrose Solutions (% w/w) | Effective Sucrose/Ethanol Ratio in 100 mL Solution | Tfest Fit % | ||
|---|---|---|---|---|---|---|
| Model 1 | Model 2 | Model 3 | ||||
| 1 | 0 | 33 | - | 55.2 | 67.8 | 96.43 |
| 2 | 44 | - | 55.56 | 68.48 | 95.84 | |
| 3 | 55 | - | 62.31 | 76.26 | 93.42 | |
| 4 | 66.67 | - | 88.98 | 80.12 | 91.75 | |
| 5 | 0.33 | 33 | 1 | 64.87 | 63.73 | 95.12 |
| 6 | 44 | 1.33 | 71.26 | 72.85 | 94.95 | |
| 7 | 55 | 1.66 | 78.31 | 76.86 | 92.33 | |
| 8 | 66.67 | 2 | 89.94 | 80.51 | 90.9 | |
| 9 | 0.66 | 33 | 0.5 | 74.3 | 65.82 | 94.74 |
| 10 | 44 | 0.66 | 75.82 | 79.5 | 94.88 | |
| 11 | 55 | 0.83 | 80.38 | 81.39 | 92.03 | |
| 12 | 66.67 | 1 | 91.5 | 83.07 | 92.92 | |
| 13 | 0.99 | 33 | 0.33 | 79.22 | 89.45 | 93.29 |
| 14 | 44 | 0.44 | 79.1 | 90.27 | 94.13 | |
| 15 | 55 | 0.55 | 83 | 91.61 | 92.07 | |
| 16 | 66.67 | 0.66 | 92.11 | 92.2 | 93.74 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rao, G.; Aghajanian, S.; Koiranen, T.; Wajman, R.; Jackowska-Strumiłło, L. Process Monitoring of Antisolvent Based Crystallization in Low Conductivity Solutions Using Electrical Impedance Spectroscopy and 2-D Electrical Resistance Tomography. Appl. Sci. 2020, 10, 3903. https://doi.org/10.3390/app10113903
Rao G, Aghajanian S, Koiranen T, Wajman R, Jackowska-Strumiłło L. Process Monitoring of Antisolvent Based Crystallization in Low Conductivity Solutions Using Electrical Impedance Spectroscopy and 2-D Electrical Resistance Tomography. Applied Sciences. 2020; 10(11):3903. https://doi.org/10.3390/app10113903
Chicago/Turabian StyleRao, Guruprasad, Soheil Aghajanian, Tuomas Koiranen, Radosław Wajman, and Lidia Jackowska-Strumiłło. 2020. "Process Monitoring of Antisolvent Based Crystallization in Low Conductivity Solutions Using Electrical Impedance Spectroscopy and 2-D Electrical Resistance Tomography" Applied Sciences 10, no. 11: 3903. https://doi.org/10.3390/app10113903
APA StyleRao, G., Aghajanian, S., Koiranen, T., Wajman, R., & Jackowska-Strumiłło, L. (2020). Process Monitoring of Antisolvent Based Crystallization in Low Conductivity Solutions Using Electrical Impedance Spectroscopy and 2-D Electrical Resistance Tomography. Applied Sciences, 10(11), 3903. https://doi.org/10.3390/app10113903








