Numerical and Experimental Study of Turbulent Mixing Characteristics in a T-Junction System
Abstract
1. Introduction
2. CFD Simulation Methodology
2.1. Mathematical Model
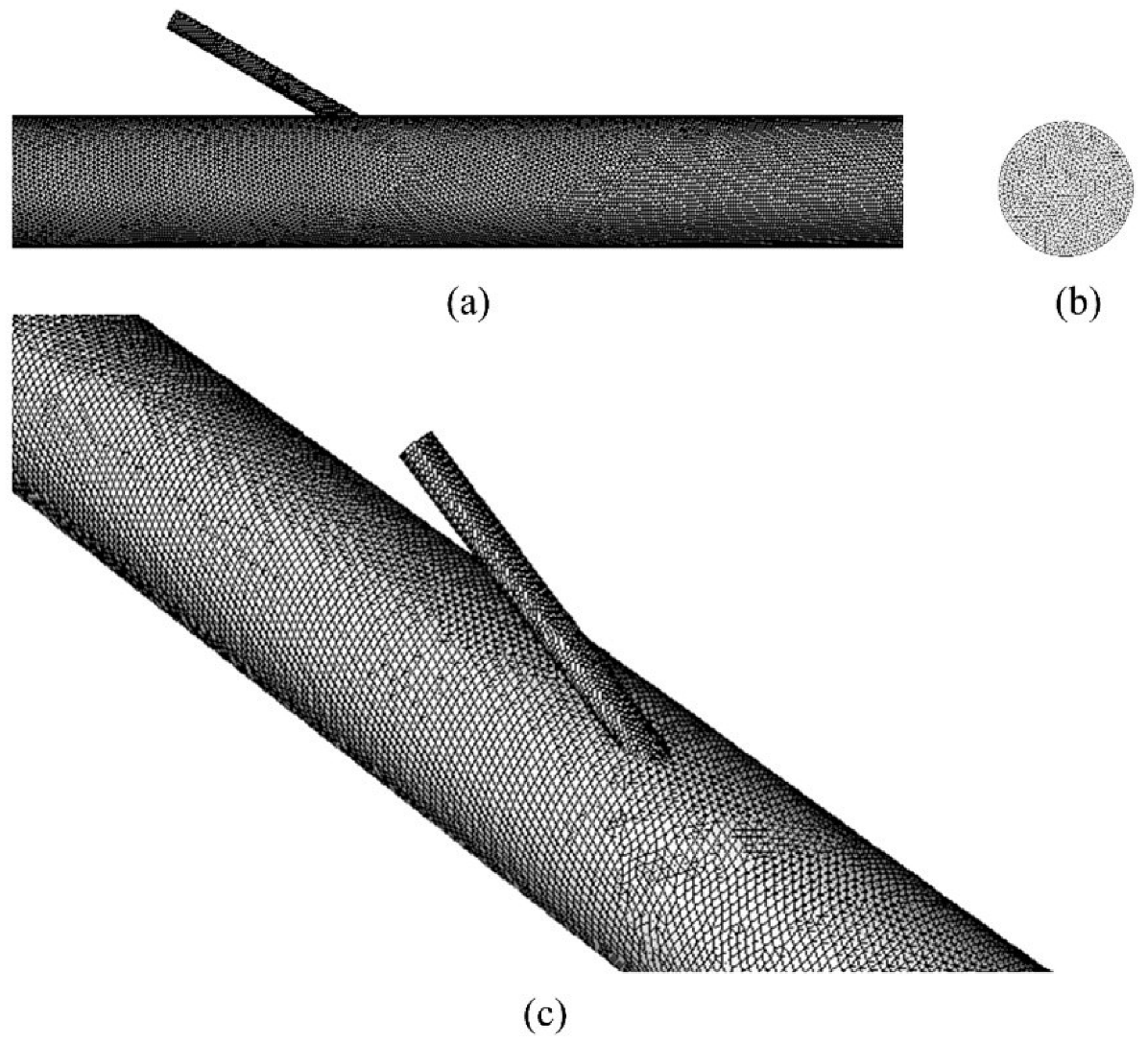
2.2. Computational Grid
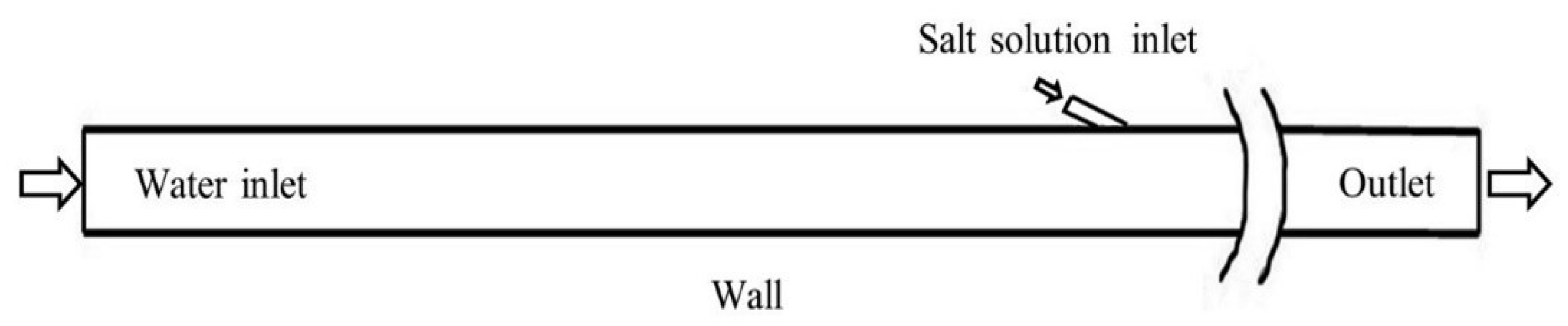
2.3. Boundary Conditions and CFD Procedures
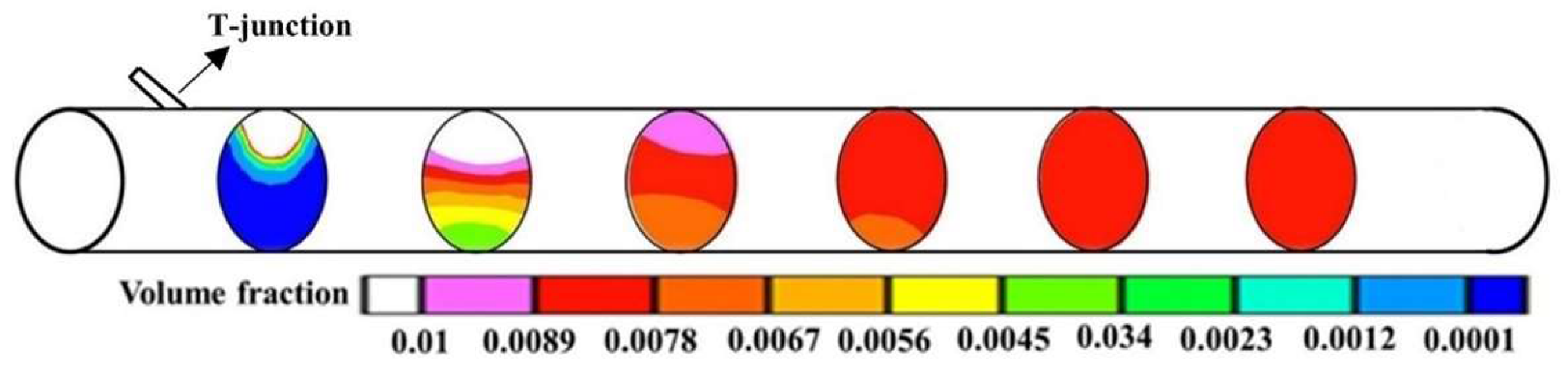
3. Experiment and Model Validation
3.1. Experimental Details
3.2. Model Validation
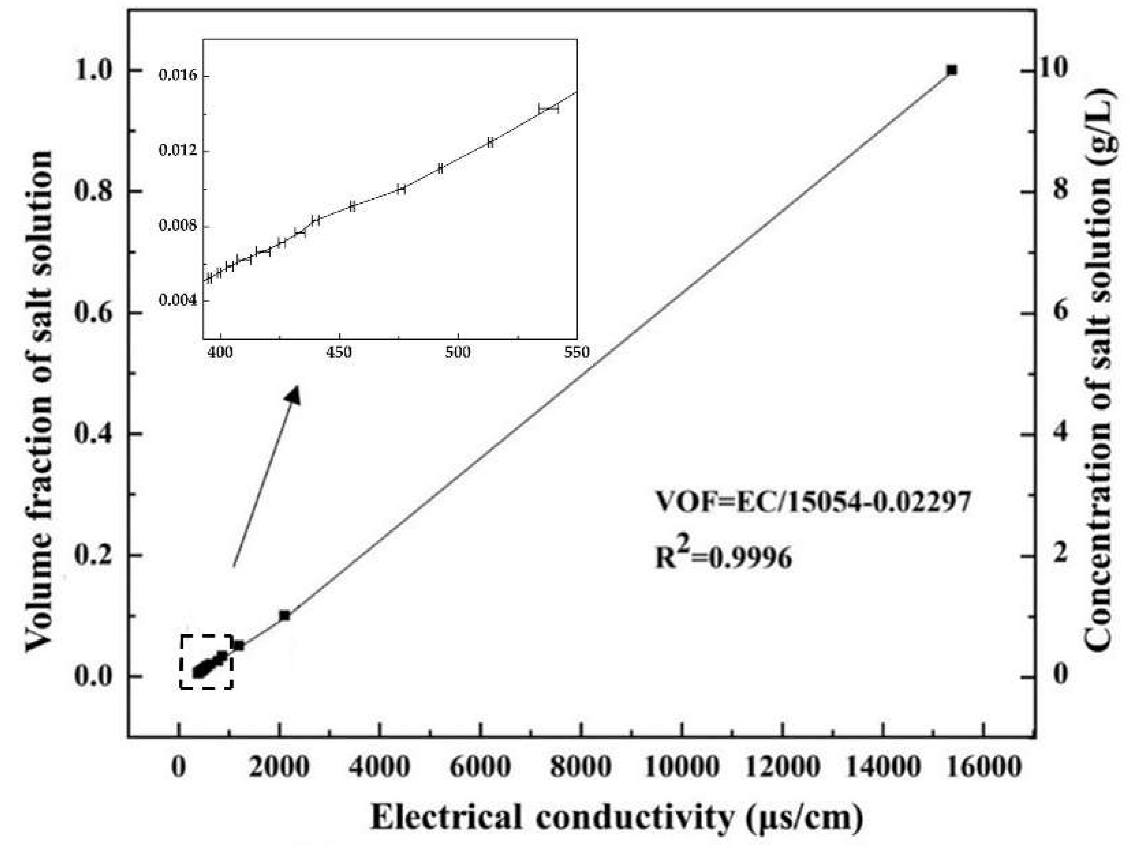
3.2.1. The Relationship between the Volume Fraction and Electrical Conductivity
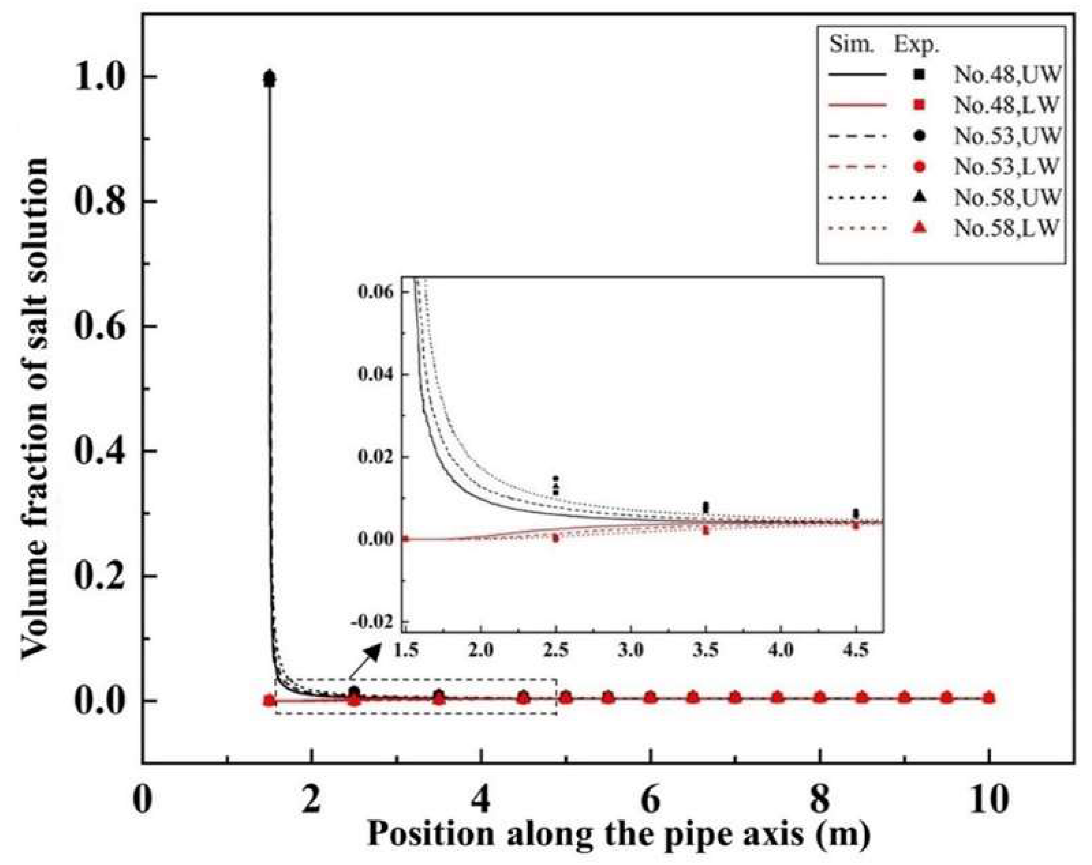
3.2.2. Comparison between Experimental Data and Simulation Results
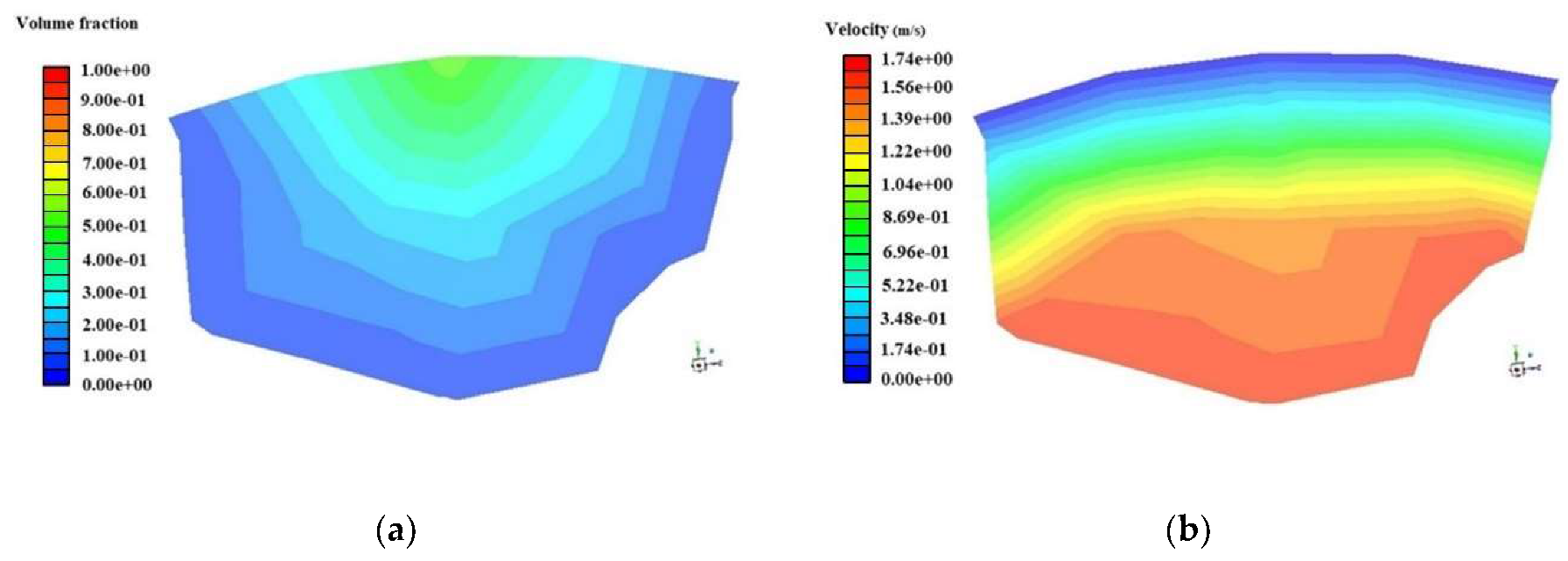
4. Results and Discussion
4.1. Influence Factors in the Mixing Process
4.1.1. The Effect of Pipe Diameter on Mixing Effect
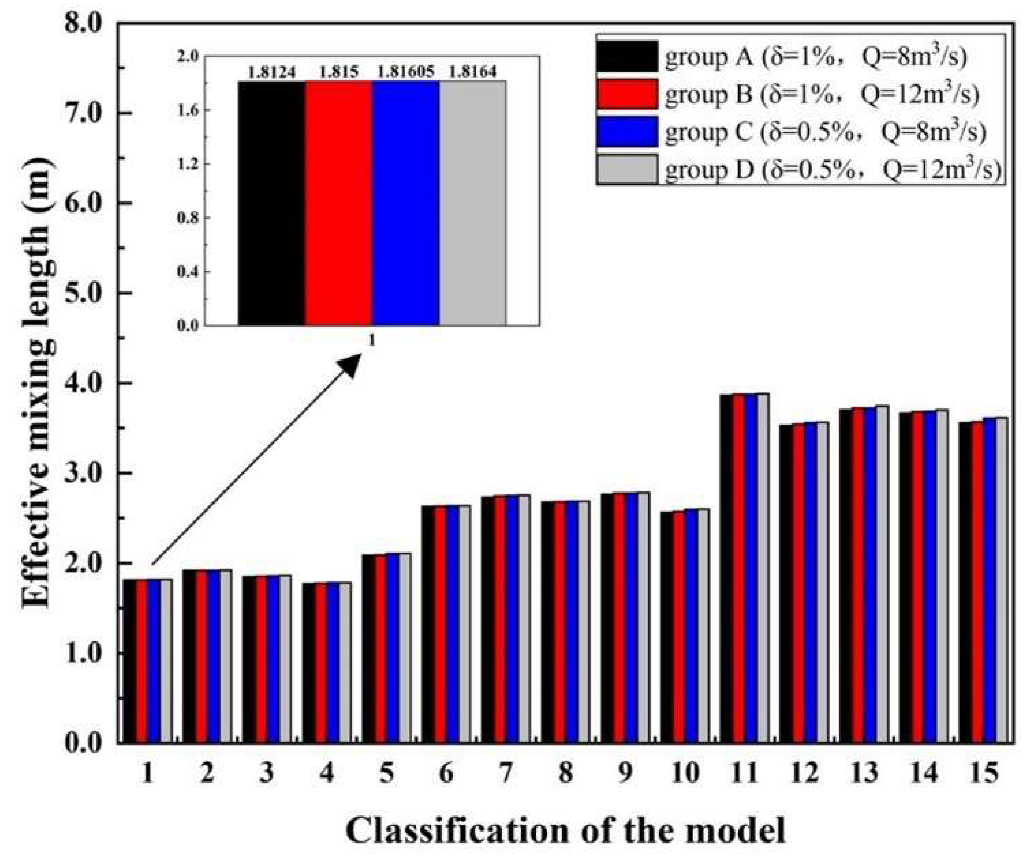
4.1.2. The Effects of Cross-Flow Flux and Mixing Ratio on Mixing Effect
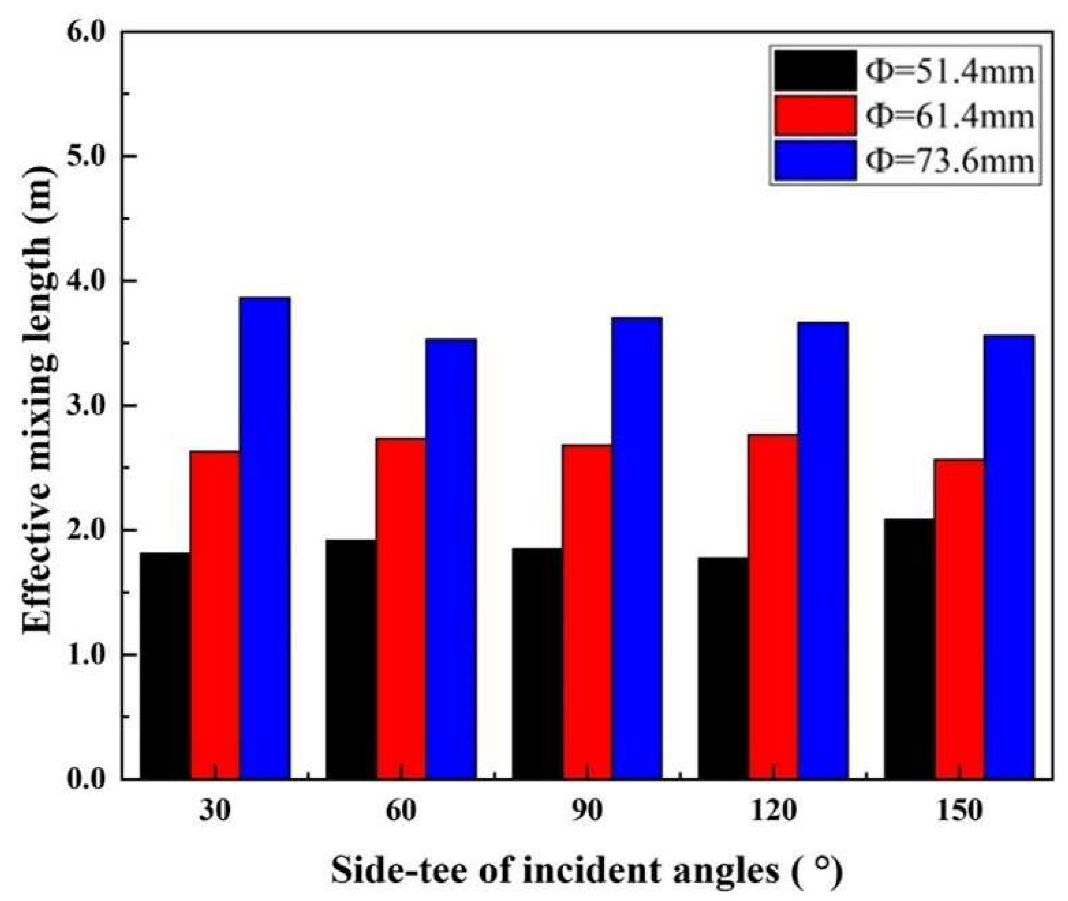
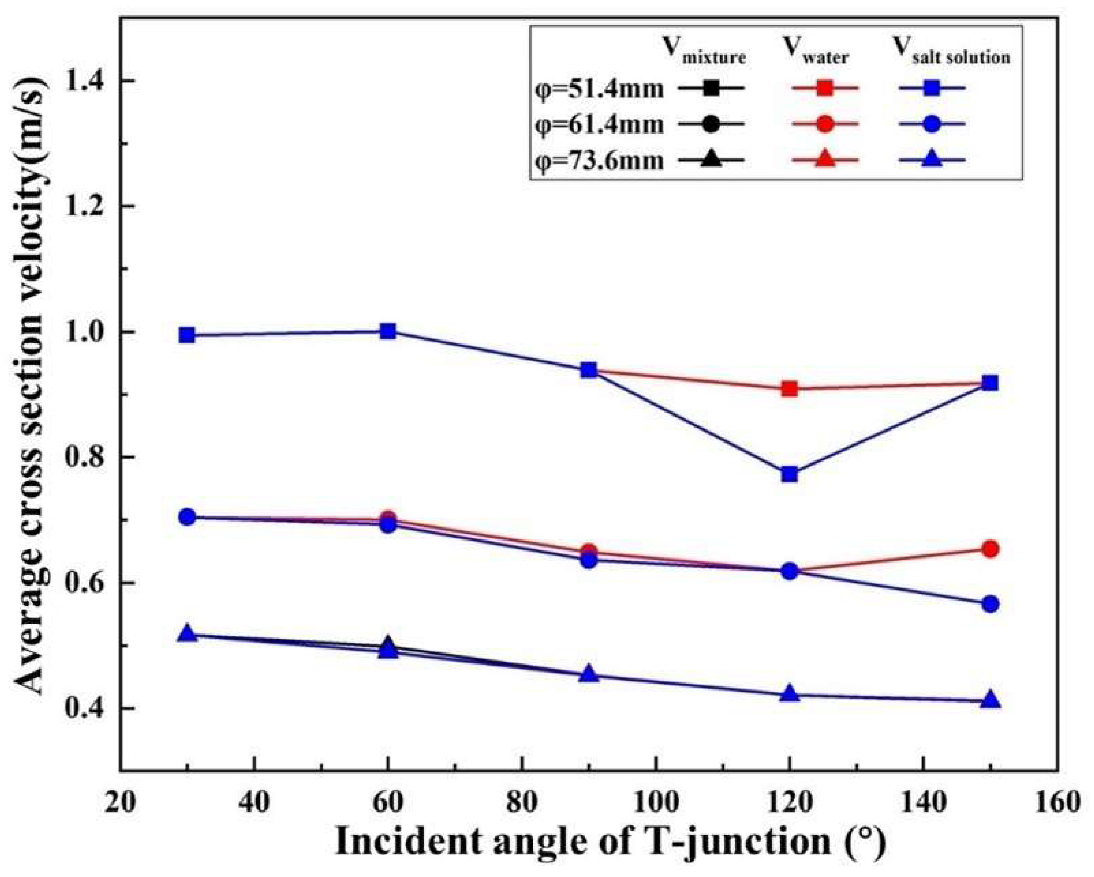
4.1.3. The Effect of Incident Angle of T-Junction on Mixing Effect
4.2. Dimensional Analysis of Effective Mixing Length
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jiang, G.M.; Keller, J.; Bond, P.L. Determining the long-term effects of H2S concentration, relative humidity and air temperature on concrete sewer corrosion. Water Res. 2014, 65, 157–169. [Google Scholar] [CrossRef] [PubMed]
- Stanev, V.G.; Iliev, F.L.; Hansen, S.; Vesselinov, V.V.; Alexandrov, B.S. Identification of release sources in advection-diffusion system by machine learning combined with Green’s function inverse method. Appl. Math. Model. 2018, 60, 64–76. [Google Scholar] [CrossRef]
- Hartmann, J.; van der Aa, M.; Wuijts, S.; Husman, A.M.D.; van der Hoek, J.P. Risk governance of potential emerging risks to drinking water quality: Analysing current practices. Environ. Sci. Policy 2018, 84, 97–104. [Google Scholar] [CrossRef]
- Wang, M.J.; Fang, D.; Xiang, Y.; Fei, Y.; Wang, Y.; Ren, W.Y.; Tian, W.X.; Su, G.H.; Qiu, S.Z. Study on the coolant mixing phenomenon in a 45 degrees T junction based on the thermal-mechanical coupling method. Appl. Therm. Eng. 2018, 144, 600–613. [Google Scholar] [CrossRef]
- Galeazzo, F.C.C.; Donnert, G.; Cardenas, C.; Sedlmaier, J.; Habisreuther, P.; Zarzalis, N.; Beck, C.; Krebs, W. Computational modeling of turbulent mixing in a jet in crossflow. Int. J. Heat Fluid Flow 2013, 41, 55–65. [Google Scholar] [CrossRef]
- Uyanwaththa, A.; Malalasekera, W.; Hargrave, G.; Dubal, M. Large Eddy Simulation of Scalar Mixing in Jet in a Cross-Flow. J. Eng. Gas Turbines Power Trans. ASME 2019, 141, 13. [Google Scholar] [CrossRef]
- Frank, T.; Lifante, C.; Prasser, H.M.; Menter, F. Simulation of turbulent and thermal mixing in T-junctions using URANS and scale-resolving turbulence models in ANSYS CFX. Nucl. Eng. Des. 2010, 240, 2313–2328. [Google Scholar] [CrossRef]
- Jayaraju, S.T.; Komen, E.M.J.; Baglietto, E. Suitability of wall-functions in Large Eddy Simulation for thermal fatigue in a T-junction. Nucl. Eng. Des. 2010, 240, 2544–2554. [Google Scholar] [CrossRef]
- Tong-Miin, L.; Chin-Chun, L.; Shih-Hui, C.; Hsin-Ming, L. Study on side-jet injection near a duct entry with various injection angles. Trans. ASME J. Fluids Eng. 1999, 121, 580–587. [Google Scholar]
- Zughbi, H.D.; Khokhar, Z.H.; Sharma, R.N. Mixing in pipelines with side and opposed tees. Ind. Eng. Chem. Res. 2003, 42, 5333–5344. [Google Scholar] [CrossRef]
- Zughbi, H.D. Effects of jet protrusion on mixing in pipelines with side-tees. Chem. Eng. Res. Des. 2006, 84, 993–1000. [Google Scholar] [CrossRef]
- Lin, C.H.; Chen, M.S.; Ferng, Y.M. Investigating thermal mixing and reverse flow characteristics in a T-junction by way of experiments. Appl. Therm. Eng. 2016, 99, 1171–1182. [Google Scholar] [CrossRef]
- Chen, M.S.; Hsieh, H.E.; Ferng, Y.M.; Pei, B.S. Experimental observations of thermal mixing characteristics in T-junction piping. Nucl. Eng. Des. 2014, 276, 107–114. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Yuki, K.; Hashizume, H. Classification of turbulent jets in a T-junction area with a 90-deg bend upstream. Int. J. Heat Mass Transf. 2008, 51, 2444–2454. [Google Scholar] [CrossRef]
- Hekmat, M.H.; Saharkhiz, S.; Izadpanah, E. Investigation on the thermal mixing enhancement in a T-junction pipe. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 11. [Google Scholar] [CrossRef]
- Wang, S.J.; Mujumdar, A.S. Flow and mixing characteristics of multiple and multi-set opposing jets. Chem. Eng. Process. Process Intensif. 2007, 46, 703–712. [Google Scholar] [CrossRef]
- Ayhan, H.; Sokmen, C.N. CFD modeling of thermal mixing in a T-junction geometry using LES model. Nucl. Eng. Des. 2012, 253, 183–191. [Google Scholar] [CrossRef]
- Rahmani, R.K.; Keith, T.G.; Ayasoufi, A. Numerical simulation and mixing study of pseudoplastic fluids in an industrial helical static mixer. J. Fluids Eng. Trans. ASME 2006, 128, 467–480. [Google Scholar] [CrossRef]
- Anselmet, F.; Ternat, F.; Amielh, M.; Boiron, O.; Boyer, P.; Pietri, L. Axial development of the mean flow in the entrance region of turbulent pipe and duct flows. Comptes Rendus Mécanique 2009, 337, 573–584. [Google Scholar] [CrossRef]
- Vijiapurapu, S.; Cui, J. Performance of turbulence models for flows through rough pipes. Appl. Math. Model. 2010, 34, 1458–1466. [Google Scholar] [CrossRef]
- Rahmani, R.K.; Keith, T.G.; Ayasoufi, A. Three-dimensional numerical simulation and performance study of an industrial helical static mixer. J. Fluids Eng.Trans. ASME 2005, 127, 467–483. [Google Scholar] [CrossRef][Green Version]
- Kamide, H.; Igarashi, M.; Kawashima, S.; Kimura, N.; Hayashi, K. Study on mixing behavior in a tee piping and numerical analyses for evaluation of thermal striping. Nucl. Eng. Des. 2009, 239, 58–67. [Google Scholar] [CrossRef]
- Vondricka, J.; Lammers, P.S. Optimization of direct nozzle injection system’s response time. In Proceedings of the Conference on Agricultural Engineering, Dusseldorf, Germany, 9–10 November 2007; pp. 507–512. [Google Scholar]
- Sonin, A.A. A generalization of the II-theorem and dimensional analysis. Proc. Natl. Acad. Sci. USA 2004, 101, 8525–8526. [Google Scholar] [CrossRef] [PubMed]


| No. | δ | Q (m3/h) | φ (mm) | θ (°) | No. | δ | Q (m3/h) | φ (mm) | θ (°) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 30 | 31 | 30 | ||||||
| 2 | 60 | 32 | 60 | ||||||
| 3 | 51.4 | 90 | 33 | 51.4 | 90 | ||||
| 4 | 120 | 34 | 120 | ||||||
| 5 | 150 | 35 | 150 | ||||||
| 6 | 30 | 36 | 30 | ||||||
| 7 | 60 | 37 | 60 | ||||||
| 8 | 8 | 61.4 | 90 | 38 | 8 | 61.4 | 90 | ||
| 9 | 120 | 39 | 120 | ||||||
| 10 | 150 | 40 | 150 | ||||||
| 11 | 30 | 41 | 30 | ||||||
| 12 | 60 | 42 | 60 | ||||||
| 13 | 73.6 | 90 | 43 | 73.6 | 90 | ||||
| 14 | 120 | 44 | 120 | ||||||
| 15 | 1% | 150 | 45 | 0.5% | 150 | ||||
| 16 | 30 | 46 | 30 | ||||||
| 17 | 60 | 47 | 60 | ||||||
| 18 | 51.4 | 90 | 48 | 51.4 | 90 | ||||
| 19 | 120 | 49 | 120 | ||||||
| 20 | 150 | 50 | 150 | ||||||
| 21 | 30 | 51 | 30 | ||||||
| 22 | 60 | 52 | 60 | ||||||
| 23 | 12 | 61.4 | 90 | 53 | 12 | 61.4 | 90 | ||
| 24 | 120 | 54 | 120 | ||||||
| 25 | 150 | 55 | 150 | ||||||
| 26 | 30 | 56 | 30 | ||||||
| 27 | 60 | 57 | 60 | ||||||
| 28 | 73.6 | 90 | 58 | 73.6 | 90 | ||||
| 29 | 120 | 59 | 120 | ||||||
| 30 | 150 | 60 | 150 |
| No | Re | No | Re | No. | Re |
|---|---|---|---|---|---|
| 1 | 616,940 | 6 | 516,461 | 11 | 430,852 |
| 16 | 925,409 | 21 | 774,691 | 26 | 646,278 |
| Diameter (mm) | Incident Angle | LEML of Group A (m) | LEML of Group B (m) | LEML of Group C (m) | LEML of Group D (m) |
|---|---|---|---|---|---|
| 30° | 1.8124 | 1.8150 | 1.8161 | 1.8164 | |
| 60° | 1.9167 | 1.9168 | 1.9172 | 1.9220 | |
| 51.4 | 90° | 1.8496 | 1.8520 | 1.8599 | 1.8610 |
| 120° | 1.7747 | 1.7753 | 1.7796 | 1.7800 | |
| 150° | 2.0830 | 2.0879 | 2.1070 | 2.1090 | |
| 30° | 2.6286 | 2.6345 | 2.6347 | 2.6353 | |
| 60° | 2.7339 | 2.7450 | 2.7520 | 2.7549 | |
| 61.4 | 90° | 2.6790 | 2.6830 | 2.6850 | 2.6882 |
| 120° | 2.7638 | 2.7754 | 2.7769 | 2.7804 | |
| 150° | 2.5650 | 2.5752 | 2.5970 | 2.5990 | |
| 30° | 3.8650 | 3.8710 | 3.8740 | 3.8790 | |
| 60° | 3.5270 | 3.5402 | 3.5600 | 3.5632 | |
| 73.6 | 90° | 3.7007 | 3.7208 | 3.7240 | 3.7439 |
| 120° | 3.6640 | 3.6808 | 3.6868 | 3.7010 | |
| 150° | 3.5600 | 3.5680 | 3.6092 | 3.6120 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, B.; Liu, Q.; Fang, H.; Zhang, C.; Lu, Y.; Zhu, S. Numerical and Experimental Study of Turbulent Mixing Characteristics in a T-Junction System. Appl. Sci. 2020, 10, 3899. https://doi.org/10.3390/app10113899
Sun B, Liu Q, Fang H, Zhang C, Lu Y, Zhu S. Numerical and Experimental Study of Turbulent Mixing Characteristics in a T-Junction System. Applied Sciences. 2020; 10(11):3899. https://doi.org/10.3390/app10113899
Chicago/Turabian StyleSun, Bin, Quan Liu, Hongyuan Fang, Chao Zhang, Yuanbo Lu, and Shun Zhu. 2020. "Numerical and Experimental Study of Turbulent Mixing Characteristics in a T-Junction System" Applied Sciences 10, no. 11: 3899. https://doi.org/10.3390/app10113899
APA StyleSun, B., Liu, Q., Fang, H., Zhang, C., Lu, Y., & Zhu, S. (2020). Numerical and Experimental Study of Turbulent Mixing Characteristics in a T-Junction System. Applied Sciences, 10(11), 3899. https://doi.org/10.3390/app10113899





