Computation of Stray Losses in Transformer Bushing Regions Considering Harmonics in the Load Current

Abstract

The presence of harmonics in the load current considerably increases stray losses in electric transformers. In this research paper, a new model for computing the electromagnetic field (EMF) and eddy current (EC) losses in transformer tank covers is derived considering harmonics. Maxwell’s equations are solved with their corresponding boundary conditions. The differential equation thus obtained is solved using the method of separation of variables. The obtained expressions do not require the use of special functions, accommodating them for practical implementation in the industry. The obtained formulas are evaluated for different spectrum contents of the load current and losses. The results are in good agreement with simulations carried out using the Altair Flux finite element (FE) software.

1. Introduction

The growing energy demand and environmental problems have led to the integration of renewable energy technologies to the power grid [1]. These technologies are integrated into the power system via inverters, requiring the HVDC system for long-distance transmission [2,3]. Their development over the past few decades, and nonlinear loads such as inverters, arc furnaces, personal computers, AC and DC drives, etc. have brought about a significant increase in harmonics [4,5,6]. Nonlinear loads are notorious for generating harmonics and require transformers to connect them safely to the network. Transformers are usually designed under the assumptions of sinusoidal conditions [7,8]. It is known [7] that the harmonic content in the load current increases losses in the transformer and eventually the temperature, resulting in its premature damage.

Bushings are perhaps the weakest parts of transformers, electrically and physically, and their failure is one of the major causes of transformer malfunctions [9]. The contribution of bushings and tank walls to transformer failures are about 20% and 21%, respectively, which is a significant percentage among all the damages caused by other parts of the transformer [10]. Therefore, with the increasing trend of nonlinear loads in the distribution network, the transformer is even more prone to fail. Consequently, to reduce power losses and heating in bushing regions, low permeability materials [11], and magnetic shunts [12] have been proposed in the literature [7].

At the industry design stage, it is very important to compute transformers stray losses caused by the alternating electromagnetic field (EMF). This way, the derivation of new formulas is desirable and is sought to improve calculation and estimation methods. Several studies have been carried out recently with these objectives in mind [13,14,15,16,17,18,19,20]. Thus, analytical approaches have proven to be useful in calculating electromagnetic losses [13]. Generally speaking, there are two analytical methods to estimate eddy current (EC) losses in transformer tanks: (i) Application of Poynting’s theorem [15] and (ii) direct calculation of the EMF by solving Maxwell’s equations [13,20]. In the first method (see Turowski’s analytical method [15]), Poynting’s theorem is used to estimate the power dissipation. However, the power dissipation formula contains semi-empirical parameters selected by nonrigorous methods. The precision of the second method is limited only by the difficulty of reproducing real geometries. In [19], the axial component of the electric field (EF) in the tank wall was ignored while solving Maxwell’s equations, which negatively impacted the accuracy of the obtained results [20].

In [20], analytical formulas for calculating EMF and EC losses in transformer tank walls were obtained by solving Maxwell’s equations in the case of the axial geometry of the tank wall. The results demonstrated a good accuracy compared with the previous methods. However, a load current with only the fundamental frequency was considered. Moreover, the obtained formulae involve Bessel functions, which might not be easily implemented in an industrial setting. None of the previously published works [13,14,15,16,17,18,19,20] consider harmonics in the load current while deriving analytical models for computing losses in transformer tank walls.

Due to the increasing applications of nonlinear loads, the computation of stray losses in transformer tanks requires the consideration of the harmonic content in the load current, with proper computation of the EMF. Therefore, it is of great importance to study the influence of the load current spectrum on the stray losses and heating of transformers. In our work, we propose simplified analytical formulas to calculate the EMF and EC losses in the presence of harmonics, which are derived for the bushing region of transformer tanks. The obtained formulas enable the analysis of the contribution of each harmonic to the power losses. Thus, it is a powerful and useful tool that can provide quick results in preliminary transformer designs without the need of expensive and high-end computational resources.

The remaining paper is structured as follows. Section 2 states the geometry of the problem and mathematical models along with the boundary conditions. In Section 3, the EMF in the tank wall is obtained solving Maxwell’s equations and employing the separation of variables technique. In Section 4, both solutions (outside and inside the tank wall) are coupled taking account of the corresponding boundary conditions. Simplified asymptotic formulas for computing EMF are obtained. The formula for calculating power losses in transformer tank walls is derived in Section 5. In Section 6, the analytical results are compared with the finite element method (FEM) simulations. Finally, the conclusions are presented in Section 7.

2. Model

The conductor passing through the bushings and tank wall of a transformer is shown in Figure 1. The tank wall is considered as a disk of radius $b$ with a hole of radius $a$ in the center. An infinitely long conductor passes at a right angle through the hole. The axial geometry of the system requires the use of the cylindrical coordinates for solving Maxwell’s equations. Figure 2 shows the schematic geometry of the system, which is divided into two regions. The hole, where the conductor is mounted, the medium above the tank wall, and the region below the wall are filled with air or any other dielectric. Region $R_I=\left\{\left(r,z\right):r_0\le r\right\}\backslash \left\{\left(r,z\right):a\le r\le b,\left|z\right|\le h/2\right\}$, where $r_0$ and $h$ are the conductor half diameter and the transformer tank thickness, respectively. Region $R_{II}=\left\{\left(r,z\right):a\le r\le b,\left|z\right|\le h/2\right\}$ represents the tank wall, which is made up of a ferromagnetic material. In this paper, the magnitude of the magnetic flux density is considered not too high so that the permeability of the tank wall can be considered constant. The values of magnetic flux density found in [21] and [22] for the tank wall studies were 0.001 T and 22 mT, respectively, which are much lower than the maximum value (1.7 T maximum for steel material [23]).

The conductor, passing through the hole, can be modeled as infinitely thin and long. With the advent of nonlinear loads in the distribution system, the current carries an infinite number of harmonics:

$$I\left(t\right)={\displaystyle {\displaystyle \sum }_{n=-\infty }^{\infty }}{I}_n{e}^{jn\omega t},$$

(1)

where $n$ enumerates harmonics, $I_n$is the respective complex amplitude, and $\omega$ is the fundamental angular frequency. The EF and MF produced by the current-carrying conductor, in both regions can be expanded to a Fourier series of the same form:

$$E={\displaystyle {\displaystyle \sum }_{n=-\infty }^{\infty }}{E}_n{e}^{jn\omega t},$$

(2)

$$H={\displaystyle {\displaystyle \sum }_{n=-\infty }^{\infty }}{H}_n{e}^{jn\omega t},$$

(3)

where $E_n$ and $H_n$ are the EF and MF in the frequency domain (complex amplitudes of harmonics), respectively. Due to the linear permeability of the tank wall, the complete system of Maxwell’s equations in the quasi-static approximation can be written for each harmonic as follows:

$$\begin{array}{c}\nabla \times E_n=-jn\omega \mu H_n, \nabla \cdot H_n=0,\\ \\ \nabla \times H_n=J_n+\sigma E_n, \nabla \cdot E_n=0,\end{array}$$

(4)

where $\mathsf{\mu }={\mathsf{\mu }}_{\mathrm{r}}{\mathsf{\mu }}_0$.

Due to the axial symmetry of the system, the solution to Equation (4) can be sought as follows:

$$H_n=H_{n,\phi }\left(r,z\right)e_{\phi }, E_n=E_{n,r}\left(r,z\right)e_r+E_{n,z}\left(r,z\right)e_z,$$

(5)

where the MF is an even function of the axial coordinate $z$: $H_{n,\phi }\left(r,-z\right)=H_{n,\phi }\left(r,z\right)$. The system of Equation (4) must be taken into account along with the boundary conditions given below in the interface of regions $R_I$ and $R_{II}$.

$$\begin{gathered} {H_{n,\phi }^{\left(I\right)}|}_{r=a}={H_{n,\phi }^{\left(II\right)}|}_{r=a}, \\ {\frac{\partial H_{n,\phi }^{\left(I\right)}}{\partial z}|}_{r=a}={\frac{\partial H_{n,\phi }^{\left(II\right)}}{\partial z}|}_{r=a}=0, \end{gathered}$$

(6)

$$\begin{gathered} {\frac{\partial H_{n,\phi }^{\left(I\right)}}{\partial r}|}_{r=a}=-{\frac{H_{n,\phi }^{\left(II\right)}}{a}|}_{r=a}, \\ {H_{n,\phi }^{\left(I\right)}|}_{r=b}={H_{n,\phi }^{\left(II\right)}|}_{r=b} , \\ {\frac{\partial H_{n,\phi }^{\left(I\right)}}{\partial z}|}_{r=b}={\frac{\partial H_{n,\phi }^{\left(II\right)}}{\partial z}|}_{r=b}=0, \end{gathered}$$

(7)

$$\begin{gathered} {\frac{\partial H_{n,\phi }^{\left(I\right)}}{\partial r}|}_{r=b}=-{\frac{H_{n,\phi }^{\left(II\right)}}{b}|}_{r=b}, \\ {\frac{1}{r}\frac{\partial \left(r{H}_{n,\phi }^{\left(I\right)}\right)}{\partial r}|}_{z=\frac{h}{2}}={\frac{1}{r}\frac{\partial \left(r{H}_{n,\phi }^{\left(II\right)}\right)}{\partial r}|}_{z=\frac{h}{2}}=0, \\ {\frac{\partial H_{n,\phi }^{\left(I\right)}}{\partial z}|}_{z=\frac{h}{2}}=0, \\ {H_{n,\phi }^{\left(I\right)}|}_{z=\frac{h}{2}}={H_{n,\phi }^{\left(II\right)}|}_{z=\frac{h}{2}}, \end{gathered}$$

(8)

where $H_{n,\phi }^{\left(I\right)}$ and $H_{n,\phi }^{\left(II\right)}$ are the MF components in regions $R_I$and $R_{II}$, respectively, and the MF in air (Region I), according to the Ampere–Maxwell law, is:

$$H_{n,\phi }^{\left(I\right)}=\frac{I_n}{2\pi r}.$$

(9)

3. Electromagnetic Field (EMF) Distribution in Region ${\mathit{R}}_{\mathit{I}\mathit{I}}$

In region $R_{II}$, the system of Equation (4) can be reduced to the following equation for the magnetic flux density:

$$\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial H_{n,\phi }^{\left(II\right)}}{\partial r}\right)+\frac{{\partial }^2{H}_{n,\phi }^{\left(II\right)}}{\partial z^2}-\frac{H_{n,\phi }^{\left(II\right)}}{r^2}-jn\omega \mu \sigma H_{n,\phi }^{\left(II\right)}=0.$$

(10)

Equation (10) can be solved using the separation of variables technique [24]. As a result, the following expression is obtained:

$$H_{n,\phi }^{\left(II\right)}\left(r,z\right)=\left(\frac{A_n}{r}+B_{n}r\right)\cosh ({\beta }_{n}z)+{\displaystyle {\displaystyle \sum }_{m=0}^{\infty }}\left\{C_{n,m}{I}_1\left({\lambda }_{n,m}r\right)+D_{n,m}{K}_1\left({\lambda }_{n,m}r\right)\right\}\cos \left(k_{m}z\right),$$

(11)

where $I_1\left({\lambda }_{n,m}r\right)$ and $K_1\left({\lambda }_{n,m}r\right)$ are the modified Bessel functions of the first order, ${\beta }_n^2=jn\omega \mu \sigma$, $k_m=\frac{\pi \left(2m+1\right)}{h},$ and ${\lambda }_{n,m}^2=k_m^2+{\beta }_n^2$, where $m=0, 1, 2,\dots$. In order to find the unknown constants $C_{n,m}$ and $D_{n,m}$, boundary conditions (6) and (7) need to be applied. Therefore, we get:

$$\{\begin{array}{l}{\beta }_n\left(\frac{A_n}{a}+B_{n}a\right)\sinh ({\beta }_{n}z)-{\displaystyle {\displaystyle \sum }_{m=0}^{\infty }}{k}_m\left\{C_{n,m}{I}_1\left({\lambda }_{n,m}a\right)+D_{n,m}{K}_1\left({\lambda }_{n,m}a\right)\right\}\sin \left(k_{m}z\right)=0,\\ {\beta }_n\left(\frac{A_n}{b}+B_{n}b\right)\sinh ({\beta }_{n}z)-{\displaystyle {\displaystyle \sum }_{m=0}^{\infty }}{k}_m\left\{C_{n,m}{I}_1\left({\lambda }_{n,m}b\right)+D_{n,m}{K}_1\left({\lambda }_{n,m}b\right)\right\}\sin \left(k_{m}z\right)=0,\end{array}$$

(12)

where $\sinh ({\beta }_{n}z)$ can be expanded in a Fourier series within the segment $z\in \left[-\frac{h}{2},\frac{h}{2}\right]$as follows (see [9]):

$$\sinh \left({\beta }_{n}z\right)={\displaystyle {\displaystyle \sum }_{m=0}^{\infty }}\frac{4{\beta }_n{\left(-1\right)}^m}{h{\lambda }_{n,m}^2}\cosh \left(\frac{{\beta }_{n}h}{2}\right)\sin \left(k_{m}z\right).$$

(13)

The substitution of (13) into the system of Equation (12) yields:

$$\{\begin{array}{l}{k}_m\left\{C_{n,m}{I}_1\left({\lambda }_{n,m}a\right)+D_{n,m}{K}_1\left({\lambda }_{n,m}a\right)\right\}={\beta }_n\left(\frac{A_n}{a}+B_{n}a\right)\frac{4{\beta }_n{\left(-1\right)}^m}{h{\lambda }_{n,m}^2}\cosh \left(\frac{{\beta }_{n}h}{2}\right),\\ k_m\left\{C_{n,m}{I}_1\left({\lambda }_{n,m}b\right)+D_{n,m}{K}_1\left({\lambda }_{n,m}b\right)\right\}={\beta }_n\left(\frac{A_n}{b}+B_{n}b\right)\frac{4{\beta }_n{\left(-1\right)}^m}{h{\lambda }_{n,m}^2}\cosh \left(\frac{{\beta }_{n}h}{2}\right).\end{array}$$

The solution to this system of equations (with respect to the constants $C_{n,m}$ and $D_{n,m}$) should be substituted into Equation (9), resulting in the following solution to Equation (10):

$$\begin{array}{cc}\hfill H_{n,\phi }^{\left(II\right)}\left(r,z\right)& =\left(\frac{A_n}{r}+B_{n}r\right)\cosh ({\beta }_{n}z)\hfill \\ & +{\displaystyle {\displaystyle \sum }_{m=0}^{\infty }}\frac{4{\beta }_n^2{\left(-1\right)}^m}{h{k}_m{\lambda }_{n,m}^2}\frac{\cosh \left(\frac{{\beta }_{n}h}{2}\right)\cos \left(k_{m}z\right)}{I_1\left({\lambda }_{n,m}a\right)K_1\left({\lambda }_{n,m}b\right)-I_1\left({\lambda }_{n,m}b\right)K_1\left({\lambda }_{n,m}a\right)}\hfill \\ & \times \{\left(\frac{A_n}{a}+B_{n}a\right)\left(I_1\left({\lambda }_{n,m}r\right)K_1\left({\lambda }_{n,m}b\right)-I_1\left({\lambda }_{n,m}b\right)K_1\left({\lambda }_{n,m}r\right)\right)\hfill \\ & +\left(\frac{A_n}{b}+B_{n}b\right)\left(I_1\left({\lambda }_{n,m}a\right)K_1\left({\lambda }_{n,m}r\right)-I_1\left({\lambda }_{n,m}r\right)K_1\left({\lambda }_{n,m}a\right)\right)\},\hfill \end{array}$$

(14)

where constants $A_n$ and $B_n$ are to be found in the next section.

4. Coupling of Solutions in Regions ${\mathit{R}}_{\mathit{I}}$ and ${\mathit{R}}_{\mathit{I}\mathit{I}}$

Solutions (9) and (14) should be appropriately coupled by employing boundary conditions (6–8). First, taking account of the fact that $\cos \left(k_{m}h/2\right)=0$, the following result for the MF on the upper surface of the tank cover can be obtained from Equation (14):

$$H_{n,\phi }^{\left(II\right)}\left(r,\frac{h}{2}\right)=\left(\frac{A_n}{r}+B_{n}r\right)\cos \mathrm{h}\left(\frac{{\beta }_{n}h}{2}\right).$$

(15)

The substitution of (15) and (9) into boundary condition (8) yields:

$$\left(\frac{A_n}{r}+B_{n}r\right)\cos \mathrm{h}\left(\frac{{\beta }_{n}h}{2}\right)=\frac{I_n}{2\pi r}.$$

(16)

Since the functions $1/r$ and $r$ are linearly independent, the following solution for the constants $A_n$ and $B_n$can be obtained:

$$A_n=\frac{I_n}{2\pi \cos \mathrm{h}\left(\frac{{\beta }_{n}h}{2}\right)}, B_n=0.$$

Finally, the substitution of these results into Equation (14) yields the following solution to Equation (10) in region $R_{II}$:

$$\begin{array}{cc}\hfill H_{n,\phi }^{\left(II\right)}\left(r,z\right)& =\frac{I_n}{2\pi r}\frac{\cosh ({\beta }_{n}z)}{\cosh \left(\frac{{\beta }_{n}h}{2}\right)}\hfill \\ & +\frac{I_n}{2\pi }{\displaystyle {\displaystyle \sum }_{m=0}^{\infty }}\frac{4{\beta }_n^2{\left(-1\right)}^m}{h{k}_m{\lambda }_{n,m}^2}\frac{\cos \left(k_{m}z\right)}{I_1\left({\lambda }_{n,m}a\right)K_1\left({\lambda }_{n,m}b\right)-I_1\left({\lambda }_{n,m}b\right)K_1\left({\lambda }_{n,m}a\right)}\hfill \\ & \times \{\frac{1}{a}\left[I_1\left({\lambda }_{n,m}r\right)K_1\left({\lambda }_{n,m}b\right)-I_1\left({\lambda }_{n,m}b\right)K_1\left({\lambda }_{n,m}r\right)\right]\hfill \\ & +\frac{1}{b}[I_1\left({\lambda }_{n,m}a\right)K_1\left({\lambda }_{n,m}r\right)-I_1\left({\lambda }_{n,m}r\right)K_1\left({\lambda }_{n,m}a\right)]\}.\hfill \end{array}$$

(17)

Both Equations (7) and (17) represent the solution to Maxwell’s equations for the nth harmonic of the MF in the entire domain. The solution depends on the tank geometry (through the hole and disc radii a and b, the wall thickness h), amplitude of the nth harmonic of the electric current, and angular frequency (through the parameters ${\lambda }_{n,m}$ and ${\beta }_n$). It can be noticed that the dependence of the solution on the disc radius $b$ is weak enough to be neglected. Indeed, according to Equation (11), ${\beta }_n=\left(1+j\right)/{\delta }_n$, where ${\delta }_n=\sqrt{2/n\omega \mu \sigma }$ is the skin-effect depth for the nth harmonic of the MF. Therefore, the following estimation can be obtained:

$${\left|{\lambda }_{n,m}\right|}^2=\left|{\left(\frac{\pi \left(2m+1\right)}{h}\right)}^2+\frac{2j}{{\delta }_n^2}\right|\ge \frac{2}{{\delta }_n^2}.$$

(18)

Therefore, $\left|{\lambda }_{n,m}\right|\ge \sqrt{2}/{\delta }_n$, which, due to the smallness of parameter ${\delta }_n$, results in the estimation: $\left|{\lambda }_{n,m}b\right|\ge \sqrt{2}b/{\delta }_n\gg 1$. This estimation leads to the following asymptotic behavior of the modified Bessel functions [25]:

$$K_1\left({\lambda }_{n,m}b\right)\propto \sqrt{\frac{\pi }{2{\lambda }_{n,m}b}}{e}^{-{\lambda }_{n,m}b}=\mathcal{O}\left(\sqrt{\frac{{\delta }_n}{b}} e^{-\frac{b}{{\delta }_n}}\right)\to 0 \mathrm{as}\frac{b}{{\delta }_n}\to \infty ,$$

(19)

where $\mathcal{O}\left(x\right)$ is the Landau big O notation [26]. Thus, the terms with $K_1\left({\lambda }_{n,m}b\right)$ and $1/b$ in solution (17) can be neglected. As a result, the following equation is obtained:

$$H_{n,\phi }^{\left(II\right)}\left(r,z\right)=\frac{I_n}{2\pi r}\frac{\cosh ({\beta }_{n}z)}{\cos \mathrm{h}\left(\frac{{\beta }_{n}h}{2}\right)}+\frac{2{\beta }_n^2{I}_n}{\pi ah}{\displaystyle {\displaystyle \sum }_{m=0}^{\infty }}\frac{{\left(-1\right)}^m}{k_m{\lambda }_{n,m}^2}\frac{K_1\left({\lambda }_{n,m}r\right)}{K_1\left({\lambda }_{n,m}a\right)}\cos \left(k_{m}z\right).$$

(20)

At the same time, if the hole radius $a$ is much greater than the skin-effect depth ${\delta }_0$ for the fundamental harmonic, i.e., $a\gg {\delta }_0$, then the following asymptotic formulas can be used for the functions $K_1\left({\lambda }_{n,m}a\right)$ and $K_1\left({\lambda }_{n,m}r\right)$, namely,

$$K_1\left({\lambda }_{n,m}a\right)\propto \sqrt{\frac{\pi }{2{\lambda }_{n,m}a}}{e}^{-{\lambda }_{n,m}a} \mathrm{and} K_1\left({\lambda }_{n,m}r\right)\propto \sqrt{\frac{\pi }{2{\lambda }_{n,m}r}}{e}^{-{\lambda }_{n,m}r}.$$

(21)

The substitution of (21) into Equation (20) results in the following approximate formula for the nth harmonic of the MF in the tank wall:

$$H_{n,\phi }^{\left(II\right)}\left(r,z\right)=\frac{I_n}{2\pi r}\frac{\cosh ({\beta }_{n}z)}{\cos \mathrm{h}\left(\frac{{\beta }_{n}h}{2}\right)}+\frac{2I_n{\beta }_n^2}{\pi h\sqrt{ar}}{\displaystyle {\displaystyle \sum }_{m=0}^{\infty }}\frac{{\left(-1\right)}^m}{k_m{\lambda }_{n,m}^2} e^{-{\lambda }_{n,m}\left(r-a\right)}\cos \left(k_{m}z\right).$$

(22)

Equation (22) is a simplified formula for computing MFs in tank walls of transformers. It does not require the use of special functions such as the modified Bessel functions, etc., which makes formula (22) advantageous for practical implementation.

5. Electric Field (EF) and Eddy Current (EC) Losses in the Tank Wall

Due to the Ohmic nature of EC losses, the average power density of losses can be expressed in the form:

$$P\left(r\right)=\frac{1}{T}{\displaystyle \underset{0}{\overset{T}{{\displaystyle \int }}}}\sigma E^2\left(r,t\right)dt,$$

(23)

where $E\left(r,t\right)$ is the EF in region $R_{II}$, which can be obtained from Maxwell’s Equation (4) in the form:

$$E=\frac{\nabla \times H}{\sigma }={\displaystyle {\displaystyle \sum }_{n=-\infty }^{+\infty }}{E}_n{e}^{jn\omega t}={\displaystyle {\displaystyle \sum }_{n=-\infty }^{+\infty }}\left(e_r{E}_{n,r}\left(r,z\right)+e_z{E}_{n,z}\left(r,z\right)\right)e^{jn\omega t}.$$

(24)

The substitution of (24) into (23) and accurate calculation of the respective integrals yields:

$$P\left(r,z\right)={\displaystyle {\displaystyle \sum }_{n=-\infty }^{+\infty }}{P}_n\left(r,z\right),$$

where

$$P_n\left(r,z\right)=\frac{1}{2}\sigma \left({\left|E_{n,r}\left(r,z\right)\right|}^2+{\left|E_{n,z}\left(r,z\right)\right|}^2\right).$$

(25)

Here, the radial component of the EF in the tank wall is:

$$\begin{array}{cc}\hfill E_{n,r}\left(r,z\right)& =-\frac{1}{\sigma }\frac{\partial H_{n,\phi }}{\partial z}\hfill \\ & =-\frac{{\beta }_n{I}_n}{2\pi r\sigma }\frac{\sinh ({\beta }_{n}z)}{\cosh \left(\frac{{\beta }_{n}h}{2}\right)}+\frac{I_n}{2\pi \sigma }{\displaystyle {\displaystyle \sum }_{m=0}^{\infty }}\frac{4{\beta }_n^2{\left(-1\right)}^m}{h{\lambda }_{n,m}^2}\frac{\sin \left(k_{m}z\right)}{I_1\left({\lambda }_{n,m}a\right)K_1\left({\lambda }_{n,m}b\right)-I_1\left({\lambda }_{n,m}b\right)K_1\left({\lambda }_{n,m}a\right)}\hfill \\ & \times \left\{\frac{1}{a}\right[I_1\left({\lambda }_{n,m}r\right)K_1\left({\lambda }_{n,m}b\right)-I_1\left({\lambda }_{n,m}b\right)K_1\left({\lambda }_{n,m}r\right)]\hfill \\ & +\frac{1}{b}[I_1\left({\lambda }_{n,m}a\right)K_1\left({\lambda }_{n,m}r\right)-I_1\left({\lambda }_{n,m}r\right)K_1\left({\lambda }_{n,m}a\right)]\},\hfill \end{array}$$

whereas the axial component takes the form:

$$\begin{array}{cc}\hfill E_{n,z}\left(r,z\right)& =\frac{1}{\sigma }\frac{1}{r}\frac{\partial \left(r{H}_{n,\phi }\right)}{\partial r}=\frac{I_n}{2\pi \sigma }{\displaystyle {\displaystyle \sum }_{m=0}^{\infty }}\frac{4{\beta }_n^2{\left(-1\right)}^m}{h{k}_m{\lambda }_{n,m}}\frac{\cos \left(k_{m}z\right)}{I_1\left({\lambda }_{n,m}a\right)K_1\left({\lambda }_{n,m}b\right)-I_1\left({\lambda }_{n,m}b\right)K_1\left({\lambda }_{n,m}a\right)}\hfill \\ & \times \left\{\frac{1}{a}\right[I_0\left({\lambda }_{n,m}r\right)K_1\left({\lambda }_{n,m}b\right)+I_1\left({\lambda }_{n,m}b\right)K_0\left({\lambda }_{n,m}r\right)]\hfill \\ & -\frac{1}{b}[I_1\left({\lambda }_{n,m}a\right)K_0\left({\lambda }_{n,m}r\right)+I_0\left({\lambda }_{n,m}r\right)K_1\left({\lambda }_{n,m}a\right)]\}.\hfill \end{array}$$

Using the same approximation as in (22), these components of the EF can be represented as follows:

$$\begin{array}{cc}\hfill E_{n,r}\left(r,z\right)& =-\frac{{\beta }_n{I}_n}{2\pi r\sigma }\frac{\sinh ({\beta }_{n}z)}{\cos \mathrm{h}\left(\frac{{\beta }_{n}h}{2}\right)}+\frac{2{\beta }_n^2{I}_n}{\pi ah\sigma }{\displaystyle {\displaystyle \sum }_{m=0}^{\infty }}\frac{{\left(-1\right)}^m}{{\lambda }_{n,m}^2}\frac{K_1\left({\lambda }_{n,m}r\right)}{K_1\left({\lambda }_{n,m}a\right)}\sin \left(k_{m}z\right)\hfill \\ & =\frac{2{\beta }_n^2{I}_n}{\pi ah\sigma }{\displaystyle {\displaystyle \sum }_{m=0}^{\infty }}\frac{{\left(-1\right)}^m}{{\lambda }_{n,m}^2}\left(\sqrt{\frac{a}{r}}{e}^{-{\lambda }_{n,m}\left(r-a\right)}-\frac{a}{r}\right)\sin \left(k_{m}z\right),\hfill \end{array}$$

(26)

$$E_{n,z}\left(r,z\right)=-\frac{2{\beta }_n^2{I}_n}{\pi ah\sigma }{\displaystyle {\displaystyle \sum }_{m=0}^{\infty }}\frac{{\left(-1\right)}^m}{k_m{\lambda }_{n,m}}\sqrt{\frac{a}{r}}{e}^{-{\lambda }_{n,m}\left(r-a\right)}\cos \left(k_{m}z\right),$$

(27)

where expansion (13) of the function $\sinh ({\beta }_{n}z)$ in a Fourier series has been used.

By taking the integral of power density losses (23) over the whole conducting disk, the total losses in the tank wall can be computed. Thus, it can be written as:

$$\begin{array}{cc}\hfill P_{\mathrm{tot}}& ={\displaystyle \underset{a}{\overset{2\pi }{{\displaystyle \int }}}}d\phi {\displaystyle \underset{a}{\overset{b}{{\displaystyle \int }}}}rdr{\displaystyle \underset{-h/2}{\overset{h/2}{{\displaystyle \int }}}}dzP\left(r,z\right)=2\pi {\displaystyle {\displaystyle \sum }_{n=-\infty }^{+\infty }}{\displaystyle \underset{a}{\overset{b}{{\displaystyle \int }}}}rdr{\displaystyle \underset{-h/2}{\overset{h/2}{{\displaystyle \int }}}}dz{P}_n\left(r,z\right)\hfill \\ & =\pi \sigma {\displaystyle {\displaystyle \sum }_{n=-\infty }^{+\infty }}{\displaystyle \underset{a}{\overset{b}{{\displaystyle \int }}}}rdr{\displaystyle \underset{-h/2}{\overset{h/2}{{\displaystyle \int }}}}dz({\left|E_{n,r}\left(r,z\right)\right|}^2+{\left|E_{n,z}\left(r,z\right)\right|}^2).\hfill \end{array}$$

(28)

Results (26) and (27) for $E_{n,r}\left(r,z\right)$ and $E_{n,z}\left(r,z\right)$ should be substituted into Equation (28), where the integration over the variable $z$ can be performed using the orthogonality of the system of functions $\left\{\sin \left(k_{m}z\right),\cos \left(k_{n}z\right)\right\}$. As a result, the following asymptotic expression for the total EC losses can be obtained:

$$\begin{array}{cc}\hfill P_{\mathrm{tot}}& \approx {\displaystyle {\displaystyle \sum }_{n=-\infty }^{+\infty }}\frac{2{\left|{\beta }_n\right|}^4{\left|I_n\right|}^2}{\pi \sigma h{a}^2} {\displaystyle {\displaystyle \sum }_{m=0}^{\infty }}\frac{1}{{\left|{\lambda }_{n,m}\right|}^4}{\displaystyle \underset{a}{\overset{b}{{\displaystyle \int }}}}rdr\{{\left|\sqrt{\frac{a}{r}}{e}^{-{\lambda }_{n,m}\left(r-a\right)}-\frac{a}{r}\right|}^2\hfill \\ & +\frac{{\left|{\lambda }_{n,m}\right|}^2}{k_m^2}\frac{a}{r}{e}^{-2\mathrm{Re}\left\{{\lambda }_{n,m}\right\}\left(r-a\right)}\}\hfill \\ & ={\displaystyle {\displaystyle \sum }_{n=-\infty }^{+\infty }}\frac{2{\left|{\beta }_n\right|}^4{\left|I_n\right|}^2}{\pi \sigma ha} {\displaystyle {\displaystyle \sum }_{m=0}^{\infty }}\frac{1}{{\left|{\lambda }_{n,m}\right|}^4}{\displaystyle \underset{a}{\overset{b}{{\displaystyle \int }}}}dr\{\frac{a}{r}+(1+\frac{{\left|{\lambda }_{n,m}\right|}^2}{k_m^2})e^{-2\mathrm{Re}\left\{{\lambda }_{n,m}\right\}\left(r-a\right)}\hfill \\ & -2\mathrm{Re}\left(\sqrt{\frac{a}{r}}{e}^{-{\lambda }_{n,m}\left(r-a\right)}\right)\}\hfill \\ & ={\displaystyle {\displaystyle \sum }_{n=-\infty }^{+\infty }}\frac{2{\left|{\beta }_n\right|}^4{\left|I_n\right|}^2}{\pi \sigma ha} {\displaystyle {\displaystyle \sum }_{m=0}^{\infty }}\frac{1}{{\left|{\lambda }_{n,m}\right|}^4}\{a\ln \frac{b}{a}+\frac{1-e^{-2\mathrm{Re}\left\{{\lambda }_{n,m}\right\}\left(b-a\right)}}{2\mathrm{Re}\left\{{\lambda }_{n,m}\right\}}\left(1+\frac{{\left|{\lambda }_{n,m}\right|}^2}{k_m^2}\right)\hfill \\ & -2\Re (\sqrt{\frac{\pi a}{{\lambda }_{n,m}}}{e}^{{\lambda }_{n,m}a}[\mathrm{erf}\left(\sqrt{{\lambda }_{n,m}b}\right)-\mathrm{erf}\left(\sqrt{{\lambda }_{n,m}a}\right)])\},\hfill \end{array}$$

where $\mathrm{erf}\left(x\right)$ is the error function [16]. Finally, taking advantage of the fact that the value of $\left|\sqrt{{\lambda }_{n,m}b}\right|$ is high we can approximately write: $\mathrm{erf}\left(\sqrt{{\lambda }_{n,m}b}\right)\approx 1$. As a result, the following approximation can be suitably used for calculating the total losses:

$$\begin{array}{cc}\hfill P_{\mathrm{tot}}& ={\displaystyle {\displaystyle \sum }_{n=-\infty }^{+\infty }}\frac{2{\left|{\beta }_n\right|}^4{\left|I_n\right|}^2}{\pi \sigma ha} {\left|\cosh \left(\frac{{\beta }_{n}h}{2}\right)\right|}^2{\displaystyle {\displaystyle \sum }_{m=0}^{\infty }}\frac{1}{{\left|{\lambda }_{n,m}\right|}^4}\{a\ln \frac{b}{a}+\frac{1}{2\mathrm{Re}\left\{{\lambda }_{n,m}\right\}}(1+\frac{{\left|{\lambda }_{n,m}\right|}^2}{k_m^2})\hfill \\ & -2\mathrm{Re}\left(\sqrt{\frac{\pi a}{{\lambda }_{n,m}}}{e}^{{\lambda }_{n,m}a}\mathrm{erfc}\left(\sqrt{{\lambda }_{n,m}a}\right)\right)\}\hfill \end{array}$$

(29)

where $\mathrm{erfc}\left(x\right)=1-\mathrm{erf}\left(x\right)$ is the complementary error function [16].

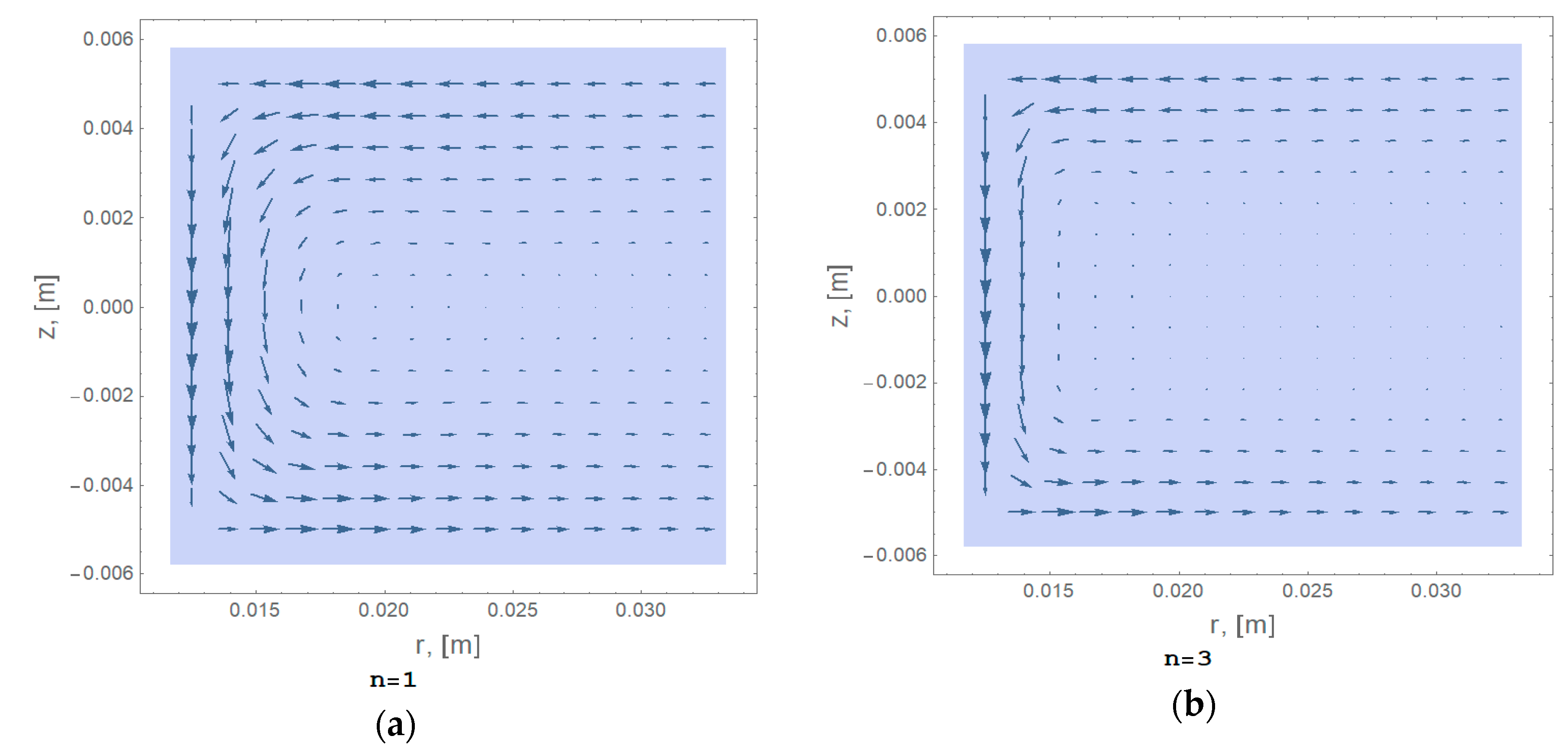
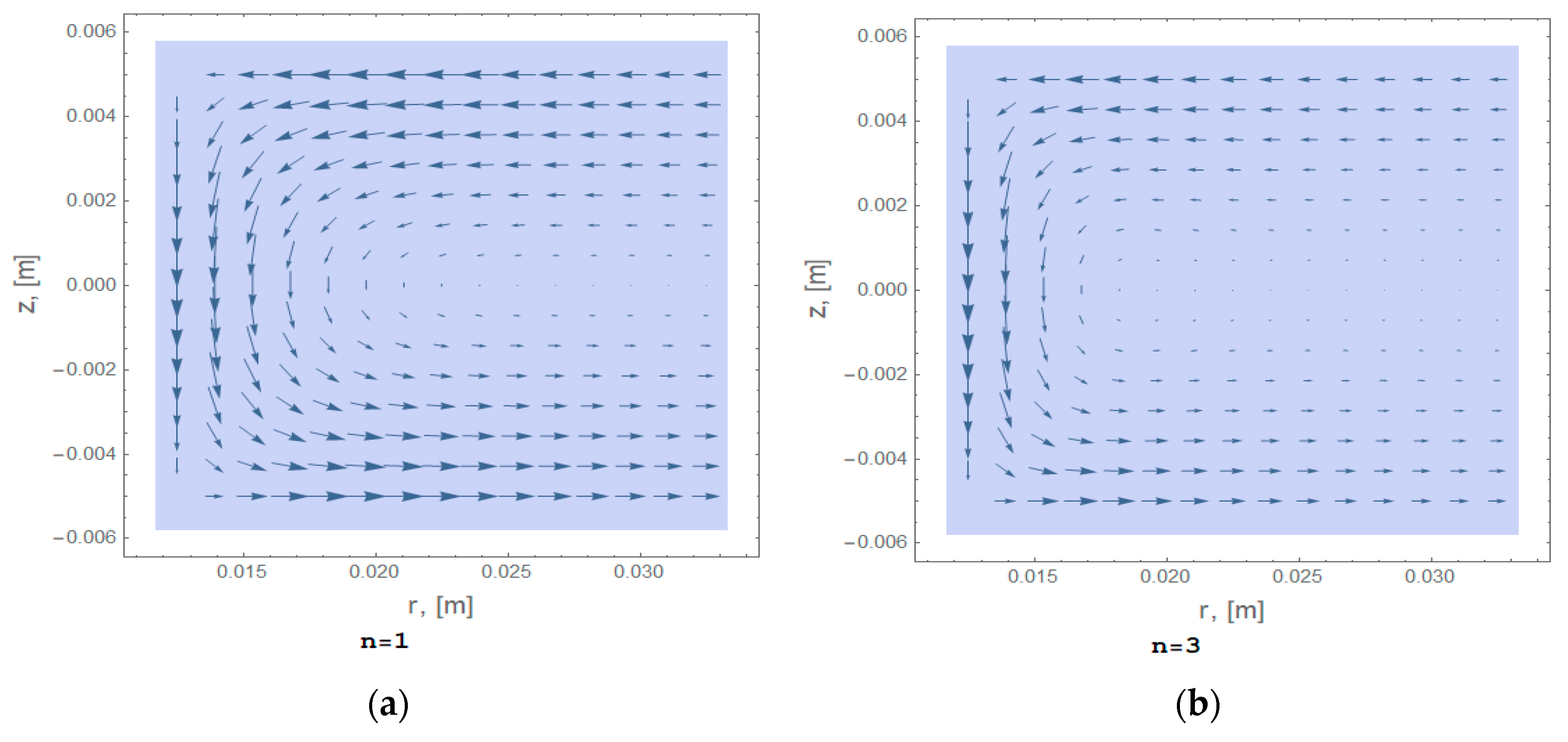
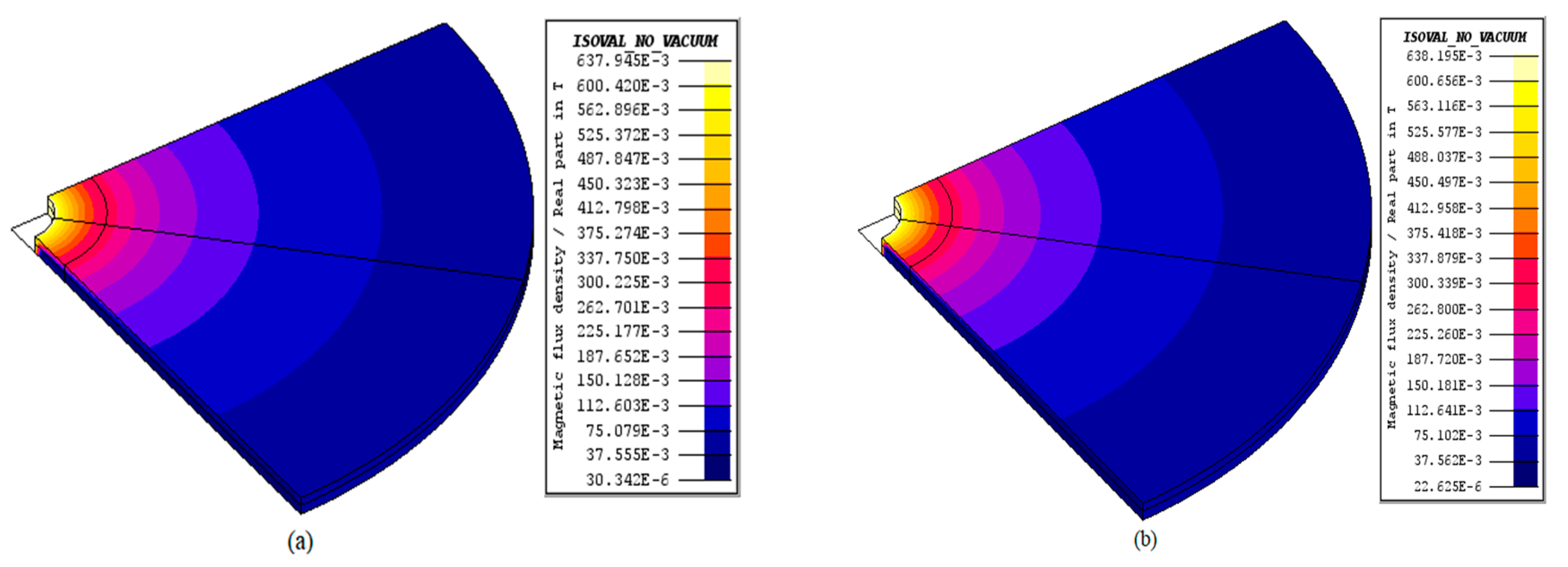
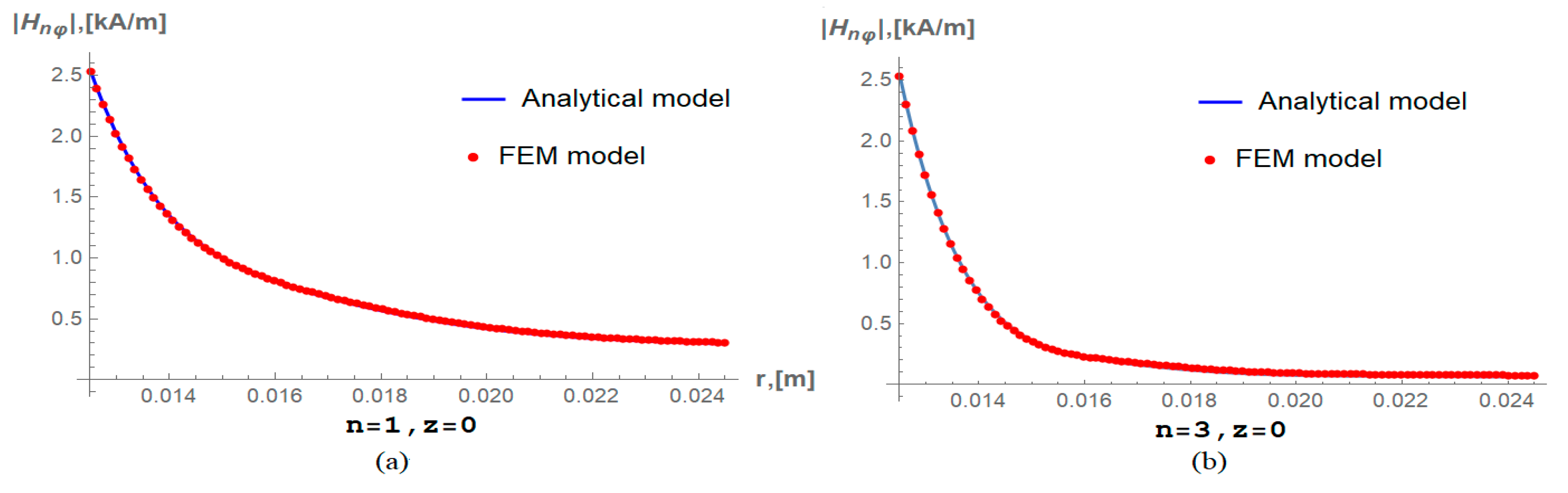
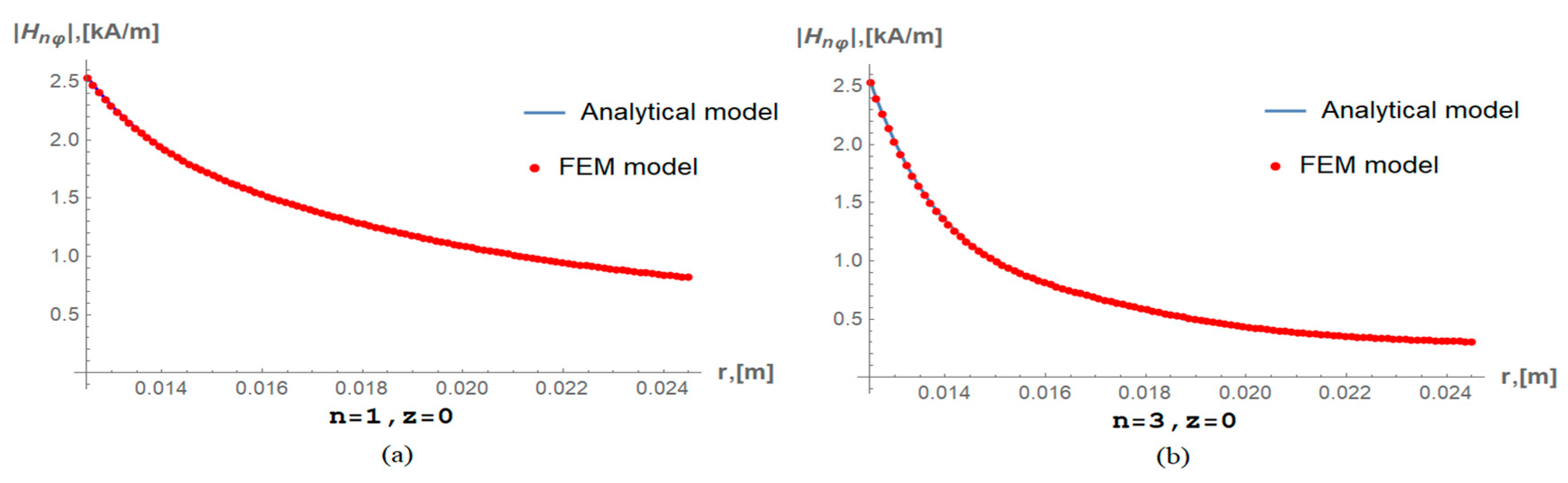
6. Simulation Results and Discussion

Several simulations were carried out in order to compare the analytical results with FEM solutions. FEM computations were carried out using the Altair Flux finite element (FE) software.

A disk with the characteristics: $h=0.010 \mathrm{m}$, $a=0.0125 \mathrm{m}$, $b=0.150 \mathrm{m}$, and ${\epsilon }_r=1$ is considered. A copper conductor with a radius $r_0=2$mm and length $1400 \mathrm{m}$m crosses the disk at the center of the hole. One quarter of the entire disc and a half of its height were considered in the simulations, taking advantage of the symmetry of the problem. The total system was enclosed in a cylinder with an inner radius of 255 mm, outer radius of 305 mm, inner half height of 700 mm, and outer half height of 800 mm.

To mesh the geometry, 66,212 volume finite elements, 14,992 surface elements, and 1292 line elements were used, which gave as a result a total number of 82,496 elements. Of good quality were 96.36% of the elements. Moreover, to properly simulate the skin-effect in a thin boundary layer of the disk and to ensure a better accuracy of computations, nine layers of FE mesh of 0.255 mm of height in each one, were generated near the upper surface of the disk as shown in Figure 3a. Additionally, a high-density mesh was created near the conductor (see Figure 3b).

Figure 4 and Figure 5 show the MF penetration in the transformer tank, computed for the first (60 Hz) and third harmonics (180 Hz) using formula (20) (Figure 4a and Figure 5a for the first and Figure 4b and Figure 5b for the third harmonics, respectively), for two different resistivities: $\mathsf{\rho }=0.25\times {10}^{-6}\mathsf{\Omega }·\mathrm{m}$ in Figure 4 and $\mathsf{\rho }=0.75\times {10}^{-6}\mathsf{\Omega }·\mathrm{m}$ in Figure 5. In order to compare the MF distribution in the magnetic disk for different harmonic numbers, both harmonics were studied with the same value of the RMS current $I_{\mathrm{rms},1}=I_{\mathrm{rms},3}=141.42$ A. In both cases, the relative permeability was considered as ${\mu }_r=200$. It can be observed in Figure 4 and Figure 5 that the higher the harmonic number, the smaller is the penetration depth of the MF in the transformer tank.

The EF distribution in the tank wall, computed using our analytical method (formulas (26) and (27)), is shown in Figure 6 and Figure 7 for the first and third harmonics, under the same conditions (Figure 6 for $\mathsf{\rho }=0.25\times {10}^{-6}\mathsf{\Omega }·\mathrm{m}$ and Figure 7 for $\mathsf{\rho }=0.75\times {10}^{-6}\mathsf{\Omega }·\mathrm{m}$, also $I_{\mathrm{rms},1}=I_{\mathrm{rms},3}=141.42$ A and ${\mu }_r=200$ in both cases). Since the EC density is proportional to the EF (${\mathbf{j}}_n=\sigma E_n$), Figure 6 and Figure 7 also qualitatively depict EC density lines in the tank wall. It can be observed that the ECs are mainly concentrated near the wall surface (skin-effect), and the concentration of the current density is higher for the third harmonic than for the first.

Figure 8a,b show the FEM-calculated magnetic flux density distribution in the transformer tank for $\mathsf{\rho }=0.25\times {10}^{-6}\mathsf{\Omega }·\mathrm{m}$ and RMS current $I_{\mathrm{rms}}=141.42$ A for the first and third harmonics, respectively. The maximum value of the magnetic flux density $\mathrm{B}=637.94\times {10}^{-3}\mathrm{T}$ was obtained on the hole surface for the first harmonic (see Figure 8a), whereas for the third harmonic it was $\mathrm{B}=638.19\times {10}^{-3}\mathrm{T}$ (Figure 8b).

The absolute value wave-form for the MF on the central plane of the tank wall (at z = 0) is shown in Figure 9 and Figure 10, where the blue line represents the analytical solution and the red points correspond to FEM simulations. Figure 9 is plotted for a resistivity of $\mathsf{\rho }=0.25\times {10}^{-6}\mathsf{\Omega }·\mathrm{m}$, whereas Figure 10 shows the MF profile for $\mathsf{\rho }=0.75\times {10}^{-6}\mathsf{\Omega }·\mathrm{m}$. Figure 9 and Figure 10 show an excellent match between the analytical and FEM computations, which validates Equations (22)–(26). On the other hand, the time taken while executing the analytical model was 0.66 s, which is notably less than the several minutes the FE software takes in execution.

To validate formula (29), total EC losses were analytically and numerically computed for eight different cases, where the radii, resistivity, and frequency were varied (see

Table 1. Transformer tank wall parameters and frequencies (${\mathsf{\mu }}_r=\mathbf{200}$)

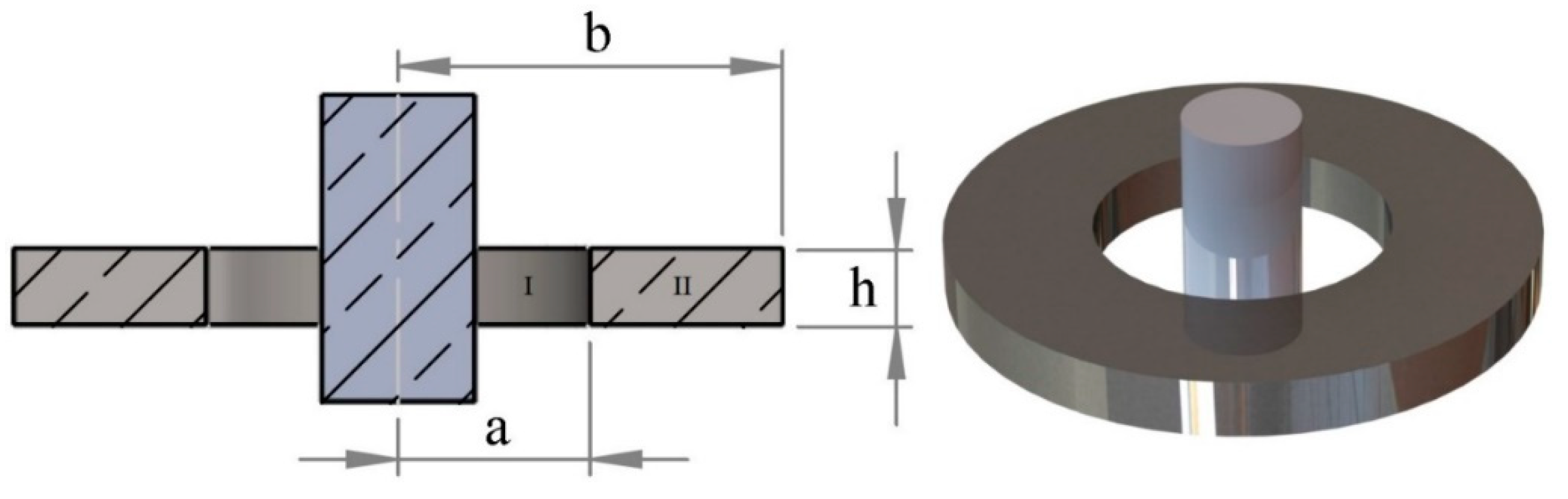
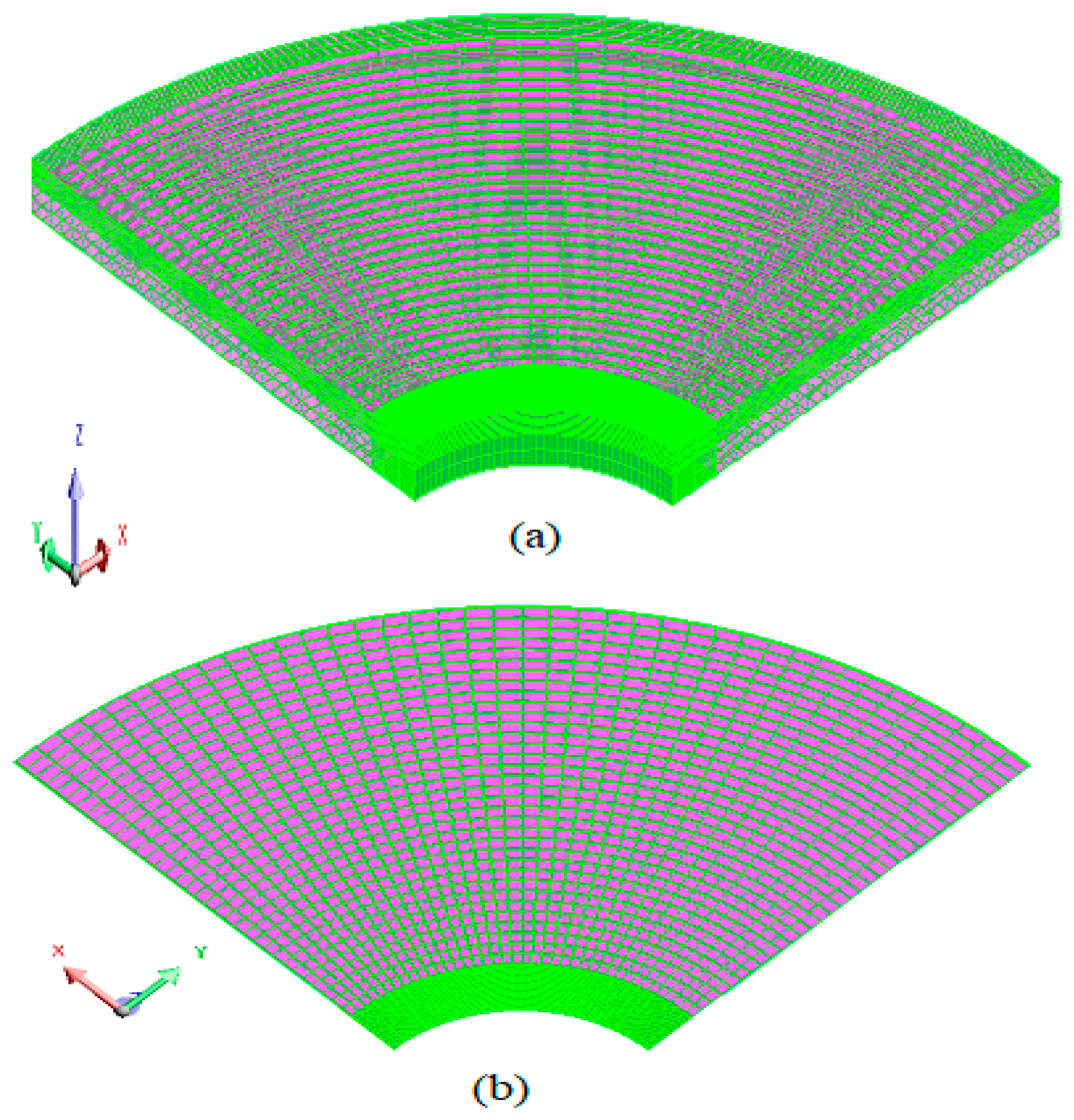
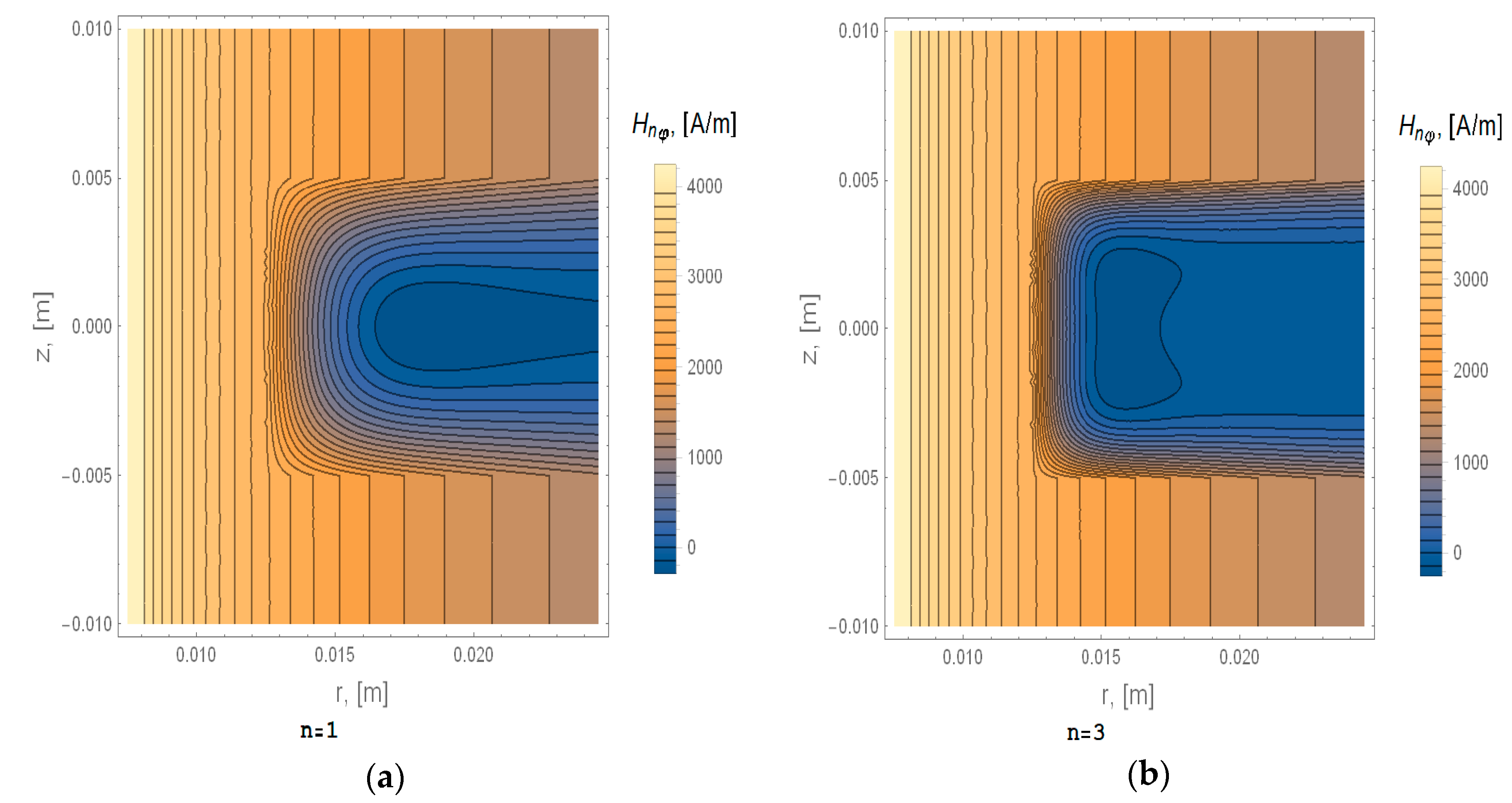
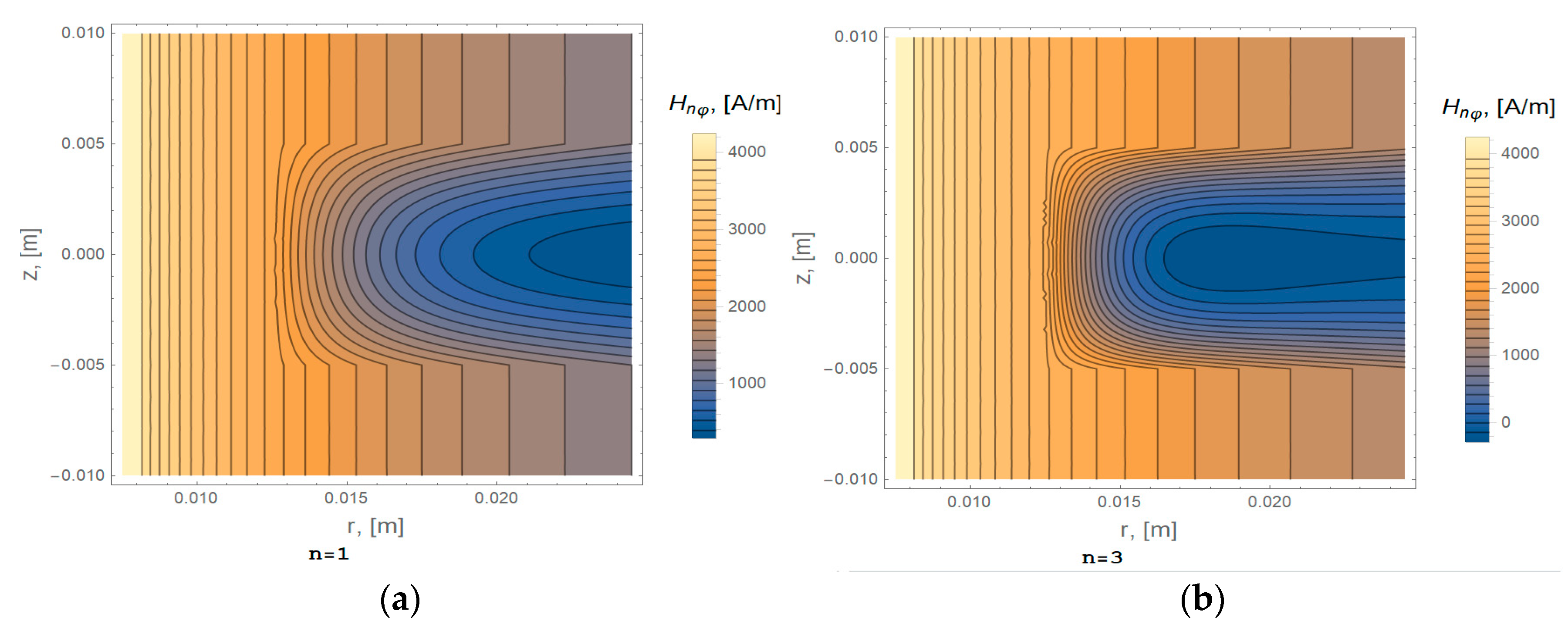
Case	A [m]	B [m]	h [m]	Irms [A]	$\mathsf{\rho }$$\left[\mathsf{\Omega }·\mathbf{m}\right]$	Harmonic
1	0.0125	0.150	0.010	141.42	$0.25\times {10}^{-6}$	n = 1
2	0.0125	0.150	0.010	141.42	$0.25\times {10}^{-6}$	n = 3
3	0.04	0.145	0.00952	141.42	$0.25\times {10}^{-6}$	n = 1
4	0.04	0.145	0.00952	141.42	$0.25\times {10}^{-6}$	n = 3
5	0.04	0.145	0.00952	141.42	$0.25\times {10}^{-6}$	n = 5
6	0.035	0.140	0.00952	141.42	$0.75\times {10}^{-6}$	n = 1
7	0.035	0.140	0.00952	141.42	$0.75\times {10}^{-6}$	n = 3
8	0.035	0.140	0.00952	141.42	$0.75\times {10}^{-6}$	n = 5

). The data are for a 17 kVA transformer with primary and secondary voltages of 120 and 240 volts, respectively that can be manufactured in the industry. Results of simulations are presented in

Table 2. Total stray losses in the disk (${\mathsf{\mu }}_r=\mathbf{200}$)

Case	Ptotal [W], Analytical	Ptotal [W], Numerical	Relative Error (%)	Skin-Effect Depth, [mm]	Harmonic
1	1.874	1.870	0.22	2.297	n = 1
2	3.276	3.267	0.27	1.326	n = 3
3	0.959	0.953	0.63	2.297	n = 1
4	1.632	1.630	0.13	1.326	n = 3
5	2.127	2.117	0.470	1.027	n = 5
6	1.614	1.588	1.610	3.979	n = 1
7	3.108	3.100	0.26	2.297	n = 3
8	3.917	3.901	0.41	1.779	n = 5

. From Table 2, it can be observed that both the analytical and FEM-calculated results are very close. The relative error between analytical and FEM solutions is in the range 0.13% to 1.610%, which proves the high accuracy of Formulas (26), (27), and (29). Moreover, although the skin-effect depth decreases for higher frequencies, the MF density in the surface layer increases, which leads to higher losses.

7. Conclusions

In this paper, new analytical formulas for the EMF and EC loss computation in transformer tank covers have been strictly derived, with proper consideration of harmonics in the load current. Noteworthy, asymptotic formulas, that do not require the use of special functions, were formally obtained using asymptotic expressions of the modified Bessel functions. These formulas allow the distribution of MF and computation of power losses due to each harmonic in the tank wall. The geometry considered accurately represents the arrangement of the conductor carrying load current with harmonics passing through the transformer tank wall.

The new formulas were successfully verified by comparing their performance with computationally expensive FEM simulations, proving their efficiency and efficacy. Hence, our results are useful for industrial applications, where transformer analysis and design demand accurate results and low-cost computational resources. It has been additionally shown that the presence of harmonics in the load current lowers the skin effect depth, they considerably increase stray losses and, therefore, must be taken into account for proper analysis and design of transformers. These formulas can be employed in the design algorithms for evaluating the impacts of harmonics on the transformer tank wall. The results can be used to improve the design of the transformer and thereby considerably reduce the possibility of hot spots in the bushing regions. Therefore, our formulas are an important advancement to the existing methods and formulas available in the literature.

Our approach provides a basis for further developments such as analysis of stray losses in the case of three-phase currents (three conductors passing through the tank wall).