The Nano-Scale Modified BaTiO₃ Morphology Influence on Electronic Properties and Ceramics Fractal Nature Frontiers

Featured Application

The nano BaTiO₃ modification could lead towards innovation in nanocoating of ceramic grains in function of submicron intergranular capacitors. The electronic parameters integration in the frame of microelectronics in intergranular phenomena by fractals is opening novel route in miniaturization and integrations. Fractal analysis and calculations provide necessary fractal corrections for sample synthesis.

Abstract

The BaTiO₃ ceramics applications based on electronic properties have very high gradient scientific and industrial-technological interests. Our scientific research has been based on nano BaTiO₃ modified with Yttrium based organometallic salt (MOD-Y). The samples have been consolidated at a sintering temperature of 1350 °C. Within the study, the new frontiers for different electronic properties between the layers of BaTiO₃ grains have been introduced. The research target was grain boundary investigations and the influence on dielectric properties. After scanning electron microscopy and dielectric measurements, it has been established that modified BaTiO₃ samples with larger grains showed a better compact state that led to a higher dielectric constant value. DC bias stability was also investigated and showed a connection between the grain size and capacitance stability. Analyses of functions that could approximate experimental curves were successfully employed. Practical application of fractal corrections was performed, based on surface (α_s) and pore size (α_p) corrections, which resulted in obtainment of the relation between the capacitance and Curie temperature. Successful introduction of fractal corrections for capacitance-Curie temperature dependence for a set of experimental data is an important step towards further miniaturization of intergranular capacitors.

1. Introduction

The processing-property-structure relation is of great importance for designing ceramic materials, samples with full control on grains, pores and their bilayers in between the grains and pores as ceramic structures constituents. Electronic properties of ceramics have put them on the top of the materials used for sensors, actuators, capacitors and other parts integrated in electronic devices [1,2,3,4]. Ferroelectric perovskite ceramics have been intensively studies over the years, from a macro towards a nano-scale approach [5,6,7,8]. Multilayer ceramic capacitors (MLCC) have enabled tailoring of the properties by the modification of ceramic layer and the interface between them, which further led to the production of high capacitance and stability capacitors [9]. Barium-titanate is one of the most widely used ceramic materials in electronic devices, due to its high dielectric constant and modification possibilities with different inorganic and organic agents [10,11]. MLCCs are sintered in a reducing atmosphere, in order to prevent oxidation of metal. However, this leads to the reduction of BaTiO₃ and consequently to the decrease in the overall dielectric constant and capacitance [12]. One approach to solving the problem is doping BaTiO₃ with acceptors or donors, most commonly with rare-earth elements, such as Yttrium and their oxides [13,14]. After the modification, grain boundary (GB) changes, inducing changes in dielectric and ferroelectric properties, occurred [15]. By investigating the phenomena at the GB, changes in dielectric properties could be understood and controlled by changing the processing parameters [16]. It is well known that the grain size increase leads to a dielectric constant value increase but also causes higher capacitance DC bias sensitivity, that is, capacitance value decreases with the increase of applied DC voltage [9]. Finding an adequate modifier for BaTiO₃ that would reduce DC bias sensitivity dependence on the grain size is a real challenge, which could be easier with the use of proper theoretical models for the dielectric properties investigation at the GB, compared to the bulk sample. Dimensional and shape analysis could be achieved by using a fractal approach, giving insight into the influence on the bulk sample properties [17,18,19,20]. Fractals are irregular geometric objects with fragmented or amorphous forms that cannot be described by Euclid’s geometry [21]. The contribution of fractals correction could be observed and explained with the intergranular Heywang capacity model, Schottky barrier, Curie-Weiss law and other parameters in the field of dielectric and ferroelectric materials. Implementation of fractals correction in the Claussius-Mossotti equation could explain dimensional influence on atom polarizability, which further leads to a dielectric constant control at the grain boundary. In this manner, dielectric constant and DC bias stability could be enhanced with proper parameters during synthesis.

The main frame and goal of this research was the modification of BaTiO₃ with rare-earth based organometallic salt (Scheme 1), in order to provide a densified compact microstructure of modified ceramic capacitor. Next to that, investigation of GB phenomena was performed using microstructural fractal analysis for the dielectric properties investigation. Obtaining intergranular microelectronic properties represents high advance in the field of electronic ceramic applications and frontiers. Modification of the grains was performed and investigated in order to obtain coated ceramics that could be implemented in an LTCC module, within the further research direction. BaTiO₃ was modified with Yttrium based organometallic salt, in order to obtain fine dispersion in organic solvents and to ensure uniform coating. Bilayers between grains were formed (thin films that coat grains), with as precise location control as possible in ceramic bulk.

2. Materials and Methods

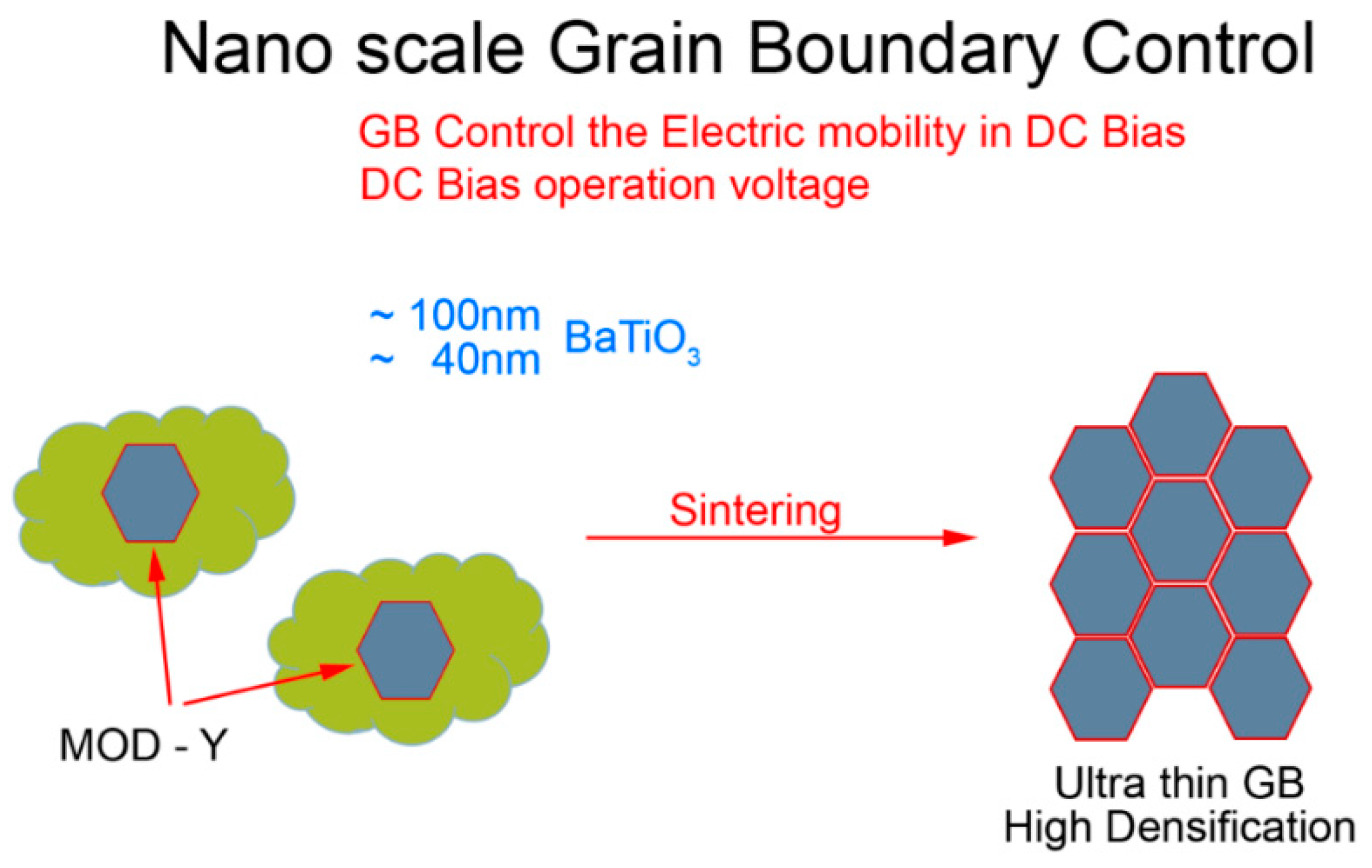
2.1. Materials and Sample Preparation

BaTiO₃ nanopowders were purchased from SAKAI CHEMICAL INDUSTRY CO. LTD., Sakai, Osaka, Japan. Nanoparticles with average diameters of around 40 nm and 112 nm were denoted KZM100 and BT02, respectively. Modified BaTiO₃ samples were prepared using solvent mixture Ethanol/Toluene/n-Butanol. Pure BaTiO₃ nano-structured powders were treated with additive metal-organic yttrium salt MOD-Y, where BaTiO₃: MOD-Y mol ratio was 3:97. This molar ratio has been chosen as the best after a series of experiments with different ratios. After the mixing, ball milling was performed for 24 h, followed by tape casting, process of lamination and sintering, where, as a result, thin films were produced. The consolidation process was carried out according to Scheme 2. All of these have been prepared by the specific and protected ITRI procedure. The sintering was performed for one hour at 1350 °C in the reducing atmosphere 5% H₂/N₂.

2.2. Characterization of Samples

Transmission electron microscopy was performed (JEOL-JEM-2100F) in order to establish whether the modification of BaTiO₃ was successful. Morphology of un-sintered and sintered ceramics was investigated via scanning electron microscopy (SEM) (EmCraft cube 2). The composition and homogeneity of the samples was investigated with energy dispersive X-ray analysis (EDX) using Cliff-Lorimer method with all the elements analyzed (Normalized). Distribution of BaTiO₃ size was obtained using Nicomp 380 DLS/ZLS Dynamic Light Scattering and Zeta Potential. Dielectric properties were measured on Microtest LCR Meter 6377@1KHz and KEITHLEY 2400 SourceMeter. Sample’s dimensions were round shaped films with a 3 mm diameter and a thickness of 0.75 mm. All the measurements were performed at room temperature (25 °C)

2.3. Fractal Analysis

Based on SEM and scanning transmission electron microscopy (STEM) images, which are characterizing the microstructure morphology, we have applied the fractal nature analysis on the same structure with four different magnifications (60 k, 100 k, 150 k and 250 k). We have successfully reconstructed the grain shape and presented it in Figure 1.

For further analysis and discussions about the influence of fractal correction on dielectric constant in Curie-Weiss law and capacitance, we obtained Hausdorf fractal dimension D_H (Figure 2) and fractal correction α_s based on grain surface influence [22,23]. Figure 2 shows the dependence of number of boxes, N, that cover the surface, on a box of size h. This dependence is shown on a logarithmic scale.

Regarding the reconstruction of the pore morphology, we must emphasize that it is a very complex procedure, more complex than for the grains, and it is based on sampling the measured dimensions inside of the pore, which become data for fractal dimensions and reconstructions of pore shape and corresponding dimensions. Finally, the pore shape is reconstructed and presented in Figure 3, with the coordinates designation omitted, as they are not significant for determining the scale invariant fractal dimension.

Coordinates designation is not significant for determining the fractal dimension, as it is scale invariant.

As for the grain surface influence, we also obtained pore Hausdorf fractal dimension D_H and corresponding fractal correction α_p based on pore shape influence [22,23]. Figure 4 shows contour length (L) dependence on ruler size (r) on a logarithmic scale.

Regarding the third influence factor α_M, it is neglected.

The implementation of fractal correction was developed within the experimental research based on a few thousand different electronic ceramics samples (BaTiO₃ with different additives) which are natural data confirming this approach with additional microstructural analysis and characterization concretely on the surface of the grains and pores. As we explained earlier, here we did not include the influence of particles’ Brownian motion because this phenomenon is not dominant in ferroelectrics and dielectric materials and processes. Regarding the influence of grain and pore surfaces, it is definitely clear that this fractal level of microstructure characteristics directly and more precisely extend the structure influence on electrophysical properties, in this paper, specifically, ferroelectric and dielectric properties. Here, in this paper we applied previous knowledge to samples based on BaTiO₃ with Ytrium additives. Fractal correction is based on grains’ and pores’ surfaces fractal dimension which has been calculated by using well known methods of Richardson plot and box-counting (Figure 2 and Figure 4).

Problems associated with determining the fractal dimension and its correctness are multiple and require detailed analysis. Our results up to now could be a useful contribution to a precise determination of D_H and problems related to it. As this is not the main topic of this paper, we can analyze this problems in future research in which results from this paper could be a contribution to further research and further clarification of this matter.

3. Results and Discussion

3.1. Microstructural Analysis

Morphological and constitutional changes after the modification with MOD-Y salt, as well as the differences caused by grain size of KZM-100 (average 41.3 nm) and BT02 (average size 112.1 nm), were investigated with STEM, FSEM and EDX.

3.1.1. STEM-EDX

The microstructure of KZM-100-MOD-Y and BT02-MOD-Y, obtained by STEM, is shown in Figure 5 and Figure 6, respectively. Increased grain growth occurred in both samples, as a consequence of liquid sintering [15,24]. After 1 h of sintering, KZM-100-MOD-Y had nonuniform grain size, up to around 400 nm in diameter.

EDX analysis using the Cliff-Lorimer method showed uniform composition in KZM100-MOD-Y around the sample, based on 7 chosen points presented in Figure 5. EDX mapping of Ba, Ti, O and Y distribution has revealed that Y is highly dispersed in the BaTiO₃, leading to a conclusion that the used modification method with Yttrium organic salt was successful.

BT02-MOD-Y exhibited more uniform size distribution than KZM100-MOD-Y but with a grain size up to 1 µm. In both cases, grain size was around 10 times larger than for pure commercial KZM-100 and BT02. In addition, BT02-MOD-Y showed higher regularity in grain shape than KZM-100-MOD-Y, while the latter had a more densified microstructure.

Similar to in sample KZM100-MOD-Y, a uniform composition was confirmed in BT02-MOD-Y, based on 7 chosen points presented in Figure 6. Yttrium was identified along the grain boundary in both samples, with over 2 times higher content in BT02-MOD-Y, which could lead to a higher dielectric constant value. A drop of O content indicates slight degradation of the BaTiO₃ phase during high temperature modification of grains.

EDX analysis in both samples showed that Ba/Ti ratio is nonstoichiometric (

Table 1. EDX analysis of different points in KZM100-MOD-Y.

Spectrum	In Stats.	O	Si	Ti	Y	Ba	Total
Spectrum 1	Yes	18.12	0.18	18.30	0.38	63.01	100.00
Spectrum 2	Yes	18.17	−0.24	18.36	0.77	62.96	100.00
Spectrum 3	Yes	16.43	0.32	19.61	1.55	62.09	100.00
Spectrum 4	Yes	16.61	0.28	17.64	1.21	64.26	100.00
Spectrum 5	Yes	19.38	0.00	17.68	1.63	61.32	100.00
Spectrum 6	Yes	15.80	0.02	16.92	1.01	66.26	100.00
Spectrum 7	Yes	17.35	−0.07	18.14	0.95	63.63	100.00
Mean		17.41	0.07	18.09	1.07	63.36	100.00
Std. deviation		1.24	0.20	0.83	0.44	1.60
Max.		19.38	0.32	19.61	1.63	66.26
Min.		15.80	−0.24	16.92	0.38	61.32

and

Table 2. EDX analysis of different points in BT02-MOD-Y (wt%).

Spectrum	In Stats.	O	Si	Ti	Y	Ba	Total
Spectrum 1	Yes	9.49	0.15	17.30	2.25	63.60	100.00
Spectrum 2	Yes	10.67	0.11	17.66	2.02	63.16	100.00
Spectrum 3	Yes	11.89	0.16	17.46	2.68	61.16	100.00
Spectrum 4	Yes	13.29	−0.10	15.76	2.37	62.73	100.00
Spectrum 5	Yes	12.19	−0.02	17.11	2.32	61.51	100.00
Spectrum 6	Yes	12.56	0.02	18.12	2.12	60.38	100.00
Spectrum 7	Yes	11.37	0.06	18.46	2.51	60.84	100.00
Mean		12.46	0.05	18.65	2.49	66.32	100.00
Std. deviation		1.26	0.09	0.87	0.23	1.25
Max.		13.29	0.16	18.46	2.68	63.60
Min.		9.49	−0.10	15.76	2.02	60.38

), indicating replacement of Ti⁴⁺ with rare earth element.

Formation of core-shell structure is presented in Figure 7. Shell thickness varies from 2 nm to 10 nm independent of the grain size, which leads to the conclusion that it depends on an amount of a doping element. It has been reported that the shell thickness has a small influence on dielectric constant, predominantly controlled by the grain size [12].

3.1.2. FESEM Analysis

Figure 8 shows FESEM images of sintered KZM-100-MOD-Y and BT02-MOD-Y, obtained under the same conditions, respectively. Compact state is important for expected dielectric properties, where higher surface coverage with a modification agent lead to the higher dielectric constant value.

As can be seen, BT02-MOD-Y (down left) has a more compact morphology after sintering, which should imply the highest dielectric constant and the potential for the application in electronic devices.

Based on different grain sizes and related structures, we can get different fractal characteristics, especially fractal dimensions, in correspondence with specific samples. Regarding the different fractal analysis results, we have evident influence of differences between the size and structures of samples, what is useful for further analysis and conclusions in this research and paper.

3.2. Dielectric Properties

It is well known that ferroelectrics exhibit spontaneous polarization and reversal without an external electric field. If DC bias is applied, spontaneous reversal and polarization direction are governed by the electric field direction, which leads to a decrease in the capacitance value [9]. Perovskite ceramic materials such as BaTiO₃ have a high dielectric constant (D_k) and therefore capacitance value but as D_k increases, they show increased sensitivity to DC bias. It is known that up to 1 µm, D_k sharply increases with the grain size [25]. BT02-MOD-Y showed by the order of magnitude higher dielectric constant value (2132), compared to KZM100-MOD-Y (182). However, consequently, it has the highest capacitance value decrease with DC bias. Figure 9 and Figure 10 show the capacitance drop with DC bias for KZM100-MOD-Y and BT02-MOD-Y respectively. Capacitance of KZM100-MOD-Y remained stable, with negligible decrease up to 73 V, where a slow drop can be observed to 67% at 96 V.

On the other side, BT02-MOD-Y showed a sharp drop around 4 V. This indicates that the amount of dopant in smaller grains induces higher capacitance stability of BaTiO₃ after the modification.

Capacitance change dependence on DC bias for KZM100-MOD-Y could be modeled within the class of reliability functions.

$$R(x)=1-F(x)=1-{\displaystyle \underset{-\infty }{\overset{x}{\int }}f(u)}du,$$

where F(x) is cumulative distribution of random variable. We chose Normal (Gaussian) distribution with scale 100 and got Scaled reliability function, ΔC. Here, we used relative capacitance change in function of voltage, which is the result of experimental research.

We propose a scaled reliability function of normal distribution:

$$\Delta C(x)=100\cdot \left(1-{\displaystyle \underset{-\infty }{\overset{x}{\int }}\frac{1}{\sqrt{2\pi {\delta }^2}}}e-\frac{{\left(u-\mu \right)}^2}{2{\sigma }^2}du\right),$$

with $\mu =90,\sigma =10$. Variable x corresponds to DC bias (V). Figure 11 presents a Scaled reliability function of normal distribution for KZM100-MOD-Y.

The selected model with a scaled reliability function was the first attempt and was found to be appropriate in comparison with experimental results presented in Figure 9 and Figure 10 diagrams. Up to this research stage, the limiting case of Gauss distribution fits experimental results but it could be more refined in the future. Possible other results for which we can improve the optimal selection of the function for a further adequate model could be expected. The physical meaning behind this starting model will be analyzed within the new experimental research.

Capacitance change with DC bias for BT02-MOD-Y could be modeled with the above scaled reliability function when $\sigma \to 0$ and it is practically inverted Dirac Delta function (Figure 12).

Increased grain size causes an increase in dielectric constant and loss tangent, from 0.023 to 0.069 for BT02-MOD-Y, which is in accordance with the literature [15,26]. The loss tangent value decrease is the consequence of intergranular free charges conduction.

3.3. Dielectric Constant Fractal Correction

Complex fractal correction is presented as

$${\alpha }_f={\alpha }_S+{\alpha }_P+{\alpha }_M,$$

where each α represents fractal correction induced by grain surface, inside pore surface and particles’ Brownian motion, respectively. Fractal correction based on Brownian motion of particles, α_M, is not included in this analysis because of its minor influence (in comparison to α_S and α_P) and to provide less complicated further analysis.

Here in this part, we applied fractal corrections α_s (grain surface) and α_p (inside pore surface) to Curie-Weiss law, introduced in References [22,23].

$${\epsilon }_r(T_f,\alpha )=\frac{C_c}{T-T_c}==\frac{C_c}{\frac{T_f}{\alpha }-T_c}$$

C_c~10⁵.

Sintering temperature T for modified BaTiO₃-ceramics must be influenced by three factors forming fractal corrective factor α_f, making the real ceramic temperature T_f, which is a corrected T; the two temperatures are connected using equation T_f = α_f*T and α_f is a complex fractal correction.

In all of these ceramics and general materials science formulas, absolute temperature is present. So, in our experiments and discussed samples and results, we have absolute temperature T, as temperature in all processes and structures. T is a measure of thermal relations in all of these processes and phenomena. The present thermal effects are in strong connection with the structural constituents grains and pores, especially their surfaces and related characteristics of intergranular-pores contacts relations and phenomena, also the ecranization effects of electronic properties influence from one to another side of the grain boundaries. So complex fractal correction α_f will be temperature fractal correction that is, T_f = α_f*T. In this case, the microfractality and associate complex fractal correction α_f have very important role on that submicrolevel and also influence on local and in summary the samples thermal effects.

As we neglected fractal correction α_M, total fractality impact is equally distributed over α_s and α_p

$$\alpha =\frac{{\alpha }_p+{\alpha }_s}{2}$$

$${\epsilon }_r(T_f,{\alpha }_p,{\alpha }_s)=\frac{C_c}{\frac{2T_f}{{\alpha }_p+{\alpha }_s}-T_c}$$

$${\epsilon }_r(T_f,{\alpha }_p,{\alpha }_s)=\frac{C_c}{\frac{2T_f}{0.34045+0.263}-T_c}=\frac{C_c}{\frac{2T_f}{0.60345}-T_c}=\frac{C_c}{3.3143T_f-T_c}.$$

The known dependence of capacitance on ε_r can be presented with equation:

$$C={\epsilon }_r{\epsilon }_0\frac{S}{d}$$

where ε₀ stands for absolute dielectric constant, S is the sample surface and d represents sample thickness. Including values for T_f (25 °C), S (3 mm) and d (0.75 mm), a function showing relation between capacitance (C) and T_c can be obtained for our experimental data:

$$C=3.54\times {10}^{-14}\frac{C_c}{936.6-T_c}$$

In this way, influence of DC bias on capacitance change can also give the insight in T_c change, which is very important for the investigation of capacitor stability under different operational conditions. According to the literature, C_c of pure BaTiO₃ is the order of magnitude 10⁵, so it can be assumed that modified BaTiO₃ could have the similar values, obtaining the dependence [27]:

$$C~\frac{3.54\times {10}^{-9}}{936.6-T_c}$$

Table 3. Full range of capacitance change with DC bias for KZM100-MOD-Y.

C change, %	100	100.32	101.28	100.97	100.64	100.64	100.32	100.16	93.13	78.90	0
DC bias, V	0	10	20	30	40	50	60	70	80	90	100

,

Table 4. Drop range of capacitance with DC bias for KZM100-MOD-Y.

C change, %	100.16	100.01	98.76	97.50	95.49	93.13	90.94	88.44	86.25	83.43	78.90	74.21	70.78	67.17	33.70
DC bias, V	70	72	74	76	78	80	82	84	86	88	90	92	94	96	98

,

Table 5. Full range of capacitance change with DC bias for BT02-MOD-Y.

C change, %	100	106.90	108.14	108.14	0
DC bias, V	0	1	2	3	3.83

and

Table 6. Increase range of capacitance with DC bias for KZM100-MOD-Y.

C change, %	100	101.28	103.14	104.40	105.64	106.90	107.21	107.52	108.14	108.14	108.14
DC bias, V	0	0.2	0.4	0.6	0.8	1	1.2	1.4	1.6	1.8	2

present data used for fractal correction of the Curie-Weiss equation. The data were read from the curve that has been produced by the device for capacitance stability measurement.

Future research should be focused on the investigation and explanation of the grain size/shape and different modifying agents influence on capacitance drop rate.

4. Conclusions

This study presents the characterization of modified BaTiO₃ ceramics for different grain sizes (40 nm and 112 nm). Modification was performed by a chemical solvent coating method, using metal-organic Yttrium salt in the mixture of organic solvents, in order to obtain uniformly modified samples. Microanalysis revealed the formation of ultra-thin second phase, which allowed effective consolidation during sintering. By using fractal analysis, successful reconstruction of grains and pore shapes was performed, which is important for the prediction and design of microstructure. Samples with higher grain size showed better compact state that led to a higher dielectric constant value. BT02-MOD-Y showed an excellent dielectric constant, over 2000, with a low dielectric loss of <1%. However, DC bias stability of smaller grain samples was significantly higher. BT02-MOD-Y showed sharp drop below 4 V, while KZM100-MOD-Y remained stable up to 80 V, with a slow drop to around 33% at 98 V. Adequate analyses of possible functions that can make an approximation of experimental curves in the best manner were successfully used, providing scaled reliability functions for capacitance change with DC bias. The practical application of fractal corrections based on α_s (grain surface) and α_p (inside pore surface), with the idea of establishing the relationship between the capacity and Curie temperature, was performed. The fractal characterization of grains and pores surfaces is important, because contacts between the grains and pores, considering the roughness of the surfaces, can influence the specific integranular relations and characteristics. This is especially important due to sensitive dielectric and ferroelectric characteristics that have influence in the field of further submicron parameters integrations, which represents the possible future research of deep level miniaturization. In this sense, surface fractal characterizations give more advanced details within this matter. In all of our previous research, the basic element is a practically existing intergranular fractal capacitor that is, capacity. This model already included the granular and pores’ surface effects integrated as intergranular capacity. Our results based on introduced complex fractal correction do not involve other possible factors, like grain size. For future research, we plan to extend all of these analyses and models with a goal to integrate, besides the surface and intergranular relations, the grain size and distribution phenomena.

According to our knowledge, this was the first time fractal correction has been used for connecting capacitance with Curie temperature. This novel approach in connecting capacitance with Curie temperature for specific experimental Yttrium concentration is opening new horizons for the experimental-theoretical calculations with the aim of explaining the phenomena corresponding to critical-crucial points from an experimental data set. Deeper insight in this field will be the scope of our future research.