Distributed Tracking Control for Connectivity-Preserving and Collision-Avoiding Formation Tracking of Underactuated Surface Vessels with Input Saturation

Abstract

This paper investigates the formation tracking control problem of a group of underactuated surface vessels (USVs) in the presence of model uncertainties and environmental disturbances. Additional constraints, such as collision avoidance, heterogeneous limited communication range and input saturation are also considered. A modified barrier Lyapunov function (BLF) is introduced to achieve the connectivity preservation, the collision avoidance and the distributed formation tracking. Extended state observer (ESO) is employed to estimate total disturbances consisting of environmental disturbances and model uncertainties. Auxiliary variables are introduced to deal with the underactuated problem and input saturation. A distributed controller is developed for each USV. Using the Lyapunov method analyze the stability of the system, it is proven that all signals are bounded and tracking errors converge to a neighborhood of the origin. Simulation results show that the proposed controller is practicable and effective.

1. Introduction

Formation tracking control of multiple underactuated surface vessels (USVs) has aroused great interest in recent years, owing to the fact that a team of USVs working together can accomplish more challenging missions than a single USV, such as surveillance, autonomous exploration, reconnaissance and perimeter security. A significant amount of research efforts has been focused on the control of multiple USVs. There are some challenges in USVs formation control, which are still worth mentioning. The first challenge is the amount of information being exchanged among the USVs in formation tracking control. In the beginning, USVs could sense their own positions, which are presented in a global coordinate system. Every USV controls its own positions to achieve the desired formation, which is prescribed by the desired positions in the global coordinate system [1,2,3]. The desired trajectory is available for all USVs. In this case, interactions are not necessarily needed because the desired formation can be achieved by position control of individual USVs [4]. This means that every USV should be equipped with advanced sensors, but this may not be practical. Considering the limitation of sensors, a distributed control law was proposed based on graph theory in [5,6,7,8]; it requires interactions to extract information from neighbors. The leader-following consensus problem of networked Lagrangian systems was investigated in [9]; both unknown control directions and uncertain dynamics were taken into consideration. Two types of distributed control protocols were proposed base on undirected graphs and directed graphs.

Output constraint is a challenge to USVs. A coordination strategy for multi-agent formation control based on a constraint function was proposed in [10]; this method could stabilize the formation error under a bounded tracking error assumption. A cooperative controller for a group of N USVs with limited sensing ranges was proposed in [11]; a novel potential function was used to solve the collision avoidance problem. Output-feedback cooperative controllers for mobile robots were designed in [12], where limited sensing was considered, and a control system based on potential functions incorporated with jump functions was designed. In [13], a group of USVs with a leader was considered, in order to make sure USVs function under asymmetric range and bearing constraints, the control design incorporated an asymmetric barrier Lyapunov function (BLF), and a fast convergent observer was designed to estimate the velocity of the leader. A nonlinearly transformed formation error without considering input saturation was developed in [14]; collision-avoiding, connectivity-preserving and limited communication ranges were considered simultaneously, and a distributed controller using the transformed error was designed for each USV.

In practice, designing a controller without considering the input saturation factor may lead closed-loop systems to instability. In [15], a basic controller base on two feedback functions was proposed, and the functions ensure the realization of the expected formation and input constraint. In [16], an output feedback controller was proposed by using additional controllers that are able to deal with the input saturation and underactuated problems simultaneously. In [17], an adaptive steering control method for uncertain ship dynamics with input constraint was designed; the method ensures the performance of the system under changing environmental conditions. In [18], uncertain strict-feedback nonlinear systems with input saturation and unknown disturbances were investigated, a dynamic surface control (DSC) combined with a backstepping method was proposed, and the effect of input saturation was approximated using a radial basis function neural network (RBFNN).

The model uncertainties and environmental disturbances are an important challenge. To overcome these difficulties, a hub motion estimation algorithm was designed in [19], where sensor fusion was employed. A controller that forces a USV to track arbitrary reference trajectories was proposed in [20]; a disturbance observer was presented to estimate environmental disturbances. In [21], an adaptive fuzzy controller for USV exposed to ocean currents and time-varying sideslip angle was designed, the dynamic uncertainties and environmental disturbances could be compensated by the fuzzy logic system. A practical adaptive sliding mode controller for an USV was proposed in [22], where an RBFNN combined with minimum the learning parameter method was designed to approximate the uncertain system dynamics online. In [23], neural network (NN)-based tracking control of underactuated systems was surveyed; unknown parameters and matched and mismatched disturbances were considered, and an adaptive control scheme incorporating multi-layer NNs was proposed.

In most of the above papers, the controller is designed by using the backstepping method, and Lyapunov function is used to analyze the stability of the system. In backstepping design, the computer explosion problem is universal. Tracking differentiators were used to solve the problem in [14].

Inspired by the above, in this paper we simultaneously consider model uncertainties, environmental disturbances, input saturation, collision avoidance and the limitations of communication distance. An extended state observer (ESO) is used for observing model uncertainties and environmental disturbances. A nonlinearly error transformation is provided for achieving the connectivity preservation, the collision avoidance and the distributed formation tracking. The USVs are interconnected through a directed communication network. Auxiliary variables are introduced to solve input saturation and the underactuated problem. Tracking differentiators are employed to calculating derivatives of virtual control variables. Finally, a distributed control law for each USV is constructed. The stability of the total closed-loop system is analyzed via Lyapunov theory.

The main contributions of this paper are summarized as follows. First, compared with [13], unknown model dynamics and environmental disturbances are estimated by ESO, and graph theory is combined with a distributed controller, which makes the controller suitable to be readily applied to formation control. Second, compared with [14], BLF is introduced into nonlinearly transformed formation error. In order to cope with input saturation, auxiliary variables are introduced into controller design.

The rest of this paper is organized as follows. The models of USVs, ESO and graph theory are introduced and the USV formation control problem is formulated in Section 2. Section 3 proposes a distributed controller and presents the stability analysis. Simulation results are shown and discussed in Section 4. Section 5 summarizes.

2. Preliminaries and Problem Formulation

2.1. Notion

The following notations will be used throughout this paper. $|·|$ is the absolute value. ${\lambda }_{min}$(.) and ${\lambda }_{max}$(.) represent minimum and maximum eigenvalue of a square matrix, respectively. $\parallel ·\parallel$ represents the Euclidean norm. $\mathrm{diag}\{·\}$ is diagonal matrix. ${\mathbb{R}}^{m\times n}$ represents the $m\times n$ dimensional Euclidean Space. $I_n$ represents the $n\times n$ dimensional identity matrix. i is used as the index of the USVs, i.e., $i=1,\cdots ,n$.

2.2. Graph Theory

Graph theory is used to describe the communication topology of $n+1$ USVs. A directed graph $G=\{V_G,\mathsf{\Theta }\}$ consists of a vertex set $V_G=\{0,1,\cdots ,n\}$ and $\mathsf{\Theta }=\{(i,j)\in \{1,\cdots ,n\}\times V_G\}$. $(i,j)\in \mathsf{\Theta }$ describes that information of the jth USV is available to the ith USV. The ith USV and the jth USV are said to be neighbors if ${\rho }_{ij}<L_j$, where $j=0,\cdots ,n$, $i\ne j$ and ${\rho }_{ij}$ is the distance between the ith USV and the jth USV. The neighbors of the ith USV are described by $N_i\left(j\right)=\{j\in V_G,(i,j)\in \mathsf{\Theta }\}$.

Assumption 1.

The total graph G is directed at $t=0$ and G has a directed spanning tree with the root node being the leader node.

2.3. Model of USVs

A group of USVs consisting of a leader and n followers are considered. Assume that the ith USV has an $x_i{z}_i$-plane of symmetry. Heave, pitch and roll motions are neglected. The body-fixed frame coordinate origin is set in the center-line of the USV. The mathematical model of the ith USV is defined as [24]:

$$\begin{array}{c}\hfill \begin{array}{c}{\dot{\eta }}_i=J_i\left({\psi }_i\right){\nu }_i\hfill \\ M_i{\dot{\nu }}_i=-C_i\left({\nu }_i\right){\nu }_i-D_i\left({\nu }_i\right){\nu }_i+d_i+{\tau }_i\hfill \end{array}\end{array}$$

(1)

where ${\eta }_i={[x_i,y_i,{\psi }_i]}^T$ is the vector denoting the ship position $(x_i,y_i)$ and yaw angle ${\psi }_i$ with coordinates in the earth-fixed frame, and ${\nu }_i={[u_i,v_i,r_i]}^T$ is the vector denoting surge, sway and yaw velocities of the ith USV in the body-fixed frame. $d_i={[d_{i,1},d_{i,2},d_{i,3}]}^T$ is the vector representing environmental disturbances. ${\tau }_i=[{\tau }_{i,u},0,$${\tau }_{i,r}]$${}^T$ is the control vector of the ith USV, which consists of the surge force ${\tau }_{i,u}$ and yaw moment ${\tau }_{i,r}$. The matrices $J_i\left({\psi }_i\right)$ are given by

$$J_i\left({\psi }_i\right)=\left[\begin{array}{ccc}\cos \left({\psi }_i\right)& -\sin \left({\psi }_i\right)& 0\\ \sin \left({\psi }_i\right)& \cos \left({\psi }_i\right)& 0\\ 0& 0& 1\end{array}\right],$$

$M_i=M_i^T\in {\mathbb{R}}^{3\times 3}$ is the inertia matrix of the ith USV. Here, we assume that the inertia matrices are diagonal. $C_i\left({\nu }_i\right)=-C_i^T\left({\nu }_i\right)\in {\mathbb{R}}^{3\times 3}$ represents a skew-symmetric matrix of Coriolis and centripetal term. $D_i\left({\nu }_i\right)\in {\mathbb{R}}^{3\times 3}$ is a nonlinear damping matrix.

The model of leader is defined as follows: a subscript “0” denotes the leader whose position ${\eta }_0={[x_0,y_0,{\psi }_0]}^T$ is generated by

$$\begin{array}{cc}\hfill {\dot{x}}_0& =u_0\cos \left({\psi }_0\right)-v_0\sin \left({\psi }_0\right),\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill {\dot{y}}_0& =u_0\sin \left({\psi }_0\right)+v_0\cos \left({\psi }_0\right),\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill {\dot{\psi }}_0& =r_0.\hfill \end{array}$$

(4)

Assumption 2.

${\eta }_0$, $u_0$, $v_0$, $r_0$ are bounded, and the data are available only for the ith USV satisfying $0\in N_i\left(0\right)$.

Assumption 3.

The disturbances $d_{i,h}$, $h=1,2,3$, are unknown but bounded so that $|d_{i,h}|\le {\overline{d}}_{i,h}$, ${\overline{d}}_{i,h}$ is a unknown positive constant.

Assumption 4.

$C_i\left({\nu }_i\right)$ and $D_i\left({\nu }_i\right)$ are assumed unknown.

2.4. Input Saturation

Considering input saturation, control vector ${\tau }_i$ is defined as follows:

$${\tau }_i=\left\{\begin{array}{cc}\hfill {\tau }_{i,max}& {\tau }_{ic}>{\tau }_{i,max}\hfill \\ \hfill {\tau }_{ic}& {\tau }_{i,min}\le {\tau }_{ic}\le {\tau }_{i,max}\hfill \\ \hfill {\tau }_{i,min}& {\tau }_{ic}<{\tau }_{i,min}\hfill \end{array}\right.$$

where ${\tau }_{i,max}$ and ${\tau }_{i,min}\in {\mathbb{R}}^3$ are the maximum and minimum control force and moment, respectively.

Define the mismatch function between input without saturation and with saturation as ${\varpi }_i={[{\varpi }_{i,u},0,{\varpi }_{i,r}]}^T$$={\tau }_{ic}-{\tau }_i$, where ${\tau }_{ic}={[{\tau }_{i,uc},0,{\tau }_{i,rc}]}^T$ with ${\tau }_{i,uc}$ and ${\tau }_{i,rc}$ are surge force and yaw moment calculated by the distributed controller, respectively. The saturated control in (1) is given by ${\tau }_i={\tau }_{ic}-{\varpi }_i$.

2.5. Extended State Observer

In this section, an ESO is used for estimating total disturbances consisting of the unknown term of the system matrix $C_i\left({\nu }_i\right)$, $D_i\left({\nu }_i\right)$ and environmental disturbances $d_i$ [25]. The ith USV dynamic (1) is rewritten as

$$\begin{array}{cc}\hfill {\dot{\eta }}_i& =J_i\left({\psi }_i\right){\nu }_i\hfill \\ \hfill {\dot{\nu }}_i& ={\zeta }_i+M_i^{-1}{\tau }_i,\hfill \end{array}$$

(5)

where ${\zeta }_i={[{\zeta }_{i,1},{\zeta }_{i,2},{\zeta }_{i,3}]}^T\in {\mathbb{R}}^3$ is total disturbances; it is a state vector expressed as

${\zeta }_i=M_i^{-1}(-C_i\left({\nu }_i\right)-D_i\left({\nu }_i\right){\nu }_i+d_i)$.

The following assumption is made during ESO design.

Assumption 5.

There exists a positive constant ${\zeta }_i^{*}$ satisfying $\left|\right|{\dot{\zeta }}_i\left|\right|\le {\zeta }_i^{*}$.

Remark 1.

Note that ${\zeta }_i=M_i^{-1}(-C_i\left({\nu }_i\right)-D_i\left({\nu }_i\right){\nu }_i+d_i)$. The velocity $v_i$ is bounded, and control inputs to drive USVs are bounded, and thus the derivative of $v_i$ is bounded. According to Assumption 3 and the disturbances $d_i$ are bounded, the derivative of $d_i$ is bounded. Then, Assumption 5 is reasonable.

An ESO is used for estimating the total disturbances as follows:

$$\begin{array}{c}\hfill \begin{array}{c}{\dot{\widehat{\eta }}}_i=-K_{i,o1}({\widehat{\eta }}_i-{\eta }_i)+J_i\left({\psi }_i\right){\widehat{\nu }}_i,\hfill \\ {\dot{\widehat{\nu }}}_i=-K_{i,o2}{J}_i^T\left({\psi }_i\right)(\widehat{{\eta }_i}-{\eta }_i)+{\widehat{\zeta }}_i+M_i^{-1}{\tau }_i,\hfill \\ {\dot{\widehat{\zeta }}}_i=-K_{i,o3}{J}_i^T\left({\psi }_i\right)({\widehat{\eta }}_i-{\eta }_i),\hfill \end{array}\end{array}$$

(6)

where ${\widehat{\eta }}_i={[{\widehat{x}}_i,{\widehat{y}}_i,{\widehat{\psi }}_i]}^T\in {\mathbb{R}}^3$, ${\widehat{\nu }}_i={[{\widehat{u}}_i,{\widehat{v}}_i,{\widehat{r}}_i]}^T\in {\mathbb{R}}^3$, $\widehat{\zeta }={[{\widehat{\zeta }}_{i,1},{\widehat{\zeta }}_{i,2},{\widehat{\zeta }}_{i,3}]}^T\in {\mathbb{R}}^3$, ${\widehat{x}}_i$, ${\widehat{y}}_i$, ${\widehat{\psi }}_i$, ${\widehat{u}}_i$, ${\widehat{v}}_i$, ${\widehat{r}}_i$, ${\widehat{\zeta }}_{i,1}$, ${\widehat{\zeta }}_{i,2}$, ${\widehat{\zeta }}_{i,3}$ are the estimates of $x_i$, $y_i$, ${\psi }_i$, $u_i$, $v_i$, $r_i$, ${\zeta }_{i,1}$, ${\zeta }_{i,2}$ and ${\zeta }_{i,3}$. $K_{i,o1}\in {\mathbb{R}}^{3\times 3}$, $K_{i,o2}\in {\mathbb{R}}^{3\times 3}$ and $K_{i,o3}\in {\mathbb{R}}^{3\times 3}$ are gain matrices.

From (5) and (6), the error dynamics of the observer can be expressed as

$$\begin{array}{cc}\hfill {\dot{\tilde{\eta }}}_i& =-K_{i,o1}\tilde{\eta }+J_i\left({\psi }_i\right){\tilde{\nu }}_i,\hfill \\ \hfill {\dot{\tilde{\nu }}}_i& =-K_{i,o2}{J}_i^T\left({\psi }_i\right)\tilde{\eta }+{\tilde{\zeta }}_i,\hfill \\ \hfill {\dot{\tilde{\zeta }}}_i& =-K_{i,o3}{J}_i^T\left({\psi }_i\right)\tilde{\eta }-{\dot{\zeta }}_i,\hfill \end{array}$$

(7)

where $\tilde{\eta }={\widehat{\eta }}_i-{\eta }_i$, $\tilde{\nu }={\widehat{\nu }}_i-{\nu }_i$ and ${\tilde{\zeta }}_i={\widehat{\zeta }}_i-{\zeta }_i$ are estimation errors. (7) can be rewritten as

$$\begin{array}{c}\hfill {\dot{\tilde{X}}}_i=-A_i{\tilde{X}}_i-B_i{\dot{\zeta }}_i,\end{array}$$

(8)

where ${\tilde{X}}_i={[{\tilde{\eta }}_i^T,{\tilde{\nu }}_i^T,{\tilde{\zeta }}_i^T]}^T\in {\mathbb{R}}^{9\times 1}$,

$$A_i=\left[\begin{array}{ccc}{K}_{i,o1}& -J_i\left({\psi }_i\right)& 0_{3\times 3}\\ K_{i,o2}{J}_i^T\left({\psi }_i\right)& 0_{3\times 3}& -I_3\\ K_{i,o3}{J}_i^T\left({\psi }_i\right)& 0_{3\times 3}& 0_{3\times 3}\end{array}\right]$$

(9)

and

$$B_i=\left[\begin{array}{c}{0}_{3\times 3}\\ 0_{3\times 3}\\ I_3\end{array}\right].$$

(10)

Theorem 1.

Consider the system (5) under Assumptions 2–5, the proposed observer (6) guarantees estimation error is bounded.

Proof. 

Consider the following Lyapunov function candidate as

$$\begin{array}{c}\hfill V_{io}=\frac{1}{2}{\tilde{X}}_i^T{\tilde{X}}_i,\end{array}$$

(11)

differentiating $V_{io}$ with respect to time and using (8),

$$\begin{array}{cc}\hfill {\dot{V}}_{io}=& {\tilde{X}}_i^T(-A_i{\tilde{X}}_i-B_i{\dot{\zeta }}_i),\hfill \end{array}$$

(12)

using Young’s inequality and Assumption 5, ${\tilde{X}}_i^T{B}_i{\dot{\zeta }}_i\le \frac{1}{2}{\tilde{X}}_i^T{B}_i{B}_i^T{\tilde{X}}_i+\frac{1}{2}{\dot{\zeta }}_i^T{\dot{\zeta }}_i\le \frac{1}{2}{\tilde{X}}_i^T{\tilde{X}}_i+\frac{1}{2}{\left({\zeta }_i^{*}\right)}^2$, then

$$\begin{array}{cc}\hfill {\dot{V}}_{io}& \le -({\lambda }_{min}\left(A_i\right)-\frac{1}{2}){\tilde{X}}_i^T{\tilde{X}}_i+\frac{1}{2}{\left({\zeta }_i^{*}\right)}^2.\hfill \end{array}$$

(13)

Select the appropriate parameters $K_{i,o1}$, $K_{i,o2}$ and $K_{i,o3}$ to make sure ${\lambda }_{min}\left(A_i\right)>\frac{1}{2}$. Equation (12) shows that the observer (6) ensures that the estimation error is bounded. □

2.6. Barrier Lyapunov Function

Definition 1

([26]). BLF is a scalar function, defined with respect to a system $\dot{x}=f\left(x\right)$ on D, which is continuous, positive definite, and an open region containing the origin. BLF has continuous first-order partial derivatives at every point of D and the property $V\left(x\right)\to \infty$ as x approaches the boundary of D, and satisfies $V\left(x\right(t\left)\right)\le b$, $\forall t\ge 0$ along the solution of $\dot{x}=f\left(x\right)$ for $x\left(0\right)\in D$ and some positive constant b.

To deal with the output constraint, a BLF is introduced as

$$V=\frac{1}{2}\ln \frac{k^2}{k^2-z^2},$$

(14)

where $k>0$ is a constant and z is variable of error.

Lemma 1.

If $\left|z\right|\le k$, $k\in \mathbb{R}$ is any constant [26], then

$$\ln \frac{k^2}{k^2-z^2}<\frac{z^2}{k^2-z^2}.$$

(15)

2.7. Problem Formulation

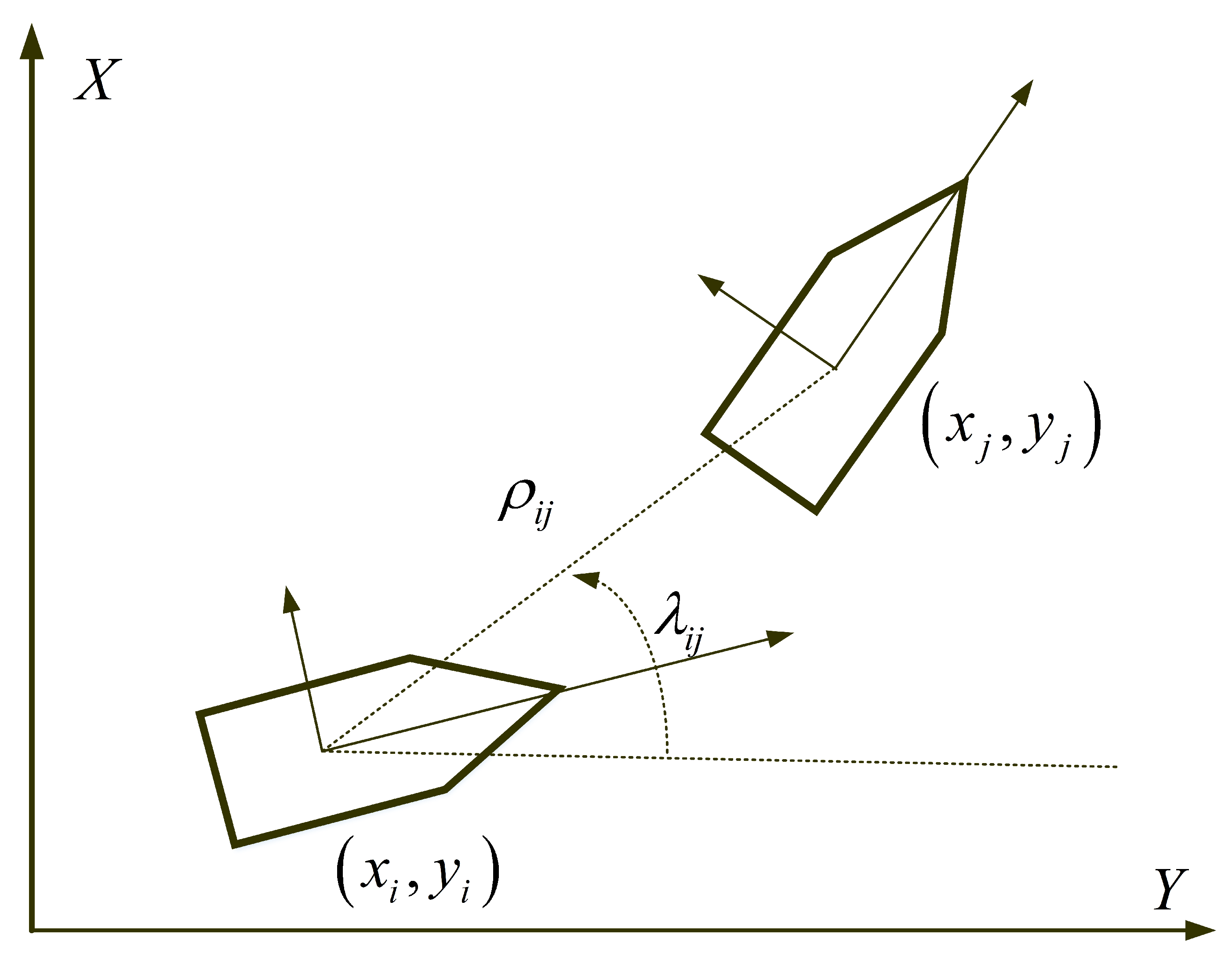
As shown in Figure 1, ${\rho }_{ij}$ is defined as the relative distance between the ith USV and the jth USV; its equation and differential equation are given as follows:

$$\begin{array}{cc}\hfill {\rho }_{ij}& =\sqrt{{(x_j-x_i)}^2+{(y_j-y_i)}^2},\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill {\dot{\rho }}_{ij}& =-u_i\cos ({\psi }_i-{\lambda }_{ij})+u_j\cos ({\psi }_j-{\lambda }_{ij})\hfill \\ \hfill & +v_i\sin ({\psi }_i-{\lambda }_{ij})-v_j\sin ({\psi }_j-{\lambda }_{ij}).\hfill \end{array}$$

(17)

${\lambda }_{ij}$ is defined as the relative angle between the ith USV and the jth USV; its equation and differential equation are given below:

$$\begin{array}{cc}\hfill {\lambda }_{ij}& =\arctan \frac{y_j-y_i}{x_j-x_i},\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill {\dot{\lambda }}_{ij}& =\frac{1}{{\rho }_{ij}}\{-u_i\sin ({\psi }_i-{\lambda }_{ij})+u_j\sin ({\psi }_j-{\lambda }_{ij})\hfill \\ \hfill & -v_i\cos ({\psi }_i-{\lambda }_{ij})+v_j\cos ({\psi }_j-{\lambda }_{ij})\}.\hfill \end{array}$$

(19)

The relative information ${\rho }_{ij}$ and ${\lambda }_{ij}$ can be measured by using local sensors, such as lidar and the gimbaled camera. If the ith USV and the jth USV are said to be neighbors, the ith USV is able to obtain the data ${\eta }_j$ and ${\nu }_j$ directly.

The control objective is to design a distributed controller for the ith USV to track the leader with model uncertainties, input saturation and limited communication ranges. Specifically, it is to achieve the following two objectives.

(1)

$\underline{R}<{\rho }_{ij}<\underline{L}$ and $\underline{\theta }<{\lambda }_{ij}<\overline{\theta }$.

where $\underline{R}=\max \{R_i,R_j\}$, $R_i$ and $R_j$ are minimum avoidance ranges of the ith USV and the jth USV, respectively. $\underline{L}=\min \{L_i,L_j\}$, $L_i$ and $L_j$ are maximum communication ranges of the ith USV and the jth USV, respectively. $\underline{\theta }$ and $\overline{\theta }$ are the minimum and maximum bearing angle of the ith USV.

(2)

${lim}_{t\to +\infty }|{\rho }_{ij}-{\rho }_{ij,d}|\le c_1$ and ${lim}_{t\to +\infty }|{\lambda }_{ij}-{\lambda }_{ij,d}|\le c_2$.

where $c_1$ and $c_2$ are positive constants that can be made small enough.

Remark 2.

Objective (1) means that the connectivity preservation and the collision avoidance are considered if the ith USV is a neighbor of the jth USV. Objective (2) represents the formation tracking problem.

3. Controller Design

In this section, the distributed controller is designed to meet the requirements of connectivity-preserving and collision avoidance. To satisfy these requirements, nonlinearly transformed error surfaces are introduced as follows:

$$\begin{array}{cc}\hfill q_{i,e}& =\sum _{j=0,j\ne i}^n{c}_{ij}(e_{ij,1}+e_{ij,2}),\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill {\psi }_{i,e}& =\sum _{j=0,j\ne i}^n{c}_{ij}({\psi }_i-{\psi }_{ij,a}),\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill u_{i,e}& =u_i-{\overline{\beta }}_{i,1}-{\gamma }_1\tanh \left({\alpha }_{i,1}\right),\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill v_{i,e}& =v_i-{\overline{\beta }}_{i,2}-\tanh \left({\alpha }_{i,2}\right),\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill r_{i,e}& =r_i-{\overline{\beta }}_{i,3}-{\gamma }_1\tanh \left({\alpha }_{i,3}\right),\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill {\omega }_{i,1}& ={\overline{\beta }}_{i,1}-{\beta }_{i,1},\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill {\omega }_{i,2}& ={\overline{\beta }}_{i,2}-{\beta }_{i,2},\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill {\omega }_{i,3}& ={\overline{\beta }}_{i,3}-{\beta }_{i,3}\hfill \end{array}$$

(27)

where $c_{ij}=1$ if the ith USV and the jth USV are neighbors, otherwise $c_{ij}=0$. $e_{ij,1}$ and $e_{ij,2}$ will be explained later. ${\psi }_{ij,a}$ is the approach angles expressed as:

$$\begin{array}{c}{\psi }_{ij,a}=[\arctan (g_{ij,1},g_{ij,2})-{\psi }_j]\tanh \left(g_{ij,3}\right)+{\psi }_j,\hfill \end{array}$$

(28)

where

$$\begin{array}{cc}\hfill g_{ij,1}& ={\rho }_{ij}\sin \left({\lambda }_{ij}\right)-{\rho }_{ij,d}\sin \left({\lambda }_{ij,d}\right),\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill g_{ij,2}& ={\rho }_{ij}\cos \left({\lambda }_{ij}\right)-{\rho }_{ij,d}\cos \left({\lambda }_{ij,d}\right),\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill g_{ij,3}& =\{{({\rho }_{ij,d}-{\rho }_{ij})}^2+{({\lambda }_{ij,d}-{\lambda }_{ij})}^2\}/{\gamma }_{ij},\hfill \end{array}$$

(31)

${\gamma }_{ij}$ is a positive constant, ${\beta }_{i,h}$, $h=1,2,3,$ is virtual control and ${\overline{\beta }}_{i,h}$, $h=1,2,3,$ is the signal derived from the following first-order low-pass filters $l_{i,h}{\dot{\overline{\beta }}}_{i,h}+{\overline{\beta }}_{i,h}={\beta }_{i,h}$, and $l_{i,h}>0$ is constant. ${\alpha }_{i,h}$, $h=1,2,3,$ is a time-varying and bounded auxiliary variable derived to deal with the underactuated problem and input saturation.

Inspired by the proposed asymmetric BLF method in [26], a nonlinearly transformed formation error combined with modified BLF was developed to achieve the connectivity preservation and the collision avoidance. Error surfaces $e_{ij,1}$ and $e_{ij,2}$ are defined as follows:

$$\begin{array}{cc}\hfill e_{ij,1}& =\frac{1}{2}\ln \left(\frac{a_{ij}^2}{a_{ij}^2-{\rho }_{ij,e}^2}\right),\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill e_{ij,2}& =\frac{1}{2}\ln \left(\frac{b_{ij}^2}{b_{ij}^2-{\lambda }_{ij,e}^2}\right),\hfill \end{array}$$

(33)

where

$$\begin{array}{cc}\hfill a_{ij}& =\frac{1-\mathrm{sign}\left({\rho }_{ij,e}\right)}{2}{a}_{ij,1}+\frac{1+\mathrm{sign}\left({\rho }_{ij,e}\right)}{2}{a}_{ij,2},\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill b_{ij}& =\frac{1-\mathrm{sign}\left({\lambda }_{ij,e}\right)}{2}{b}_{ij,1}+\frac{1+\mathrm{sign}\left({\lambda }_{ij,e}\right)}{2}{b}_{ij,2},\hfill \end{array}$$

(35)

$a_{ij,1}=\underline{R}-{\rho }_{ij,d}$, $a_{ij,2}=\underline{L}-{\rho }_{ij,d}$, ${\rho }_{ij,e}={\rho }_{ij}-{\rho }_{ij,d}$, ${\lambda }_{ij,e}={\lambda }_{ij}-{\lambda }_{ij,d}$, $b_{ij,1}=\underline{\theta }-{\lambda }_{ij,d}$ and $b_{ij,2}=\overline{\theta }-{\lambda }_{ij,d}$.

Remark 3.

The error surfaces $e_{ij,1}$ and $e_{ij,2}$ are introduced to realize the connectivity preservation and the collision avoidance. According to definition of objective (1) $\underline{R}<{\rho }_{ij}<\underline{L}$, then $\underline{R}-{\rho }_{ij,d}<{\rho }_{ij,e}<\underline{L}-{\rho }_{ij,d}$. From definition of $a_{ij,1}=\underline{R}-{\rho }_{ij,d}$ and $a_{ij,2}=\underline{L}-{\rho }_{ij,d}$, such that $a_{ij,1}<{\rho }_{ij,e}<a_{ij,2}$. One notes that $a_{ij,1}<0$ and $a_{ij,2}>0$, thus ${\rho }_{ij,e}>a_{ij,1}$ if ${\rho }_{ij,e}<0$ and ${\rho }_{ij,e}<a_{ij,2}$ if ${\rho }_{ij,e}>0$. It holds that the connectivity preservation and the collision avoidance are achieved as ${\rho }_{ij,e}>a_{ij,1}$ if ${\rho }_{ij,e}<0$ and ${\rho }_{ij,e}<a_{ij,2}$ if ${\rho }_{ij,e}>0$. From Equation (32), the definition of $e_{ij.1}$ implies $-a_{ij}<{\rho }_{ij,e}<a_{ij}$. According to the definition of $a_{ij}$, ${\rho }_{ij,e}<a_{ij,2}$ if ${\rho }_{ij,e}>0$, $a_{ij,1}<{\rho }_{ij,e}$ if ${\rho }_{ij,e}<0$. Then the distance constraint $\underline{R}<{\rho }_{ij}<\underline{L}$ can be satisfied. The angle constraint $\underline{\theta }<{\lambda }_{ij}<\overline{\theta }$ is similar to the distance constraint.

A distributed controller using the nonlinearly transformed error is presented.

Step 1:

Differentiating $q_{i,e}$ along (17) and (19) yields

$$\begin{array}{cc}\hfill {\dot{q}}_{i,e}=& \sum _{j=0,j\ne i}^n{c}_{ij}[(\frac{{\rho }_{ij,e}}{a_{ij}^2-{\rho }_{ij,e}^2}(-u_i\cos ({\psi }_i-{\lambda }_{ij})\hfill \\ \hfill & +u_j\cos ({\psi }_j-{\lambda }_{ij})+v_i\sin ({\psi }_i-{\lambda }_{ij})\hfill \\ \hfill & -v_j\sin ({\psi }_j-{\lambda }_{ij})-{\dot{\rho }}_{ij,d})\hfill \\ \hfill & +\frac{{\lambda }_{ij,e}}{{\rho }_{ij}(b_{ij}^2-{\lambda }_{ij,e}^2)}(-u_i\sin ({\psi }_i-{\lambda }_{ij})\hfill \\ \hfill & +u_j\sin ({\psi }_j-{\lambda }_{ij})-v_i\cos ({\psi }_i-{\lambda }_{ij})\hfill \\ \hfill & +v_j\cos ({\psi }_j-{\lambda }_{ij}))-{\dot{\lambda }}_{ij,d}]\hfill \\ \hfill =& \sum _{j=0,j\ne i}^n{c}_{ij}{A}_{ij}{B}_{ij}(-{\mathsf{\Xi }}_{ij,1}{z}_i+{\mathsf{\Xi }}_{ij,2}{z}_j-D_{ij,d}),\hfill \end{array}$$

(36)

where

$$\begin{array}{c}\hfill A_{ij}=\left[\begin{array}{cc}\frac{{\rho }_{ij,e}}{a_{ij}^2-{\rho }_{ij,e}^2}& \frac{{\lambda }_{ij,e}}{b_{ij}^2-{\lambda }_{ij,e}^2}\end{array}\right],\end{array}$$

(37)

$B_{ij}=\mathrm{diag}\{1,\frac{1}{{\rho }_{ij}}\}$,

$${\mathsf{\Xi }}_{ij,1}=\left[\begin{array}{cc}\cos ({\psi }_i-{\lambda }_{ij})& -\sin ({\psi }_i-{\lambda }_{ij})\\ \sin ({\psi }_i-{\lambda }_{ij})& \cos ({\psi }_i-{\lambda }_{ij})\end{array}\right],$$

(38)

$${\mathsf{\Xi }}_{ij,2}=\left[\begin{array}{cc}\cos ({\psi }_j-{\lambda }_{ij})& -\sin ({\psi }_j-{\lambda }_{ij})\\ \sin ({\psi }_j-{\lambda }_{ij})& \cos ({\psi }_j-{\lambda }_{ij})\end{array}\right],$$

(39)

$z_i={[u_i,v_i]}^T$, $z_j={[u_j,v_j]}^T$ and $D_{ij,d}={[{\dot{\rho }}_{ij,d},{\dot{\lambda }}_{ij,d}]}^T$. Then, ${\dot{q}}_{i,e}$ is rewritten as follows:

$${\dot{q}}_{i,e}=A_i{B}_i(-{\mathsf{\Xi }}_{i,1}{z}_i+{\mathsf{\Xi }}_{i,2}-D_{i,d}),$$

(40)

where

$$A_i=\left[\begin{array}{ccc}{c}_{i,h_{i,1}}{A}_{i,h_{i,1}},& \cdots & c_{i,h_{i,B}}{A}_{i,h_{i,B}}\end{array}\right]\in {\mathbb{R}}^{1\times 2n},$$

(41)

$$B_i=\left[\begin{array}{ccc}{B}_{i,h_{i,1}}& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & B_{i,h_{i,B}}\end{array}\right]\in {\mathbb{R}}^{2n\times 2n},$$

(42)

$${\mathsf{\Xi }}_{i,1}=\left[\begin{array}{c}{\mathsf{\Xi }}_{i{h}_{i,1},1}\\ ⋮\\ {\mathsf{\Xi }}_{i{h}_{i,B},1}\end{array}\right]\in {\mathbb{R}}^{2n\times 2},$$

(43)

$${\mathsf{\Xi }}_{i,2}=\left[\begin{array}{c}{\mathsf{\Xi }}_{i{h}_{i,1},2}{z}_{h_{i,1}}\\ ⋮\\ {\mathsf{\Xi }}_{i{h}_{i,B},2}{z}_{h_{i,B}}\end{array}\right]\in {\mathbb{R}}^{2n\times 1},$$

(44)

and

$$D_{i,d}=\left[\begin{array}{c}{D}_{i{h}_{i,1},d}\\ ⋮\\ D_{i{h}_{i,B},d}\end{array}\right]\in {\mathbb{R}}^{2n\times 1}.$$

(45)

In these expressions, $h_{i,1},\cdots ,h_{i,B}$ are the elements of the set $h_i=\{h_{i,1},\cdots ,h_{i,B}\}=\left\{j\right|c_{ij}\ne 0\}$.

Define $f_i={\left[f_{i,1}{f}_{i,2}\right]}^T=A_i{B}_i{\mathsf{\Xi }}_{i,1}$, and $f_i$ is bounded and $\parallel f_i\parallel <f_i^{*}$, $f_i^{*}$ is an unknown positive constant.

Remark 4.

From the definition of ${\mathsf{\Xi }}_{i,1}$, $A_i$ and $B_i$ and Equations (41)–(43), one notes that $\parallel {\mathsf{\Xi }}_{i,1}\parallel \le 1$, $A_i$ and $B_i$ are bounded, so $\parallel f_i\parallel <f_i^{*}$ is reasonable.

In order to stabilize ${\dot{q}}_{i,e}$, the desired virtual control ${\beta }_i$ is given as:

$$\begin{array}{c}\hfill {\beta }_i={\overline{\mathsf{\Xi }}}_{i,1}^{-1}(K_i{B}_i^{-1}{P}_i+{\mathsf{\Xi }}_{i,2}-D_{i,d})+{\overline{f}}_{i,2},\end{array}$$

(46)

where ${\beta }_i={[{\beta }_{i,1},{\beta }_{i,2}]}^T$, ${\overline{\mathsf{\Xi }}}_{i,1}^{-1}={\mathsf{\Xi }}_{i,1}^T{\left({\mathsf{\Xi }}_{i,1}{\mathsf{\Xi }}_{i,1}^T\right)}^{-1}$, $K_i\in {\mathbb{R}}^{2n\times 2n}$ is a positive definite matrix,

$$P_i={\left[\begin{array}{ccc}{P}_{i,h_{i,1}}& \cdots & P_{i,h_{i,B}}\end{array}\right]}^T\in {\mathbb{R}}^{2n\times 1},$$

(47)

$h_{i,1},\cdots ,h_{i,B}$ are the elements of the set $h_i=\left\{j\right|c_{ij}\ne 0\}$, $P_{i,h_i}=[{\rho }_{i{h}_i,e},{\lambda }_{i{h}_i,e}]$, ${\overline{f}}_{i,2}={[0,\tanh (f_{i,2}/{ϵ}_{i,1})]}^T$, and ${ϵ}_{i,1}>0$ is a constant. Notice that the matrix $B_i$ is invertible owing to ${\rho }_{ij}\ne 0$. Notice that based on Lemma 1, we have $\ln \frac{k^2}{k^2-z^2}<\frac{z^2}{k^2-z^2}$ and define $k_{i,1}={\lambda }_{min}\left(K_{i,1}\right)$, then $-A_i{K}_{i,1}{P}_i<-2k_{i,1}{q}_{i,e}$.

Step 2:

Differentiating ${\psi }_{i,e}$ along (21) yields

$$\begin{array}{cc}\hfill {\dot{\psi }}_{i,e}=& {\vartheta }_{i,1}{r}_i-{\vartheta }_{i,2},\hfill \end{array}$$

(48)

where ${\vartheta }_{i,1}={\sum }_{j=0,j\ne i}^n{c}_{ij}$ and ${\vartheta }_{i,2}={\sum }_{j=0,j\ne i}^n{c}_{ij}{\dot{\psi }}_{ij,a}$.

The stabilizing function ${\beta }_{i,3}$ is chosen as:

$$\begin{array}{c}{\beta }_{i,3}=\frac{1}{{\vartheta }_{i,1}}(-k_{i,2}{\psi }_{i,e}+{\vartheta }_{i,2}),\hfill \end{array}$$

(49)

where $k_{i,2}$ is a positive constant.

Remark 5.

The virtual controllers (46) and (49) are composed of the error surfaces (20) and (21), the distributed vectors $P_i$, and matrices ${\mathsf{\Xi }}_{i,1}$ and ${\mathsf{\Xi }}_{i,2}$. The link weights $c_{ij}$ of the distributed error surfaces (20) and (21) depict the directed graph among USVs that satisfies Assumption 1. Thus, the proposed formation approach is in a fully distributed formation manner.

Step 3:

Differentiating (22)–(24)

$$\begin{array}{cc}\hfill {\dot{u}}_{i,e}& ={\zeta }_{i,1}+({\tau }_{i,uc}-{\varpi }_{i,u})/m_{i,11}-{\dot{\overline{\beta }}}_{i,1}-{\gamma }_1\frac{{\dot{\alpha }}_{i,1}}{{\cosh }^2\left({\alpha }_{i,1}\right)},\hfill \end{array}$$

(50)

$$\begin{array}{cc}\hfill {\dot{v}}_{i,e}& ={\zeta }_{i,2}-{\dot{\overline{\beta }}}_{i,2}-\frac{{\dot{\alpha }}_{i,2}}{{\cosh }^2\left({\alpha }_{i,2}\right)},\hfill \end{array}$$

(51)

$$\begin{array}{cc}\hfill {\dot{r}}_{i,e}& ={\zeta }_{i,3}+({\tau }_{i,rc}-{\varpi }_{i,r})/m_{i,33}-{\dot{\overline{\beta }}}_{i,3}-{\gamma }_1\frac{{\dot{\alpha }}_{i,3}}{{\cosh }^2\left({\alpha }_{i,3}\right)}.\hfill \end{array}$$

(52)

The update law of additional controls ${\alpha }_{i,1}$, ${\alpha }_{i,2}$ and ${\alpha }_{i,3}$ is given by

$$\begin{array}{cc}\hfill {\dot{\alpha }}_{i,1}& ={\cosh }^2\left({\alpha }_{i,1}\right)\{-T_u{\alpha }_{i,1}-{\varpi }_{i,u}/m_{i,11}\}/{\gamma }_1,\hfill \end{array}$$

(53)

$$\begin{array}{cc}\hfill {\dot{\alpha }}_{i,2}& ={\cosh }^2\left({\alpha }_{i,2}\right)({\widehat{\zeta }}_{i,2}+k_{i,4}{v}_{i,e}-f_{i,2}-{\dot{\overline{\beta }}}_{i,2}),\hfill \end{array}$$

(54)

$$\begin{array}{cc}\hfill {\dot{\alpha }}_{i,3}& ={\cosh }^2\left({\alpha }_{i,3}\right)\{-T_r{\alpha }_{i,3}-{\varpi }_{i,r}/m_{i,33}\}/{\gamma }_1,\hfill \end{array}$$

(55)

where $k_{i,4}$, $T_u$ and $T_r>0$ are positive constants.

Step 4:

To stabilize the system, kinetic control laws are designed as

$$\begin{array}{cc}\hfill {\tau }_{i,uc}& =-k_{i,3}{u}_{i,e}-m_{i,11}({\widehat{\zeta }}_{i,1}+T_u{\alpha }_{i,1}-{\dot{\overline{\beta }}}_{i,1})+f_{i,1},\hfill \end{array}$$

(56)

$$\begin{array}{cc}\hfill {\tau }_{i,rc}& =-k_{i,5}{r}_{i,e}-m_{i,33}({\widehat{\zeta }}_{i,3}+T_r{\alpha }_{i,3}-{\dot{\overline{\beta }}}_{i,3})-{\psi }_{i,e}{\vartheta }_{i,1},\hfill \end{array}$$

(57)

where $k_{i,3}$ and $k_{i,5}$ are positive constants.

Theorem 2.

Consider that the system consist of USV (1), the control law (56) and (57), the observer (6) and the update law of additional controls (53)–(55), with environmental disturbances, input saturation and limited communication ranges under Assumptions 1–5. The proposed controller guarantees all signals in the closed-loop system are bounded and two objectives are achieved.

Proof. 

Consider the Lyapunov function as follows:

$$V=\sum _{i=1}^n\{q_{i,e}+{\psi }_{i,e}^2+1/2(m_{i,11}{u}_{i,e}^2+v_{i,e}^2+m_{i,33}{r}_{i,e}^2)+\sum _{h=1}^3{\omega }_{i,h}^2\},$$

(58)

along with (40), (48) and (50)–(52), the differentiation of V is given as

$$\begin{array}{cc}\hfill \dot{V}=& \sum _{i=1}^n\{A_i{B}_i(-{\mathsf{\Xi }}_{i,1}{z}_i+{\mathsf{\Xi }}_{i,2}-D_{i,d})+{\psi }_{i,e}({\vartheta }_{i,1}{r}_i-{\vartheta }_{i,2})\hfill \\ \hfill & +u_{i,e}(m_{i,11}({\zeta }_{i,1}-{\dot{\overline{\beta }}}_{i,1}-{\gamma }_1\frac{{\dot{\alpha }}_{i,1}}{{\cosh }^2\left({\alpha }_{i,1}\right)})+{\tau }_{i,uc}\hfill \\ \hfill & -{\varpi }_{i,u})+v_{i,e}({\zeta }_{i,2}-{\dot{\overline{\beta }}}_{i,2}-{\gamma }_1\frac{{\dot{\alpha }}_{i,2}}{\cos h^2\left({\alpha }_{i,2}\right)})\hfill \\ \hfill & +r_{i,e}(m_{i,33}({\zeta }_{i,3}-{\dot{\overline{\beta }}}_{i,3}-{\gamma }_1\frac{{\dot{\alpha }}_{i,3}}{\cos h^2\left({\alpha }_{i,3}\right)})\hfill \\ \hfill & +{\tau }_{i,rc}-{\varpi }_{i,r})+\sum _{h=1}^3{\omega }_{i,h}({\dot{\overline{\beta }}}_{i,h}-{\dot{\beta }}_{i,h})\},\hfill \end{array}$$

(59)

where $h=1,2,3$.

Furthermore, substituting virtual controls (46) and (49), additional controls (53)–(55), control laws (56) and (57) into (59) leads to

$$\begin{array}{cc}\hfill \dot{V}\le & \sum _{i=1}^n\{-2k_{i,1}{q}_{i,e}-k_{i,2}{\psi }_{i,e}^2-k_{i,3}{u}_{i,e}^2-k_{i,4}{v}_{i,e}^2\hfill \\ \hfill & -k_{i,5}{r}_{i,e}^2-f_i(z_{i,e}+{\overline{\alpha }}_i+{\omega }_i+{\overline{f}}_{i,2}+{\gamma }_1{\overrightarrow{\alpha }}_{i,1})\hfill \\ \hfill & +{\psi }_{i,e}{\vartheta }_{i,1}({\omega }_{i,3}+{\gamma }_1\tanh \left({\alpha }_{i,3}\right))\hfill \\ \hfill & -u_{i,e}(m_{i,11}{\tilde{\zeta }}_{i,1}-f_{i,1})-v_{i,e}({\tilde{\zeta }}_{i,2}-f_{i,2})\hfill \\ \hfill & -r_{i,e}{m}_{i,33}{\tilde{\zeta }}_{i,3}-\sum _{h=1}^3{\omega }_{i,h}(\frac{{\omega }_{i,h}}{l_{i,h}}+{\dot{\beta }}_{i,h})\},\hfill \end{array}$$

(60)

where $h=1,2,3$, ${\overline{\alpha }}_i={[0,\tanh \left({\alpha }_{i,2}\right)]}^T$, $z_{i,e}=z_i-{\overline{\alpha }}_i-{\omega }_i-{\beta }_i-{\gamma }_1{\overrightarrow{\alpha }}_{i,1}$, ${\omega }_i={[{\omega }_{i,1},{\omega }_{i,2}]}^T$ and ${\overrightarrow{\alpha }}_{i,1}={[\tanh \left({\alpha }_{i,1}\right),0]}^T$.

From the definition of $f_i$ and $z_{i,e}$, the following can be attained.

$$\begin{array}{c}\hfill f_i{z}_{i,e}=u_{i,e}{f}_{i,1}+v_{i,e}{f}_{i,2},\end{array}$$

(61)

where $f_i=\left[f_{i,1}{f}_{i,2}\right]$. From [27], we have

$$\begin{array}{cc}\hfill -f_i({\overline{\alpha }}_i+{\overline{f}}_{i,2})& =-f_{i,2}\tanh \left({\alpha }_i\right)-f_{i,2}\tanh (f_{i,2}/{ϵ}_{i,1})\hfill \\ \hfill & \le |f_{i,2}|-f_{i,2}\tanh (f_{i,2}/{ϵ}_{i,1})\le 0.2875{ϵ}_{i,1}.\hfill \end{array}$$

(62)

According to ${\gamma }_1\left|\right|{\overrightarrow{\alpha }}_{i,1}\left|\right|\le {\gamma }_1$ and $\left|\right|f_i\left|\right|\le f_i^{*}$, we have

$$\begin{array}{c}\hfill -f_i{\gamma }_1{\overrightarrow{\alpha }}_{i,1}\le {\gamma }_1{f}_i^{*}.\end{array}$$

(63)

According to Young’s inequality, then:

$$\begin{array}{cc}\hfill {\psi }_{i,e}{\vartheta }_{i,1}{\gamma }_1& \le \frac{1}{2}{\psi }_{i,e}^2+\frac{1}{2}{\vartheta }_{i,1}^2{\gamma }_1^2,\hfill \end{array}$$

(64)

$$\begin{array}{cc}\hfill -u_{i,e}{m}_{i,11}{\tilde{\zeta }}_{i,1}& \le \frac{1}{2}{u}_{i,e}^2+\frac{1}{2}{m}_{i,11}^2{\tilde{\zeta }}_{i,1}^2,\hfill \end{array}$$

(65)

$$\begin{array}{cc}\hfill -v_{i,e}{\tilde{\zeta }}_{i,2}& \le \frac{1}{2}{v}_{i,e}^2+\frac{1}{2}{\tilde{\zeta }}_{i,2}^2,\hfill \end{array}$$

(66)

$$\begin{array}{cc}\hfill -r_{i,e}{m}_{i,33}{\tilde{\zeta }}_{i,3}& \le \frac{1}{2}{r}_{i,e}^2+\frac{1}{2}{m}_{i,33}^2{\tilde{\zeta }}_{i,3}^2,\hfill \end{array}$$

(67)

Equation (60) can be rewritten as follows:

$$\begin{array}{cc}\hfill \dot{V}\le & \sum _{i=1}^n\{-2k_{i,1}{q}_{i,e}-(k_{i,2}-\frac{1}{2}){\psi }_{i,e}^2-(k_{i,3}-\frac{1}{2})u_{i,e}^2\hfill \\ \hfill & -(k_{i,4}-\frac{1}{2})v_{i,e}^2-(k_{i,5}-\frac{1}{2})r_{i,e}^2+\frac{1}{2}{m}_{i,11}^2{\tilde{\zeta }}_{i,1}^2\hfill \\ \hfill & +\frac{1}{2}{\tilde{\zeta }}_{i,2}^2+\frac{1}{2}{m}_{i,33}^2{\tilde{\zeta }}_{i,3}^2-f_i{\omega }_i+{\psi }_{i,e}{\vartheta }_{i,1}{\omega }_{i,3}\hfill \\ \hfill & -\sum _{h=1}^3{\omega }_{i,h}(\frac{{\omega }_{i,h}}{l_{i,h}}+{\dot{\beta }}_i)\}+{\mu }_1\hfill \end{array}$$

(68)

where ${\mu }_1={\sum }_{i=1}^n\{({\vartheta }_{i,1}^2{\gamma }_1^2)/2+{\gamma }_1{f}_i^{*}+0.2875{ϵ}_{i,1}\}$.

Define $\overline{m}=max\{\frac{1}{2}{m}_{i,11}^2,\frac{1}{2},\frac{1}{2}{m}_{i,33}^2\}$, then

$$\begin{array}{cc}\hfill \frac{1}{2}{m}_{i,11}^2{\tilde{\zeta }}_{i,1}^2+\frac{1}{2}{\tilde{\zeta }}_{i,2}^2+\frac{1}{2}{m}_{i,33}^2{\tilde{\zeta }}_{i,3}^2\le & \overline{m}{\tilde{\zeta }}_i^T{\tilde{\zeta }}_i\hfill \\ \hfill \le & \overline{m}{\tilde{X}}_i^T{\tilde{X}}_i.\hfill \end{array}$$

(69)

Consider the total function

$$\begin{array}{c}\hfill V_t=V+\sum _{i=1}^n{V}_{io},\end{array}$$

(70)

Using (12), (68) and (69), the derivative of $V_t$ is given by

$$\begin{array}{cc}\hfill {\dot{V}}_t\le & \sum _{i=1}^n\{-2k_{i,1}{q}_{i,e}-(k_{i,2}-\frac{1}{2}){\psi }_{i,e}^2-(k_{i,4}-\frac{1}{2})u_{i,e}^2\hfill \\ \hfill & -(k_{i,3}-\frac{1}{2})v_{i,e}^2-(k_{i,5}-\frac{1}{2})r_{i,e}^2-\sum _{h=1}^3(\frac{{\omega }_{i,h}^2}{l_{i,h}}-\hfill \\ \hfill & \frac{{\omega }_{i,h}^2{\mathsf{\Omega }}_{i,h}^2}{2{\varrho }_i})-({\lambda }_{min}\left(A_i\right)-\frac{1}{2}-\overline{m}){\tilde{X}}_i^T{\tilde{X}}_i\}+{\mu }_2,\hfill \end{array}$$

(71)

where ${\mathsf{\Omega }}_{i,1}={\dot{\beta }}_{i,1}-f_{i,1}$, ${\mathsf{\Omega }}_{i,2}={\dot{\beta }}_{i,2}-f_{i,2}$ and ${\mathsf{\Omega }}_{i,3}={\dot{\beta }}_{i,3}+{\psi }_{i,e}{\vartheta }_{i,1}$. According to Young’s inequality, ${\omega }_{i,h}{\mathsf{\Omega }}_{i,h}$$\le \frac{1}{2{\varrho }_i}{\omega }_{i,h}^2{\mathsf{\Omega }}_{i,h}^2+\frac{{\varrho }_i}{2}$ with ${\varrho }_i$ being a small positive constant and ${\mu }_2={\mu }_1+\frac{3{\varrho }_i}{2}+{\sum }_{i=1}^n\frac{1}{2}{\left({\zeta }_i^{*}\right)}^2$. Consider the sets ${\prod }_i:\{{\sum }_{j=1}^i{q}_{j,e}$$+{\psi }_{j,e}^2+m_{j,11}{u}_{j.e}^2+v_{j,e}^2+m_{j,33}{r}_{j,e}^2+{\sum }_{h=1}^3{\omega }_{j,h}^2+\frac{1}{2}{\tilde{X}}_j^T{\tilde{X}}_j\le 2{\rho }_{\rho }\}$ and $O_o:=\{{\eta }_0^T{\eta }_0+{\dot{\eta }}_0^T{\dot{\eta }}_0\le {\eta }_0^{*}\}$ where ${\rho }_{\rho }$ and ${\eta }_0^{*}$ are positive constants. Since ${\prod }_i\times O_o$ is compact in ${\mathbb{R}}^{8i+6}$, there exist a constant $s_{i,h}>0$ such that $|{\mathsf{\Omega }}_{i,h}|\le s_{i,h}$ on ${\prod }_i\times O_o$.

Choosing $k_{i,n}=\frac{1}{2}+k_{i,n}^{*}$ with $n=2,3,4,5$, and constants $k_{i,n}^{*}\ge 0$ and $\frac{1}{l_{i,h}}=s_{i,h}^2/\left(2{\varrho }_i\right)+l_{i,h}^{*}$ with $l_{i,h}^{*}>0$ is a constants. The following can be attained:

$$\begin{array}{cc}\hfill {\dot{V}}_t\le & \sum _{i=1}^n[-2k_{i,1}{q}_{i,e}-k_{i,2}^{*}{\psi }_{i,e}^2-k_{i,3}^{*}{u}_{i,e}^2-k_{i,4}^{*}{v}_{i,e}^2\hfill \\ \hfill & -k_{i,5}^{*}{r}_{i,e}^2-\sum _{h=1}^3{l}_{i,h}^{*}{\mathsf{\omega }}_{i,h}^2-\sum _{h=1}^3(1-\frac{{\mathsf{\Omega }}_{i,h}^2}{s_{i,h}^2})\frac{{\omega }_{i,h}^2{s}_{i,h}^2}{2{\varrho }_i}\hfill \\ \hfill & -({\lambda }_{min}\left(A_i\right)-\frac{1}{2}-\overline{m}){\tilde{X}}_i^T{\tilde{X}}_i]+{\mu }_2.\hfill \end{array}$$

(72)

Owing to $|{\mathsf{\Omega }}_{i,h}|\le s_{i,h}$ on $V={\rho }_{\rho }$, the inequality (72) becomes

$$\begin{array}{c}{\dot{V}}_t\le -{\mu }_0{V}_t\left(t\right)+{\mu }_2,\hfill \end{array}$$

(73)

where ${\mu }_0=\min \{2k_{i,1},2k_{i,2},2k_{i,3}^{*}/m_{i,11},2k_{i,4}^{*},2k_{i,5}^{*}/m_{i,33},$ $2l_{i,h}^{*},{\lambda }_{min}\left(A_i\right)-\frac{1}{2}-\overline{m}\}$. This implies that:

$$\begin{array}{c}\hfill V_t\left(t\right)\le (V_t\left(0\right)-\frac{{\mu }_2}{{\mu }_0})e^{-{\mu }_{0}t}+\frac{{\mu }_2}{{\mu }_0}.\end{array}$$

(74)

From the definition of $V_t$, it can be concluded that $q_{i,e}$ is bounded. From Assumption 1, there exists i and j such that $\underline{R}<{\rho }_{ij}\left(0\right)<\underline{L}$ for $j\in N_i\left(0\right)$ where $j=0,\cdots ,N,$ and $i\ne j$. From the definition of $q_{i,e}$, the boundedness of $q_{i,e}\left(t\right)$ leads to $\underline{R}<{\rho }_{ij}<\underline{L}$ and $\underline{\theta }<{\lambda }_{ij}<\overline{\theta }$. Thus, if $\underline{R}<{\rho }_{ij}\left(0\right)<\underline{L}$ for $j\in N_i\left(0\right)$, then $\underline{R}<{\rho }_{ij}\left(t\right)<\underline{L}$ and $\underline{\theta }<{\lambda }_{ij}\left(t\right)<\overline{\theta }$. This completes the proof of (1).

From (74), $q_e={[q_{1.e},\cdots ,q_{N,e}]}^T$ exponentially converges to the compact set $\prod =\{q_e|\parallel q_e\parallel \le 2{\mu }_2/{\mu }_0\}$ that can be made arbitrarily small by adjusting $u_0$. From (20), $e_{ij,1}$ and $e_{ij,2}$ can be reduced to be arbitrarily small; this leads to the conclusion that ${\rho }_{ij,e}$ and ${\lambda }_{ij,e}$ can be also reduced to be arbitrarily small. Then, it holds that ${lim}_{x\to +\infty }|{\rho }_{ij}\left(t\right)-{\rho }_{ij,d}|\le c_1$ and ${lim}_{x\to +\infty }|{\lambda }_{ij}\left(t\right)-{\lambda }_{ij,d}|\le c_2$, and the proof of (2) is completed. □

The distributed controller is composed of the local virtual control laws (46) and (49) and the auxiliary dynamics and the actual control laws (56) and (57). In (1), there is no control input on the sway dynamics, and this causes difficulty in the control of sway. To make sure of the stability of the sway dynamics, auxiliary variable ${\alpha }_{i,2}$ is introduced to solve the problem, and auxiliary variables ${\alpha }_{i,1}$ and ${\alpha }_{i,3}$ are introduced to solve the problem of input saturation. The $\tanh (.)$ function guarantees that the introduced variables $\tanh \left({\alpha }_{i,h}\right)$, $h=1,2,3$ are smooth and differentiable. By designing ${\dot{\alpha }}_{i,2}$ in (54) and substituting it into (59), the boundedness and convergence of $v_{i,e}$ can be achieved.

According to (72), the following conditions determine the stability of the entire system: $k_{i,1}>0$, $k_{i,2}>\frac{1}{2}$, $k_{i,3}>\frac{1}{2}$, $k_{i,4}>\frac{1}{2}$, $k_{i,5}>\frac{1}{2}$, and ${\lambda }_{min}\left(A_i\right)>\frac{1}{2}+\overline{m}$. According to (13), the size of the eigenvalues of parameters $K_{i,o1}$, $K_{i,o2}$ and $K_{i,o3}$ determines the convergence speed of estimation error. Note that ${\lambda }_{min}\left(A_i\right)$ affects both the stability of the observer and of the whole system.

4. Simulation Results and Discussion

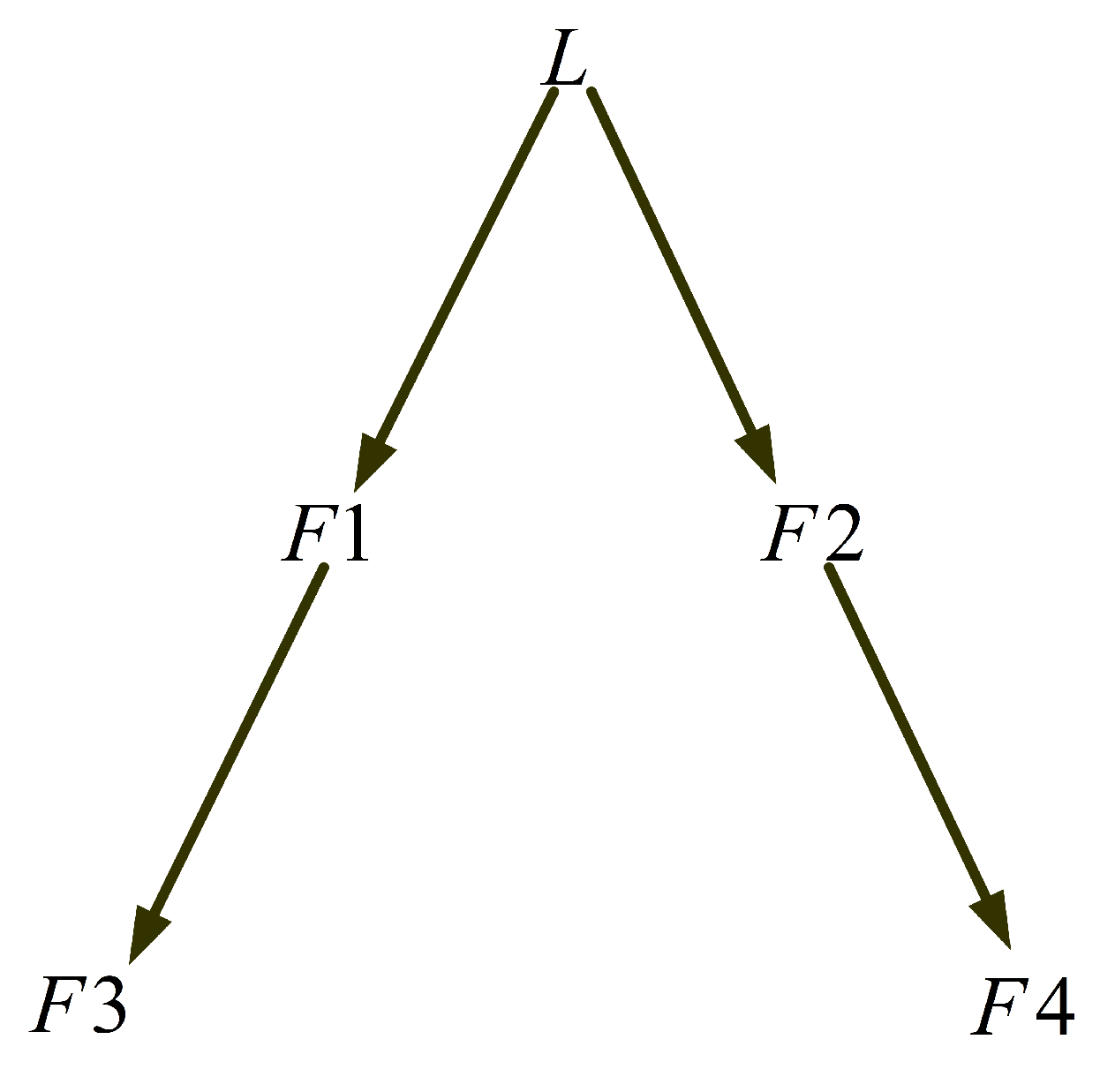
In this section, the formation is composed of one leader and four followers. From the defined heterogeneous communication and avoidance ranges, the directed communication graph is given in Figure 2. The model of USV is taken from [28], and the main parameters are $M_i=\mathrm{diag}\{23.8,33.8,2.764\}$,

$$D_i=\left[\begin{array}{ccc}2& 0& 0\\ 0& 7& 0.1\\ 0& 0.1& 0.5\end{array}\right].$$

Environmental disturbances are chosen as a superposition of zero mean white noise and constant interference. Standard deviation of white noise is chosen as 0.4, constant interference is chosen as 0.1. The parameters for ESO are set to $K_{i,o1}=7·I_3$, $K_{i,o2}=45·I_3$, and $K_{i,o3}=80·I_3$. The control forces and moment are constrained as ${\tau }_{i,max}={[{\tau }_{i,umax},0,{\tau }_{i,rmax}]}^T$, ${\tau }_{i,min}={[{\tau }_{i,umin},0,{\tau }_{i,rmin}]}^T$, ${\tau }_{i,umax}=-{\tau }_{i,umin}=2\mathrm{N}$, and ${\tau }_{i,rmax}=-{\tau }_{i,rmin}=1.5\mathrm{Nm}$. The design parameters of control laws are chosen as $K_i=0.3·I_2$, $k_{i,2}=6$, $k_{i,3}=8$, $k_{i,4}=5$, $k_{i,5}=5$, $l_{i,1}=l_{i,2}=l_{i,3}=l_{i,4}$$=0.01$, and ${\gamma }_{ij}=0.01$. The heterogeneous communication ranges of USVs are $L_0=8$ m, $L_1=7$ m, $L_2=7$ m, $L_3=5$ m and $L_4=5$ m. The avoidance ranges are $R_i=1$ m and $i=0,1,2,3,4$. The path of the leader is generated by $u_0=0.1$ m/s and $r_0=0$ rad/s for $0\le t<40$ s, $u_0=0.1$ m/s and $r_0=0.1\sin (\pi t/20)$ rad/s for $40\le t<80$ s, $u_0=0.1$ m/s and $r_0=0$ rad/s for $80\le t<140$ s. The initial positions of USVs are chosen as ${\eta }_0\left(0\right)=[0$ m, 0 m, 0 rad${]}^T$, ${\eta }_1\left(0\right)=[0$ m, $-5$ m, 0 rad${]}^T$, ${\eta }_2\left(0\right)=[0$ m, 5 m, 0 rad${]}^T$, ${\eta }_3\left(0\right)=[7$ m, 8 m, 0 rad${]}^T$, ${\eta }_4\left(0\right)=[7$ m, $-8$ m, 0 rad${]}^T$. Desired distances and angles are chosen as ${\rho }_{10,d}={\rho }_{20,d}={\rho }_{31,d}={\rho }_{42,d}=5$ m, ${\lambda }_{10,d}=-25\pi /180$ rad, ${\lambda }_{20,d}=25\pi /180$ rad, ${\lambda }_{31,d}=-25\pi /180$ rad, and ${\lambda }_{42,d}=25\pi /180$ rad.

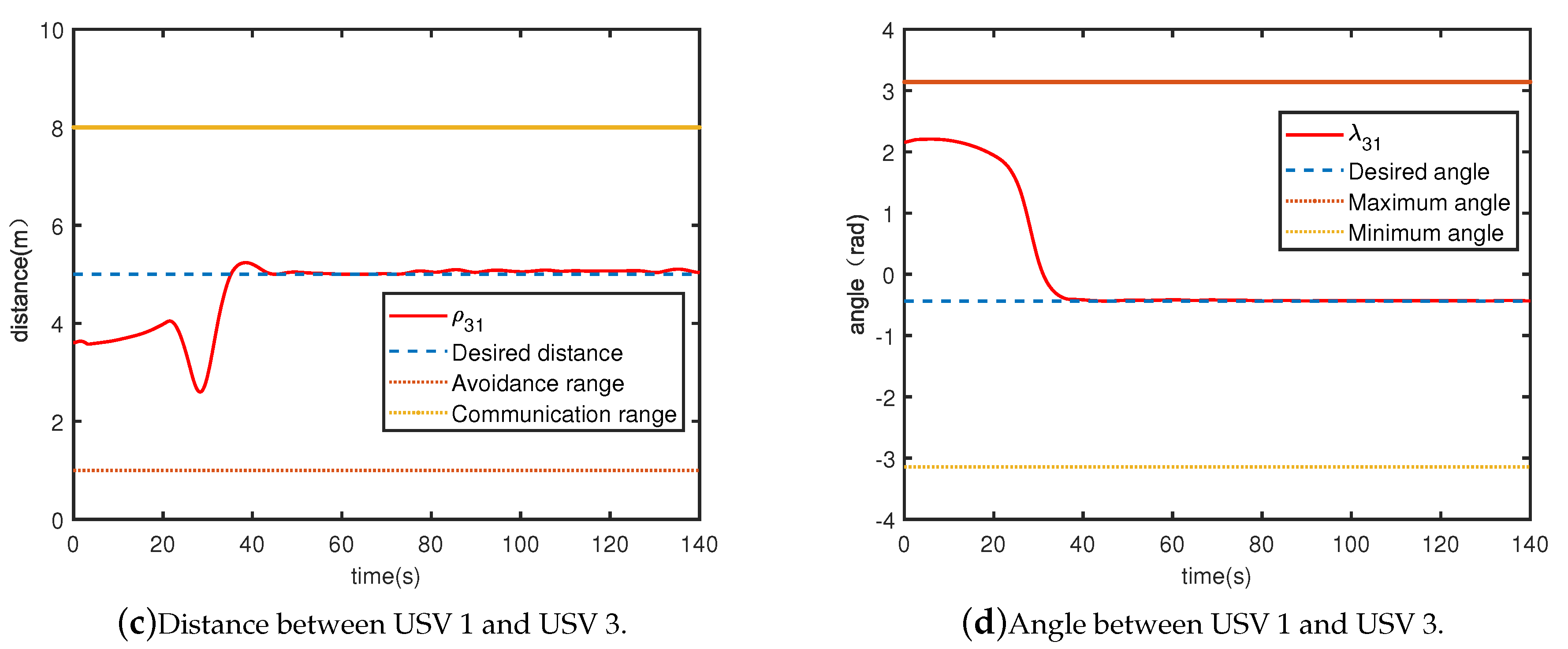
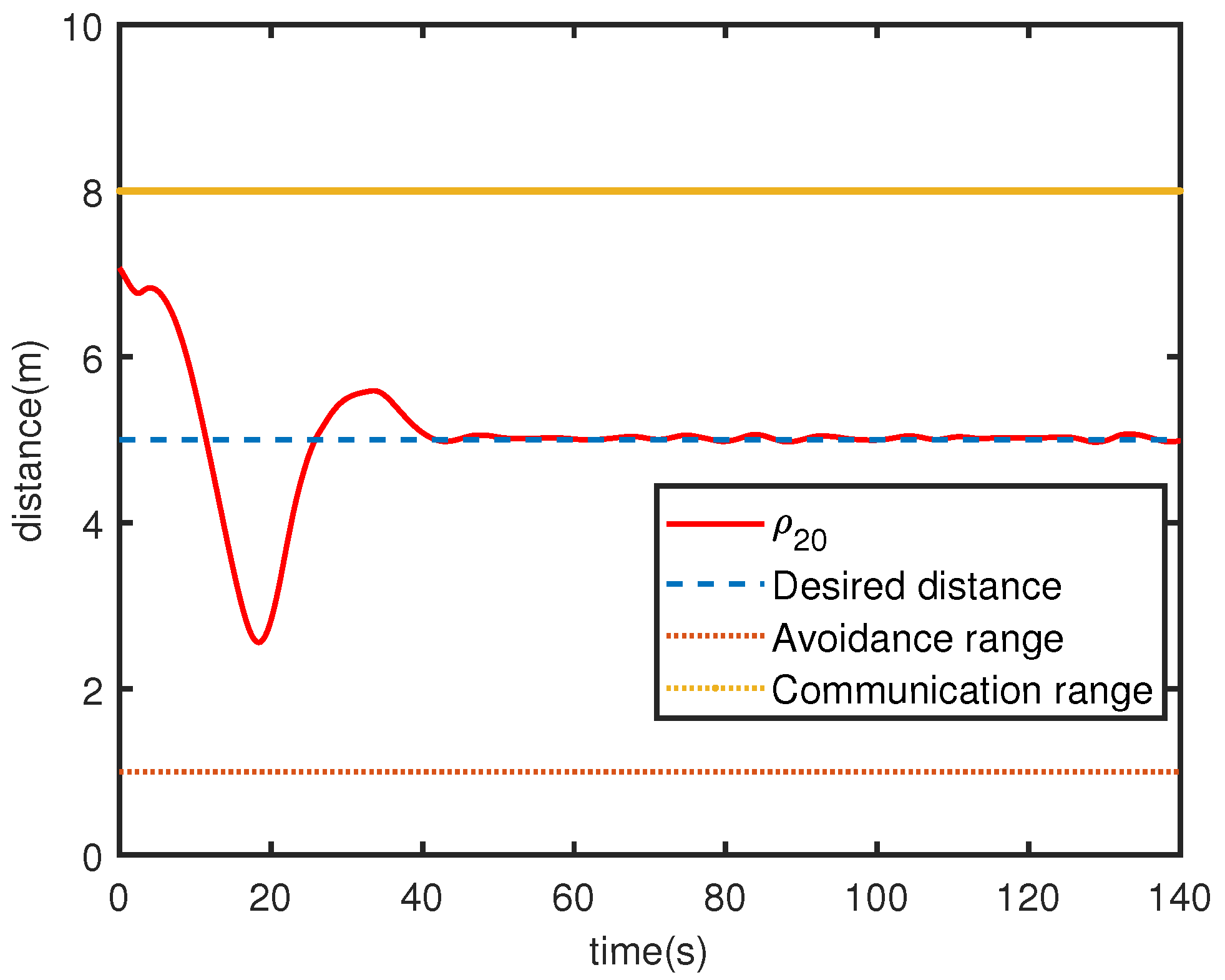
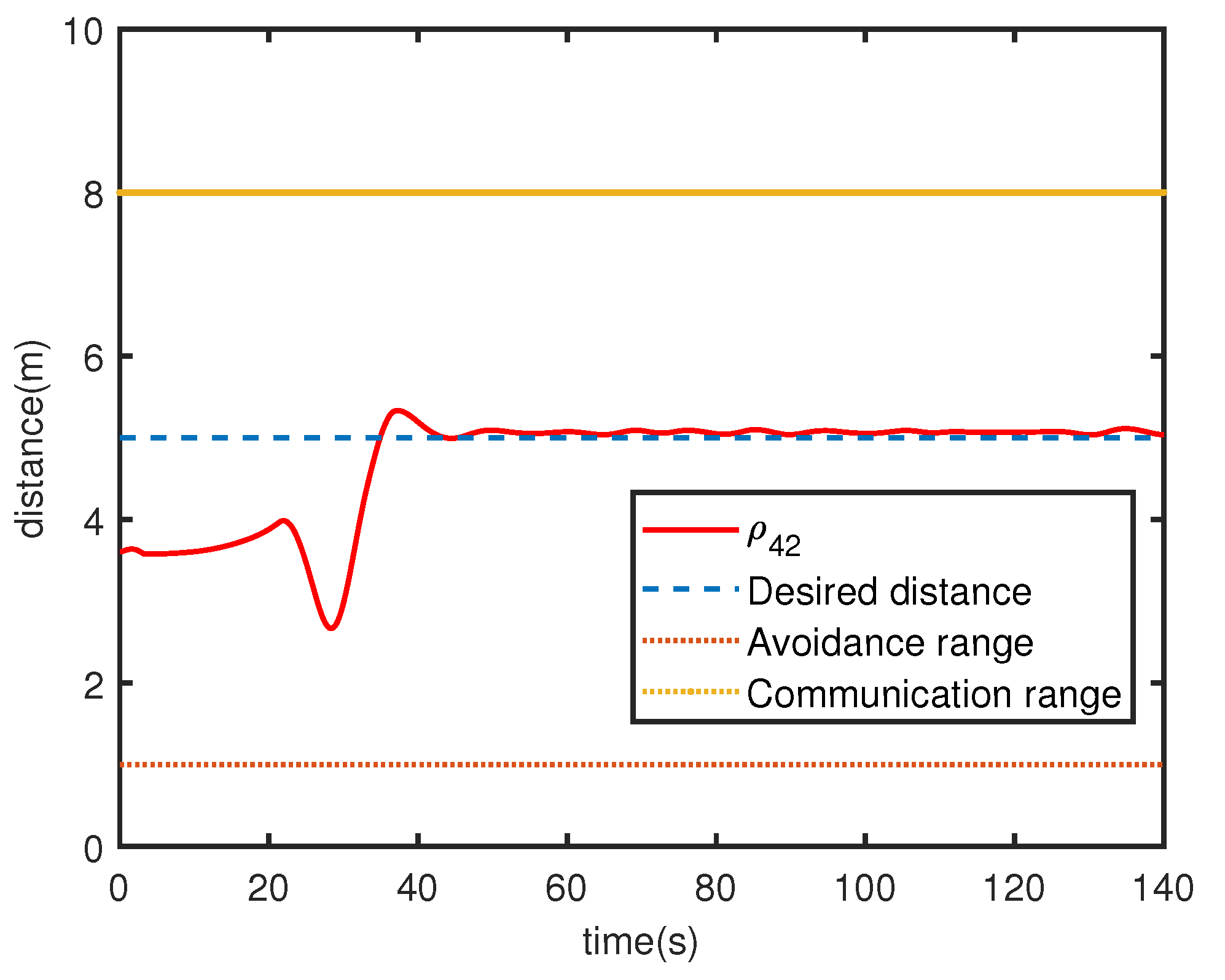
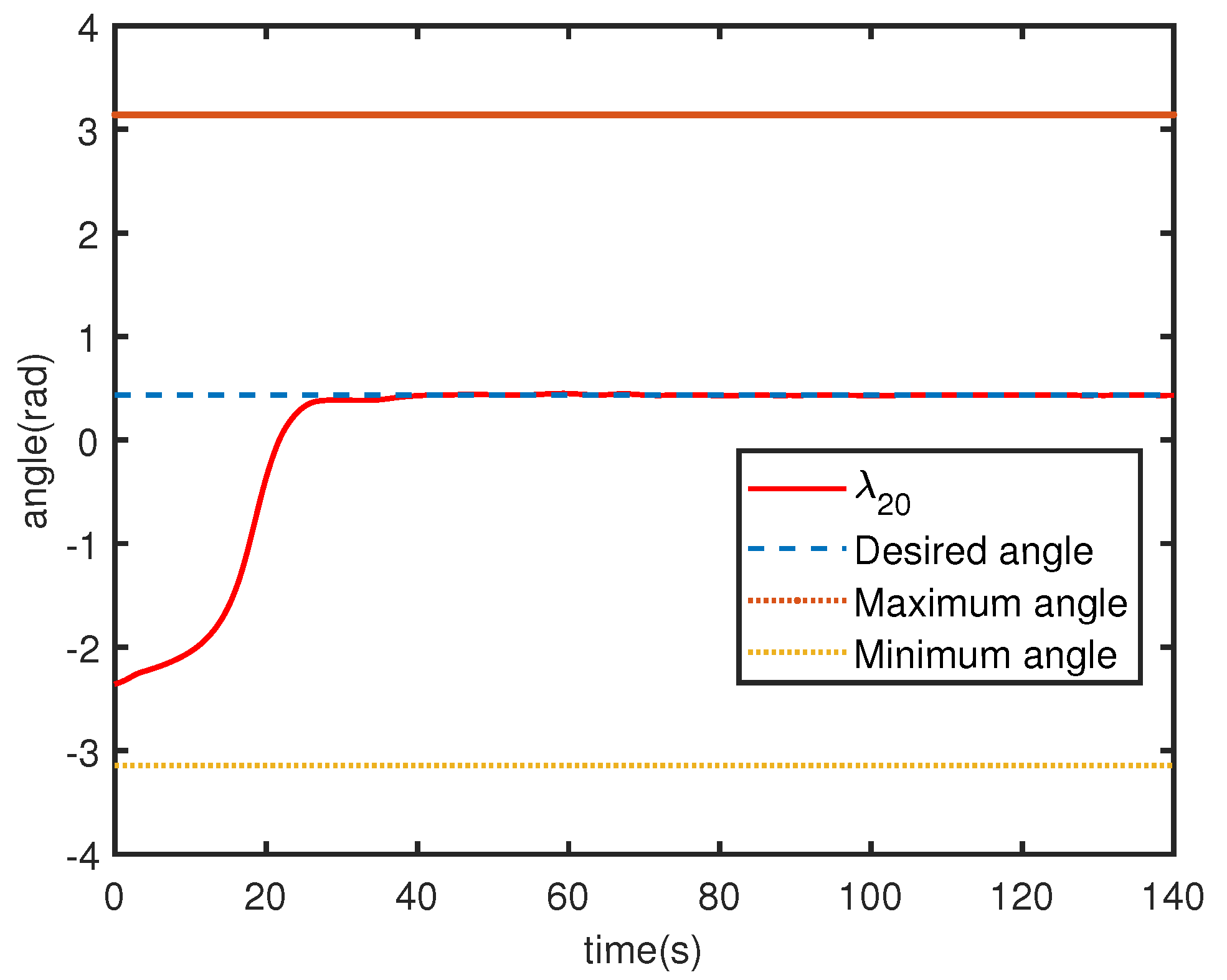
The formation tracking result is shown in Figure 3. Figure 4a,c, Figure 5 and Figure 6 show the the distance errors ${\rho }_{ij}-{\rho }_{ij,d}$, and Figure 4b,d, Figure 7 and Figure 8 show the angle errors ${\lambda }_{ij}-{\lambda }_{ij,d}$. As shown in Figure 3, one can see that all the USVs are able to track the formation. Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 show trends of relative distance and angle, and the connectivity-preserving and collision-avoiding is achieved. 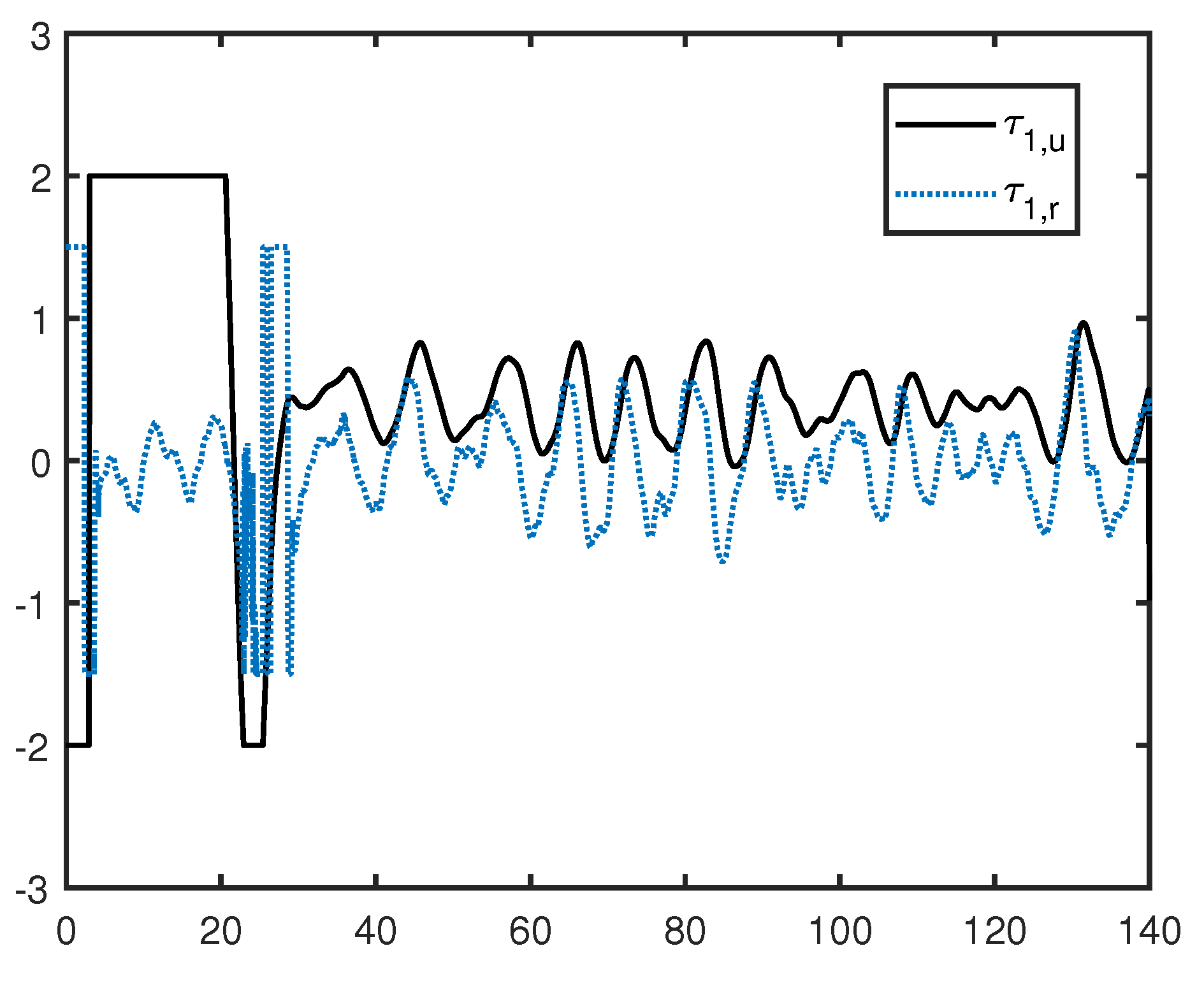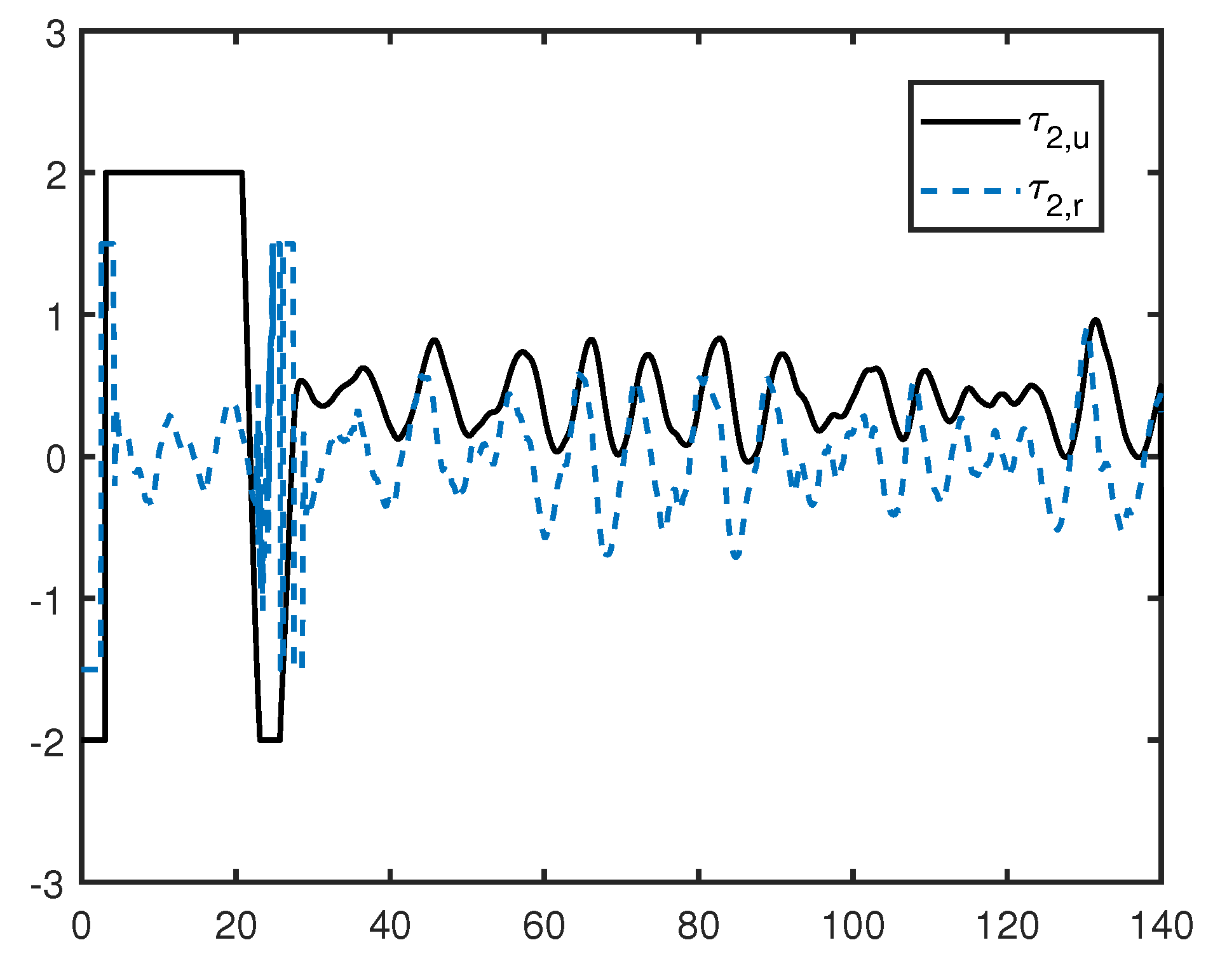Figure 9, Figure 10, Figure 11 and Figure 12 depict the control inputs of the follower. In the beginning, since the initial heading angles of followers are 0 rad, all followers turn around and travel in the opposite direction for a certain period of time, then the followers take a turn to avoid collision, and the control inputs ${\tau }_i$ are saturated and suffer from sudden jumps. The control inputs ${\tau }_i$ become smaller and unsaturated when the follower catches up with the leader.

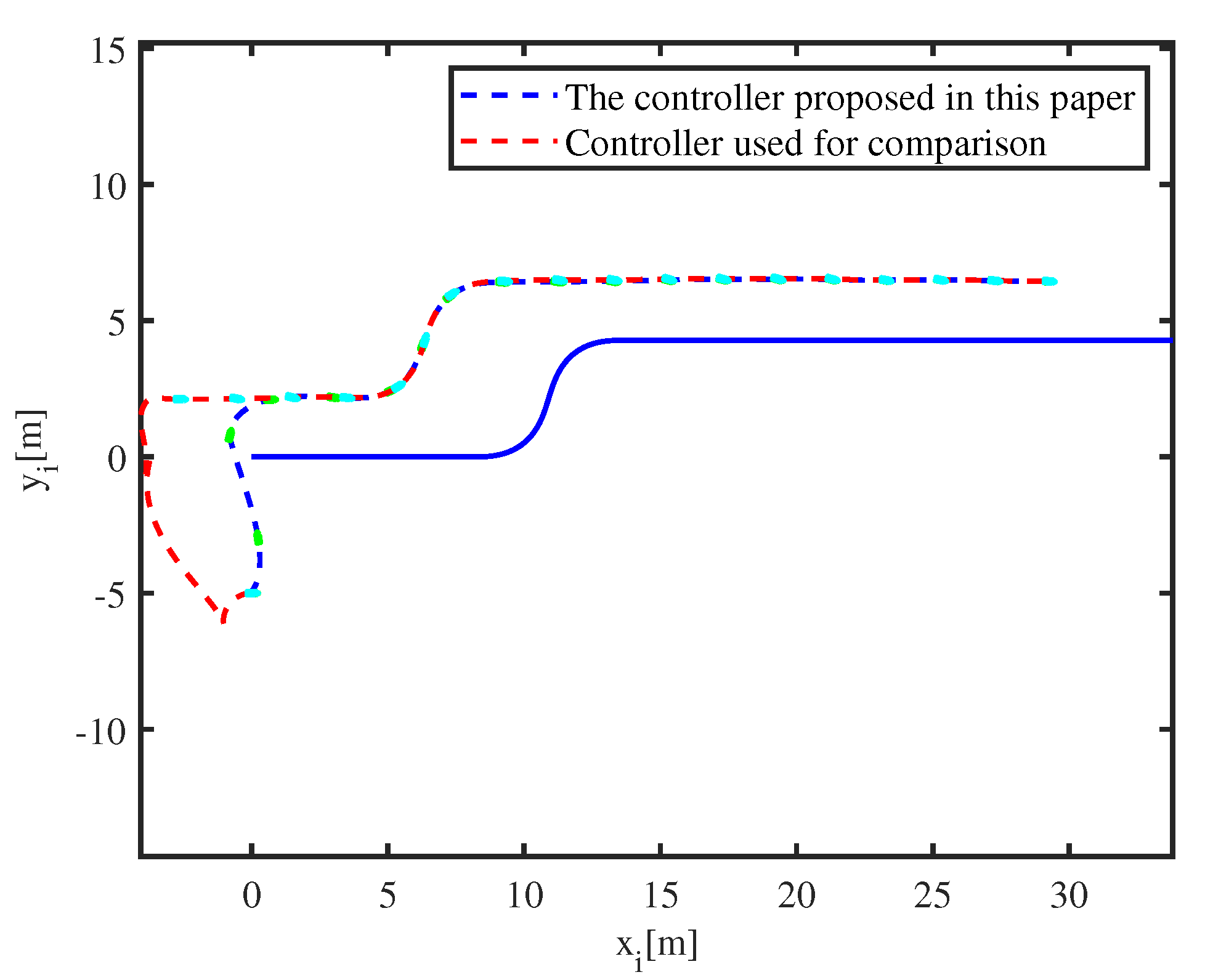
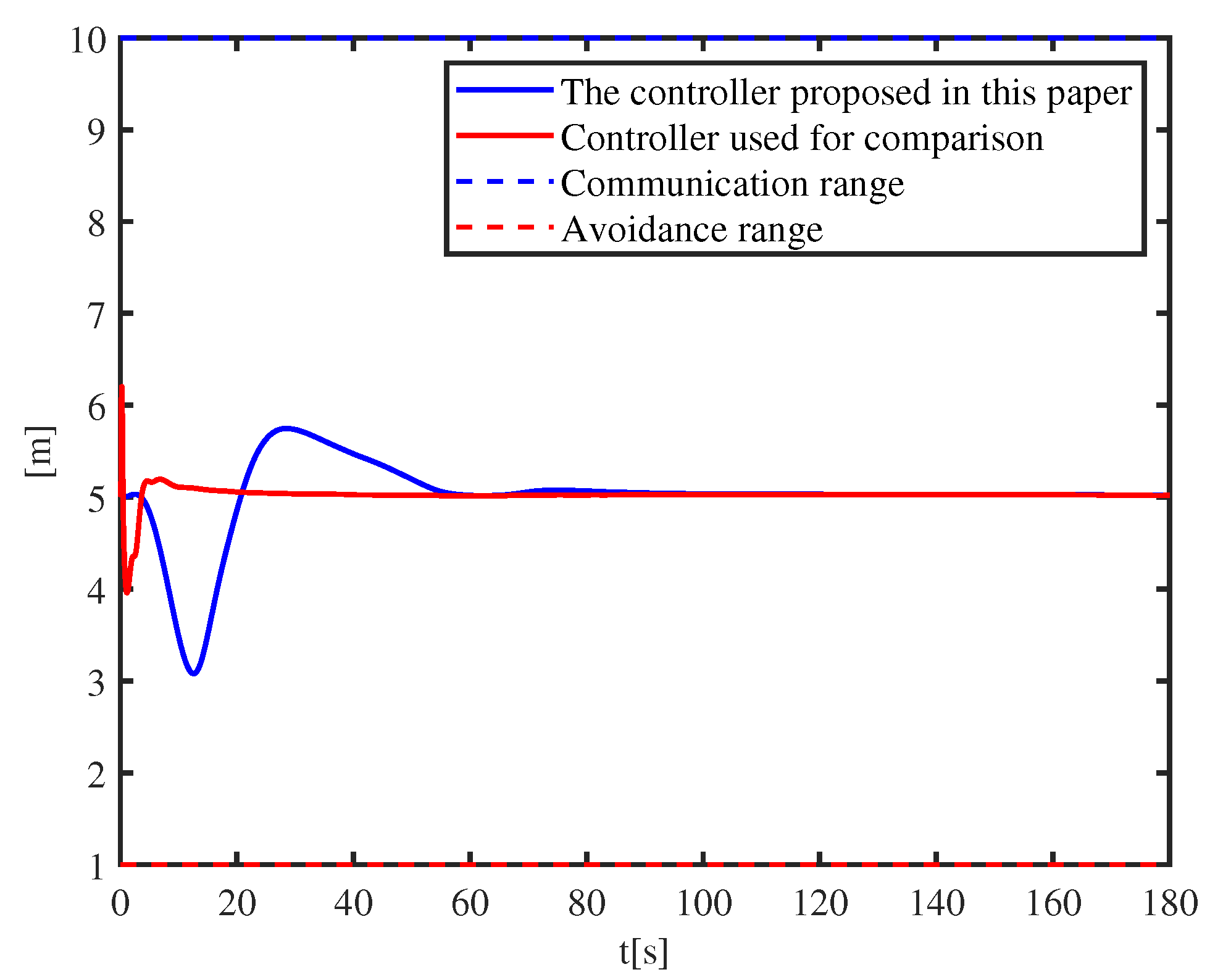
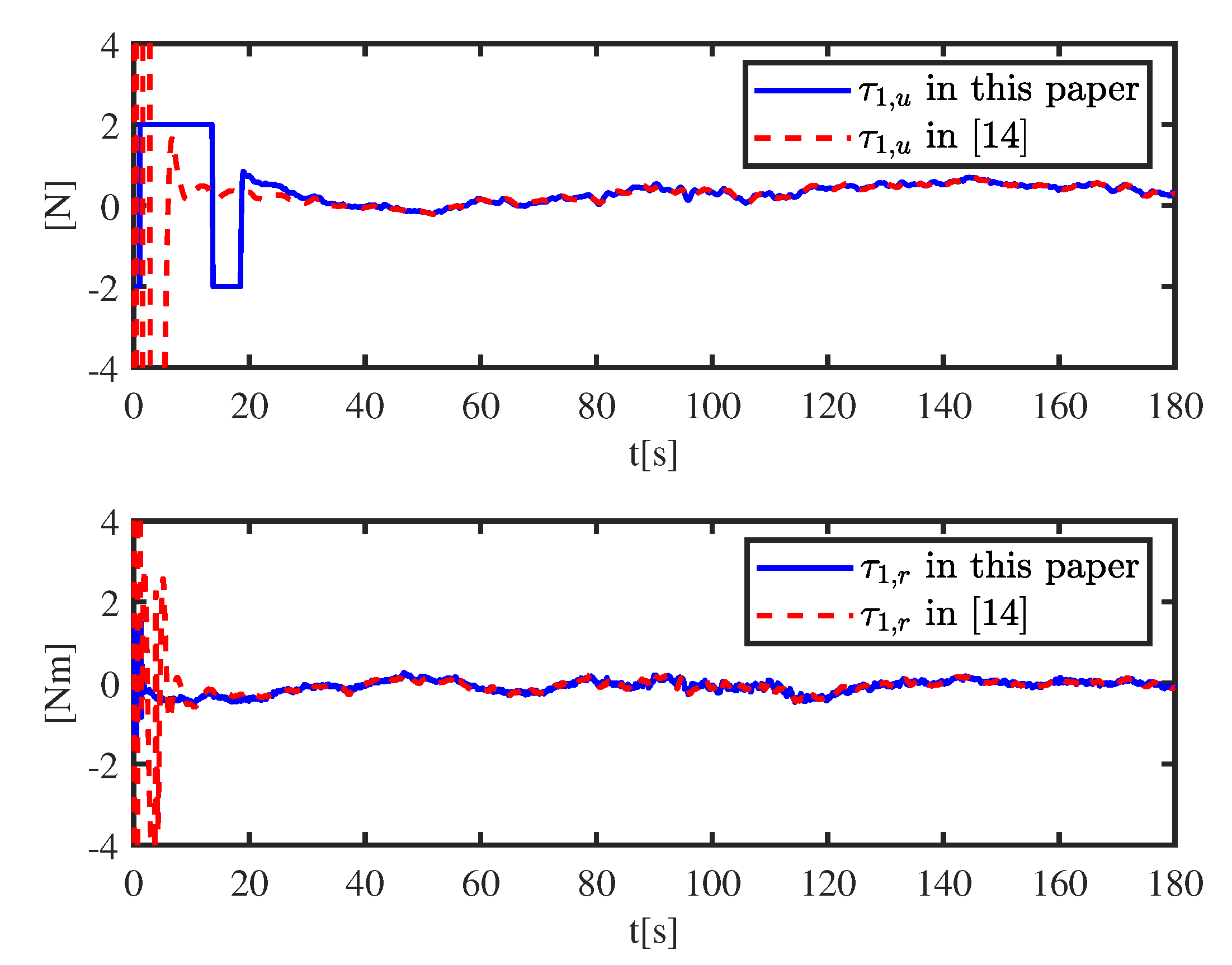
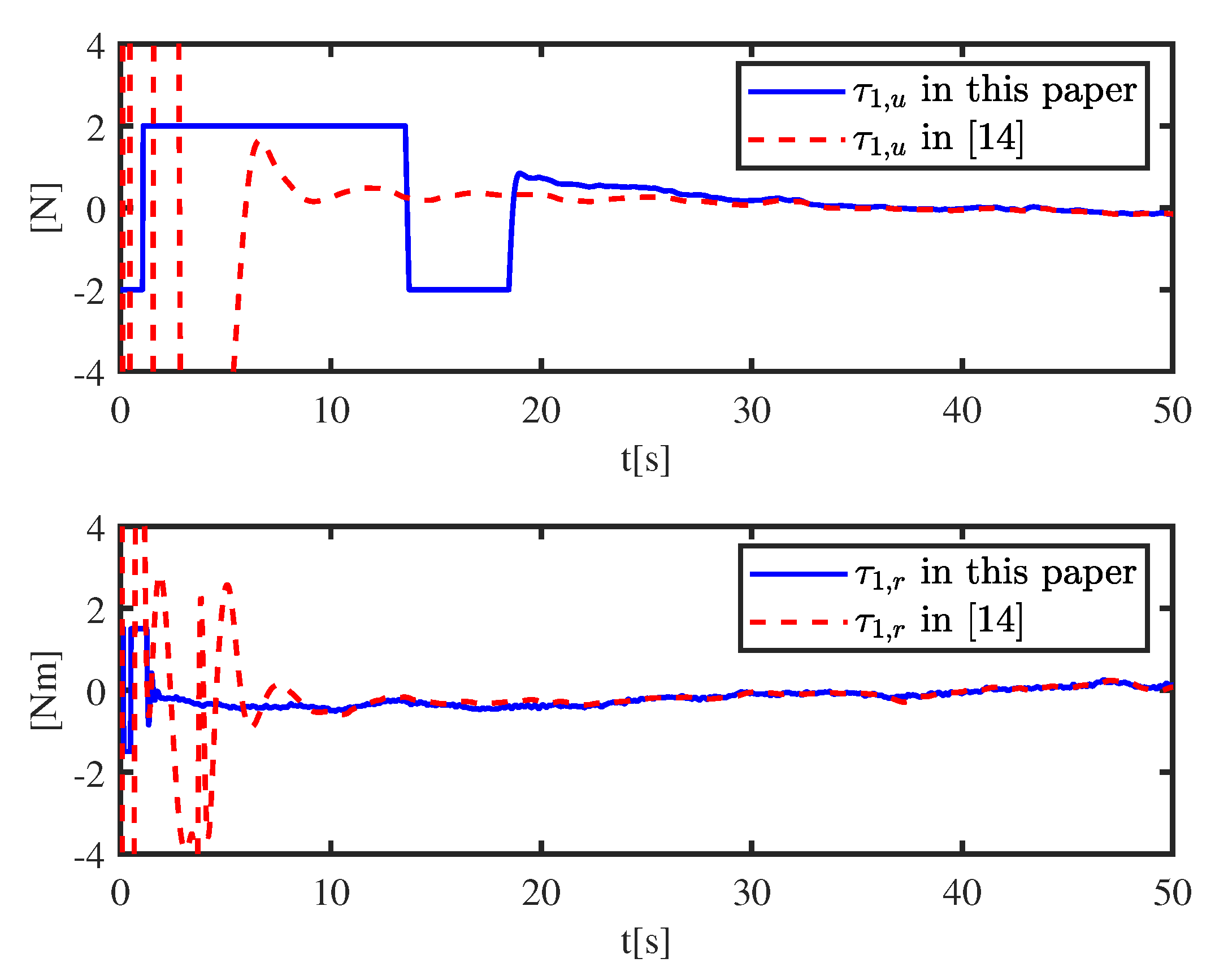
Comparison with the controller proposed in [14] is given though Matlab simulation in Figure 13, Figure 14, Figure 15 and Figure 16; the simulation result is provided to validate the effectiveness and feasibility of the proposed controller. Comparison is designed under the same environmental disturbances, and the standard deviation of white noise is chosen as 0.4 while the constant interference is chosen as 0.1, with the same initial position ${\eta }_1\left(0\right)=[0$ m, $-5$ m, 0 rad${]}^T$ and the same objective ${\rho }_{10,d}=5$ and ${\lambda }_{10,d}=-25\pi /180$ rad. Figure 13 shows that USV 1 could track the leader accurately in a different controller. Figure 14 shows that the controller proposed in [14] accomplishes faster convergence and tracing speed. Not taking input saturation into consideration, the result is a more aggressive tracking trajectory, which is difficult to implement. In Figure 15, control inputs under different controllers are given. A local enlarged drawing of the control input is given in Figure 16. In the beginning, the input signal in this paper is saturated, and the position of the USV changes relatively slowly. At about 60 s, the follower catches up with the leader. The input signal in [14] is huge, and the position of the USV changes rapidly. At about 10 s, the follower has caught up with the leader. Unlike the controller proposed in this paper, it is extremely difficult to avoid a huge input signal and a drastic change of input signal.

By using the modified barrier Lyapunov function, the connectivity preservation and the collision avoidance are achieved. By using ESO and the proposed controller, the followers can track the leader accurately. By using an auxiliary variable, the input saturation is solved. Positive definitions of matrix $K_{io1}$, $K_{io2}$ and $K_{io3}$ make sure that convergence of estimation error is achieved. By adjusting $u_0$, the track error can be made arbitrarily small.

Both controllers are designed based on Assumption 2, and ${\eta }_0$, $u_0$, $v_0$, $r_0$ are bounded, meaning that the formation control problem is solved only when the follower starts in a certain neighborhood of the leader. In [29], the path following the control problem of USVs was investigated and the system could provide global asymptotic stability. How to design a controller which could makes the system have global asymptotic stability is an interesting challenge. Both controllers are designed without considering the saturation rate of the actuator, meaning that the conclusion is relatively radical. How to design a controller with the rate saturation factor for formation control will be considered in future work.

5. Conclusions

This paper proposed an error-transformation-based design strategy for tracking control for multiple USVs with limited communication ranges and input saturation. ESO was used for estimating model uncertainties and unknown disturbances. The distributed tracker for each follower was designed by using a modified BLF. Auxiliary variables were used to solve input saturation and underactuated problems. From the Lyapunov stability sense, all error signals in the closed-loop were bounded. A simulation verified the effectiveness of the proposed distributed controller.