Viscoelastic Finite Line Contact of Thin Bonded Layered Solids of Low Elastic Modulus
Abstract
1. Introduction
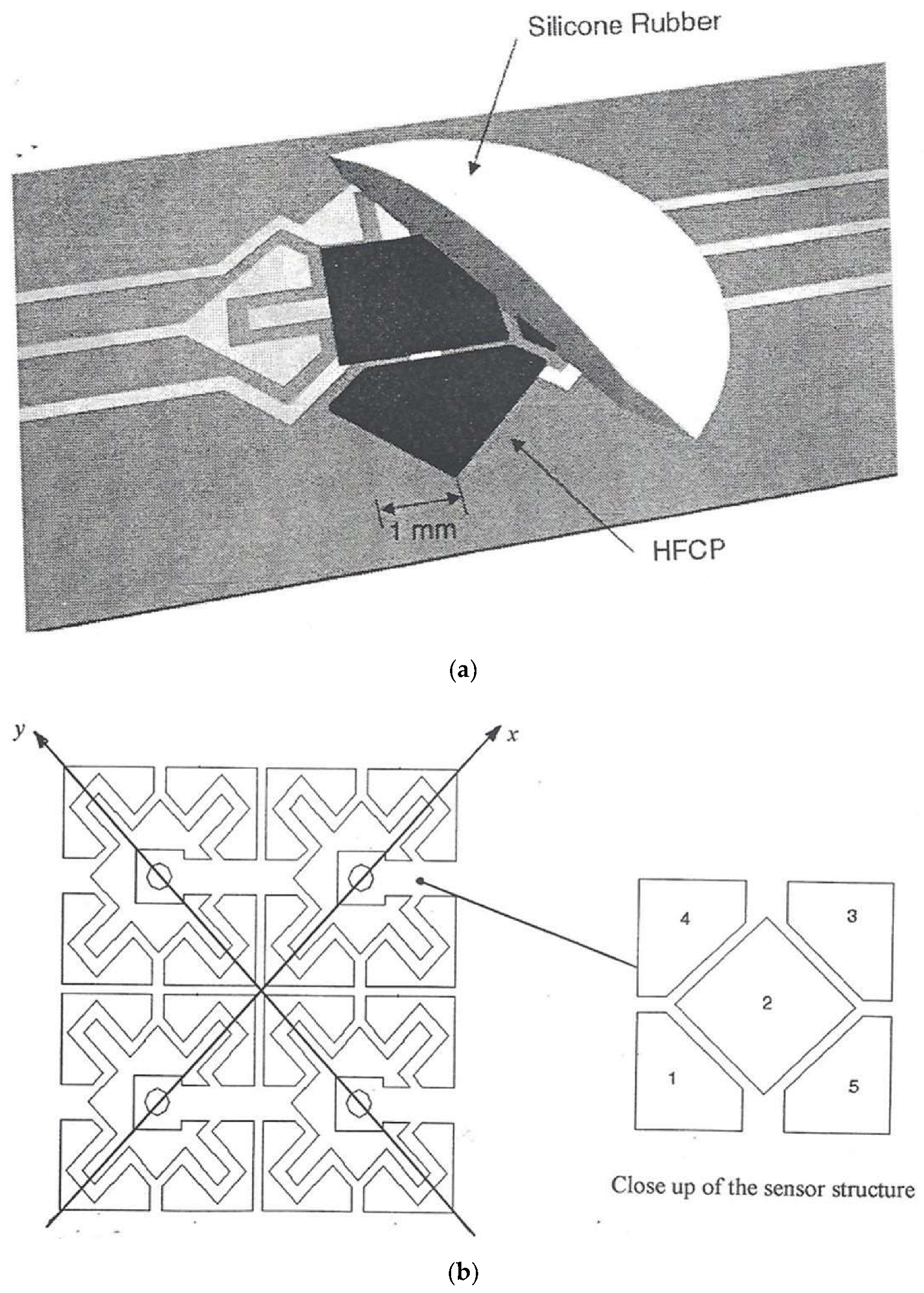
2. The Layered Bonded Sensor Structure
3. Experimental Procedure
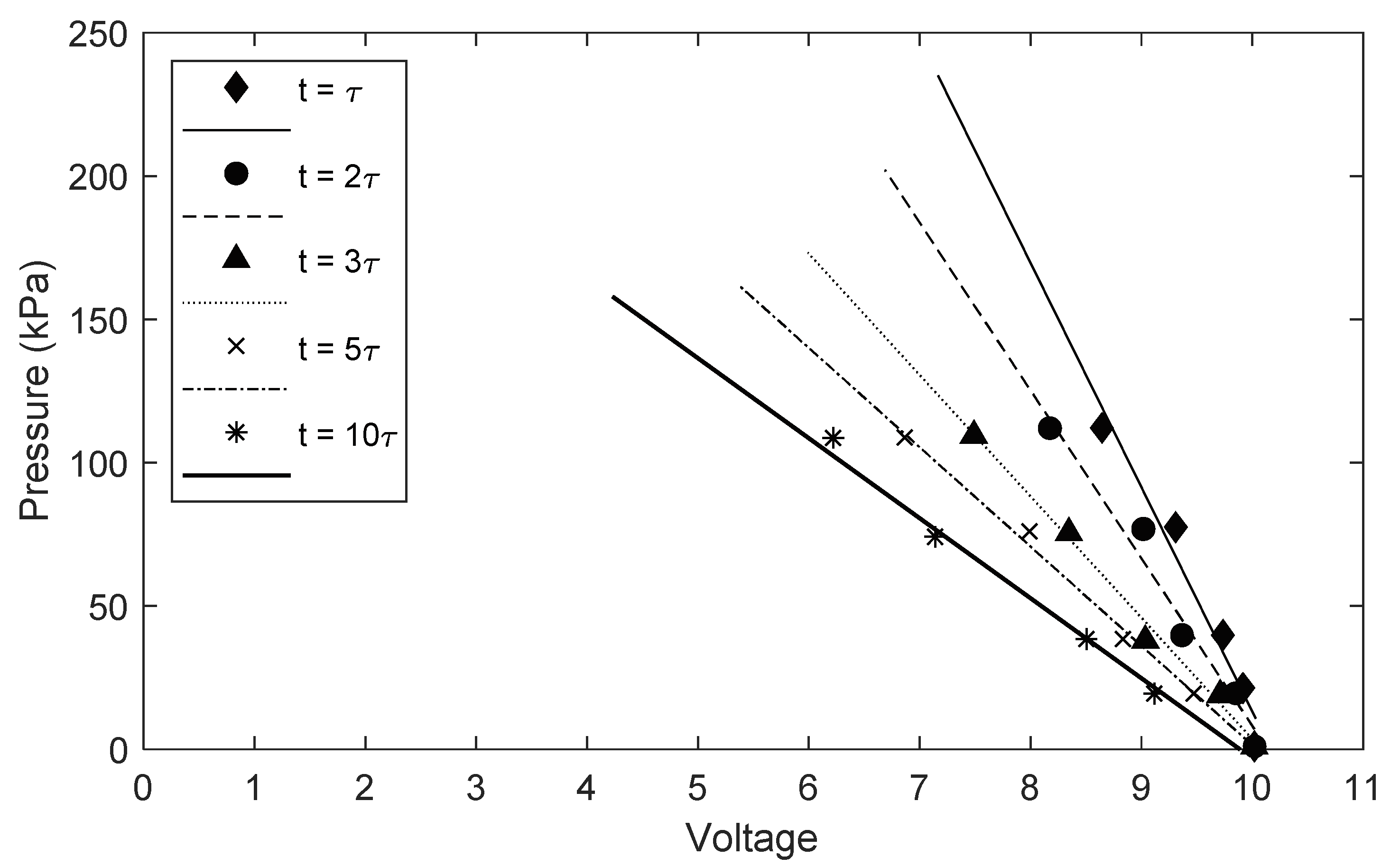
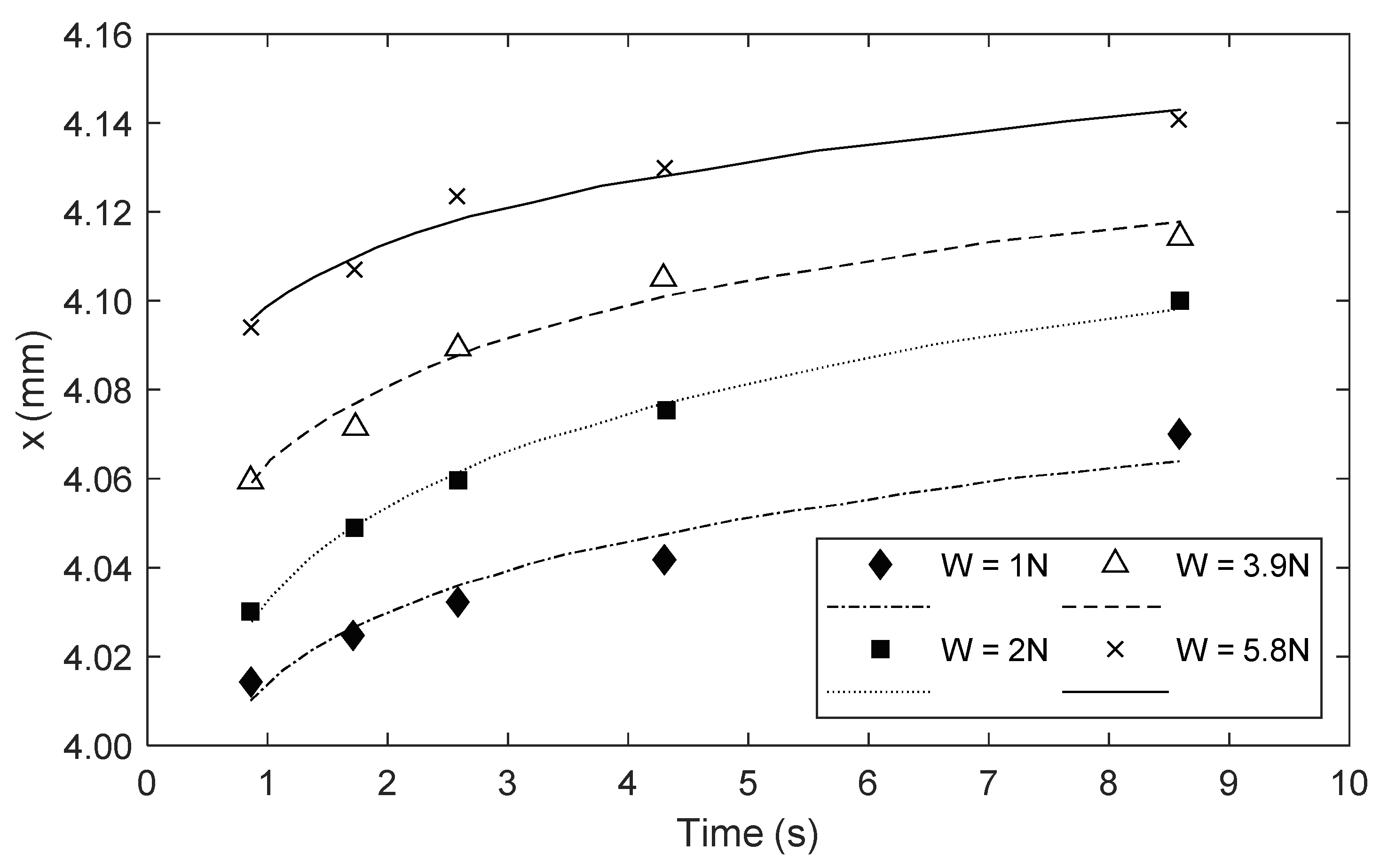
4. Experimental Results
5. Finite Element Analysis of Layered Bonded Viscoelastic Solids
5.1. The Formulation Method
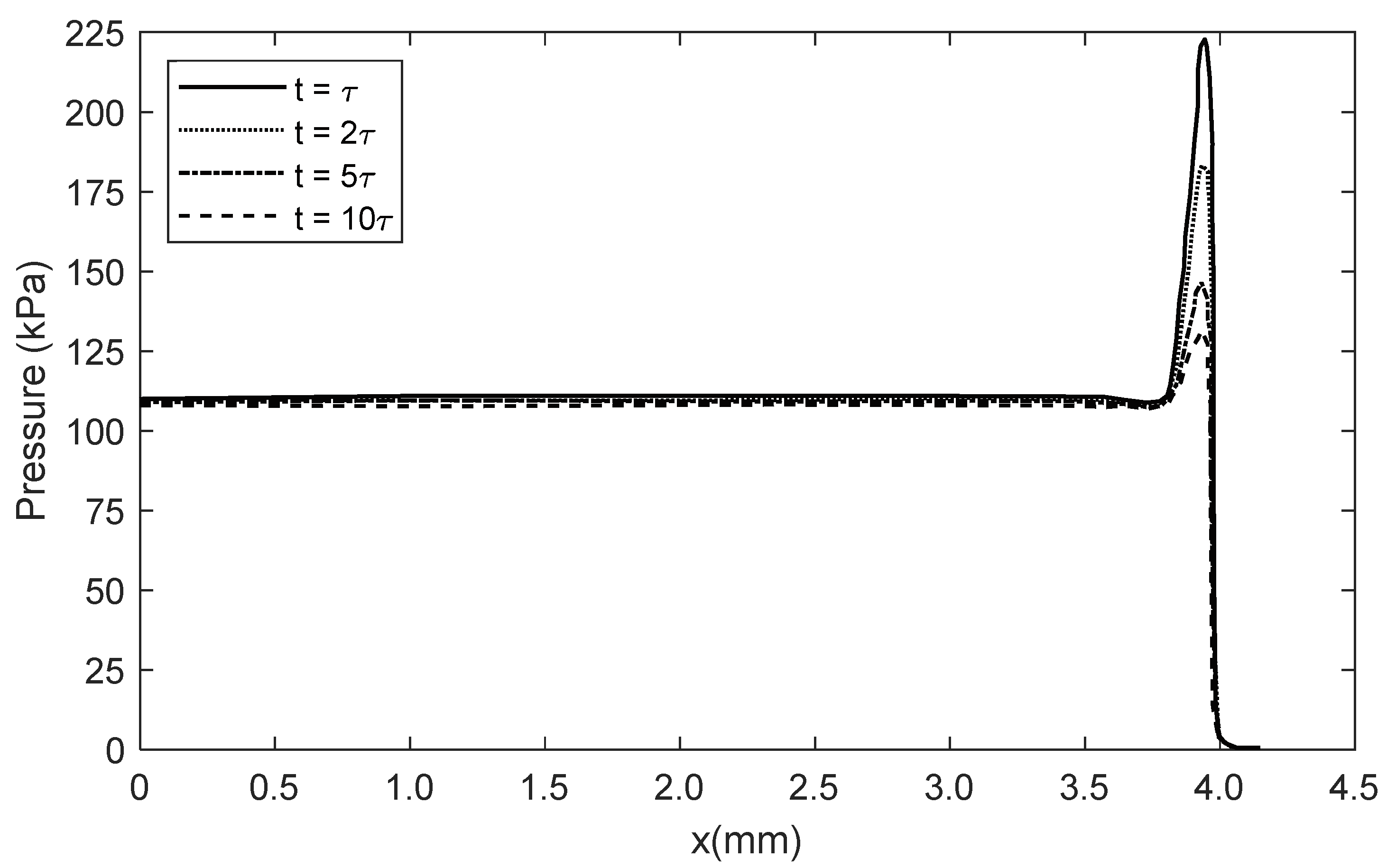
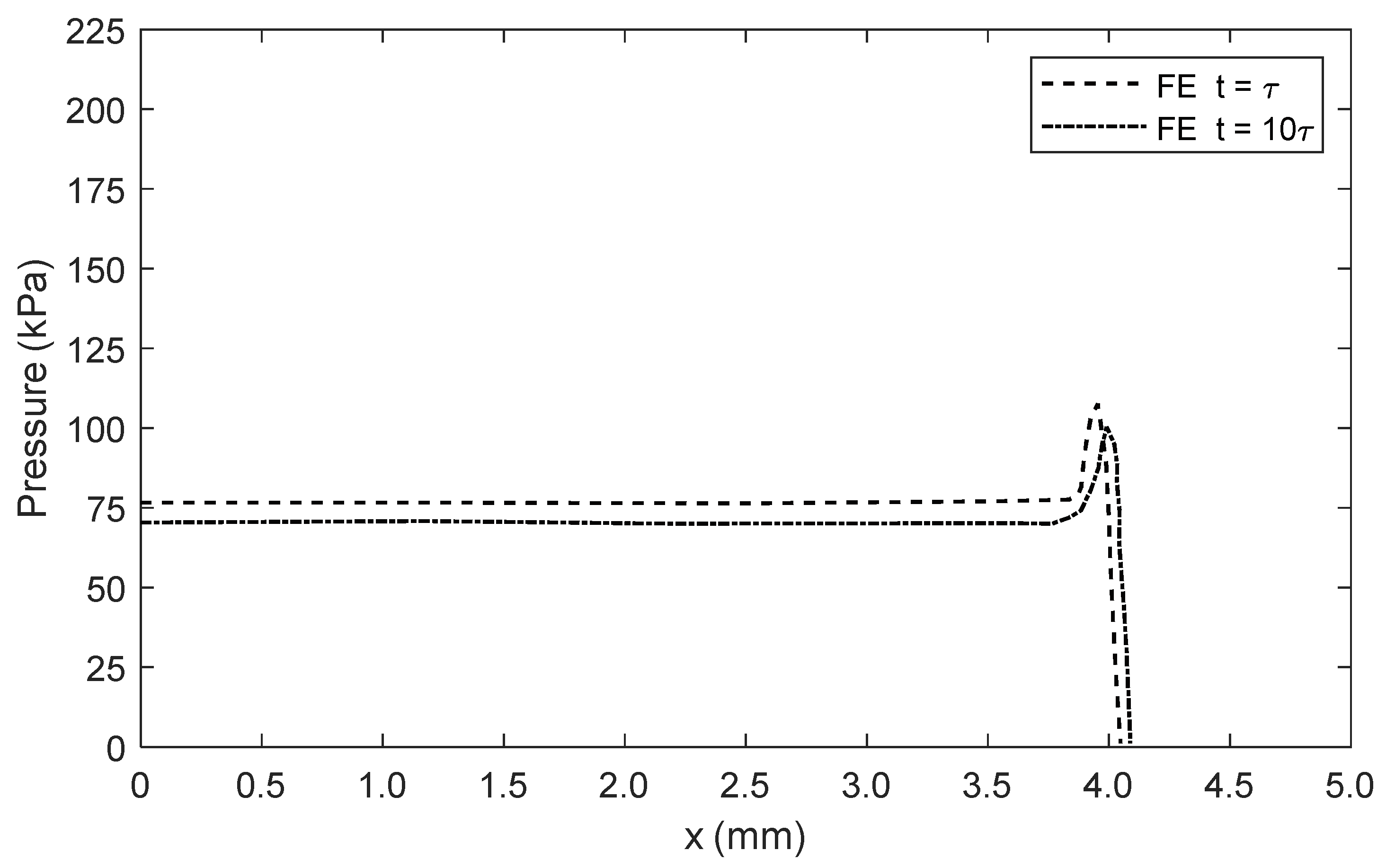
5.2. Numerical Prediction and Experiment Verification
6. Concluding Remarks
Author Contributions
Conflicts of Interest
Nomenclature
| A | Area of contact |
| e | Volumetric strain |
| G | Modulus of rigidity |
| i | Relaxation time step |
| K | Bulk modulus |
| n | Iteration step |
| P | Pressure |
| t | Time |
| ε | Shear strain |
| υ | Poisson’s ratio |
| σ | Stress |
| τ | Relaxation time |
| φ | e or ε |
| Subscript | |
| 0 | Instantaneous value |
References
- Thomsen, K.; Klit, P. A study on compliant layers and its influence on dynamic response of a hydrodynamic journal bearing. Tribol. Int. 2011, 44, 1872–1877. [Google Scholar] [CrossRef]
- Simmons, G.F.; Varela, A.C.; Santos, I.F.; Glavatskih, S. Dynamic characteristics of polymer faced tilting pad journal bearings. Tribol. Int. 2014, 74, 20–27. [Google Scholar] [CrossRef]
- Flitney, B. Advances in understanding of polymer seals for rotating applications. Seal. Technol. 2010, 11, 7–11. [Google Scholar] [CrossRef]
- Thomine, M.; Degrange, J.M.; Vigier, G.; Chazeau, L.; Pelletier, J.M.; Kapsa, P.; Guerbe, L.; Dudragne, G. Study of relations between viscoelasticity and tribological behaviour of filled elastomer for lip seal application. Tribol. Int. 2007, 40, 405–411. [Google Scholar] [CrossRef]
- Kozuch, E.; Nomikos, P.; Rahmani, R.; Morris, N.; Rahnejat, H. Effect of shaft surface roughness on the performance of radial lip seals. Lubricants 2018, 6, 99. [Google Scholar] [CrossRef]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Naghieh, G.R.; Rahnejat, H.; Jin, Z.M. Characteristics of frictionless contact of bonded elastic and viscoelastic layered solids. Wear 1999, 232, 243–249. [Google Scholar] [CrossRef]
- Hertz, H. On the contact of elastic solids. Z. Reine Angew. Mathematik. 1881, 92, 156–171. [Google Scholar]
- Naghieh, G.R.; Jin, Z.M.; Rahnejat, H. Contact characteristics of viscoelastic bonded layers. Appl. Math. Model. 1998, 22, 569–581. [Google Scholar] [CrossRef]
- Johns, P.M.; Gohar, R. Roller bearings under radial and eccentric loads. Tribol. Int. 1981, 14, 131–136. [Google Scholar] [CrossRef]
- Kushwaha, M.; Rahnejat, H.; Gohar, R. Aligned and misaligned contacts of rollers to races in elastohydrodynamic finite line conjunctions. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2002, 216, 1051–1070. [Google Scholar] [CrossRef]
- Kushwaha, M.; Rahnejat, H. Transient elastohydrodynamic lubrication of finite line conjunction of cam to follower concentrated contact. J. Phys. D Appl. Phys. 2002, 35, 2872. [Google Scholar] [CrossRef]
- Najjari, M.; Guilbault, R. Edge contact effect on thermal elastohydrodynamic lubrication of finite contact lines. Tribol. Int. 2014, 71, 50–61. [Google Scholar] [CrossRef]
- Hultqvist, T.; Shirzadegan, M.; Vrcek, A.; Baubet, Y.; Prakash, B.; Marklund, P.; Larsson, R. Elastohydrodynamic lubrication for the finite line contact under transient loading Conditions. Tribol. Int. 2018, 127, 489–499. [Google Scholar] [CrossRef]
- Nambiar, S.; Yeow, J.T. Conductive polymer-based sensors for biomedical applications. Biosens. Bioelectron. 2011, 26, 1825–1832. [Google Scholar] [CrossRef]
- Mehdian, M.; Rahnejat, H. Blood flow measurement using a highly filled carbon polymer sandwich sensor and an elasto-pseudo compressible vascular flow. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 1996, 210, 289–296. [Google Scholar] [CrossRef]
- Koç, İ.M.; Aksu, C. Tactile sensing of constructional differences in fabrics with a polymeric fingertip. Tribol. Int. 2013, 59, 339–349. [Google Scholar] [CrossRef]
- Rahnejat, H.; Bera, H. Sensors, Special purpose. In International Encyclopedia of Robotics; Dorf, R.C., Nof, S.Y., Eds.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1988; pp. 1536–1544. [Google Scholar]
- Sferrazza, C.; Wahlsten, A.; Trueeb, C.; D’Andrea, R. Ground truth force distribution for Learning-based tactile sensing: A finite element approach. IEEE Access 2019, 7, 173438–173449. [Google Scholar] [CrossRef]
- Wijesinghe, P.; Sampson, D.D.; Kennedy, B.F. Computational optical palpation: A finite-element approach to micro-scale tactile imaging using a compliant sensor. J. R. Soc. Interface 2017, 14, 20160878. [Google Scholar] [CrossRef]
- Conway, H.D.; Lee, H.C.; Bayer, R.G. The impact between a rigid sphere and a thin layer. Trans. ASME J. Appl. Mech. 1970, 37, 159–162. [Google Scholar] [CrossRef]
- Teodorescu, M.; Rahnejat, H.; Gohar, R.; Dowson, D. Harmonic decomposition analysis of contact mechanics of bonded layered elastic solids. Appl. Math. Model. 2009, 33, 467–485. [Google Scholar] [CrossRef]
- Mehdian, M.; Rahnejat, H. A dexterous anthropomorphic hand for robotic and prosthetic Applications. Robotica 1994, 12, 455–463. [Google Scholar] [CrossRef]
- Cutkosky, M.R.; Jourdain, J.M.; Wright, P.K. Skin materials for robotic fingers. In Proceedings of the IEEE International Conference on Robotics and Automation, Raleigh, NC, USA, 31 March–3 April 1987; pp. 1649–1654. [Google Scholar]
- Naghieh, G.R.; Rahnejat, H.; Jin, Z.M. Contact mechanics of viscoelastic layered surface. In Computational Methods in Contact Mechanics III; Aliabadi, M.H., Samartin, A., Eds.; WIT Press: Southampton, UK, 1997; pp. 59–68. [Google Scholar]
- Kadiric, A.; Sayles, R.S.; Zhou, X.B.; Ioannides, E. A numerical study of the contact mechanics and sub-surface stress effects experienced over a range of machined surface coatings in rough surface contacts. J. Tribol. 2003, 125, 720–730. [Google Scholar] [CrossRef]
- Teodorescu, M.; Kushwaha, M.; Rahnejat, H.; Rothberg, S.J. Multi-physics analysis of valve train systems: From system level to microscale interactions. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2007, 221, 349–361. [Google Scholar] [CrossRef]
- Altenbach, H.; Eremeyev, V.A. On the bending of viscoelastic plates made of polymer foams. Acta Mech. 2009, 204, 137. [Google Scholar] [CrossRef]



| Time (s) | Element 1 | Element 2 | Element 3 | Element 4 | Element 5 |
|---|---|---|---|---|---|
| τ | 9.305 | 8.793 | 8.213 | 8.238 | 8.113 |
| 2τ | 9.02 | 8.573 | 7.699 | 7.925 | 7.854 |
| 3τ | 8.34 | 7.987 | 7.03 | 7.24 | 6.975 |
| 5τ | 7.995 | 7.693 | 6.75 | 6.78 | 6.575 |
| 10τ | 7.15 | 7.04 | 5.89 | 6.17 | 5.75 |
| Relaxation Time (s) | Contact Area (mm2) |
|---|---|
| τ | 51.785 |
| 2τ | 52.104 |
| 3τ | 52.553 |
| 5τ | 52.939 |
| 10τ | 54.015 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Votsios, V.; Johns-Rahnejat, P.; Rahnejat, H. Viscoelastic Finite Line Contact of Thin Bonded Layered Solids of Low Elastic Modulus. Appl. Sci. 2020, 10, 3363. https://doi.org/10.3390/app10103363
Votsios V, Johns-Rahnejat P, Rahnejat H. Viscoelastic Finite Line Contact of Thin Bonded Layered Solids of Low Elastic Modulus. Applied Sciences. 2020; 10(10):3363. https://doi.org/10.3390/app10103363
Chicago/Turabian StyleVotsios, Vasilis, Patricia Johns-Rahnejat, and Homer Rahnejat. 2020. "Viscoelastic Finite Line Contact of Thin Bonded Layered Solids of Low Elastic Modulus" Applied Sciences 10, no. 10: 3363. https://doi.org/10.3390/app10103363
APA StyleVotsios, V., Johns-Rahnejat, P., & Rahnejat, H. (2020). Viscoelastic Finite Line Contact of Thin Bonded Layered Solids of Low Elastic Modulus. Applied Sciences, 10(10), 3363. https://doi.org/10.3390/app10103363







