A Hydraulic Experimental Study of a Movable Barrier on a Revetment to Block Wave Overtopping
Abstract
:1. Introduction
2. Physical Experiment
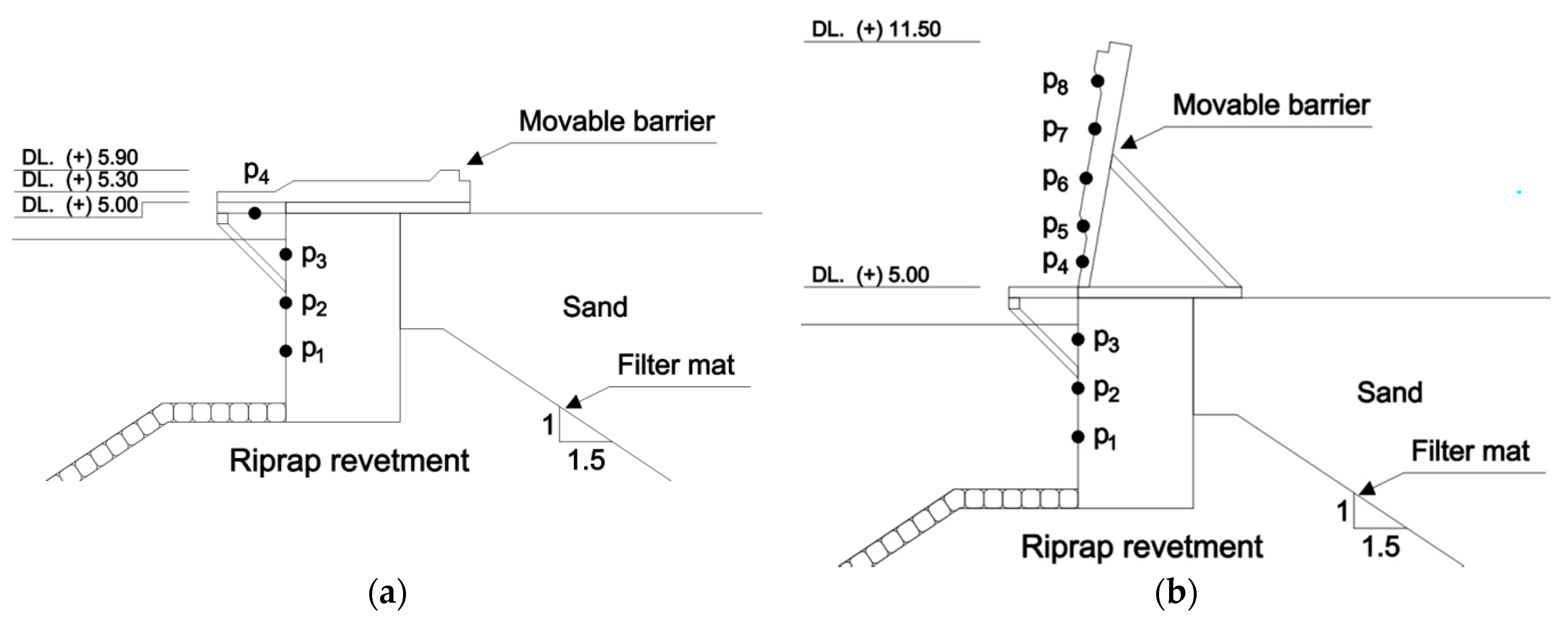
2.1. Experimental Setup
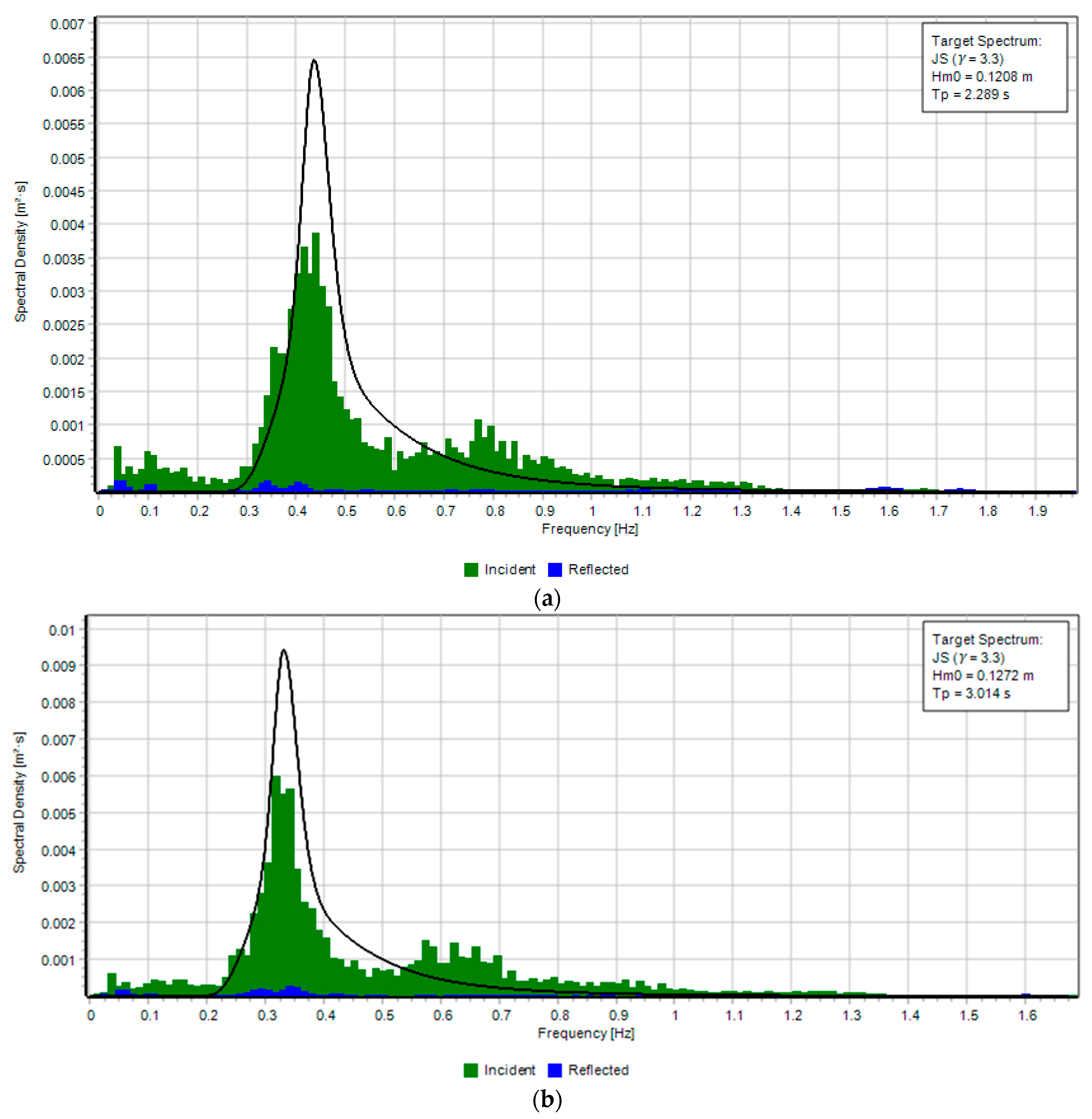
2.2. Wave Conditions
3. Results and Discussion of the Physical Experiment
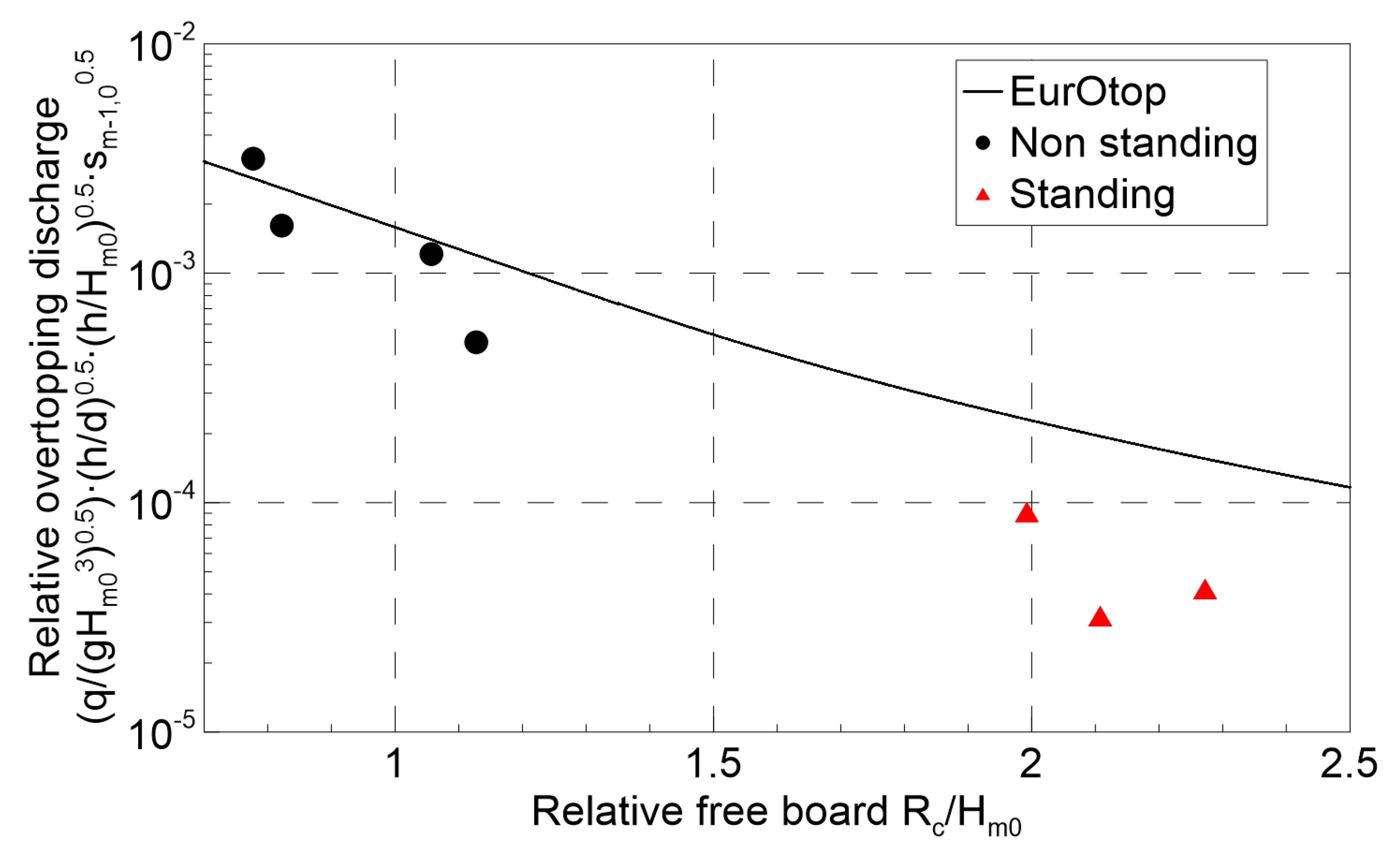
3.1. Wave Overtopping
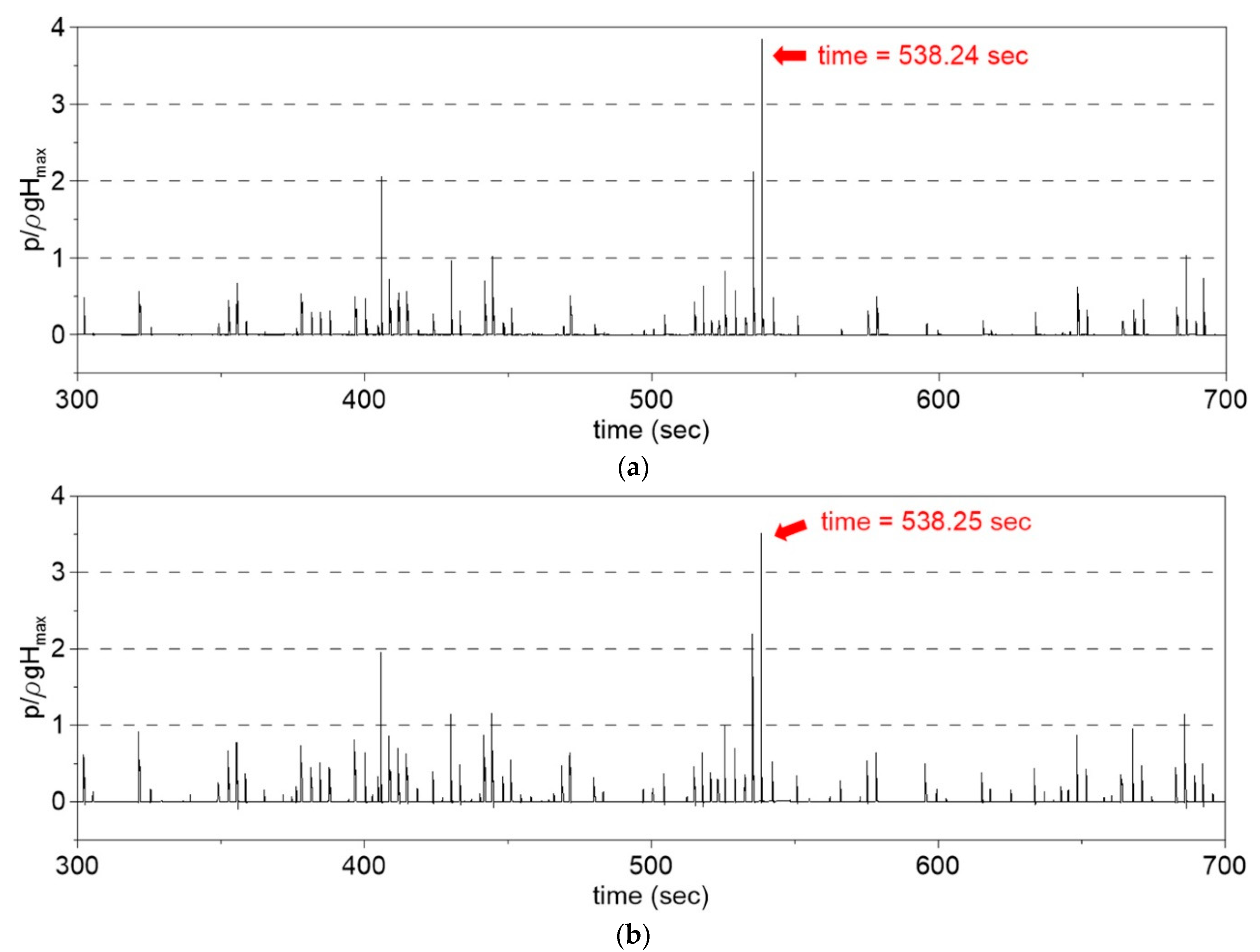
3.2. Uplift Pressure and Wave Pressure
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yamada, Y.; Satoh, M.; Sugi, M.; Kodama, C.; Noda, A.T.; Nakano, M.; Nasuno, T. Response of tropical cyclone activity and structure to global warming in a high-resolution global nonhydrostatic model. J. Clim. 2017, 30, 9703–9724. [Google Scholar] [CrossRef]
- The Intergovernmental Panel on Climate Change. Global Warming of 1.5 °C; The Intergovernmental Panel on Climate Change: Geneva, Switzerland, 2019.
- Van der Meer, J.W.; Allsop, N.W.H.; Bruce, T.; De Rouck, J.; Kortenhaus, A.; Pullen, T.; Schüttrumpf, H.; Troch, P.; Zanuttigh, B. Manual on wave overtopping of sea defences and related structures. An overtopping manual largely based on European research, but for worldwide application. EurOtop. 2018. Available online: www.overtopping-manual.com (accessed on 20 December 2019).
- Gensen, M. Wave Overtopping in Harbour Areas. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, March 2017. [Google Scholar]
- Lehmann, H.A.; Jasper, H. Tidal barriers at the North and Baltic Sea Coast. Die Küste 74 ICCE 2008, 74, 212–232. [Google Scholar]
- Kendrick, M. The Thames Barrier. Coast. Eng. 1988, 16, 57–68. [Google Scholar] [CrossRef]
- Bol, R. Flooding and Environmental Challenges for Venice and Its Lagoon: State of Knowledge, 1st ed.; Cambridge University Press: Cambridge, UK, 2005; pp. 311–316. [Google Scholar]
- Hunter, P. The St Petersburg Flood Protection Barrier: Design and Construction; CETMEF PIANC: Paris, France, 2012. [Google Scholar]
- Venice Flood Barrier: MOSE Project Keeps the Sea at Bay. Available online: http://eandt.theiet.org/ magazine/2014/08/venice-master-of-water.cfm (accessed on 8 December 2019).
- Seo, J.; Lee, B.W.; Park, W.S.; Won, D. Behavior of a moveable barrier on revetment for mitigation of disaster by wave overtopping. J. Korean Soc. Coast. Ocean Eng. 2018, 30, 10–18. (In Korean) [Google Scholar] [CrossRef]
- Cuomo, G.; Allsop, W.; Bruce, T.; Pearson, J. Breaking wave loads at vertical seawalls and breakwaters. Coast. Eng. 2010, 57, 424–439. [Google Scholar] [CrossRef] [Green Version]
- Oh, S.H.; Lee, J.S.; Lee, J. Introduction to Physical Experiment Building of KIOST in Busan. In Proceedings of the 10th International Conference on Asian and Pacific Coasts 2019 (APAC 2019), Hanoi, Vietnam, 25–28 September 2019; Trung Viet, N., Xiping, D., Thanh Tung, T., Eds.; Springer: Singapore, 2020; pp. 221–226. [Google Scholar]
- Lykke Andersen, T.; Clavero, M.; Firgaard, P.; Losada, M.; Puyol, J.I. A new active absorption system and its performance to linear and non-linear waves. Coast. Eng. 2016, 114, 47–60. [Google Scholar] [CrossRef]
- Meinert, P.; Lykke Andersen, T.; Frigaard, P. AwaSys 7 User Manual; Aalborg University: Aalborg, Denmark, 2017. [Google Scholar]
- Oh, S.H.; Lee, J.; Lee, J.S. Experimental investigation of the wave force on the caisson according to different coverage of armor units. In Proceedings of the 10th International Conference on Asian and Pacific Coasts 2019 (APAC 2019), Hanoi, Vietnam, 25–28 September 2019; Trung Viet, N., Xiping, D., Thanh Tung, T., Eds.; Springer: Singapore, 2020; pp. 987–993. [Google Scholar]
- Hasselmann, K.; Barnett, T.P.; Bouws, E.; Carlson, H.; Cartwright, D.E.; Enke, K.; Ewing, J.A.; Gienapp, H.; Hasselmann, D.E.; Kruseman, P.; et al. Measurements of Wind-wave Growth and Swell Decay During the Joint North Sea Wave Project (JONSWAP); Deutches Hydrographisches Institut: Hamburg, Germany, 1973.
- Lykke Andersen, T.; Eldrup, M.R.; Firgaard, P. Estimation of incident and reflected components in highly nonlinear regular waves. Coast. Eng. 2017, 119, 51–64. [Google Scholar] [CrossRef]
- Haeundae-gu Office. Feasibility Study and Master Plan Report for Storm Surge Risk Zone on Suyeong Bay; Haeundae-gu Office: Busan, Korea, 2016. (In Korean) [Google Scholar]
- Korea Hydrographic and Oceanographic Administration. Analysis and Prediction for Sea Level Fluctuation, 5th ed.; Korea Hydrographic and Oceanographic Administration: Busan, Korea, 2013. (In Korean)
- Korea Real Time Database for NEAR-GOOS by Korea Hydrographic and Oceanographic Administration. Available online: http://www.khoa.go.kr/koofs/eng/observation/obs_real.do (accessed on 8 December 2019).
- Ministry of Maritime Affairs and Fisheries. Basic and Detailed Design for Development Project of Marina Port on Haeundae-Gu; Ministry of Maritime Affairs and Fisheries: Busan, Korea, 2019. (In Korean)
- Ministry of Maritime Affairs and Fisheries. Harbor and Fishery Design Criteria; Ministry of Maritime Affairs and Fisheries: Busan, Korea, 2017. (In Korean)
- Oh, S.H. Analysis of the effect of reducing wave overtopping by wave return walls. J. Korean Soc. Coast. Ocean Eng. 2016, 28, 1–6. (In Korean) [Google Scholar] [CrossRef]
- Kerpen, N.B.; Schoonees, T.; Schlurmann, T. Wave overtopping of stepped revetments. Water 2019, 11, 1035. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.S.; An, D.H.; Chun, I.S. Wave impact pressures acting on the underwater tunnel bulkhead under construction—Numerical analysis and hydraulic model experiment. J. Korean Soc. Coast. Ocean Eng. 2011, 23, 139–146. (In Korean) [Google Scholar] [CrossRef] [Green Version]
- Park, W.S.; Ahn, H.D. An efficient model for dynamic analysis of caisson breakwaters under impulsive wave loadings. J. Korean Soc. Coast. Ocean Eng. 1995, 7, 108–115. (In Korean) [Google Scholar]
- Takahashi, S.; Tanimoto, K.; Suzumura, S. Generation mechanism of impulsive pressure by breaking wave on a vertical wall. Rep. Port Harb. Res. Inst. 1983, 22, 3–31. (In Japanese) [Google Scholar]







 | Manufacturer | SSK Company, Japan |
| Model | P310 | |
| Material | Stainless steel | |
| Rated capacity | 49.05 kPa | |
| Natural oscillation frequency | 7.8 kHz |
| No. | Designed Sea Level | Return Period (year) | Target Wave | Estimated Test Wave | |||
|---|---|---|---|---|---|---|---|
| Hs (cm) | Ts (s) | Hs (cm) | Ts (s) | Hr (cm) | |||
| 1 | Approx. H.H.W. | 10 | 12.08 | 2.18 | 12.00 | 2.17 | 3.29 |
| 2 | Approx. H.H.W. | 50 | 12.72 | 2.87 | 12.80 | 3.00 | 3.92 |
| 3 | Sea level during storm surge + SLR | 10 | 12.08 | 2.18 | 12.10 | 2.23 | 3.05 |
| 4 | Sea level during storm surge + SLR | 50 | 12.72 | 2.87 | 12.80 | 3.00 | 3.36 |
| State of Movable Barrier | Designed Sea Level | Return Period (year) | Overtopping Discharge (q, m3/(m s)) | |
|---|---|---|---|---|
| Model Scale | Full Scale | |||
| Non-standing | Approx. H.H.W. | 10 | 1.366 × 10−4 | 0.0295 |
| Approx. H.H.W. | 50 | 5.043 × 10−4 | 0.1089 | |
| Sea level during storm surge + SLR | 10 | 5.572 × 10−4 | 0.1204 | |
| Sea level during storm surge + SLR | 50 | 1.598 × 10−3 | 0.3453 | |
| Standing | Approx. H.H.W. | 10 | 0 | 0 |
| Approx. H.H.W. | 50 | 1.749 × 10−5 | 0.0038 | |
| Sea level during storm surge + SLR | 10 | 1.106 × 10−5 | 0.0024 | |
| Sea level during storm surge + SLR | 50 | 4.602 × 10−5 | 0.0099 | |
| State of Movable Barrier | Designed Sea Level | Return Period (year) | Hm0 (m) | Tm−1,0 (sec) | d (m) | h (m) | Rc/Hm0 | Lm−1,0 (m) | Sm−1,0 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Non-standing | Approx. H.H.W. | 10 | 0.120 | 2.17 | 0.0388 | 0.254 | 1.127 | 7.352 | 0.0163 | 0.0112 |
| Approx. H.H.W. | 50 | 0.128 | 3.00 | 0.0388 | 0.254 | 1.106 | 14.052 | 0.0091 | 0.0055 | |
| Sea level during storm surge + SLR | 10 | 0.121 | 2.23 | 0.0746 | 0.290 | 0.822 | 7.764 | 0.0155 | 0.0230 | |
| Sea level during storm surge + SLR | 50 | 0.128 | 3.00 | 0.0746 | 0.290 | 0.777 | 14.052 | 0.0091 | 0.0120 | |
| Standing | Approx. H.H.W. | 50 | 0.128 | 3.00 | 0.0388 | 0.254 | 2.272 | 14.052 | 0.0091 | 0.0055 |
| Sea level during storm surge + SLR | 10 | 0.121 | 2.23 | 0.0746 | 0.290 | 2.107 | 7.764 | 0.0155 | 0.0230 | |
| Sea level during storm surge + SLR | 50 | 0.128 | 3.00 | 0.0746 | 0.290 | 1.992 | 14.052 | 0.0091 | 0.0120 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, B.W.; Seo, J.; Park, W.-S.; Won, D. A Hydraulic Experimental Study of a Movable Barrier on a Revetment to Block Wave Overtopping. Appl. Sci. 2020, 10, 89. https://doi.org/10.3390/app10010089
Lee BW, Seo J, Park W-S, Won D. A Hydraulic Experimental Study of a Movable Barrier on a Revetment to Block Wave Overtopping. Applied Sciences. 2020; 10(1):89. https://doi.org/10.3390/app10010089
Chicago/Turabian StyleLee, Byeong Wook, Jihye Seo, Woo-Sun Park, and Deokhee Won. 2020. "A Hydraulic Experimental Study of a Movable Barrier on a Revetment to Block Wave Overtopping" Applied Sciences 10, no. 1: 89. https://doi.org/10.3390/app10010089
APA StyleLee, B. W., Seo, J., Park, W.-S., & Won, D. (2020). A Hydraulic Experimental Study of a Movable Barrier on a Revetment to Block Wave Overtopping. Applied Sciences, 10(1), 89. https://doi.org/10.3390/app10010089






