Design and Control of a 1-DOF Robotic Lower-Limb System Driven by Novel Single Pneumatic Artificial Muscle
Abstract
1. Introduction
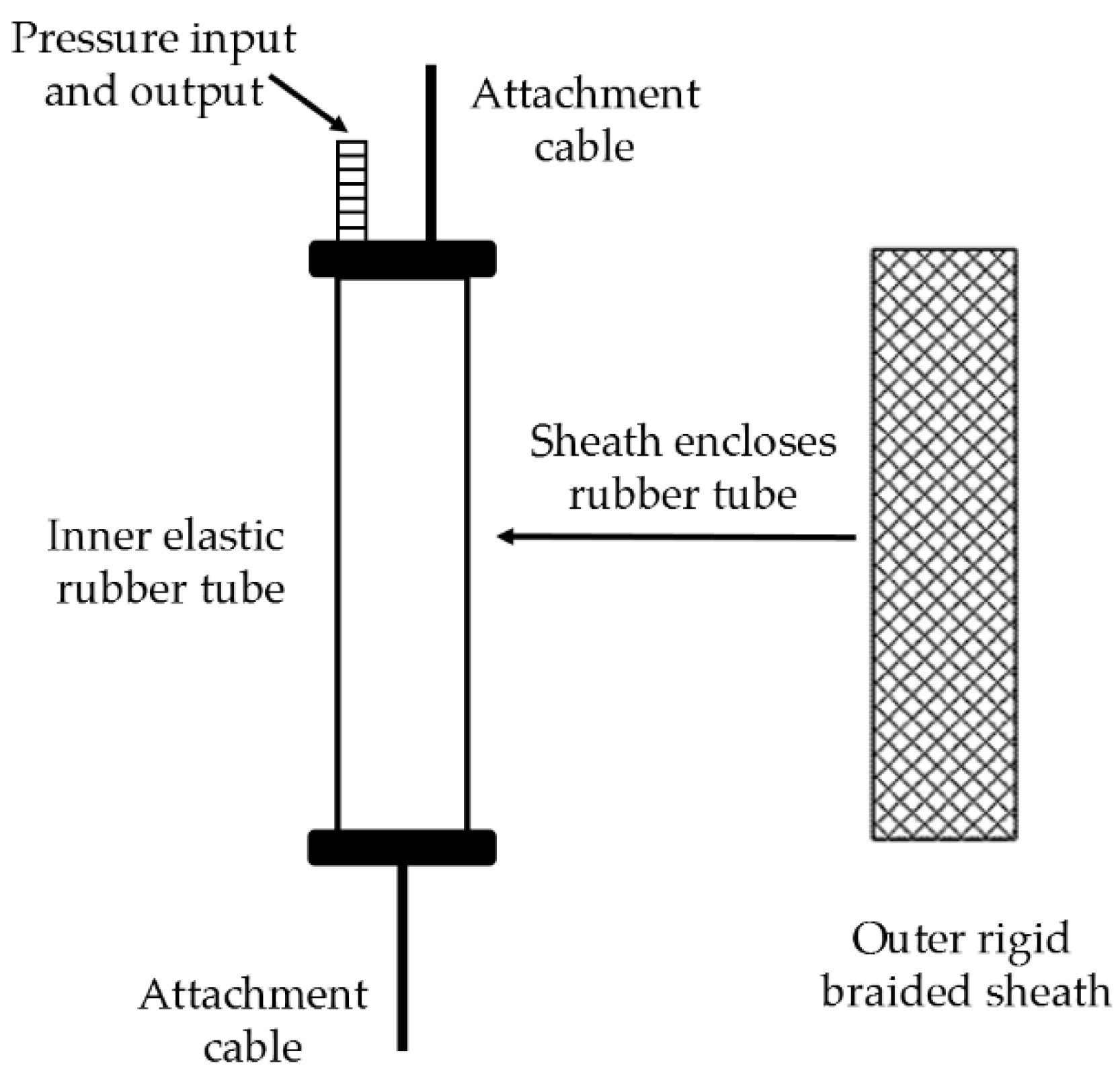
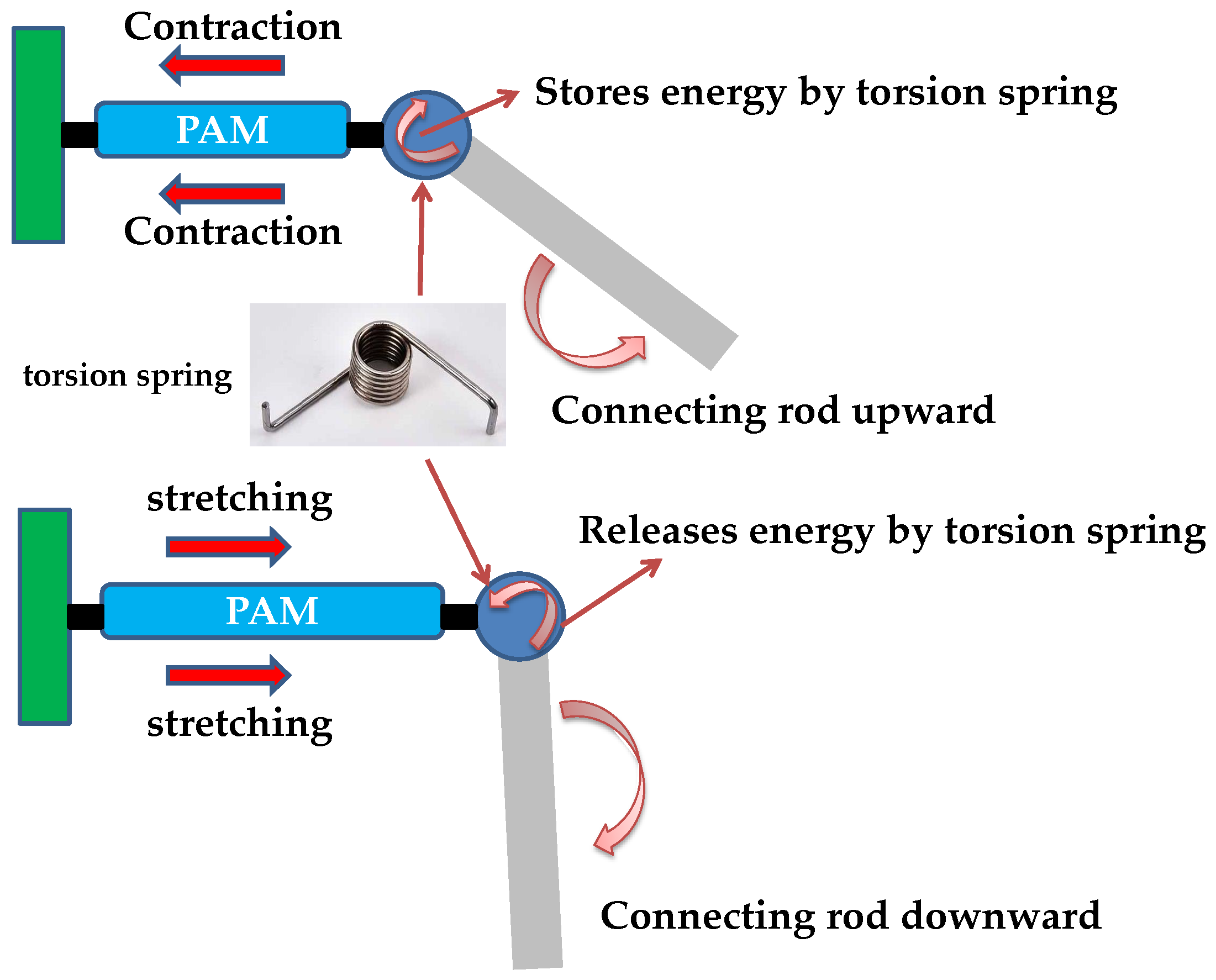
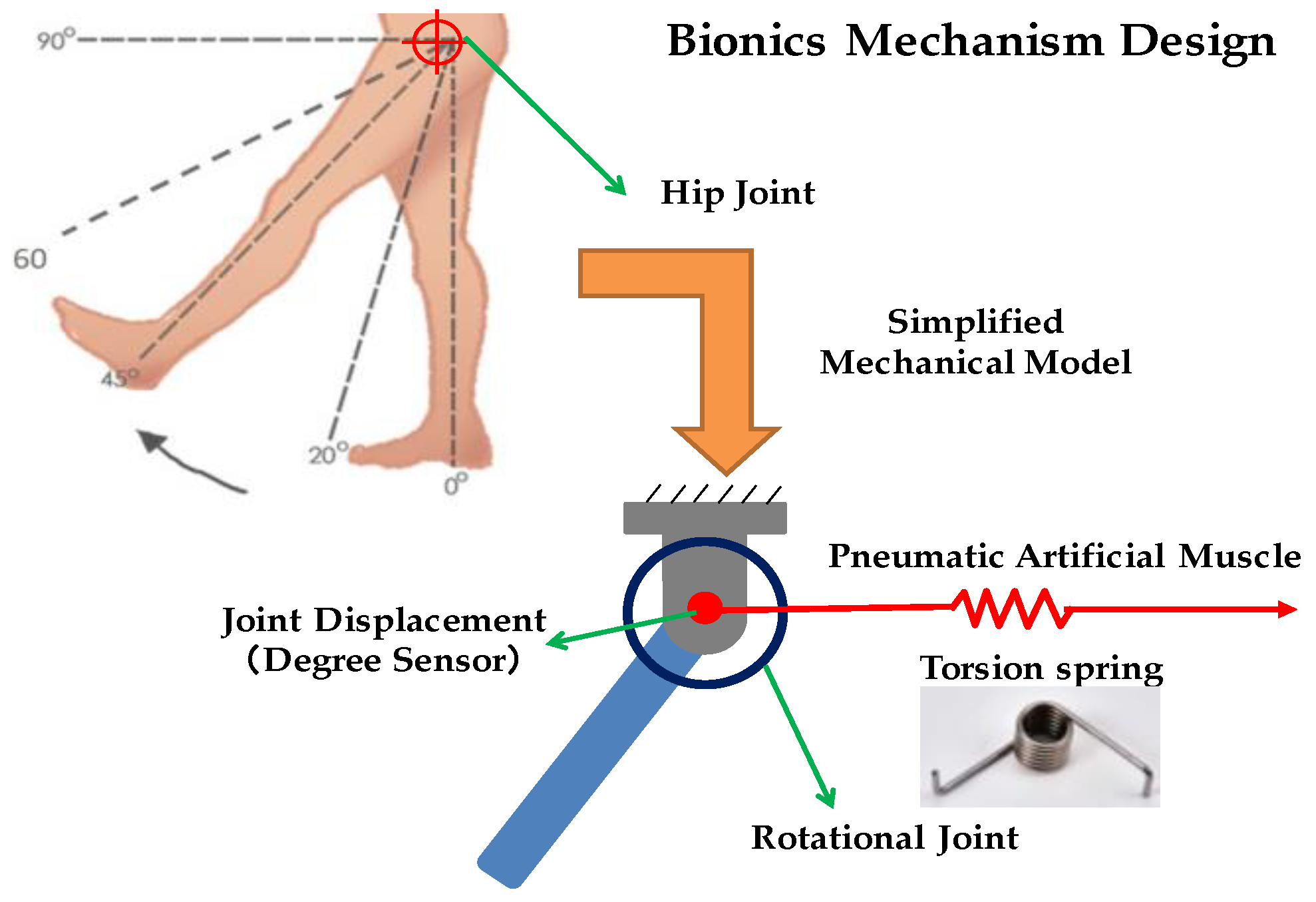
2. Mechanism Design of Novel Single-Pneumatic Artificial Muscle (PAM) System
- Shock absorption: when the mechanical sudden impact load occurs, the spring can absorb the vibration energy to make the vibration more moderate.
- Force generation: the most common function of the spring applied to the machine is to use the elasticity of the spring to generate force or torque to maintain contact between the parts.
- Energy storage: the spring can generate elastic energy due to deformation, so the spring can be used to store energy.
- Force measurement: when the spring is deformed, the amount of deformation maintains a certain proportional relationship with the external force. With this characteristic, it can be used to measure the magnitude of the external force.
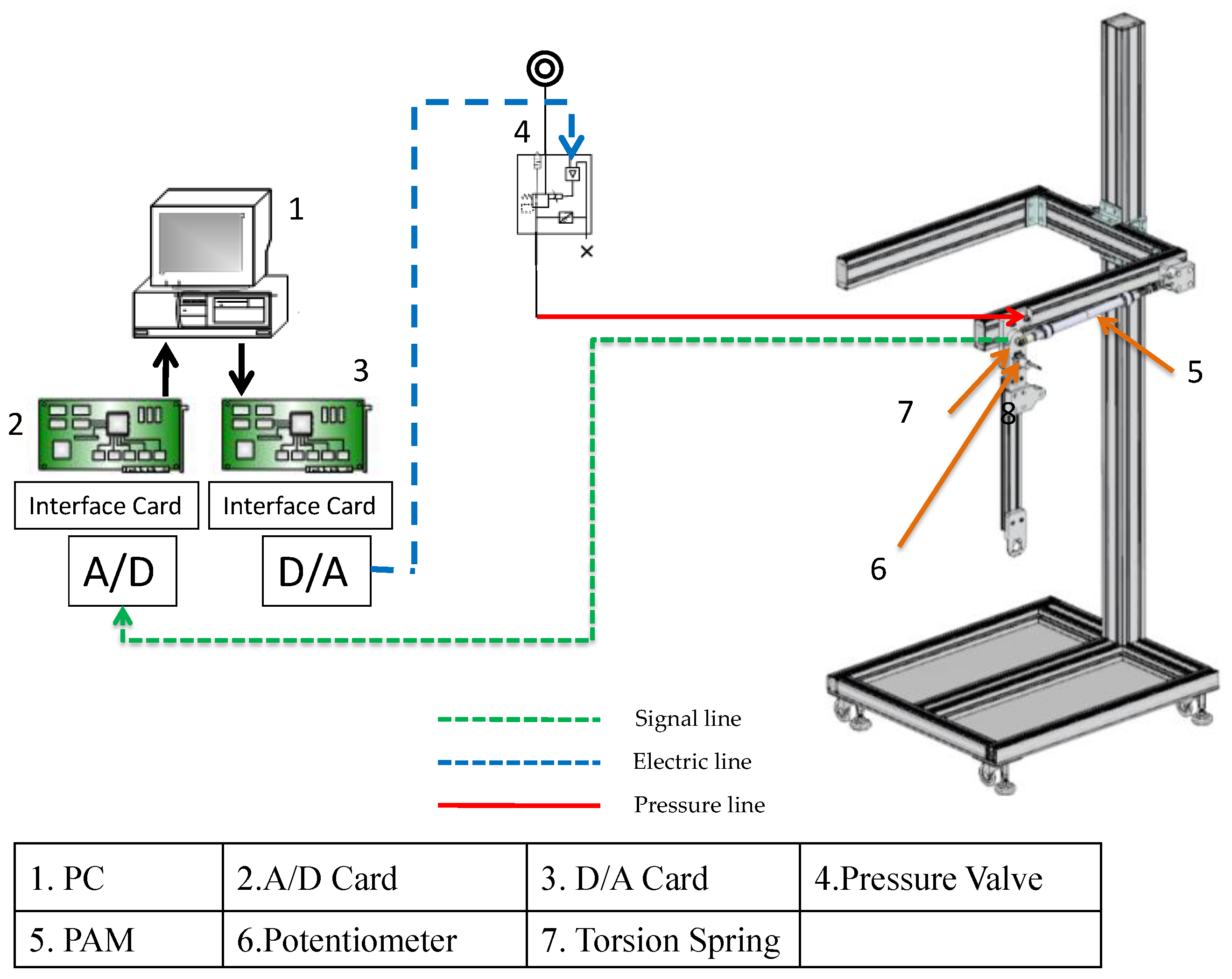
3. Layout of Test Rig
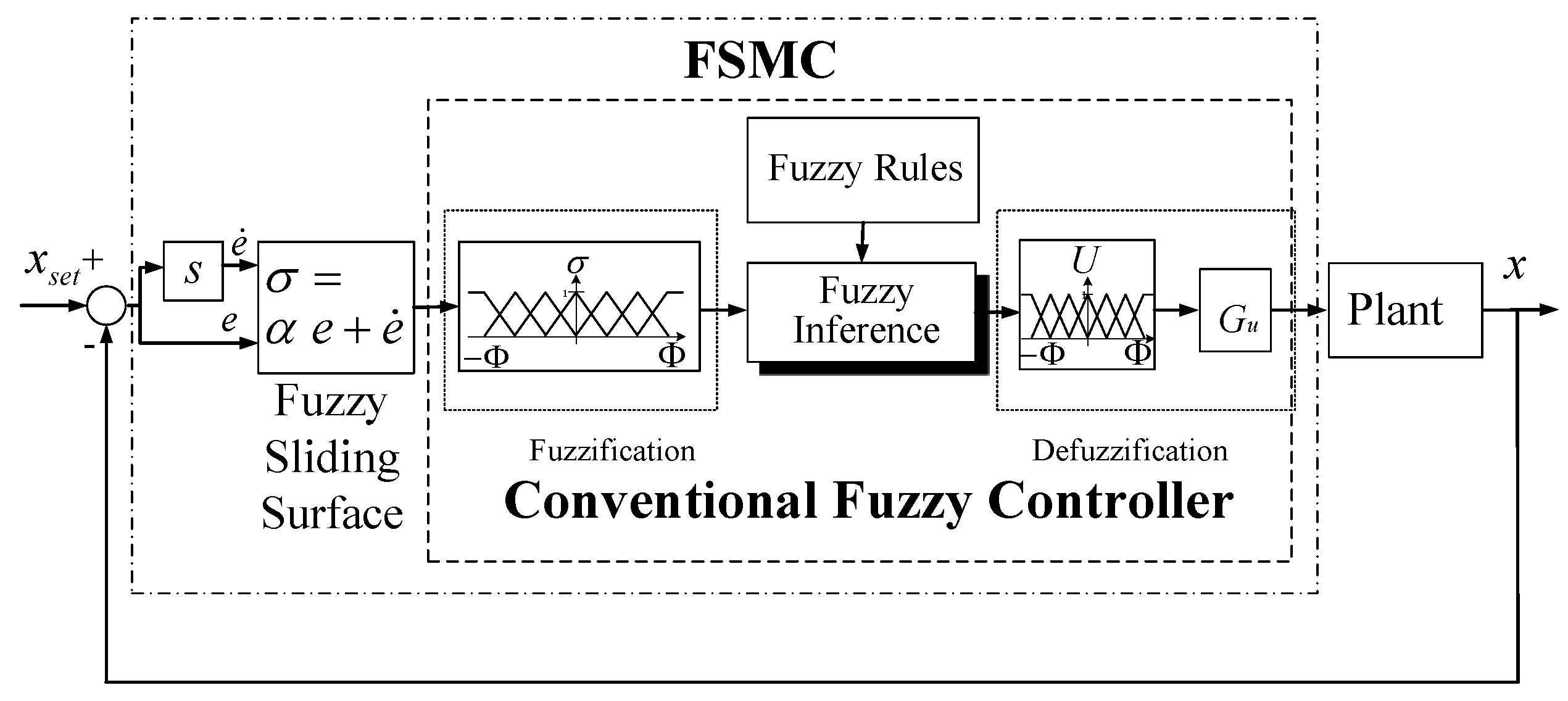
4. Controller Design
4.1. Control Strategy
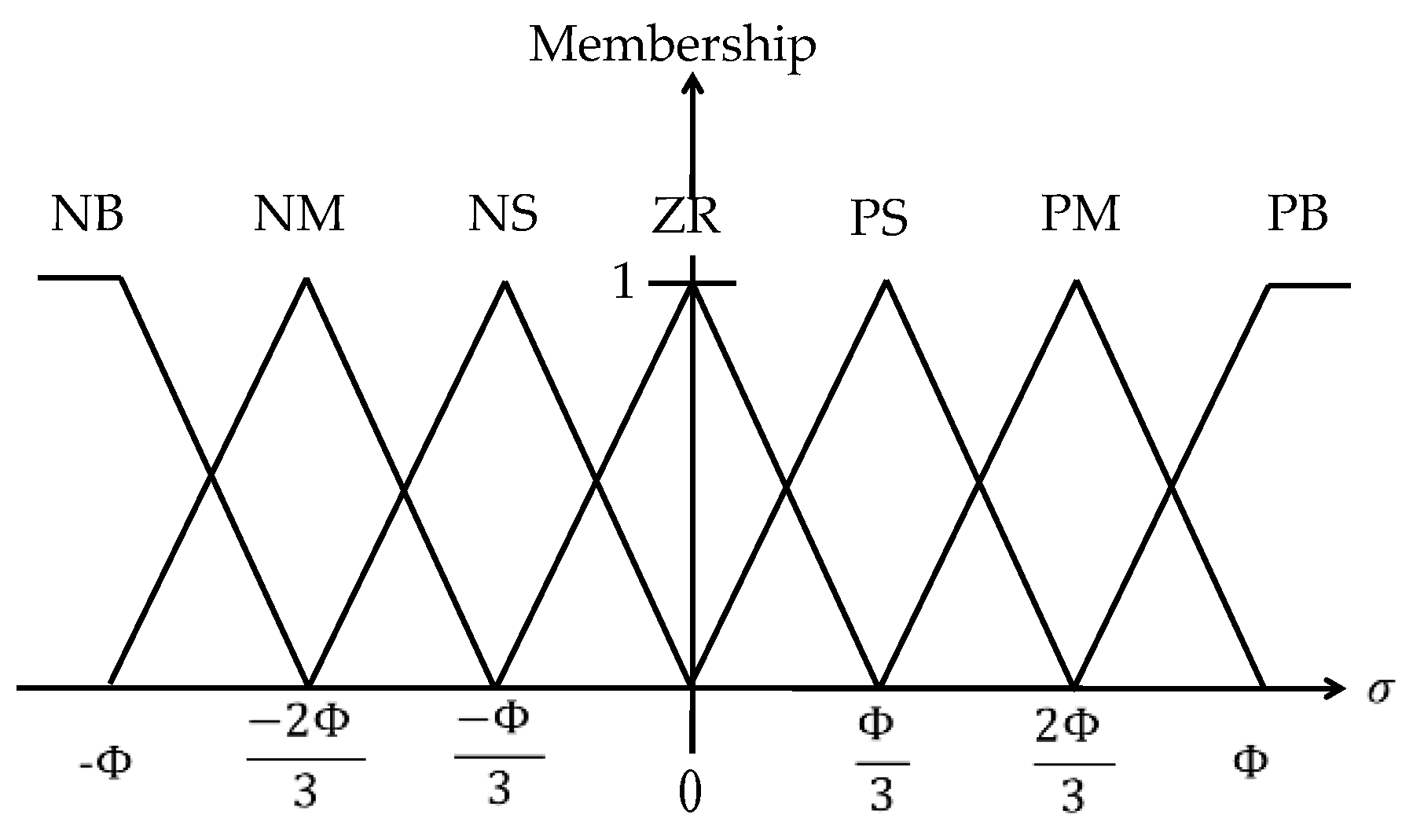
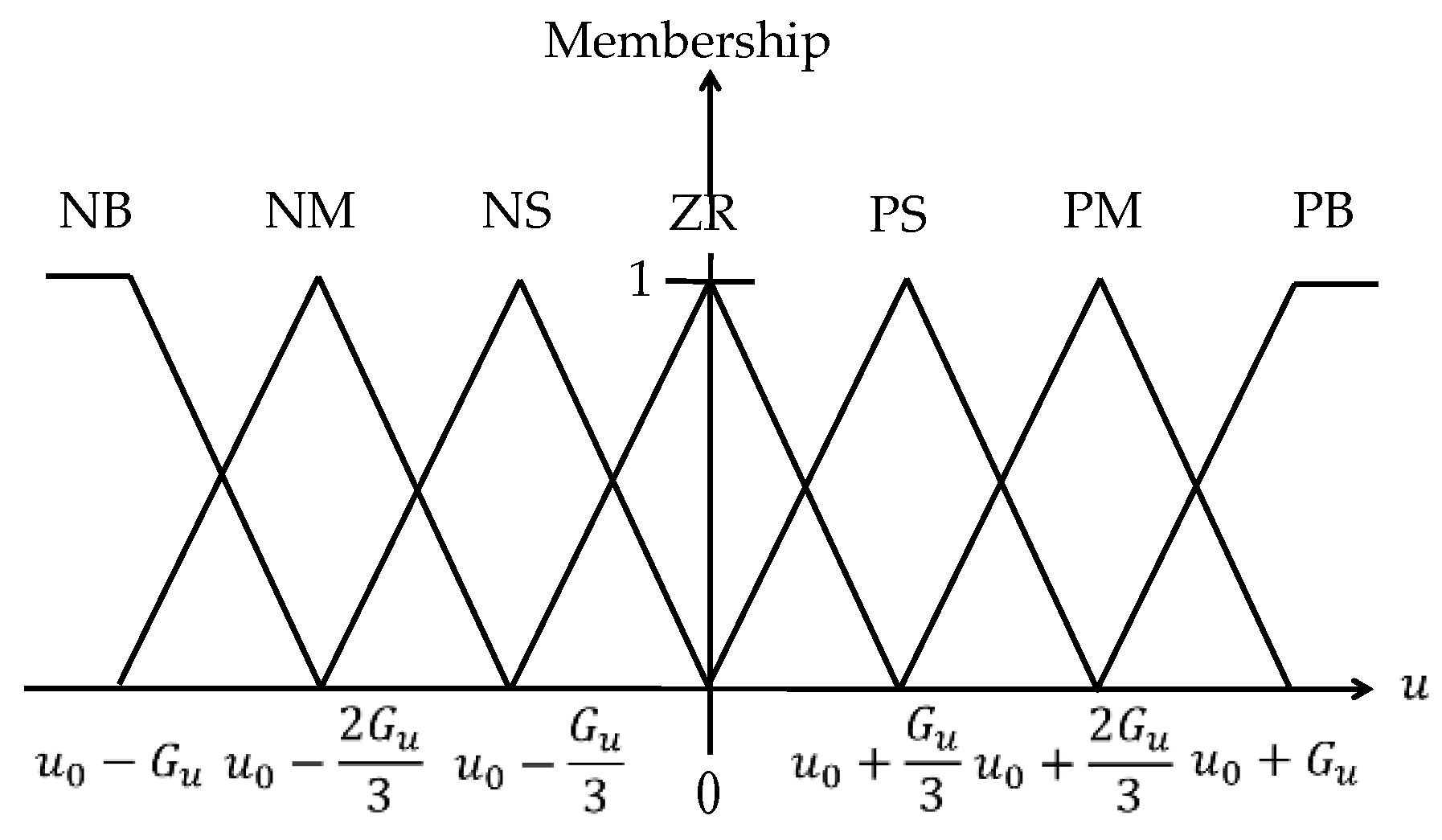
4.2. Design of Fuzzy Sliding Mode Control (FSMC) for Path-Positioning Controller
5. Experiments
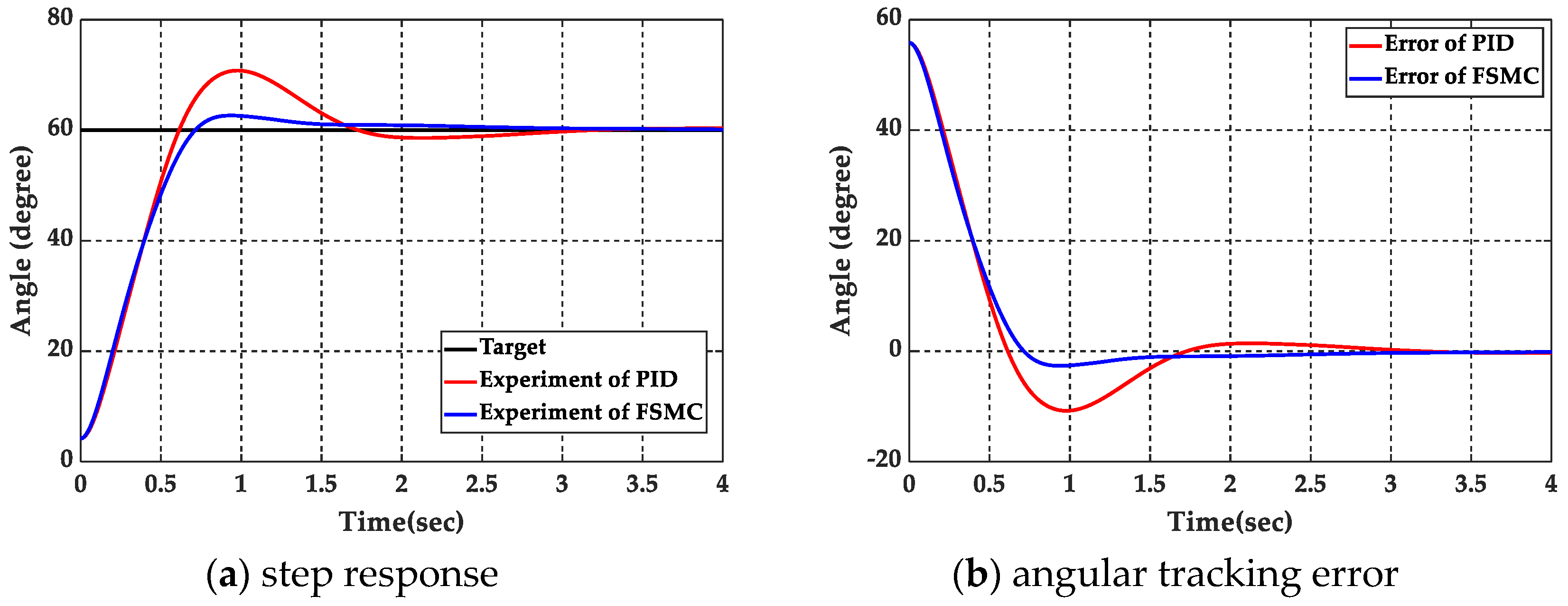
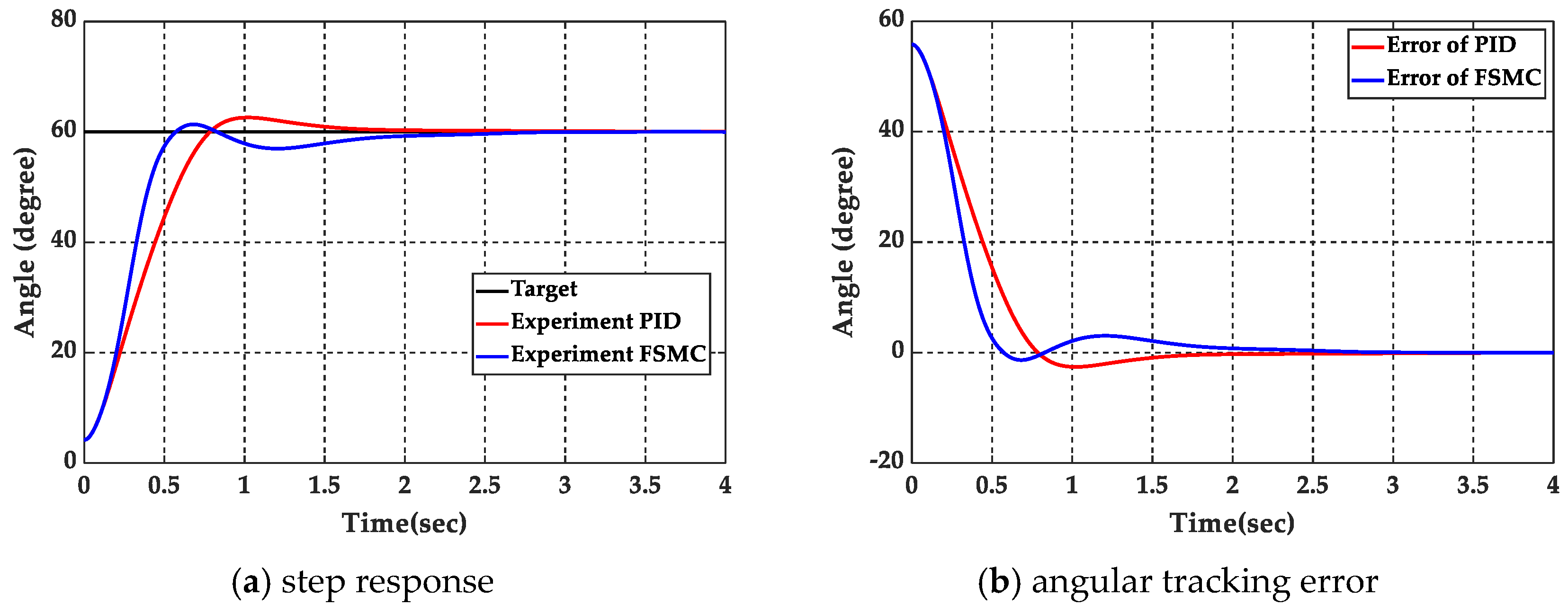
5.1. Step Response Experiment
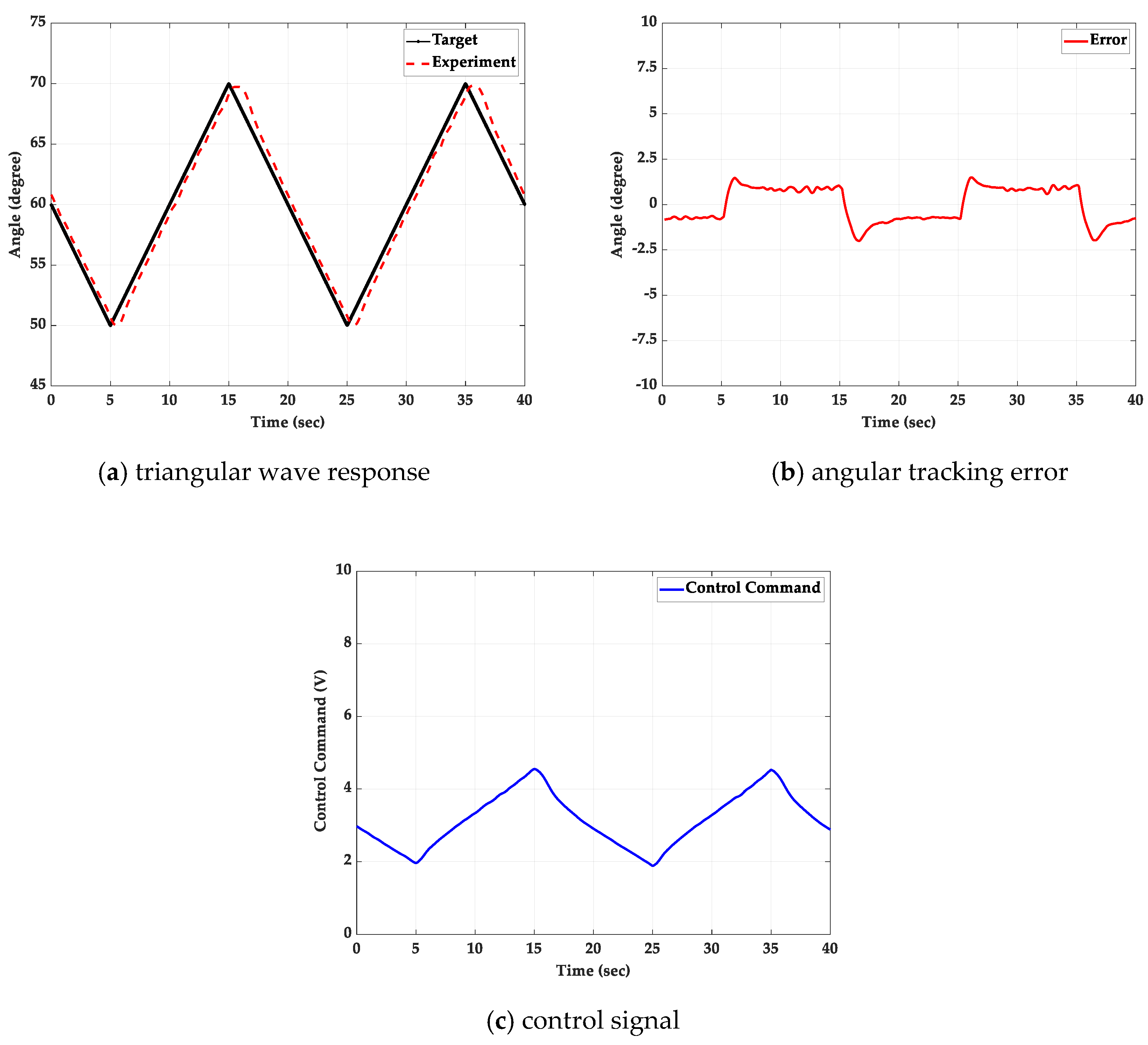
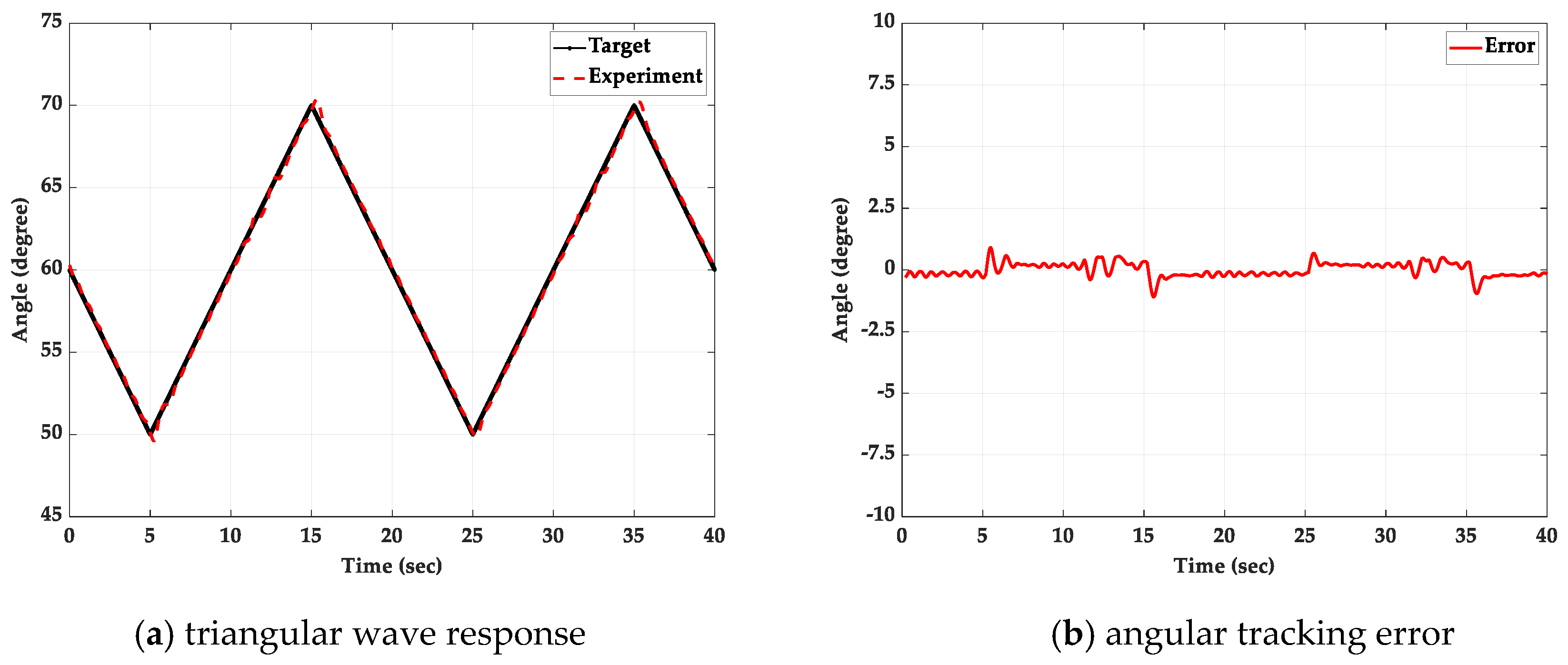
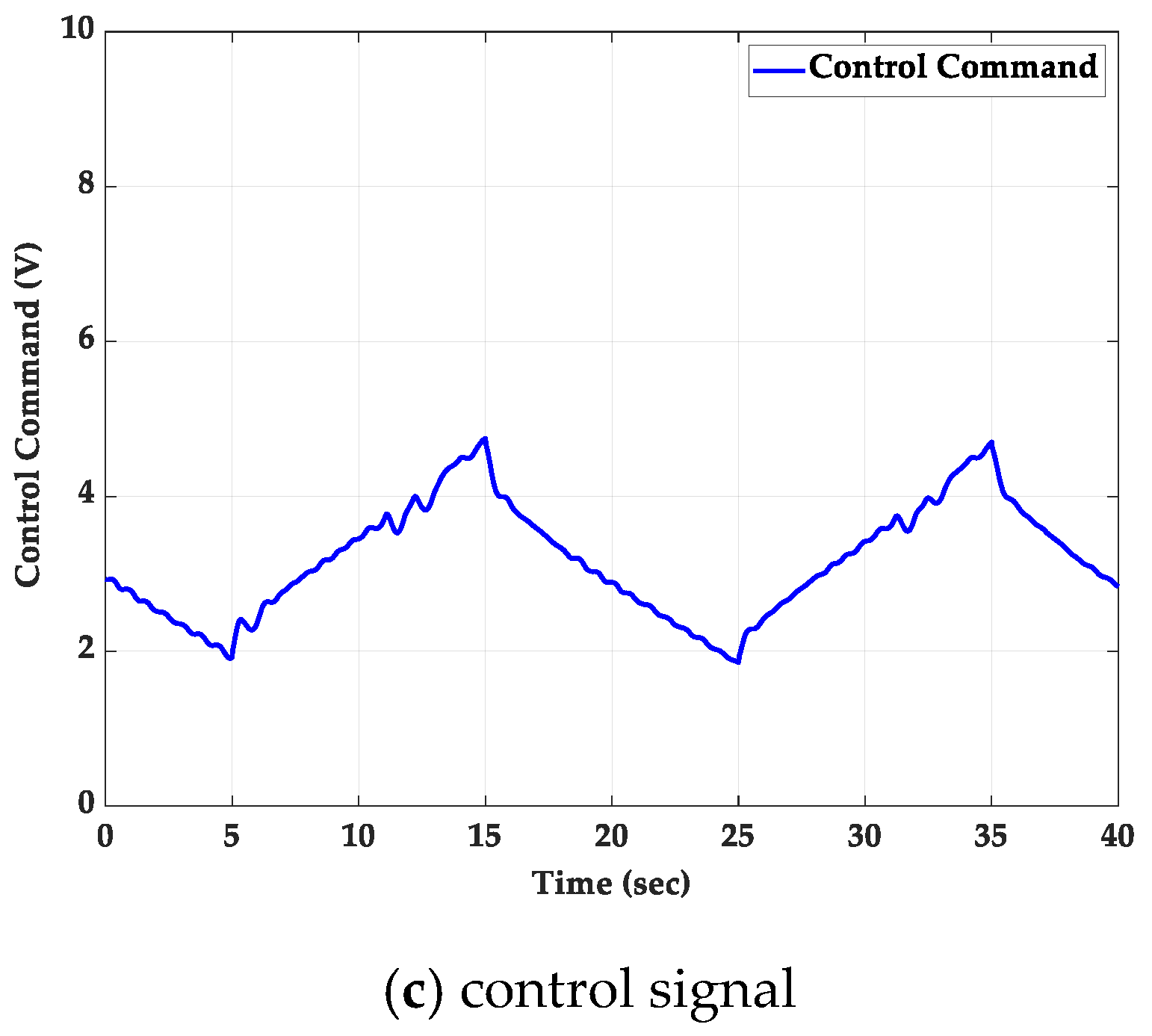
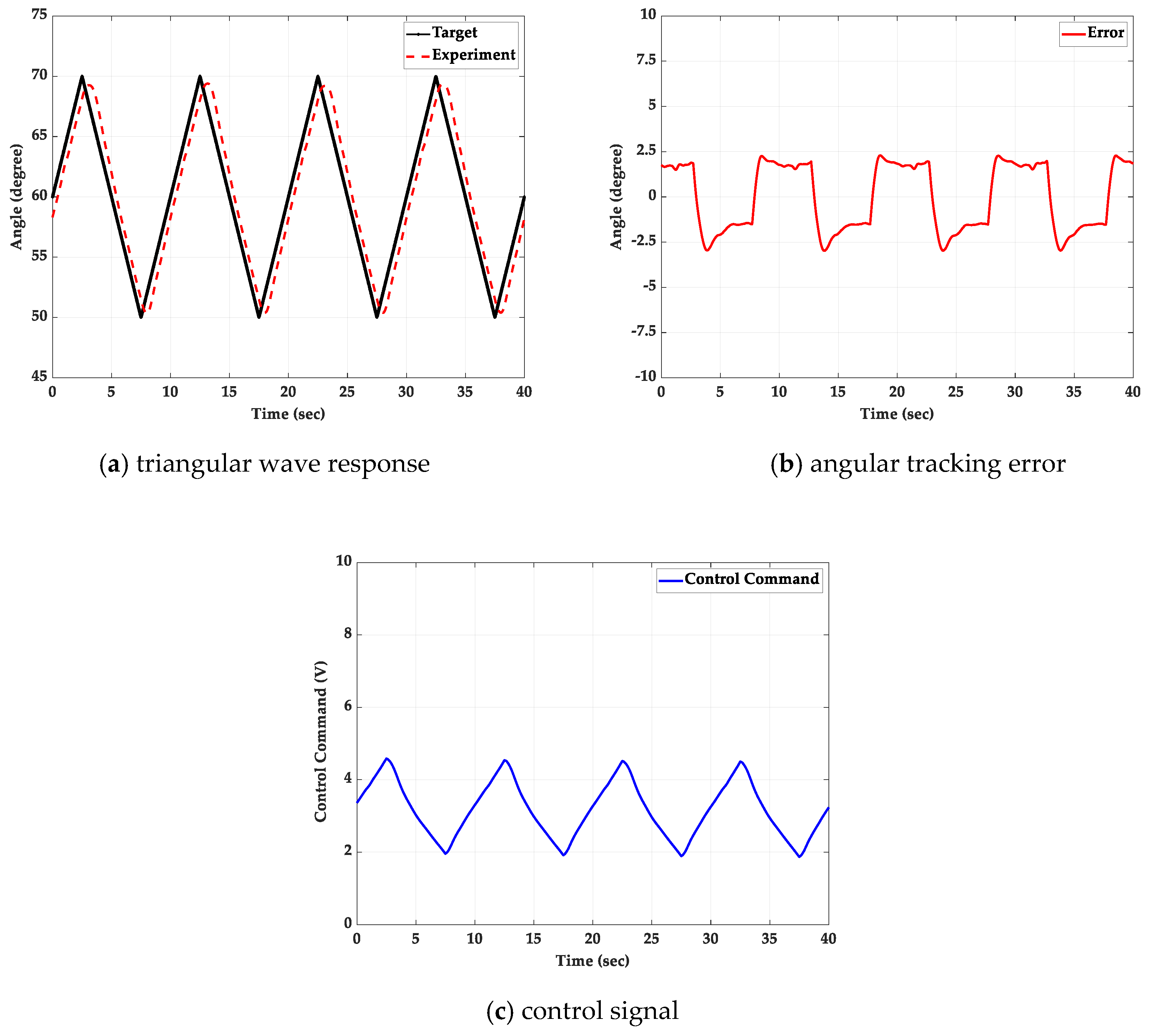
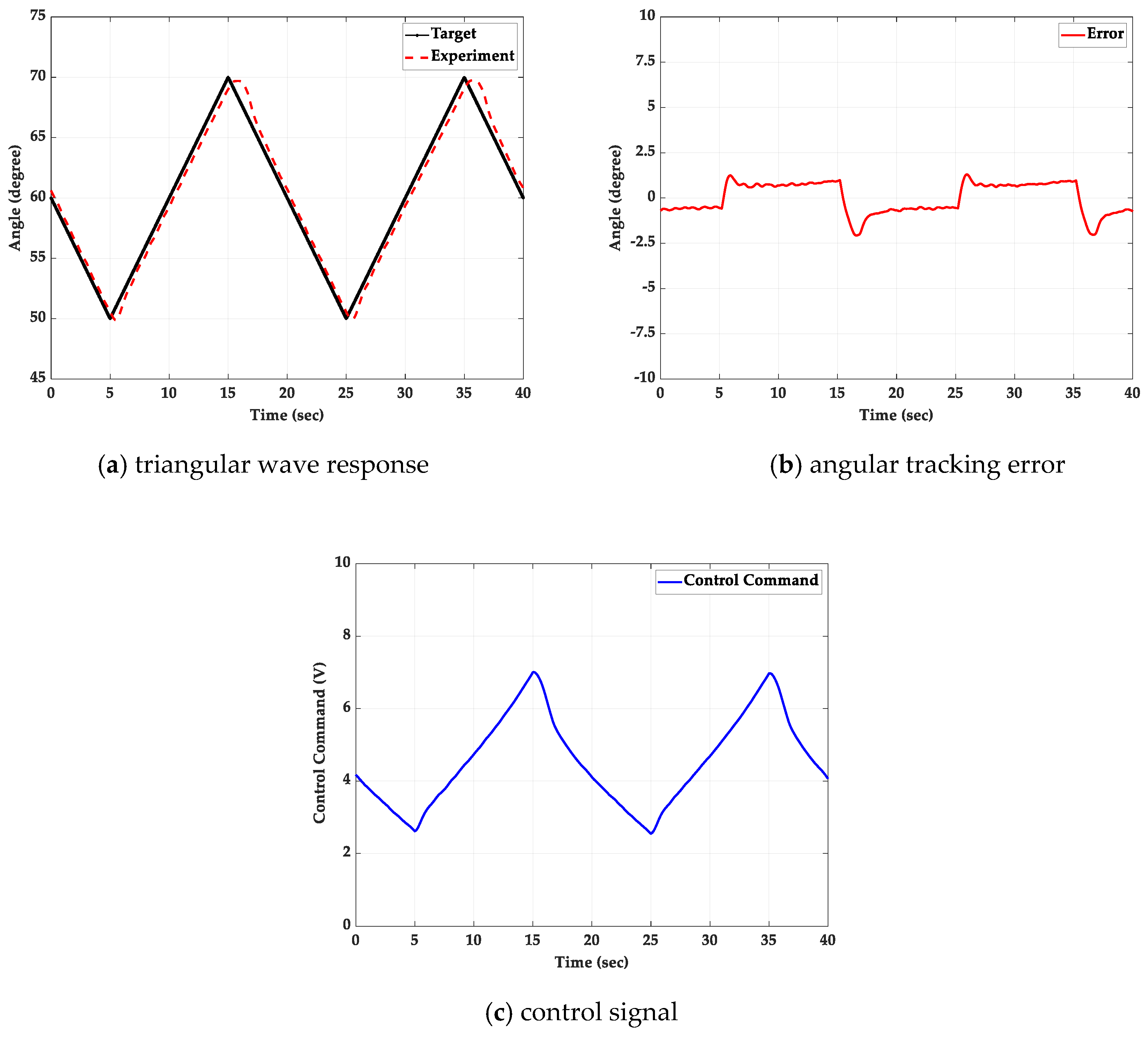
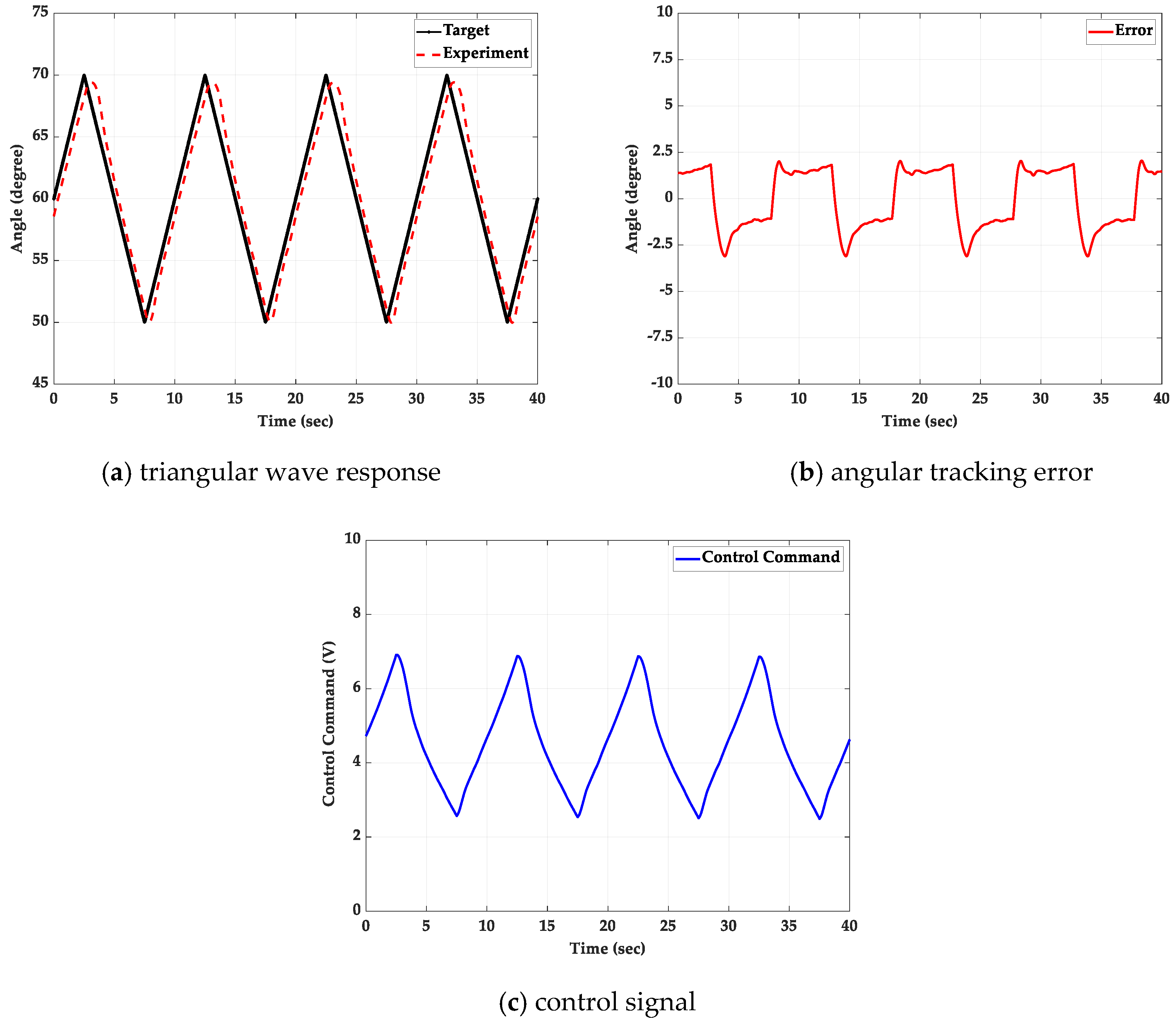
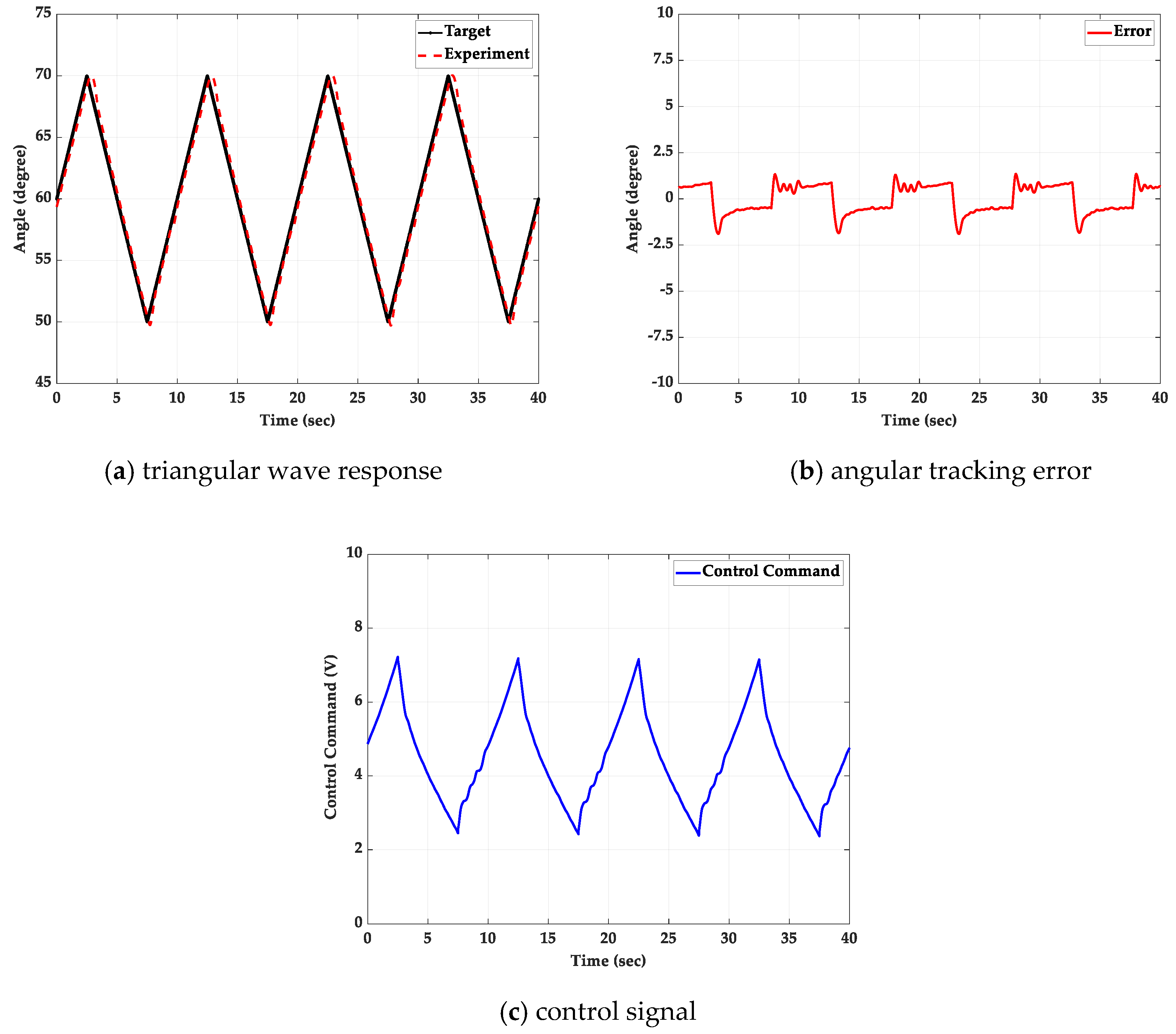
5.2. Triangular Wave Path-Tracking Control Experiment
5.2.1. Without Additional Loading
5.2.2. With a 2 kg Loading Mass
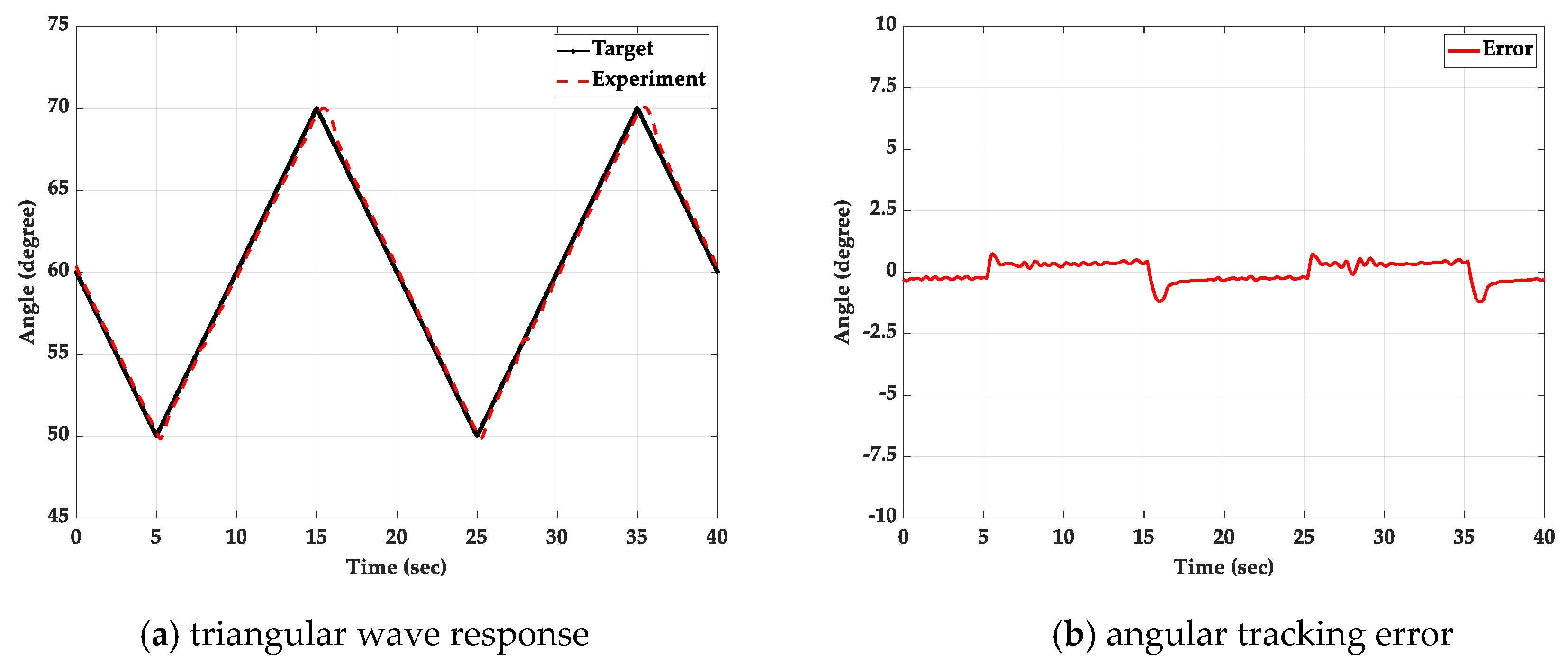
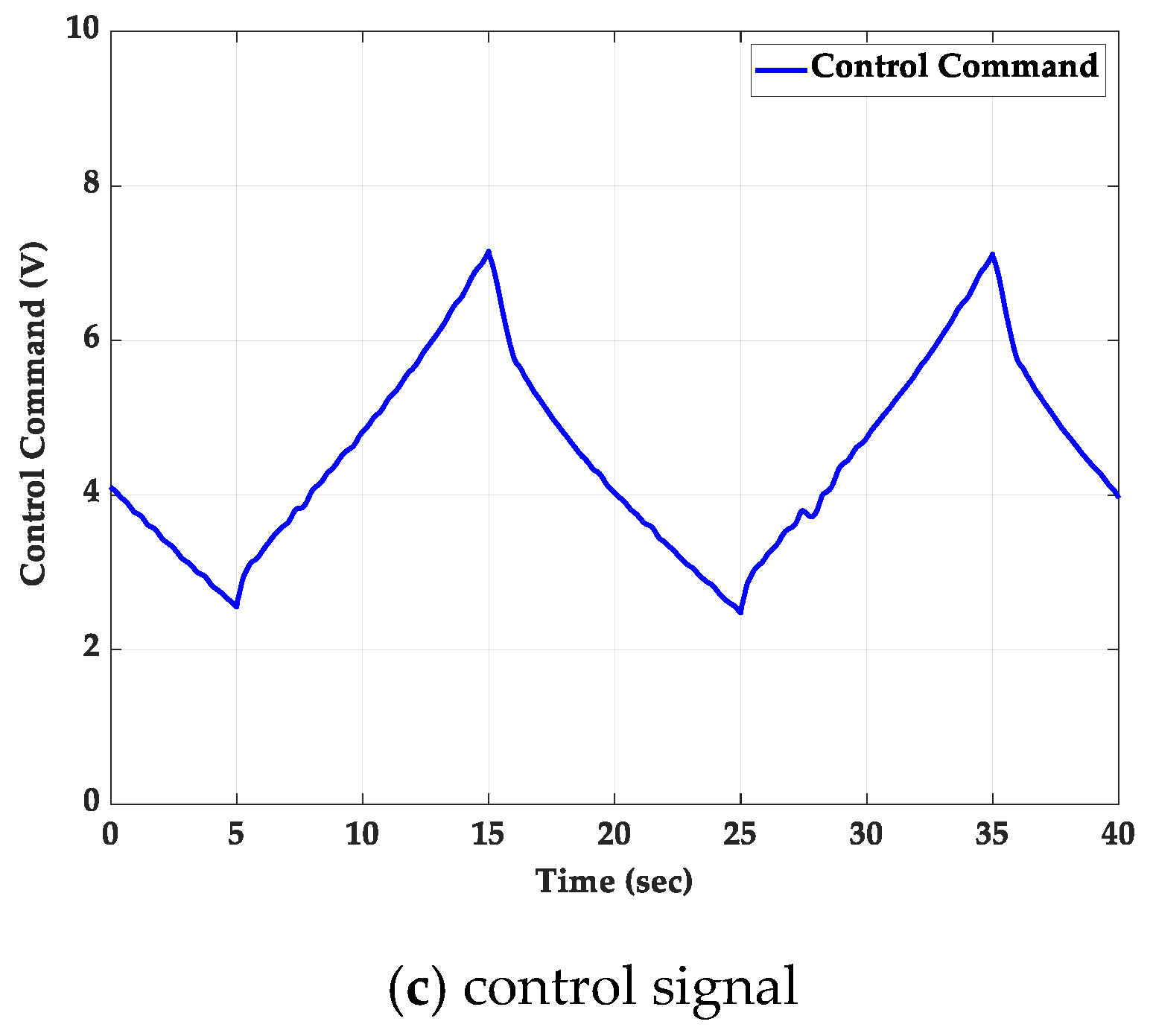
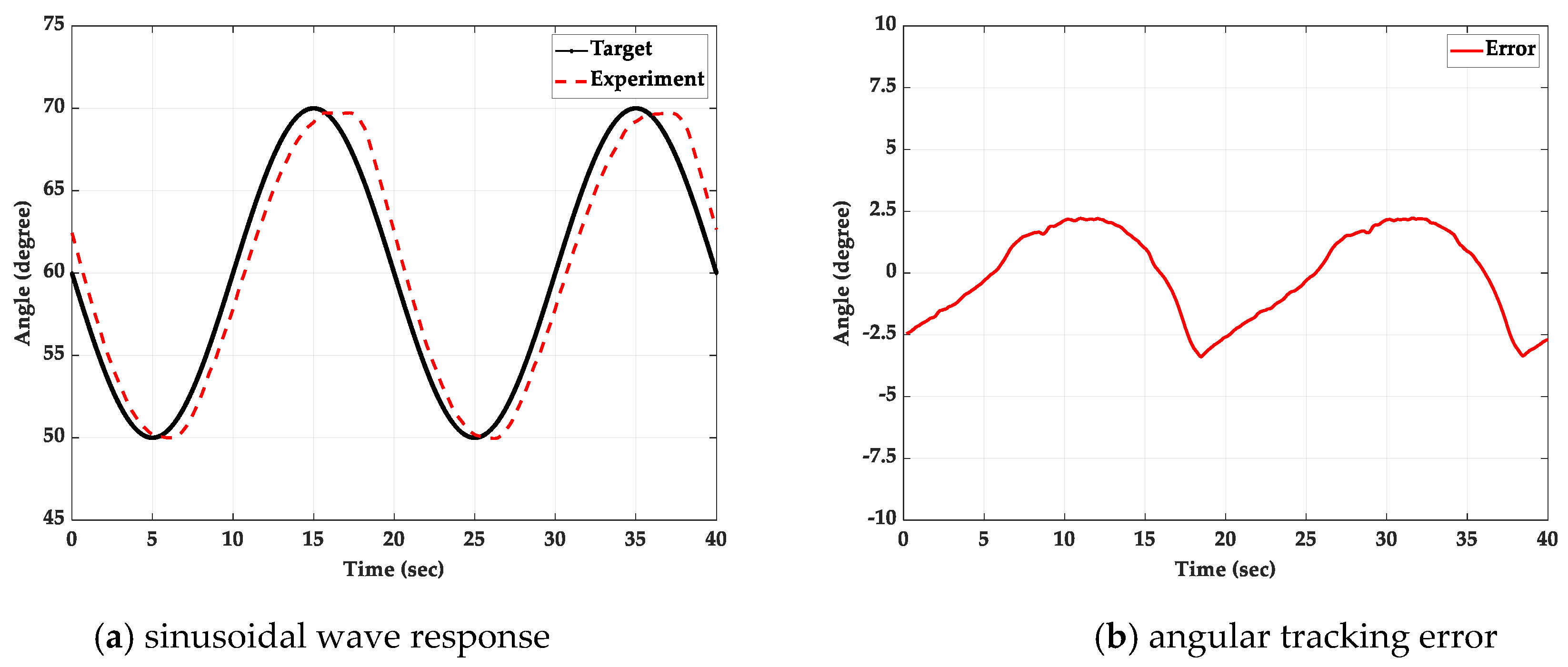
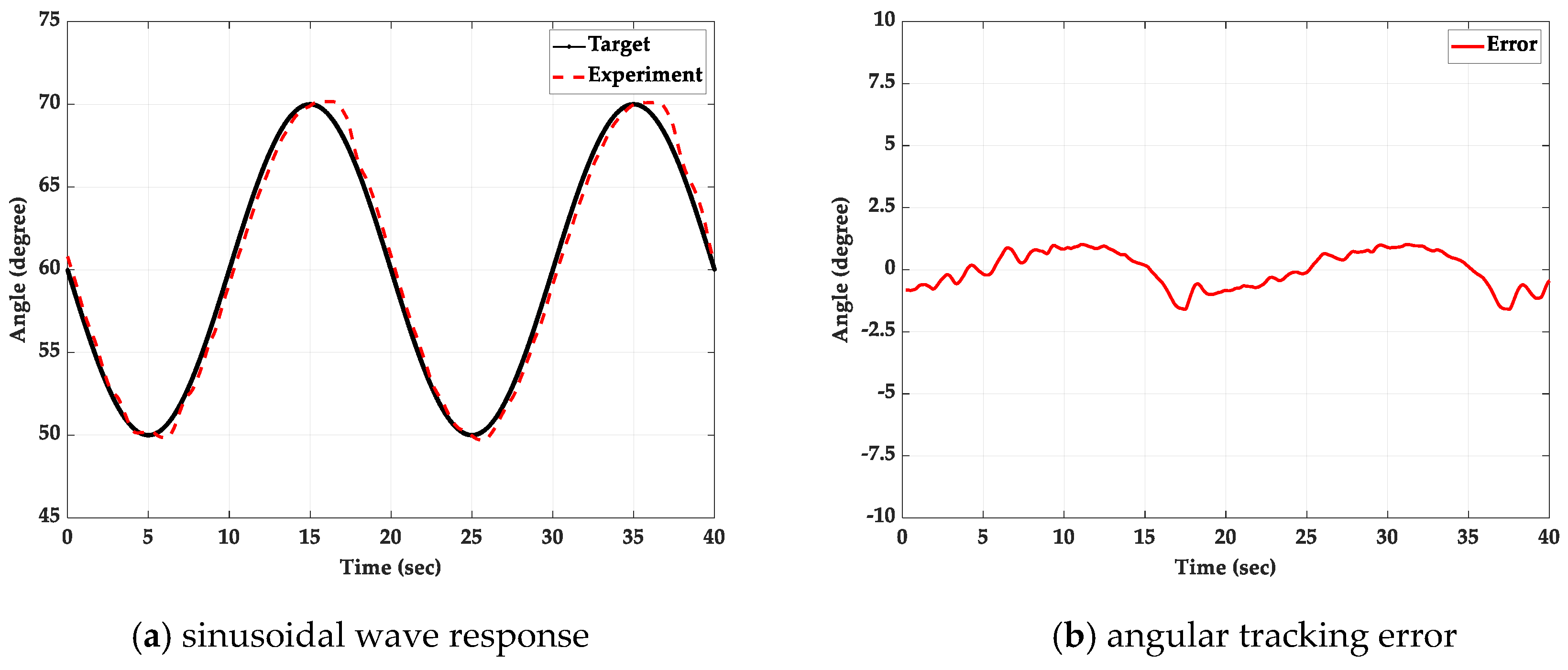
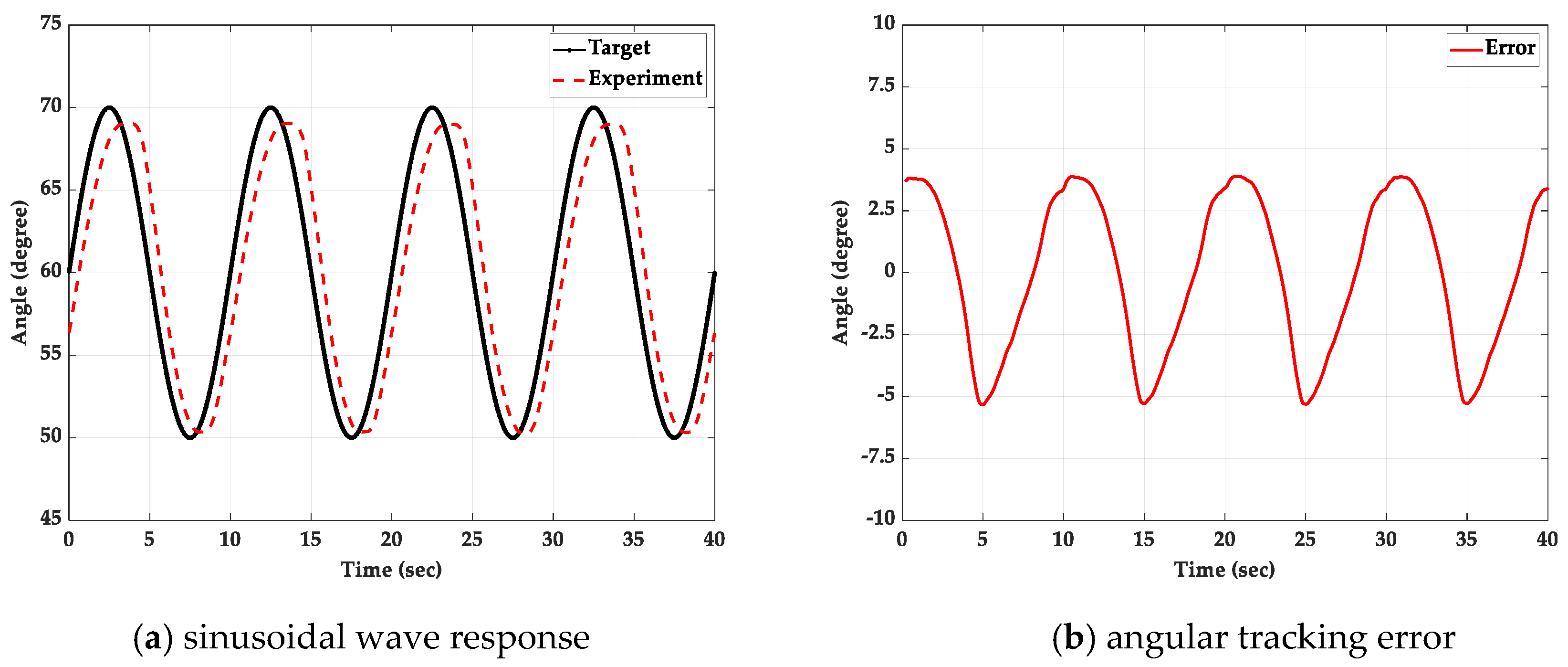
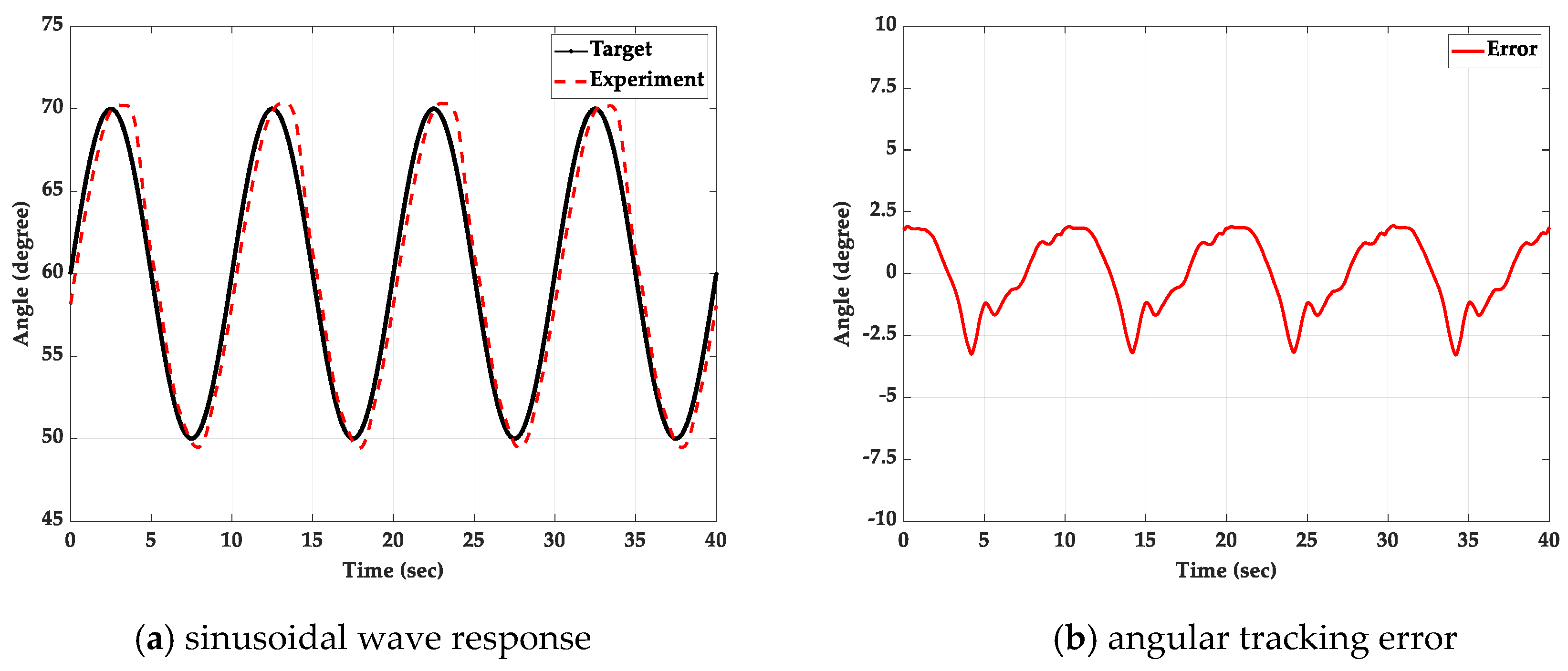
5.3. Sinusoidal Wave Path-Tracking Experiment with a 2 kg Loading Mass
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| PAM | Pneumatic artificial muscle |
| FSMC | Fuzzy sliding mode control |
References
- Schulte, H.F. The characteristics of the McKibben artificial pneumatic muscle. In the Application of External Power in Prosthetics and Orthotics; Appendix H. Publ. 874; National Academy of Sciences: Washington, DC, USA, 1961; pp. 94–115. [Google Scholar]
- Caldwell, D.G.; Medrano-Cerda, G.A.; Goodwin, M. Control of pneumatic muscle actuators. IEEE Control Syst. Mag. 1995, 15, 40–48. [Google Scholar]
- Chou, C.P.; Hannaford, B. Static and dynamic characteristics of McKibben pneumatic artificial muscles. In Proceedings of the 1994 IEEE International Conference on Robotics and Automation, San Diego, CA, USA, 8–13 May 1994; pp. 281–286. [Google Scholar]
- Chou, C.P.; Hannaford, B. Measurement and modeling of McKibben pneumatic artificial muscles. IEEE Int. Conf. Robot. Autom. 1996, 12, 90–102. [Google Scholar] [CrossRef]
- Lilly, J.H.; Quesada, P.M. A two-input sliding-mode controller for a planar arm actuated by four pneumatic muscle groups. IEEE Trans. Neural Syst. Rehabil. Eng. 2004, 12, 349–359. [Google Scholar] [CrossRef] [PubMed]
- Chang, M.K. An adaptive self-organizing fuzzy sliding mode controller for a 2-DOF rehabilitation robot actuated by pneumatic muscle actuators. Control Eng. Pract. 2010, 18, 13–22. [Google Scholar] [CrossRef]
- Anh, H.P.H. Online tuning gain scheduling MIMO neural PID control of the 2-axes pneumatic artificial muscle (PAM) robot arm. Expert Syst. Appl. 2010, 37, 6547–6560. [Google Scholar] [CrossRef]
- Jahanabadi, H.; Mailah, M.; Md-Zain, M.Z.; Hooi, H.M. Active force with fuzzy logic control of a two-link arm driven by pneumatic artificial muscles. J. Bionic Eng. 2011, 8, 474–484. [Google Scholar] [CrossRef]
- Medrano-Cerda, G.A.; Bowler, C.J.; Caldwell, D.G. Adaptive position control of antagonistic pneumatic muscle actuators. In Proceedings of the 1995 IEEE/RSJ International Conference on Intelligent Robots and Systems, Pittsburgh, PA, USA, 5–9 August 1995; Volume 1, pp. 378–383. [Google Scholar]
- Ahn, K.K.; Thanh, T.D.C.; Ahn, Y.K. Intelligent switching control of pneumatic artificial muscle manipulator. JSME Int. J. 2005, 48, 657–667. [Google Scholar] [CrossRef]
- Tondu, B.; Lopez, Y. Modeling and control of Mckibben artificial muscle robot actuators. IEEE Control Syst. Mag. 2005, 20, 15–38. [Google Scholar]
- Mao, Y.; Wang, J.; Li, S.; Han, Z. Energy-efficient control of pneumatic muscle actuated biped robot joints. In Proceedings of the 6th World Congress on Intelligent Control and Automatic, Dalian, China, 21–23 June 2006; Volume 2, pp. 8881–8885. [Google Scholar]
- Jutras, D.; Bigras, P. Control of an actuator made of two antagonist Mckibben muscles via LMI optimization. In Proceedings of the IEEE International Symposium on Industrial Electronics, Montreal, QC, Canada, 9–13 July 2006; Volume 4, pp. 3072–3077. [Google Scholar]
- Chang, M.K.; Yen, P.L.; Yuan, T.H. Angle control of a one-dimension pneumatic muscle arm using self-organizing fuzzy control. In Proceedings of the IEEE International Conference on Systems, Man and Cybernetics, Taipei, Taiwan, 8–11 October 2006; Volume 5, pp. 3834–3838. [Google Scholar]
- Kato, T.; Higashi, T.; Shimizu, K. Teleoperation of a Robot Arm System Using Pneumatic Artificial Rubber Muscles: Teleoperation over the Internet Using UDP and a Web Camera. In Proceedings of the International Conference on Broadband, Wireless Computing, Communication and Applications, Fukuoka, Japan, 4–6 November 2010; pp. 714–718. [Google Scholar]
- Muramatsu, Y.; Kobayashi, H.; Sato, Y.; Jiaou, H.; Hashimoto, T.; Kobayashi, H. Quantitative performance analysis of muscle suit—Estimation by Oxyhemoglobin and deoxyhemoglobin. In Proceedings of the IEEE International Conference on Robotics and Biomimetics, Karon Beach, Phuket, Thailand, 7–11 December 2011; pp. 293–298. [Google Scholar]
- Perry, J. Burnfield, J.M. Gait analysis: Normal and pathological function. J. Pediatric Orthop. 1992, 12, 815. [Google Scholar] [CrossRef]
- Hung, J.Y.; Gao, W.; Hung, J.C. Variable structure control: A survey. Industrial Electronics. IEEE Trans. Mechatron. 1993, 40, 2–22. [Google Scholar]
- Kim, S.-W.; Lee, J.-J. Design of a fuzzy controller with fuzzy sliding surface. Fuzzy Sets Syst. 1995, 71, 359–367. [Google Scholar] [CrossRef]
- Wu, J.C.; Liu, T.S. A sliding-mode approach to fuzzy control design. IEEE Trans. Control Syst. Technol. 1996, 4, 141–151. [Google Scholar] [CrossRef]
- Behrens, H.; Jaschke, P.; Steinhausen, J.; Waller, H. Modeling of Technical Systems: Application to Hydrodynamic Torque Converters and Couplings. Math. Comput. Modeling Dyn. Syst. 2002, 6, 223–250. [Google Scholar] [CrossRef]





| Components | Company | Type | Specifications |
|---|---|---|---|
| A/D (Analog to Digital) Interface Card | Advantech | PCI-1720U | 4 channels12-bit D/A Output range: ±10 V |
| D/A (Digital to Analog) Interface Card | Advantech | PCI-1710 | 32 channels12-bit A/D Maximum input range: ±10 V |
| Pneumatic Muscle | FESTO | DMSP-20-200N-25cm | Max. stroke: 25% Max. force output: 1500 N Input pressure: 0~6 bar |
| Proportional Valve | FESTO | VPPM-8L-L-1-G14-0L6H-V1P | Input voltage: 0~10 V Output pressure: 0~6 bar |
| Potentiometer | Mitingen (Taiwan mitingen co., ltd.) | MTR22A | Range: 0~120 degree Output voltage: 0~5 V |
| Parameters | Value | Unity |
|---|---|---|
| Wire diameter | 3.5 | mm |
| Center diameter | 26.5 | mm |
| Number of laps | 4 | loop |
| Installation angle | −10 | degree |
| Installation torque | 794 | N·mm |
| Free angle | 0 | degree |
| Working angle | 54 | degree |
| Working torque | 4280 | N·mm |
| Rules | ||
|---|---|---|
| If is PB | Then is PB | |
| If is PM | Then is PM | |
| If is PS | Then is PS | |
| If is ZR | Then is ZR | |
| If is NS | Then is NS | |
| If is NM | Then is NM | |
| If is NB | Then is NB |
| NB | NM | NS | ZR | PS | PM | PB | |
|---|---|---|---|---|---|---|---|
| NB | NM | NS | ZR | PS | PM | PB | |
| Parameters | Description | Value |
|---|---|---|
| The slope of the fuzzy sliding surface | 1 | |
| The fuzzy sliding surface | ||
| The offset of the control signal input | 0 | |
| The convergence boundary of the fuzzy sliding surface | ||
| The membership function of the input variable | ||
| The membership function of the output variable | ||
| The scale factor | 5.8 |
| Parameters | Loading | Rising Time (s) | Settling Time (s) | Peak Time (s) | Overshoot (%) | Steady State Error (Degree) | |
|---|---|---|---|---|---|---|---|
| Controller | |||||||
| PID Controller | No | 0.4313 | 2.4066 | 0.9780 | 18.1499 | 0.0850 | |
| FSMC | 0.4873 | 1.4733 | 0.9730 | 4.4194 | 0.0030 | ||
| PID Controller | Yes | 0.5370 | 1.4254 | 1.0210 | 4.2278 | 0.0566 | |
| FSMC | 0.3389 | 1.7927 | 0.6820 | 2.2125 | 0.0338 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsai, T.-C.; Chiang, M.-H. Design and Control of a 1-DOF Robotic Lower-Limb System Driven by Novel Single Pneumatic Artificial Muscle. Appl. Sci. 2020, 10, 43. https://doi.org/10.3390/app10010043
Tsai T-C, Chiang M-H. Design and Control of a 1-DOF Robotic Lower-Limb System Driven by Novel Single Pneumatic Artificial Muscle. Applied Sciences. 2020; 10(1):43. https://doi.org/10.3390/app10010043
Chicago/Turabian StyleTsai, Tsung-Chin, and Mao-Hsiung Chiang. 2020. "Design and Control of a 1-DOF Robotic Lower-Limb System Driven by Novel Single Pneumatic Artificial Muscle" Applied Sciences 10, no. 1: 43. https://doi.org/10.3390/app10010043
APA StyleTsai, T.-C., & Chiang, M.-H. (2020). Design and Control of a 1-DOF Robotic Lower-Limb System Driven by Novel Single Pneumatic Artificial Muscle. Applied Sciences, 10(1), 43. https://doi.org/10.3390/app10010043




