A Bio-Inspired Flapping Wing Rotor of Variant Frequency Driven by Ultrasonic Motor
Abstract
1. Introduction
2. Structure Design and Numerical Method
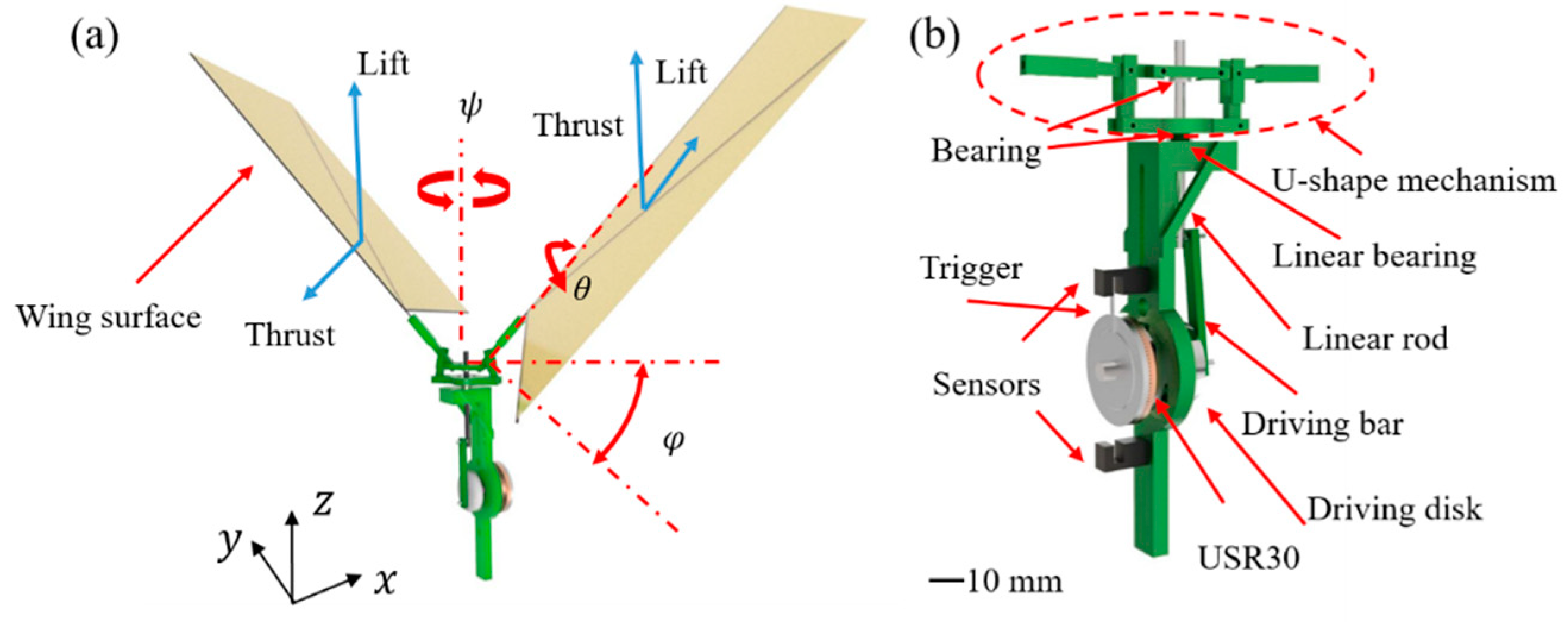
2.1. Flapping Wing Rotor Model
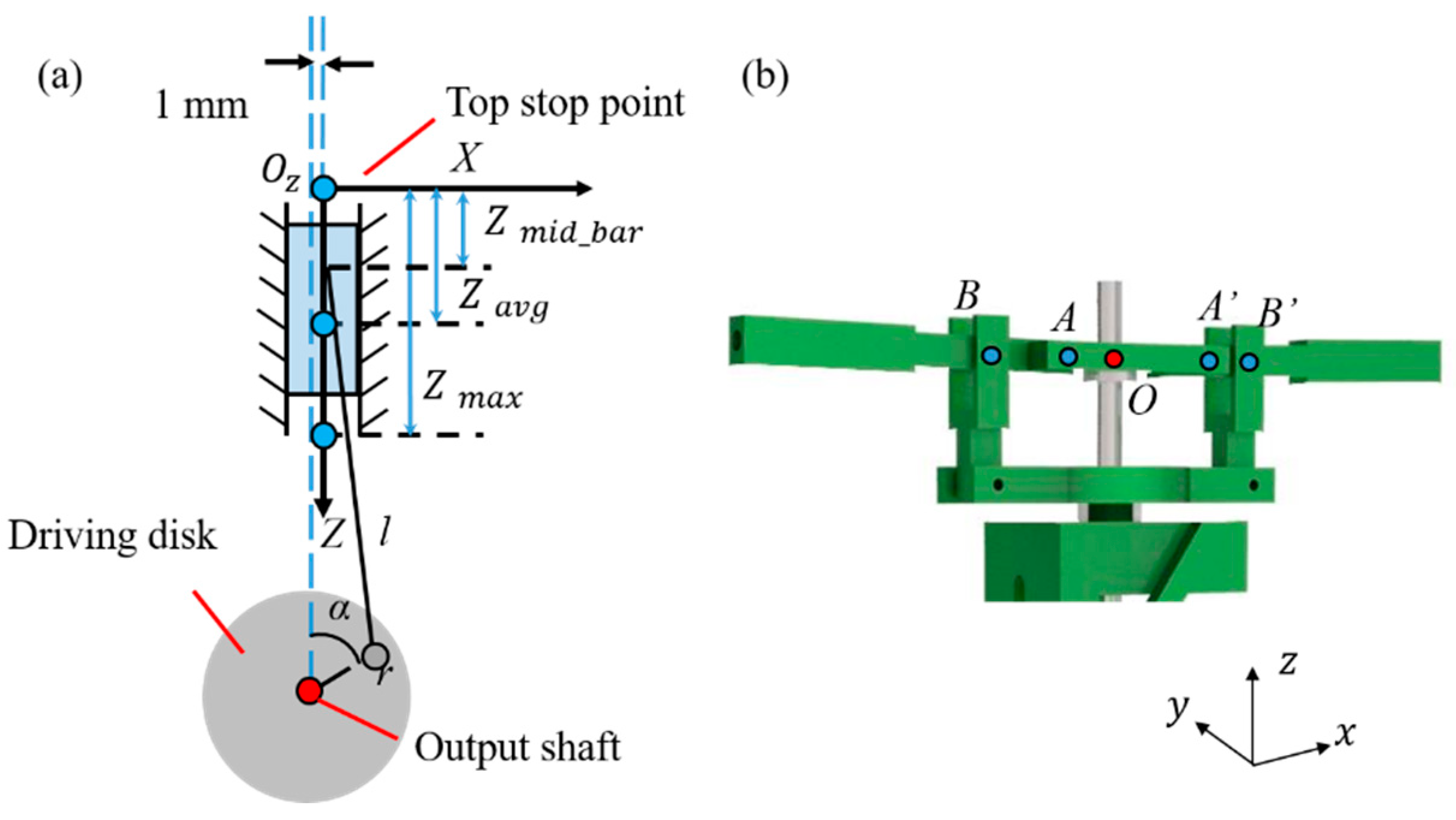
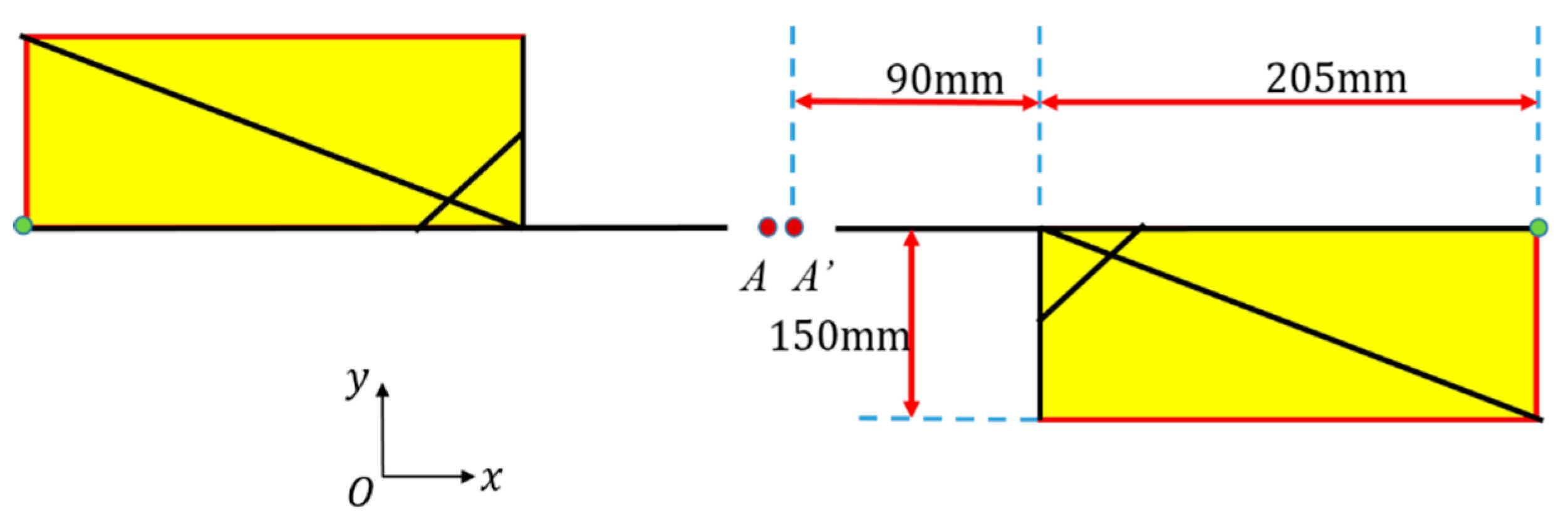
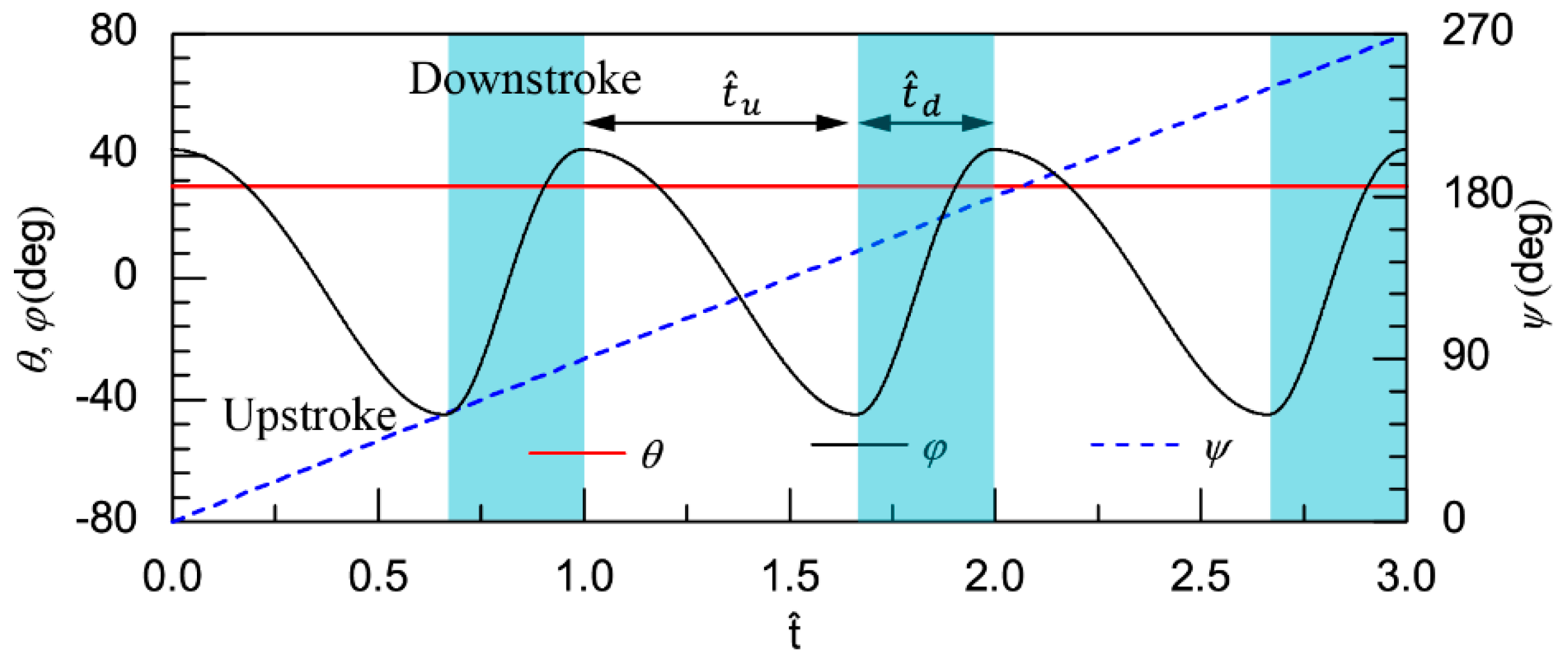
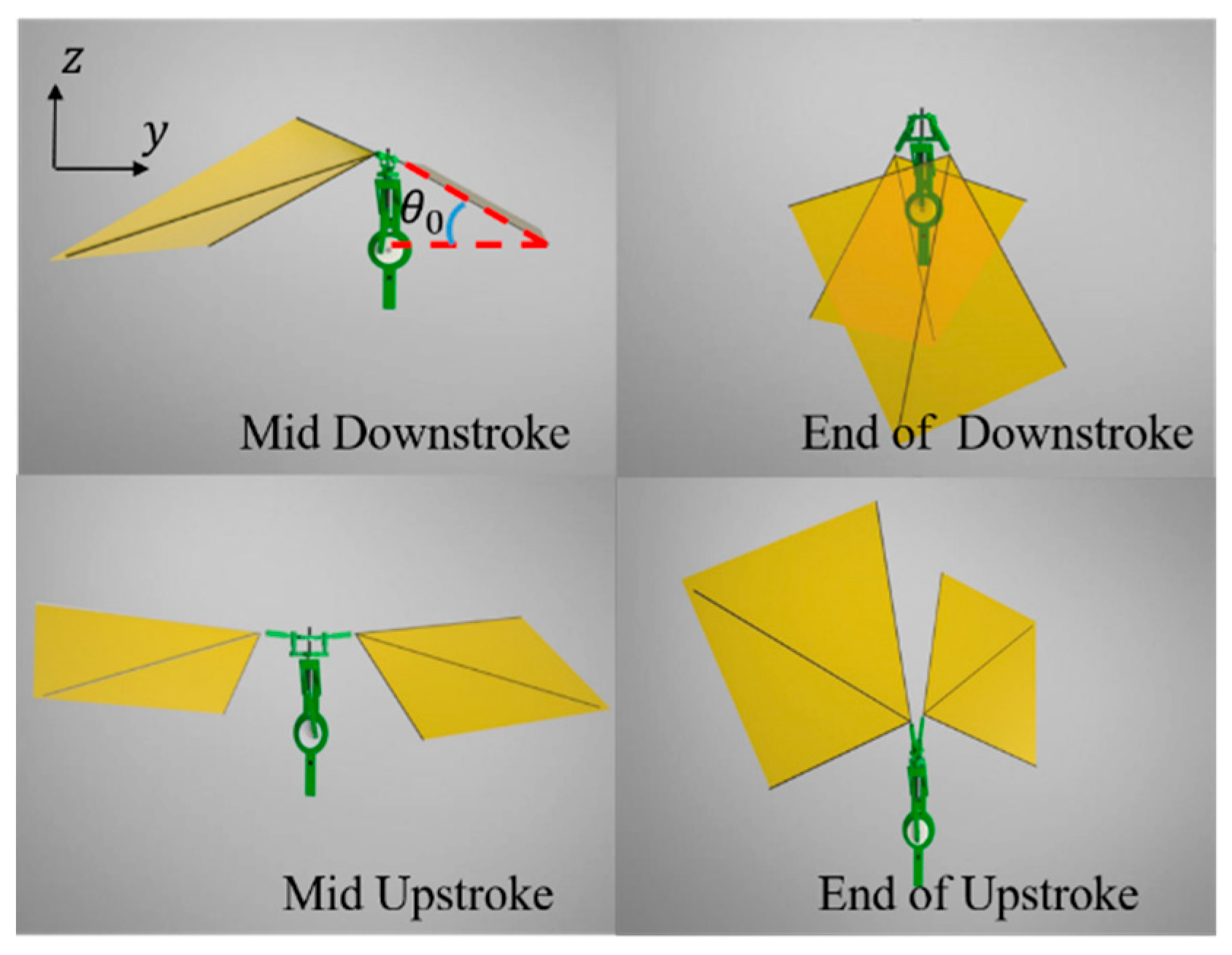
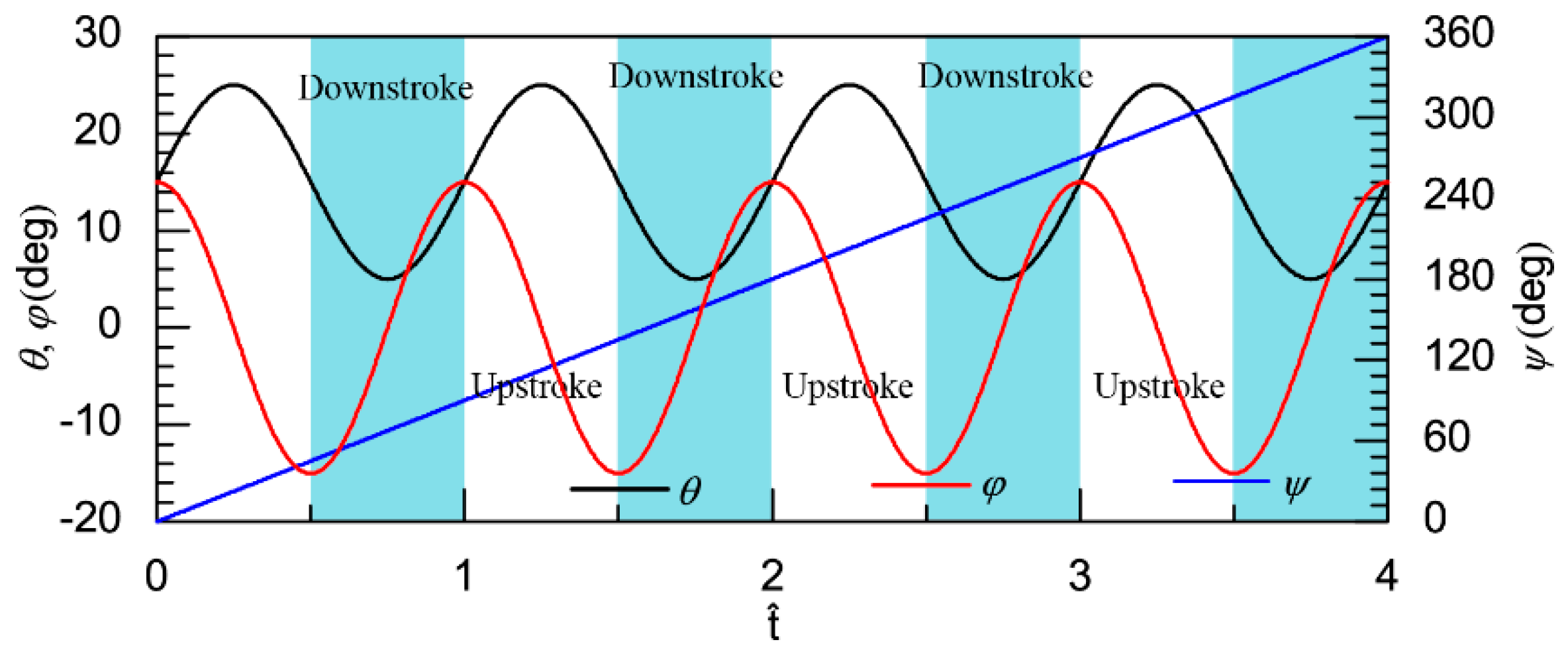
2.2. Kinematics of the Flapping Wing Rotor
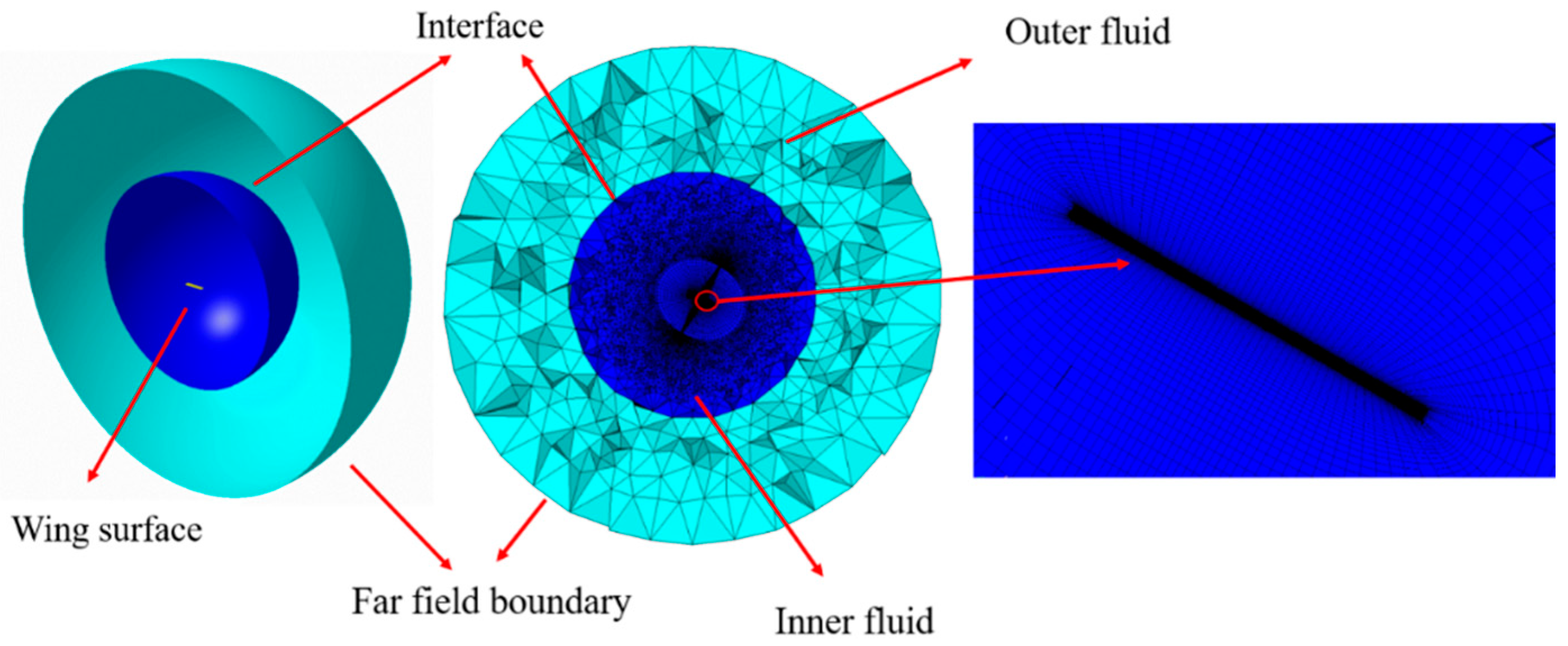
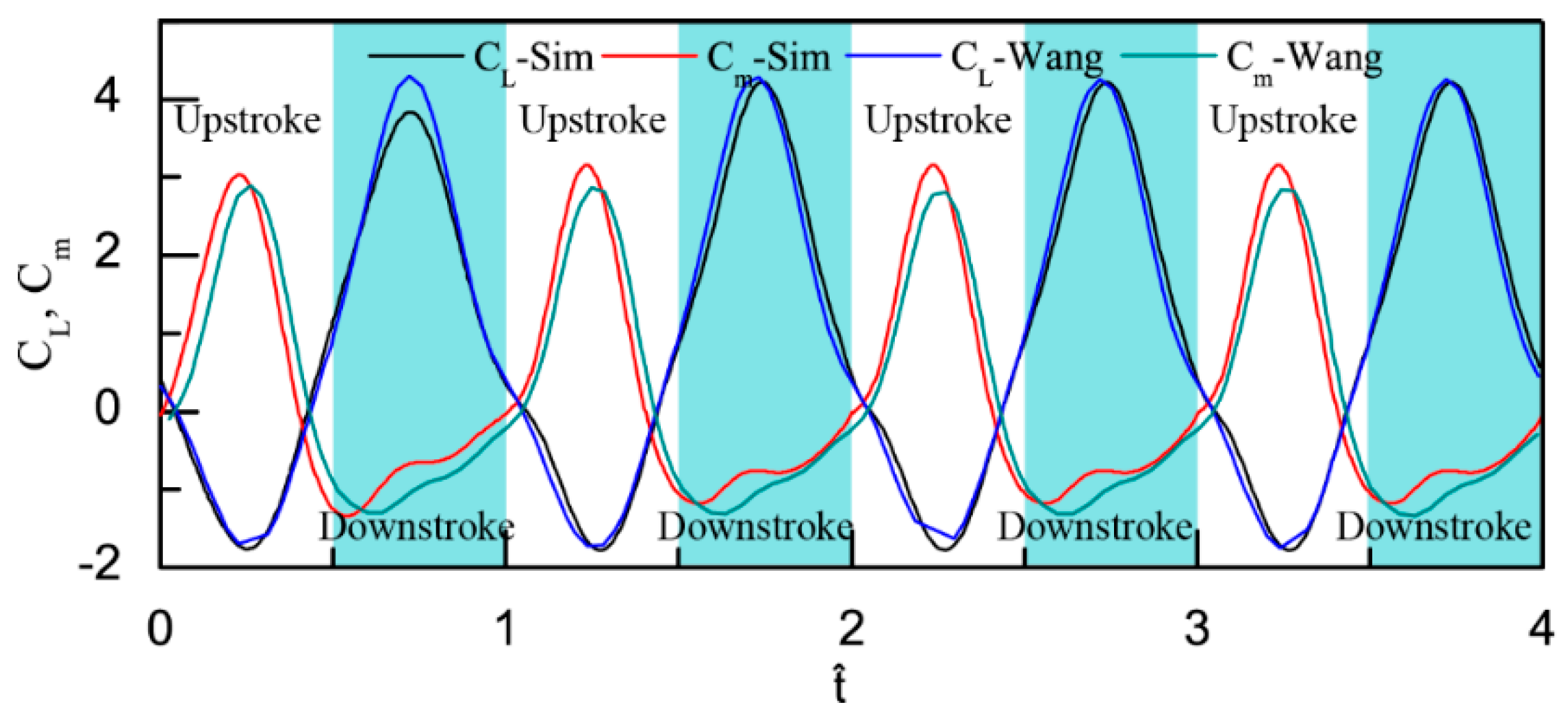
2.3. CFD Model and Validation
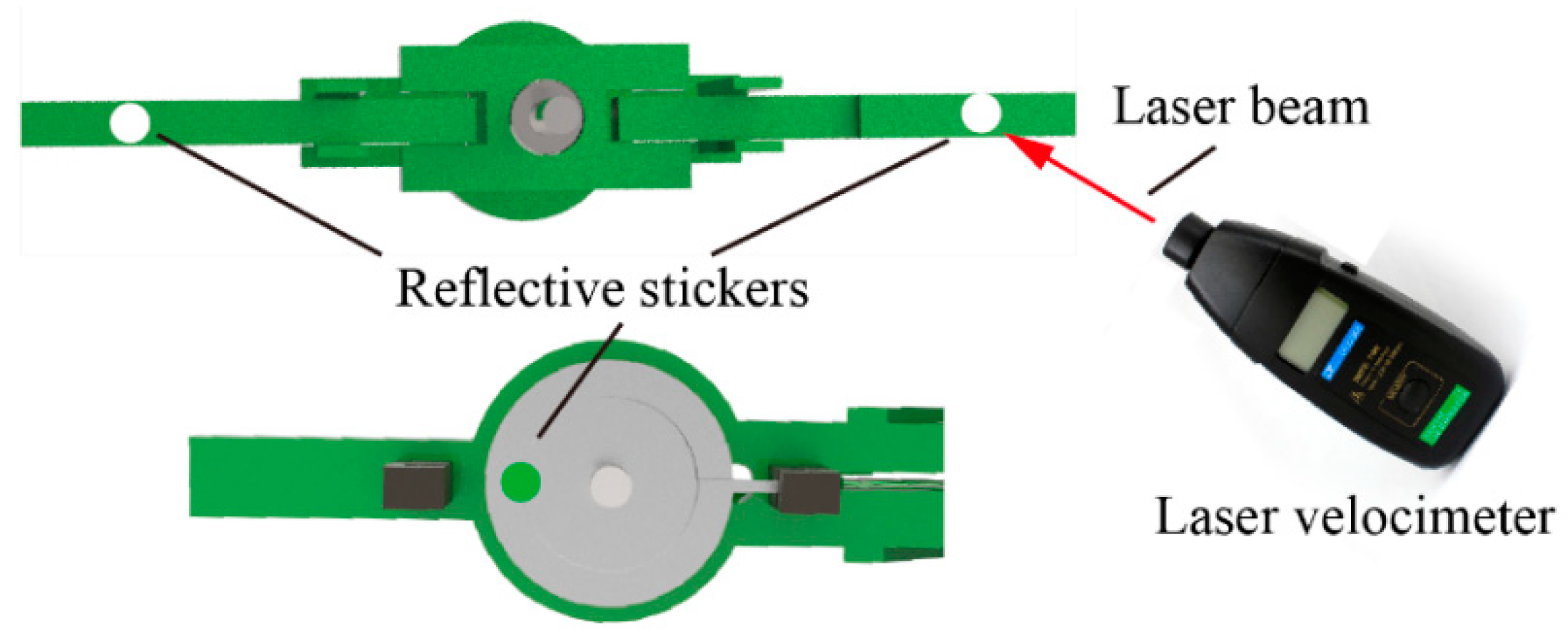
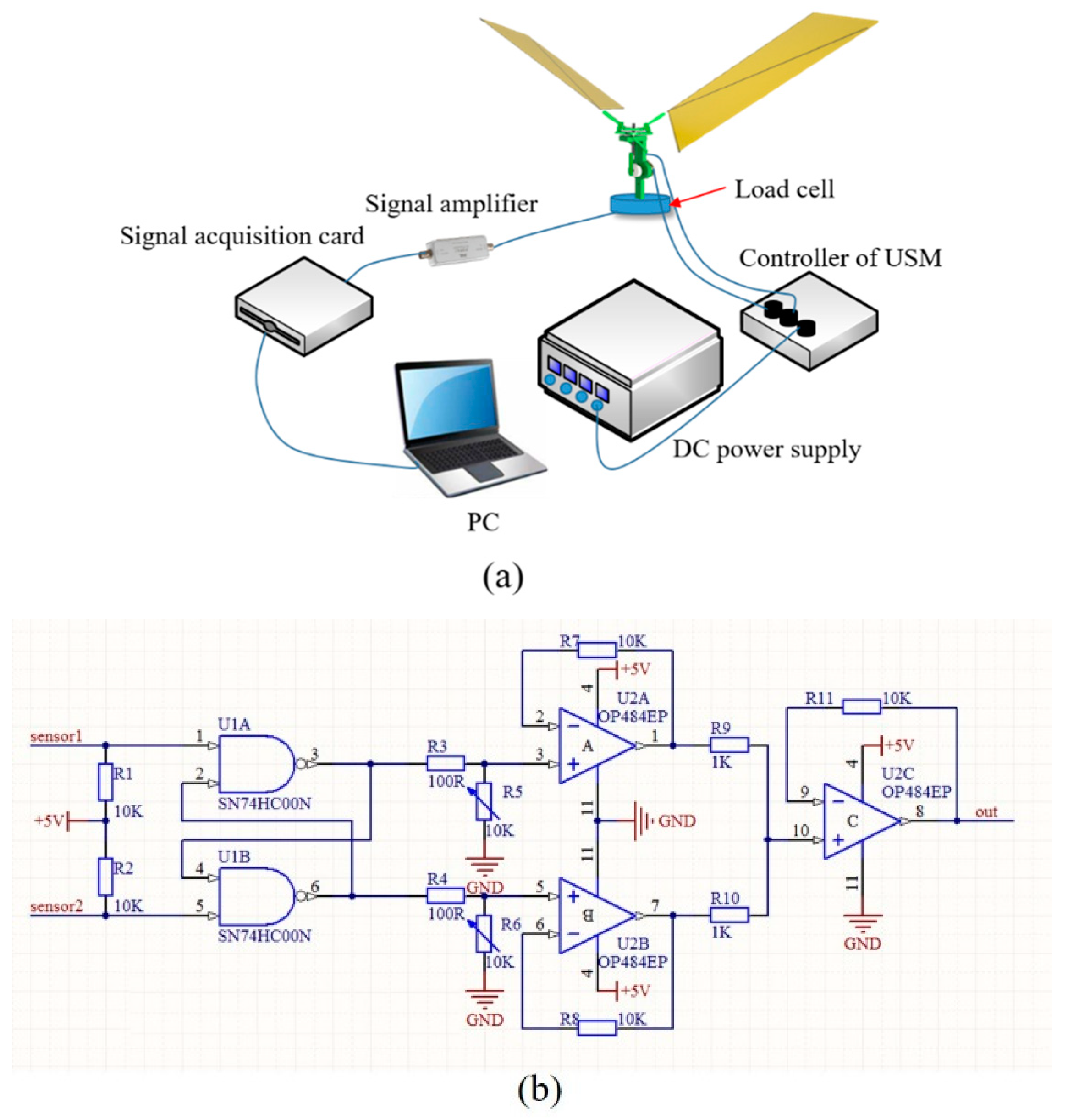
2.4. Assembly of Experimental Devices
3. Experiment Results and Discussion
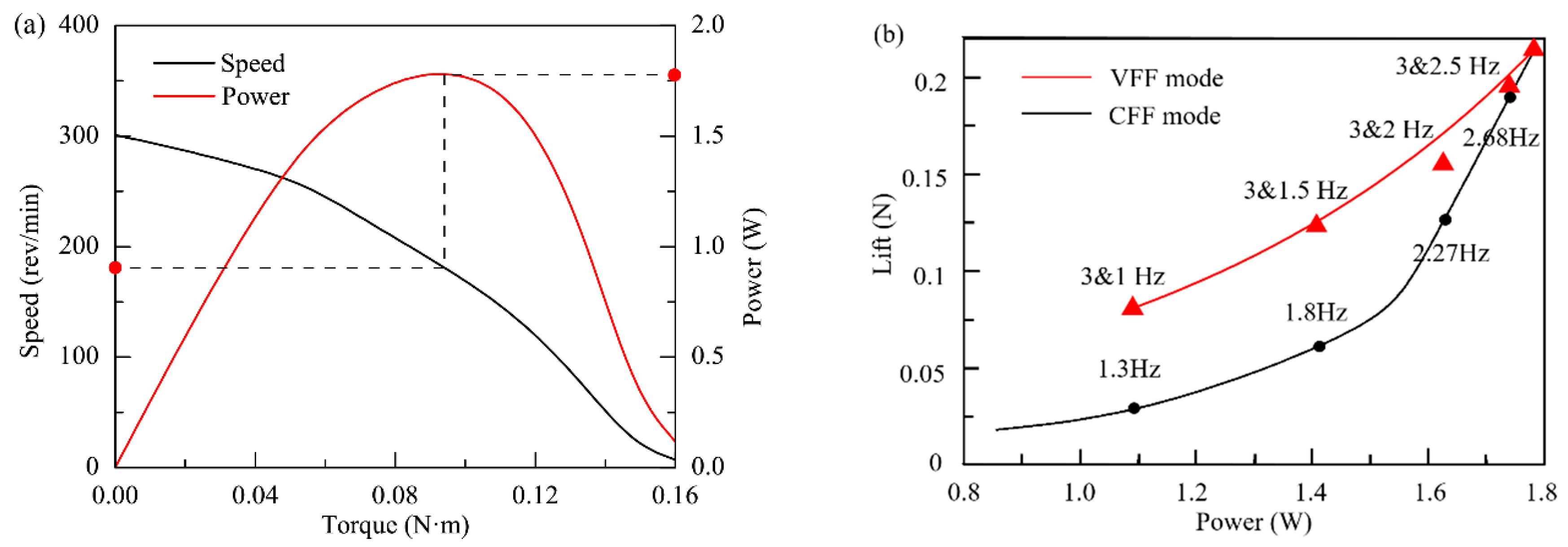
3.1. Parametric Study for the Effect of Flapping Frequency Variation
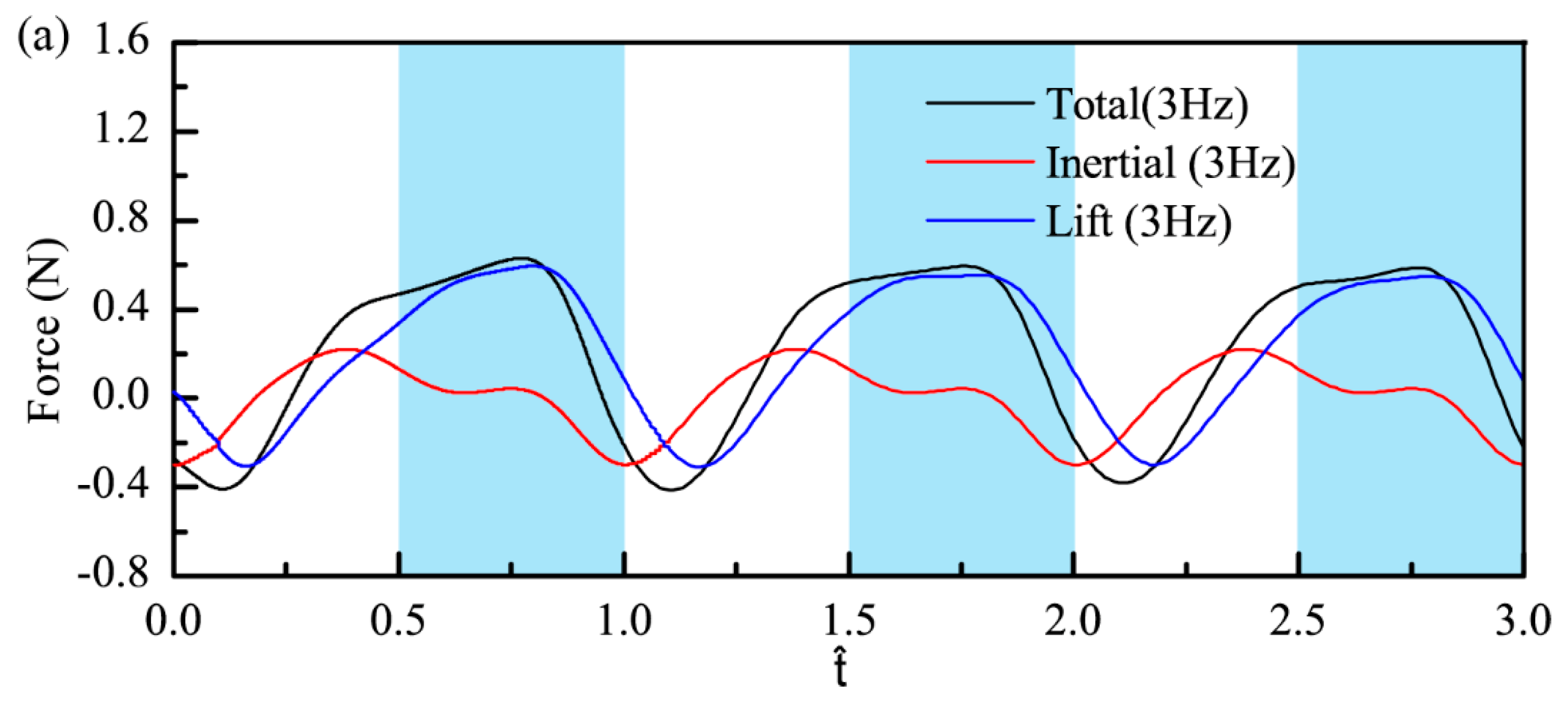
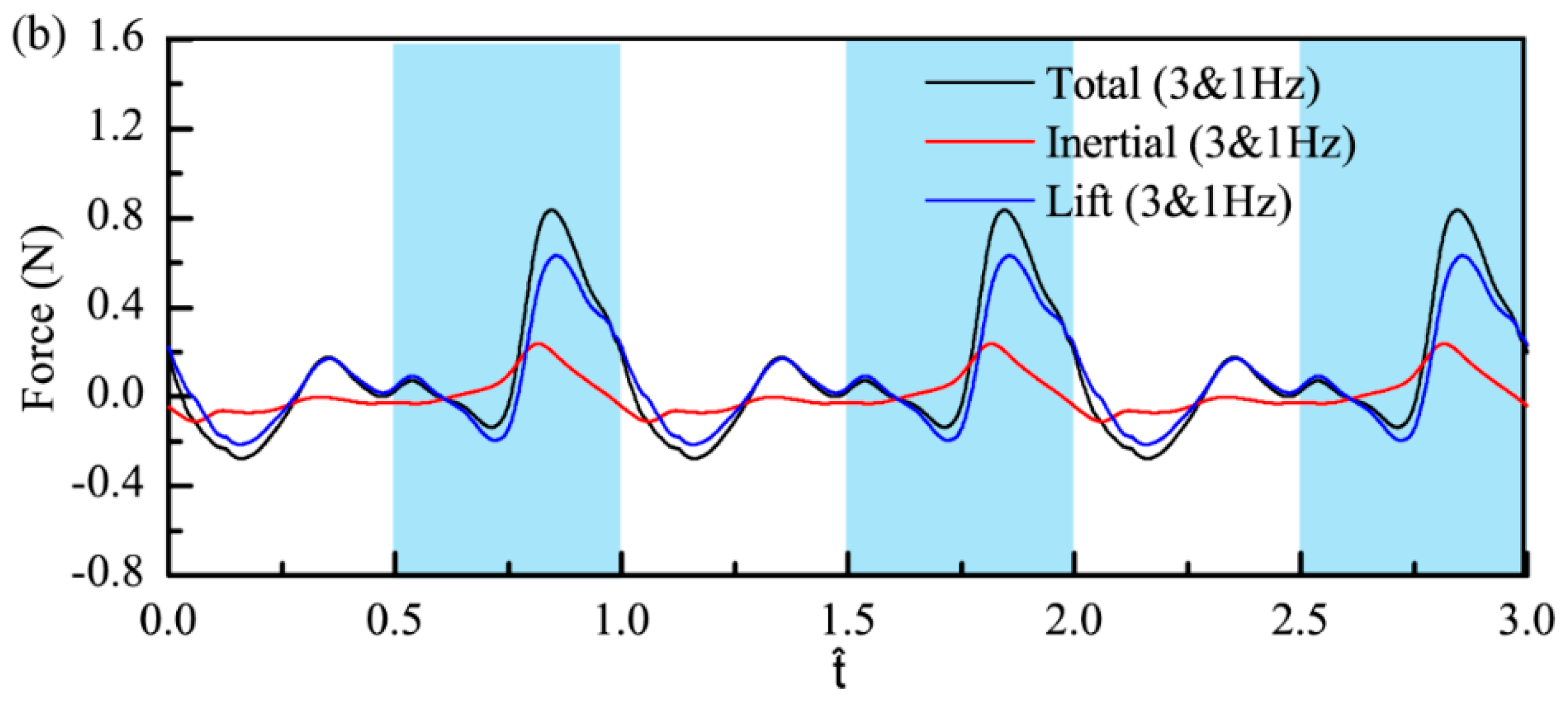
3.2. Experimental Results of the VFF Effect on Inertial Force
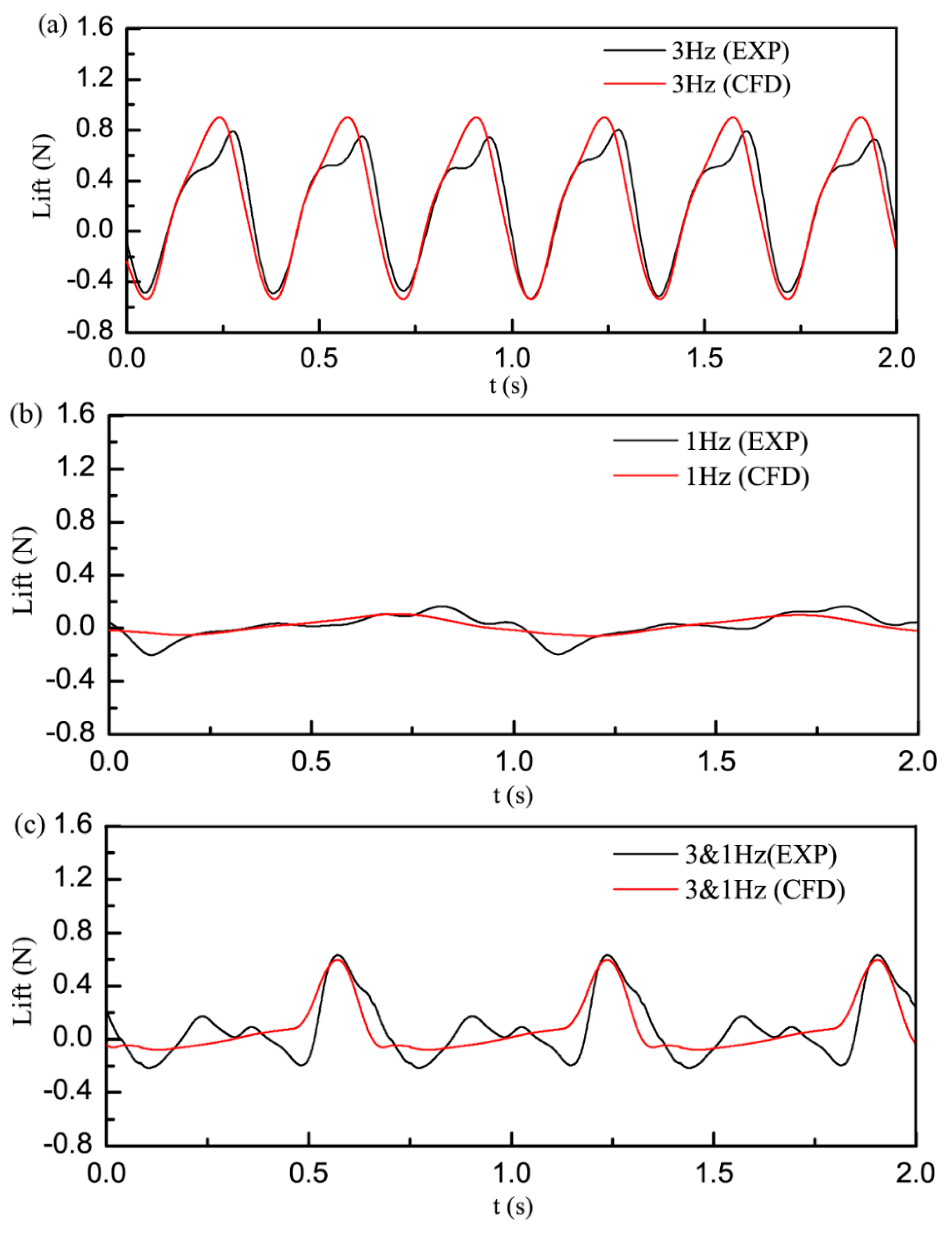
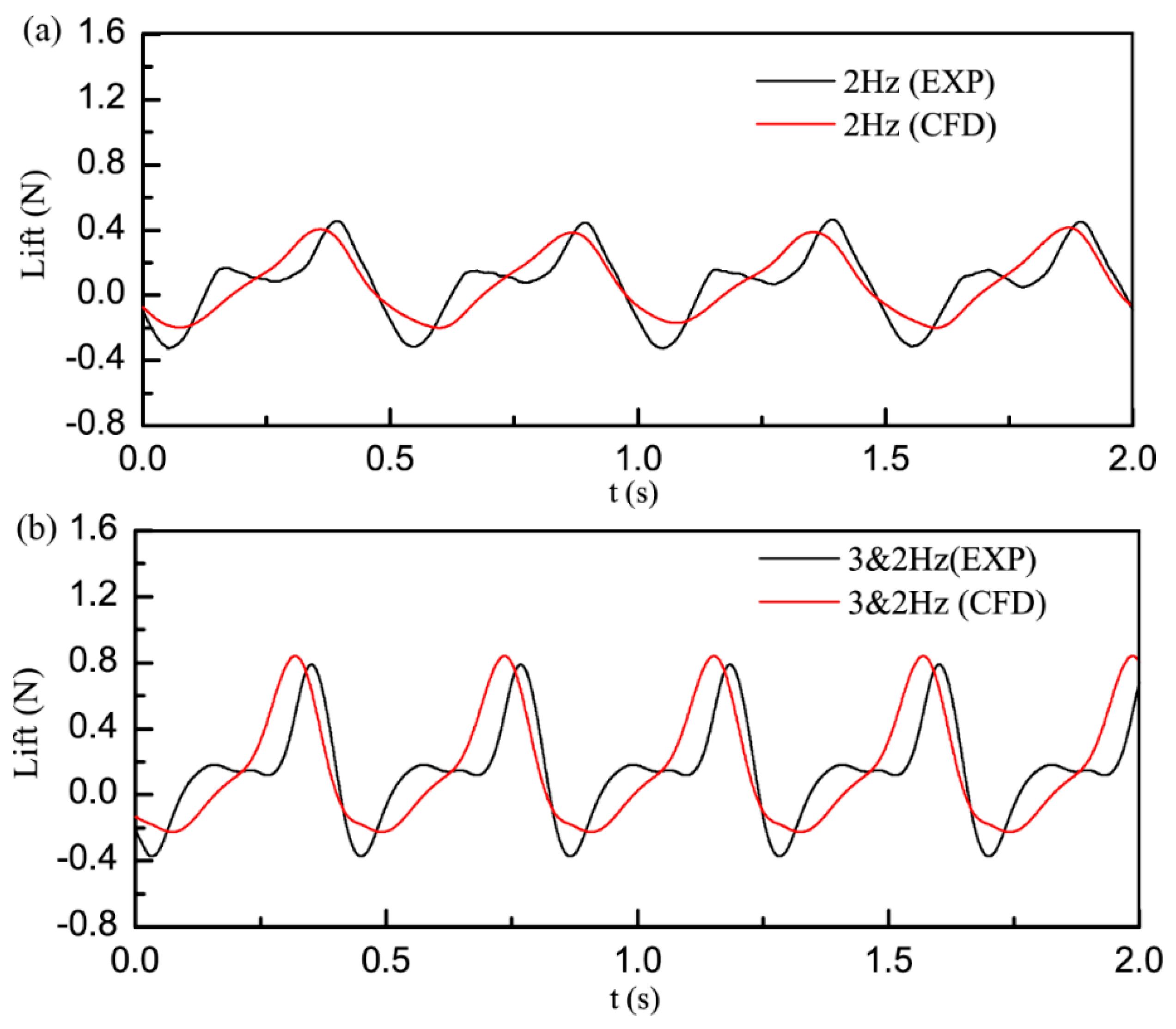
3.3. Experimental and CFD Simulation Comparison
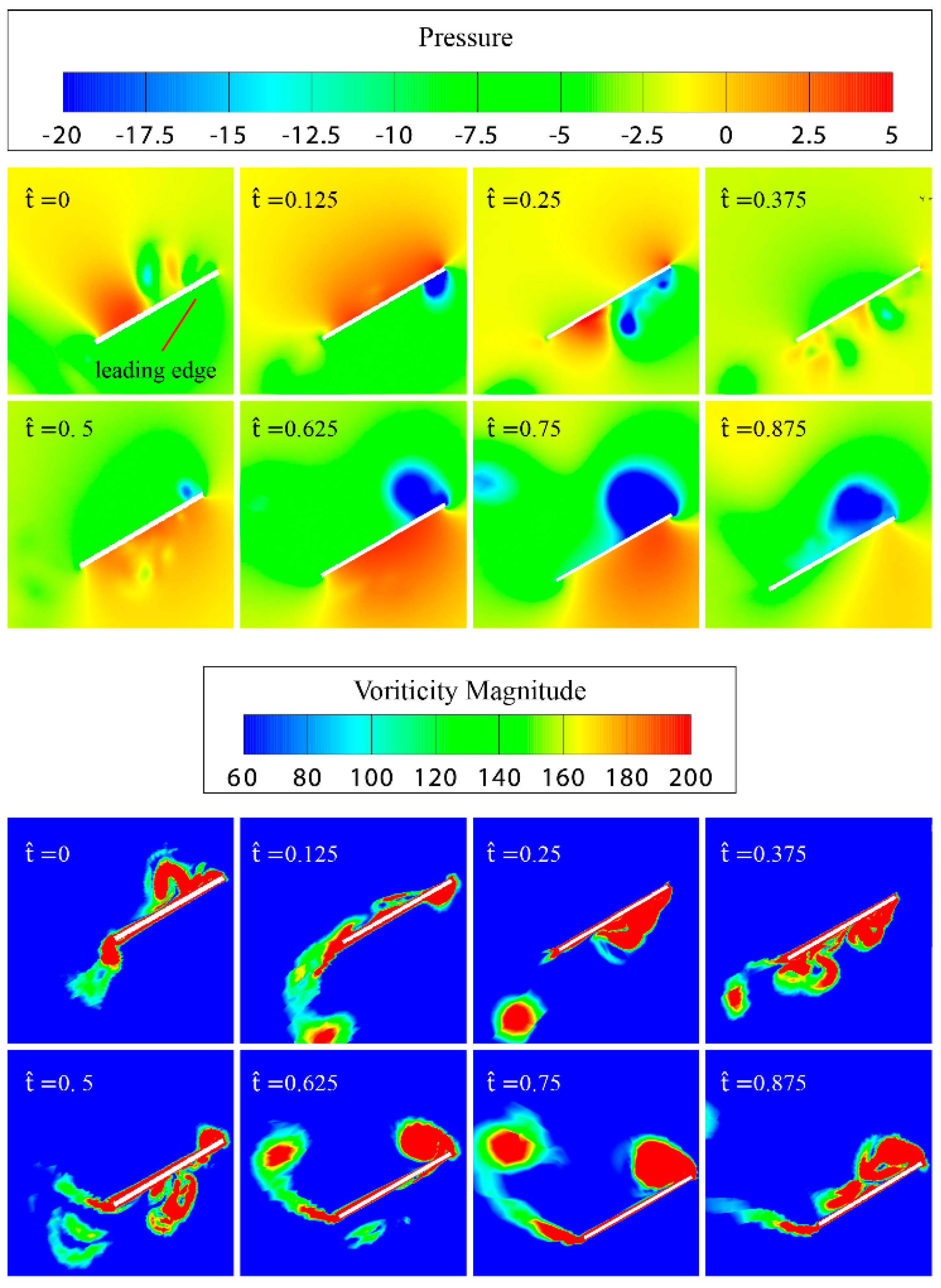
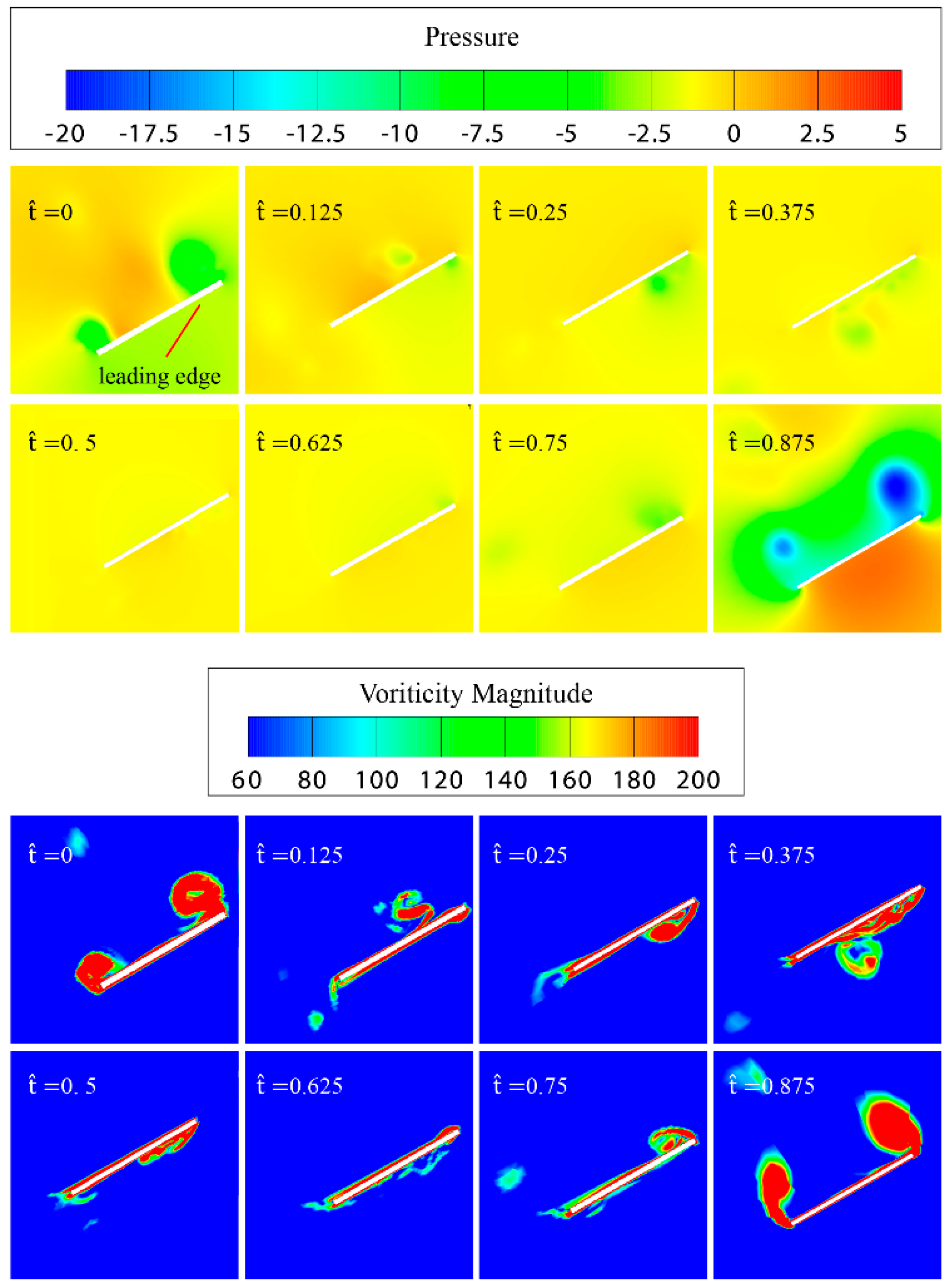
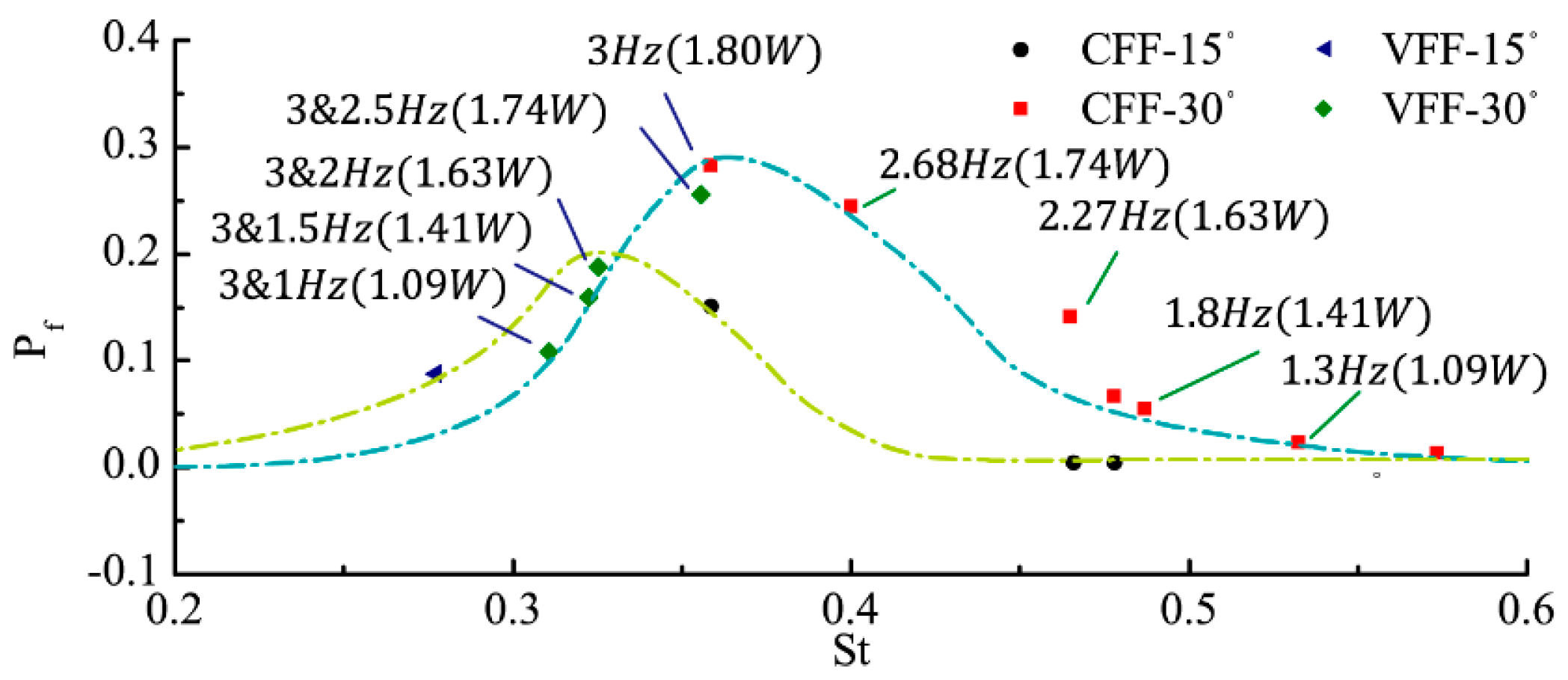
3.4. Flow Field Simulation and Analysis by CFD Method
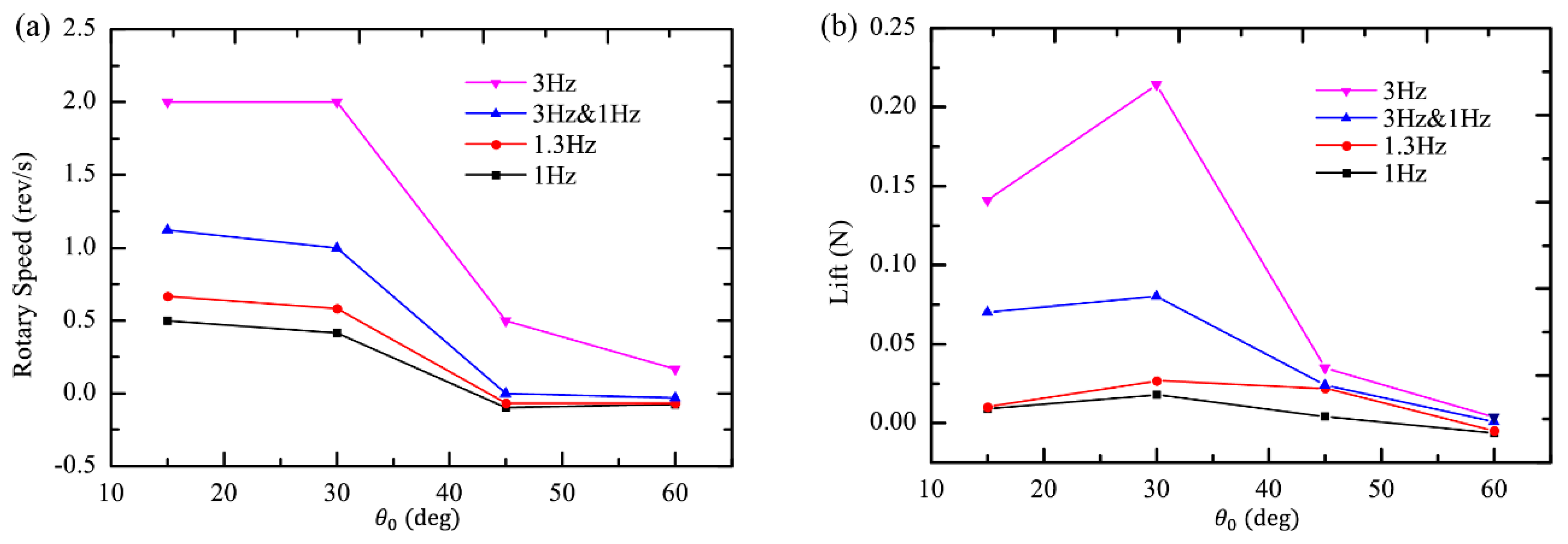
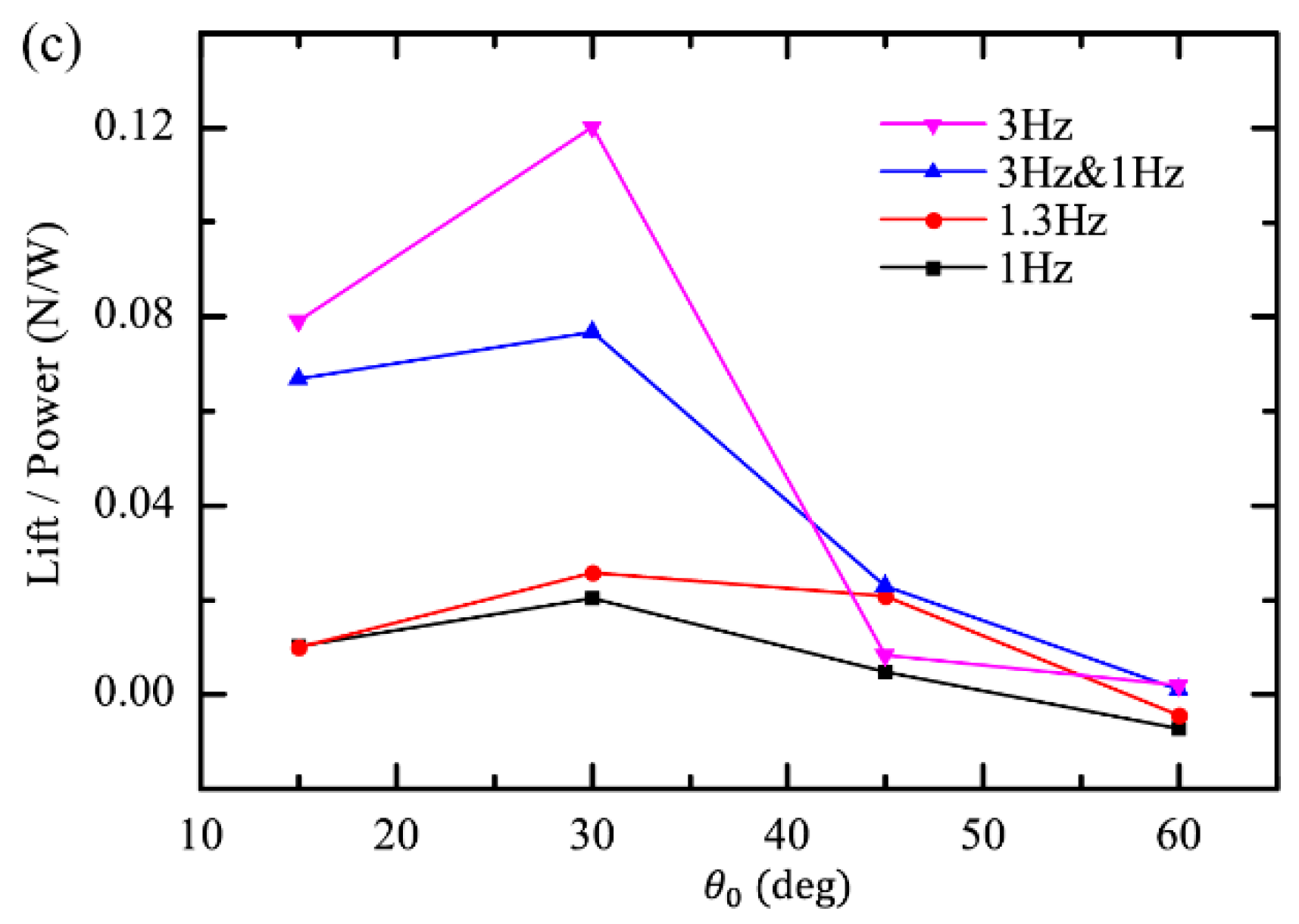
3.5. The Effect of Different Installation Angles on the Lift Generation and Rotational Speed Generation
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jubin, J.; Tornow, J.D. The DARPA Packet Radio Network Protocols. Proc. IEEE 1987, 75, 21–32. [Google Scholar] [CrossRef]
- Lentink, D. Biomimetics: Flying like a fly. Nature 2013, 498, 306–307. [Google Scholar] [CrossRef] [PubMed]
- Mishra, S.; Tripathi, B.; Garg, S.; Kumar, A.; Kumar, P. Design and Development of a Bio-Inspired Flapping Wing Type Micro Air Vehicle. Procedia Mater. Sci. 2015, 10, 519–526. [Google Scholar] [CrossRef]
- Kim, D.K.; Han, J.H.; Kwon, K.J. Wind tunnel tests for a flapping wing model with a changeable camber using macro-fiber composite actuators. Smart Mater. Struct. 2009, 18, 24–32. [Google Scholar] [CrossRef]
- Phan, H.V.; Kang, T.; Park, H. Design and stable flight of a 21 g insect-like tailless flapping wing micro air vehicle with angular rates feedback control. Bioinspir. Biomim. 2017, 12, 1–17. [Google Scholar] [CrossRef]
- Hsiao, F.-Y.; Yang, L.; Lin, S.-H.; Chen, C.-L.; Shen, J.-F. Autopilots for ultra lightweight robotic birds: Automatic altitude control and system integration of a sub-10 g weight flapping-wing micro air vehicle. IEEE Control Syst. 2012, 32, 35–48. [Google Scholar]
- Arabagi, V.; Hines, L.; Sitti, M. Design and manufacturing of a controllable miniature flapping wing robotic platform. Int. J. Robot. Res. 2012, 31, 785–800. [Google Scholar] [CrossRef]
- Ansari, S.A.; Zbikowski, R.; Knowles, K. Non-linear unsteady aerodynamic model for insect-like flapping wings in the hover. Part 1: Methodology and analysis. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2006, 220, 169–186. [Google Scholar] [CrossRef]
- Ansari, S.; Phillips, N.; Stabler, G.; Wilkins, P.; Żbikowski, R.; Knowles, K. Erratum to: Experimental investigation of some aspects of insect-like flapping flight aerodynamics for application to micro air vehicles. Exp. Fluids 2012, 46, 777–798. [Google Scholar] [CrossRef]
- Guo, S.; Li, D.; Wu, J. Theoretical and experimental study of a piezoelectric flapping wing rotor for micro aerial vehicle. Aerosp. Sci. Technol. 2012, 23, 429–438. [Google Scholar] [CrossRef]
- Chung, H.C.; Kummari, K.L.; Croucher, S.J.; Lawson, N.J.; Guo, S.; Whatmore, R.W.; Huang, Z. Development of piezoelectric fans for flapping wing application. Sens. Actuators A Phys. 2009, 149, 136–142. [Google Scholar] [CrossRef]
- Lal Kummari, K.; Li, D.; Guo, S.; Huang, Z. Development of piezoelectric actuated mechanism for flapping wing micro-aerial vehicle applications. Adv. Appl. Ceram. 2010, 109, 175–179. [Google Scholar] [CrossRef]
- Sreetharan, P.S.; Wood, R.J. Passive torque regulation in an underactuated flapping wing robotic insect. Auton. Robots 2011, 31, 225–234. [Google Scholar] [CrossRef]
- Mateti, K.; Byrne-Dugan, R.A.; Rahn, C.D.; Tadigadapa, S.A. Monolithic SUEX flapping wing mechanisms for pico air vehicle applications. J. Microelectromech. Syst. 2013, 22, 527–535. [Google Scholar] [CrossRef]
- Mateti, K.; Byrne-Dugan, R.A.; Tadigadapa, S.A.; Rahn, C.D. Wing rotation and lift in SUEX flapping wing mechanisms. Smart Mater. Struct. 2013, 22, 14–25. [Google Scholar] [CrossRef]
- Buck, M.; Razavi, S.; Derose, R.; Inoue, T.; Silver, P.A.; Subsoontorn, P.; Endy, D.; Gerchman, Y.; Collins, C.H.; Arnold, F.H.; et al. Controlled Flight of a Biologically. Science 2013, 340, 603–607. [Google Scholar]
- Li, D.; Guo, S.; Matteo, N.D.; Yang, D.; Student, P. Design, Experiment and Aerodynamic Calculation of a Flapping Wing Rotor Micro Aerial Vehicle. In Proceedings of the 52nd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Denver, CO, USA, 4–7 April 2011; pp. 1–9. [Google Scholar]
- Zhou, C.; Wu, J.; Guo, S.; Li, D. Experimental study on the lift generated by a flapping rotary wing applied in a micro air vehicle. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2014, 228, 2083–2093. [Google Scholar] [CrossRef]
- Li, H.; Guo, S. Aerodynamic efficiency of a bioinspired flapping wing rotor at low Reynolds number. R. Soc. Open Sci. 2018, 5, 1–15. [Google Scholar] [CrossRef]
- Zhou, C.; Wu, J.H.; Guo, S.J. Experimental study of a mechanical flapping rotary wing model. Appl. Mech. Mater. 2013, 390, 23–27. [Google Scholar] [CrossRef]
- Chen, L.; Yan, W.; Wu, J. Experimental Validation on Lift Increment of a Flapping Rotary Wing with Boring-hole Design. Procedia Eng. 2015, 99, 1543–1547. [Google Scholar]
- Wu, J.; Wang, D.; Zhang, Y. Aerodynamic Analysis of a Flapping Rotary Wing at a Low Reynolds Number. AIAA J. 2015, 53, 2951–2966. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, Y.; Wu, J.; Zhang, Y. Aerodynamics on Flapping Rotary Wing in Low Reynolds Number. Am. Inst. Aeronaut. Astronaut. 2013, 37, 1–14. [Google Scholar]
- Yang, L.J.; Huang, H.; Liou, J.; Esakki, B.; Chandrasekhar, U. 2D Quasi-Steady Flow Simulation of an Actual Flapping Wing. J. Unmanned Syst. Technol. 2015, 2, 10–16. [Google Scholar]
- Yang, L.; Feng, A.-L.; Lee, H.-C.; Esakki, B.; He, W. The Three-Dimensional Flow Simulation of a Flapping Wing. J. Mar. Sci. Technol. 2018, 26, 297–308. [Google Scholar]
- Li, H.; Guo, S.; Zhang, Y.L.; Zhou, C.; Wu, J.H. Unsteady aerodynamic and optimal kinematic analysis of a micro flapping wing rotor. Aerosp. Sci. Technol. 2016, 63, 1–19. [Google Scholar] [CrossRef]
- Zhao, C. Ultrasonic Motors Technologies and Applications; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Liu, L.; Li, H.; Ang, H.; Xiao, T. Numerical investigation of flexible flapping wings using computational fluid dynamics/computational structural dynamics method. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2018, 232, 85–95. [Google Scholar] [CrossRef]
- Granlund, K.O.; Ol, M.V.; Bernal, L.P. Unsteady pitching flat plates. J. Fluid Mech. 2013, 733, R5. [Google Scholar] [CrossRef]
- Ramesh, K.; Gopalarathnam, A.; Edwards, J.R.; Ol, M.V.; Granlund, K. An unsteady airfoil theory applied to pitching motions validated against experiment and computation. Theor. Comput. Fluid Dyn. 2013, 27, 843–864. [Google Scholar] [CrossRef]
- Taylor, G.K.; Nudds, R.L.; Thomas, A.L.R. Flying and swimming animals cruise at a Strouhal number tuned for high power efficiency. Nature 2003, 425, 707–711. [Google Scholar] [CrossRef]
- Ellington, C.P. The Aerodynamics of Hovering Insect Flight: II. Morphological Parameters. Philos. Trans. R. Soc. Lond. 1984, 303, 605–654. [Google Scholar] [CrossRef]

| Variables | r | l | ||
|---|---|---|---|---|
| Dimensions (mm) | 6 | 35 | 9 | 8 |
| Case No. | Flapping Mode | (Hz) | (Hz) | (Hz) |
|---|---|---|---|---|
| 1 | CFF | 3 | 3 | 2 |
| 2 | CFF | 2 | 2 | 1 |
| 3 | CFF | 1 | 1 | 0.41 |
| 4 | VFF | 3 | 1 | 1 |
| 5 | VFF | 3 | 2 | 1.67 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; Wang, L.; Guo, S.; Zhao, C.; Tong, M. A Bio-Inspired Flapping Wing Rotor of Variant Frequency Driven by Ultrasonic Motor. Appl. Sci. 2020, 10, 412. https://doi.org/10.3390/app10010412
Chen S, Wang L, Guo S, Zhao C, Tong M. A Bio-Inspired Flapping Wing Rotor of Variant Frequency Driven by Ultrasonic Motor. Applied Sciences. 2020; 10(1):412. https://doi.org/10.3390/app10010412
Chicago/Turabian StyleChen, Si, Le Wang, Shijun Guo, Chunsheng Zhao, and Mingbo Tong. 2020. "A Bio-Inspired Flapping Wing Rotor of Variant Frequency Driven by Ultrasonic Motor" Applied Sciences 10, no. 1: 412. https://doi.org/10.3390/app10010412
APA StyleChen, S., Wang, L., Guo, S., Zhao, C., & Tong, M. (2020). A Bio-Inspired Flapping Wing Rotor of Variant Frequency Driven by Ultrasonic Motor. Applied Sciences, 10(1), 412. https://doi.org/10.3390/app10010412






