Improvement in Land Cover and Crop Classification based on Temporal Features Learning from Sentinel-2 Data Using Recurrent-Convolutional Neural Network (R-CNN)
Abstract
1. Introduction
2. Related Work
2.1. Temporal Feature Representation
2.2. Pixel-Based Crops Classification
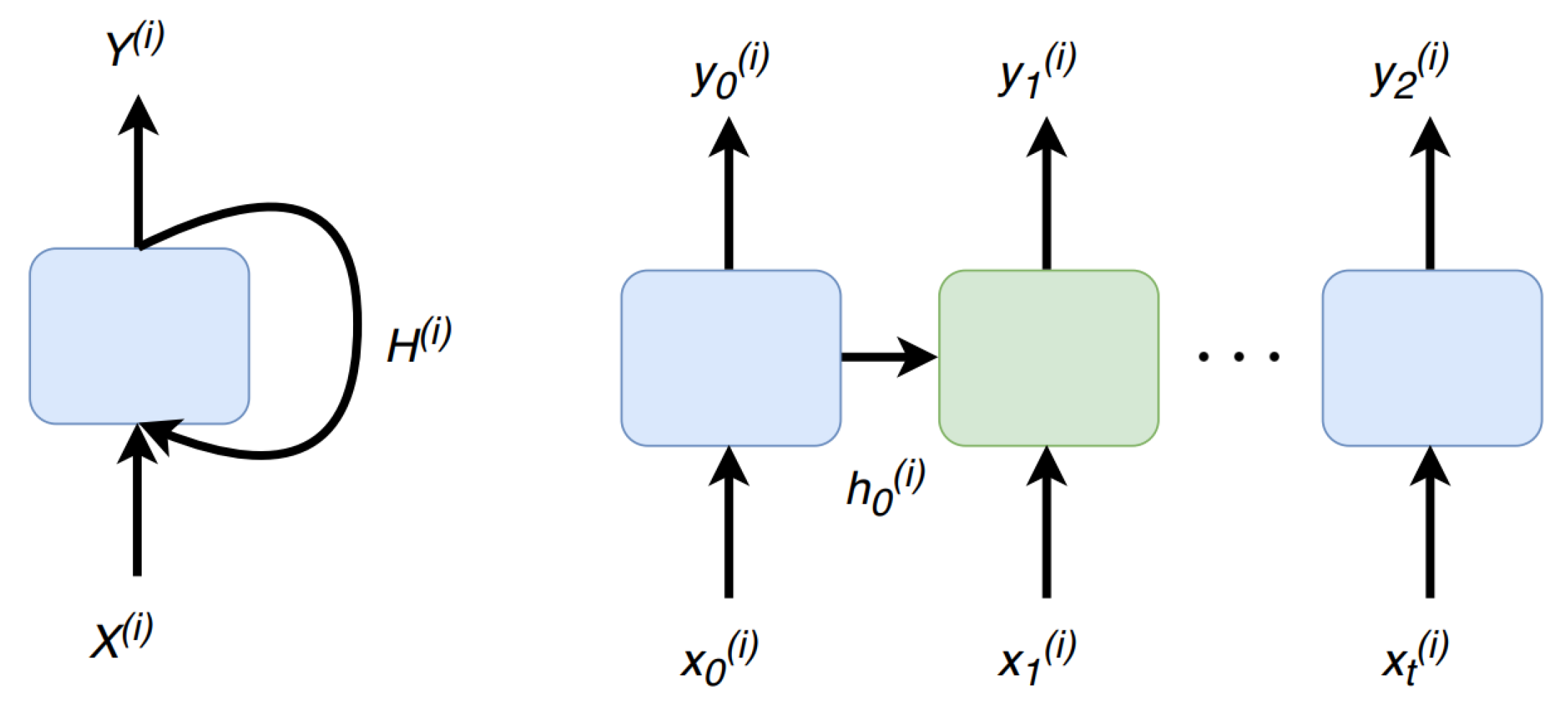
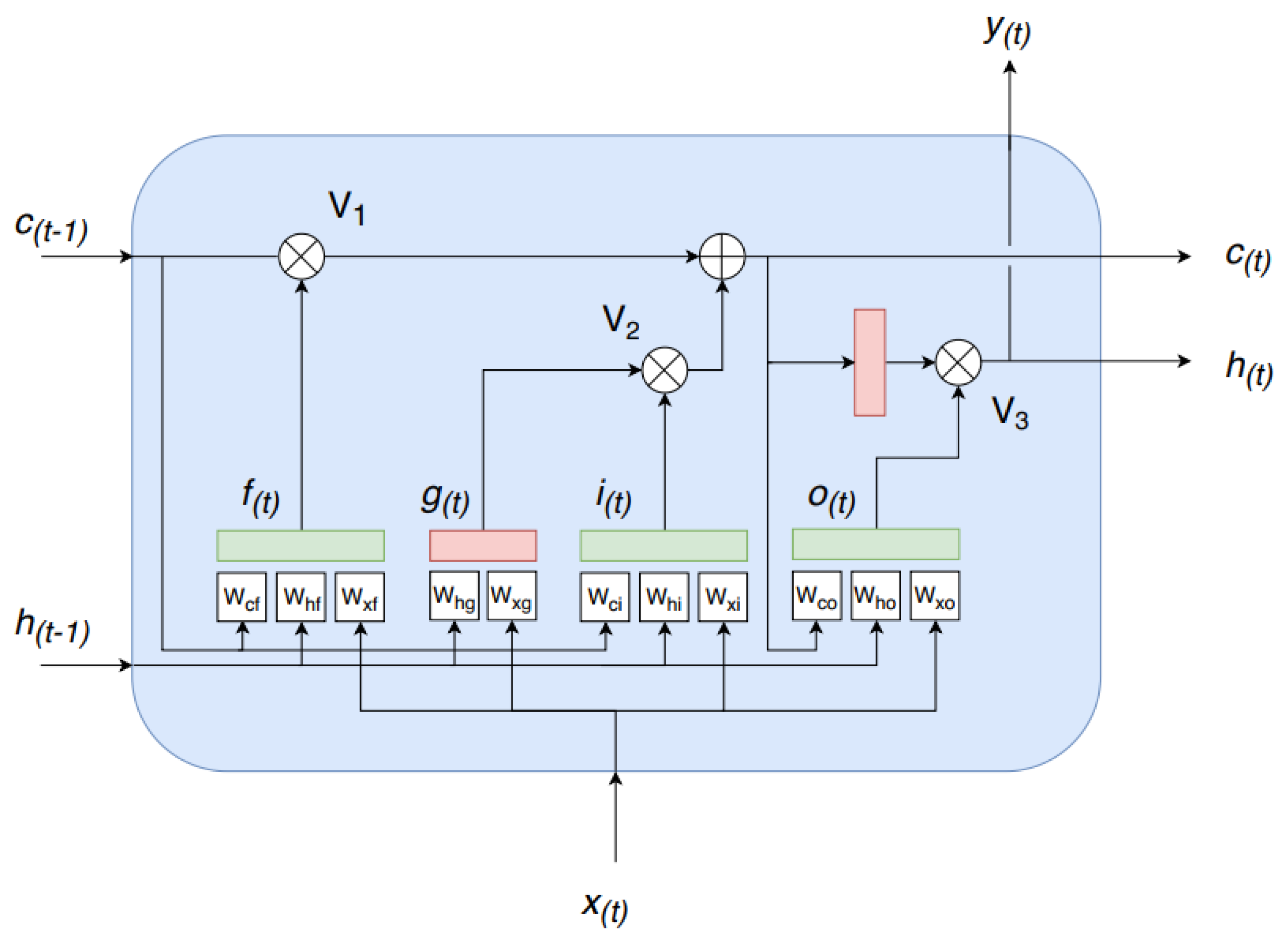
2.3. Recurrent Neural Network (RNN)
2.4. Convolutional Neural Network (CNN)
3. Study Area and Data
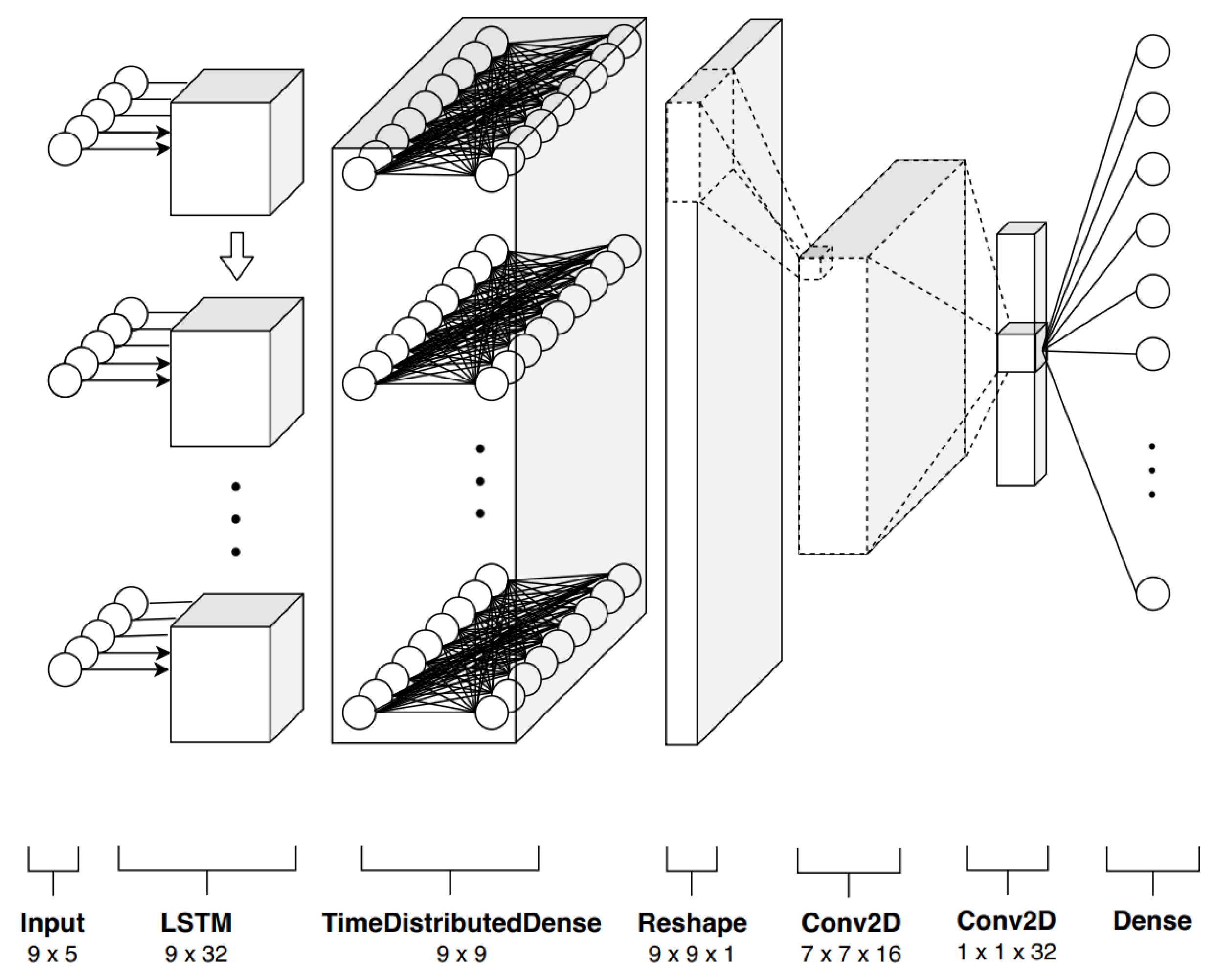
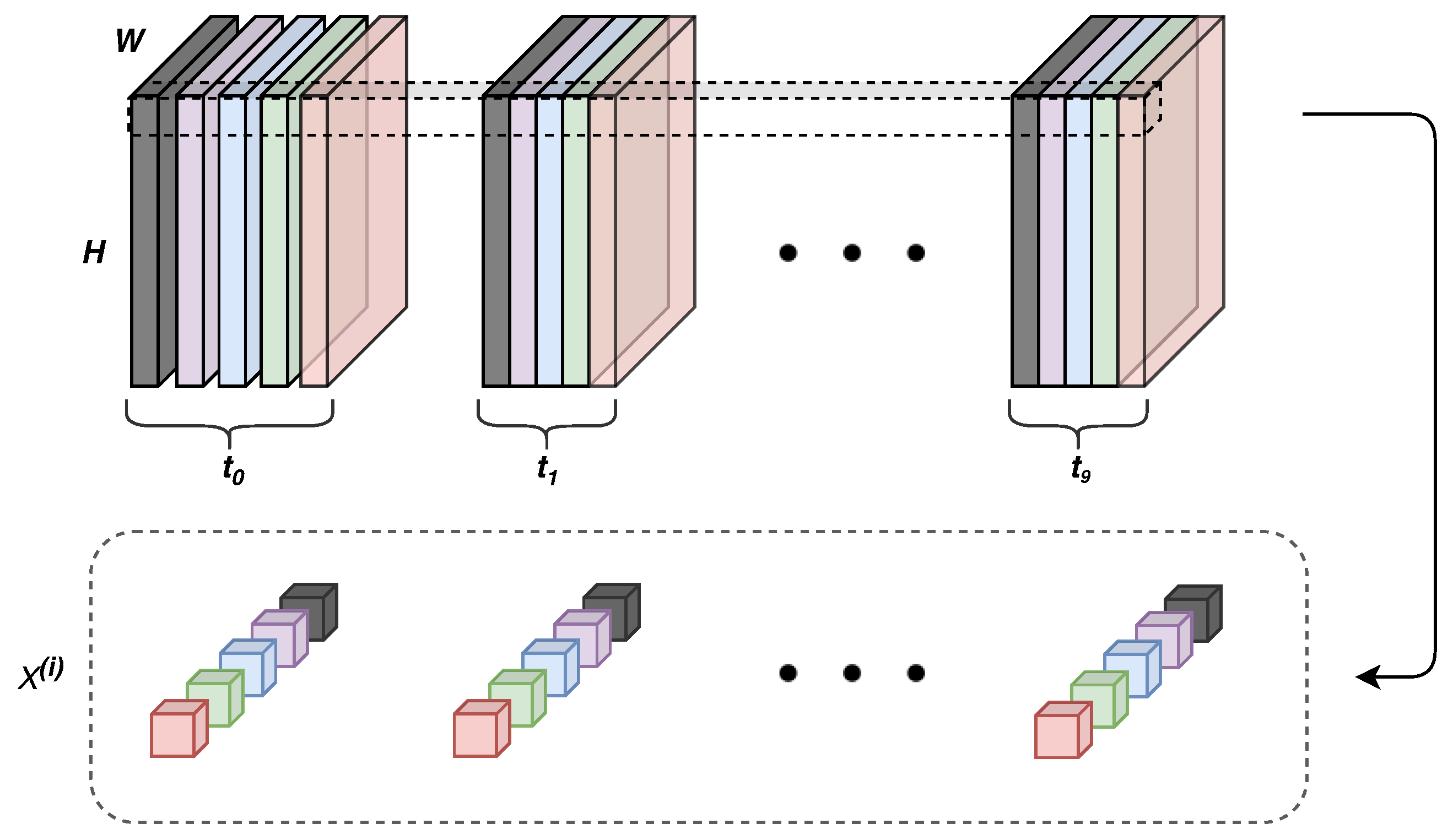
4. Convolutional and Recurrent Neural Networks for Pixel-Based Crops Classification
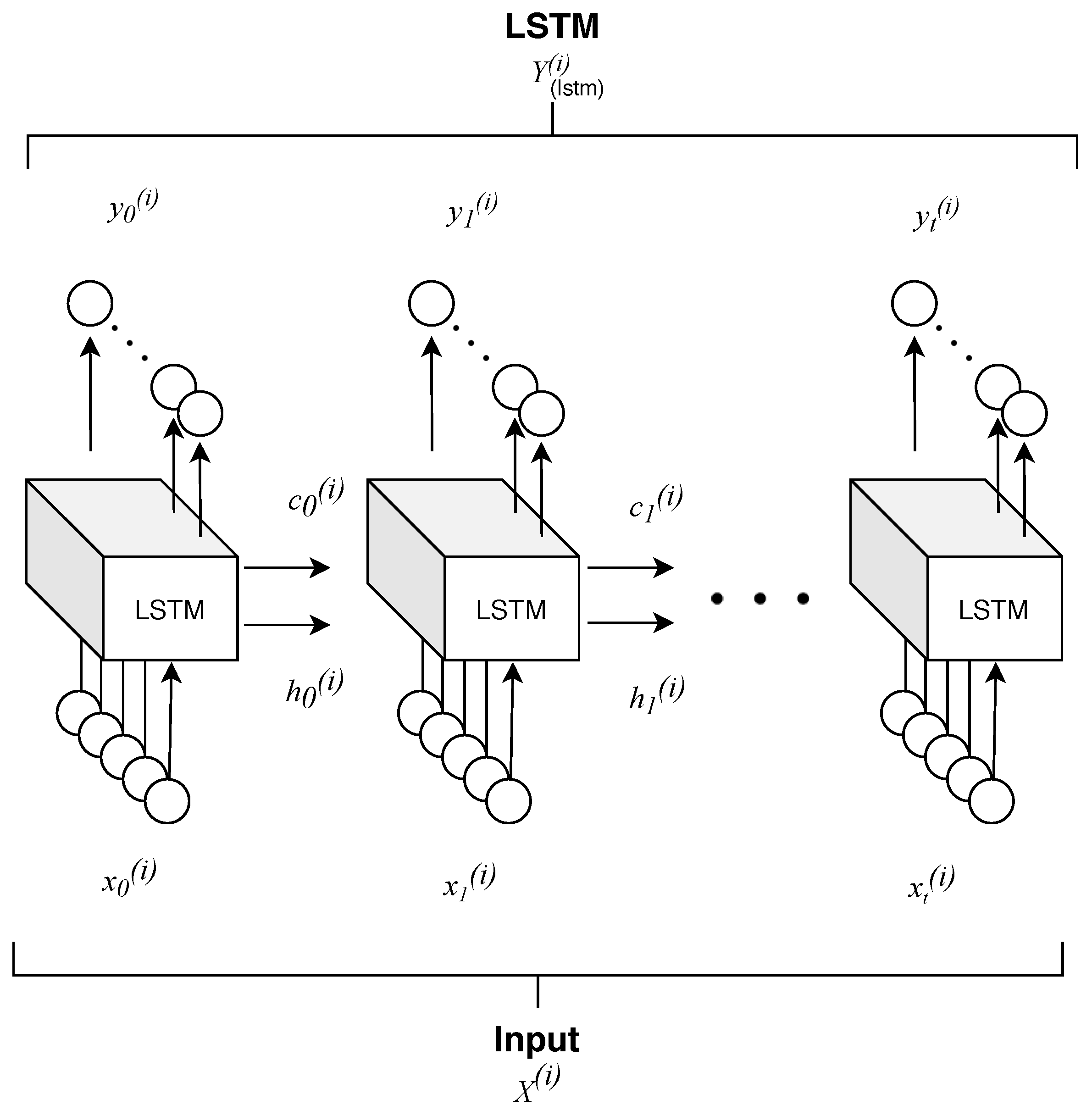
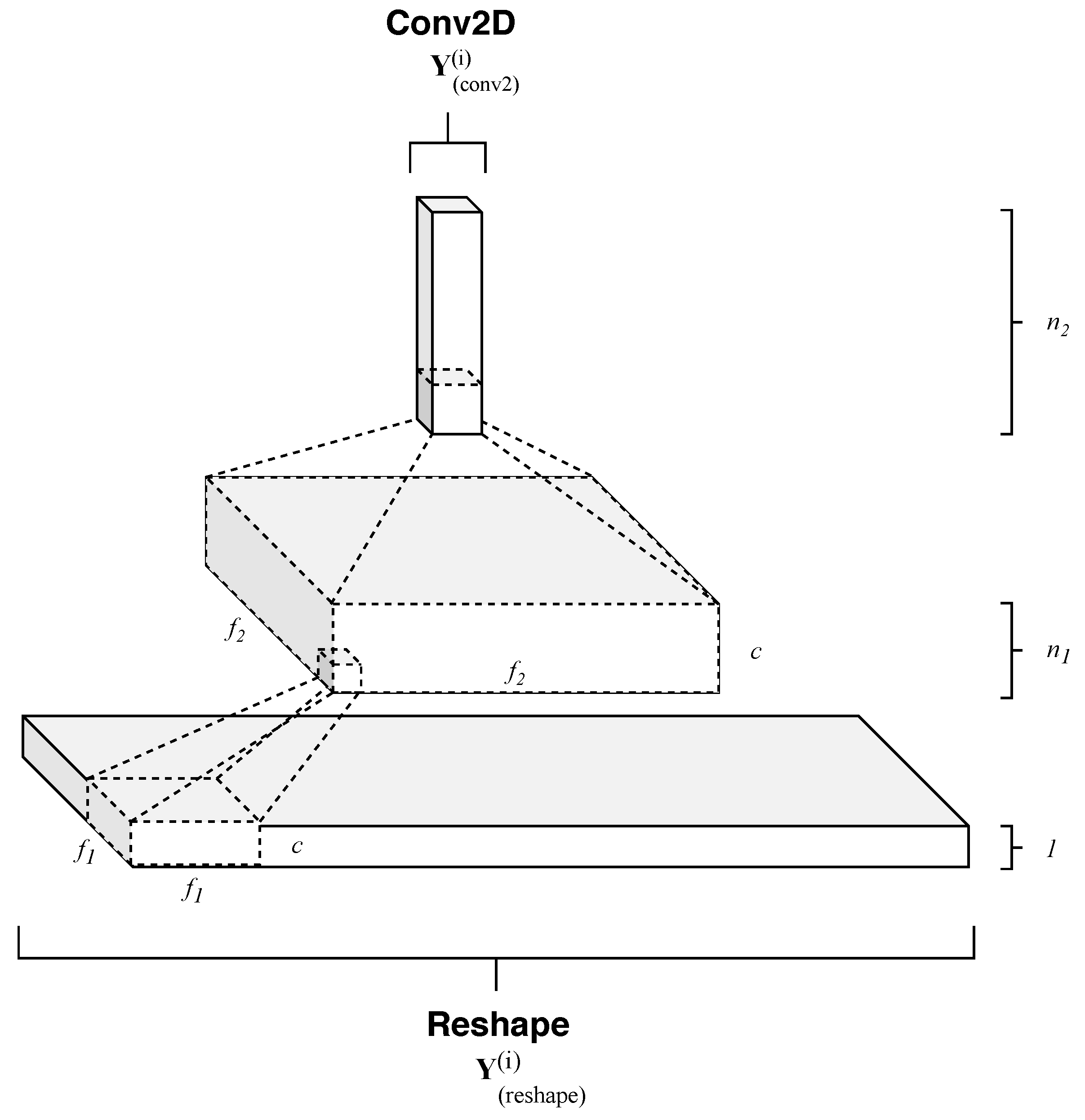
4.1. Formulation
- Time correlation representations—this operation extracts temporal correlations from multi-spectral, temporal pixels exploiting a sequence-to-sequence recurrent neural network based on long short-term memory (LSTM) cells. A final time-distributed layer is used to compress and maintain a sequence like structure, preserving the multidimensionality nature of the data. In this way, it is possible to take advantage of temporal and spectral correlations simultaneously.
- Temporal pattern extraction—this operation consists of a series of convolutional operations followed by rectifier activation functions that non linearly maps each elaborated temporal and spectral patterns onto high dimensional representations. So, RNN output temporal sequences are processed by a subsequent cascade of filters, which in a hierarchical fashion, extracts essential features for the successive stage.
- Multiclass classification—this final operation maps the feature space with a probability distribution with K different probabilities, where K, as previously stated, is equal to the number of classes.
4.1.1. Time Correlation Representation
4.1.2. Temporal Patterns Extraction
4.1.3. Multiclass Classification
4.2. Training
5. Experimental Results and Discussion
5.1. Training Data
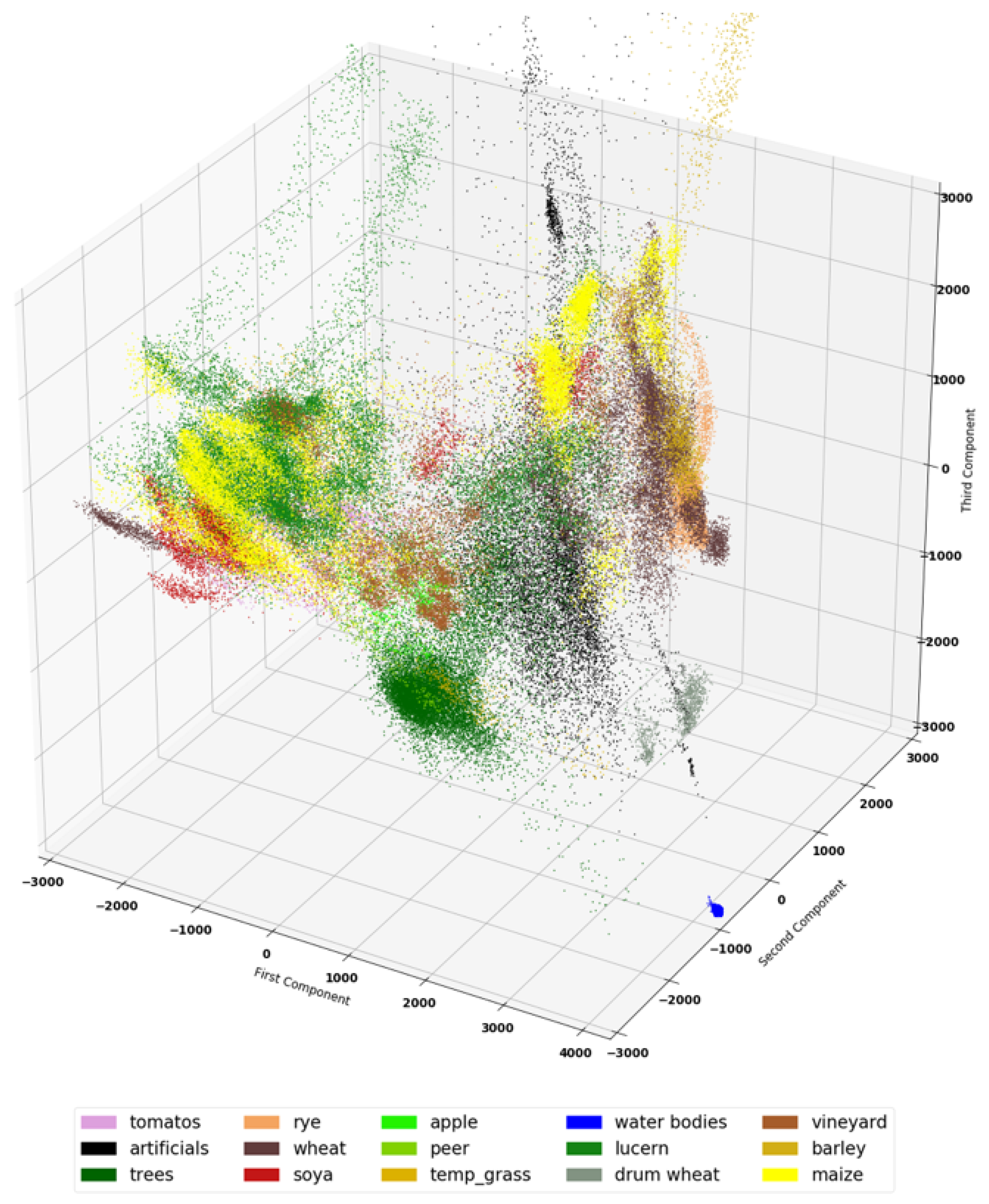
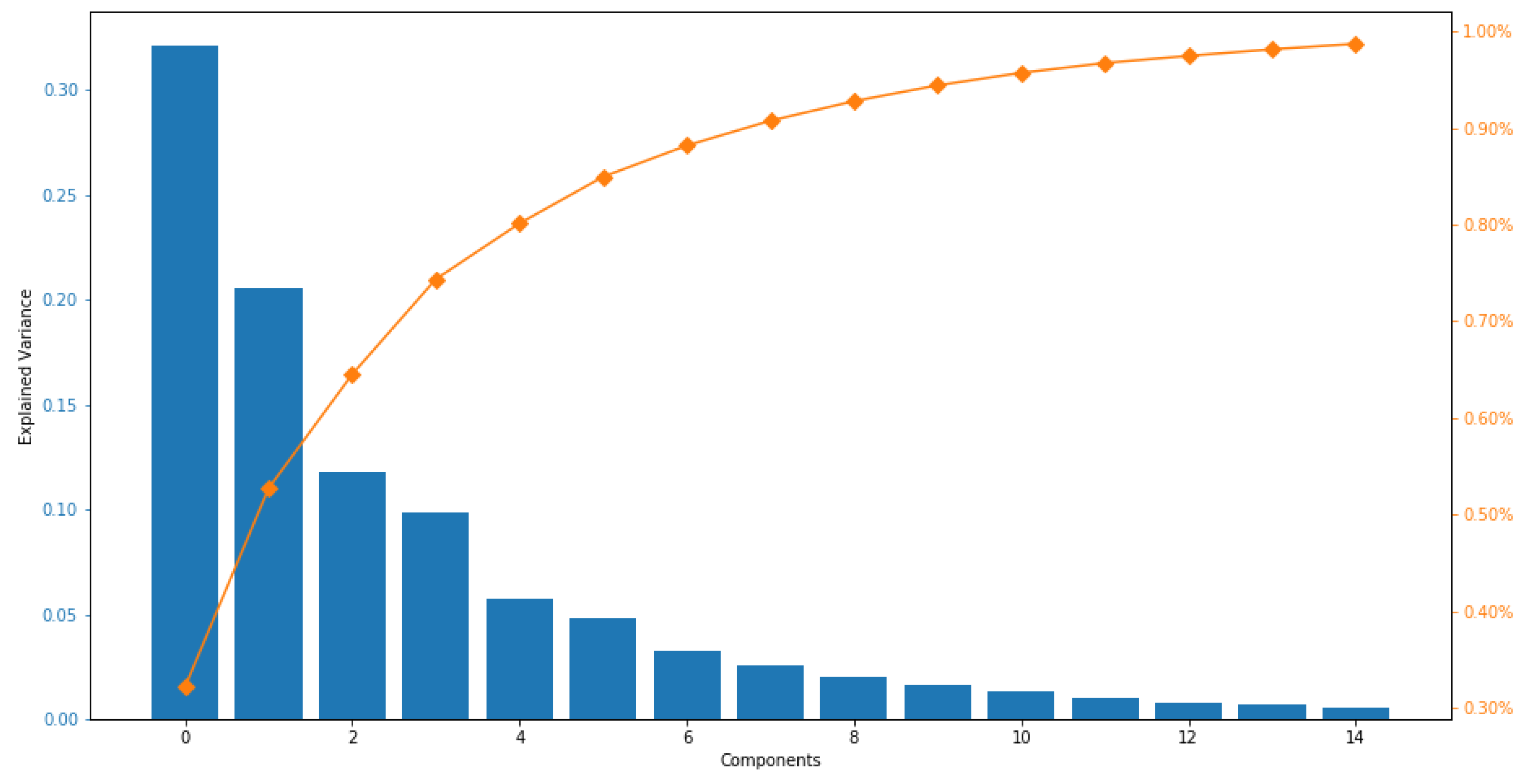
5.2. Dataset Visualization
5.3. Experimental Settings
5.4. Classification
5.5. Non Deep Learning Classifiers
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gomez, C.; White, J.C.; Wulder, M.A. Optical remotely sensed time series data for land cover classification: A review. ISPRS J. Photogramm. Remote Sens. 2016, 116, 55–72. [Google Scholar] [CrossRef]
- Wu, W.-B.; Yu, Q.-Y.; Peter, V.H.; You, L.-Z.; Yang, P.; Tang, H.-J. How Could Agricultural Land Systems Contribute to Raise Food Production Under Global Change? J. Integr. Agric. 2014, 13, 1432–1442. [Google Scholar] [CrossRef]
- Jin, Z.; Azzari, G.; You, C.; Di Tommaso, S.; Aston, S.; Burke, M.; Lobell, D.B. Smallholder maize area and yield mapping at national scales with Google Earth Engine. Remote Sens. Environ. 2019, 228, 115–128. [Google Scholar] [CrossRef]
- Yang, P.; Wu, W.-B.; Tang, H.-J.; Zhou, Q.-B.; Zou, J.-Q.; Zhang, L. Mapping Spatial and Temporal Variations of Leaf Area Index for Winter Wheat in North China. Agric. Sci. China 2007, 6, 1437–1443. [Google Scholar] [CrossRef]
- Wang, L.A.; Zhou, X.; Zhu, X.; Dong, Z.; Guo, W. Estimation of biomass in wheat using random forest regression algorithm and remote sensing data. Crop. J. 2016, 4, 212–219. [Google Scholar] [CrossRef]
- Matton, N.; Canto, G.; Waldner, F.; Valero, S.; Morin, D.; Inglada, J.; Defourny, P. An automated method for annual cropland mapping along the season for various globally-distributed agrosystems using high spatial and temporal resolution time series. Remote Sens. 2015, 7, 13208–13232. [Google Scholar] [CrossRef]
- Guan, K.; Berry, J.A.; Zhang, Y.; Joiner, J.; Guanter, L.; Badgley, G.; Lobell, D.B. Improving the monitoring of crop productivity using spaceborne solar-induced fluorescence. Glob. Chang. Biol. 2016, 22, 716–726. [Google Scholar] [CrossRef]
- Battude, M.; Al Bitar, A.; Morin, D.; Cros, J.; Huc, M.; Marais Sicre, C.; Le Dantec, V.; Demarez, V. Estimating maize biomass and yield over large areas using high spatial and temporal resolution Sentinel-2 like remote sensing data. Remote Sens. Environ. 2016, 184, 668–681. [Google Scholar] [CrossRef]
- Huang, J.; Tian, L.; Liang, S.; Ma, H.; Becker-Reshef, I.; Huang, Y.; Su, W.; Zhang, X.; Zhu, D.; Wu, W. Improving winter wheat yield estimation by assimilation of the leaf area index from Landsat TM and MODIS data into the WOFOST model. Agric. For. Meteorol. 2015, 204, 106–121. [Google Scholar] [CrossRef]
- Toureiro, C.; Serralheiro, R.; Shahidian, S.; Sousa, A. Irrigation management with remote sensing: Evaluating irrigation requirement for maize under Mediterranean climate condition. Agric. Water Manag. 2017, 184, 211–220. [Google Scholar] [CrossRef]
- Yu, Q.; Shi, Y.; Tang, H.; Yang, P.; Xie, A.; Liu, B.; Wu, W. eFarm: A Tool for Better Observing Agricultural Land Systems. Sensors 2017, 17, 453. [Google Scholar] [CrossRef] [PubMed]
- Boryan, C.; Yang, Z.; Mueller, R.; Craig, M. Monitoring US agriculture: the US department of agriculture, national agricultural statistics service, cropland data layer program. Geocarto Int. 2011, 26, 341–358. [Google Scholar] [CrossRef]
- Xie, Y.; Sha, Z.; Yu, M. Remote sensing imagery in vegetation mapping: A review. Plant Ecol. 2008, 1, 9–23. [Google Scholar] [CrossRef]
- Johnson, D.M. A comprehensive assessment of the correlations between field crop yields and commonly used MODIS products. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 65–81. [Google Scholar] [CrossRef]
- Senf, C.; Leitão, P.J.; Pflugmacher, D.; van der Linden, S.; Hostert, P. Mapping land cover in complex Mediterranean landscapes using Landsat: Improved classification accuracies from integrating multi-seasonal and synthetic imagery. Remote Sens. Environ. 2015, 156, 527–536. [Google Scholar] [CrossRef]
- Jin, H.; Li, A.; Wang, J.; Bo, Y. Improvement of spatially and temporally continuous crop leaf area index by integration of CERES-Maize model and MODIS data. Eur. J. Agron. 2016, 78, 1–12. [Google Scholar] [CrossRef]
- Liaqat, M.U.; Cheema, M.J.M.; Huang, W.; Mahmood, T.; Zaman, M.; Khan, M.M. Evaluation of MODIS and Landsat multiband vegetation indices used for wheat yield estimation in irrigated Indus Basin. Comput. Electron. Agric. 2017, 138, 39–47. [Google Scholar] [CrossRef]
- Senf, C.; Pflugmacher, D.; Heurich, M.; Krueger, T. A Bayesian hierarchical model for estimating spatial and temporal variation in vegetation phenology from Landsat time series. Remote Sens. Environ. 2017, 194, 155–160. [Google Scholar] [CrossRef]
- Kussul, N.; Lemoine, G.; Gallego, F.J.; Skakun, S.V.; Lavreniuk, M.; Shelestov, A.Y. Parcel-based crop classification in ukraine using landsat-8 data and sentinel-1A data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 2500–2508. [Google Scholar] [CrossRef]
- Xiong, J.; Thenkabail, P.S.; Gumma, M.K.; Teluguntla, P.; Poehnelt, J.; Congalton, R.G.; Thau, D. Automated cropland mapping of continental Africa using Google Earth Engine cloud computing. ISPRS J. Photogramm. Remote Sens. 2017, 126, 225–244. [Google Scholar] [CrossRef]
- Yan, L.; Roy, D.P. Improved time series land cover classification by missing-observation-adaptive nonlinear dimensionality reduction. Remote Sens. Environ. 2015, 158, 478–491. [Google Scholar] [CrossRef]
- Xiao, J.; Wu, H.; Wang, C.; Xia, H. Land Cover Classification Using Features Generated From Annual Time-Series Landsat Data. IEEE Geosci. Remote Sens. Lett. 2018, 15, 739–743. [Google Scholar] [CrossRef]
- Khaliq, A.; Peroni, L.; Chiaberge, M. Land cover and crop classification using multitemporal Sentinel-2 images based on crops phenological cycle. In IEEE Workshop on Environmental, Energy, and Structural Monitoring Systems (EESMS); IEEE: Piscataway, NJ, USA, 2018; pp. 1–5. [Google Scholar]
- Gallego, J.; Craig, M.; Michaelsen, J.; Bossyns, B.; Fritz, S. Best Practices for Crop Area Estimation with Remote Sensing; Joint Research Center: Ispra, Italy, 2008. [Google Scholar]
- Zhou, F.; Zhang, A.; Townley-Smith, L. A data mining approach for evaluation of optimal time-series of MODIS data for land cover mapping at a regional level. ISPRS J. Photogramm. Remote Sens. 2013, 84, 114–129. [Google Scholar] [CrossRef]
- Arvor, D.; Jonathan, M.; Meirelles, M.S.P.; Dubreuil, V.; Durieux, L. Classification of MODIS EVI time series for crop mapping in the state of Mato Grosso, Brazil. Remote Sens. 2011, 32, 7847–7871. [Google Scholar] [CrossRef]
- Zhong, L.; Gong, P.; Biging, G.S. Phenology-based crop classification algorithm and its implications on agricultural water use assessments in California’s Central Valley. Photogramm. Eng. Remote Sens. 2012, 78, 799–813. [Google Scholar] [CrossRef]
- Wardlow, B.D.; Egbert, S.L. A comparison of MODIS 250-m EVI and NDVI data for crop mapping: A case study for southwest Kansas. Int. J. Remote Sens. 2012, 31, 805–830. [Google Scholar] [CrossRef]
- Löw, F.; Michel, U.; Dech, S.; Conrad, C. Impact of feature selection on the accuracy and spatial uncertainty of per-field crop classification using support vector machines. ISPRS J. Photogramm. Remote Sens. 2013, 85, 102–119. [Google Scholar] [CrossRef]
- Hao, P.; Zhan, Y.; Wang, L.; Niu, Z.; Shakir, M. Feature selection of time series MODIS data for early crop classification using random forest: A case study in Kansas, USA. Remote Sens. 2015, 7, 5347–5369. [Google Scholar] [CrossRef]
- Blaschke, T. Object based image analysis for remote sensing. ISPRS J. Photogramm. Remote Sens. 2010, 65, 2–16. [Google Scholar] [CrossRef]
- Novelli, A.; Aguilar, M.A.; Nemmaoui, A.; Aguilar, F.J.; Tarantino, E. Performance evaluation of object based greenhouse detection from Sentinel-2 MSI and Landsat 8 OLI data: A case study from Almería (Spain). Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 403–411. [Google Scholar] [CrossRef]
- Long, J.A.; Lawrence, R.L.; Greenwood, M.C.; Marshall, L.; Miller, P.R. Object-oriented crop classification using multitemporal ETM+ SLC-off imagery and random forest. GIsci. Remote Sens. 2013, 50, 418–436. [Google Scholar] [CrossRef]
- Li, Q.; Wang, C.; Zhang, B.; Lu, L. Object-based crop classification with Landsat-MODIS enhanced time-series data. Remote Sens. 2015, 7, 16091–16107. [Google Scholar] [CrossRef]
- Walker, J.J.; De Beurs, K.M.; Wynne, R.H. Dryland vegetation phenology across an elevation gradient in Arizona, USA, investigated with fused MODIS and Landsat data. Remote Sens. Environ. 2014, 144, 85–97. [Google Scholar] [CrossRef]
- Walker, J.J.; De Beurs, K.M.; Henebry, G.M. Land surface phenology along urban to rural gradients in the US Great Plains. Remote Sens. Environ. 2015, 165, 42–52. [Google Scholar] [CrossRef]
- Simonneaux, V.; Duchemin, B.; Helson, D.; Er-Raki, S.; Olioso, A.; Chehbouni, A.G. The use of high-resolution image time series for crop classification and evapotranspiration estimate over an irrigated area in central Morocco. Int. J. Remote Sens. 2008, 29, 95–116. [Google Scholar] [CrossRef]
- Shao, Y.; Lunetta, R.S.; Wheeler, B.; Iiames, J.S.; Campbell, J.B. An evaluation of time-series smoothing algorithms for land-cover classifications using MODIS-NDVI multi-temporal data. Remote Sens. Environ. 2016, 174, 258–265. [Google Scholar] [CrossRef]
- Galford, G.L.; Mustard, J.F.; Melillo, J.; Gendrin, A.; Cerri, C.C.; Cerri, C.E. Wavelet analysis of MODIS time series to detect expansion and intensification of row-crop agriculture in Brazil. Remote Sens. Environ. 2008, 112, 576–587. [Google Scholar] [CrossRef]
- Funk, C.; Budde, M.E. Phenologically-tuned MODIS NDVI-based production anomaly estimates for Zimbabwe. Remote Sens. Environ. 2009, 113, 115–125. [Google Scholar] [CrossRef]
- Siachalou, S.; Mallinis, G.; Tsakiri-Strati, M. A hidden Markov models approach for crop classification: Linking crop phenology to time series of multi-sensor remote sensing data. Remote Sens. 2015, 7, 3633–3650. [Google Scholar] [CrossRef]
- Xin, Q.; Broich, M.; Zhu, P.; Gong, P. Modeling grassland spring onset across the Western United States using climate variables and MODIS-derived phenology metrics. Remote. Sens. Environ. 2015, 161, 63–77. [Google Scholar] [CrossRef]
- Gonsamo, A.; Chen, J.M. Circumpolar vegetation dynamics product for global change study. Remote. Sens. Environ. 2016, 182, 13–26. [Google Scholar] [CrossRef]
- Dannenberg, M.P.; Song, C.; Hwang, T.; Wise, E.K. Empirical evidence of El Niño–Southern Oscillation influence on land surface phenology and productivity in the western United States. Remote Sens. Environ. 2015, 159, 167–180. [Google Scholar] [CrossRef]
- Khatami, R.; Mountrakis, G.; Stehman, S.V. A meta-analysis of remote sensing research on supervised pixel-based land-cover image classification processes: General guidelines for practitioners and future research. Remote Sens. Environ. 2016, 177, 89–100. [Google Scholar] [CrossRef]
- Gislason, P.O.; Benediktsson, J.A.; Sveinsson, J.R. Random forests for land cover classification. Pattern Recognit. Lett. 2006, 27, 294–300. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to sequence learning with neural networks. In Proceedings of the Twenty-Eighth Conference on Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2014; pp. 3104–3112. [Google Scholar]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to forget: Continual prediction with LSTM. Neural Comput. 2000, 850–855. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. In Proceedings of the NIPS 2014 Deep Learning and Representation Learning Workshop, Montreal, QC, Canada, 12 December 2014. [Google Scholar]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural machine translation by jointly learning to align and translate. In Proceedings of the ICLR 2015: International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Gated feedback recurrent neural networks. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 2067–2075. [Google Scholar]
- Lyu, H.; Lu, H.; Mou, L. Learning a transferable change rule from a recurrent neural network for land cover change detection. Remote Sens. 2016, 8, 506. [Google Scholar] [CrossRef]
- Lyu, H.; Lu, H.; Mou, L.; Li, W.; Wright, J.; Li, X.; Gong, P. Long-term annual mapping of four cities on different continents by applying a deep information learning method to landsat data. Remote Sens. 2018, 10, 471. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Hubel, D.H.; Wiesel, T.N. Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex. J. Physiol. 1962, 160, 106–154. [Google Scholar] [CrossRef]
- Szeliski, R. Computer vision: Algorithms and applications. In Springer Science & Business Media; Springer: London, UK, 2010. [Google Scholar]
- Dalal, N.; Triggs, B. Histograms of oriented gradients for human detection. In Proceedings of the International Conference on Computer Vision & Pattern Recognition (CVPR ’05), San Diego, CA, USA, 20–26 June 2005; pp. 886–893. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Twenty-Sixth Conference on Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–8 December 2012; pp. 1097–1105. [Google Scholar]
- Zeiler, M.D.; Fergus, R. Visualizing and understanding convolutional networks. In European Conference on Computer Vision; Springer: Cham, Switzerland, 2014; pp. 818–833. [Google Scholar]
- Wan, X.; Zhao, C.; Wang, Y.; Liu, W. Stacked sparse autoencoder in hyperspectral data classification using spectral-spatial, higher order statistics and multifractal spectrum features. Infrared Phys. Technol. 2017, 86, 77–89. [Google Scholar] [CrossRef]
- Mou, L.; Ghamisi, P.; Zhu, X.X. Unsupervised spectral–spatial feature learning via deep residual Conv–Deconv network for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 56, 391–406. [Google Scholar] [CrossRef]
- Kampffmeyer, M.; Salberg, A.B.; Jenssen, R. Semantic segmentation of small objects and modeling of uncertainty in urban remote sensing images using deep convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 1–9. [Google Scholar]
- Maggiori, E.; Tarabalka, Y.; Charpiat, G.; Alliez, P. High-resolution aerial image labeling with convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 2017, 55, 7092–7103. [Google Scholar] [CrossRef]
- Audebert, N.; Le Saux, B.; Lefèvre, S. Beyond RGB: Very high resolution urban remote sensing with multimodal deep networks. IISPRS J Photogramm. Remote Sens. 2018, 140, 20–32. [Google Scholar] [CrossRef]
- Kussul, N.; Lavreniuk, M.; Skakun, S.; Shelestov, A. Deep learning classification of land cover and crop types using remote sensing data. IEEE Geosci. Remote Sens. Lett. 2017, 14, 778–782. [Google Scholar] [CrossRef]
- Land Use and Coverage Area frame Survey (LUCAS) Details. Available online: https://ec.europa.eu/eurostat/web/lucas (accessed on 14 January 2019).
- Sentinel-2 MSI Technical Guide. Available online: https://sentinel.esa.int/web/sentinel/technical-guides/sentinel-2-msi (accessed on 14 January 2019).
- Kaufman, Y.J.; Sendra, C. Algorithm for automatic atmospheric corrections to visible and near-IR satellite imagery. Int. J. Remote Sens. 1988, 9, 1357–1381. [Google Scholar] [CrossRef]
- Mellet, E.; Tzourio, N.; Crivello, F.; Joliot, M.; Denis, M.; Mazoyer, B. Functional anatomy of spatial mental imagery generated from verbal instructions. Open J. Neurosci. 1996, 16, 6504–6512. [Google Scholar] [CrossRef]
- Reddi, S.J.; Kale, S.; Kumar, S. On the convergence of adam and beyond. In Proceedings of the ICLR 2018 Conference Track, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference on Learning Representations (ICLR2015), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Smith, L.N. Cyclical learning rates for training neural networks. In Proceedings of the 2017 IEEE Winter Conference on Applications of Computer Vision (WACV), Santa Rosa, CA, USA, 24–31 March 2017; pp. 464–472. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Congalton, R.G. A review of assessing the accuracy of classifications of remotely sensed data. Remote Sens. Environ. 1991, 37, 35–46. [Google Scholar] [CrossRef]
- Conrad, C.; Dech, S.; Dubovyk, O.; Fritsch, S.; Klein, D.; Löw, F.; Zeidler, J. Derivation of temporal windows for accurate crop discrimination in heterogeneous croplands of Uzbekistan using multitemporal RapidEye images. Comput. Electron. Agric. 2014, 103, 63–74. [Google Scholar] [CrossRef]
- Skakun, S.; Kussul, N.; Shelestov, A.Y.; Lavreniuk, M.; Kussul, O. Efficiency assessment of multitemporal C-band Radarsat-2 intensity and Landsat-8 surface reflectance satellite imagery for crop classification in Ukraine. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 9, 3712–3719. [Google Scholar] [CrossRef]
- Rußwurm, M.; Körner, M. Multi-temporal land cover classification with sequential recurrent encoders. ISPRS Int. J. Geoinf. 2018, 7, 129. [Google Scholar] [CrossRef]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Vuolo, F.; Neuwirth, M.; Immitzer, M.; Atzberger, C.; Ng, W.T. How much does multi-temporal Sentinel-2 data improve crop type classification? Int. J. Appl. Earth Obs. Geoinf. 2018, 72, 122–130. [Google Scholar] [CrossRef]
- Peña-Barragán, J.M.; Ngugi, M.K.; Plant, R.E.; Six, J. Object-based crop identification using multiple vegetation indices, textural features and crop phenology. Remote sens. Environ. 2011, 115, 1301–1316. [Google Scholar] [CrossRef]
- Fernández-Delgado, M.; Cernadas, E.; Barro, S.; Amorim, D. Do we need hundreds of classifiers to solve real world classification problems? J. Mach. Learn. Res. 2014, 15, 3133–3181. [Google Scholar]
- Shi, D.; Yang, X. An assessment of algorithmic parameters affecting image classification accuracy by random forests. Photogramm. Eng. Remote Sens. 2016, 82, 407–417. [Google Scholar] [CrossRef]
- Lawrence, R.L.; Wood, S.D.; Sheley, R.L. Mapping invasive plants using hyperspectral imagery and Breiman Cutler classifications (RandomForest). Remote Sens. Environ. 2006, 100, 356–362. [Google Scholar] [CrossRef]
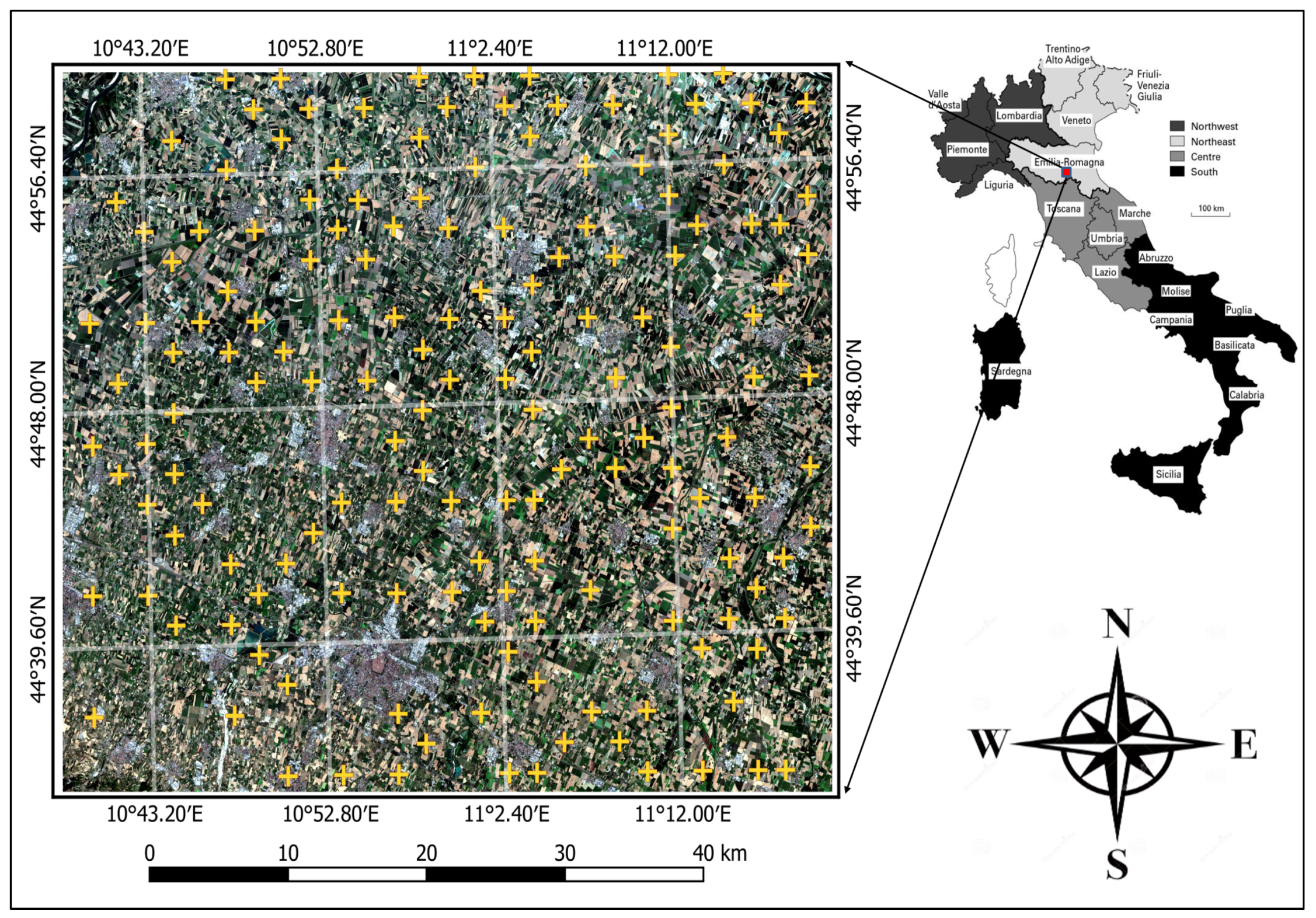


| Bands Used | Description | Central Wavelength (m) | Resolution (m) |
|---|---|---|---|
| Band 2 | Blue | 0.49 | 10 |
| Band 3 | Green | 0.56 | 10 |
| Band 4 | Red | 0.665 | 10 |
| Band 8 | Near-infrared | 0.705 | 10 |
| NDVI | (Band8-Band4)/(Band8+Band4) | - | 10 |
| Date | Doy | Sensing Orbit # | Cloud Pixel Percentage |
|---|---|---|---|
| 7/4/2015 | 185 | 22-Descending | 0 |
| 8/3/2015 | 215 | 22-Descending | 0.384 |
| 9/2/2015 | 245 | 22-Descending | 4.795 |
| 9/12/2015 | 255 | 22-Descending | 7.397 |
| 10/22/2015 | 295 | 22-Descending | 7.606 |
| 2/19/2016 | 50 | 22-Descending | 5.8 |
| 3/20/2016 | 80 | 22-Descending | 19.866 |
| 4/29/2016 | 120 | 22-Descending | 18.61 |
| 6/18/2016 | 170 | 22-Descending | 15.52 |
| 7/18/2016 | 200 | 22-Descending | 0 |
| Class | Pixels | Percentage |
|---|---|---|
| Tomatoes | 3020 | 3.20% |
| Artificials | 9343 | 10.14% |
| Trees | 7384 | 8.01% |
| Rye | 4382 | 4.75% |
| Wheat | 12,826 | 13.92% |
| Soya | 5836 | 6.33% |
| Apple | 849 | 0.92% |
| Peer | 495 | 0.53% |
| Temp Grass | 1744 | 1.89% |
| Water | 2451 | 2.66% |
| Lucerne | 17,942 | 19.47% |
| Durum Wheat | 1188 | 1.28% |
| Vineyard | 6110 | 6.63% |
| Barley | 2549 | 2.76% |
| Maize | 15,997 | 17.37% |
| Total | 92,116 | 100% |
| Ground Truth | Classified Classes | Total | PA | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TM | AR | TR | RY | WH | SY | AP | PR | GL | WT | LN | DW | VY | BL | MZ | |||
| Tomatoes (TM) | 1096 | 0 | 0 | 0 | 4 | 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1111 | 98% |
| Artificial (AR) | 0 | 3752 | 8 | 1 | 2 | 0 | 2 | 1 | 9 | 9 | 12 | 2 | 6 | 0 | 4 | 3808 | 99% |
| Trees (TR) | 0 | 31 | 2967 | 1 | 0 | 0 | 0 | 3 | 10 | 0 | 17 | 0 | 2 | 0 | 0 | 3031 | 98% |
| Rye (RY) | 0 | 1 | 0 | 1960 | 25 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 5 | 0 | 1991 | 98% |
| Wheat (WH) | 38 | 7 | 0 | 221 | 4981 | 6 | 0 | 0 | 10 | 0 | 14 | 1 | 2 | 38 | 42 | 5360 | 93% |
| Soya (SY) | 3 | 0 | 0 | 0 | 3 | 1226 | 0 | 0 | 0 | 0 | 11 | 0 | 3 | 0 | 41 | 1287 | 95% |
| Apple (AP) | 0 | 0 | 0 | 0 | 0 | 0 | 142 | 0 | 0 | 0 | 2 | 0 | 21 | 0 | 0 | 165 | 86% |
| Peer (PR) | 0 | 0 | 11 | 0 | 0 | 0 | 27 | 124 | 0 | 0 | 0 | 0 | 6 | 0 | 0 | 168 | 73% |
| Grassland (GL) | 0 | 39 | 3 | 7 | 0 | 1 | 0 | 0 | 239 | 0 | 72 | 0 | 3 | 0 | 4 | 368 | 65% |
| Water (WT) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 906 | 0 | 0 | 0 | 0 | 0 | 906 | 100% |
| Lucerne (LN) | 0 | 0 | 0 | 2 | 0 | 2 | 0 | 0 | 48 | 0 | 7250 | 0 | 26 | 0 | 10 | 7338 | 98% |
| Durum.Wheat (W) | 0 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 322 | 0 | 0 | 0 | 328 | 98% |
| Vineyard (VY) | 11 | 7 | 4 | 4 | 11 | 1 | 50 | 1 | 21 | 0 | 93 | 0 | 2139 | 0 | 7 | 2349 | 91% |
| Barley (BL) | 0 | 1 | 0 | 2 | 24 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 817 | 0 | 846 | 96% |
| Maize (MZ) | 17 | 14 | 0 | 0 | 10 | 24 | 0 | 3 | 10 | 0 | 16 | 1 | 6 | 0 | 7689 | 7790 | 99% |
| Total | 1165 | 3856 | 2993 | 2198 | 5060 | 1271 | 221 | 132 | 350 | 915 | 7488 | 326 | 2214 | 860 | 7797 | ||
| UA | 94% | 97% | 99% | 89% | 98% | 96% | 64% | 93% | 68% | 99% | 96% | 99% | 96% | 95% | 98% | ||
| Study | Details | ||||
|---|---|---|---|---|---|
| Sensor | Features | Classifier | Accuracy | Classes | |
| Our | Sentinel-2 | BOA Reflectances | Pixel R-CNN | 96.50% | 15 |
| Rußwurm and Körner [78], 2018 | Sentinel-2 | TOA Reflectances | Recurrent Encoders | 90% | 17 |
| Skakun et al. [77], 2016 | Radarsat-2 + Landsat-8 | Optical+SAR | NN and MLPs | 90% | 11 |
| Conrad et al. [76], 2014 | RapidEye | Vegetation Indices | RF and OBIA | 86% | 9 |
| Vuolo et al. [80], 2018 | Sentinel-2 | Optical | RF | 91–95% | 9 |
| Hao et al. [30], 2015 | MODIS | Stat + phenological | RF | 89% | 6 |
| J.M. Pea-Barragán [81], 2011 | ASTER | Vegetation Indices | OBIA+DT | 79% | 13 |
| Model | Parameters | OA |
|---|---|---|
| SVM | C: 0.01, 0.1, 1, 10, 100, 1000 | 79.50% |
| Kernel: linear | ||
| C: 0.01, 0.1, 1, 10, 100, 1000 | ||
| Kernel SVM | Kernel: rbf | 76.20% |
| Gamma: 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8 | ||
| Random Forest | n_estimators: 10, 20, 100, 200, 500 max_depth: 5, 10, 15, 30 min_samples_split: 3, 5, 10, 15, 30 min_samples_leaf: 1, 3, 5, 10 | 77.90% |
| XGBoost | learning_rate: 0.01, 0.02, 0.05, 0.1 | 77.60% |
| gamma: 0.05, 0.1, 0.5, 1 | ||
| max_depth: 3, 7, 9, 20, 25 min_child_weight: 1, 5, 7, 9 | ||
| subsamples: 0.5, 0.7, 1 | ||
| colsample_bytree: 0.5, 0.7, 1 | ||
| reg_labda: 0.01, 0.1, 1 | ||
| reg_alpha: 0, 0.1, 0.5, 1 | ||
| Pixel R-CNN | Mentioned in experimental settings | 96.50% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mazzia, V.; Khaliq, A.; Chiaberge, M. Improvement in Land Cover and Crop Classification based on Temporal Features Learning from Sentinel-2 Data Using Recurrent-Convolutional Neural Network (R-CNN). Appl. Sci. 2020, 10, 238. https://doi.org/10.3390/app10010238
Mazzia V, Khaliq A, Chiaberge M. Improvement in Land Cover and Crop Classification based on Temporal Features Learning from Sentinel-2 Data Using Recurrent-Convolutional Neural Network (R-CNN). Applied Sciences. 2020; 10(1):238. https://doi.org/10.3390/app10010238
Chicago/Turabian StyleMazzia, Vittorio, Aleem Khaliq, and Marcello Chiaberge. 2020. "Improvement in Land Cover and Crop Classification based on Temporal Features Learning from Sentinel-2 Data Using Recurrent-Convolutional Neural Network (R-CNN)" Applied Sciences 10, no. 1: 238. https://doi.org/10.3390/app10010238
APA StyleMazzia, V., Khaliq, A., & Chiaberge, M. (2020). Improvement in Land Cover and Crop Classification based on Temporal Features Learning from Sentinel-2 Data Using Recurrent-Convolutional Neural Network (R-CNN). Applied Sciences, 10(1), 238. https://doi.org/10.3390/app10010238







