An Analysis of Rhythmic Patterns with Unsupervised Learning
Abstract
:1. Introduction
1.1. Related Work
1.1.1. Established MIR Tasks
1.1.2. Models for Music Understanding
1.2. Motivation
2. The Compositional Hierarchical Model for Rhythm Modeling
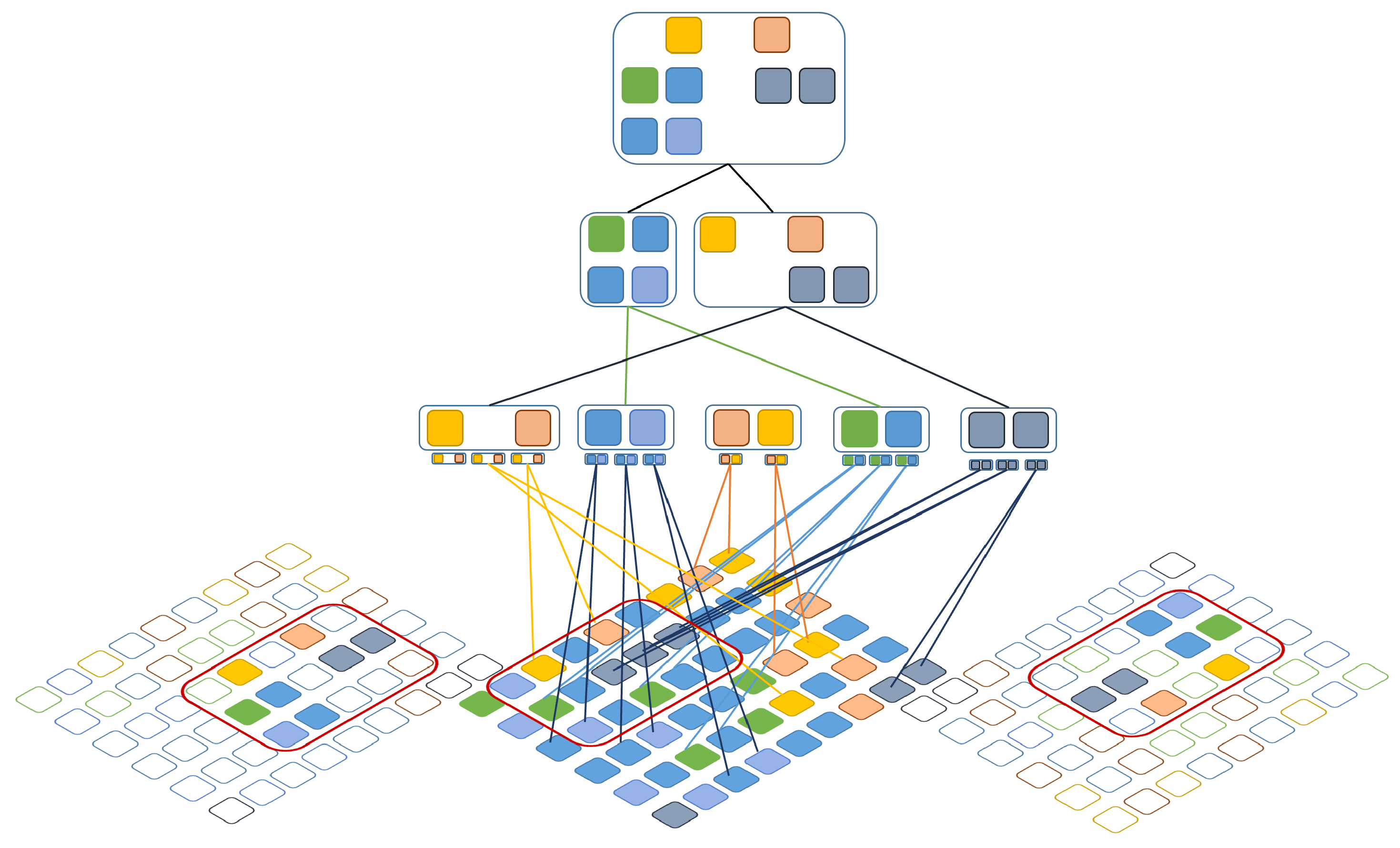
2.1. Model Description
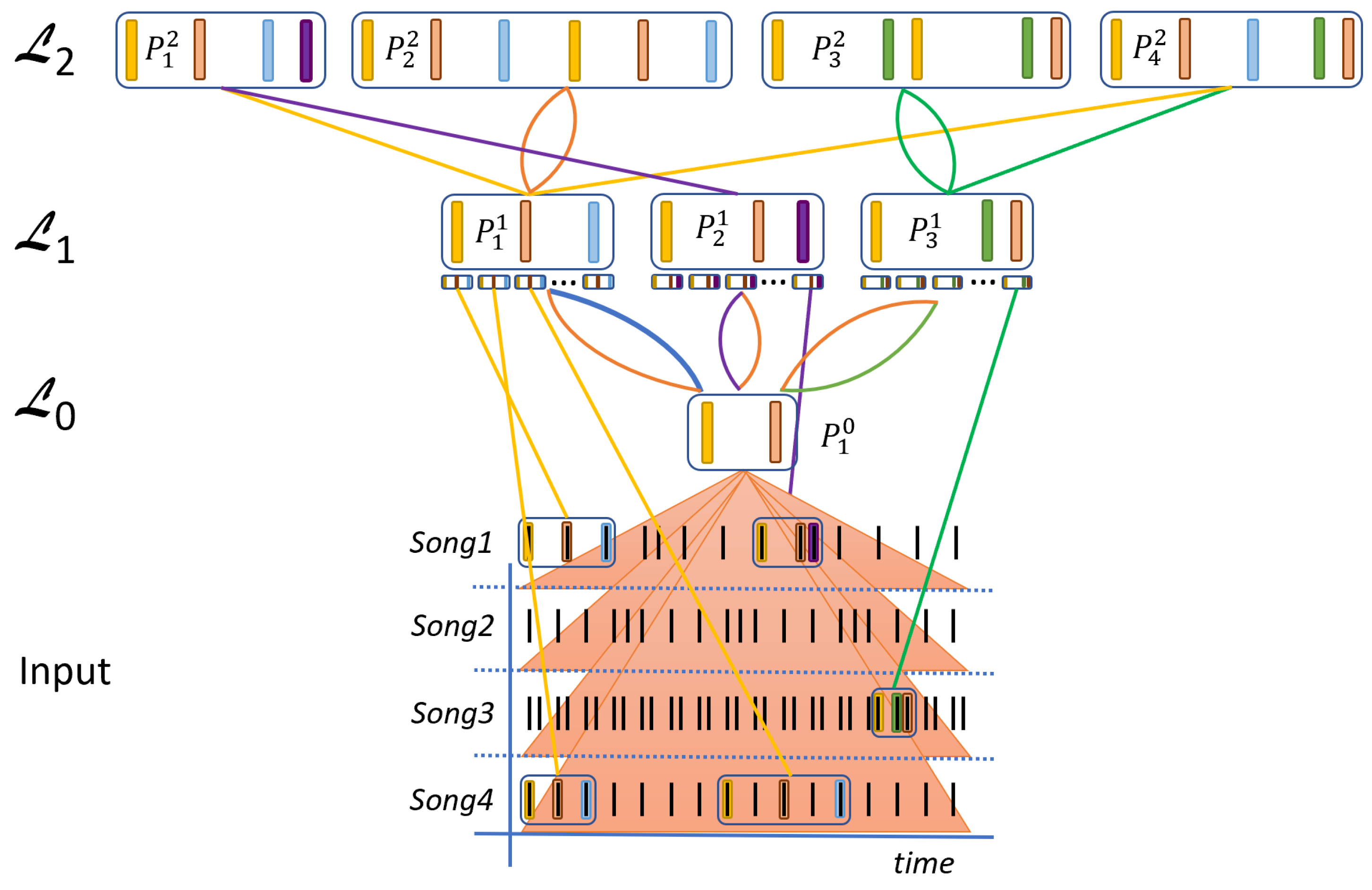
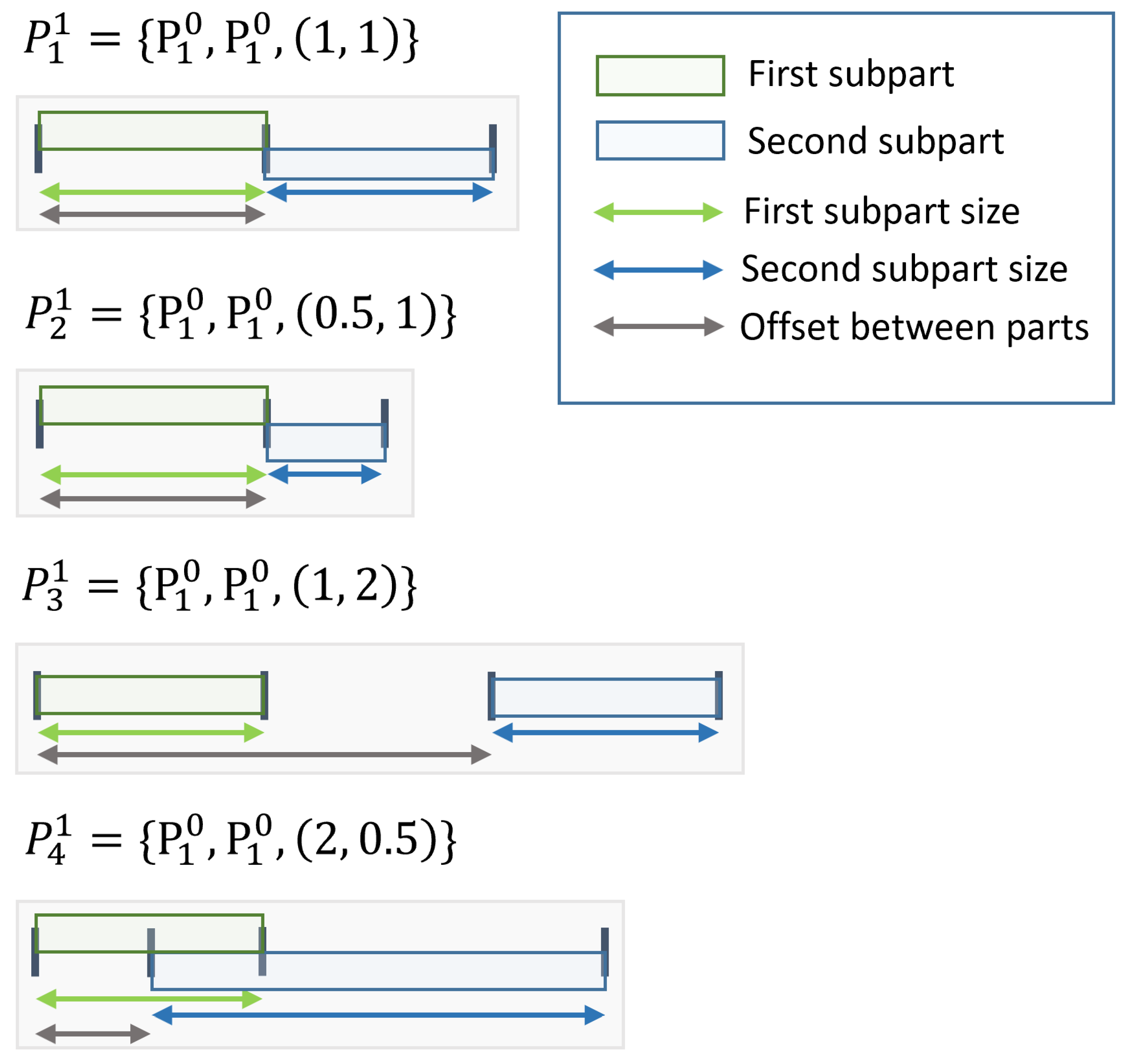
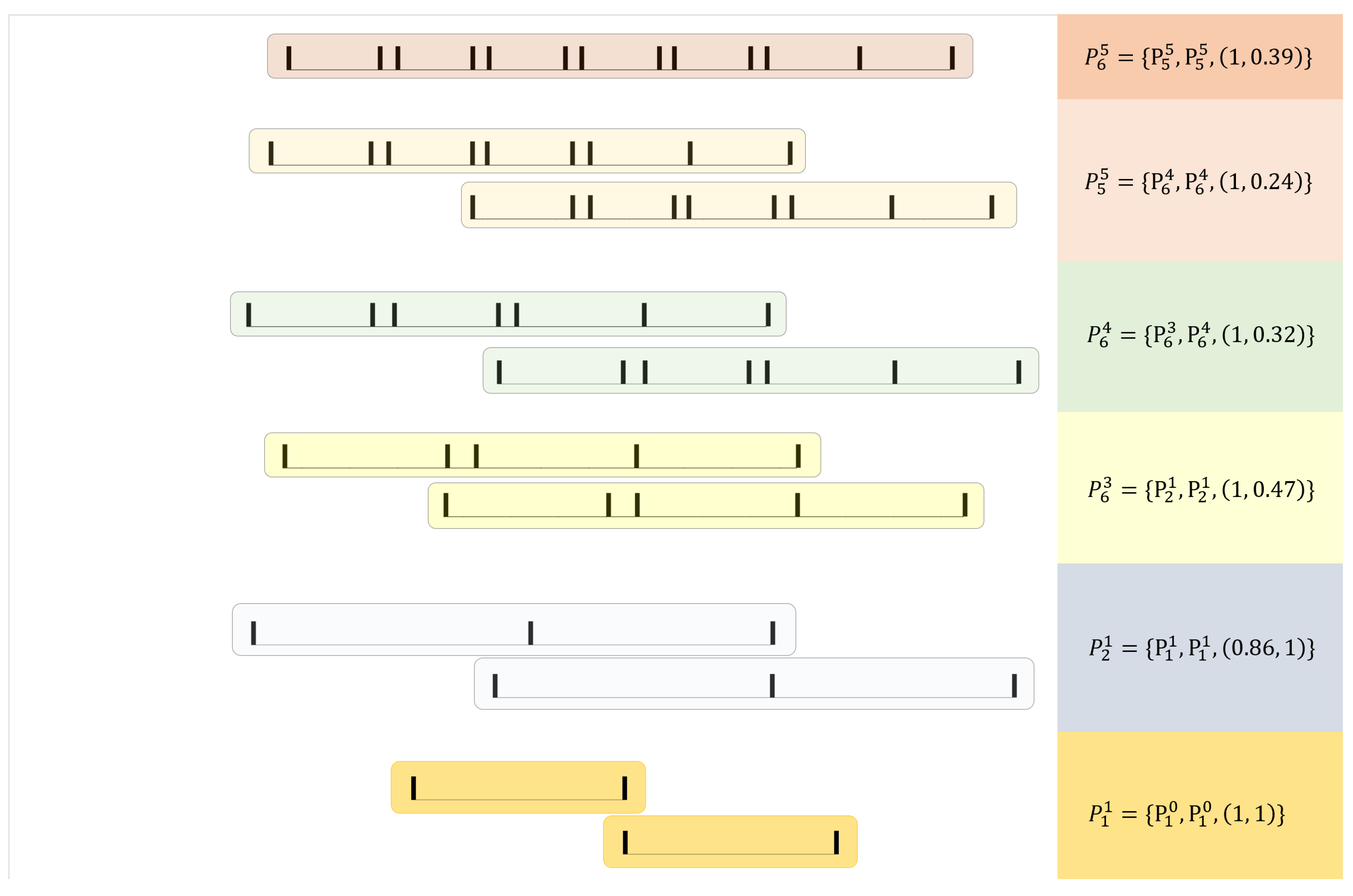
2.1.1. Rhythmic Compositions
2.1.2. Activations of Parts on Higher Layers
2.2. Learning and Inference
2.2.1. The Learning Algorithm
- coverage of each part (events that part activations explain in the training set) is calculated,
- the part that adds most to the coverage of the entire training set is chosen. This ensures that only compositions that provide enough coverage of “new” data with regard to the currently selected set of parts will be added,
- the algorithm stops when the added coverage falls below the learning threshold or the overall coverage reaches the threshold .
2.2.2. Inference
3. Analyses
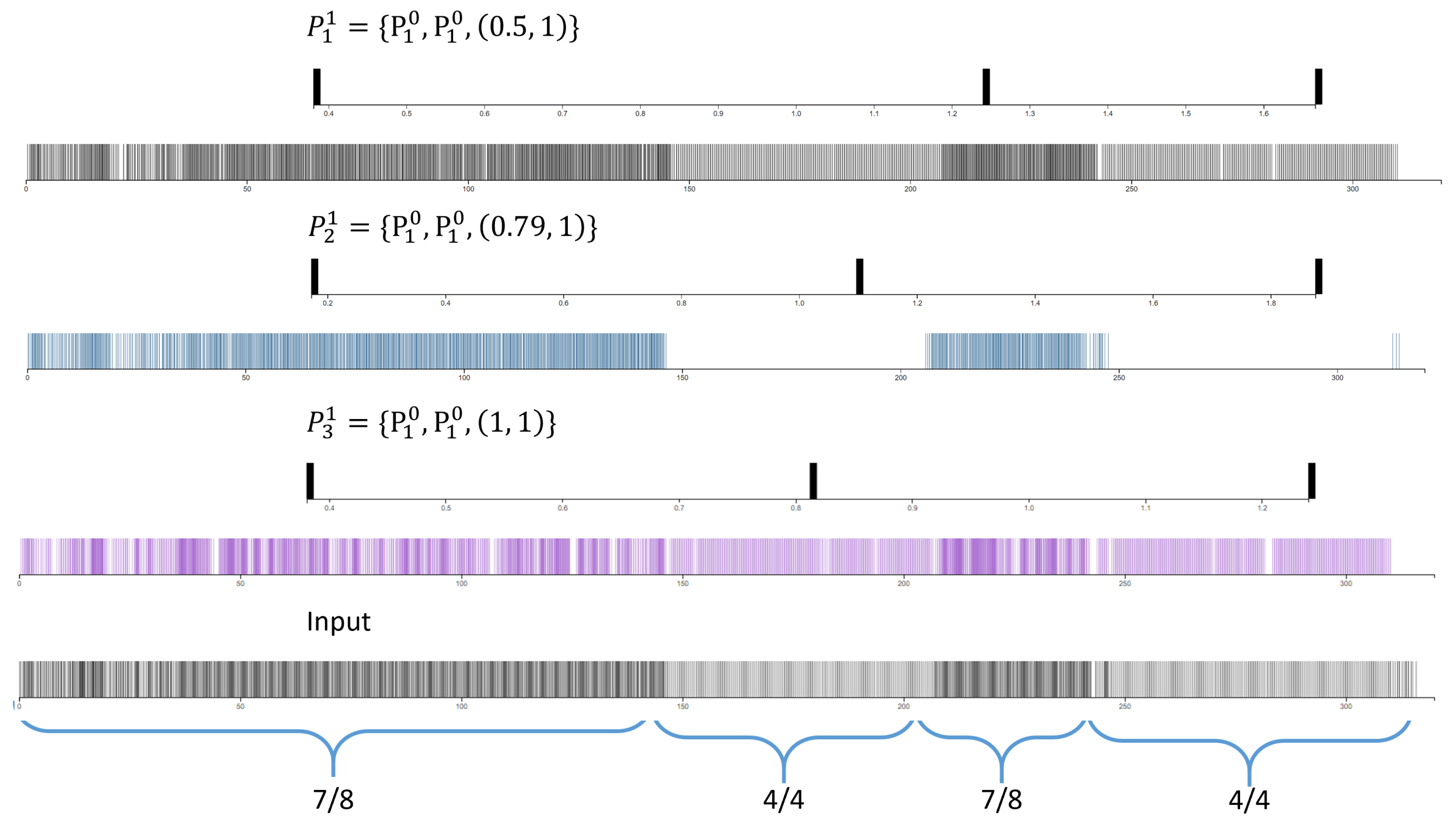
3.1. Experiment 1: Analyzing Ballroom Dances
3.1.1. Jive
3.1.2. Samba
3.1.3. Rumba and Cha Cha
3.1.4. Tango
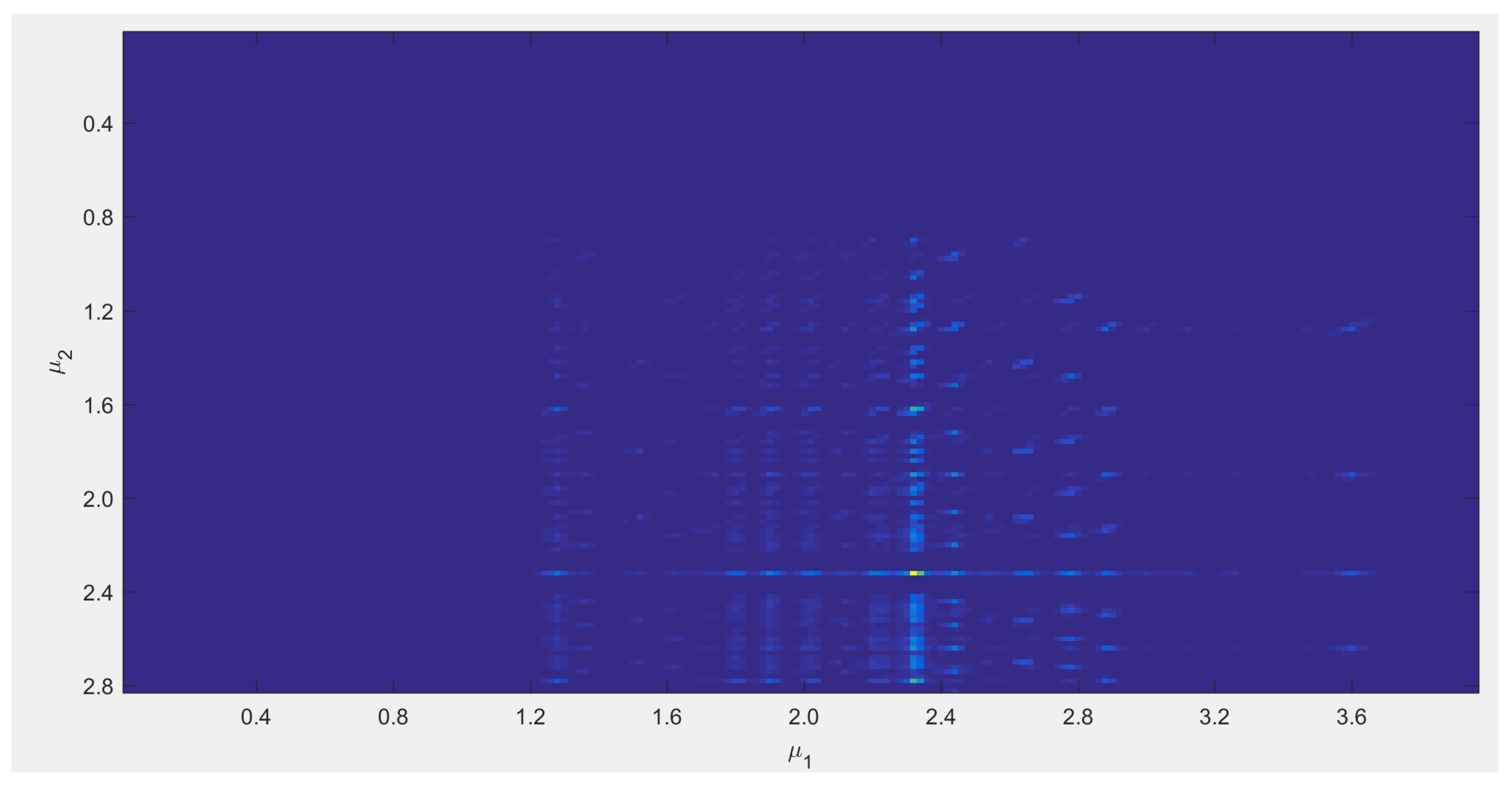
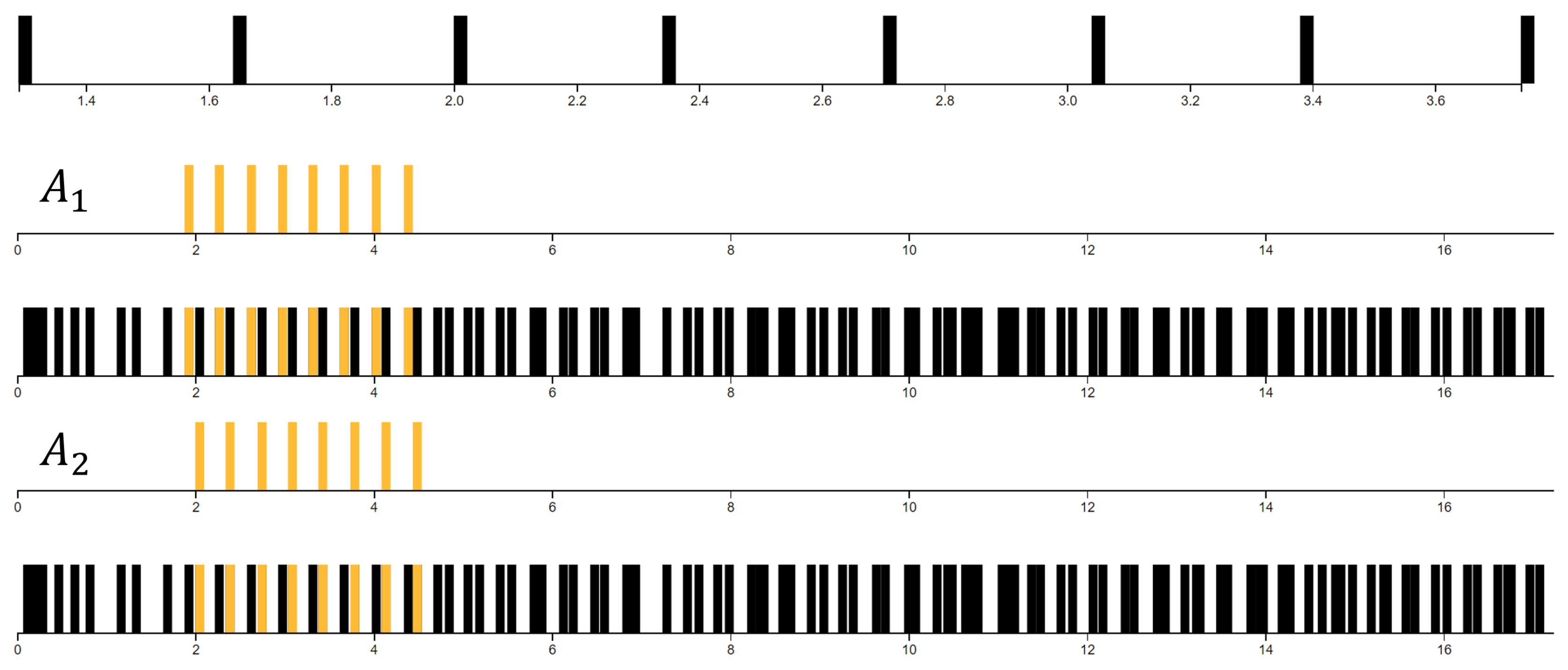
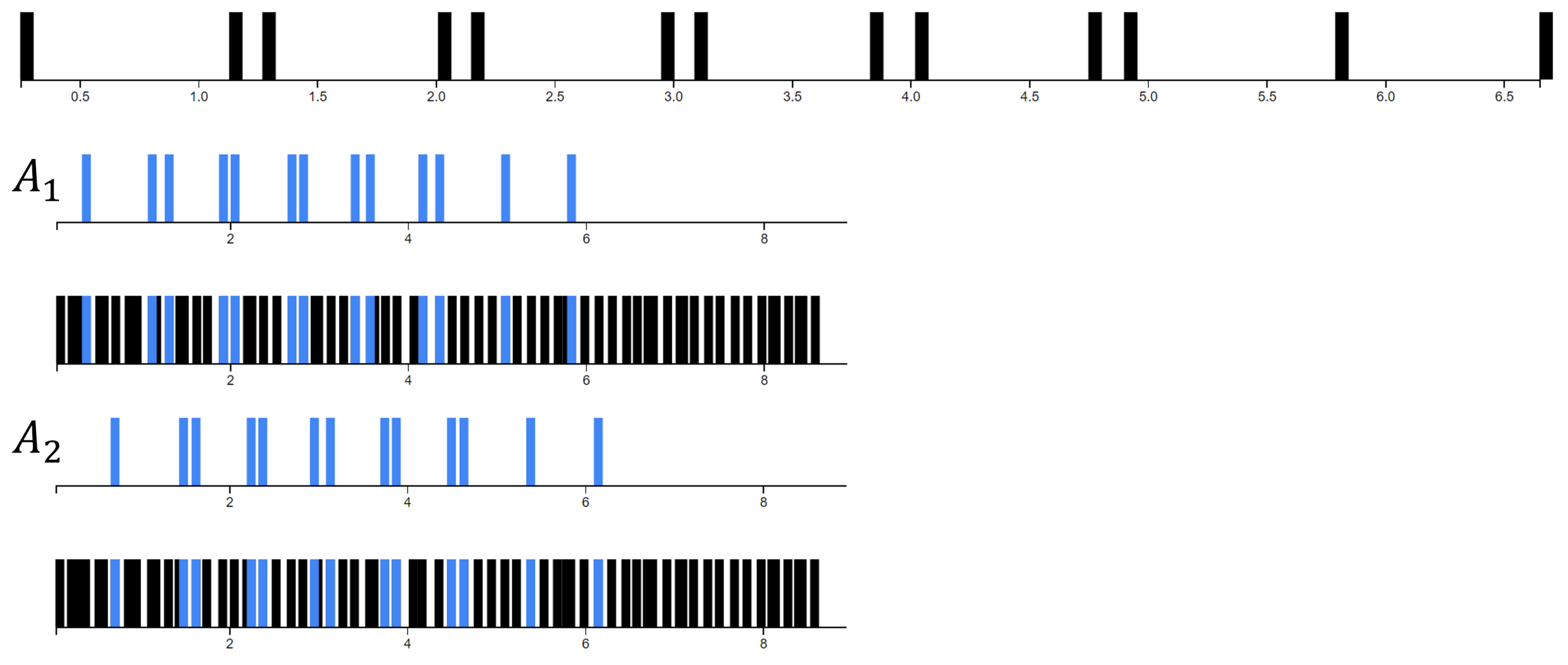
3.2. Experiment 2: Robustness of the Model to Timing and Tempo Variations
4. Scalability and Visualization
4.1. Scalability
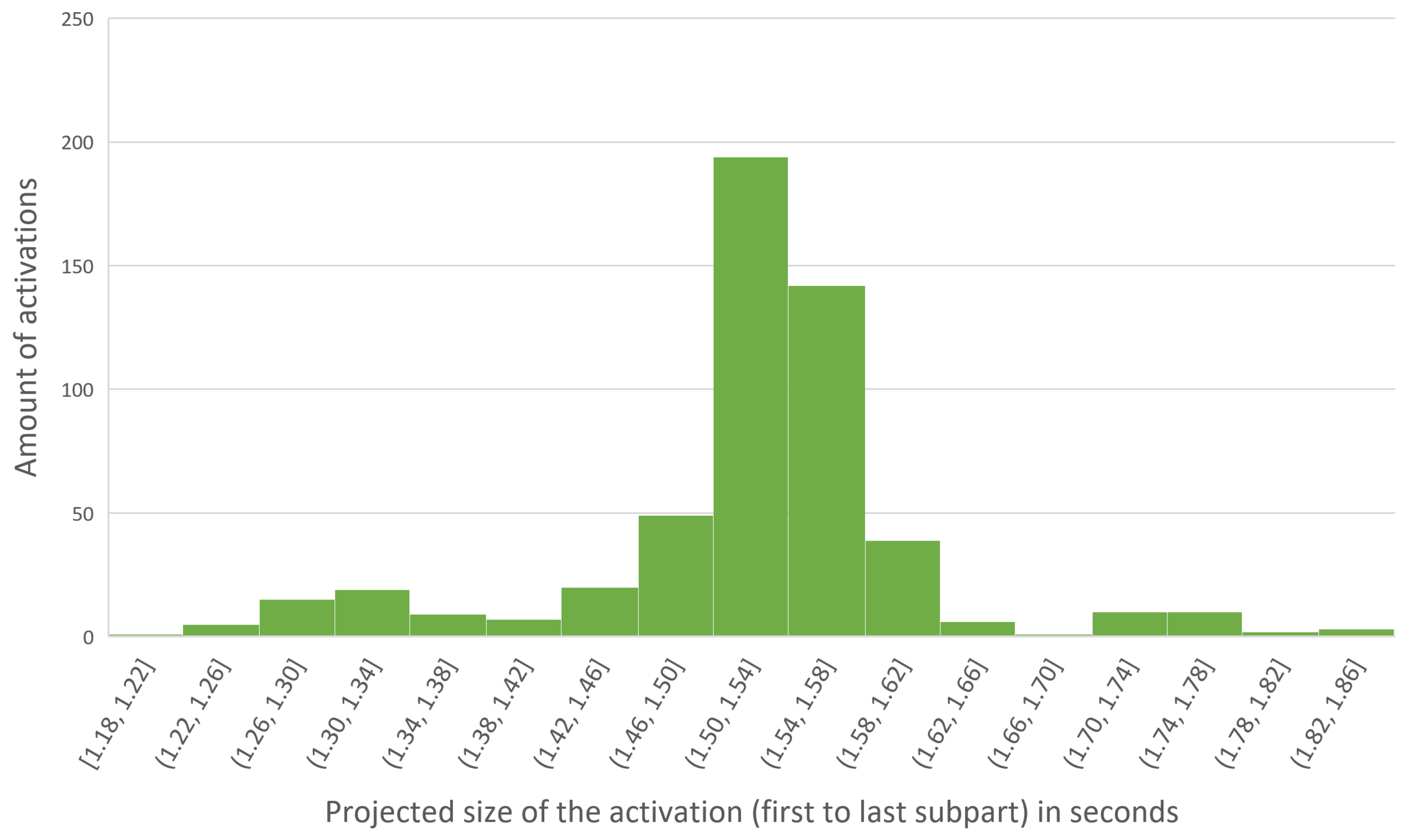
4.2. Visualizing the Patterns
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Brochard, R.; Abecasis, D.; Potter, D.; Ragot, R.; Drake, C. The “Ticktock” of Our Internal Clock: Direct Brain Evidence of Subjective Accents in Isochronous Sequences. Psychol. Sci. 2003, 14, 362–366. [Google Scholar] [CrossRef] [PubMed]
- Hansen, N.C.; Sadakata, M.; Pearce, M. Nonlinear Changes in the Rhythm of European Art Music: Quantitative Support for Historical Musicology. Music Percept. Interdiscip. J. 2016, 33, 414–431. [Google Scholar] [CrossRef]
- Toussaint, G.T. The Geometry of Musical Rhythm; Chapman and Hall/CRC: Boca Raton, FL, USA, 2016. [Google Scholar] [CrossRef]
- Bello, J.P.; Rowe, R.; Guedes, C.; Toussaint, G. Five Perspectives on Musical Rhythm. J. New Music Res. 2015, 44, 1–2. [Google Scholar] [CrossRef] [Green Version]
- Sachs, C. Rhythm and Tempo: An Introduction. Music. Q. 1952, 38, 384–398. [Google Scholar] [CrossRef]
- Downie, J.S. The music information retrieval evaluation exchange (2005–2007): A window into music information retrieval research. Acoust. Sci. Technol. 2008, 29, 247–255. [Google Scholar] [CrossRef] [Green Version]
- Dixon, S.; Gouyon, F.; Widmer, G. Towards Characterisation of Music via Rhythmic Patterns. In Proceedings of the International Conference on Music Information Retrieval (ISMIR), Barcelona, Spain, 10–14 October 2004; pp. 509–516. [Google Scholar]
- Esparza, T.M.; Bello, J.P.; Humphrey, E.J. From Genre Classification to Rhythm Similarity: Computational and Musicological Insights. J. New Music Res. 2015, 44, 39–57. [Google Scholar] [CrossRef]
- Böck, S.; Krebs, F.; Widmer, G. Accurate Tempo Estimation Based on Recurrent Neural Networks and Resonating Comb Filters. In Proceedings of the International Conference on Music Information Retrieval (ISMIR), Málaga, Spain, 26–30 October 2015; pp. 625–631. [Google Scholar]
- Bock, S. Submission to the MIREX 2018: BeatTracker. In Proceedings of the MIREX 2018, Paris, France, 23–27 September 2018; pp. 1–2. [Google Scholar]
- Bock, S.; Krebs, F. Submission to the MIREX 2018: DBNBeatTracker. In Proceedings of the MIREX 2018, Paris, France, 23–27 September 2018; pp. 1–2. [Google Scholar]
- Krebs, F.; Böck, S.; Widmer, G. Rhythmic pattern modeling for beat and downbeat tracking in musical audio. In Proceedings of the International Conference on Music Information Retrieval (ISMIR), Curitiba, Brazil, 4–8 November 2013; pp. 1–6. [Google Scholar]
- Huron, D. Tone and Voice: A Derivation of the Rules of Voice-Leading from Perceptual Principles. Music Percept. 2001, 19, 1–64. [Google Scholar] [CrossRef]
- Huron, D.B. Sweet Anticipation: Music and the Psychology of Expectation; MIT Press: Cambridge, MA, USA, 2006; p. 462. [Google Scholar]
- Abdallah, S.; Plumbley, M. Information dynamics: Patterns of expectation and surprise in the perception of music. Connect. Sci. 2009, 21, 89–117. [Google Scholar] [CrossRef] [Green Version]
- Sioros, G.; Davies, M.E.P.; Guedes, C. A generative model for the characterization of musical rhythms. J. New Music Res. 2018, 47, 114–128. [Google Scholar] [CrossRef]
- Foscarin, F.; Jacquemard, F.; Rigaux, P. Modeling and Learning Rhythm Structure. In Proceedings of the Sound & Music Computing Conference, Málaga, Spain, 28–31 May 2019. [Google Scholar]
- Simonetta, F.; Carnovalini, F.; Orio, N.; Rodà, A. Symbolic Music Similarity through a Graph-Based Representation. In Proceedings of the Audio Mostly 2018 on Sound in Immersion and Emotion—AM’18, Wrexham, UK, 12–14 September 2018; ACM Press: New York, NY, USA, 2018; pp. 1–7. [Google Scholar] [CrossRef] [Green Version]
- Temperley, D. A Unified Probabilistic Model for Polyphonic Music Analysis. J. New Music Res. 2009, 38, 3–18. [Google Scholar] [CrossRef]
- Temperley, D. Modeling Common-Practice Rhythm. Music Percept. Interdiscip. J. 2010, 27, 355–376. [Google Scholar] [CrossRef]
- Holzapfel, A. Relation Between Surface Rhythm and Rhythmic Modes in Turkish Makam Music. J. New Music Res. 2015, 44, 25–38. [Google Scholar] [CrossRef] [Green Version]
- London, J.; Polak, R.; Jacoby, N. Rhythm histograms and musical meter: A corpus study of Malian percussion music. Psychon. Bull. Rev. 2017, 24, 474–480. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Panteli, M.; Dixon, S. On the Evaluation of Rhythmic and Melodic Descriptors for Music Similarity. In Proceedings of the International Conference on Music Information Retrieval (ISMIR), New York, NY, USA, 7–11 August 2016; pp. 468–474. [Google Scholar]
- Pesek, M.; Leonardis, A.; Marolt, M. Robust Real-Time Music Transcription with a Compositional Hierarchical Model. PLoS ONE 2017, 12. [Google Scholar] [CrossRef] [PubMed]
- Pesek, M.; Leonardis, A.; Marolt, M. SymCHM—An Unsupervised Approach for Pattern Discovery in Symbolic Music with a Compositional Hierarchical Model. Appl. Sci. 2017, 7, 1135. [Google Scholar] [CrossRef] [Green Version]
- Pesek, M.; Žerovnik, M.; Leonardis, A.; Marolt, M. Modeling song similarity with unsupervised learning. In Proceedings of the Folk Music Analysis Workshop, Thessaloniki, Greece, 26–29 June 2018; pp. 1–3. [Google Scholar]
- Pesek, M.; Leonardis, A.; Marolt, M. A compositional hierarchical model for music information retrieval. In Proceedings of the International Conference on Music Information Retrieval (ISMIR), Taipei, Taiwan, 27–31 October 2014; pp. 131–136. [Google Scholar]
- Schluter, J.; Bock, S. Musical Onset Detection with Convolutional Neural Networks. In Proceedings of the 6th International Workshop on Machine Learning and Music, Held in Conjunction with the European Conference on Machine Learning and Principles and Practice of Knowledge Discovery in Databases, ECML/PKDD 2013, Prague, Czech Republic, 23 September 2013. [Google Scholar]
- Ren, I.Y.; Volk, A.; Swierstra, W.; Veltkamp, R.C. Analysis by Classification: A Comparative Study of Annotated and Algorithmically Extracted Patterns in Symbolic Music Data. In Proceedings of the International Conference on Music Information Retrieval (ISMIR), Paris, France, 23–27 September 2018; pp. 539–546. [Google Scholar]








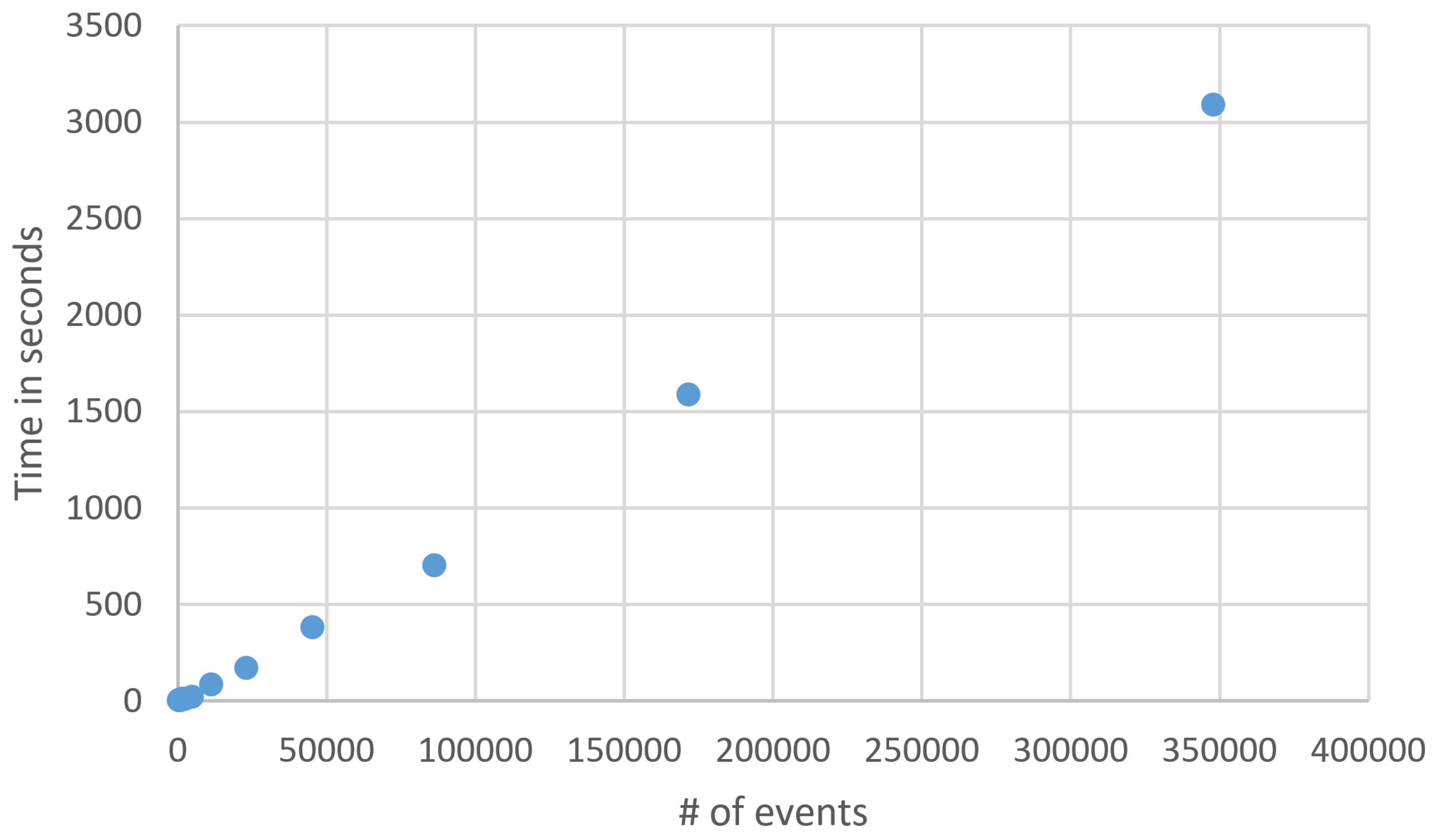

| # of Files | Time (s) | Events | # of Parts | |||||
|---|---|---|---|---|---|---|---|---|
| 2 | 3.77 | 389 | 2 | 6 | 9 | 10 | 9 | 36 |
| 4 | 5.16 | 660 | 3 | 10 | 9 | 9 | 10 | 41 |
| 8 | 10.43 | 1175 | 5 | 10 | 9 | 9 | 10 | 43 |
| 16 | 9.16 | 2307 | 3 | 10 | 9 | 8 | 9 | 39 |
| 32 | 20.13 | 4754 | 3 | 9 | 9 | 8 | 8 | 37 |
| 64 | 86.98 | 11,097 | 4 | 9 | 10 | 8 | 9 | 40 |
| 128 | 171.00 | 22,892 | 4 | 9 | 9 | 8 | 8 | 38 |
| 256 | 382.47 | 45,229 | 4 | 10 | 9 | 9 | 9 | 41 |
| 512 | 704.29 | 86,118 | 4 | 10 | 10 | 8 | 8 | 40 |
| 1024 | 1587.78 | 171,585 | 4 | 10 | 10 | 9 | 9 | 42 |
| 2048 | 3092.72 | 347,863 | 4 | 10 | 10 | 10 | 10 | 44 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pesek, M.; Leonardis, A.; Marolt, M. An Analysis of Rhythmic Patterns with Unsupervised Learning. Appl. Sci. 2020, 10, 178. https://doi.org/10.3390/app10010178
Pesek M, Leonardis A, Marolt M. An Analysis of Rhythmic Patterns with Unsupervised Learning. Applied Sciences. 2020; 10(1):178. https://doi.org/10.3390/app10010178
Chicago/Turabian StylePesek, Matevž, Aleš Leonardis, and Matija Marolt. 2020. "An Analysis of Rhythmic Patterns with Unsupervised Learning" Applied Sciences 10, no. 1: 178. https://doi.org/10.3390/app10010178
APA StylePesek, M., Leonardis, A., & Marolt, M. (2020). An Analysis of Rhythmic Patterns with Unsupervised Learning. Applied Sciences, 10(1), 178. https://doi.org/10.3390/app10010178






