Existence, Uniqueness and Stability of Market Equilibrium in Oligopoly Markets

Abstract

In this paper we build a pragmatic model on competition in oligopoly markets. To achieve this goal, we use an approach based on studying the response functions of each market participant, thus making it possible to address both Cournot and Bertrand industrial structures with a unified formal method. In contrast to the restrictive theoretical constructs of duopoly equilibrium, our study is able to account for real-world limitations like minimal sustainable production levels and exclusive access to certain resources. We prove and demonstrate that by using carefully constructed response functions it is possible to build and calibrate a model that reflects different competitive strategies used in extremely concentrated markets. The response functions approach makes it also possible to take into consideration different barriers to entry. By fitting to the response functions rather than the profit maximization of the payoff functions problem we alter the classical optimization problem to a problem of coupled fixed points, which has the benefit that considering corner optimum, corner equilibria and convexity condition of the payoff function can be skipped.

1. Introduction

Markets dominated by a small number of players are getting more common than ever. This process has been fueled by industry consolidation, rise in international expansion and natural desire to benefit from economies in scale, all resulting in a number of mergers and acquisitions that leave few companies dominating a particular market. Cournot in 1838, in Cournot (1897), was the first to build a complete model of a market where few players control the price and supply quantity of the goods being traded. The original model is able to correctly estimate equilibrium conditions provided that market participants comply with the following requirements:

(i)

There are two players each with sufficient market power to affect the price of the goods being sold;

(ii)

There is no product differentiation;

(iii)

Decisions on production output are taken simultaneously;

(iv)

There is no cooperation between market participants and each one reacts in a rational way, seeking to maximize its profit.

If the two companies are not necessarily rational, a different solution can be found as for example in (Rubinstein 2019; Ueda 2019).

Cournot’s approach is known nowadays as a static oligopoly model, which means that each company, participating in the oligopoly market considers the production of others to remain fixed at least for a given period of time, i.e., player i assumes that in time t the other participants produce the quantities that they have produced in time $t-1$. In the dynamic case, each company attempts to guess what change of production the other players will make in time t Cellini and Lambertini (2004).

Cournot’s duopoly model can be divided into two kinds—symmetric and asymmetric Sinha (2016). In the latter case, we consider an efficient company and a less-efficient one, producing homogeneous goods. Both are asymmetric in terms of their pre-innovation production costs. While both companies may have a fixed marginal cost of production, the efficient one has a lower cost $c_1$, and the less-efficient one has a higher cost $c_2$—where $c_1<c_2$. Companies still compete in quantities, as in Cournot’s duopoly. In the symmetric case both firms are equally efficient. It is important to note under which case a particular market falls, because asymmetric oligopoly may also end up dealing with products that are similar but of different quality. This is a question that falls beyond the scope of our study and we shall assume that there is no significant difference in the quality characteristics of the products produced and sold by each market participant.

Considering the demand, there are two distinct cases that have to be analyzed:

(i)

Demand is known and does not change. In this case the Cournot’s duopoly solution applies as it is.

(ii)

Demand may change over time. In the case, it is possible to reach a situation in which there is uncertainty about market equilibrium—as in Zapata et al. (2019).

We analyze a special case of Cournot’s duopoly in which the participating companies face different market demand in each of the scenarios.

A generalization of Cournot’s model is the Stackelberg duopoly Anderson and Engers (1992), where one firm is a leader and the other is a follower. This model is applicable when firms choose their output sequentially and not simultaneously. Cournot’s model and equilibrium are in fact the direct predecessor of Nash’s equilibrium point. Bertrand has introduced another kind of a duopoly model, where firms compete on prices rather than on outputs.

Contemporary markets can be subject to different regulations and barriers. Thus there are constraints applicable that influence the stability of market equilibrium and time required to reach it. We can summarize these constraints as:

(a)

The number of market participants;

Starting with the duopoly case in Cournot’s seminal work Cournot (1897) it is important to take into account the scalability of suggested solutions, due to the fact that there are various market structures in contemporary economics with high concentration and limited number of players.

(b)

The interdependence, availability, and access to information;

Companies operating in an environment with high concentration ratios (as measured by share of the largest participants compared to the total market volume) cannot take decisions in a completely isolated way. They need to take into account the effects their decisions have on the other participants, as well as their imminent reaction.

(c)

The price and non-price competition terms;

In order to account for the actual behavior of companies operating under oligopoly markets, it is necessary to take into consideration the non-price competition. In some cases, product differentiation may not exist (for example in the case of raw materials) but there may be loyalty schemes or aggressive advertisement campaigns that affect the equilibrium in an indirect way.

(d)

Consistency of behavior and time dependence of market conditions;

Solutions that consider time-dependency of company behavior and market changes Barbagallo and Cojocaru (2009) and Chan et al. (2018) are better able to describe contemporary oligopoly markets.

(e)

Market entry and exit barriers;

Entry and exit barriers can directly influence the number of companies operating on the oligopoly market. They also play an important role in shaping the decisions of each participant as barriers can be considered as additional limiting/boundary conditions.

(f)

Goals and profit maximization behavior;

We assume that profit maximization is the sole purpose of all market participants in the oligopoly markets. It is possible that there are periods of time, or even specific markets in which this is not the case (for example as described in Klemm 2004) and the resulting equilibrium is different. In the long term, economic agents would need to go back to profit maximization as they may be otherwise subject to acquisition or change in management.

(g)

Linear and non-linear changes in market conditions and firm behavior.

Taking into consideration these critical factors is very important in order to create a formal description of oligopoly markets that is adequate to the reality we live in.

Restraints could emerge as milestones at every production stage, at a different scale, size and intensity. Moreover, each of the restraints could influence each other, in a different direction and with different strength, and in parallel they could be influenced by the introduced production system and the existing market environment. The market is a vital substance, and the environment in which it functions and “breathes” would challenge the play of both actors, and could perform various scenarios of their action. Hence, these influences could affect the preliminary set up goals and price-polices of each of the observed players.

An extensive study on the oligopoly markets can be found in Bischi et al. (2010); Matsumoto and Szidarovszky (2018); Okuguchi (1976); Okuguchi and Szidarovszky (1990). Some recent results on Oligopoly markets are Alavifard et al. (2020); Geraskin (2020); Siegert and Ulbricht (2020); Strandholm (2020); Xiao and Wang (2020) and especially in duopoly markets Baik and Lee (2020); Liu and Sun (2020); Wang et al. (2020). All these items cannot be exhausted, even the published research on the subject in 2020. It is seen from the cited items that different techniques can be applied. We will present a different approach for the investigation of equilibrium in duopoly markets, based on the response functions, cyclic maps and coupled fixed (or best proximity) points.

2. Modeling Real-World Oligopoly Markets

Let us consider two companies that offer identical goods or services. These could range from health-care in a specific region to simple grocery delivery in a neighborhood. While the assumption for having homogeneous goods is quite restrictive, it helps to start with a simple model and then extend it by adding non-price competition and brand loyalty, to name a few extra factors. In support of the approach we have used, it should be noted that oligopoly markets with heterogeneous goods can be analyzed with the same instruments as the ones we employ. The only requirement is to define and estimate parameters of the response function of each market participant. In the case of identical goods it is much easier to do this. For complex products that include a variety of factors, such as positioning through non-price attributes, response functions may be harder to define and are often composite ones.

To investigate the existence and uniqueness of market equilibrium we employ game theory terminology. This is supported by the notion that company profits depend on its own output, as well as on the production of the other market participants. Under duopoly markets the result fits naturally into game theory basic cases of strategic interaction. Thus the static Cournot’s oligopoly is a fully rational game, based on the following assumptions:

(i)

Each company, in taking its optimal production decision rationally, must know before hand all its rival’s production and both firms should take their decisions simultaneously;

(ii)

Each firm has a perfect knowledge of the market demand function.

The dynamic model is a game in which case restrictive assumption (i) is replaced by some kind of expectation on the rivals’ outputs. While the simplest way is to use naive expectation that production or each market participant will remain at its most recent level, it is also possible to impose more realistic views as in McManus and Quandt (1961); Teocharis (1960). As a starting point, let us consider a situation in which there are two players ”A“ and ”B“ producing at moment $n+1$ goods $F(x_n,y_n)$ and $f(x_n,y_n)$, provided that at moment n they have produced $x_n$ and $y_n$ respectively. Such general notation does not yet imply anything regarding market participants. Depending on the functions $F(x_n,y_n)$ and $f(x_n,y_n)$ the model can be static or dynamic, as well as symmetric or asymmetric.

However in order to have market equilibrium, the pair $(x,y)$ should satisfy the equations $x=F(x,y)$ and $y=f(x,y)$.

Thus we will search for sufficient conditions, depending only on the response functions, that will ensure the existence and uniqueness of the equilibrium pair. Compared to the classical approaches in oligopoly markets, this way has several important advantages:

• It is possible to account for protective capacity present in contemporary production environments, which allows to have minimal (or even zero) marginal costs within some output ranges;
• It is possible to assess whether the marker can reach equilibrium, regardless of the initial position;
• And finally it is possible to assess the time necessary to reach equilibrium and whether this situation can remain stable.

3. The Basic Model

Let us first start with a duopoly model Friedman (2007) and Smith (1987)—two companies competing for the same consumers and striving to meet the demand with overall production of $Z=x+y$. The market price is defined as $P(Z)=P(x+y)$, which is the inverse of the demand function. Market players have cost functions $c_1(x)$ and $c_2(y)$, respectively. Assuming that both firms are acting rationally, the profit functions are ${\Pi }_1(x,y)=xP(x+y)-c_1(x)$ and ${\Pi }_2(x,y)=yP(x+y)-c_2(y)$ of the first and the second firm, respectively. The goal of each company is to maximize its profit, i.e., $max\{{\Pi }_1(x,y):x,\mathrm{assuming}\mathrm{that}y\mathrm{is}\mathrm{fixed}\}$ and $max\{{\Pi }_2(x,y):y,\mathrm{assuming}\mathrm{that}x\mathrm{is}\mathrm{fixed}\}$. Provided that functions P and $c_i$, $i=1,2$ are differentiable, we get the equations

$$\left|\begin{array}{c}\frac{\partial {\Pi }_1(x,y)}{\partial x}=P(x+y)+x{P}^{\prime }(x+y)-c_1^{\prime }(x)=0\hfill \\ \frac{\partial {\Pi }_2(x,y)}{\partial y}=P(x+y)+y{P}^{\prime }(x+y)-c_2^{\prime }(y)=0.\hfill \end{array}\right.$$

(1)

The solution of (1) presents the equilibrium pair of production in the duopoly market Friedman (2007); Smith (1987).

Often Equations (1) have solutions in the form of $x=b_1(y)$ and $y=b_2(x)$, which are called response functions (Friedman 2007).

It may turn out difficult or impossible to solve (1) thus it is often advised to search for an approximate solution. Another drawback, when searching for an approximate solution is that it may not be stable. Fortunately we can find an implicit formula for the response function in (1) i.e.,

$$x=\frac{c_1^{\prime }(x)-P(x+y)}{P^{\prime }(x+y)}=F(x,y)\mathrm{and}y=\frac{c_2^{\prime }(y)-P(x+y)}{P^{\prime }(x+y)}=f(x,y).$$

It is still possible that we may end up with response functions, that do not lead to maximization of the profit $\Pi$. As it is often assumed, each participant response depends on its own production level and that of the pother payers. For example, if at a moment n the output quantities are $(x_n,y_n)$, and the first player changes its productions to $x_{n+1}=F(x_n,y_n)$, then the second one will also change its output to $y_{n+1}=f(x_n,y_n)$. We will define the iterated sequence ${\{(x_n,y_n)\}}_{n=1}^{\infty }$ in the Appendix A in Definition A5. We have an equilibrium if there are two productions x and y, such that $x=F(x,y)$ and $y=f(x,y)$. The functions ${\Pi }_i$ are called payoff functions. To ensure that the solutions of (1) will present a maximization of the payoff functions, a sufficient condition is that ${\Pi }_i$ are concave functions Bischi et al. (2010); Matsumoto and Szidarovszky (2018); Okuguchi and Szidarovszky (1990), by using of response function we alter the maximization problem into a coupled fixed point one thus all assumptions of concavity and differentiability can be skipped. The problem of solving the equations $x=F(x,y)$ and $y=f(x,y)$ is the problem of finding coupled fixed points for an ordered pair of maps $(F,f)$ Guo and Lakshmikantham (1987). Yet an important limitation may be that players cannot change the output too fast and thus the player may not perform to maximize their profits.

Focusing on response functions, allows to put together Cournot and Bertand models. Indeed let the first company have reaction be $F(X,Y)$ and the second one $f(X,Y)$, where $X=(x,p)$ and $Y=(y,q)$. Here x and y denote the output quantity and $(p,q)$ are the prices set by players. In this case companies can compete in terms of both price and quantity.

4. Existence and Uniqueness in Duopoly Models

In the case of two major players taking all or most of the market, we need to consider special cases depending on intersection of production set. The situation in which production sets of both companies have an empty intersection may seem extreme, but it is not impossible. For example if one of the companies is working at a very large scale it may simply be impractical to sustain a low level of output. On the other hand, if the company is just too small to undertake large projects it may also happen that expanding its production beyond a certain limit is not feasible. Therefore, it is possible that long term contracts or technical issues prohibit a certain type of action and impose special limitations. The mathematical justifications of the results are presented in Appendix A.

4.1. Players’ Production Sets Have a Nonempty Intersection

Assumption 1.

Let there be a duopoly market, satisfying the following assumptions:

(1) 

The two firms are producing homogeneous goods that are perfect substitutes.

(2) 

The first firm can produce qualities from the set $A_x$ and the second firm can produce qualities from the set $A_y$, where $A_x$ and $A_y$ be closed, nonempty subsets of a complete metric space $(X,\rho )$.

(3) 

Let there exist a closed subset $D\subseteq A_x\times A_y$ and maps $F:D\to A_x$ and $f:D\to A_y$, such that $(F(x,y),f(x,y))\subseteq D$ for every $(x,y)\in D$, be the response functions for firm one and two respectively.

(4) 

Let there exist $\alpha ,\beta ,\gamma ,\delta >0$, $max\{\alpha +\gamma ,\beta +\delta \}<1$, such that the inequality

$$\rho (F(x,y),F(u,v))+\rho (f(z,w),f(t,s))\le \alpha \rho (x,u)+\beta \rho (y,v)+\gamma \rho (z,t)+\delta \rho (w,s)$$

(2)

holds for all $(x,y),(u,v),(z,w),(t,s)\in A_x\times A_y$.

Then

(I)

There exists a unique pair $(\xi ,\eta )$ in D, such that $\xi =F(\xi ,\eta )$ and $\eta =f(\xi ,\eta )$, i.e., a market equilibrium pair. Moreover the iteration sequences ${\{x_n\}}_{n=0}^{\infty }$ and ${\{y_n\}}_{n=0}^{\infty }$, defined in Definition A5 converge to $\xi$ and $\eta$ respectively.

(II)

A priori error estimates hold

$$max\left\{\rho (x_n,\xi ),\rho (y_n,\eta )\right\}\le \frac{k^n}{1-k}(\rho (x_1,x_0)+\rho (y_1,y_0));$$

(3)

(III)

A posteriori error estimates hold

$$max\left\{\rho (x_n,\xi ),\rho (y_n,\eta )\right\}\le \frac{k}{1-k}(\rho (x_{n-1},x_n)+\rho (y_{n-1},y_n));$$

(4)

(IV)

The rate of convergence for the sequences of successive iterations is given by

$$\rho (x_n,\xi )+\rho (y_n,\eta )\le k\left(\rho (x_{n-1},\xi )+(y_{n-1},\eta )\right),$$

(5)

where $k=max\{\alpha +\gamma ,\beta +\delta \}$.

If in addition $f(x.y)=F(y,x)$ then the coupled fixed point $(x,y)$ satisfies $x=y$.

The proof is a direct consequence of Theorem A1.

Remark 1.

Let the two players have one and the same response function. That is if player one has a production x and player two has a production y then the first player reaction will be $F(x,y)$ and the second player reaction will be $f(x,y)=F(y,x)$. It follows that the equilibrium pair $(x,y)$ will satisfy $x=y$, i.e., both firms will have equal production. This means that if both firms have one and the same technology, one and the same knowledge on the market that will affect to one and the same response functions, then the equilibrium will be reached at the level of equal productions.

4.2. Equilibrium, When Players’ Production Sets Have a Nonempty Intersection

Let us consider a duopoly market. Let the two firms produce qualities from the set $A_x$ and the second firm can produce qualities from the set $A_y$, where $A_x$ and $A_y$ are nonempty subsets of a complete metric space $(X,\rho )$. Any of the firms can produce a bundle of products $x=(x_1,x_2,\cdots x_n)\in X$. Assumption 1 ensures the existence and uniqueness of the production bundles $(x_1,x_2,\cdots x_n),(y_1,y_2,\cdots y_n)\in X$ of n-goods, that present the equilibrium in a duopoly economy.

4.2.1. A Linear Case, When Each Player Is Producing a Single Product, Goods Being Perfect Substitutes

Let us consider a market with two competing firms, each firm producing just one product, and both goods are perfect substitutes. Let the two firms produce quantities $x\in A_x$ and $y\in A_y$, respectively, where $A_x,A_y\subset [0,+\infty )$ and $(X,\rho )$ be the complete metric space $(\mathbb{R},|·|)$. Let us consider the response functions of player one $F(x,y)=a-s-px-qy$ and player two $f(x,y)=a-r-\mu y-\nu x$, where

(1)

$a,s,r,p,q,\mu ,\nu >0$, $s<a$, $r<a$, $max\{p+\mu ,q+\nu \}<1$

(2)

$A_x=\left[0,\frac{a-s}{p}\right]\cap \left[0,\frac{a-r}{\mu }\right]$ and $A_y=\left[0,\frac{a-s}{q}\right]\cap \left[0,\frac{a-r}{\nu }\right]$

(3)

D can be defined in three ways:

(3a)

$D=\left[0,\frac{a\mu -aq-s\mu -qr}{\mu p-\nu q}\right]\times \left[0,\frac{ap-a\nu +s\nu -pr}{\mu p-\nu q}\right]$, provided that

$$a-s\le \frac{a\mu -aq-s\mu -qr}{\mu p-\nu q}\mathrm{and}a-r\le \frac{ap-a\nu +s\nu -pr}{\mu p-\nu q}$$

(3b)

$D=\left[0,a-s\right]\times \left[0,a-r\right]$, provided that $\mu r+\nu s-a\mu -a\nu +a-r>0$ and $ps+qr-ap-aq+a-s>0$

(3c)

$D=\left\{\begin{array}{c}{\displaystyle 0\le x\le \frac{a-s}{p}}\hfill \\ {\displaystyle 0\le y\le \frac{a-r-\mu x}{\nu }.}\hfill \end{array}\right.$

It is easy to check that $F:D\subset A_x\times A_y\to A_x$, $f:D\subset A_x\times A_y\to A_y$ and $(F(D),f(D))\subseteq D$.

Indeed let us consider case (3a). From the assumptions that $a,s,r,p,q,\mu ,\nu >0$ we get

$$F(x,y)\le F(0,0)=a-s\le \frac{a\mu -aq+s\mu -qr}{\mu p-\nu q},$$

$$F(x,y)\ge F\left(\frac{a\mu -aq+s\mu -qr}{\mu p-\nu q},\frac{ap-a\nu +s\nu -pr}{\mu p-\nu q}\right)=0,$$

and

$$f(x,y)\le f(0,0)=a-r\le \frac{ap-a\nu +s\nu -pr}{\mu p-\nu q},$$

$$f(x,y)\ge f\left(\frac{a\mu -aq+s\mu -qr}{\mu p-\nu q},\frac{ap-a\nu +s\nu -pr}{\mu p-\nu q}\right)=0.$$

Therefore $F:D\to A_x$, $f:D\to A_y$ and $(F(D),f(D))\subseteq D$.

It can be proven in a similar fashion that $(F(D),f(D))\subseteq D$ and for the cases (3b) and (3c).

From the inequalities

$$\left|F(x,y)-F(u,v)\right|=\left|p(x-u)+q(y-v)\right|\le p|x-u|+q|y-v|$$

and

$$\left|f(z,w)-f(t,s)\right|=\left|\mu (z-t)+\nu (w-s)\right|\le \mu |z-t|+\nu |w-s|$$

it follows that

$$\left|F(x,y)-F(u,v)\right|+\left|f(z,w)-f(t,s)\right|\le p|x-u|+q|y-v|+\mu |z-t|+\nu |w-s|$$

and thus the ordered pair $(F,f)$ satisfies Assumption 1 with constants $\alpha =p$, $\beta =q$, $\gamma =\mu$, $\delta =\nu$, because $max\{p+\mu ,q+\nu \}<0$. Consequently there exists an equilibrium pair $(x,y)$ and for any initial start in the economy the iterated sequences $(x_n,y_n)$ converge to the market equilibrium $(x,y)$. The equilibrium pair is

$$x=\frac{a\mu -aq-s\mu +qr+a-s}{\mu p-\nu q+\mu +p+1},y=\frac{ap-a\nu +s\nu -pr-a+r}{\mu p-\nu q+\mu +p+1}.$$

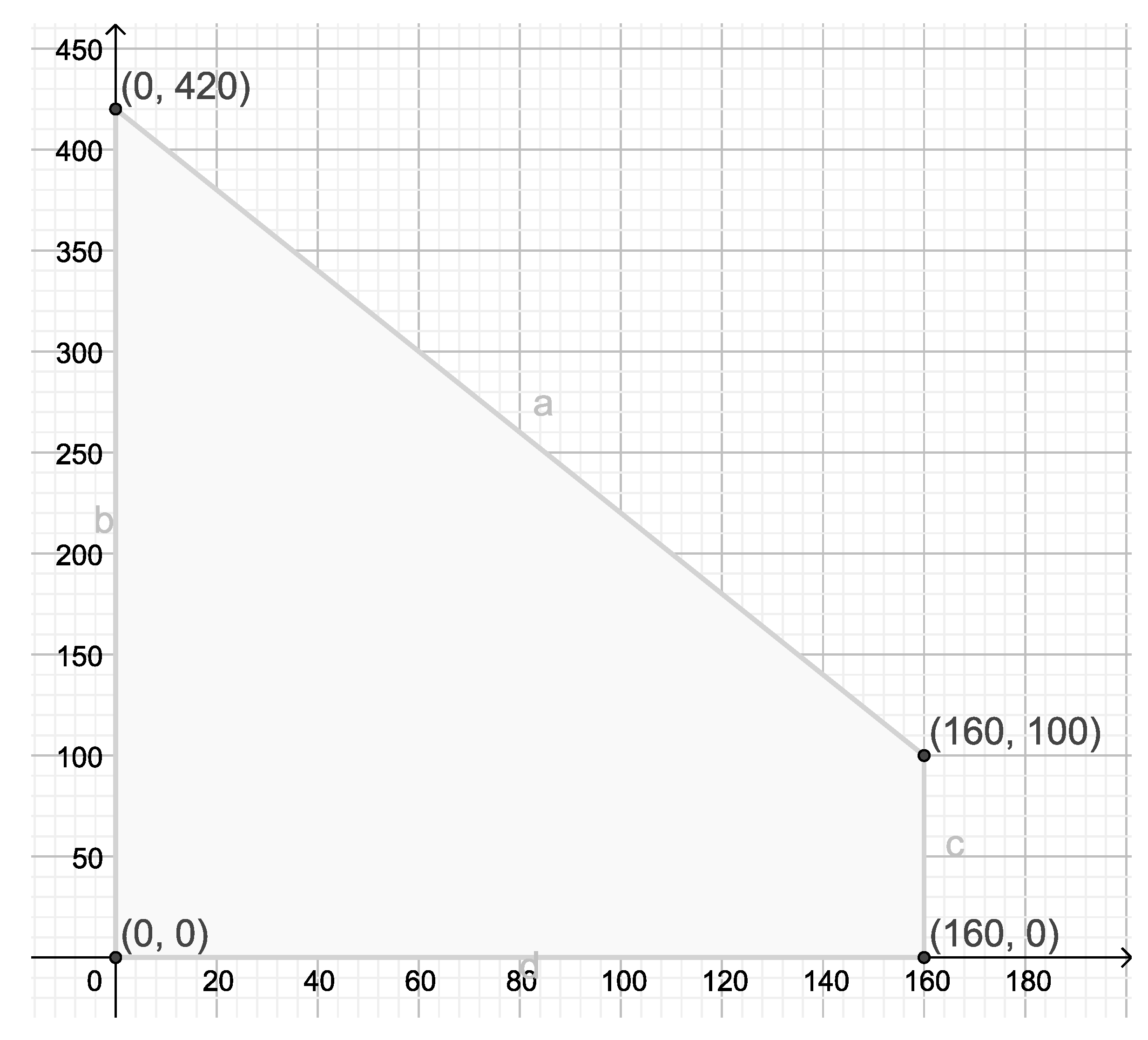
Let us consider a particular case: $a=100$, $s=20$, $r=30$, $p=\frac{1}{2}$, $q=\frac{1}{8}$, $\mu =\frac{1}{3}$, $\nu =\frac{1}{6}$.

Values selected for this case are arbitrarily chosen with only general conditions in mind. However, in an actual situation the values of p, q, $\mu$ and $\nu$ reflect the actual management and marketing policy of the market participants.

In this case $F(x,y)=80-\frac{x}{2}-\frac{y}{8}$, $f(x,y)=70-\frac{x}{3}-\frac{y}{6}$, $A_x=[0,210]$, $A_y=[0,320]$. The subset D can be considered either $D=[0,110]\times [0,200]$ (3a) or $D=\{0\le x\le 160,0\le y\le 420-2x\}$ (3c) (see Figure 1).

We get in this case that the equilibrium pair of the production of the two firms is $(49.51,45.85)$ and the total production will be $x+y=95.36$. Values of the iterated sequence are presented in

Table 1. Values of the iterated sequence $(x_n,y_n)$ if started with $(40,60)$.

n	0	1	2	5	10	20	30
$x_n$	40	52.5	47.92	49.85	49.49	49.51205	49.51219
$y_n$	60	46.6	44.72	46.11	45.83	45.85354	45.85366

and numbers of iterations needed for the a priori and a posteriori error estimate are shown in

Table 2. Number n of iterations needed by the a priori estimate if stared with $(100,20)$.

$\epsilon$	0.1	0.01	0.001	0.0001	0.00001
n	41	53	66	79	91

and

Table 3. Number n of iterations needed by the a posteriori estimate if started with $(100,20)$.

$\epsilon$	0.1	0.01	0.001	0.0001	0.00001
n	14	18	23	27	32

, respectively.

To get the data to fill the above tables and the tables in the forthcoming examples we use Maple 2016 software.

Let us consider a classic example, where the price function is linear and so are the cost functions of both players. Assuming the feasible market price is defined by $P(x,y)=120-x-y$, it is expected that additional output x from the first company as well as extra production y of the second one will cause a decrease in prices. Therefore under equilibrium conditions $x+y$ will be the total production of the two firms and it will also be reflected in prices. Let the two firms have cost functions equal to $30x$ and $20y$, respectively. The profit of the first one is

$${\Pi }_1(x,y)=xP(x,y)-30x=x(120-x-y)-30x=90x-x^2-xy$$

and the profit of the second one is

$${\Pi }_2(x,y)=yP(x,y)-20y=y(120-x-y)-20y=100y-y^2-xy.$$

Following the Cournot model after solving (1) we get the response functions $F:D\to A_x$ and $f:D\to A_y$ of the two firms $F(y)=\frac{90-y}{2}$ and $f(x)=\frac{100-x}{2}$, where $A_y=[0,90]$, $A_x=[0,100]$ and $D=A_x\times A_y$. Consequently it is a special case of the general example with $a=60$, $s=15$, $r=10$, $p=0$, $q=\frac{1}{2}$, $\mu =\frac{1}{2}$, $\nu =0$.

It is possible to find the constants in this case with the help of some Computer Algebra System (CAS), such as Maple, MathLab, MathCad or Mathematica. We will illustrate it by using Maple 2016. Writing the command

$$solve\left(\left\{\left|\frac{90-y}{2}-\frac{90-v}{2}\right|\le p|y-v|,0\le y\le 90,0\le v\le 90\right\},a\right);$$

the software returns that $p\ge \frac{1}{2}$. The same result can be obtained and for the inequality $|f(x)-f(u)|\le \mu |x-u|$. Unfortunately when trying to solve the forthcoming more complicated examples Maple was not of good use, therefore we have preferred to use some of the classical inequalities and to make the calculations by hand.

Thus there exists an equilibrium pair $(x,y)$ and for any initial start in the economy where iterated sequences $(x_n,y_n)$ converge to the market equilibrium $(x,y)$. We estimate in this case that the equilibrium pair of the production is $(80/3,110/3)$ and the total output will be $a=190/3$.

Let us assume that the two firms have started with output $x_0=40$ and $y_0=60$. In the following table (see

Table 4. Values of the iterated sequence $(x_n,y_n)$ if started with $(40,60)$.

n	0	1	2	5	10	20
$x_n$	40	15	30.0	25.94	26.68	26.67
$y_n$	60	30	42.5	36.25	36.69	36.67

) we present how, depending on the response functions F and f the output of each company will change.

Let us assume that the two firms have started from productions $x_0=100$ and $y_0=20$. In the next table (see

Table 5. Values of the iterated sequence $(x_n,y_n)$ if started with $(100,20)$.

n	0	1	2	5	10	20
$x_n$	100	35	45.0	27.19	26.74	26.67
$y_n$	20	0	32.5	34.38	36.65	36.67

) we present how using the response functions F and f the productions of the two firms will change.

Numbers of iterations needed for the a priori and a posteriori error estimate are shown in

Table 6. Number n of iterations needed by the a priori estimate if started with $(100,20)$.

$\epsilon$	0.1	0.01	0.001	0.0001	0.00001
n	11	15	18	21	25

and

Table 7. Number n of iterations needed by the a posteriori estimate if started with $(100,20)$.

$\epsilon$	0.1	0.01	0.001	0.0001	0.00001
n	11	15	18	21	25

are presented in the case $(x_0=100,y_0=20)$, respectively.

4.2.2. A Nonlinear Case, When Each Player Is Producing a Single Product, While Goods Sold Are Perfect Substitutes

Let us consider a market with two competing firms, producing perfect substitute products with quantities $x\in A_x$ and $y\in A_y$, respectively, where $A_x,A_y\subset [0,+\infty )$ and $(X,\rho )$ is the complete metric space $(\mathbb{R},|·|)$. Let us assume that each firm produces at least one item, i.e., $x,y\ge 1$. Let us consider the response functions of player one $F(x,y)=\frac{90-x-\frac{y}{8}-\frac{\sqrt{y}}{2}}{2}$ and player two $f(x,y)=\frac{100-\frac{x}{4}-y-\sqrt{x}}{3}$, where

• $A_x=[1,44]$ and $A_y=[1,33]$
• D can be defined as $D=A_x\times A_y$

It is easy to check that $F:D=A_x\times A_y\to A_x$, $f:D=A_x\times A_y\to A_y$ and $(F(D),f(D))\subseteq D$.

Indeed, we get

$$F(x,y)\le F(1,1)=44,F(x,y)\ge F\left(44,33\right)=13.31$$

and

$$f(x,y)\le f(1,1)=32.33<33,f(x,y)\ge f\left(44,33\right)=5.46$$

and therefore $F:D\to A_x$, $f:D\to A_y$ and $(F(D),f(D))\subseteq D$.

There exists $\xi$ between the points y and v so that there holds $\left|\sqrt{y}-\sqrt{v}\right|=\frac{1}{2\sqrt{\xi }}|y-v|$. From the assumption that $y,v\ge 1$ we get that $\left|\sqrt{y}-\sqrt{v}\right|\le \frac{1}{2}|y-v|$. Using this last inequality we obtain

$$\left|F(x,y)-F(u,v)\right|\le \frac{1}{2}\left|x-u\right|+\frac{1}{16}\left|y-v\right|+\frac{1}{8}\left|y-v\right|=\frac{1}{2}\left|x-u\right|+\frac{3}{16}\left|y-v\right|$$

and

$$\left|f(z,w)-f(t,s)\right|\le \frac{1}{12}\left|z-t\right|+\frac{1}{3}\left|w-s\right|+\frac{1}{6}\left|w-s\right|=\frac{1}{12}\left|z-t\right|+\frac{1}{2}\left|w-s\right|.$$

Therefore

$${\displaystyle \left|F(x,y)-F(u,v)\right|+\left|f(z,w)-f(t,s)\right|\le \frac{1}{2}\left|x-u\right|+\frac{3}{16}\left|y-v\right|+\frac{1}{12}\left|z-t\right|+\frac{1}{2}\left|w-s\right|}$$

and thus the ordered pair $(F,f)$ satisfies Assumption 1 with constants $\alpha =1/2$, $\beta =3/16$, $\gamma =1/12$ and $\delta =1/2$, $max\{1/2+1/12,3/16+1/2\}=max\{7/12,11/16\}=7/12$. Consequently there exists an equilibrium pair $(x,y)$ and for any initial start in the economy the iterated sequences $(x_n,y_n)$ converge to the market equilibrium $(x,y)$. We get in this case that the equilibrium pair of the production of the two firms is $(28.3,21.9)$ (see

Table 8. Values of the iterated sequence $(x_n,y_n)$ if started with $(10,50)$.

n	0	1	2	5	10	20	30
$x_n$	10	35.10	25.56	28.61	28.29	28.30747	28.30750
$y_n$	50	14.77	23.50	21.99	21.89	21.90064	21.90066

) and the total production will be $a=50.2$. Number of the needed iterations is presented in

Table 9. Number n of iterations needed by the a priori estimate if started with $(10,50)$.

$\epsilon$	0.1	0.01	0.001	0.0001	0.00001
n	39	50	62	73	84

and

Table 10. Number n of iterations needed by the a posteriori estimate if started with $(10,50)$.

$\epsilon$	0.1	0.01	0.001	0.0001	0.00001
n	12	16	20	24	28

.

If we try to solve the system of equations $x=F(x,y)$ and $y=f(x,y)$ from the previous section, where for example $F(x,y)=80-\frac{x}{2}-\frac{y}{8}$ and $f(x,y)=70-\frac{x}{3}-\frac{y}{6}$, with the help of Maple then we will get the exact result. Unfortunately when the response functions are not linear the software can give us just some approximation. No information is available about the uniqueness and the stability of the solution. The same observations have been made in Zlatanov (2021), the exact solution is possible to find with the help of the theory of coupled best proximity points, but the approximation solution, regardless of the precision, is never the exact one.

Let us consider again a case with two players, producing two products, but let them know the market demand function and behave rational, i.e., they are trying to maximize their profits, assuming that the rival player will do the same.

Let there be no limit on the market, but let us assume that the total consumption is $100\%$. That is, the market will consume a constant 1, which is $100\%$, and the production of both firms will be a percentage of the consumption x and y, respectively, i.e., $x,y\in [0,1]$. Let the market price be defined by $P(x,y)=1-\frac{x+y}{2}-\frac{x^2+y^2}{24}$, where x is the production of one of the firms, y is the production of the other one, assuming that number 1 presents $100\%$. Let the two firms have cost functions equal to $C_x(x)=x/2+x^2/16$ and $y/6+y^2/12$, respectively. The profit of the first firm is

$${\Pi }_1(x,y)=xP(x,y)-C_x(x)=\frac{7x}{8}-\frac{9x^2}{16}-\frac{xy}{2}-\frac{x^3}{24}-\frac{x{y}^2}{24}$$

and the profit of the second firm is

$${\Pi }_2(x,y)=yP(x,y)-C_y=\frac{5y}{6}-\frac{13y^2}{24}-\frac{xy}{2}-\frac{y^3}{24}-\frac{x^{2}y}{24}.$$

Following Cournot model after solving (1) we get the response functions F and f of the two players

$$F(x,y)=\frac{7}{8}-\frac{x}{8}-\frac{y}{2}-\frac{x^2}{8}-\frac{y^2}{24}\mathrm{and}f(x,y)=\frac{5}{6}-\frac{x}{2}-\frac{y}{12}-\frac{y^2}{8}-\frac{x^2}{24},$$

which satisfy $F:[0,1]\times [0,1]\to [0,1]$ and $f:[0,1]\times [0,1]\to [0,1]$, i.e., $D=[0,1]\times [0,1]$. Using the inequality $|x^2-y^2|=2\xi |x-y|\le 2|x-y|$, for any $x,y\in [0,1]$ and some $\xi$ between x and y we obtain

$$\left|F(x,y)-F(u,v)\right|\le \frac{3}{8}|x-u|+\frac{7}{12}|y-v|$$

and

$$\left|f(z,w)-f(s,t)\right|\le \frac{7}{12}|z-t|+\frac{7}{24}\left|w-s\right|.$$

Therefore

$${\displaystyle \left|F(x,y)-F(u,v)\right|+\left|f(z,w)-f(s,t)\right|\le \frac{3}{8}\left|x-u\right|+\frac{7}{12}|y-v|+\frac{7}{12}|z-s|+\frac{7}{24}\left|w-t\right|}$$

and thus the ordered pair $(F,f)$ satisfies Assumption 1 with constants $\alpha =3/8$, $\beta =7/12$, $\gamma =7/12$ and $\delta =7/24$. There holds $max\{\alpha +\gamma ,\beta +\delta \}<0.958$. Thus there exists an equilibrium pair $(x,y)$ and for any initial start in the economy the iterated sequences $(x_n,y_n)$ converge to the market equilibrium $(x,y)$. We get in this case that the equilibrium pair of the production of the two firms is $(0.537,0.451)$, i.e., the first firm will have a share of $53.7\%$ and the second one a share of $45.1\%$ of the sold goods (see

Table 11. Values of the iterated sequence $(x_n,y_n)$ if started with $(50\%,50\%)$.

n	0	1	2	5	10	20
$x_n$	50%	51.8%	53.3%	53.66%	53.735%	53.732%
$y_n$	50%	46.4%	45.9%	45.17%	45.184%	45.181%

if the starting point is $(50\%,50\%)$,

Table 12. Values of the iterated sequence $(x_n,y_n)$ if started with $(10\%,90\%)$.

n	0	1	2	5	10	20
$x_n$	10%	34.6%	49.2%	53.16%	53.749%	53.732%
$y_n$	90%	58.4%	52.4%	45.19%	45.201%	45.181%

if the starting point is $(10\%,90\%)$ and

Table 13. Values of the iterated sequence $(x_n,y_n)$ if started with $(100\%,0\%)$.

n	0	1	2	5	10	20
$x_n$	100%	66.6%	61.4%	53.68%	53.757%	53.732%
$y_n$	0%	25.0%	40.6%	44.55%	45.201%	45.181%

if the starting point is $(100\%,0\%)$). The total production will be $0.989$, i.e., $98.9\%$ of the total demand of the market.

4.2.3. Each Player Is Producing Two Product Types, Goods from Each Type Being Perfect Substitutes

Let us consider a market with two competing firms, and each firm is producing two product types. For simplicity we assume that goods from each type produced by major players are perfect substitutes. While it is possible that two types have nothing it common, it still means that within each type customers can freely replace a product from the first company with one manufactured by the second one. Let us assume that each firm produces at least one item from each product, i.e., $x=(x_1,x_2),y=(y_1,y_2),x_1,x_2,y_1,y_2\ge 1$. Let us denote the production of the two players by $x=(x_1,x_2)$ and $y=(y_1,y_2)$, respectively.

Let the market of the two goods be endowed with the p norm, $p\in [1,\infty )$, i.e.,

$$\rho ((x_1,x_2),(y_1,y_2))={\parallel (x_1,x_2)-(y_1,y_2)\parallel }_p={\left(|x_1-y_1{|}^p+{|x_2-y_2|}^p\right)}^{1/p}.$$

Let us consider the response functions $F(x,y)=(F_1(x,y),F_2(x,y))$ and $f(x,y)=(f_1(x,y),f_2(x,y))$ defined by

$$F(x,y)=\left\{\begin{array}{c}{\displaystyle \frac{{\displaystyle 90-\frac{x_1+x_2}{2}-\frac{y_1+y_2}{3}}}{3},}\hfill \\ {\displaystyle \frac{{\displaystyle 90-\frac{x_1+x_2}{2}-\frac{y_1+y_2}{3}}}{3};}\hfill \end{array}\right.f(x,y)=\left\{\begin{array}{c}{\displaystyle \frac{{\displaystyle 100-\frac{x_1+x_2}{4}-\frac{y_1+y_2}{3}}}{4}}\hfill \\ {\displaystyle \frac{{\displaystyle 100-\frac{x_1+x_2}{4}-\frac{y_1+y_2}{3}}}{4}.}\hfill \end{array}\right.$$

where

• $A_x=[0,30]\times [0,30]$ and $A_y=[0,25]\times [0,25]$
• $D=[0,30]\times [0,30]\times [0,25]\times [0,25]$

It is easy to see that $(F(x,y),f(x,y))\subseteq D$, whenever $(x,y)=((x_1,x_2),(y_1,y_2))\in D$.

Using the inequality $\frac{a+b}{2}\le \frac{{(a^p+b^p)}^{1/p}}{2^{1/p}}$, which holds for any $a,b\ge 0$ we get the chain of inequalities

$$\begin{array}{ccc}{∥F(x,y)-F(u,v)∥}_p\hfill & =\hfill & {∥\left(F_1(x,y),F_2(x,y)\right)-\left(F_1(u,v),F_2(u,v)\right)∥}_p\hfill \\ & =\hfill & {∥\left(\frac{\frac{(u_1+u_2)-(x_1+x_2)}{2}+\frac{v_1+v_2-(y_1+y_2)}{3}}{3},\frac{\frac{(u_1+u_2)-(x_1+x_2)}{2}+\frac{v_1+v_2-(y_1+y_2)}{3}}{3}\right)∥}_p\hfill \\ & \le \hfill & \frac{2}{3}\left(\frac{|u_1-x_1|+|u_2-x_2|}{2}+\frac{|v_1-y_1|+|v_2-y_2|}{3}\right)=\frac{2}{3}\frac{|u_1-x_1|+|u_2+x_2|}{2}+\frac{4}{9}\frac{|v_1-y_1|+|v_2+y_2|}{2}\hfill \\ & \le \hfill & \frac{2^{\frac{p-1}{p}}}{3}{\left(|x_1-u_1{|}^p+{|x_2-y_2|}^p\right)}^{1/p}+\frac{2^{\frac{p-1}{p}+1}}{9}{\left(|y_1-v_1{|}^p+{|y_2-v_2|}^p\right)}^{1/p}\hfill \\ & =\hfill & \frac{2^{\frac{p-1}{p}}}{3}\parallel (x_1,x_2)-(u_1,u_2){\parallel }_p+\frac{2^{\frac{p-1}{p}+1}}{9}{\parallel (y_1,v_2)-(y_1,v_2)\parallel }_p\hfill \\ & =\hfill & \frac{2^{\frac{p-1}{p}}}{3}{\parallel x-u\parallel }_p+\frac{2^{\frac{p-1}{p}+1}}{9}{\parallel y-v\parallel }_p\hfill \end{array}$$

and

$$\begin{array}{ccc}{∥f(x,y)-f(u,v)∥}_p\hfill & =\hfill & {∥\left(f_1(x,y),f_2(x,y)\right)-\left(f_1(u,v),f_2(u,v)\right)∥}_p\hfill \\ & =\hfill & {∥\left(\frac{\frac{(u_1+u_2)-(x_1+x_2)}{4}+\frac{v_1+v_2-(y_1+y_2)}{3}}{3},\frac{\frac{(u_1+u_2)-(x_1+x_2)}{4}+\frac{v_1+v_2-(y_1+y_2)}{3}}{3}\right)∥}_p\hfill \\ & \le \hfill & \frac{2}{3}\left(\frac{|u_1-x_1|+|u_2-x_2|}{4}+\frac{|v_1-y_1|+|v_2-y_2|}{3}\right)=\frac{2}{6}\frac{|u_1-x_1|-|u_2+x_2|}{2}+\frac{4}{9}\frac{|v_1-y_1|+|v_2+y_2|}{2}\hfill \\ & \le \hfill & \frac{2^{\frac{p-1}{p}}}{6}{\left(|x_1-u_1{|}^p+{|x_2-y_2|}^p\right)}^{1/p}+\frac{2^{\frac{p-1}{p}+1}}{9}{\left(|y_1-v_1{|}^p+{|y_2-v_2|}^p\right)}^{1/p}\hfill \\ & =\hfill & \frac{2^{\frac{p-1}{p}}}{6}\parallel (x_1,x_2)-(u_1,u_2){\parallel }_p+\frac{2^{\frac{p-1}{p}+1}}{9}{\parallel (y_1,v_2)-(y_1,v_2)\parallel }_p\hfill \\ & =\hfill & \frac{2^{\frac{p-1}{p}}}{6}{\parallel x-u\parallel }_p+\frac{2^{\frac{p-1}{p}+1}}{9}{\parallel y-v\parallel }_p.\hfill \end{array}$$

Therefore

$$∥F(x,y)-F(u,v)∥+∥f(z,w)-f(t,s)∥\le 2^{\frac{p-1}{p}}\left({\displaystyle \frac{∥x-u∥}{3}+\frac{∥z-t∥}{6}}\right)+2^{\frac{2p-1}{p}}\left(\frac{∥y-v∥}{9}+\frac{∥w-s∥}{9}\right).$$

From the inequalities $\frac{2^{\frac{p-1}{p}}}{3}+\frac{2^{\frac{p-1}{p}}}{6}<\frac{2}{3}+\frac{1}{3}=1$ and $\frac{2^{\frac{2p-1}{p}}}{9}+\frac{2^{\frac{2p-1}{p}}}{9}\le 2\frac{4}{9}<1$ it follows that the ordered pair $(F,f)$ satisfies Assumption 1 with constants $\alpha =\frac{2^{\frac{p-1}{p}}}{3}$, $\beta =\frac{2^{\frac{p-1}{p}+1}}{9}$, $\gamma =\frac{2^{\frac{p-1}{p}}}{6}$ and $\delta =\frac{2^{\frac{p-1}{p}+1}}{9}$. Thus there exists an equilibrium pair $(x,y)$ and for any initial start in the economy the iterated sequences $(x_n,y_n)$ converge to the market equilibrium $(x,y)$. We get in this case that the equilibrium pair of the production of the two firms is $x=(19.27,19.27)$, $y=(19.36,19.36)$ (see

Table 14. Values of the iterated sequence $(x_n,y_n)$ if started with $x=(10,10)$, $y=(50,50)$.

n	0	1	2
$x_n$	(10, 10)	(15.56, 15.56)	(21.39, 21.39)
$y_n$	(50, 50)	(15.42, 15.42)	(20.49, 20.49)

and

Table 15. Values of the iterated sequence $(x_n,y_n)$ if started with $x=(10,10)$, $y=(50,50)$.

n	5	10	20
$x_n$	(19.09, 19.09)	(19.28, 19.28)	(19.27, 19.27)
$y_n$	(19.28, 19.28)	(19.36, 19.36)	(19.36, 19.36)

) and the total production will be $a=(38.63,38.63)$. Numbers of iterations, that a needed to ensure the a priori (see

Table 16. Number n of iterations needed by the a priori estimate if started with $x=(19.27,19.27)$, $y=(19.36,19.36)$ and $p=2$.

$\epsilon$	0.1	0.01	0.001	0.0001	0.00001
n	16	21	26	31	36

) and the a posteriori (see

Table 17. Number n of iterations needed by the a posteriori estimate if started with $x=(19.27,19.27)$, $y=(19.36,19.36)$ and $p=2$.

$\epsilon$	0.1	0.01	0.001	0.0001	0.00001
n	9	12	15	18	20

) are calculated.

4.3. The Players Are Producing a Single Product and Compete on Both Quantities and Prices

There is a large number of goods where companies can compete on both quality and prices. In this case the equilibrium would depend on a balanced decision on what market share to target at a reasonable price. Let us assume that there are only two major players that produce homogeneous products. The first company can produce qualities from the set $A_x\subseteq [0,\infty )$ at a price $p\in P_x\subseteq [0,\infty )$ and the second one can produce qualities from the set $A_y\subseteq [0,\infty )$ at a price $p\in P_x\subseteq [0,\infty )$, where $A_x$, $A_y$, $P_x$, $P_y$ are nonempty subsets. Let $A_x\times P_x$, $A_y\times P_y$ be subsets of a complete metric space $({\mathbb{R}}^2,\rho )$.

Assumption 2.

Let there be a duopoly market, satisfying the following assumptions:

(1) 

The two firms are producing homogeneous, perfect substitute products.

(2) 

The first firm can produce qualities from the set $A_x$ at a price $p\in P_x$ and the second firm can produce qualities from the set $A_y$ at a price $p\in P_x$, where $A_x\times P_x$, $A_y\times P_y$ are nonempty, closed subsets of a complete metric space $({\mathbb{R}}^2,\rho )$.

(3) 

Let there exist a closed subset $D\subseteq A_x\times P_x\times A_y\times P_y\to A_x$, such that $F:D\to A_x\times P_x$, $f:D\to A_y\times P_y$ and $(F(x,p,y,q),f(x,p,y,q))\subseteq D$ for every $(x,p,y,q)\in D$ be the response functions for firm one and two respectively.

(4) 

Let there exist $\alpha ,\beta ,\gamma ,\delta >0$, $max\{\alpha +\gamma ,\beta +\delta \}<1$, such that the inequality

$$\rho (F(X,Y),F(U,V))+\rho (f(Z,W),f(T,S))\le \alpha \rho (X,U)+\beta \rho (Y,V)+\gamma \rho (Z,T)+\delta \rho (W,S),$$

(6)

where we use thenotations $X=(x,p_1)$, $Y=(y,q_1)$, $U=(u,p_2)$, $V=(v,q2)$, $Z=(z,p_3)$, $W=(w,q_3)$, $T=(t,p_4)$, $S=(s,q_4)$, holds for all $(x,p_1,y,q_1),(u,p_2,v,q_2),(z,p_3,w,q_3),(t,p_4,s,q_4)\in D$.

Then

(I)

There exists a unique pair $(\xi ,p,\eta ,q)$ in $A_x\times P_x\times A_y\times P_y$, which is a common coupled fixed point for the maps F and f, i.e., a market equilibrium pair. Moreover the iteration sequences ${\{x_n\}}_{n=0}^{\infty }$, ${\{p_n\}}_{n=0}^{\infty }$, ${\{y_n\}}_{n=0}^{\infty }$ and ${\{q_n\}}_{n=0}^{\infty }$, defined in Definition A5 converge to $\xi$, p, $\eta$, and q respectively.

(II)

A priori error estimates hold

$$\begin{array}{ccc}{S}_1\hfill & =\hfill & max\left\{\rho ((x_n,p_n),(\xi ,p)),\rho ((y_n,q_n),(\eta ,q))\right\}\hfill \\ \hfill & \le \hfill & \frac{k^n}{1-k}(\rho ((x_1,p_1),(x_0,p_0))+\rho ((y_1,q_1),(y_0,q_0)));\hfill \end{array}$$

(7)

(III)

A posteriori error estimates hold

$$\begin{array}{ccc}{S}_2\hfill & =\hfill & max\left\{\rho ((x_n,p_n),(\xi ,p)),\rho ((y_n,q_n),(\eta ,q))\right\}\hfill \\ \hfill & \le \hfill & \frac{k}{1-k}(\rho ((x_{n-1},p_{n-1}),(x_n,p_n))+\rho ((y_{n-1},p_{n-1}),(y_n,q_n)));\hfill \end{array}$$

(8)

(IV)

The rate of convergence for the sequences of successive iterations is given by

$$\begin{array}{ccc}{S}_3\hfill & =\hfill & \rho ((x_n,p_n),(\xi ,p))+\rho ((y_n,q_n),(\eta ,q))\hfill \\ \hfill & \le \hfill & k\left(\rho ((x_{n-1},p_{n-1},(\xi ,p))+\rho ((y_{n-1},p_{n-1}),(\eta ,q))\right),\hfill \end{array}$$

(9)

where $k=max\{\alpha +\gamma ,\beta +\delta \}$.

If in addition $f(X,Y)=F(Y,X)$ then the coupled fixed point $(X,Y)$ satisfies $X=Y$, i.e., $x=y$ and $p=q$.

The proof is a direct consequence of Theorem A1.

Remark 2.

If we consider Bertrand’s model with the same assumption of equal response functions then not only the quantities will be equal but also and the prices.

Example of a Duopoly Model, Where Players Compete on Quantities and Prices Simultaneously

Let us consider a market with two competing firms, producing the same product, and selling it at a price p and q respectively, i.e., $X=(x,p),Y=(y,q)$. Let us consider the response functions $F(X,Y)=(F_1(X,Y),F_2(X,Y))$ and $f(X,Y)=(f_1(X,Y),f_2(X,Y))$ defined by

$$F(X,Y)=\left\{\begin{array}{c}{\displaystyle \frac{{\displaystyle 90-\frac{x}{2}-\frac{y}{3}}}{3},}\hfill \\ {\displaystyle \frac{{\displaystyle 4-\frac{p}{2}-\frac{q}{3}}}{3};}\hfill \end{array}\right.f(X,Y)=\left\{\begin{array}{c}{\displaystyle \frac{{\displaystyle 100-\frac{x}{4}-\frac{y}{3}}}{4}}\hfill \\ {\displaystyle \frac{{\displaystyle 5-\frac{p}{4}-\frac{q}{3}}}{4}.}\hfill \end{array}\right.$$

Let $X=(x,p)$ and $Y=(y,q)$ be subsets of $({\mathbb{R}}^2,\parallel ·{\parallel }_2)$ (the two dimensional Euclidean space). Let

• $A_x=[0,100]\times [0,5]$ and $A_y=[0,100]\times [0,4]$
• $D=[0,100]\times [0,5]\times [0,100]\times [0,4]$

It is easy to see that $F:D\to [0,100]\times [0,5]$, $f:D\to [0,100]\times [0,4]$ and $(F(x,p,y,q),f(x,p,y,q))\subseteq D$ for every $(x,p,y,q)\in D$.

Using the inequality $\frac{a+b}{2}\le \frac{{(a^2+b^2)}^{1/2}}{2^{1/2}}$, which holds for any $a,b\ge 0$ we get the chain of inequalities we obtain

$$\begin{array}{ccc}{S}_4\hfill & =\hfill & {∥F(x,p_1,y,q_1)-F(u,p_2,v,q_2)∥}_2\hfill \\ & =\hfill & {∥\left({\displaystyle \frac{{\displaystyle 90-\frac{x}{2}-\frac{y}{3}}}{3},\frac{{\displaystyle 4-\frac{p_1}{2}-\frac{q_1}{3}}}{3}}\right)-\left({\displaystyle \frac{{\displaystyle 90-\frac{u}{2}-\frac{v}{3}}}{3},\frac{{\displaystyle 4-\frac{p_2}{2}-\frac{q_2}{3}}}{3}}\right)∥}_2\hfill \\ & =\hfill & {∥\left({\displaystyle \frac{{\displaystyle \frac{u-x}{2}+\frac{v-y}{3}}}{3},\frac{{\displaystyle \frac{p_1-p_2}{2}+\frac{q_1-q_2}{3}}}{3}}\right)∥}_2\hfill \\ & \le \hfill & {\displaystyle \frac{1}{3}\sqrt{{\displaystyle {\left(\frac{|u-x|+|v-y|}{2}\right)}^2+{\left(\frac{|p_1-p_2|+|q_1-q_2|}{2}\right)}^2}}}\hfill \\ & \le \hfill & {\displaystyle \frac{1}{3}\left({\displaystyle \frac{|u-x|+|v-y|}{2}+\frac{|p_1-p_2|+|q_1-q_2|}{2}}\right)}\hfill \\ & =\hfill & {\displaystyle \frac{1}{3}\left({\displaystyle \frac{|u-x|+|p_1-p_2|}{2}+\frac{|v-y|+|q_1-q_2|}{2}}\right)}\hfill \\ & \le \hfill & {\displaystyle \frac{1}{3\sqrt{2}}\sqrt{{|u-x|}^2+{|p_1-p_2|}^2}+\frac{1}{3\sqrt{2}}\sqrt{|v-y|+|q_1-q_2|}}\hfill \\ & =\hfill & {\displaystyle \frac{1}{3\sqrt{2}}\rho (U,X)+\frac{1}{3\sqrt{2}}\rho (V,Y)}\hfill \end{array}$$

and

$$\begin{array}{ccc}{S}_5\hfill & =\hfill & {∥f(x,p_1,y,q_1)-f(u,p_2,v,q_2)∥}_2\hfill \\ & =\hfill & {∥\left({\displaystyle \frac{{\displaystyle 100-\frac{x}{4}-\frac{y}{3}}}{4},\frac{{\displaystyle 5-\frac{p_1}{4}-\frac{q_1}{3}}}{4}}\right)-\left({\displaystyle \frac{{\displaystyle 100-\frac{u}{4}-\frac{v}{3}}}{4},\frac{{\displaystyle 5-\frac{p_2}{4}-\frac{q_2}{3}}}{4}}\right)∥}_2\hfill \\ & =\hfill & {∥\left({\displaystyle \frac{{\displaystyle \frac{u-x}{4}+\frac{v-y}{3}}}{4},\frac{{\displaystyle \frac{p_1-p_2}{4}+\frac{q_1-q_2}{3}}}{4}}\right)∥}_2\hfill \\ & \le \hfill & {\displaystyle \frac{1}{4}\sqrt{{\displaystyle {\left(\frac{|u-x|+|v-y|}{3}\right)}^2+{\left(\frac{|p_1-p_2|+|q_1-q_2|}{3}\right)}^2}}}\hfill \\ & \le \hfill & {\displaystyle \frac{1}{4}\left({\displaystyle \frac{|u-x|+|v-y|}{3}+\frac{|p_1-p_2|+|q_1-q_2|}{3}}\right)}\hfill \\ & <\hfill & {\displaystyle \frac{1}{4}\left({\displaystyle \frac{|u-x|+|p_1-p_2|}{2}+\frac{|v-y|+|q_1-q_2|}{2}}\right)}\hfill \\ & \le \hfill & {\displaystyle \frac{1}{4\sqrt{2}}\sqrt{{|u-x|}^2+{|p_1-p_2|}^2}+\frac{1}{4\sqrt{2}}\sqrt{|v-y|+|q_1-q_2|}}\hfill \\ & =\hfill & {\displaystyle \frac{1}{4\sqrt{2}}\rho (U,X)+\frac{1}{4\sqrt{2}}\rho (V,Y).}\hfill \end{array}$$

Therefore

$${\displaystyle ∥F(X,Y)-F(U,V)∥+∥f(Z,W)-f(T,S)∥\le \frac{∥X-U∥}{3\sqrt{2}}+\frac{∥Y-V∥}{3\sqrt{2}}+\frac{∥Z-T∥}{4\sqrt{2}}+\frac{∥W-S∥}{4\sqrt{2}}.}$$

From the inequalities $\frac{1}{3\sqrt{2}}+\frac{1}{4\sqrt{2}}<1$ it follows that the ordered pair $(F,f)$ satisfies Assumption 2 with constants $\alpha =\frac{1}{3\sqrt{2}}$, $\beta =\frac{1}{3\sqrt{2}}$, $\gamma =\frac{1}{4\sqrt{2}}$ and $\delta =\frac{1}{4\sqrt{2}}$. Thus there exists an equilibrium pair $(x,y)$ and for any initial start in the economy the iterated sequences $(x_n,y_n)$ converge to the market equilibrium $(x,y)$. We get in this case that the equilibrium pair of the production of the two firms is $x=(23.64,1.03)$, $y=(21.71,1.09)$.

4.4. Players’ Production Sets Have an Empty Intersection

Assumption 3.

Let there be a duopoly market, satisfying the following assumptions:

1. 

The two firms are producing homogeneous perfect substitute products.

2. 

The first firm can produce qualities from the set $A_x$ and the second firm can produce qualities from the set $A_y$, where $A_x$ and $A_y$ are nonempty, closed and convex subsets of a uniformly convex Banach space $(X,\parallel ·\parallel )$

3. 

Let there exist a closed and convex subset $D\subseteq A_x\times A_y$ and maps $F:D\to A_x$ and $f:D\to A_y$, such that $(F(x,y),f(x,y))\subseteq D$ for every $(x,y)\in D$, are the response functions for firm one and two respectively

4. 

Let there exist $\alpha ,\beta >0$, $\alpha +\beta <1$, such that

$$\parallel F(x,y)-f(u,v)\parallel \le \alpha \parallel x-v\parallel +\beta \parallel y-u\parallel +(1-(\alpha +\beta ))d$$

(10)

for all $(x,y),(u,v)\in A_x\times A_y$, where $d=\mathrm{dist}(A_x,A_y)=inf\{\parallel x-y\parallel :x\in A_x,y\in A_y\}$.

Then there exists a unique pair $(\xi ,\eta )$ in $A_x\times A_y$, which is a coupled best point for the pair of maps $(F,f)$, i.e., a market equilibrium pair. Moreover the iteration sequences ${\{x_n\}}_{n=0}^{\infty }$ and ${\{y_n\}}_{n=0}^{\infty }$, defined in Definition A5 converge to $\xi$ and $\eta$ respectively.

If in addition $(X,\parallel ·\parallel )$ has a modulus of convexity of power type with constants $C>0$ and $q>1$, then

• A priori error estimates hold

  $$∥\xi -x_m∥\le M_0\sqrt[q]{\frac{max\{W_{0,1}(x,y),W_{0,0}(x,y)\}}{Cd}}·\frac{\sqrt[q]{{(\alpha +\beta )}^m}}{1-\sqrt[q]{\alpha +\beta }};$$

  (11)

  $$∥\eta -y_m∥\le N_0\sqrt[q]{\frac{max\{W_{0,1}(y,x),W_{0,0}(y,x)\}}{Cd}}·\frac{\sqrt[q]{{(\alpha +\beta )}^m}}{1-\sqrt[q]{\alpha +\beta }};$$

  (12)
• A posteriori error estimates hold

  $$∥\xi -x_n∥\le M_{n-1}\sqrt[q]{\frac{max\{W_{n-1,n}(x,y),W_{n-1,n-1}(x,y)\}}{Cd}}c.$$

  (13)

  $$∥\eta -y_{2n}∥\le N_{n-1}\sqrt[q]{\frac{max\{W_{n-1,n}(y,x),W_{n-1,n-1}(y,x)\}}{Cd}}c,$$

  (14)

  where $W_{n,m}(x,y)=\parallel x_n-x_m\parallel -d$, $M_{n}max\{\parallel x_n-y_n\parallel ,\parallel x_n-y_{n+1}\parallel \}$, $N_{n}max\{\parallel x_n-y_n\parallel ,\parallel y_n-x_{n+1}\parallel \}$ and $c=\frac{\sqrt[q]{\alpha +\beta }}{1-\sqrt[q]{\alpha +\beta }}$.

The proof is a direct consequence of Theorem A2.

Players’ Production Sets Have an Empty Intersection, Each Player Is Producing Two Goods

Let us consider a market with two competing firms, each firm produces two products and any one of the items is completely replaceable with a similar product of the other firm. Let us assume that the first firm can produce much less quantities than the second one, i.e., if $x_1,x_2$ are the quantities produced by the first firm and $y_1,y_2$ are the quantities produced by the second one and, then $x_1,x_2\in [0,1]$ and $y_1,y_2\in [2,3]$. Let $A_x=[0,1]\times [0,1]$$A_y=[2,3]\times [2,3]$ be considered as subsets of $({\mathbb{R}}^2,\parallel ·\parallel )$, which is a uniformly convex Banach space with modulus of convexity ${\delta }_{{\parallel ·\parallel }_2}(\epsilon )\ge \frac{{\epsilon }^2}{3}$ of power type Zlatanov (2016). Let us consider the response functions $F(x_1,x_2,y_1,y_2)$ and $f(x_1,x_2,y_1,y_2)$ defined by

$$F(x,y)=\left\{\begin{array}{c}\frac{3x_1}{8}+\frac{x_2}{8}-\frac{3y_1}{16}-\frac{y_2}{16}+1\hfill \\ \frac{x_1}{8}+\frac{3x_2}{8}-\frac{y_1}{16}-\frac{3y_2}{16}+1\hfill \end{array}\right.,f(x,y)=\left\{\begin{array}{c}-\frac{3x_1}{16}-\frac{x_2}{16}+\frac{3y_1}{4}+\frac{y_2}{4}+\frac{5}{4}\hfill \\ -\frac{x_1}{16}-\frac{3x_2}{16}+\frac{y_1}{4}+\frac{3y_2}{4}+\frac{5}{4}\hfill \end{array}\right..$$

It is easy to see that $F:[0,1]\times [0,1]\times [2,3]\times [2,3]\to [0,1]\times [0,1]$ and $f:[0,1]\times [0,1]\times [2,3]\times [2,3]\to [2,3]\times [2,3]$

Indeed the inequalities $0\le \frac{3x_1}{8}+\frac{x_2}{8}-\frac{3y_1}{16}-\frac{y_2}{16}+1\le 1$ are equivalent to

$$\left|\begin{array}{ccc}\hfill \frac{3y_1}{16}+\frac{y_2}{16}& \le & \frac{3x_1}{8}+\frac{x_2}{8}+1\hfill \\ \hfill \frac{3x_1}{8}+\frac{x_2}{8}& \le & \frac{3y_1}{16}+\frac{y_2}{16}\hfill \end{array}\right.$$

for $(x_1,x_2,y_1,y_2)\in [0,1]\times [0,1]\times [2,3]\times [2,3]$.

The inequalities $2\le -\frac{3u_1}{16}-\frac{u_2}{16}+\frac{3v_1}{4}+\frac{v_2}{4}+\frac{5}{4}\le 3$ are equivalent to

$$\left|\begin{array}{ccc}\hfill \frac{3u_1}{16}+\frac{u_2}{16}& \le & \frac{3v_1}{4}+\frac{v_2}{4}\hfill \\ \hfill \frac{3v_1}{4}+\frac{v_2}{4}& \le & \frac{7}{4}+\frac{3u_1}{16}+\frac{u_2}{16}\hfill \end{array}\right.$$

for $(u_1,u_2,v_1,v_2)\in [0,1]\times [0,1]\times [2,3]\times [2,3]$.

Using the inequality ${\left(\frac{3a}{4}+\frac{b}{4}\right)}^2\le \frac{3}{4}{a}^2+\frac{1}{4}{b}^2$, i.e., $\left|\frac{3a}{4}+\frac{b}{4}\right|\le \frac{\sqrt{3a^2+b^2}}{2}$ we obtain

$$\begin{array}{ccc}{S}_6\hfill & =\hfill & \parallel F(x_1,x_2,y_1,y_2)-f(u_1,u_2,v_1,v_2){\parallel }_2\hfill \\ & =\hfill & ∥\left(\frac{3x_1}{8}+\frac{x_2}{8}-\frac{3y_1}{16}-\frac{y_2}{16}+1,\frac{x_1}{8}+\frac{3x_2}{8}-\frac{y_1}{16}-\frac{3y_2}{16}+1\right)\hfill \\ & & {-\left(-\frac{3u_1}{16}-\frac{u_2}{16}+\frac{3v_1}{4}+\frac{v_2}{4}+\frac{5}{4},-\frac{u_1}{16}-\frac{3u_2}{16}+\frac{v_1}{4}+\frac{3v_2}{4}+\frac{5}{4}\right)∥}_2\hfill \\ & =\hfill & {∥\left(\frac{1}{4}+\frac{3(x_1-v_1)}{8}+\frac{x_2-v_2}{8},\frac{1}{4}+\frac{3(u_1-y_1)}{16}+\frac{u_2-y_2}{16}\right)∥}_2\hfill \\ & \le \hfill & {∥\left(\frac{1}{4},\frac{1}{4}\right)∥}_2+{∥\left(\frac{3(x_1-v_1)}{8}+\frac{x_2-v_2}{8},\frac{3(u_1-y_1)}{16}+\frac{u_2-y_2}{16}\right)∥}_2\hfill \\ & \le \hfill & \frac{\sqrt{2}}{4}+{∥\left(\frac{3(x_1-v_1)}{8}+\frac{x_2-v_2}{8},0\right)∥}_2+{∥\left(0,\frac{3(u_1-y_1)}{16}+\frac{u_2-y_2}{16}\right)∥}_2\hfill \\ & =\hfill & \frac{\sqrt{2}}{4}+\frac{1}{2}{∥\left(\frac{3(x_1-v_1)}{4}+\frac{x_2-v_2}{4},0\right)∥}_2+\frac{1}{4}{∥\left(0,\frac{3(u_1-y_1)}{4}+\frac{u_2-y_2}{4}\right)∥}_2\hfill \\ & =\hfill & \frac{\sqrt{2}}{4}+\frac{1}{2}\left|\frac{3(x_1-v_1)}{4}+\frac{x_2-v_2}{4}\right|+\frac{1}{4}{\left|\frac{3(u_1-y_1)}{4}+\frac{u_2-y_2}{4}\right|}_2\hfill \\ & \le \hfill & \frac{\sqrt{2}}{4}+\frac{\sqrt{3|x_1-v_1{|}^2+{|x_2-v_2|}^2}}{4}+\frac{\sqrt{3|u_1-y_1{|}^2+{|u_2-y_2|}^2}}{8}\hfill \\ & \le \hfill & \frac{\sqrt{2}}{4}+\frac{\sqrt{3}}{4}\sqrt{|x_1-v_1{|}^2+{|x_2-v_2|}^2}+\frac{\sqrt{3}}{8}\sqrt{|u_1-y_1{|}^2+{|u_2-y_2|}^2}\hfill \\ & =\hfill & \frac{\sqrt{3}}{4}{\parallel x-v\parallel }_2+\frac{\sqrt{3}}{8}{\parallel y-u\parallel }_2+\frac{\sqrt{2}}{4}\hfill \\ & \le \hfill & \frac{\sqrt{3}}{4}{\parallel x-v\parallel }_2+\frac{\sqrt{3}}{8}{\parallel y-u\parallel }_2+\left(1-\frac{\sqrt{3}}{4}-\frac{\sqrt{3}}{8}\right)\sqrt{2}\hfill \\ & =\hfill & \frac{\sqrt{3}}{4}{\parallel x-v\parallel }_2+\frac{\sqrt{3}}{8}{\parallel y-u\parallel }_2+\left(1-\frac{\sqrt{3}}{4}-\frac{\sqrt{3}}{8}\right)d,\hfill \end{array}$$

where $d=\mathrm{dist}([0,1]\times [0,1],[2,3]\times [2,3])=\sqrt{2}$. Therefore the ordered pair $(F,f)$ satisfies Assumption 3 with constants $\alpha =\frac{\sqrt{3}}{4}$, $\beta =\frac{\sqrt{3}}{8}$. Thus there exists an equilibrium pair $(x,y)=((x_1,x_2),(y_1,y_2))$ and for any initial start in the economy, the iterated sequence $(x^n,y^n)=((x_1^n,x_2^n),(y_1^n,y_2^n))$ converges to the market equilibrium $(x,y)$. We get in this case that the equilibrium pair of the production of the two firms is $x=(1,1)$, $y=(2,2)$ (see

Table 18. Values of the iterated sequence $(x^n,y^n)$ if started with $((0.01,0.2),(2.9,2.1))$.

n	0	1	2
$(x_1^n,x_2^n)$	(0.01, 0.9)	(0.44, 0.76)	(0.66, 0.75)
$(y_1^n,y_2^n)$	(2.90, 2.1)	(2.44, 2.33)	(2.31, 2.27)

and

Table 19. Values of the iterated sequence $(x^n,y^n)$ if started with $((0.01,0.2),(2.9,2.1))$.

n	5	10	20
$(x_1^n,x_2^n)$	(0.87, 0.88)	(0.97, 0.97)	(1, 1)
$(y_1^n,y_2^n)$	(2.12, 2.12)	(2.03, 2.03)	(2, 2)

) and the total production will be $a=(3,3)$.

4.5. Equilibrium in the Case, When the Two Players Are Producing Just One Good and the Production Set Has an Empty Intersection

Let us point out that the properties of the modulus of convexity ${\delta }_{\parallel ·\parallel }$ are investigated if the Banach space is at least two dimensional. As far as $\mathbb{R}$, endowed with its canonical norm is a subspace of ${\mathbb{R}}_2^2$ we get that ${\delta }_{(\mathbb{R},|·|)}(\epsilon )\ge {\delta }_{({\mathbb{R}}_2^2,\parallel ·{\parallel }_2)}(\epsilon )=\frac{{\epsilon }^2}{8}$. It is easy to observe that in $\mathbb{R}$ there holds the equality ${\delta }_{(\mathbb{R},|·|)}(\epsilon )=\frac{\epsilon }{2}$. Indeed $B_{(\mathbb{R},|·|)}=[-1,1]$. Then ${\delta }_{(\mathbb{R},|·|)}(\epsilon )=inf\left\{\left|1-\frac{x+y}{2}\right|:x,y\in [-1,1],|x-y|\ge \epsilon \right\}$. The infimum is attained, when $x=1$ and $y=1-\epsilon$. Therefore ${\delta }_{(\mathbb{R},|·|)}(\epsilon )=\left|1-\frac{1+(1-\epsilon )}{2}\right|=\frac{\epsilon }{2}$ Ilchev and Zlatanov (2016).

We will formulate Assumption 3 in the case when the underlying Banach space is $(\mathbb{R},|·|)$.

Assumption 4.

Let there is a duopoly market, satisfying the following assumptions:

1. 

The two firms are producing homogeneous perfect substitute products

2. 

The first firm can produce qualities from the set $A_x$ and the second firm can produce qualities from the set $A_y$, where $A_x$ and $A_y$ are nonempty closed intervals of $(\mathbb{R},|·|)$

3. 

Let there exist a close and convex subset $D\subseteq A_x\times A_y$ and maps $F:D\to A_x$ and $f:D\to A_y$, such that $(F(x,y),f(x,y))\subseteq D$ for every $(x,y)\in D$, be the response functions for firm one and two respectively

4. 

Let there exist $\alpha ,\beta >0$, $\alpha +\beta <1$, such that

$$|F(x,y)-f(u,v)|\le \alpha |x-v|+\beta |y-u|+(1-(\alpha +\beta ))d$$

(15)

for all $(x,y),(u,v)\in A_x\times A_y$, where $d=\mathrm{dist}(A_x,A_y)=inf\{|x-y|:x\in A_x,y\in A_y\}$.

Then there exists a unique pair $(\xi ,\eta )$ in $A_x\times A_y$, which is a coupled best point for the pair of maps $(F,f)$, i.e., a market equilibrium pair. Moreover the iteration sequences ${\{x_n\}}_{n=0}^{\infty }$ and ${\{y_n\}}_{n=0}^{\infty }$, defined in Definition A5 converge to $\xi$ and $\eta$ respectively.

• A priori error estimates hold

  $$\left|\xi -x_m\right|\le 2max\{|x_0-y_0|,|x_0-y_1|\}\frac{max\{W_{0,1}(x,y),W_{0,0}(x,y)\}}{d}·\frac{{(\alpha +\beta )}^m}{1-(\alpha +\beta )};$$

  (16)

  $$∥\eta -y_m∥\le 2max\{|x_0-y_0|,|x_1-y_0|\}\frac{max\{W_{0,1}(y,x),W_{0,0}(y,x)\}}{d}·\frac{{(\alpha +\beta )}^m}{1-(\alpha +\beta )};$$

  (17)
• A posteriori error estimates hold

  $$\left|\xi -x_n\right|\le 2max\{|x_{n-1}-y_{n-1}|,|x_{n-1}-y_n|\}\frac{max\{W_{n-1,n}(x,y),W_{n-1,n-1}(x,y)\}}{d(1-(\alpha +\beta ))}(\alpha +\beta );$$

  (18)

  $$\left|\eta -y_n\right|\le 2max\{|x_{n-1}-y_{n-1}|,|x_n-y_{n-1}|\}\frac{max\{W_{n-1,n}(y,x),W_{n-1,n-1}(y,x)\}}{d(1-(\alpha +\beta ))}(\alpha +\beta ),$$

  (19)

  where $W_{n,m}(x,y)=|x_n-x_m|-d$.

The proof is a direct consequence of Theorem A2 and the remark that $(\mathbb{R},|·|)$ is a uniformly convex Banach space with modulus of convexity ${\delta }_{|·|}(\epsilon )=\frac{\epsilon }{2}$.

Example When the Two Players Are Producing Just One Good

Let us consider a market with two competing firms, producing two products, that are perfect substitutes. Let us assume that the first firm can produce much smaller quantities than the second one, i.e., $x,y$, so that $x\in [0,1]$ and $y\in [2,3]$. Let us consider the response functions $F(x,y)$ and $f(x,y)$ defined by

$$F(x,y)=\frac{x}{2}-\frac{y}{4}+1,f(x,y)=-\frac{u}{4}+\frac{v}{2}+\frac{5}{4}$$

It is easy to see that $F:[0,1]\times [2,3]\to [0,1]$ and $f:[0,1]\times [2,3]\to [2,3]$

Indeed the inequalities $0\le \frac{x}{2}-\frac{y}{4}+1\le 1$ are equivalent to

$$\left|\begin{array}{ccc}\hfill \frac{y}{4}& \le & \frac{x}{2}+1\hfill \\ \hfill \frac{x}{2}& \le & \frac{y}{4}\hfill \end{array}\right.$$

for $(x,y)\in [0,1]\times [2,3]$.

The inequalities $2\le -\frac{u}{4}+\frac{v}{2}+\frac{5}{4}\le 3$ are equivalent to

$$\left|\begin{array}{ccc}\hfill \frac{3}{4}+\frac{u}{4}& \le & \frac{v}{2}\hfill \\ \hfill \frac{v}{2}& \le & \frac{7}{4}+\frac{u}{4}\hfill \end{array}\right.$$

for $(u,v)\in [0,1]\times [2,3]$.

Then we obtain

$$\begin{array}{ccc}|F(x,y)-f(u,v)|\hfill & =\hfill & {\displaystyle \left|{\displaystyle -\frac{u}{4}+\frac{v}{2}+\frac{5}{4}-\left(\frac{x}{2}-\frac{y}{4}+1\right)}\right|\le \frac{|v-x|}{2}+\frac{|y-u|}{4}+\left|\frac{5}{4}-1\right|}\hfill \\ & =\hfill & {\displaystyle \frac{|v-x|}{2}+\frac{|y-u|}{4}+\frac{1}{4}=\frac{|v-x|}{2}+\frac{|y-u|}{4}+\left(1-\left(\frac{1}{2}+\frac{1}{4}\right)\right)d.}\hfill \end{array}$$

Therefore the ordered pair $(F,f)$ satisfies Assumption 4 with constants $\alpha =\frac{1}{2}$, $\beta =\frac{1}{4}$. Thus there exists an equilibrium pair $(x,y)$ and for any initial start in the economy the iterated sequences $(x_n,y_n)$ converge to the market equilibrium $(x,y)$. We get in this case that the equilibrium pair of the production of the two firms is $x=1$, $y=2$ (see

Table 20. Values of the iterated sequence $(x_n,y_n)$ if started with $(0.2,2.8)$.

n	0	1	2	5	10	20	30
$x_n$	0.2	0.4	0.55	0.81	0.95	0.997	0.9998
$y_n$	2.8	2.6	2.45	2.18	2.04	2.002	2.0001

,

Table 21. Number n of iterations needed by the a priori estimate if started with $(0.2,2.8)$.

$\epsilon$	0.1	0.01	0.001	0.0001	0.00001
n	21	29	37	45	53

and

Table 22. Number n of iterations needed by the a posteriori estimate if started with $(100,20)$.

$\epsilon$	0.1	0.01	0.001	0.0001	0.00001
n	17	25	33	41	49

) and the total production will be $a=3$.

5. Conclusions

Markets dominated by a small group of players are not uncommon even in a fast moving global economy. Therefore it is essential to analyze these cases, understand what leads to equilibrium and how different companies respond to changes in the economic environment. In this paper we have built a model on existence and uniqueness of market equilibrium in oligopoly markets that can be derived from response functions of major players. We assume that goods produced by different market players are perfect substitutes as this simplifies the mathematical description of the model. Due to the fact that response functions can also account for differences in product qualities, the model can also be applied to situations where price is not the only factor on which companies compete. With a carefully constructed response function it is possible to fully comprehend all five basic factors influencing competition—product features, number of sellers, information ability and barriers to entry.

Use of the suggested model can help understand better markets with limited number of players. By solving the inverse problem—estimate response functions based on historical prices and output series, it is also possible to understand how companies make decisions and react on regulations and changes in the environment. Compared to other approaches that also allow to estimate how market participants change their behavior, our suggestion is more flexible and can be extended to include different limitations.

Response functions also support the concept of having protective capacity and the ability to change output within certain limits, with minimal changes in total costs. While this matches the way contemporary businesses are run, it also provides for building more realistic views of the market. That is of particular importance for taking regulatory measures and estimating how changes in economic conditions may affect certain industries. It should be noted that our approach is important also for a wider audience when we consider that there are rare metals and raw materials markets with oligopolistic structure. Such special cases have influence reaching beyond the trade with a particular good.

Existence and uniqueness of equilibrium can be analyzed with both linear and non-linear response functions which proves to be a very flexible approach when studying different markets, which despite being dominated by a small number of companies may have quite different characteristics. Applications of the suggested model when production sets of market participants have empty intersection are particularly important when it is necessary to account for real world limitations like huge economies of scale or unique resources available to some players. One specific application and advantage of the suggested model is that calibration of response functions can be performed in a way that matches observed past behavior (output and prices) or major market players. This way it is possible to assess not only equilibrium stability but also the way that different companies react to changes in the environment.