Modern Optimization and Simulation Methods in Managerial and Business Economics: A Review
Abstract
1. Introduction
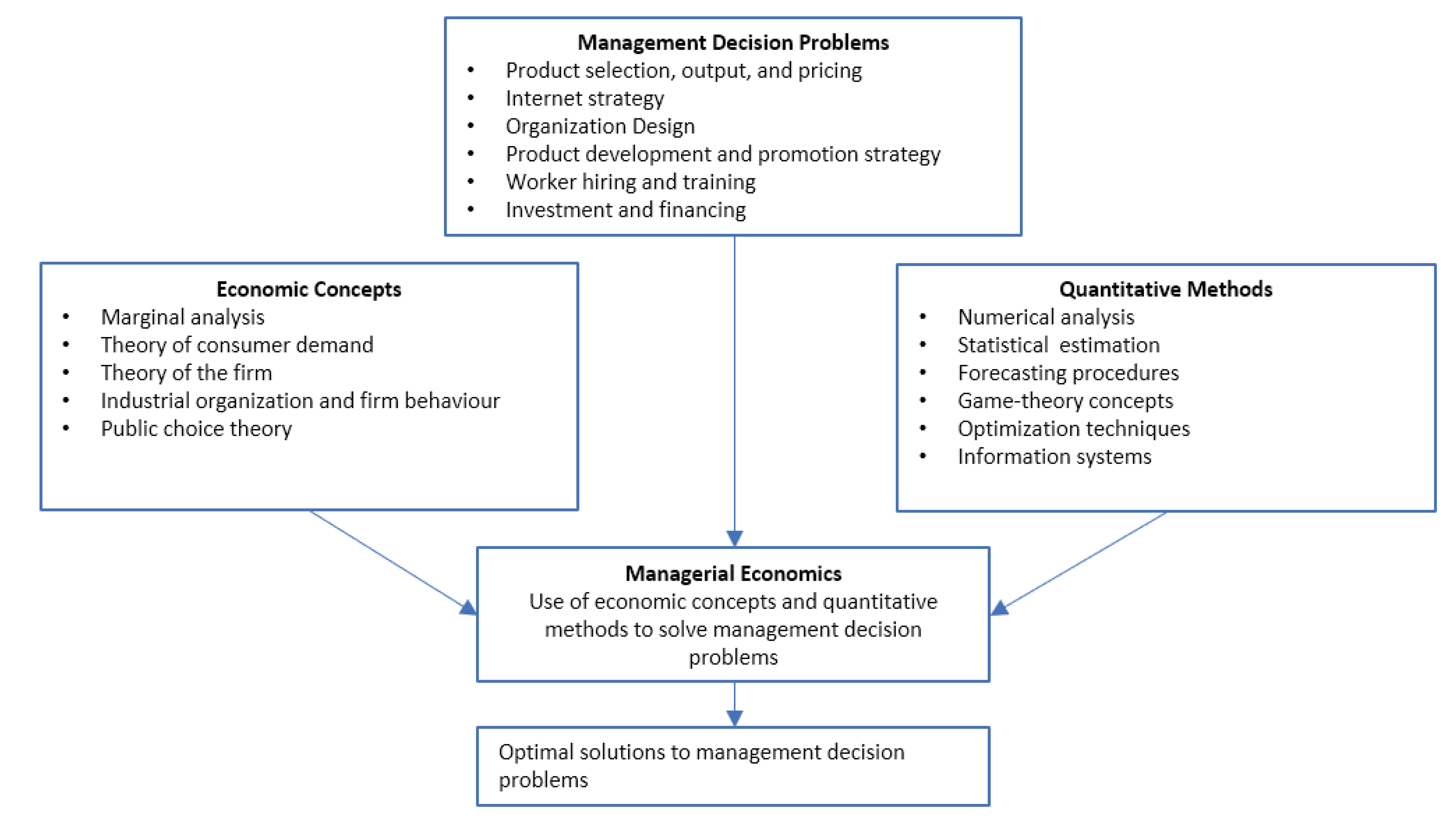
2. Overview of Managerial Economics
3. Overview of Heuristic Optimization and Simulation Methods
- Continuous simulation refers to the modeling of a system with random variables that change continuously over time. This methodology makes use of differential equations and frequently employs numerical approaches for their resolution (Amaran et al. 2016).
- Discrete-event simulation points out to the modeling of a system with random variables that can vary over time (i.e., dynamic systems) but just in a discrete way (when specific events happen during a time). This approach is traditionally utilized to analyze the behavior of time-dependent network systems, such as a supply chain (Fishman 2013).
- Monte Carlo simulation (MCS) employs random sampling for addressing stochastic problems that do not evolve over time (i.e., static systems). This method is extensively used for dealing with not analytically tractable stochastic optimization problems (Bianchi et al. 2009).
- Optimization integrated with simulation: In this approach, the optimization is used to evaluate a specific problem. Then, the result comes back to the simulation, which then re-starts its activity. For instance, the ordering of jobs could be re-scheduled according to the current state of the simulation (Dias et al. 2018).
- Simulation as objective function: In this case, the optimization provides a feasible solution, evaluated through the simulation. Then, these results are used by the optimization in order to generate alternative solutions. This, for instance, can be applied for determining the staff assigned to a given project (Zhang et al. 2019).
- Simulation results as a start for optimization: Using this combination, the simulation is conducted before the optimization, and is the one that provides the initialization parameters for the optimization process. For instance, the determination of the required staff for a certain production process and, afterward, using the optimization to allocate this staff (Rezaeiahari and Khasawneh 2020).
- Optimization for configuring simulation: Here, the simulation is employed to evaluate the feasibility of a solution found by the optimization (Yang et al. 2019).
4. Applications in Competitive Markets
5. Applications in Imperfect Markets
5.1. Monopolies and Monopsonies
5.2. Monopolistic Competition
5.3. Oligopolies and Oligopsonies
6. Public Sector and Public-Private Partnerships
- Monopoly power: (a) breaking up existing monopolies, (b) preventing monopolistic practices, (c) preventing mergers that reduce competition, and (d) preventing collusion.
- Negative externalities: (a) taxes, (b) government standards, (c) permits (either tradable or not), (d) liability rules, and bargaining among affected parties.
- Positive externalities: (a) promoting literacy and education, ) improving health, (c) promoting research, (d) patent system, and copyright.
- Imperfect information: (a) banning some drugs, (b) taxing unhealthy products, (c) mandating compulsory education, and (d) requiring producers to provide information (e.g., warning labels on cigarettes).
6.1. Regulation
6.2. Public Goods
7. Common Trends and Open Challenges
- The first challenge is the adaptability of the used techniques. In fact, a particular decision-making problem can be answered by different methodologies (Tsao et al. 2020) and, in other cases, a particular methodology can provide a solution for different sets of decision-making requirements. That is, within the same industry, firms are most likely to face similar problems or have similar goals. However, and independently of their goals, their necessities cannot be answered by the same methodology, since the firm environment can be diametrically opposite and can vary over time (Salamat et al. 2016). For example, collaborators (i.e., they may be based in local, national, or international region), target customers (i.e., with different demographics and living patterns) and market environment (i.e., perfect or imperfect competition), among others. Thus, it is in these cases where an intelligent design that allows adaptation and evolution of decision-making mechanisms play a fundamental role in the competitiveness of firms. In a similar line, it is also necessary to develop dynamic procedures that include uncertainty (Kumar and Chatterjee 2015; Mathur et al. 2017).
- The second challenge is the reliability of some of the simulation outputs. Some authors, like Zhang et al. (2019), point out about the discrepancies between the simulation outputs and the observed data in practice, due to multiple nuances that were not incorporated in the models in complex environments. This statement is particularly true in those cases where consumers’ behavior may intervene (e.g., hospitals). As a consequence, the aforementioned discrepancies in output may affect the reliability of the model insights, especially when those insights are implemented in high-risk practice.
- The third challenge is the applicability, i.e., the horizon of repercussion to which the decision to make belongs. The previous literature review shows that firms and researchers are making an attempt to design and implement possible simulation and metaheuristic algorithms for better decision, but in most of the studies referenced in this work, the utilization of the aforementioned techniques is limited to the strategic decision level (considering the importance of these decisions for the survival of the firm). However, there is no impediment to use them as a support system in all decision making processes. Reinforcing this idea, some authors, such as Mendoza-Gómez et al. (2018), advocate its massive implementation as a support technique in the decision-making process in regular basis (i.e., tactical and operational levels).
- Finally, the fourth challenge refers to the dissemination of these techniques as a decision tool, the uniqueness in the solution. The procedures described in this study can provide more than one good and feasible solution, such that, according to Tang et al. (2017) this can generate controversy when making a decision. It is possible that in this scenario, in which two equally good solutions are available, the managers of the firms doubt the effectiveness of these tools and dismiss it as effective tools by not providing a single solution.
8. Potential use of Simheuristics and Learnheuristics
- Pricing strategies in oligopolies or monopolistic competition usually are subject to incomplete/ uncertain information, such as the pricing strategies and cost of competitors or characteristics of potential entrants. Taking into account this uncertainty is key for the economical sustainability of an organization.
- The best market segment strategy may depend on the strategies of the competitors, current and future technologies, and customer demands, among many other factors. All these factors are impossible to predict perfectly and may change over time very fast.
- Public transportation has many relevant positive externalities. To design efficient systems is required to estimate the number of users, but such predictions tend to have a high margin error. Moreover, the number of users of a given system, for instance a shuttle bus service, may depend on many factors that may change over time: prices in the car market, environmental awareness, characteristics of other public alternatives, etc.
- Public/private portfolio design is usually a multiobjective optimization problem with many restrictions. Completion times, cost and even the preferences of decision-makers and available funding may be fuzzy and change over time.
9. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ACO | Ant colony optimization |
| BE | Business economics |
| DE | Differential evolution |
| GA | Genetic algorithm |
| ICA | Imperialist competitive algorithm |
| ILS | Iterated local search |
| LP | Linear programming |
| MCS | Monte Carlo simulation |
| ME | Managerial economics |
| PSO | Particle swarm optimization |
| TS | Tabu search |
| SA | Simulated annealing |
| VNS | Variable neighbourhood search |
References
- Agarwal, Rajshree, and Constance E. Helfat. 2009. Strategic renewal of organizations. Organization Science 20: 281–93. [Google Scholar] [CrossRef]
- Ahuja, H. L., and Amit Ahuja. 2017. Managerial Economics: Analysis of Managerial Decision Making. New Delhi: S Chand Limited. [Google Scholar]
- Al Shehhi, Mohammed, and Andreas Karathanasopoulos. 2020. Forecasting hotel room prices in selected GCC cities using deep learning. Journal of Hospitality and Tourism Management 42: 40–50. [Google Scholar] [CrossRef]
- Alhabeeb, Musaddak J., and L. Joe Moffitt. 2012. Managerial Economics: A Mathematical Approach. New York: John Wiley & Sons. [Google Scholar]
- Allen, Richard, Richard Hemming, and Barry Potter. 2013. The International Handbook of Public Financial Management. Berlin: Springer. [Google Scholar]
- Alvarez, Antonio M., Eduardo G. Fidalgo, Richard J. Sexton, and Mingxia Zhang. 2000. Oligopsony power with uniform spatial pricing: Theory and application to milk processing in Spain. European Review of Agricultural Economics 27: 347–64. [Google Scholar] [CrossRef]
- Amaran, Satyajith, Nikolaos V. Sahinidis, Bikram Sharda, and Scott J. Bury. 2016. Simulation optimization: A review of algorithms and applications. Annals of Operations Research 240: 351–80. [Google Scholar]
- Amelian, Sayed Shahab, Seyed Mojtaba Sajadi, Mehrzad Navabakhsh, and Majid Esmaelian. 2019. Multi-objective optimization for stochastic failure-prone job shop scheduling problem via hybrid of NSGA-II and simulation method. Expert Systems, e12455. [Google Scholar] [CrossRef]
- Annicchiarico, Barbara, and Enrico Marvasi. 2019. Protection for sale under monopolistic competition: Beyond the CES. European Journal of Political Economy 60: 101802. [Google Scholar] [CrossRef]
- Aringhieri, Roberto, Paolo Landa, Patrick Soriano, Elena Tànfani, and Angela Testi. 2015. A two level metaheuristic for the operating room scheduling and assignment problem. Computers & Operations Research 54: 21–34. [Google Scholar]
- Arnau, Quim, Angel A. Juan, and Isabel Serra. 2018. On the use of learnheuristics in vehicle routing optimization problems with dynamic inputs. Algorithms 11: 208. [Google Scholar] [CrossRef]
- Azadeh, Ali, Reza Skandari, and Babak Maleki-Shoja. 2010. An integrated ant colony optimization approach to compare strategies of clearing market in electricity markets: Agent-based simulation. Energy Policy 38: 6307–19. [Google Scholar] [CrossRef]
- Balderas, Fausto, Eduardo Fernandez, Claudia Gomez-Santillan, Nelson Rangel-Valdez, and Laura Cruz. 2019. An interval-based approach for evolutionary multi-objective optimization of project portfolios. International Journal of Information Technology & Decision Making 18: 1317–58. [Google Scholar]
- Baringo, Luis, and Raquel Sánchez Amaro. 2017. A stochastic robust optimization approach for the bidding strategy of an electric vehicle aggregator. Electric Power Systems Research 146: 362–70. [Google Scholar] [CrossRef]
- Baye, Michael R., Jeff Prince, and Jay Squalli. 2006. Managerial Economics and Business Strategy. New York: McGraw-Hill, vol. 5. [Google Scholar]
- Belkaid, Fayçal, Farouk Yalaoui, and Zaki Sari. 2016. An efficient approach for the reentrant parallel machines scheduling problem under consumable resources constraints. International Journal of Information Systems and Supply Chain Management (IJISSCM) 9: 1–25. [Google Scholar] [CrossRef]
- Besanko, David, David Dranove, Mark Shanley, and Scott Schaefer. 2009. Economics of Strategy. New York: John Wiley & Sons. [Google Scholar]
- Bhattacharya, Anagha, Swapan Kr Goswami, and Tanima Kole Bhowmik. 2017. Developing an optimization method for bidding strategies in an open electricity market. International Journal of Electrical Energy 5: 71–75. [Google Scholar] [CrossRef]
- Bianchi, Leonora, Marco Dorigo, Luca Maria Gambardella, and Walter J. Gutjahr. 2009. A survey on metaheuristics for stochastic combinatorial optimization. Natural Computing 8: 239–87. [Google Scholar] [CrossRef]
- Brass, Daniel J., Joseph Galaskiewicz, Henrich R. Greve, and Wenpin Tsai. 2004. Taking stock of networks and organizations: A multilevel perspective. Academy of Management Journal 47: 795–817. [Google Scholar]
- Buer, Tobias, and Herbert Kopfer. 2014. A pareto-metaheuristic for a bi-objective winner determination problem in a combinatorial reverse auction. Computers & Operations Research 41: 208–20. [Google Scholar]
- Cabrera, Guillem, Angel A. Juan, Daniel Lazaro, Joan M. Marques, and Iuliia Proskurnia. 2014. A simulation-optimization approach to deploy internet services in large-scale systems with user-provided resources. Simulation 90: 644–59. [Google Scholar] [CrossRef]
- Cai, Xiaowei, Kyle W. Stiegert, and Stephen R. Koontz. 2011. Oligopsony fed cattle pricing: Did mandatory price reporting increase meatpacker market power? Applied Economic Perspectives and Policy 33: 606–22. [Google Scholar] [CrossRef]
- Calvet, Laura, Jesica de Armas, David Masip, and Angel A. Juan. 2017. Learnheuristics: Hybridizing metaheuristics with machine learning for optimization with dynamic inputs. Open Mathematics 15: 261–80. [Google Scholar] [CrossRef]
- Calvet, Laura, Albert Ferrer, M. Isabel Gomes, Angel A. Juan, and David Masip. 2016. Combining statistical learning with metaheuristics for the multi-depot vehicle routing problem with market segmentation. Computers & Industrial Engineering 94: 93–104. [Google Scholar]
- Castillo-López, Iván, and Héctor A. López-Ospina. 2015. School location and capacity modification considering the existence of externalities in students school choice. Computers & Industrial Engineering 80: 284–94. [Google Scholar]
- Ciaffi, Francesco, Ernesto Cipriani, and Marco Petrelli. 2012. Feeder bus network design problem: A new metaheuristic procedure and real size applications. Procedia-Social and Behavioral Sciences 54: 798–807. [Google Scholar] [CrossRef]
- Crispim, José, Nazaré Rego, and Jorge Pinho de Sousa. 2015. Stochastic partner selection for virtual enterprises: A chance-constrained approach. International Journal of Production Research 53: 3661–77. [Google Scholar] [CrossRef]
- David, A. Kumar, and Fushuan Wen. 2000. Strategic bidding in competitive electricity markets: A literature survey. Paper presented at 2000 IEEE Power Engineering Society Summer Meeting (Cat. No. 00CH37134), Seattle, WA, USA, March 16–20, vol. 4, pp. 2168–73. [Google Scholar]
- Dean, Joel. 1951. Measurement of profits for executive decisions. The Accounting Review 26: 185–96. [Google Scholar]
- Dias, Lisia S., Richard C. Pattison, Calvin Tsay, Michael Baldea, and Marianthi G. Ierapetritou. 2018. A simulation-based optimization framework for integrating scheduling and model predictive control, and its application to air separation units. Computers & Chemical Engineering 113: 139–51. [Google Scholar]
- Douglas, Evan J. 1983. Managerial Economics: Theory, Practice, and Problems. New York: Prentice Hall. [Google Scholar]
- Dunke, Fabian, and Stefan Nickel. 2017. Evaluating the quality of online optimization algorithms by discrete event simulation. Central European Journal of Operations Research 25: 831–58. [Google Scholar] [CrossRef]
- Feenstra, Robert C. 2010. Measuring the gains from trade under monopolistic competition. Canadian Journal of Economics/Revue canadienne d’économique 43: 1–28. [Google Scholar] [CrossRef]
- Fernandez, Eduardo, Edy Lopez, Gustavo Mazcorro, Rafael Olmedo, and Carlos A. Coello. 2013. Application of the non-outranked sorting genetic algorithm to public project portfolio selection. Information Sciences 228: 131–49. [Google Scholar] [CrossRef]
- Ferone, Daniele, Aljoscha Gruler, Paola Festa, and Angel A. Juan. 2019. Enhancing and extending the classical GRASP framework with biased randomisation and simulation. Journal of the Operational Research Society 70: 1362–75. [Google Scholar] [CrossRef]
- Fikar, Christian, Angel A. Juan, Enoc Martinez, and Patrick Hirsch. 2016. A discrete-event driven metaheuristic for dynamic home service routing with synchronised trip sharing. European Journal of Industrial Engineering 10: 323–40. [Google Scholar] [CrossRef]
- Fishman, George S. 2013. Discrete-Event Simulation: Modeling, Programming, and Analysis. Berlin: Springer Science & Business Media. [Google Scholar]
- Fonseca, Fagno, Marcelo Lisboa, David Prata, and Patrick Letouze. 2015. A decision-making technique for financial grant allocation to research projects. International Proceedings of Economics Development and Research 85: 119. [Google Scholar]
- Ghosh, Piyali, and Purba Roy Chowdhury. 2008. Managerial Economics. New York: McGraw-Hill Education. [Google Scholar]
- Göçken, Mustafa, Mehmet Özçalıcı, Aslı Boru, and Ayşe Tuğba Dosdoğru. 2016. Integrating metaheuristics and artificial neural networks for improved stock price prediction. Expert Systems with Applications 44: 320–31. [Google Scholar] [CrossRef]
- Gonzalez-Martin, Sergio, Angel A. Juan, Daniel Riera, Monica G. Elizondo, and Juan J. Ramos. 2018. A simheuristic algorithm for solving the arc routing problem with stochastic demands. Journal of Simulation 12: 53–66. [Google Scholar] [CrossRef]
- Gonzalez-Neira, Eliana Maria, Daniele Ferone, Sara Hatami, and Angel A Juan. 2017. A biased-randomized simheuristic for the distributed assembly permutation flowshop problem with stochastic processing times. Simulation Modelling Practice and Theory 79: 23–36. [Google Scholar] [CrossRef]
- Graham, J. Edward, Carlos Lassala, and Belén Ribeiro-Navarrete. 2019. A fuzzy-set analysis of conditions influencing mutual fund performance. International Review of Economics & Finance 61: 324–36. [Google Scholar]
- Grasas, Alex, Angel A. Juan, Javier Faulin, Jesica de Armas, and Helena Ramalhinho. 2017. Biased randomization of heuristics using skewed probability distributions: A survey and some applications. Computers & Industrial Engineering 110: 216–28. [Google Scholar]
- Gravetter, Frederick J., and Lori-Ann B. Forzano. 2018. Research Methods for the Behavioral Sciences. Boston: Cengage Learning. [Google Scholar]
- Gruler, Aljoscha, Christian Fikar, Angel A. Juan, Patrick Hirsch, and C. Contreras-Bolton. 2017. Supporting multi-depot and stochastic waste collection management in clustered urban areas via simulation–optimization. Journal of Simulation 11: 11–19. [Google Scholar] [CrossRef]
- Gruler, Aljoscha, Javier Panadero, Jesica de Armas, Jose A. Moreno, and Angel A. Juan. 2018. Combining variable neighborhood search with simulation for the inventory routing problem with stochastic demands and stock-outs. Computers & Industrial Engineering 123: 278–88. [Google Scholar]
- Gruler, Aljoscha, Javier Panadero, Jesica de Armas, Jose A. Moreno, and Angel A. Juan. 2020. A variable neighborhood search simheuristic for the multiperiod inventory routing problem with stochastic demands. International Transactions in Operational Research 27: 314–35. [Google Scholar] [CrossRef]
- Gruler, Aljoscha, Carlos L. Quintero-Araújo, Laura Calvet, and Angel A. Juan. 2017. Waste collection under uncertainty: A simheuristic based on variable neighbourhood search. European Journal of Industrial Engineering 11: 228–55. [Google Scholar] [CrossRef]
- Gupta, Rajan, Sunil Kumar Muttoo, and Saibal K. Pal. 2019. Meta-heuristic algorithms to improve fuzzy c-means and k-means clustering for location allocation of telecenters under e-governance in developing nations. International Journal of Fuzzy Logic and Intelligent Systems 19: 290–98. [Google Scholar] [CrossRef]
- Haase, Knut, Lukas Knörr, Ralf Krohn, Sven Müller, and Michael Wagner. 2019. Facility location in the public sector. In Location Science. Berlin: Springer, pp. 745–64. [Google Scholar]
- Hamid, Mahdi, Mahdi Bastan, Mojtaba Hamid, and Farrokh Sheikhahmadi. 2019. Solving a stochastic multi-objective and multi-period hub location problem considering economic aspects by meta-heuristics: Application in public transportation. International Journal of Computer Applications in Technology 60: 183–202. [Google Scholar] [CrossRef]
- Hatami, Sara, Laura Calvet, Victor Fernandez-Viagas, Jose M. Framinan, and Angel A. Juan. 2018. A simheuristic algorithm to set up starting times in the stochastic parallel flowshop problem. Simulation Modelling Practice and Theory 86: 55–71. [Google Scholar] [CrossRef]
- Hirschey, Mark, and Eric Bentzen. 2016. Managerial Economics. Boston: Cengage Learning. [Google Scholar]
- Hussain, Kashif, Mohd Najib Mohd Salleh, Shi Cheng, and Yuhui Shi. 2019. Metaheuristic research: A comprehensive survey. Artificial Intelligence Review 52: 2191–2233. [Google Scholar] [CrossRef]
- Iliopoulou, Christina, Konstantinos Kepaptsoglou, and Eleni Vlahogianni. 2019. Metaheuristics for the transit route network design problem: A review and comparative analysis. Public Transport 11: 487–521. [Google Scholar] [CrossRef]
- Iliopoulou, Christina, Ioannis Tassopoulos, Konstantinos Kepaptsoglou, and Grigorios Beligiannis. 2019. Electric transit route network design problem: Model and application. Transportation Research Record 2673: 264–74. [Google Scholar] [CrossRef]
- Ivanov, Dmitry. 2017. Simulation-based ripple effect modelling in the supply chain. International Journal of Production Research 55: 2083–2101. [Google Scholar] [CrossRef]
- Jaafari, Abolfazl, Seyed Vahid Razavi Termeh, and Dieu Tien Bui. 2019. Genetic and firefly metaheuristic algorithms for an optimized neuro-fuzzy prediction modeling of wildfire probability. Journal of Environmental Management 243: 358–69. [Google Scholar] [CrossRef]
- Jourdan, Laetitia, Matthieu Basseur, and El-Ghazali Talbi. 2009. Hybridizing exact methods and metaheuristics: A taxonomy. European Journal of Operational Research 199: 620–29. [Google Scholar] [CrossRef]
- Juan, Angel A., W. David Kelton, Christine S. M. Currie, and Javier Faulin. 2018. Simheuristics applications: Dealing with uncertainty in logistics, transportation, and other supply chain areas. Paper presented at 2018 IEEE Winter Simulation Conference, Gothenburg, Sweden, December 9–12; pp. 3048–59. [Google Scholar]
- Karbowski, Adam. 2019. Cooperative and non-cooperative R&D in product innovation and firm performance. Journal of Business Economics and Management 20: 1121–42. [Google Scholar]
- Khalfalli, Marwa, Fouad Ben Abdelaziz, and Hichem Kamoun. 2019. Multi-objective surgery scheduling integrating surgeon constraints. Management Decision 57: 445–60. [Google Scholar] [CrossRef]
- Krugman, Paul, Robin Wells, and Kathryn Graddy. 2007. Economics: European Edition. New York: Worth Publishers. [Google Scholar]
- Kumar, Soumojit, and Ashis Kumar Chatterjee. 2015. A profit maximising product line optimisation model under monopolistic competition. International Journal of Production Research 53: 1584–95. [Google Scholar] [CrossRef]
- Ladjici, Ahmed A., Ahmed Tiguercha, and Mohamed Boudour. 2014. Nash equilibrium in a two-settlement electricity market using competitive coevolutionary algorithms. International Journal of Electrical Power & Energy Systems 57: 148–55. [Google Scholar]
- Law, Averill M. 2014. Simulation Modeling and Analysis, 5th ed. McGraw-Hill Series in Industrial Engineering and Management Science; New York: McGraw-Hill. [Google Scholar]
- Li, Hong-Nan, and Yu-Jing Li. 2019. Interactive multiobjective optimization for life-cycle analysis in seismic design of bridges. Journal of Engineering Mechanics 145: 04019050. [Google Scholar] [CrossRef]
- Lian, Kunlei, Chaoyong Zhang, Xinyu Shao, and Liang Gao. 2012. Optimization of process planning with various flexibilities using an imperialist competitive algorithm. The International Journal of Advanced Manufacturing Technology 59: 815–28. [Google Scholar] [CrossRef]
- Lin, Boliang, Yinan Zhao, and Ruixi Lin. 2020. Optimization for courier delivery service network design based on frequency delay. Computers & Industrial Engineering 139: 106144. [Google Scholar]
- Longo, Francesco, Luigi Siciliani, Hugh Gravelle, and Rita Santos. 2017. Do hospitals respond to rivals’ quality and efficiency? a spatial panel econometric analysis. Health Economics 26: 38–62. [Google Scholar] [CrossRef]
- Lopez-Garcia, Pedro, Eneko Osaba, Enrique Onieva, Antonio D. Masegosa, and Asier Perallos. 2016. Short-term traffic congestion forecasting using hybrid metaheuristics and rule-based methods: A comparative study. Paper presented at the Conference of the Spanish Association for Artificial Intelligence, Salamanca, Spain, September 14–16; Berlin: Springer, pp. 290–99. [Google Scholar]
- Lu, Xiaoshan, Jian Li, and Fengmei Yang. 2010. Analyses of location-price game on networks with stochastic customer behavior and its heuristic algorithm. Journal of Systems Science and Complexity 23: 701–14. [Google Scholar] [CrossRef]
- Luke, Sean. 2013. Essentials of Metaheuristics. Raleigh: Lulu. [Google Scholar]
- Luong, Binh, Pulkit Parikh, and Satish V. Ukkusuri. 2014. Metaheuristic approach for repositioning bicycles in a public bike-sharing system. Paper presented at the Transportation Research Board 93rd Annual Meeting, Washington, DC, USA, January 12–16. [Google Scholar]
- Ma, Xiao-Zhi, and Wen-Yuan Lv. 2019. Joint optimization of production and maintenance using monte carlo method and metaheuristic algorithms. Mathematical Problems in Engineering 2019: 1–22. [Google Scholar] [CrossRef]
- Manavizadeh, Neda, M. A. Yavari, and Hamed Farrokhi-Asl. 2017. Using metaheuristic algorithm to solve a multi objective portfolio selection problem: Application in renewable energy investment policy. International Journal of Applied 7: 21–44. [Google Scholar]
- Marynissen, Joren, and Erik Demeulemeester. 2019. Literature review on multi-appointment scheduling problems in hospitals. European Journal of Operational Research 272: 407–419. [Google Scholar] [CrossRef]
- Mathur, Somendra P. S., Anoop Arya, and Manisha Dubey. 2017. Optimal bidding strategy for price takers and customers in a competitive electricity market. Cogent Engineering 4: 1358545. [Google Scholar] [CrossRef]
- McGuigan, Jim. 2010. Creative labour, cultural work and individualisation. International Journal of Cultural Policy 16: 323–35. [Google Scholar] [CrossRef]
- Memmah, Mohamed-Mahmoud, Françoise Lescourret, Xin Yao, and Claire Lavigne. 2015. Metaheuristics for agricultural land use optimization: A review. Agronomy for Sustainable Development 35: 975–98. [Google Scholar] [CrossRef]
- Mendoza-Gómez, Rodolfo, Roger Z. Ríos-Mercado, and Karla B. Valenzuela-Ocaña. 2018. An iterated greedy algorithm with variable neighborhood descent for the planning of specialized diagnostic services in a segmented healthcare system. Journal of Industrial & Management Optimization 13: 1. [Google Scholar]
- Miskovic, Stefan, and Zorica Stanimirovic. 2016. Hybrid metaheuristic method for solving a multi-period emergency service location problem. Information Technology and Control 45: 321–37. [Google Scholar] [CrossRef]
- Moayedi, Hossein, Mahdy Khari, Mehdi Bahiraei, Loke Kok Foong, and Dieu Tien Bui. 2020. Spatial assessment of landslide risk using two novel integrations of neuro-fuzzy system and metaheuristic approaches; ardabil province, iran. Geomatics, Natural Hazards and Risk 11: 230–58. [Google Scholar] [CrossRef]
- Monahan, Kelly. 2018. How Behavioral Economics Influences Management Decision-Making: A New Paradigm. New York: Academic Press. [Google Scholar]
- Mousavi, Seyed Hosein, Ali Nazemi, and Ashkan Hafezalkotob. 2015. Using and comparing metaheuristic algorithms for optimizing bidding strategy viewpoint of profit maximization of generators. Journal of Industrial Engineering International 11: 59–72. [Google Scholar] [CrossRef][Green Version]
- Nolz, Pamela C., Karl F. Doerner, Walter J. Gutjahr, and Richard F. Hartl. 2010. A bi-objective metaheuristic for disaster relief operation planning. In Advances in Multi-Objective Nature Inspired Computing. Berlin: Springer, pp. 167–87. [Google Scholar]
- Pages-Bernaus, Adela, Helena Ramalhinho, Angel A. Juan, and Laura Calvet. 2019. Designing e-commerce supply chains: A stochastic facility–location approach. International Transactions in Operational Research 26: 507–528. [Google Scholar] [CrossRef]
- Pan, Quan-Ke, Liang Gao, Li Xin-Yu, and Framinan M. Jose. 2019. Effective constructive heuristics and meta-heuristics for the distributed assembly permutation flowshop scheduling problem. Applied Soft Computing 81: 105492. [Google Scholar] [CrossRef]
- Panadero, Javier, Jana Doering, Renatas Kizys, Angel A. Juan, and Angels Fito. 2020. A variable neighborhood search simheuristic for project portfolio selection under uncertainty. Journal of Heuristics 26: 353–75. [Google Scholar] [CrossRef]
- Panin, Artem A., Mikhail G. Pashchenko, and Aleksandr V. Plyasunov. 2014. Bilevel competitive facility location and pricing problems. Automation and Remote Control 75: 715–27. [Google Scholar] [CrossRef]
- Parenti, Mathieu, Philip Ushchev, and Jacques-François Thisse. 2017. Toward a theory of monopolistic competition. Journal of Economic Theory 167: 86–115. [Google Scholar] [CrossRef]
- Perloff, Jeffrey M., and James A. Brander. 2017. Managerial Economics and Strategy. Londo: Pearson. [Google Scholar]
- Porter, Michael E. 2011. Competitive Advantage of Nations: Creating and Sustaining Superior Performance. New York: Simon and Schuster. [Google Scholar]
- Pourghasemi, Hamid Reza, Seyed Vahid Razavi-Termeh, Narges Kariminejad, Haoyuan Hong, and Wei Chen. 2020. An assessment of metaheuristic approaches for flood assessment. Journal of Hydrology 582: 124536. [Google Scholar] [CrossRef]
- Rabe, Markus, Maik Deininger, and Angel A. Juan. 2020. Speeding up computational times in simheuristics combining genetic algorithms with discrete-event simulation. Simulation Modelling Practice and Theory 103: 102089. [Google Scholar] [CrossRef]
- Raza, Syed Asif, Faseela Chakkalakkal Abdullakutty, Sivakumar Rathinam, and Srikrishna Madhumohan Govindaluri. 2019. Multi-objective framework for process mean selection and price differentiation with leakage effects under price-dependent stochastic demand. Computers & Industrial Engineering 127: 698–708. [Google Scholar]
- Rego, Nazaré, João Claro, and Jorge Pinho de Sousa. 2014. A hybrid approach for integrated healthcare cooperative purchasing and supply chain configuration. Health Care Management Science 17: 303–20. [Google Scholar] [CrossRef]
- Rezaeiahari, Mandana, and Mohammad T. Khasawneh. 2020. Simulation optimization approach for patient scheduling at destination medical centers. Expert Systems with Applications 140: 112881. [Google Scholar] [CrossRef]
- Robbins, Matthew J., and Brian J. Lunday. 2016. A bilevel formulation of the pediatric vaccine pricing problem. European Journal of Operational Research 248: 634–45. [Google Scholar] [CrossRef]
- Rodriguez, Diego A., Paola P. Oteiza, and Nélida B. Brignole. 2019. An urban transportation problem solved by parallel programming with hyper-heuristics. Engineering Optimization 51: 1965–79. [Google Scholar] [CrossRef]
- Sadeghi, Ali, and Mostafa Zandieh. 2011. A game theory-based model for product portfolio management in a competitive market. Expert Systems with Applications 38: 7919–23. [Google Scholar] [CrossRef]
- Salamat, Vahid Reza, Alireza Aliahmadi, Mir Saman Pishvaee, and Khalid Hafeez. 2016. Assessing partnership alternatives in an IT network employing analytical methods. Scientific Programming 2016: 1–18. [Google Scholar] [CrossRef]
- Samuelson, William, and Stephen G. Marks. 2015. Managerial Economics, 8th ed. New York: John Wiley & Sons. [Google Scholar]
- Sauvey, Christophe, Teresa Melo, and Isabel Correia. 2020. Heuristics for a multi-period facility location problem with delayed demand satisfaction. Computers & Industrial Engineering 139: 106171. [Google Scholar]
- Spencer, Milton H., and Louis Siegelman. 1959. Managerial Economics. Merced County: Irwin. [Google Scholar]
- Talbi, El-Ghazali. 2009. Metaheuristics: From Design to Implementation. New York: John Wiley & Sons, vol. 74. [Google Scholar]
- Tang, Yi, Jing Ling, Tingting Ma, Ning Chen, Xiaofeng Liu, and Bingtuan Gao. 2017. A game theoretical approach based bidding strategy optimization for power producers in power markets with renewable electricity. Energies 10: 627. [Google Scholar] [CrossRef]
- Tsao, Yu-Chung, Thuy-Linh Vu, and Lu-Wen Liao. 2020. Hybrid heuristics for the cut ordering planning problem in apparel industry. Computers & Industrial Engineering 144: 106478. [Google Scholar]
- Turek, Wojciech, Leszek Siwik, Marek Kisiel-Dorohinicki, Sebastian Łakomy, Piotr Kala, and Aleksander Byrski. 2017. Real-time metaheuristic-based urban crossroad management with multi-variant planning. Journal of Computational Science 23: 240–48. [Google Scholar] [CrossRef]
- Uvaraja, Vikneswary, and Lai Soon Lee. 2017. Metaheuristic approaches for urban transit scheduling problem: A review. Journal of Advanced Review on Scientific Research 34: 11–25. [Google Scholar]
- Vanderbei, Robert J. 2015. Linear Programming. Berlin: Springer. [Google Scholar]
- Wang, Jian, and De-bi Cao. 2008. Relationships between two approaches for planning manufacturing strategy: A strategic approach and a paradigmatic approach. International Journal of Production Economics 115: 349–61. [Google Scholar] [CrossRef]
- Wen, Fushuan, and A. Kumar David. 2001. Optimal bidding strategies for competitive generators and large consumers. International Journal of Electrical Power & Energy Systems 23: 37–43. [Google Scholar]
- Werden, Gregory J., Luke M. Froeb, and Steven Tschantz. 2005. The effects of merger efficiencies on consumers of differentiated products. European Competition Journal 1: 245–64. [Google Scholar] [CrossRef][Green Version]
- Xavier, Clahildek Matos, Marly Guimarães Fernandes Costa, and Cícero Ferreira Fernandes Costa Filho. 2020. Combining facility-location approaches for public schools expansion. IEEE Access 8: 24229–241. [Google Scholar] [CrossRef]
- Xie, Lin, Marius Merschformann, Natalia Kliewer, and Leena Suhl. 2017. Metaheuristics approach for solving personalized crew rostering problem in public bus transit. Journal of Heuristics 23: 321–47. [Google Scholar] [CrossRef]
- Xu, Haitao, and Jing Ying. 2019. A hybrid and adaptive metaheuristic for the rebalancing problem in public bicycle systems. International Journal of Intelligent Transportation Systems Research 17: 161–70. [Google Scholar] [CrossRef]
- Yang, Sheng Luo, Z. G. Xu, and J. Y. Wang. 2019. Modelling and production configuration optimization for an assembly shop. International Journal of Simulation Modelling 18: 366–77. [Google Scholar] [CrossRef]
- Zhang, Hui, Thomas J. Best, Anton Chivu, and David O. Meltzer. 2019. Simulation-based optimization to improve hospital patient assignment to physicians and clinical units. Health Care Management Science 23: 117–41. [Google Scholar] [CrossRef]
- Zhang, Tao, Gang Ren, and Yang Yang. 2020. Transit route network design for low-mobility individuals using a hybrid metaheuristic approach. Journal of Advanced Transportation 2020: 1–12. [Google Scholar] [CrossRef]
- Zhou, Wenhui, and Weixiang Huang. 2016. Contract designs for energy-saving product development in a monopoly. European Journal of Operational Research 250: 902–13. [Google Scholar] [CrossRef]




© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Calvet, L.; de la Torre, R.; Goyal, A.; Marmol, M.; Juan, A.A. Modern Optimization and Simulation Methods in Managerial and Business Economics: A Review. Adm. Sci. 2020, 10, 47. https://doi.org/10.3390/admsci10030047
Calvet L, de la Torre R, Goyal A, Marmol M, Juan AA. Modern Optimization and Simulation Methods in Managerial and Business Economics: A Review. Administrative Sciences. 2020; 10(3):47. https://doi.org/10.3390/admsci10030047
Chicago/Turabian StyleCalvet, Laura, Rocio de la Torre, Anita Goyal, Mage Marmol, and Angel A. Juan. 2020. "Modern Optimization and Simulation Methods in Managerial and Business Economics: A Review" Administrative Sciences 10, no. 3: 47. https://doi.org/10.3390/admsci10030047
APA StyleCalvet, L., de la Torre, R., Goyal, A., Marmol, M., & Juan, A. A. (2020). Modern Optimization and Simulation Methods in Managerial and Business Economics: A Review. Administrative Sciences, 10(3), 47. https://doi.org/10.3390/admsci10030047





