Modelling the Kinetics of Elements Release from a Zeolitic-Rich Tuff
Abstract
1. Introduction
- (i)
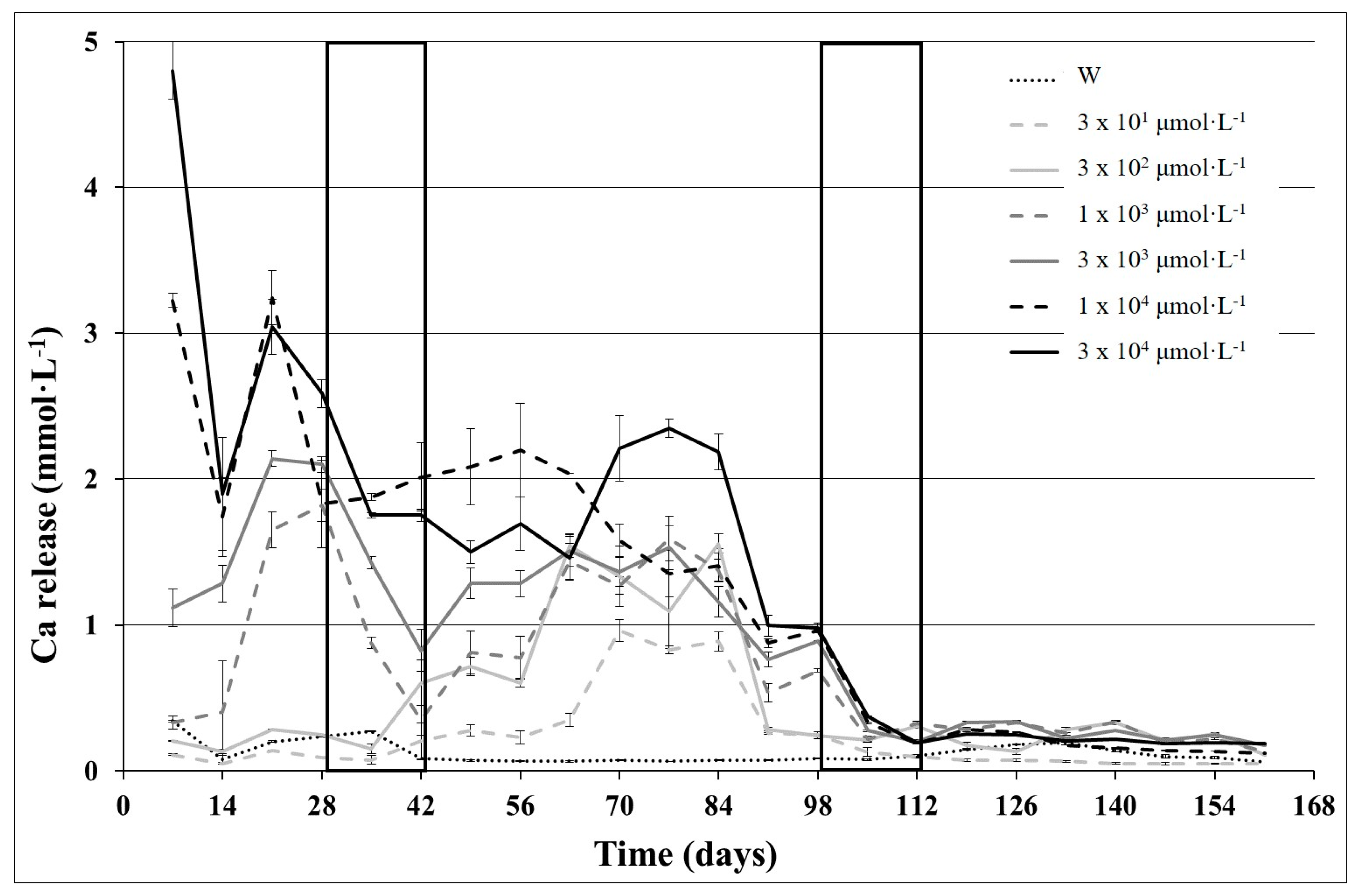
- the weathering effectiveness of the different solutions is quite proportional to the order of exponential magnitude of the TA concentration, viz. 0 < n × 101 µmol·L−1 ≅ n × 102 µmol·L−1 < n × 103 µmol·L−1 < n × 104 µmol·L−1;
- (ii)
- the variability of electrical conductivity and proton budget activity of rock/solutions, as well as the elements release seem to be differentiated in three distinct temporal stages, probably due to the weathering of different mineralogical phases over time.
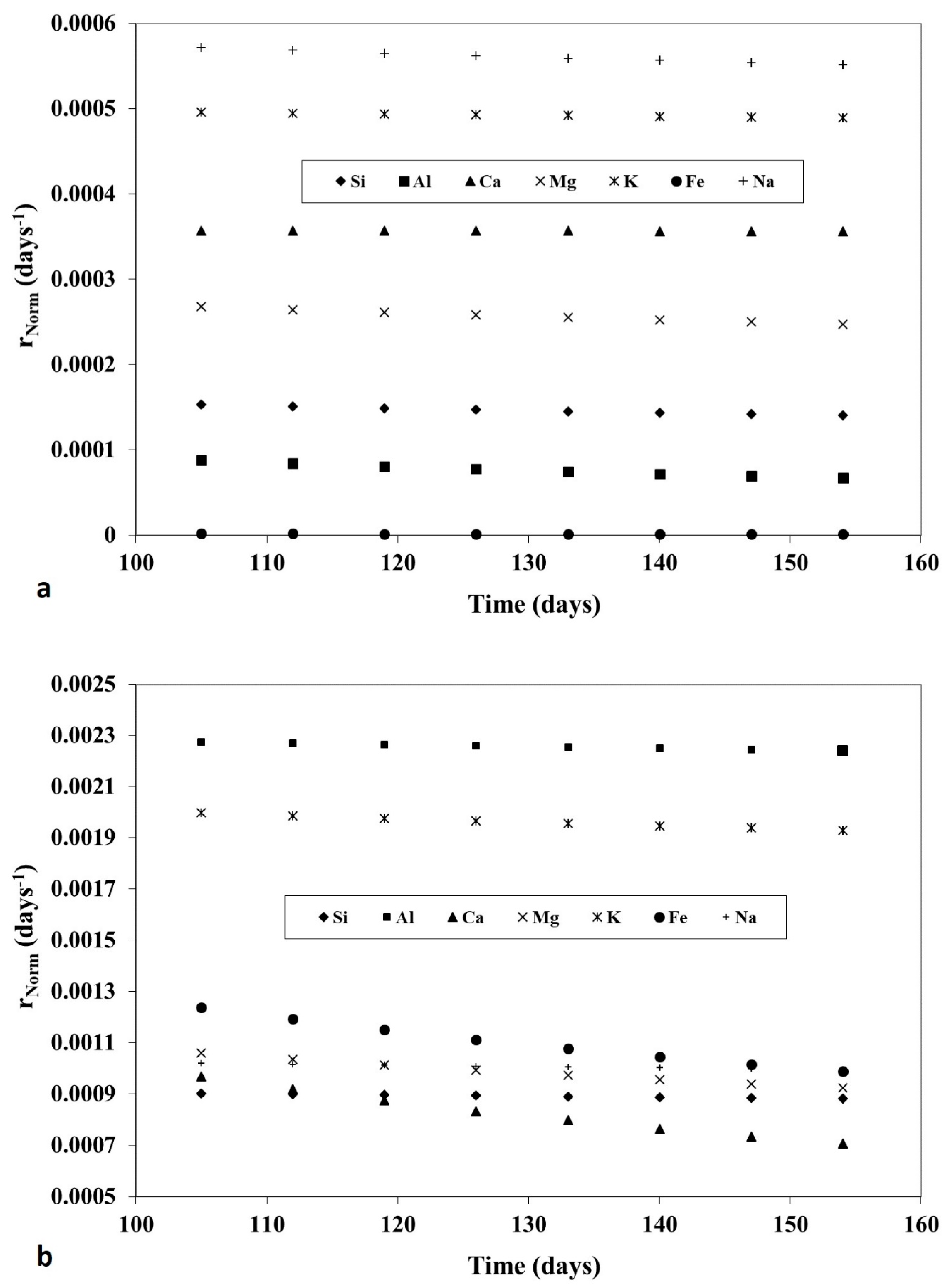
- ▪ finding kinetic models best fitting the observed, complex elements release;
- ▪ identifying the mineral phases involved, step by step, on elements release, with special reference to potassium taking into account its already mentioned importance as plant nutrient (vide supra).
2. Materials and Methods
2.1. Previous Phlegraean Yellow Tuff (PYT) Weathering Experiment
2.2. Kinetic Models
3. Results
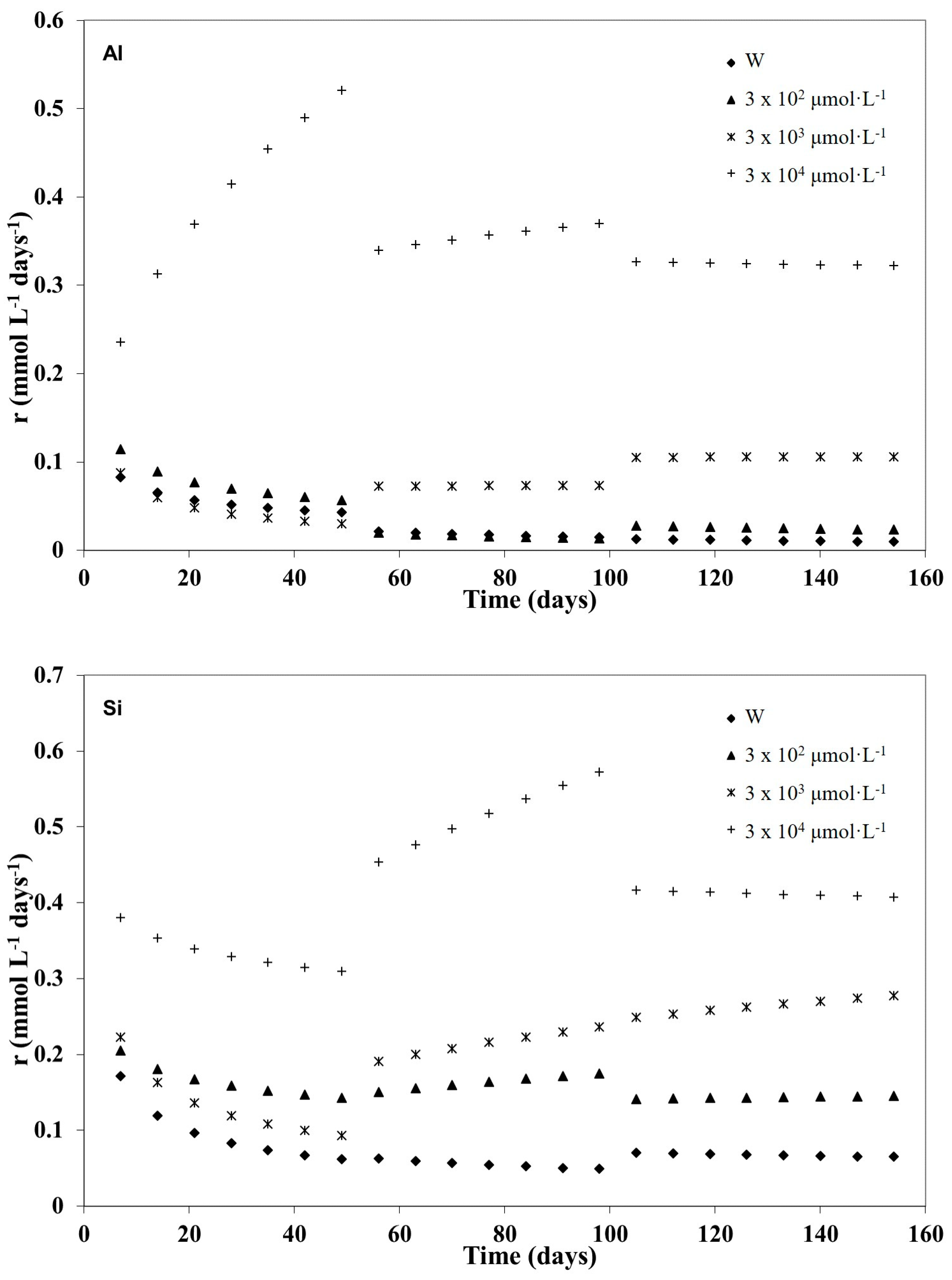
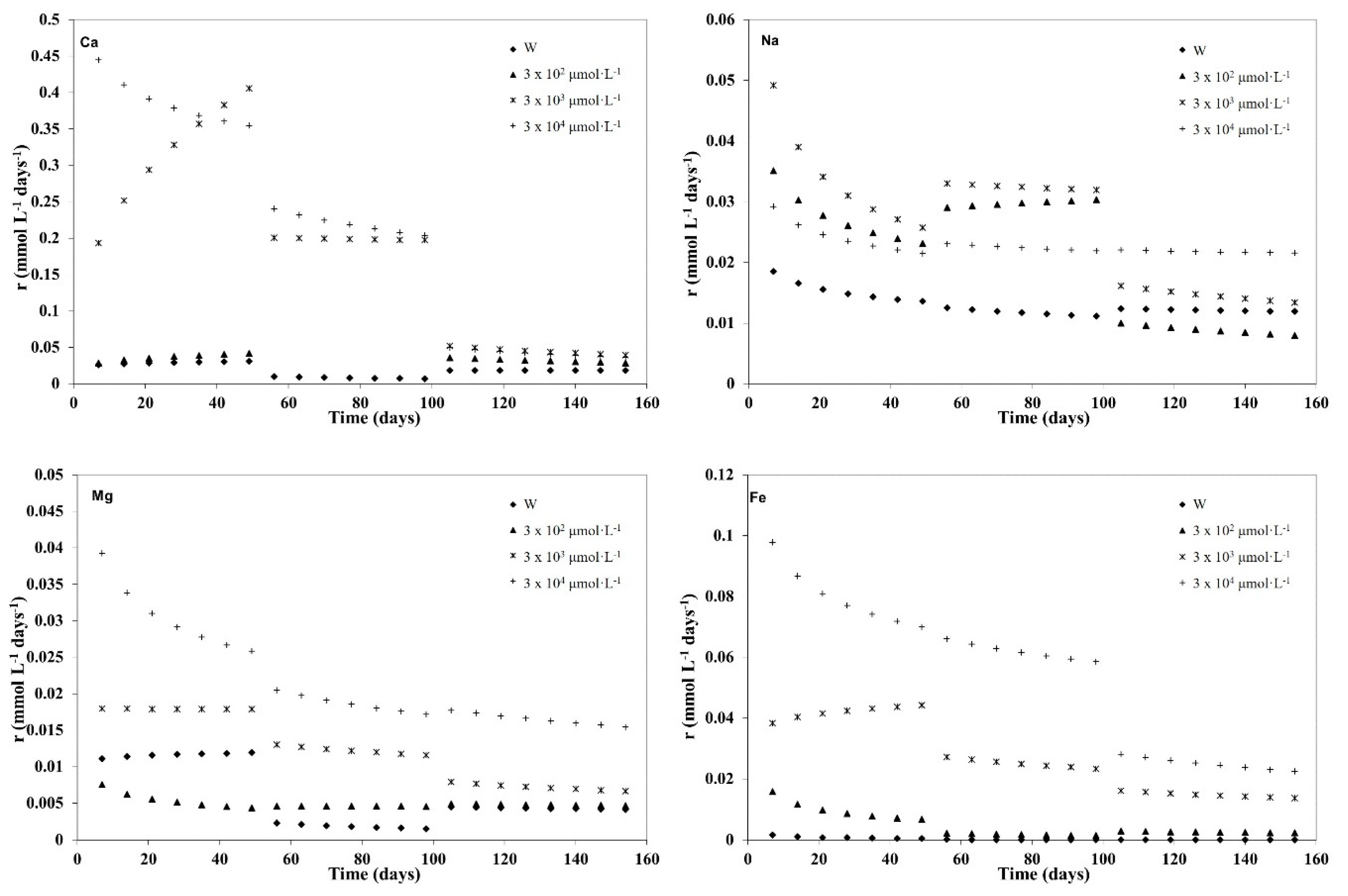
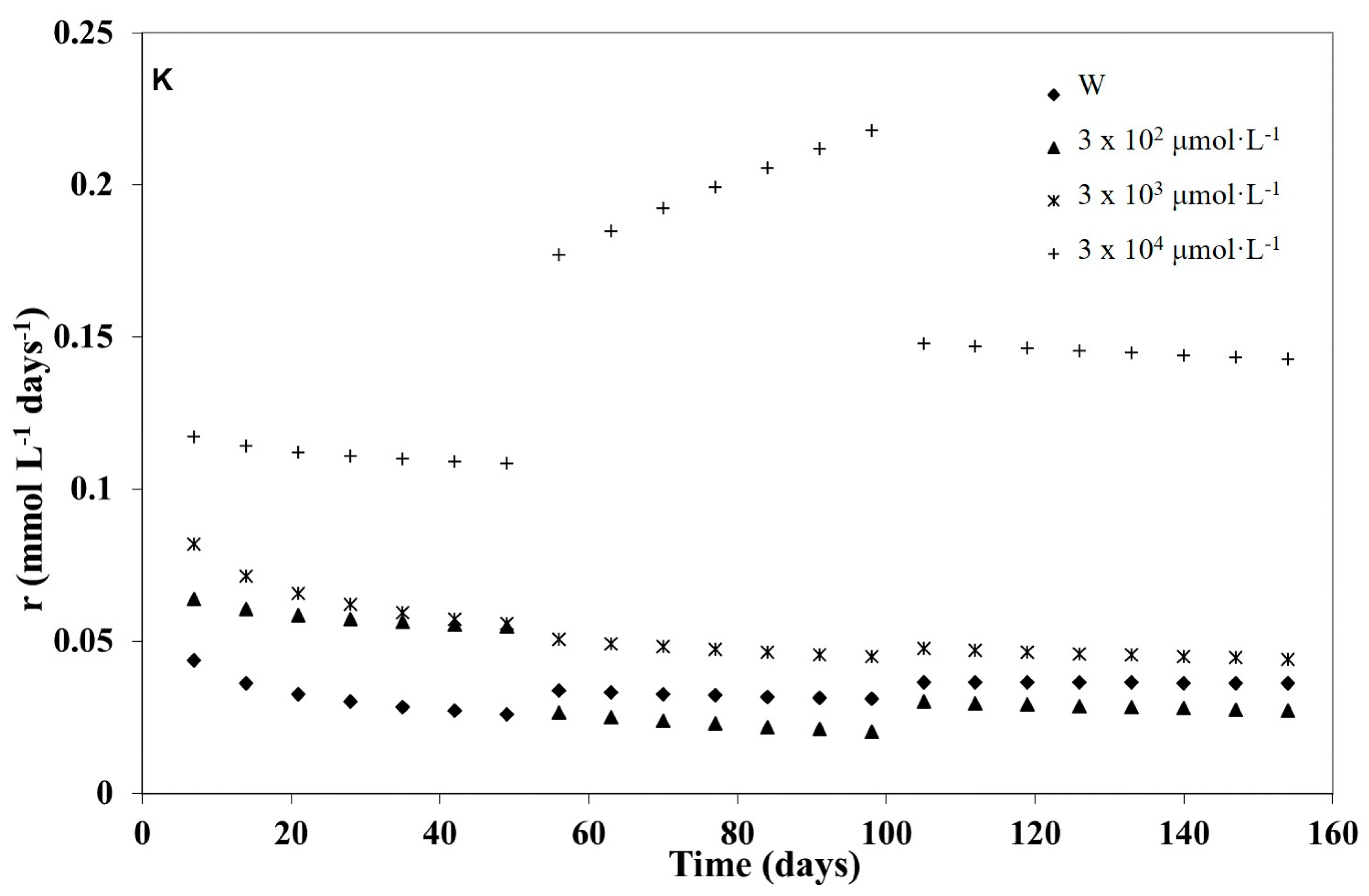
3.1. Kinetic Modelling
3.2. Kinetic Analysis of the Three Weathering Stages
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Aainaa, H.N.; Ahmed, O.H.; Majid, N.M.A. Effects of clinoptilolite zeolite on phosphorus dynamics and yield of Zea Mays L. cultivated on an acid soil. PLoS ONE 2018, 13, e0204401. [Google Scholar] [CrossRef]
- Ming, D.W.; Allen, E.R. Use of natural zeolites in agronomy, horticulture, and environmental soil remediation. Rev. Mineral. Geochem. 2001, 45, 618–654. [Google Scholar] [CrossRef]
- Doula, M.K.; Kavvadias, V.A.; Elaiopoulos, K. Zeolites in soil remediation processes. In Handbook of Natural Zeolites; Bentham Science Publishers: Sharjah, UAE, 2012; pp. 519–568. [Google Scholar]
- Hamidpour, M.; Shariatmadari, H.; Soleimani, M. Zeoponic systems. In Handbook of Natural Zeolites; Bentham Science Publishers: Sharjah, UAE, 2012; pp. 588–600. [Google Scholar]
- Margeta, K.; Zabukovec, N.; Siljeg, M.; Farkas, A. Natural Zeolites in Water Treatment—How Effective is Their Use. In Water Treatment; InTechOpen Ltd.: London, UK, 2013. [Google Scholar]
- Filcheva, E.; Chakalov, K. Soil fertility management with zeolite amendments. i. effect of zeolite on carbon sequestration: A review. In Agricultural Practices and Policies for Carbon Sequestration in Soil; CRC Press: Boca Raton, FL, USA, 2016; pp. 223–228. [Google Scholar]
- Soudejani, H.T.; Kazemian, H.; Inglezakis, V.J.; Zorpas, A.A. Application of zeolites in organic waste composting: A review. Biocatal. Agric. Biotechnol. 2019, 22, 101396. [Google Scholar] [CrossRef]
- Montalvo, S.; Huiliñir, C.; Borja, R.; Sánchez, E.; Herrmann, C. Application of zeolites for biological treatment processes of solid wastes and wastewaters—A review. Bioresour. Technol. 2020, 301. [Google Scholar] [CrossRef] [PubMed]
- Salvestrini, S.; Vanore, P.; Iovino, P.; Leone, V.; Capasso, S. Adsorption of simazine and boscalid onto acid-activated natural clinoptilolite. Environ. Eng. Manag. J. 2015, 14, 1705–1712. [Google Scholar] [CrossRef]
- Gkotsis, P.; Peleka, E.; Zouboulis, A. The Use of Natural Minerals in a Pilot-Scale MBR for Membrane Fouling Mitigation. Separations 2020, 7, 24. [Google Scholar] [CrossRef]
- Vera-Puerto, I.; Saravia, M.; Olave, J.; Arias, C.; Alarcon, E.; Valdes, H. Potential Application of Chilean Natural Zeolite as a Support Medium in Treatment Wetlands for Removing Ammonium and Phosphate from Wastewater. Water 2020, 12, 1156. [Google Scholar] [CrossRef]
- Salvestrini, S.; Sagliano, P.; Iovino, P.; Capasso, S.; Colella, C. Atrazine adsorption by acid-activated zeolite-rich tuffs. Appl. Clay Sci. 2010, 49, 330–335. [Google Scholar] [CrossRef]
- Leone, V.; Canzano, S.; Iovino, P.; Salvestrini, S.; Capasso, S. A novel organo-zeolite adduct for environmental applications: Sorption of phenol. Chemosphere 2013, 91, 415–420. [Google Scholar] [CrossRef]
- Kuntubek, A.; Kinayat, N.; Meiramkulova, K.; Poulopoulos, S.; Bear, J.C.; Inglezakis, V.J. Catalytic Oxidation of Methylene Blue by Use of Natural Zeolite-Based Silver and Magnetite Nanocomposites. Processes 2020, 8, 471. [Google Scholar] [CrossRef]
- Leone, V.; Iovino, P.; Salvestrini, S.; Capasso, S. Sorption of non-ionic organic pollutants onto a humic acids-zeolitic tuff adduct: Thermodynamic aspects. Chemosphere 2014, 95, 75–80. [Google Scholar] [CrossRef]
- Naumova, L.; Gorlenko, N.; Kurzina, I. Photocatalytic Activity of the Iron-Containing Natural Composites in the Reaction of Oxidative Destruction of Oxalic Acid and Phenol. Environments 2018, 5, 16. [Google Scholar] [CrossRef]
- Buondonno, A.; Coppola, E.; Bucci, M.; Battaglia, G.; Colella, A.; Langella, A.; Colella, C. Zeolitized tuffs as pedogenic substrate for soil re-building. Early evolution of zeolite/organic matter proto-horizons. Stud. Surf. Sci. Catal. 2002, 142, 1751–1758. [Google Scholar]
- Buondonno, A.; Colella, A.; Coppola, E.; de Gennaro, B.; de’ Gennaro, M.; Gargiulo, N.; Langella, A.; Leone, A.P.; Letizia, A.; Rubino, M.; et al. Properties of zeolitized tuff/organic matter aggregates relevant for their use in pedotechnique. III: Organic matter stability and exchange properties. Stud. Surf. Sci. Catal. 2007, 170, 2141–2146. [Google Scholar]
- Buondonno, A.; Colella, A.; Coppola, E.; de Gennaro, B.; Gargiulo, N.; Langella, A.; Letizia, A.; Colella, C. Properties of zeolitized tuff/organic matter aggregates relevant for their use in pedotechnique. IIb: Structural characterization with emphasis on surface and porosity properties. Stud. Surf. Sci. Catal. 2008, 174, 517–520. [Google Scholar] [CrossRef]
- Buondonno, A.; Grilli, E.; Capra, G.F.; Glorioso, C.; Langella, A.; Leone, A.P.; Leone, N.; Odierna, P.; Vacca, S.; Vigliotti, R.C. Zeolitized tuffs in pedotechnique for the reclamation of abandoned quarries. A case study in the Campania region (Italy). J. Environ. Manage. 2013, 122, 25–30. [Google Scholar] [CrossRef] [PubMed]
- Bucci, M.; Buondonno, A.; Colella, C.; Coppola, E.; Leone, A.P.; Mammucari, M. Properties of zeolitized tuff/organic matter aggregates relevant for their use in pedotechnique I. Chemical and physical-chemical properties. Stud. Surf. Sci. Catal. 2005, 155, 103–116. [Google Scholar]
- De Gennaro, B.; Aprea, P.; Colella, C.; Buondonno, A. Comparative ion-exchange characterization of zeolitic and clayey materials for pedotechnical applications-Part 1: Interaction with noxious cations. J. Porous Mater. 2007, 14, 349–356. [Google Scholar] [CrossRef]
- De Gennaro, B.; Aprea, P.; Colella, C.; Buondonno, A. Comparative ion-exchange characterization of zeolitic and clayey materials for pedotechnical applications—Part 2: Interaction with nutrient cations. J. Porous Mater. 2009, 16, 667–673. [Google Scholar] [CrossRef]
- Capra, G.F.; Buondonno, A.; Coppola, E.; Duras, M.G.; Vacca, S.; Colella, C. Zeolitized tuffs in pedotechniques to improve soil resilience against the impact of treatment by municipal sewage: Balance of nutrient and noxious cations. Clay Miner. 2011, 46, 261–278. [Google Scholar] [CrossRef]
- Capra, G.F.; Duras, M.G.; Vacca, S.; Grilli, E.; Buondonno, A. Issues concerning soils treated with wastewater: Pedotechnical management with zeolitized tuffs as an option for turning N and P pollutants into potential fertilizers. Microporous Mesoporous Mater. 2013, 167, 22–29. [Google Scholar] [CrossRef]
- Capra, G.F.; Grilli, E.; Macci, C.; Vacca, S.; Masciandaro, G.; Ceccanti, B.; Bondi, G.; Duras, M.G.; Dessena, M.A.; Marras, G.; et al. Lake-dredged material (LDM) in pedotechnique for the restoration of Mediterranean soils affected by erosion/entisolization processes. J. Soils Sediments 2014, 15, 32–46. [Google Scholar] [CrossRef]
- Wilson, G.; van Ouwerkerk, C. Pedotechnique, the link between pedology and engineering. Soil Tillage Res. 1987, 10, 1–3. [Google Scholar] [CrossRef]
- Koolen, A.J.; Rossignol, J.P. Introduction to symposium 19: Construction and use of artificial soils. Soil Tillage Res. 1998, 47, 151–155. [Google Scholar]
- Ming, D.W.; Boettinger, J.L. Zeolites in Soil Environments. Rev. Mineral. Geochem. 2018, 45, 323–346. [Google Scholar] [CrossRef]
- Grilli, E.; Colella, A.; Coppola, E.; Langella, A.; Buondonno, A. Modelling pedogenization of zeolitized tuff: Effects of water and phenolic substances on weathering rates of the Campanian Ignimbrite (yellow facies). Clay Miner. 2011, 46, 311–327. [Google Scholar] [CrossRef]
- Buondonno, A.; Colella, A.; Colella, C.; Coppola, E.; de’ Gennaro, B.; de’ Gennaro, M.; Gargiulo, N.; Grilli, E.; Langella, A.; Rubino, M. Modeling pedogenization of zeolitized tuffs. II: Medium-term weathering of phlegraean yellow tuff and red tuff with black scoriae by water and humic acids. Stud. Surf. Sci. Catal. 2007, 170, 2092–2097. [Google Scholar]
- Robarge, W.P. Precipitation/dissolution reactions in soils. In Soil Physical Chemistry, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2018; pp. 193–238. [Google Scholar]
- De Vivo, B.; Rolandi, G.; Gans, P.B.; Calvert, A.; Bohrson, W.A.; Spera, F.J.; Belkin, H.E. New constraints on the pyroclastic eruptive history of the Campanian volcanic Plain (Italy). Mineral. Petrol. 2001, 73, 47–65. [Google Scholar] [CrossRef]
- Kuo, S.; Lotse, E.G. Kinetics of Phosphate Adsorption and Desorption By Lake Sediments. Soil Sci. Soc. Am. J. 1974, 38, 50–54. [Google Scholar] [CrossRef]
- Havlin, J.L.; Westfall, D.G. Potassium Release Kinetics and Plant Response in Calcareous Soils. Soil Sci. Soc. Am. J. 1985, 49, 366–370. [Google Scholar] [CrossRef]
- Zhang, H.; Bloom, P.R. Dissolution Kinetics of Hornblende in Organic Acid Solutions. Soil Sci. Soc. Am. J. 1999, 63, 815–822. [Google Scholar] [CrossRef]
- Acosta-Vigil, A.; London, D.; Dewers, T.A.; Morgan VI, G.B. Dissolution of corundum and andalusite in H2O-saturated haplogranitic melts at 800 °C and 200 MPa: Constraints on diffusivities and the generation of peraluminous melts. J. Petrol. 2002, 43, 1885–1908. [Google Scholar] [CrossRef]
- Canzano, S.; Iovino, P.; Leone, V.; Salvestrini, S.; Capasso, S. Use and misuse of sorption kinetic data: A common mistake that should be avoided. Adsorpt. Sci. Technol. 2012, 30, 217–225. [Google Scholar] [CrossRef]
- Weber, W. Kinetics of Adsorption on Carbon from Solution. J. Sanit. Eng. Div. 1963, 89, 31–60. [Google Scholar]
- Salvestrini, S.; Vanore, P.; Bogush, A.; Mayadevi, S.; Campos, L.C. Sorption of metaldehyde using granular activated carbon. J. Water Reuse Desalin. 2017, 7, 280–287. [Google Scholar] [CrossRef]
- Gupta, G.S.; Prasad, G.; Singh, V.N. Removal of chrome dye from carpet effluents using coal-ii (rate processes). Environ. Technol. Lett. 1988, 9, 1413–1422. [Google Scholar] [CrossRef]
- Cheknane, B.; Zermane, F.; Baudu, M.; Bouras, O.; Basly, J.P. Sorption of basic dyes onto granulated pillared clays: Thermodynamic and kinetic studies. J. Colloid Interface Sci. 2012, 381, 158–163. [Google Scholar] [CrossRef]
- Salvestrini, S.; Canzano, S.; Iovino, P.; Leone, V.; Capasso, S. Modelling the biphasic sorption of simazine, imidacloprid, and boscalid in water/soil systems. J. Environ. Sci. Heal. B Pestic. Food Contam. Agric. Wastes 2014, 49, 578–590. [Google Scholar] [CrossRef]
- Chianese, S.; Fenti, A.; Iovino, P.; Musmarra, D.; Salvestrini, S. Sorption of organic pollutants by humic acids: A review. Molecules 2020, 25, 918. [Google Scholar] [CrossRef]
- Da Silva, A.D.A.S.; Sampaio, J.A.; Da Luz, A.B.; França, S.C.A.; Ronconi, C.M. Modeling controlled potassium release from phlogopite in solution: Exploring the viability of using crushed phlogopitite rock as an alternative potassium source in Brazilian soil. J. Braz. Chem. Soc. 2013, 24, 1366–1372. [Google Scholar] [CrossRef]
- Luce, R.W.; Bartlett, R.W.; Parks, G.A. Dissolution kinetics of magnesium silicates. Geochim. Cosmochim. Acta 1972, 36, 35–50. [Google Scholar] [CrossRef]
- Lin, F.C.; Clemency, C.V. The dissolution kinetics of brucite, antigorite, talc, and phlogopite at room temperature and pressure. Am. Mineral. 1981, 66, 801–806. [Google Scholar]
- Freund, T. Diffusion and gas sorption rates obeying the elovich equation. J. Chem. Phys. 1957, 26, 713. [Google Scholar] [CrossRef]
- He, Z.L.; Yao, H.; Calvert, D.V.; Stoffella, P.J.; Yang, X.E.; Chen, G.; Lloyd, G.M. Dissolution characteristics of central Florida phosphate rock in an acidic sandy soil. Plant Soil 2005, 273, 157–166. [Google Scholar] [CrossRef]
- Ding, Z.; Yin, Z.; Hu, H.; Chen, Q. Dissolution kinetics of zinc silicate (hemimorphite) in ammoniacal solution. Hydrometallurgy 2010, 104, 201–206. [Google Scholar] [CrossRef]
- Salvestrini, S. New insights into the interaction mechanism of humic acids with phillipsite. React. Kinet. Mech. Catal. 2017, 120, 735–752. [Google Scholar] [CrossRef]
- Colella, A.; de Gennaro, B.; Salvestrini, S.; Colella, C. Surface interaction of humic acids with natural and synthetic phillipsite. J. Porous Mater. 2015, 22, 501–509. [Google Scholar] [CrossRef]
- Lin, J.; Zhan, Y.; Zhu, Z.; Xing, Y. Adsorption of tannic acid from aqueous solution onto surfactant-modified zeolite. J. Hazard. Mater. 2011, 193, 102–111. [Google Scholar] [CrossRef]
- Iglesias, J.; García de Saldaña, E.; Jaén, J.A. On the tannic acid interaction with metallic iron. Hyperfine Interact. 2001, 134, 109–114. [Google Scholar] [CrossRef]
- Iffat, A.T.; Maqsood, Z.T.; Fatima, N. Study of complex formation of Fe(III) with tannic acid. J. Chem. Soc. Pakistan 2005, 27, 174–177. [Google Scholar]

| Kinetic Model | TA (μmol L−1) | Element | χ2 | R2 | Element | χ2 | R2 | Element | χ2 | R2 |
|---|---|---|---|---|---|---|---|---|---|---|
| Power function | 0 | Si | 5.68 | 0.969 | K | 0.06 | 0.999 | Na | 0.01 | 0.999 |
| 3 × 102 | 13.19 | 0.985 | 0.15 | 0.997 | 0.34 | 0.980 | ||||
| 3 × 103 | 96.40 | 0.967 | 0.19 | 0.999 | 0.17 | 0.994 | ||||
| 3 × 104 | 79.81 | 0.992 | 18.61 | 0.987 | 0.03 | 0.999 | ||||
| Weber–Morris equation | 0 | Si | 4.04 | 0.978 | K | 1.76 | 0.973 | Na | 0.15 | 0.980 |
| 3 × 102 | 61.37 | 0.931 | 0.35 | 0.994 | 0.22 | 0.987 | ||||
| 3 × 103 | 318.88 | 0.891 | 2.8 | 0.980 | 0.14 | 0.995 | ||||
| 3 × 104 | 695.75 | 0.934 | 66.9 | 0.952 | 0.85 | 0.970 | ||||
| Elovich equation | 0 | Si | 19.27 | 0.894 | K | 8.86 | 0.865 | Na | 0.92 | 0.884 |
| 3 × 102 | 177.67 | 0.802 | 4.14 | 0.926 | 0.99 | 0.943 | ||||
| 3 × 103 | 768.35 | 0.737 | 16.39 | 0.881 | 1.59 | 0.940 | ||||
| 3 × 104 | 2113.4 | 0.799 | 245.41 | 0.826 | 3.97 | 0.860 | ||||
| Power function | 0 | Al | 0.76 | 0.973 | Fe | <0.01 | 0.780 | Ca | 0.29 | 0.976 |
| 3 × 102 | 1.22 | 0.978 | 0.05 | 0.918 | 28.78 | 0.922 | ||||
| 3 × 103 | 19.80 | 0.968 | 0.40 | 0.983 | 40.17 | 0.955 | ||||
| 3 × 104 | 68.84 | 0.989 | 1.75 | 0.986 | 74.96 | 0.955 | ||||
| Weber–Morris equation | 0 | Al | 0.85 | 0.97 | Fe | <0.01 | 0.766 | Ca | 0.45 | 0.963 |
| 3 × 102 | 1.21 | 0.978 | 0.01 | 0.978 | 24.57 | 0.933 | ||||
| 3 × 103 | 68.38 | 0.891 | 0.17 | 0.993 | 25.19 | 0.972 | ||||
| 3 × 104 | 198.58 | 0.968 | 0.80 | 0.994 | 66.56 | 0.960 | ||||
| Elovich equation | 0 | Al | 0.43 | 0.985 | Fe | <0.01 | 0.781 | Ca | 1.49 | 0.878 |
| 3 × 102 | 3.04 | 0.946 | 0.04 | 0.934 | 57.44 | 0.845 | ||||
| 3 × 103 | 165.83 | 0.735 | 0.70 | 0.970 | 37.38 | 0.959 | ||||
| 3 × 104 | 881.94 | 0.857 | 4.97 | 0.960 | 77.48 | 0.953 | ||||
| Power function | 0 | Mg | 0.03 | 0.968 | ||||||
| 3 × 102 | 0.02 | 0.983 | ||||||||
| 3 × 103 | 0.05 | 0.992 | ||||||||
| 3 × 104 | 0.08 | 0.997 | ||||||||
| Weber–Morris equation | 0 | Mg | 0.03 | 0.969 | ||||||
| 3 × 102 | 0.08 | 0.94 | ||||||||
| 3 × 103 | 0.02 | 0.997 | ||||||||
| 3 × 104 | 0.31 | 0.987 | ||||||||
| Elovich equation | 0 | Mg | 0.05 | 0.938 | ||||||
| 3 × 102 | 0.24 | 0.819 | ||||||||
| 3 × 103 | 0.41 | 0.939 | ||||||||
| 3 × 104 | 2.27 | 0.902 |
| Element | TA (μmol L−1) | First Weathering Stage (0–49 Days) | Middle Weathering Stage (49–98 Days) | Late Weathering Stage (98–161 Days) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| k | n | χ2 | R2 | k | n | χ2 | R2 | k | n | χ2 | R2 | ||
| Si | 0 | 1.01 | 0.47 | 0.06 | 0.995 | 0.70 | 0.55 | 0.02 | 0.996 | 0.25 | 0.78 | 0.09 | 0.991 |
| 3 × 102 | 0.36 | 0.81 | 0.12 | 0.984 | 0.04 | 1.27 | 7.14 | 0.898 | 0.09 | 1.08 | 0.59 | 0.991 | |
| 3 × 103 | 0.97 | 0.55 | 0.12 | 0.988 | 0.03 | 1.38 | 3.24 | 0.981 | 0.05 | 1.29 | 0.23 | 0.999 | |
| 3 × 104 | 0.52 | 0.89 | 0.71 | 0.988 | 0.06 | 1.42 | 4.63 | 0.994 | 0.58 | 0.94 | 5.37 | 0.989 | |
| Al | 0 | 0.24 | 0.66 | 0.09 | 0.983 | 0.82 | 0.35 | <0.01 | 0.998 | 1.02 | 0.31 | 0.01 | 0.982 |
| 3 × 102 | 0.36 | 0.64 | 0.36 | 0.939 | 1.21 | 0.29 | 0.01 | 0.899 | 0.50 | 0.52 | 0.04 | 0.989 | |
| 3 × 103 | 0.56 | 0.45 | 0.03 | 0.979 | 0.07 | 1.02 | 0.06 | 0.978 | 0.09 | 1.02 | 4.28 | 0.955 | |
| 3 × 104 | 0.08 | 1.41 | 1.77 | 0.975 | 0.16 | 1.15 | 0.52 | 0.991 | 0.41 | 0.96 | 10.51 | 0.989 | |
| Mg | 0 | 0.01 | 1.04 | <0.01 | 0.994 | 0.15 | 0.28 | <0.01 | 0.987 | 0.01 | 0.79 | <0.01 | 0.973 |
| 3 × 102 | 0.02 | 0.72 | <0.01 | 0.991 | 0.005 | 0.98 | <0.01 | 0.998 | 0.01 | 0.86 | <0.01 | 0.989 | |
| 3 × 103 | 0.02 | 1.00 | <0.01 | 0.999 | 0.04 | 0.79 | <0.01 | 0.998 | 0.12 | 0.54 | <0.01 | 0.987 | |
| 3 × 104 | 0.08 | 0.78 | <0.01 | 0.998 | 0.11 | 0.68 | <0.01 | 0.996 | 0.15 | 0.64 | 0.08 | 0.806 | |
| K | 0 | 0.10 | 0.73 | 0.01 | 0.985 | 0.07 | 0.85 | <0.01 | 0.999 | 0.04 | 0.97 | 0.01 | 0.997 |
| 3 × 102 | 0.08 | 0.92 | <0.01 | 0.998 | 0.34 | 0.52 | <0.01 | 0.995 | 0.14 | 0.73 | 0.02 | 0.997 | |
| 3 × 103 | 0.15 | 0.80 | <0.01 | 0.999 | 0.15 | 0.78 | 0.01 | 0.995 | 0.16 | 0.79 | 0.01 | 0.999 | |
| 3 × 104 | 0.13 | 0.96 | <0.01 | 0.999 | 0.03 | 1.37 | <0.01 | 0.999 | 0.25 | 0.91 | 0.10 | 0.990 | |
| Fe | 0 | 0.01 | 0.39 | <0.01 | 0.997 | 0.03 | 0.15 | <0.01 | 0.998 | 0.05 | 0.07 | <0.01 | 0.898 |
| 3 × 102 | 0.07 | 0.56 | <0.01 | 0.929 | 0.17 | 0.26 | <0.01 | 0.996 | 0.09 | 0.44 | <0.01 | 0.967 | |
| 3 × 103 | 0.03 | 1.07 | <0.01 | 0.999 | 0.11 | 0.73 | 0.01 | 0.985 | 0.21 | 0.57 | 0.01 | 0.953 | |
| 3 × 104 | 0.16 | 0.83 | <0.01 | 0.999 | 0.20 | 0.78 | <0.01 | 0.998 | 1.05 | 0.41 | <0.01 | 0.997 | |
| Na | 0 | 0.03 | 0.84 | <0.01 | 0.999 | 0.04 | 0.78 | <0.01 | 0.999 | 0.02 | 0.91 | <0.01 | 0.999 |
| 3 × 102 | 0.07 | 0.78 | 0.01 | 0.990 | 0.02 | 1.07 | <0.01 | 0.998 | 0.39 | 0.40 | <0.01 | 0.995 | |
| 3 × 103 | 0.14 | 0.67 | 0.02 | 0.984 | 0.04 | 0.94 | <0.01 | 0.999 | 0.30 | 0.52 | <0.01 | 0.998 | |
| 3 × 104 | 0.05 | 0.84 | <0.01 | 0.998 | 0.04 | 0.91 | <0.01 | 0.992 | 0.03 | 0.94 | 0.01 | 0.997 | |
| Ca | 0 | 0.02 | 1.09 | 0.02 | 0.943 | 0.26 | 0.40 | <0.01 | 0.997 | 0.02 | 0.99 | 0.02 | 0.965 |
| 3 × 102 | 0.02 | 1.20 | <0.01 | 0.988 | ND * | ND * | ND * | ND * | 1.37 | 0.41 | 0.04 | 0.995 | |
| 3 × 103 | 0.07 | 1.38 | 0.05 | 0.997 | 0.23 | 0.97 | 0.01 | 0.999 | 4.87 | 0.29 | 0.55 | 0.966 | |
| 3 × 104 | 0.63 | 0.88 | 1.95 | 0.940 | 1.12 | 0.70 | 0.24 | 0.991 | 12.50 | 0.18 | 1.22 | 0.923 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grilli, E.; Ganga, A.; Salvestrini, S. Modelling the Kinetics of Elements Release from a Zeolitic-Rich Tuff. Environments 2020, 7, 41. https://doi.org/10.3390/environments7060041
Grilli E, Ganga A, Salvestrini S. Modelling the Kinetics of Elements Release from a Zeolitic-Rich Tuff. Environments. 2020; 7(6):41. https://doi.org/10.3390/environments7060041
Chicago/Turabian StyleGrilli, Eleonora, Antonio Ganga, and Stefano Salvestrini. 2020. "Modelling the Kinetics of Elements Release from a Zeolitic-Rich Tuff" Environments 7, no. 6: 41. https://doi.org/10.3390/environments7060041
APA StyleGrilli, E., Ganga, A., & Salvestrini, S. (2020). Modelling the Kinetics of Elements Release from a Zeolitic-Rich Tuff. Environments, 7(6), 41. https://doi.org/10.3390/environments7060041







