The Use of Sentinel-3 Imagery to Monitor Cyanobacterial Blooms
Abstract
:1. Introduction
2. Materials and Methods
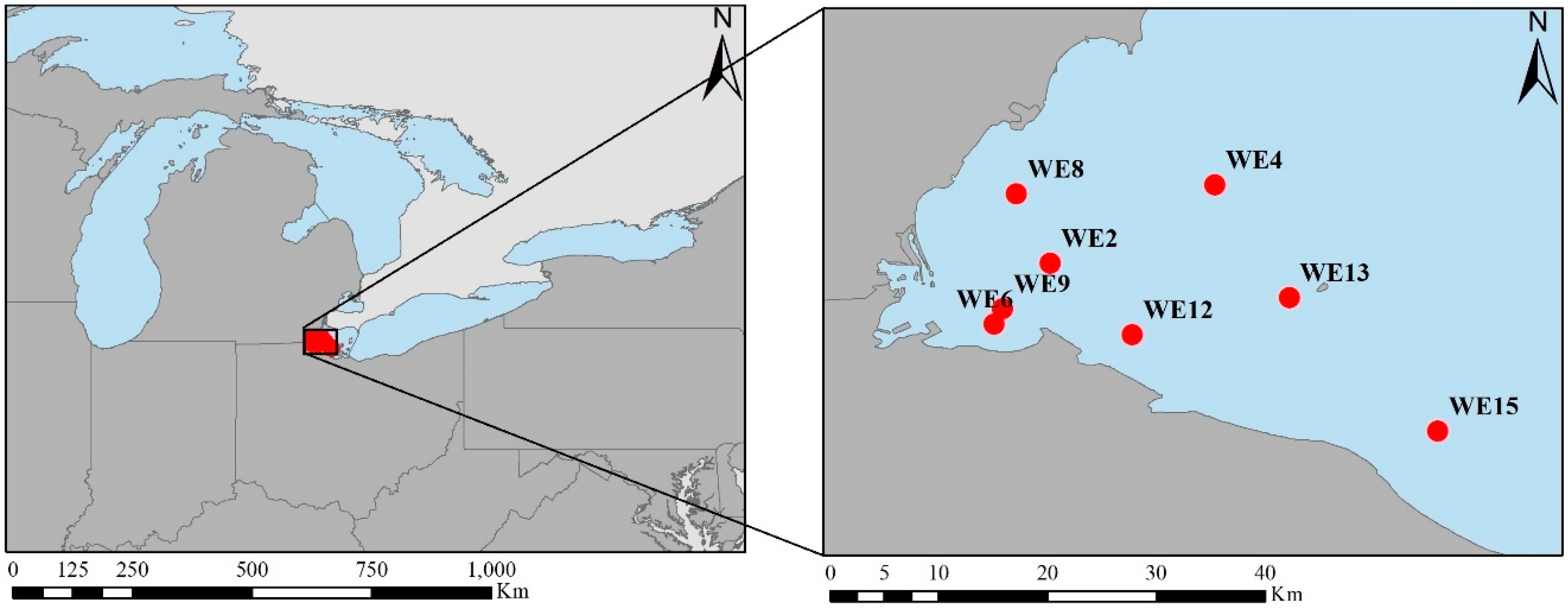
2.1. Study Site
2.2. Measured Pigments
2.3. Satellite Imagery
2.3.1. Data Acquisition
2.3.2. Atmospheric Correction
2.4. Evaluation of OLCI Imagery to Retrieve PC and chl-a
2.4.1. Atmospheric Correction Comparison
2.4.2. Remote Sensing Algorithms Comparison
2.4.3. OLCI Spectral Bands and Cyanobacterial Pigments
3. Results
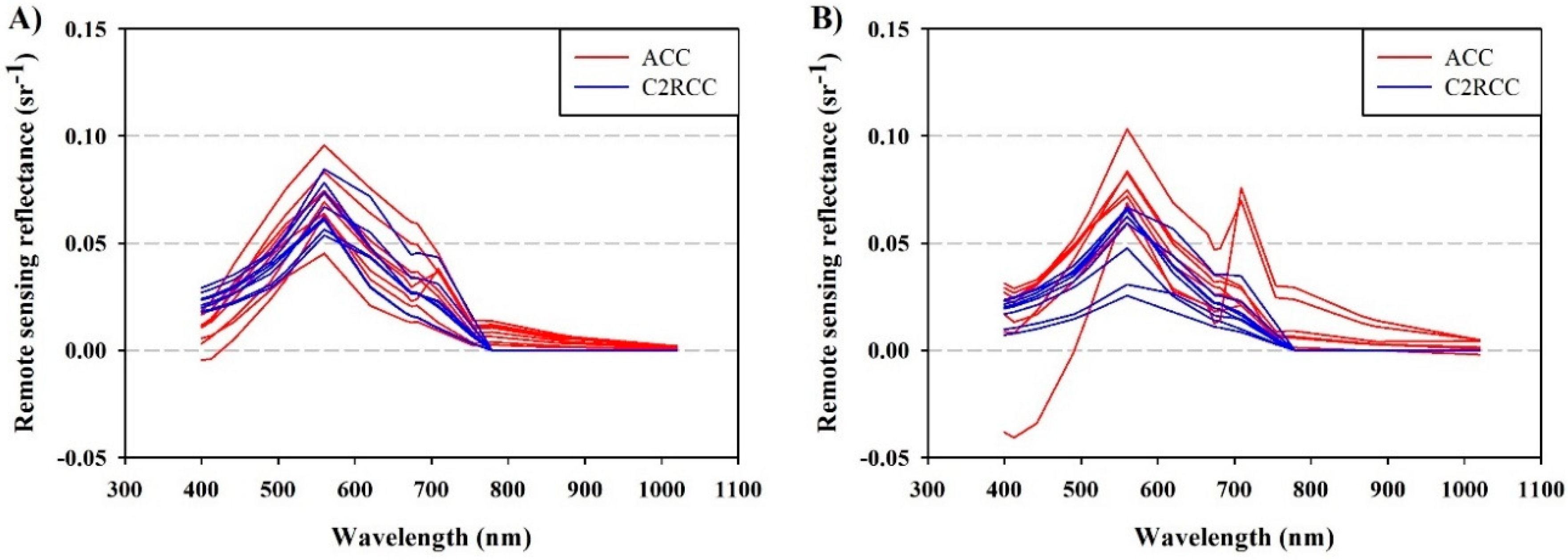
3.1. Atmospheric Correction of OLCI Images
3.2. Remote Sensing Models Evaluation
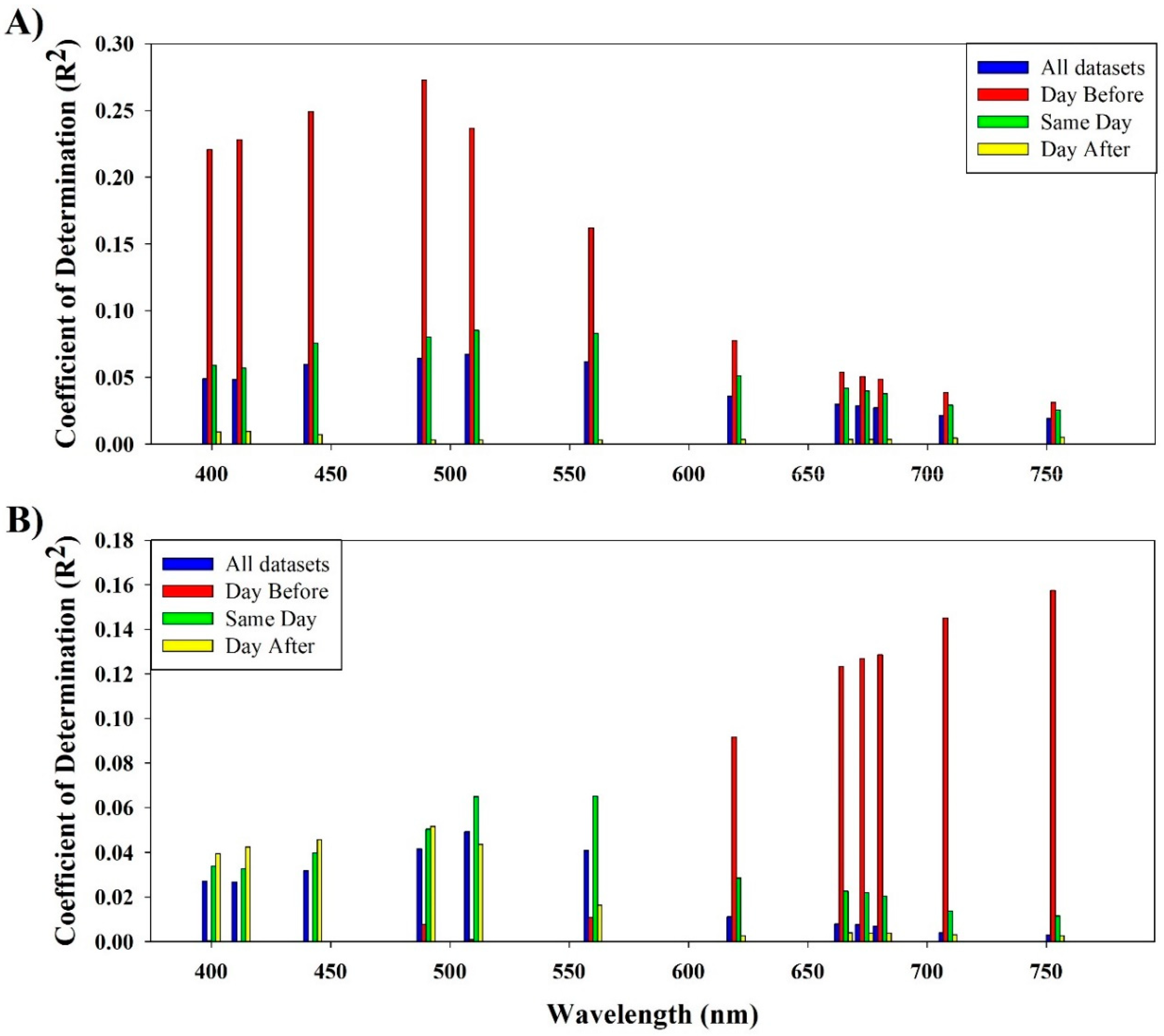
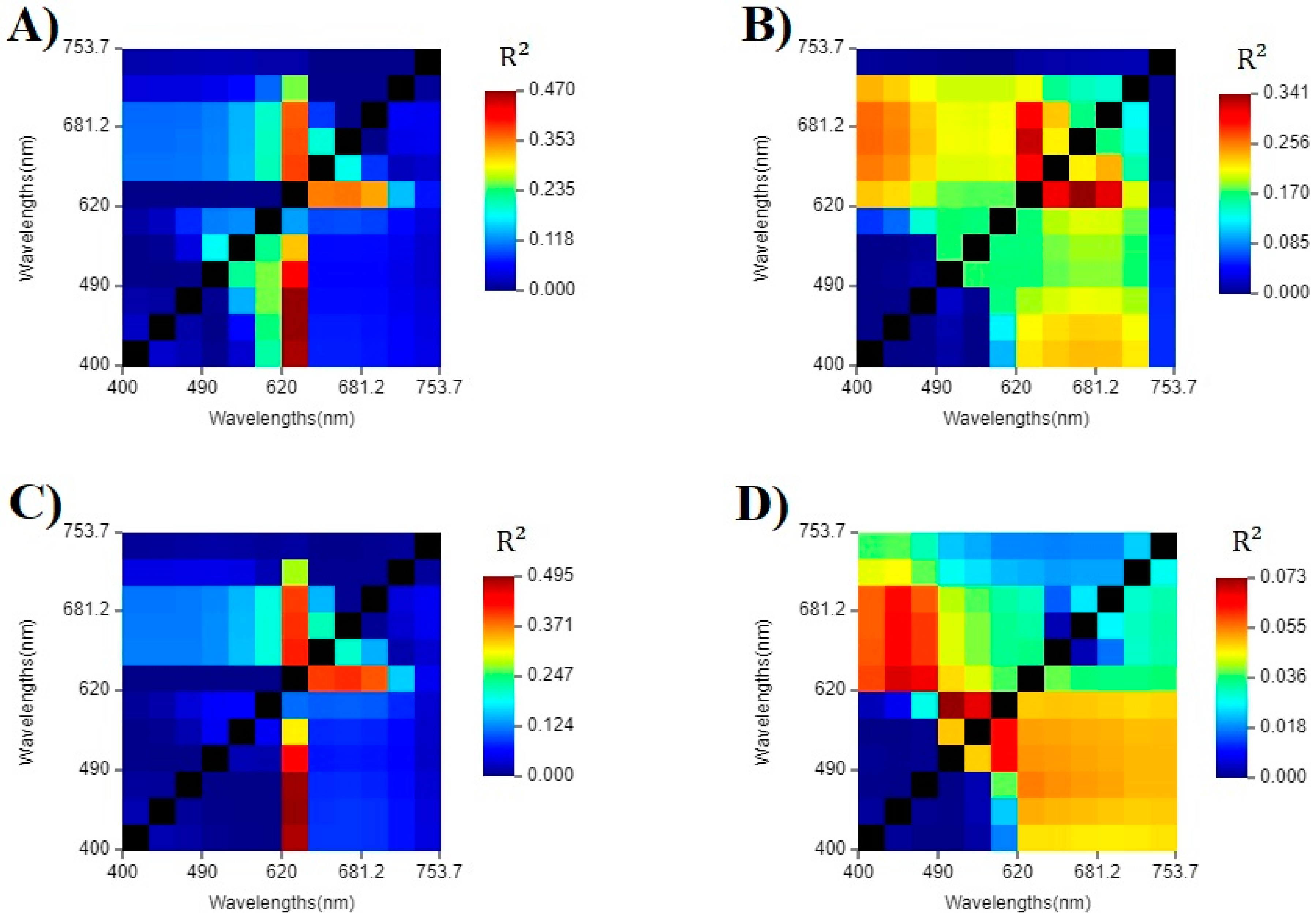
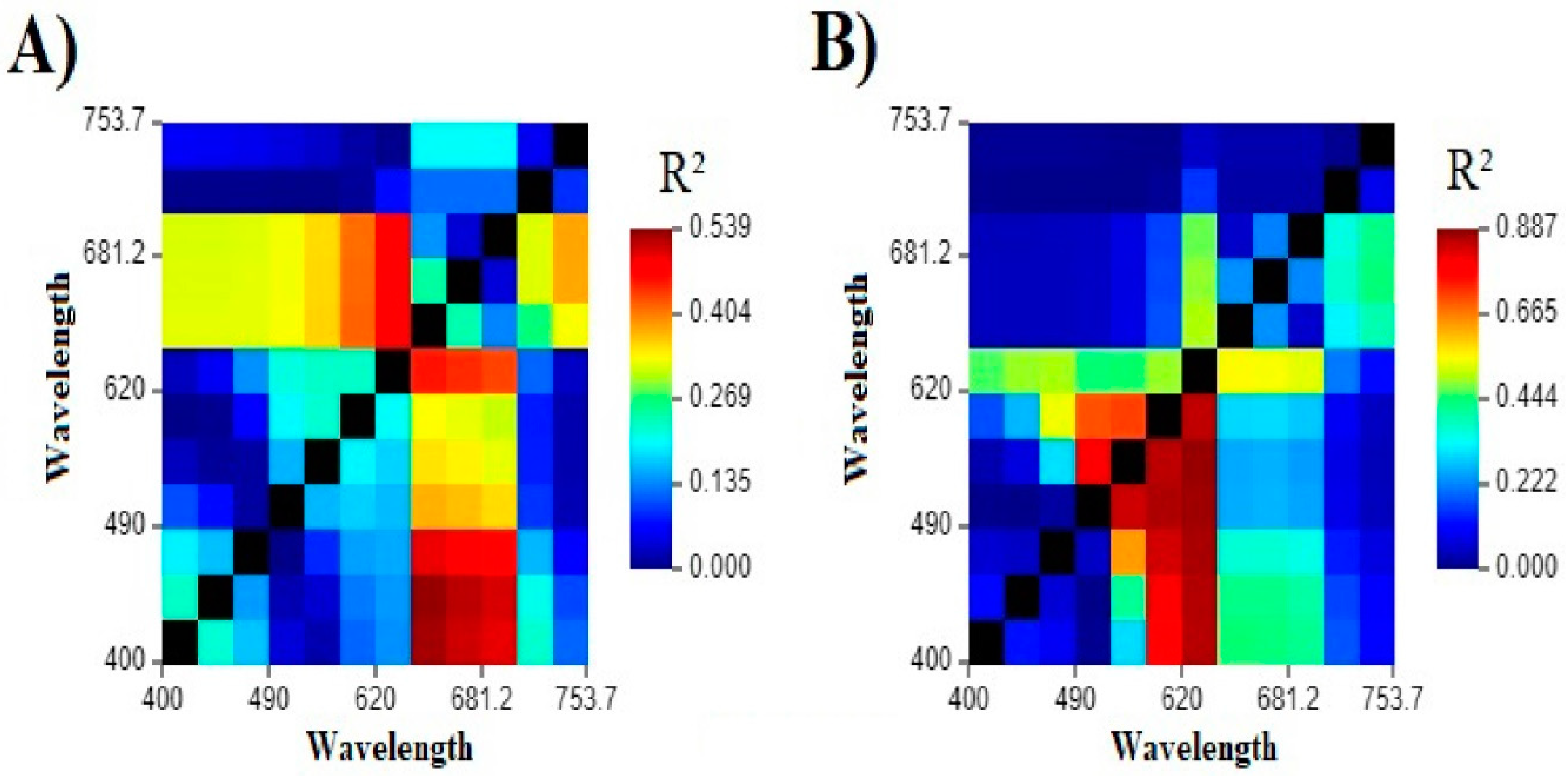
3.3. Single and Band Ratio Evaluation
4. Discussion
4.1. Sensitivity to Lower Concentrations
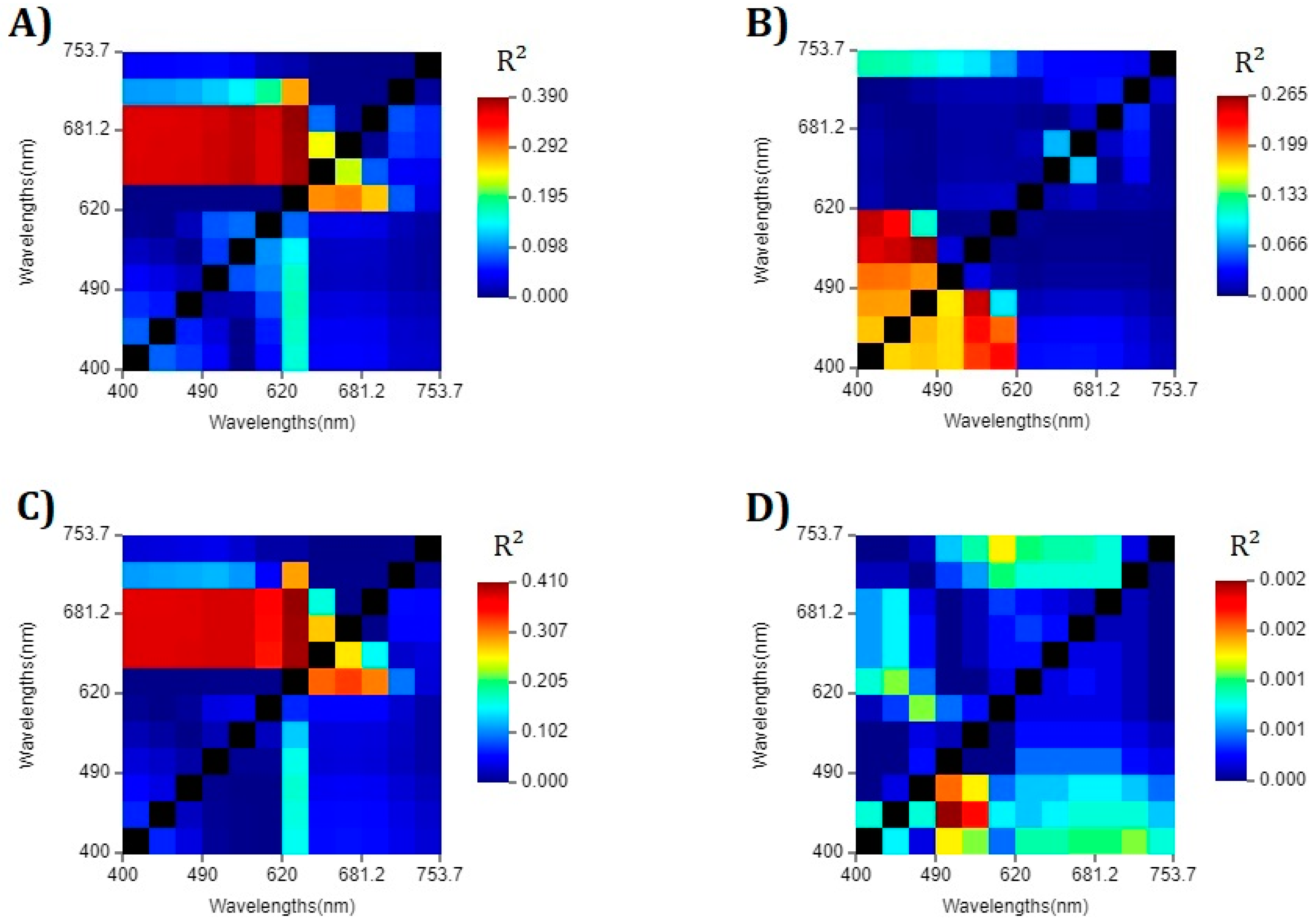
4.2. Band Selection for the Development of Algorithms
5. Conclusions
Funding
Conflicts of Interest
References
- Palmer, S.C.; Kutser, T.; Hunter, P.D. Remote sensing of inland waters: Challenges, progress and future directions. Remote. Sens. Environ. 2015, 157, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Donlon, C.; Berruti, B.; Buongiorno, A.; Ferreira, M.-H.; Féménias, P.; Frerick, J.; Goryl, P.; Klein, U.; Laur, H.; Mavrocordatos, C.; et al. The Global Monitoring for Environment and Security (GMES) Sentinel-3 mission. Remote. Sens. Environ. 2012, 120, 37–57. [Google Scholar] [CrossRef]
- Reinart, A.; Kutser, T. Comparison of different satellite sensors in detecting cyanobacterial bloom events in the Baltic Sea. Remote. Sens. Environ. 2006, 102, 74–85. [Google Scholar] [CrossRef]
- Ogashawara, I.; Mishra, D.R.; Mishra, S.; Curtarelli, M.P.; Stech, J.L. A Performance Review of Reflectance Based Algorithms for Predicting Phycocyanin Concentrations in Inland Waters. Remote. Sens. 2013, 5, 4774–4798. [Google Scholar] [CrossRef] [Green Version]
- Hunter, P.; Tyler, A.; Presing, M.; Kovacs, A.; Preston, T. Spectral discrimination of phytoplankton colour groups: The effect of suspended particulate matter and sensor spectral resolution. Remote. Sens. Environ. 2008, 112, 1527–1544. [Google Scholar] [CrossRef]
- Dekker, A.G. Detection of Optical Water Quality Parameters for Eutrophic Waters by High Resolution Remote Sensing. Ph.D. Thesis, Vrije Universiteit, Amsterdam, The Netherlands, 1993. [Google Scholar]
- Vincent, R.K.; Qin, X.; McKay, R.L.; Miner, J.; Czajkowski, K.; Savino, J.; Bridgeman, T. Phycocyanin detection from LANDSAT TM data for mapping cyanobacterial blooms in Lake Erie. Remote. Sens. Environ. 2004, 89, 381–392. [Google Scholar] [CrossRef]
- Simis, S.G.H.; Peters, S.W.M.; Gons, H.J. Remote sensing of the cyanobacterial pigment phycocyanin in turbid inland water. Limnol. Oceanogr. 2005, 50, 237–245. [Google Scholar] [CrossRef]
- Li, L.; Sengpiel, R.E.; Pascual, D.L.; Tedesco, L.P.; Wilson, J.S.; Soyeux, E. Using hyperspectral remote sensing to estimate chlorophyll-aand phycocyanin in a mesotrophic reservoir. Int. J. Sens. 2010, 31, 4147–4162. [Google Scholar] [CrossRef]
- Lunetta, R.S.; Schaeffer, B.A.; Stumpf, R.P.; Keith, D.; Jacobs, S.A.; Murphy, M.S. Evaluation of cyanobacteria cell count detection derived from MERIS imagery across the eastern USA. Remote. Sens. Environ. 2015, 157, 24–34. [Google Scholar] [CrossRef]
- Woźniak, M.; Bradtke, K.M.; Darecki, M.; Krężel, A. Empirical Model for Phycocyanin Concentration Estimation as an Indicator of Cyanobacterial Bloom in the Optically Complex Coastal Waters of the Baltic Sea. Remote. Sens. 2016, 8, 212. [Google Scholar] [CrossRef]
- Beck, R.; Xu, M.; Zhan, S.; Liu, H.; Johansen, R.A.; Tong, S.; Yang, B.; Shu, S.; Wu, Q.; Wang, S.; et al. Comparison of satellite reflectance algorithms for estimating phycocyanin values and cyanobacterial total biovolume in a temperate reservoir using coincident hyperspectral aircraft imagery and dense coincident surface observations. Remote. Sens. 2017, 9, 538. [Google Scholar] [CrossRef]
- Mishra, D.R.; Mishra, S. A novel remote sensing algorithm to quantify phycocyanin in cyanobacterial algal blooms. Environ. Lett. 2014, 9, 114003. [Google Scholar] [CrossRef]
- Liu, G.; Simis, S.G.H.; Li, L.; Wang, Q.; Li, Y.; Song, K.; Lyu, H.; Zheng, Z.; Shi, K. A four-band semi-analytical model for estimating phycocyanin in inland waters from simulated MERIS and OLCI data. IEEE T. Geosci. Remote Sens. 2017, 56, 1374–1385. [Google Scholar] [CrossRef]
- Lake Erie LaMP. Lake Erie Binational Nutrient Management Strategy: Protecting Lake Erie by Managing Phosphorus. Available online: https://www.epa.gov/sites/production/files/2015-10/documents/binational_nutrient_management.pdf (accessed on 02 March 2019).
- Allinger, L.E.; Reavie, E.D. The ecological history of Lake Erie as recorded by the phytoplankton community. J. Great Lakes 2013, 39, 365–382. [Google Scholar] [CrossRef]
- Michalak, A.M.; Anderson, E.J.; Beletsky, D.; Boland, S.; Bosch, N.S.; Bridgeman, T.B.; Chaffin, J.D.; Cho, K.; Confesor, R.; Daloğlu, I.; et al. Record-setting algal bloom in Lake Erie caused by agricultural and meteorological trends consistent with expected future conditions. Proc. Natl. Acad. Sci. USA 2013, 110, 6448–6452. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Paerl, H.W.; Gardner, W.S.; McCarthy, M.J.; Peierls, B.L.; Wilhelm, S.W. Algal blooms: Noteworthy nitrogen. Science 2014, 346, 175. [Google Scholar] [CrossRef]
- Michalak, A.M. Study role of climate change in extreme threats to water quality. Nature 2016, 535, 349–350. [Google Scholar] [CrossRef]
- Speziale, B.J.; Schreiner, S.P.; Giammatteo, P.A.; Schindler, J.E. Comparison of N,N-Dimethylformamide, Dimethyl Sulfoxide, and Acetone for Extraction of Phytoplankton Chlorophyll. Can. J. Fish. Aquat. Sci. 1984, 41, 1519–1522. [Google Scholar] [CrossRef]
- Horváth, H.; Kovacs, A.W.; Riddick, C.; Présing, M. Extraction methods for phycocyanin determination in freshwater filamentous cyanobacteria and their application in a shallow lake. Eur. J. Phycol. 2013, 48, 278–286. [Google Scholar] [CrossRef] [Green Version]
- Copernicus Online Data Access. Available online: https://coda.eumetsat.int/#/home (accessed on 2 March 2019).
- Alternative Atmospheric Correction (Neural Network). Available online: https://sentinel.esa.int/web/sentinel/technical-guides/sentinel-3-olci/level-2/alternative-atmospheric-correction (accessed on 2 March 2019).
- Brockmann, C.; Doerffer, R.; Peters, M.; Kerstin, S.; Embacher, S.; Ruescas, A. Evolution of the C2RCC neural network for Sentinel 2 and 3 for the retrieval of ocean colour products in normal and extreme optically complex waters. In Proceedings of the Living Planet Symposium 2016, Prague, Czech Republic, 9–13 May 2016. [Google Scholar]
- Ogashawara, I. Terminology and classification of bio-optical algorithms. Sens. Lett. 2015, 6, 613–617. [Google Scholar] [CrossRef]
- Beck, R.; Zhan, S.; Liu, H.; Tong, S.; Yang, B.; Xu, M.; Ye, Z.; Huang, Y.; Shu, S.; Wu, Q.; et al. Comparison of satellite reflectance algorithms for estimating chlorophyll-a in a temperate reservoir using coincident hyperspectral aircraft imagery and dense coincident surface observations. Remote. Sens. Environ. 2016, 178, 15–30. [Google Scholar] [CrossRef] [Green Version]
- Augusto-Silva, P.B.; Ogashawara, I.; Barbosa, C.C.F.; De Carvalho, L.A.S.; Jorge, D.S.F.; Fornari, C.I.; Stech, J.L. Analysis of MERIS reflectance algorithms for estimating chlorophyll-a concentration in a Brazilian reservoir. Remote. Sens. 2014, 6, 11689–11707. [Google Scholar] [CrossRef]
- Gómez, J.A.D.; Alonso, C.A.; García, A.A. Remote sensing as a tool for monitoring water quality parameters for Mediterranean Lakes of European Union water framework directive (WFD) and as a system of surveillance of cyanobacterial harmful algae blooms (SCyanoHABs). Environ. Monit. Assess. 2011, 181, 317–334. [Google Scholar] [CrossRef] [PubMed]
- Dall’Olmo, G.; Gitelson, A.A.; Dall’Olmo, G. Effect of bio-optical parameter variability on the remote estimation of chlorophyll-a concentration in turbid productive waters: experimental results. Appl. Opt. 2005, 44, 412. [Google Scholar] [CrossRef] [PubMed]
- Gitelson, A.A.; Gritz, Y.; Merzlyak, M.N. Relationships between leaf chlorophyll content and spectral reflectance and algorithms for non-destructive chlorophyll assessment in higher plant leaves. J. Plant Physiol. 2003, 160, 271–282. [Google Scholar] [CrossRef] [PubMed]
- Mishra, S.; Mishra, D.R. Normalized difference chlorophyll index: A novel model for remote estimation of chlorophyll-a concentration in turbid productive waters. Remote. Sens. Environ. 2012, 117, 394–406. [Google Scholar] [CrossRef]
- Ogashawara, I.; Curtarelli, M.P.; Souza, A.F.; Augusto-Silva, P.B.; Alcântara, E.H.; Stech, J.L. Interactive Correlation Environment (ICE)—A statistical web tool for data collinearity analysis. Remote. Sens. 2014, 6, 3059–3074. [Google Scholar] [CrossRef]
- Ruiz-Verdú, A.; Simis, S.G.; De Hoyos, C.; Gons, H.J.; Peña-Martinez, R. An evaluation of algorithms for the remote sensing of cyanobacterial biomass. Remote. Sens. Environ. 2008, 112, 3996–4008. [Google Scholar] [CrossRef]
- Ohio Environmental Protection Agency. Public Water System Harmful Algal Bloom Response Strategy. Available online: http://epa.ohio.gov/Portals/28/documents/habs/PWS_HAB_Response_Strategy.pdf (accessed on 2 March 2019).
- Gitelson, A. The peak near 700 nm on radiance spectra of algae and water: relationships of its magnitude and position with chlorophyll concentration. Int. J. Sens. 1992, 13, 3367–3373. [Google Scholar] [CrossRef]
- Schalles, J.F.; Yacobi, Y.Z. Remote detection and seasonal patterns of phycocyanin, carotenoid, and chlorophyll pigments in eutrophic waters. Arch. Hydrobiol. 2000, 55, 153–168. [Google Scholar]
- Wynne, T.T.; Stumpf, R.P.; Tomlinson, M.C.; Warner, R.A.; Tester, P.A.; Dyble, J.; Fahnenstiel, G.L. Relating spectral shape to cyanobacterial blooms in the Laurentian Great Lakes. Int. J. Sens. 2008, 29, 3665–3672. [Google Scholar] [CrossRef]
- Wynne, T.T.; Tomlinson, M.C.; Stumpf, R.P.; Dyble, J. Characterizing a cyanobacterial bloom in Western Lake Erie using satellite imagery and meteorological data. Limnol. Oceanogr. 2010, 55, 2025–2036. [Google Scholar] [CrossRef] [Green Version]
- Lake Erie HAB Bulletin. Available online: https://www.glerl.noaa.gov/res/HABs_and_Hypoxia/lakeErieHABArchive/ (accessed on 2 March 2019).
- Claustre, H.; Bricaud, A.; Babin, M.; Morel, A. Variability in the chlorophyll-specific absorption coefficients of natural phytoplankton: Analysis and parameterization. J. Geophys. Res. Biogeosci. 1995, 100, 13321. [Google Scholar]
| Pigment | Acronym | Formulation | Range of Concentration (mg/m3) | References |
|---|---|---|---|---|
| PC | 2BDA-PC | 0.8–79.8 | [4,8] | |
| PC | 3BDA-PC * | N/A | [5] | |
| PC | NDPCI | 45–330 | [28] | |
| Chl-a | 2BDA-CL | 4–236 | [29] | |
| Chl-a | 3BDA-CL | 4–236 | [29,30] | |
| Chl-a | NDCI | 0.9–28.1 | [31] |
| Image Date | Spectral Band (nm) | Normality | U or T | p-Value | Difference |
|---|---|---|---|---|---|
| 08/22/2016 | 400 | P = 0.818 | −4.465 | <0.001 | Yes |
| 412.5 | P = 0.652 | −3.707 | 0.002 | Yes | |
| 442.5 | P = 0.986 | −1.106 | 0.287 | No | |
| 490 | P = 0.940 | 0.913 | 0.377 | No | |
| 510 | P = 0.871 | 1.115 | 0.284 | No | |
| 560 | P = 0.998 | 0.597 | 0.560 | No | |
| 620 | P = 0.717 | 0.107 | 0.916 | No | |
| 665 | P = 0.491 | 0.887 | 0.390 | No | |
| 673.75 | P = 0.461 | 0.969 | 0.349 | No | |
| 681 | P = 0.437 | 1.030 | 0.321 | No | |
| 708.75 | P = 0.817 | 1.051 | 0.311 | No | |
| 753.78 | P = 0.859 | 0.441 | 0.666 | No | |
| 09/13/2016 | 400 | P < 0.050 | 20 | 0.620 | No |
| 412.5 | P < 0.050 | 24 | 1.000 | No | |
| 442.5 | P < 0.050 | 19 | 0.535 | No | |
| 490 | P < 0.050 | 12 | 0.128 | No | |
| 510 | P < 0.050 | 10 | 0.073 | No | |
| 560 | P = 0.659 | 2.790 | 0.016 | Yes | |
| 620 | P = 0.620 | 1.002 | 0.336 | No | |
| 665 | P = 0.260 | 1.645 | 0.126 | No | |
| 673.75 | P = 0.890 | 1.370 | 0.196 | No | |
| 681 | P = 0.747 | 1.511 | 0.157 | No | |
| 708.75 | P < 0.050 | 7 | 0.026 | Yes | |
| 753.78 | P < 0.050 | 12 | 0.128 | No |
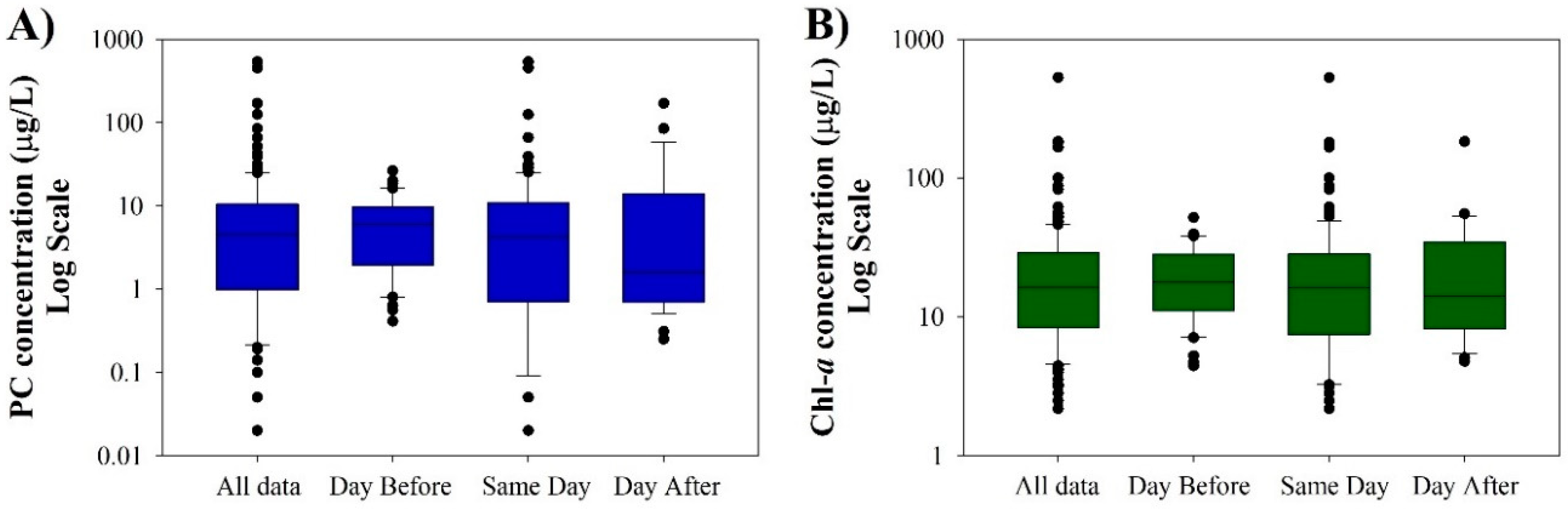
| Algorithm | All Images (n = 164) | Day Before (n = 40) | Same Day (n = 97) | Day After (n = 27) |
|---|---|---|---|---|
| NDPCI | R2 = 0.011 | R2 = 0.010 | R2 = 0.014 | R2 < 0.001 |
| RMSE = 69.925 | RMSE = 6.265 | RMSE = 88.609 | RMSE = 37.127 | |
| 3BDA-PC | R2 = 0.051 | R2 = 0.136 | R2 = 0.075 | R2 < 0.001 |
| RMSE = 68.501 | RMSE = 5.851 | RMSE = 85.829 | RMSE = 37.125 | |
| 2BDA-PC | R2 = 0.011 | R2 = 0.009 | R2 = 0.015 | R2 < 0.001 |
| RMSE = 69.922 | RMSE = 6.267 | RMSE = 88.597 | RMSE = 37.119 | |
| NDCI | R2 = 0.003 | R2 = 0.159 | R2 = 0.0150 | R2 = 0.002 |
| RMSE = 47.860 | RMSE = 10.363 | RMSE = 58.780 | RMSE = 35.307 | |
| 3BDA-CL | R2 = 0.002 | R2 = 0.155 | R2 = 0.013 | R2 = 0.014 |
| RMSE = 47.882 | RMSE = 10.386 | RMSE = 58.842 | RMSE = 35.497 | |
| 2BDA-CL | R2 = 0.002 | R2 = 0.163 | R2 = 0.012 | R2 = 0.020 |
| RMSE = 47.882 | RMSE = 10.337 | RMSE = 58.852 | RMSE = 35.391 |
| Type | All Images | Day Before | Same Day | Day After |
|---|---|---|---|---|
| Best remote sensing algorithm (PC) | R2 = 0.051 | R2 = 0.136 | R2 = 0.075 | R2 < 0.001 |
| Best single band (PC) | R2 = 0.067 | R2 = 0.272 | R2 = 0.085 | R2 = 0.009 |
| Best band ratio (PC) | R2 = 0.390 | R2 = 0.265 | R2 = 0.410 | R2 = 0.002 |
| Best remote sensing algorithm (Chl-a) | R2 = 0.003 | R2 = 0.163 | R2 = 0.015 | R2 = 0.020 |
| Best single band (Chl-a) | R2 = 0.049 | R2 = 0.157 | R2 = 0.065 | R2 = 0.051 |
| Best band ratio (Chl-a) | R2 = 0.470 | R2 = 0.341 | R2 = 0.495 | R2 = 0.073 |
| Pigment | NDI | 3BDA | 2BDA |
|---|---|---|---|
| PC >50 µg/L (n = 8) | R2 = 0.192; RMSE = 210.432 | R2 = 0.217; RMSE = 207.167 | R2 = 0.185; RMSE = 211.407 |
| Chl-a > 50 µg/L (n = 13) | R2 = 0.384; RMSE = 107.585 | R2 = 0.243; RMSE = 119.201 | R2 = 0.335; RMSE = 111.752 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ogashawara, I. The Use of Sentinel-3 Imagery to Monitor Cyanobacterial Blooms. Environments 2019, 6, 60. https://doi.org/10.3390/environments6060060
Ogashawara I. The Use of Sentinel-3 Imagery to Monitor Cyanobacterial Blooms. Environments. 2019; 6(6):60. https://doi.org/10.3390/environments6060060
Chicago/Turabian StyleOgashawara, Igor. 2019. "The Use of Sentinel-3 Imagery to Monitor Cyanobacterial Blooms" Environments 6, no. 6: 60. https://doi.org/10.3390/environments6060060





