Fractal and Long-Memory Traces in PM10 Time Series in Athens, Greece
Abstract
:1. Introduction
2. Experimental Methods
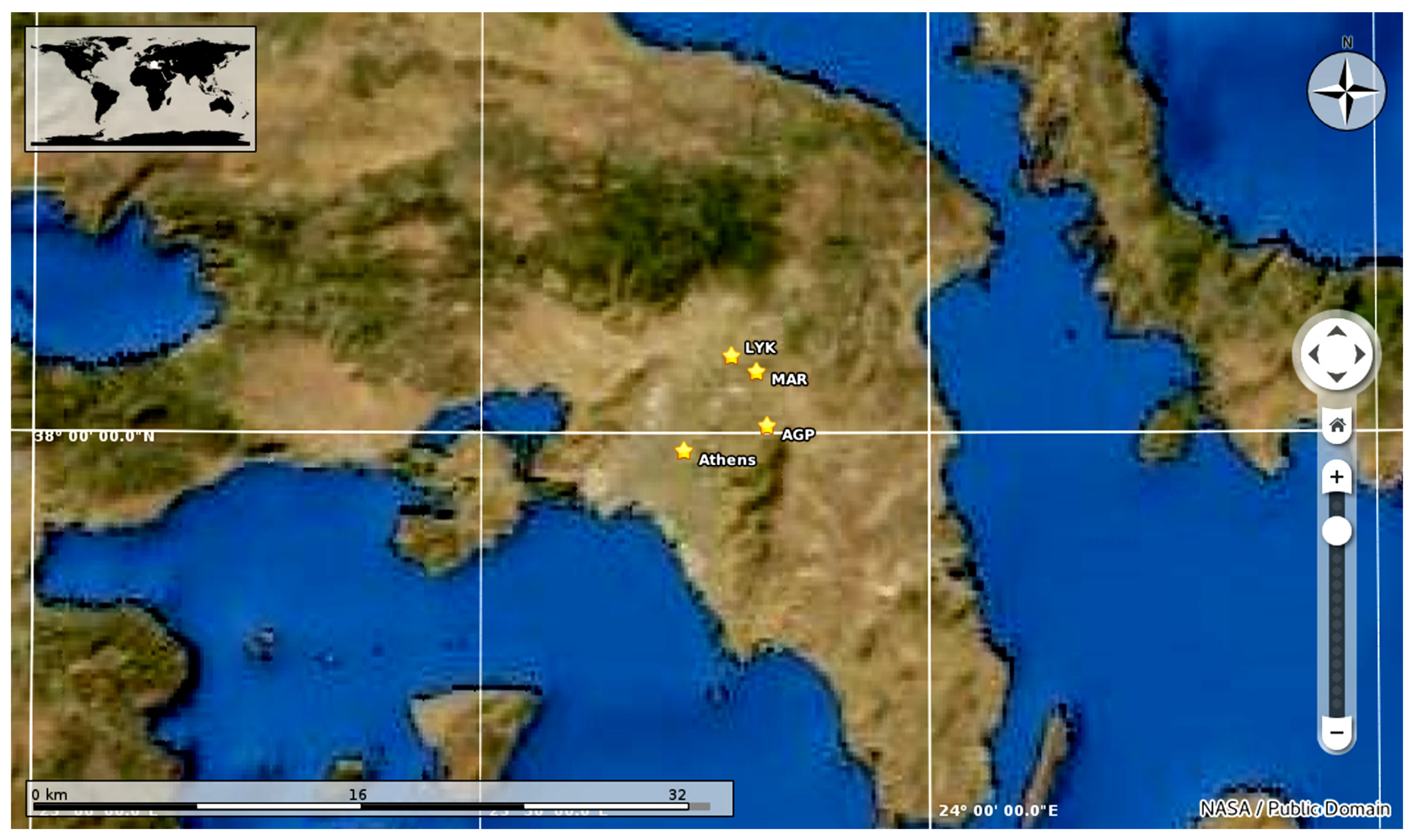
2.1. Area of Study
2.2. Measurement Methodology
3. Chaos Analysis Methods
3.1. Fractality and Long-Memory
3.2. Hurst Exponent
- (i)
- If 0.5 < H < 1, there is a positive long-range autocorrelation in the associated time series. If so, high present values are followed, most probably, by high future values, while the trend continues long into the future (persistency);
- (ii)
- if 0 < H < 0.5, there are long-lasting changes between low and high values. When this happens, low present values are followed by high future values, and vice versa. This low–high value change continues long into the future of the time series (antipersistency);
- (iii)
- if H = 0.5, the time series is random and uncorrelated.
3.3. Fractal-Dimension Analysis
3.3.1. Katz’s Method
3.3.2. Higuchi’s Method
3.3.3. Sevcik Method
3.3.4. Computational Methodology of Fractal Dimension
- The signal was divided into windows of 64 samples (approximately two months’ duration).
- In each segment, the fractal dimension was calculated as follows:
- Katz’s method: As D from Equation (4) for and = 1 sample per day, namely, the distance between the points of the series that feed parameter L.
- Higuchi’s method: As slope D of the best-fit line of the log-log plot of Equation (9), namely, versus , for .
- Sevcik ’s method: As from Equation (12) for N = 64, namely, equal to the length of the series in each window.
- The window slid one sample, and Steps (i–ii) were repeated until the end of the signal.
3.4. Rescaled-Range Analysis
Computational Methodology of R/S Analysis
- The signal was divided in windows of 64 samples (approximately two months’ duration).
- In each segment, the least-square fit was applied to the linear representation of Equation (6). Successful representations were considered those exhibiting squares of Spearman’s correlation coefficient above 0.95.
- The window slid one sample, and steps (i–ii) were repeated until the end of the signal.
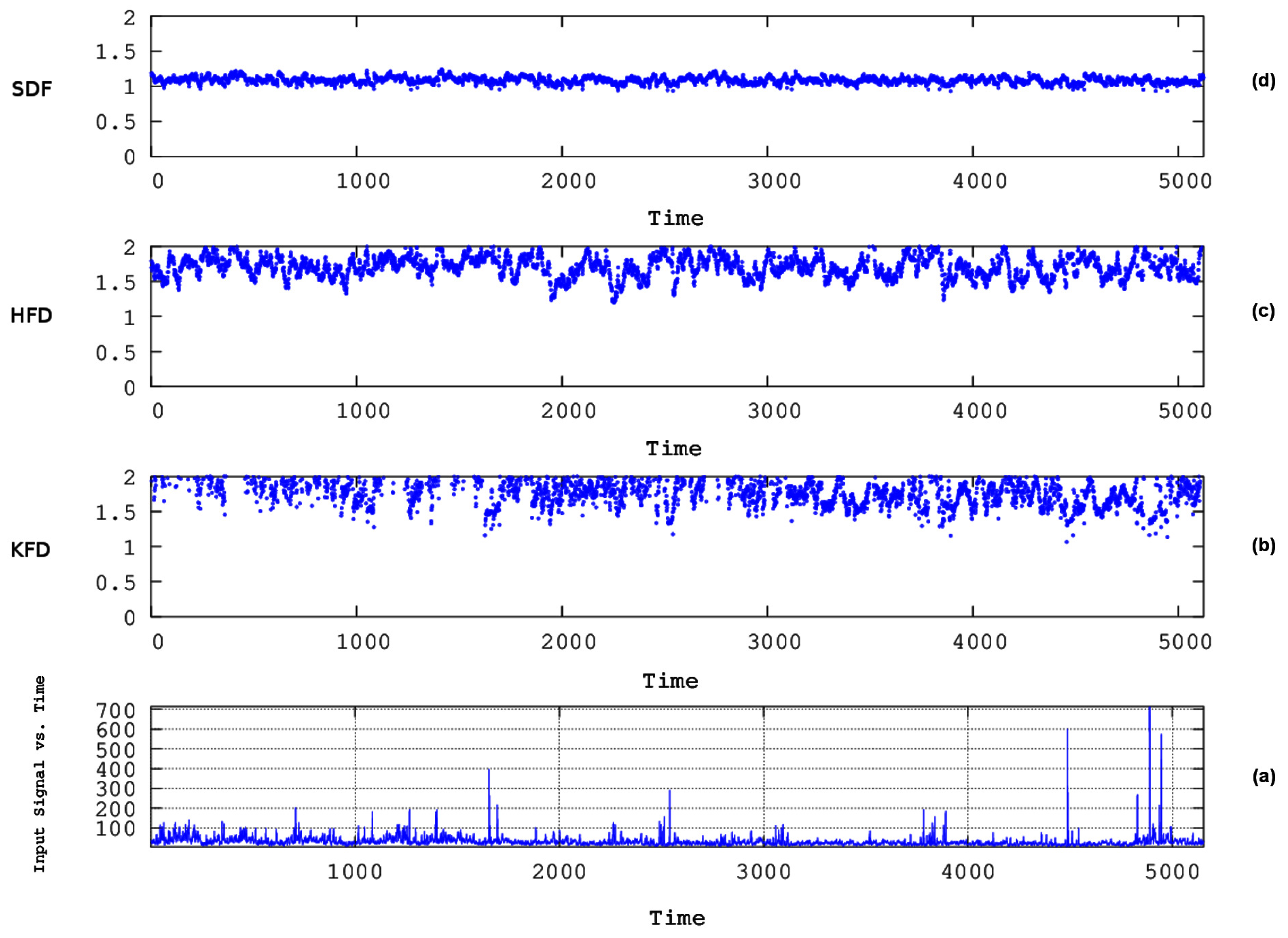
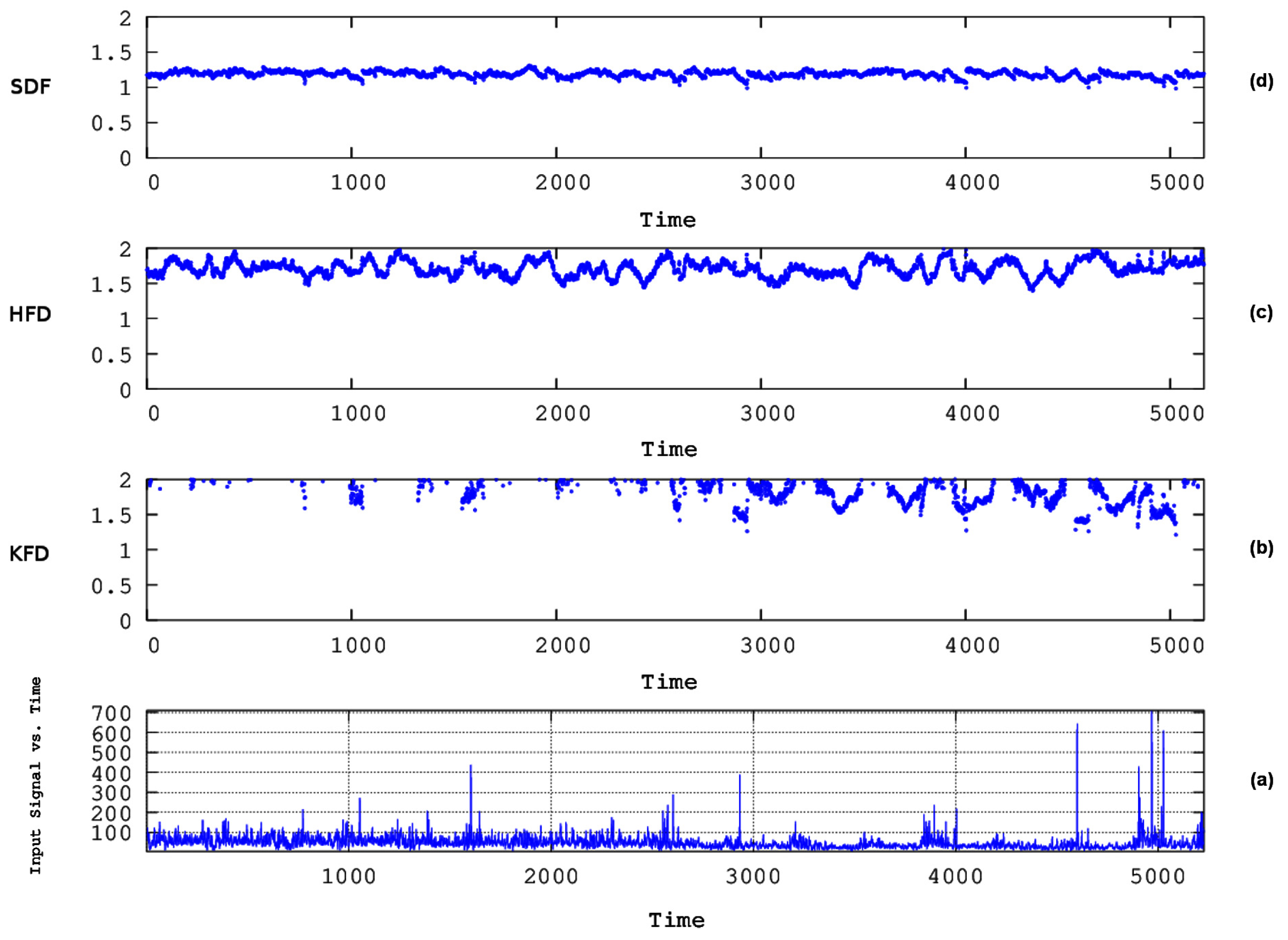
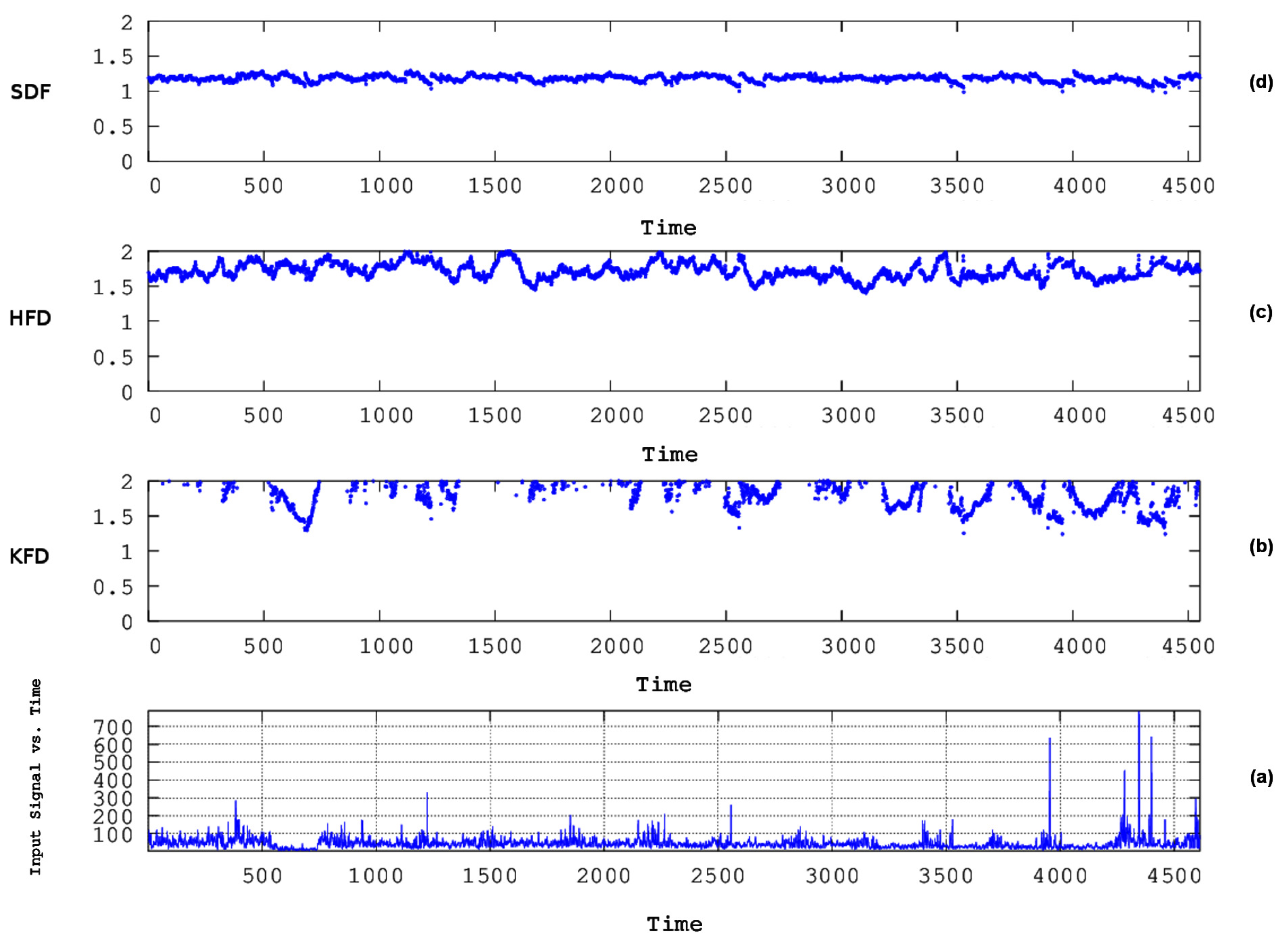
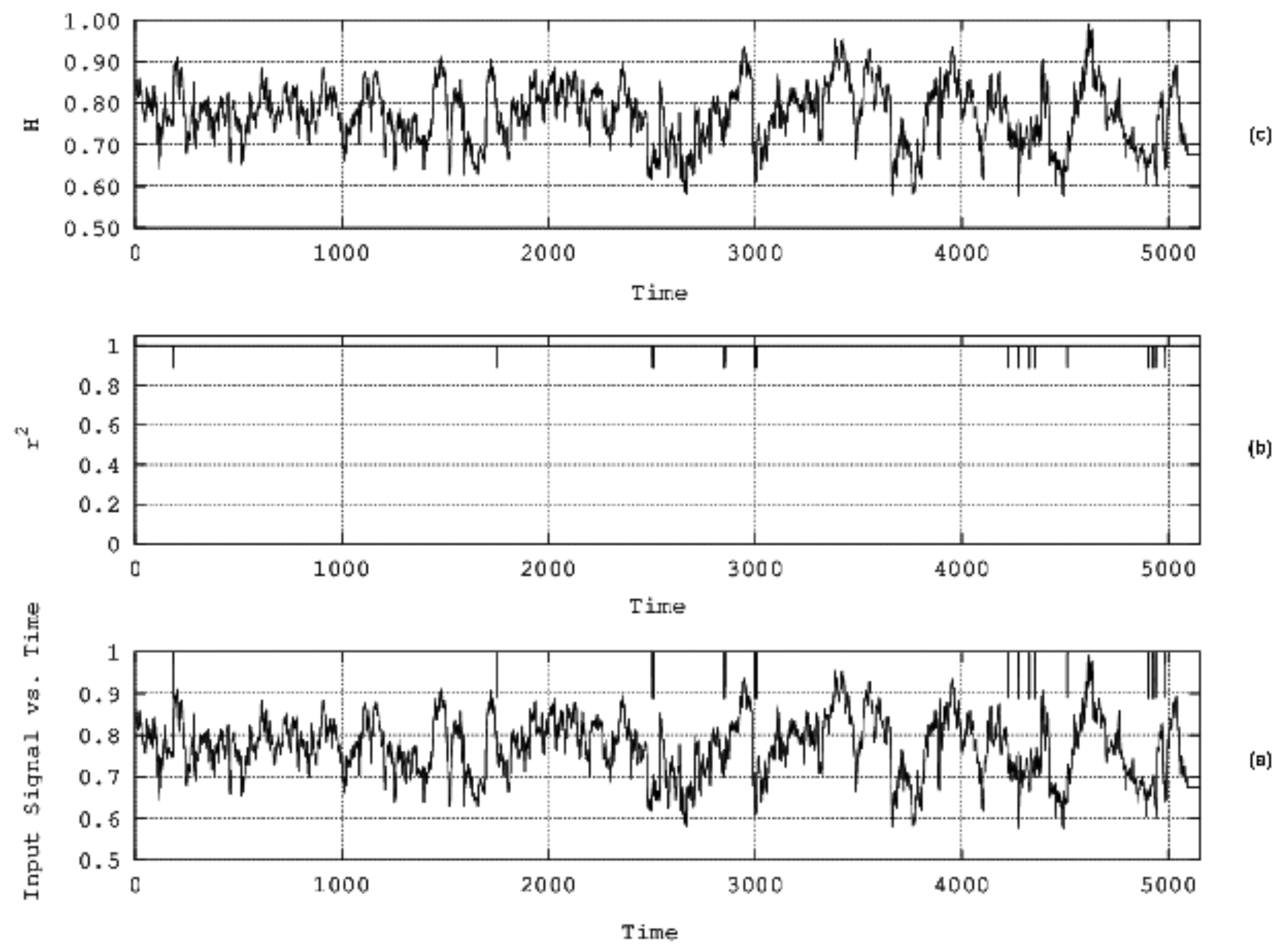
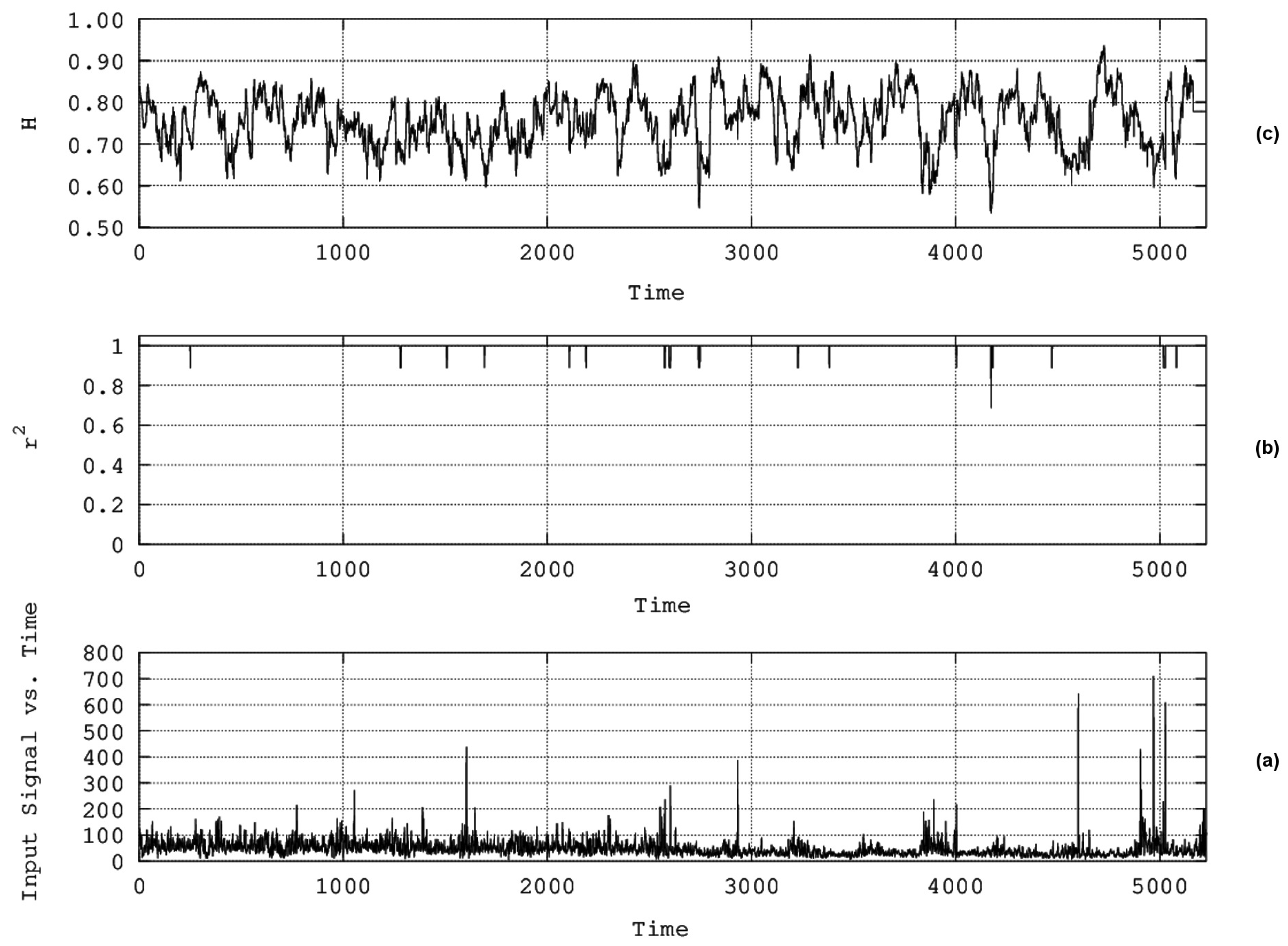
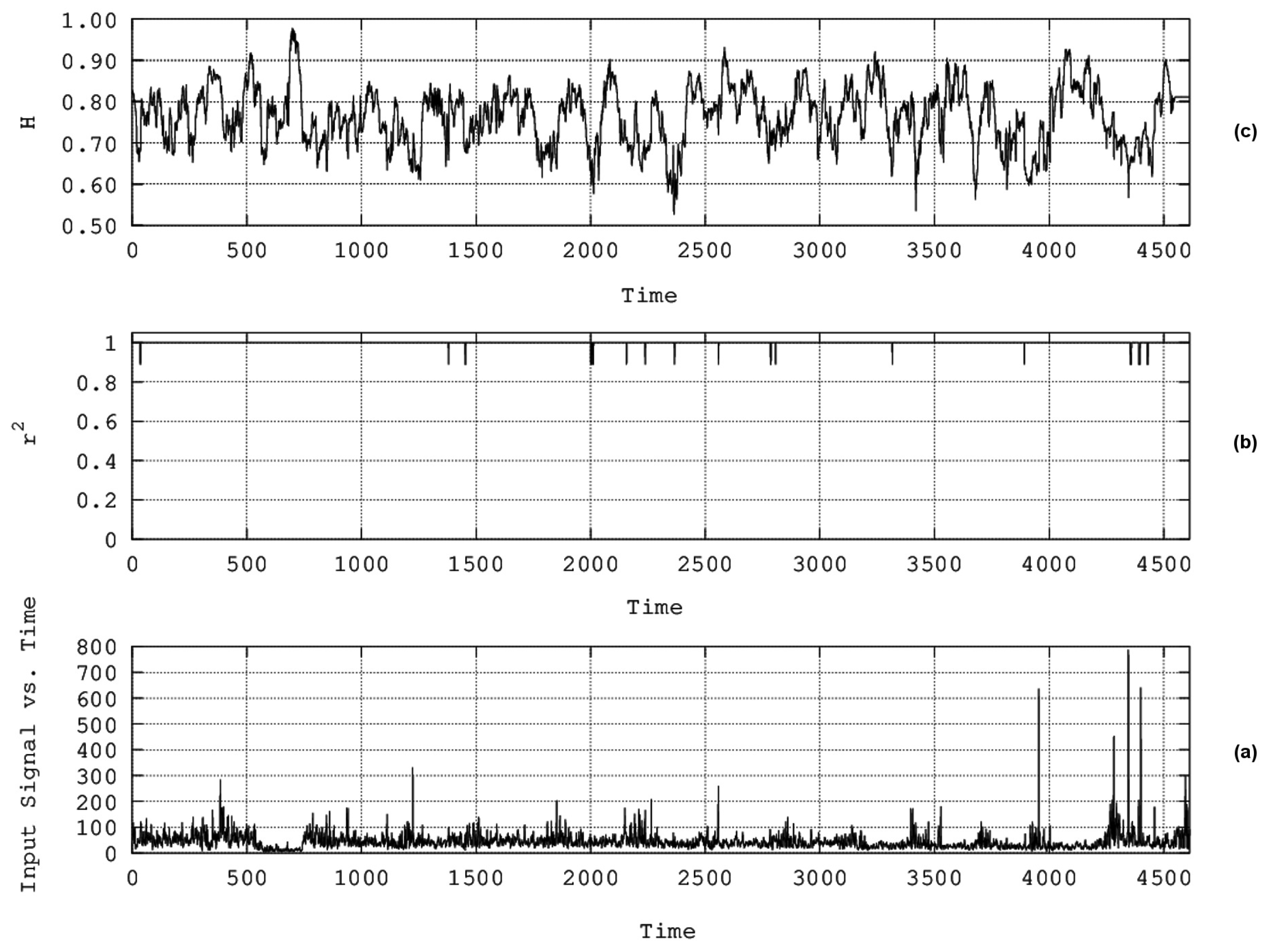
4. Results and Discussion
5. Conclusions
- The algorithms of Katz, Higuchi, and Sevcik were employed together with R/S analysis via sliding windows of two months’ duration to investigate the existence of chaos and long memory in three 16-year-long PM10 concentration time series recorded in Athens, Greece.
- Several segments were found with dynamical complex fractal behaviour and long memory. Via specific thresholds, computational calculations were performed on all possible combinations of two or more techniques for the data of all stations under study. The best combination of methods for the data of all stations was the one not including Katz’s algorithm in the meta-analysis.
- Twelve dates of coincidence were identified from this combination of techniques.
Author Contributions
Funding
Conflicts of Interest
References
- Chan, C.K.; Yao, X. Air pollution in mega cities in China. Atmos. Environ. 2008, 42, 1–42. [Google Scholar]
- Fang, M.; Chan, C.K.; Yao, X.H. Managing air quality in a rapidly developing nation: China. Atmos. Environ. 2009, 43, 79–86. [Google Scholar]
- Liu, N.; Yu, Y.; He, J.; Zhao, S. Integrated modeling of urban-scale pollutant transport: Application in a semi-arid urban valley, Northwestern China. Atmos. Pollut. Res. 2013, 4, 306–314. [Google Scholar]
- Liu, Z.; Wang, L.; Zhu, H. A time-scaling property of air pollution indices: A case study of Shanghai. China Atmos. Pollut. Res. 2015, 6, 886–892. [Google Scholar]
- Ibarra-Berastegi, G.; Elias, A.; Barona, A.; Saenz, J.; Ezcurra, A.; de Argandona, J.D. From diagnosis to prognosis for forecasting air pollution using neural networks: Air pollution monitoring in Bilbao. Environ. Model. Softw. 2008, 23, 622–637. [Google Scholar]
- Kourentzes, N.; Barrow, D.K.; Crone, S.F. Neural network ensemble operators for time series forecasting. Expert Syst. Appl. 2014, 41, 4235–4244. [Google Scholar]
- Pérez, P.; Trier, A.; Reyes, J. Prediction of PM2.5 concentrations several hours in advance using neural networks in Santiago, Chile. Atmos. Environ. 2000, 34, 1189–1196. [Google Scholar]
- Hooyberghs, J.; Mensink, C.; Dumont, G.; Fierens, F.; Brasseur, O. A neural network forecast for daily average PM10 concentrations in Belgium. Atmos. Environ. 2005, 39, 3279–3289. [Google Scholar]
- Grivas, G.; Chaloulakou, A. Artificial neural network models for prediction of PM10 hourly concentrations in the Greater Area of Athens, Greece. Atmos. Environ. 2006, 40, 1216–1229. [Google Scholar]
- Barai, S.V.; Dikshit, A.K.; Sharma, S. Neural Network Models for Air Quality Prediction: A Comparative Study. In Soft Computing in Industrial Applications; Saad, A., Dahal, K., Sarfraz, M., Roy, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; Volume 39. [Google Scholar]
- Díaz-Robles, L.A.; Ortega, J.C.; Fu, J.S.; Reed, G.D.; Chow, J.C.; Watson, J.G.; Moncada-Herrera, J. A hybrid ARIMA and artificial neural networks model to forecast particulate matter in urban areas: The case of Temuco, Chile. Atmos. Environ. 2008, 42, 8331–8340. [Google Scholar]
- Antanasijević, D.Z.; Pocajt, V.V.; Povrenović, D.S.; Ristić, M.D.; Perić-Grujić, A.A. PM10 emission forecasting using artificial neural networks and genetic algorithm input variable optimization. Sci. Total. Environ. 2013, 443, 511–519. [Google Scholar] [PubMed]
- Moustris, K.P.; Ziomas, I.C.; Paliatsos, A.G. 3-Day-Ahead Forecasting of Regional Pollution Index for the pollutants NO2, CO, SO2 and O3 using Artificial Neural Networks in Athens, Greece. Water Air Soil. Pollut. 2010, 224, 29–43. [Google Scholar]
- Moustris, K.P.; Nastos, P.T.; Larisssi, I.K.; Paliatsos, A.G. Application of Multiple Linear Regression Models and Artificial Neural Networks on the surface ozone forecast in the greater Athens area, Greece. Adv. Meteorol. 2012, 2012, 1–8. [Google Scholar]
- Moustris, K.P.; Larisssi, I.K.; Nastos, P.T.; Koukouletsos, K.V.; Paliatsos, A.G. Development and Application of Artificial Neural Network Modeling in Forecasting PM10 Levels in a Mediterranean City. Water Air Soil Pollut. 2013, 224. [Google Scholar]
- Moustris, K.P.; Proias, G.T.; Larisssi, I.K.; Nastos, P.T.; Koukouletsos, K.V.; Paliatsos, A.G. Air quality prognosis using artificial neural networks modeling in the urban environment of Volos, Central Greece. Fres. Environ. Bull. 2014, 13, 2967–2975. [Google Scholar]
- Hong, L. Decomposition and forecast for financial time series with high-frequency based on empirical mode decomposition. Energy Procedia 2011, 5, 1333–1340. [Google Scholar]
- Maheswaran, R.; Khosa, R. Wavelet Volterra Coupled Models for forecasting of nonlinear and non–stationary time series. Neurocomputing 2015, 149, 1074–1084. [Google Scholar]
- Sefidmazgi, G.; Sayemuzzaman, M.; Homaifar, M.; Jha, M.K.; Liess, S. Trend analysis using non-stationary time series clustering based on the finite element method. Nonlinear Process. Geophys. 2014, 21, 605–615. [Google Scholar]
- Lorentzen, T. Statistical analysis of temperature data sampled at Station-M in the Norwegian Sea. J. Mar. Syst. 2014, 130, 31–45. [Google Scholar]
- Samet, H.; Marzbani, F. Quantizing the deterministic nonlinearity in wind speed time series. Renew. Sustain. Energy Rev. 2014, 39, 1143–1154. [Google Scholar]
- Chelani, A.B. Persistence analysis of extreme CO, NO2 and O3 concentrations in ambient air of Delhi. Atmos. Res. 2012, 108, 128–134. [Google Scholar]
- Gan, M.; Cheng, Y.; Liu, K.; Zhang, G.L. Seasonal and trend time series forecasting based on a quasi-linear autoregressive model. Appl. Soft Comput. 2014, 24, 13–18. [Google Scholar]
- Shi, K.; Liu, C.Q.; Ai, N.S.; Zhang, X.H. Using three methods to investigate time-scaling properties in air pollution indexes time series. Nonlinear Anal. Real World Appl. 2008, 9, 693–707. [Google Scholar]
- Lee, C.K.; Ho, D.S.; Yu, C.C.; Wang, C.C.; Hsiao, H.T. Simple multifractal cascade model for the air pollutant concentration time series. Environmetrics 2003, 14, 255–269. [Google Scholar]
- Lau, J.C.; Hung, W.T.; Yuen, D.D.; Cheung, C.S. Long-memory characteristics of urban roadside air quality. Transp. Res. D 2009, 14, 353–359. [Google Scholar]
- Perez, I.A.; Sanchez, M.L.; Garcia, M.A.; Paredes, V. Persistence analysis of CO2 concentrations recorded at a rural site in the upper Spanish plateau. Atmos. Res. 2011, 100, 45–50. [Google Scholar]
- Scott, L.S.; Varian, H.R. Predicting the present with bayesian structural time series. Int. J. Math. Model. Numer. Optim. 2014, 5, 4–23. [Google Scholar]
- Shi, K.; Liu, C.Q.; Ai, N.S. Monofractal and multifractal approaches in investigating temporal variation of air pollution indexes. Fractals 2009, 17, 513–521. [Google Scholar]
- Varotsos, C.; Kirk-Davidoff, D. Long-memory processes in ozone and temperature variations at the region 60 0 S–600 N. Atmos. Chem. Phys. 2006, 6, 4093–4100. [Google Scholar]
- Varotsos, C.; Ondov, J.; Efstathiou, M. Scaling properties of air pollution in Athens, Greece and Baltimore, Maryland. Atmos. Environ. 2005, 39, 4041–4047. [Google Scholar]
- Varotsos, C.A.; Ondov, J.M.; Cracknell, A.P.; Efstathiou, M.N.; Assimakopoulos, M.N. Long-range persistence in global aerosol index dynamics. Int. J. Remote Sens. 2006, 27, 3593–3603. [Google Scholar]
- Yuval; Broday, D.M. Studying the time scale dependence of environmental variables predictability using fractal analysis. Environ. Sci. Technol. 2010, 44, 4629–4634. [Google Scholar] [PubMed]
- Weng, Y.C.; Chang, N.B.; Lee, T.Y. Nonlinear time series analysis of ground-level ozone dynamics in Southern Taiwan. J. Environ. Manag. 2008, 87, 405–414. [Google Scholar]
- Windsor, H.L.; Toumi, R. Scaling and persistence of UK pollution. Atmos. Environ. 2001, 35, 4545–4556. [Google Scholar]
- Zhu, J.; Liu, Z. Long-range persistence of acid deposition. Atmos. Environ. 2003, 37, 613. [Google Scholar]
- Schlink, U.; Herbarth, O.; Richter, M.; Dorling, S.; Nunnari, G.; Cawley, G.; Pelikan, E. Statistical models to assess the health effects and to forecast ground—Level ozone. Environ. Model. Softw. 2006, 21, 547–558. [Google Scholar]
- Eftaxias, K.; Panin, V.; Deryugin, Y. Evolution-EM signals before earthquakes in terms of mesomechanics and complexity. Phys. Chem. Earth 2007, 29, 445–451. [Google Scholar]
- Eftaxias, K.; Balasis, G.; Contoyiannis, Y.; Papadimitriou, C.; Kalimeri, M. Unfolding the procedure of characterizing recorded ultra low frequency, kHZ and MHz electromagnetic anomalies prior to the L’Aquila earthquake as pre-seismic one—Part 2. Nat. Hazard Earth Syst. 2010, 10, 275–294. [Google Scholar]
- Nikolopoulos, D.; Petraki, E.; Marousaki, A.; Potirakis, S.; Koulouras, G.; Nomicos, C.; Panagiotaras, D.; Stonhamb, J.; Louizi, A. Environmental monitoring of radon in soil during a very seismically active period occurred in South West Greece. J. Environ. Monit. 2012, 14, 564–578. [Google Scholar] [PubMed]
- Nikolopoulos, D.; Cantzos, D.; Petraki, E.; Yannakopoulos, P.H.; Nomicos, C. Traces of long-memory in pre-seismic MHz electromagnetic time series-Part1: Investigation through the R/S analysis and time-evolving spectral fractals. J. Earth Sci. Clim. Chang. 2016, 7, 359. [Google Scholar]
- Nikolopoulos, D.; Petraki, E.; Cantzos, D.; Yannakopoulos, P.H.; Panagiotaras, D.; Nomicos, C. Fractal Analysis of Pre-Seismic Electromagnetic and Radon Precursors: A Systematic Approach. J. Earth Sci. Clim. Chang. 2016, 7, 1–11. [Google Scholar]
- Nikolopoulos, D.; Matsoukas, C.; Yannakopoulos, P.H.; Petraki, E.; Cantzos, D.; Nomicos, C. Long-Memory and Fractal Trends in Variations of Environmental Radon in Soil: Results from Measurements in Lesvos Island in Greece. J. Earth Sci. Clim. Chang. 2018, 9, 1–11. [Google Scholar]
- Nikolopoulos, D.; Yannakopoulos, P.H.; Petraki, E.; Cantzos, D.; Nomicos, C. Long-Memory and Fractal Traces in kHz-MHz Electromagnetic Time Series Prior to the ML = 6.1, 12/6/2007 Lesvos, Greece Earthquake: Investigation through DFA and Time-Evolving Spectral Fractals. J. Earth Sci. Clim. Chang. 2018, 9, 1–15. [Google Scholar]
- Petraki, E. Electromagnetic Radiation and Radon-222 Gas Emissions as Precursors of Seismic Activity. Ph.D. Thesis, Department of Electronic and Computer Engineering, Brunel University, London, UK, 2016. [Google Scholar]
- Petraki, E.; Nikolopoulos, D.; Fotopoulos, A.; Panagiotaras, D.; Koulouras, G.; Zisos, A.; Nomicos, C.; Louizi, A.; Stonham, J. Self-organised critical features in soil radon and MHz electromagnetic disturbances: Results from environmental monitoring in Greece. Appl. Radiat. Isotop. 2013, 72, 39–53. [Google Scholar]
- Nikolopoulos, D.; Petraki, E.; Nomicos, C.; Koulouras, G.; Kottou, S.; Yannakopoulos, P.H. Long-Memory Trends in Disturbances of Radon in Soil Prior ML = 5.1 Earthquakes of 17 November 2014 Greece. J. Earth Sci. Clim. Chang. 2015, 6, 1–11. [Google Scholar]
- Telesca, L.; Lapenna, V.; Vallianatos, F. Monofractal and multifractal approaches in investigating scaling properties in temporal patterns of the 1983–2000 seismicity in the Western Corinth Graben, Greece. Phys. Earth Planet. Int. 2002, 131, 63–79. [Google Scholar]
- Telesca, L.; Lapenna, V.; Macchiato, M. Mono- and multi-fractal investigation of scaling properties in temporal patterns of seismic sequences. Chaos Solit. Fract. 2004, 19, 1–15. [Google Scholar]
- Lee, C.K.; Juang, L.C.; Wang, C.C.; Liao, Y.Y.; Yu, C.C.; Liu, Y.C.; Ho, D.S. Scaling characteristics in ozone concentration time series (OCTS). Chemosphere 2006, 62, 934–946. [Google Scholar] [PubMed]
- Xue, Y.; Pan, W.; Lu, W.z.; He, H.D. Multifractal nature of particulate matters (PMs) in Hong Kong urban air. Sci. Total Environ. 2015, 532, 744–751. [Google Scholar] [PubMed]
- Dong, Q.; Wang, Y.; Li, P. Multifractal behavior of an air pollutant time series and the relevance to the predictability. Environ. Pollut. 2017, 222, 444–457. [Google Scholar] [PubMed]
- Vlachogianni, A.; Kassomenos, P. One day ahead prediction of morning max CO concentration in Athens, Greece. In Proceedings of the International Conference on Environmental Management Engineering, Planning and Economics, Skiathos Island, Greece, 2–4 June 2007; pp. 2411–2416. [Google Scholar]
- Larissi, I.K.; Koukouletsos, K.V.; Moustris, K.P.; Antoniou, A.; Paliatsos, A.G. PM10 concentration levels in the greater Athens area, Greece. Fresen. Environ. Bull. 2010, 19, 226–231. [Google Scholar]
- Nastos, P.T.; Philandras, C.M.; Paliatsos, A.G. Fourier analysis of the mean monthly NOx concentrations in the Athens basin. Glob. Nest 2002, 4, 145–152. [Google Scholar]
- Mandelbrot, B.B.; Ness, J.W.V. Fractional Brownian motions, fractional noises and applications. J. Soc. Ind. Appl. Math. 1968, 10, 422–437. [Google Scholar]
- Morales, I.O.; Landa, O.; Fossion, R.; Frank, A. Scale invariance, self-similarity and critical behaviour in classical and quantum system. J. Phys. Conf. Ser. 2012, 380, 012020. [Google Scholar]
- Musa, M.; Ibrahim, K. Existence of long memory in ozone time series. Sains Malays. 2012, 41, 1367–1376. [Google Scholar]
- May, R.M. Simple mathematical models with very complicated dynamics. Nature 1976, 261, 459–467. [Google Scholar] [PubMed]
- Sugihara, G.; May, R. Nonlinear forecasting as a way of distinguishing chaos from measurement error in time series. Nature 1990, 344, 734–741. [Google Scholar] [PubMed]
- Nikolopoulos, D.; Valais, I.; Michail, C.; Bakas, A.; Fountzoula, C.; Cantzos, D.; Bhattacharyya, D.; Sianoudis, I.; Fountos, G.; Yannakopoulos, P.H.; et al. Radioluminescence properties of the CdSe/ZnS Quantum Dot nanocrystals with analysis of long-memory trends. Radiat. Meas. 2016, 92, 19–31. [Google Scholar]
- Hurst, H. Long term storage capacity of reservoirs. Trans. Am. Soc. Civ. Eng. 1951, 116, 770–808. [Google Scholar]
- Hurst, H.; Black, R.; Simaiki, Y. Long-term Storage: An Experimental Study; Constable: London, UK, 1965. [Google Scholar]
- Nikolopoulos, D.; Petraki, E.; Vogiannis, E.; Chaldeos, Y.; Giannakopoulos, P.; Kottou, S.; Nomicos, C.; Stonham, J. Traces of self-organisation and long-range memory in variations of environmental radon in soil: Comparative results from monitoring in Lesvos Island and Ileia (Greece). J. Radioanal. Nucl. Chem. 2014, 299, 203–219. [Google Scholar]
- Lopez, T.; Martınez-Gonzalez, C.; Manjarrez, J.; Plascencia, N.; Balankin, A. Fractal Analysis of EEG Signals in the Brain of Epileptic Rats, with and without Biocompatible Implanted Neuroreservoirs. AMM 2009, 15, 127–136. [Google Scholar]
- Kilcik, A.; Anderson, C.; Rozelot, J.; Ye, H.; Sugihara, G.; Ozguc, A. Nonlinear Prediction of Solar Cycle 24. Astrophys. J. 2009, 693, 1173–1177. [Google Scholar]
- Gilmore, M.; Yu, C.; Rhodes, T.; Peebles, W. Investigation of rescaled range analysis, the Hurst exponent, and long-time correlations in plasma turbulence. Phys. Plasmas 2002, 9, 1312–1317. [Google Scholar]
- Granero, M.S.; Segovia, J.T.; Perez, J.G. Some comments on Hurst exponent and the long memory processes on capital Markets. Phys. A 2008, 387, 5543–5551. [Google Scholar]
- Dattatreya, G. Hurst Parameter Estimation from Noisy Observations of Data Traffic Traces. In Proceedings of the 4th WSEAS International Conference on Electronics, Control And Signal Processing, Miami, FL, USA, 17–19 November 2005; pp. 193–198. [Google Scholar]
- Contoyiannis, Y.F.; Diakonos, F.K.; Kapiris, P.G.; Peratzakis, A.S.; Eftaxias, K.A. Intermittent dynamics of critical pre-seismic electromagnetic fluctuations. Phys. Chem. Earth 2004, 29, 397–408. [Google Scholar]
- Fujinawa, Y.; Takahashi, K. Electromagnetic radiations associated with major earthquakes. Phys. Earth Planet. Int. 1998, 105, 249–259. [Google Scholar]
- Hayakawa, M.; Ida, Y.; Gotoh, K. Multifractal analysis for the ULF geomagnetic data during the Guam earthquake. Electromagnetic Compatibility and Electromagnetic Ecology. In Proceedings of the IEEE 6th International Symposium on Electromagnetic Compatibility and Electromagnetic Ecology, Saint Petersburg, Russia, 21–24 June 2005; pp. 239–243. [Google Scholar]
- Hayakawa, M. VLF/LF radio sounding of ionospheric perturbations associated with earthquakes. Sensors 2007, 7, 1141–1158. [Google Scholar]
- Kalimeri, M.; Papadimitriou, C.; Balasis, G.; Eftaxias, K. Dynamical complexity detection in pre-seismic emissions using non-additive Tsallis entropy. Phys. A 2008, 387, 1161–1172. [Google Scholar]
- Li, X.; Polygiannakis, J.; Kapiris, P.; Peratzakis, A.; Eftaxias, K.; Yao, X. Fractal spectral analysis of pre-epileptic seizures in terms of criticality. J. Neural Eng. 2005, 2, 11–16. [Google Scholar] [PubMed]
- Rehman, S.; Siddiqi, A. Wavelet based Hurst exponent and fractal dimensional analysis of Saudi climatic dynamics. Chaos Solit. Fract. 2009, 39, 1081–1090. [Google Scholar]
- Katz, M. Fractals and the analysis of waveforms. Comput. Biol. Med. 1988, 18, 145–156. [Google Scholar] [PubMed]
- Raghavendra, B.; Dutt, D.N. Computing Fractal Dimension of Signals using Multiresolution Box-counting Method. Int. J. Electr. Comput. Energ. Electron. Commun. Eng. 2010, 4, 183–198. [Google Scholar]
- De la Torre, F.C.; Ramirez-Rojas, A.; Pavia-Miller, C.; Angulo-Brown, F.; Yepez, E.; Peralta, J.A. A comparison between spectral and fractal methods in electrotelluric time series. Revista Mexicana Fisica 1999, 45, 298–302. [Google Scholar]
- De la Torre, F.C.; Gonzaalez-Trejo, J.; Real-Ramírez, C.; Hoyos-Reyes, L. Fractal dimension algorithms and their application to time series associated with natural phenomena. J. Phys. Conf. Ser. 2013, 475, 1–10. [Google Scholar]
- Higuchi, T. Approach to an irregular time series on basis of the fractal theory. Phys. D 1988, 31, 277–283. [Google Scholar]
- Sevcik, C. On fractal dimension of waveforms. Chaos Solit. Fract. 2006, 27, 579–580. [Google Scholar]
- Benjamin, N.; Sharma, S.; Pendharker, U.; Shrivastava, J.K. Air quality prediction using artificial neural network. Int. J. Chem. Stud. 2014, 2, 7–9. [Google Scholar]
- Carrizosa, E.; Olivares-Nadal, A.V.; Ramírez-Cobo, P. Time series interpolation via global optimization of moments fitting. Eur. J. Oper. Res. 2013, 230, 97–112. [Google Scholar]
- Eftaxias, K. Footprints of non-extensive Tsallis statistics, self-affinity and universality in the preparation of the L’Aquila earthquake hidden in a pre-seismic EM emission. Phys. A 2010, 389, 133–140. [Google Scholar]
- Petraki, E.; Nikolopoulos, D.; Fotopoulos, A.; Panagiotaras, D.; Nomicos, C.; Yannakopoulos, P.; Kottou, S.; Zisos, A.; Louizi, A.; Stonham, J. Long-range memory patterns in variations of environmental radon in soil. Anal. Methods 2013, 5, 4010–4020. [Google Scholar]
- Varotsos, P.; Sarlis, N.; Skordas, E. Magnetic field variations associated with SES. The instrumentation used for investigating their detectability. Proc. Jpn. Acad. Ser. B 2001, 77, 87–92. [Google Scholar]
- Varotsos, P.; Sarlis, N.; Skordas, E. Long-range correlations in the electric signals that precede rupture: Further investigations. Phys. Rev. E 2003, 67, 021109. [Google Scholar]
- Varotsos, P.; Sarlis, N.; Skordas, E. Scale-specific order parameter fluctuations of seismicity in natural time before mainshocks. EPL 2011, 96, 1–6. [Google Scholar]
- Varotsos, P.; Sarlis, N.; Skordas, E. Identifying the occurrence time of an impending major earthquake: A review. Earthq. Sci. 2017, 30, 209–218. [Google Scholar]
- Peng, C.; Mietus, J.; Havlin, S.; Stanley, H.; Goldberger, A. Long-range anti-correlations and non-Gaussian behavior of the heartbeat. Phys. Rev. Lett. 1993, 70, 1343–1346. [Google Scholar]
- Peng, C.; Buldyrev, S.; Simons, M.; Havlin, S.; Stanley, H.; Goldberger, A. On the mosaic organization of DNA sequences. Phys. Rev. E 1994, 49, 1685–1689. [Google Scholar]
- Peng, C.; Havlin, S.; Stanley, H.; Goldberger, A. Quantification of scaling exponents and crossover phenomena in nonstationary heartbeat time series. Chaos 1995, 5, 82–87. [Google Scholar] [PubMed]
- Peng, C.; Hausdor, J.; Havlin, S.; Mietus, J.; Stanley, H.; Goldberger, A. Multiple-time scales analysis of physiological time series under neural control. Phys. A 1998, 249, 491–500. [Google Scholar]
- Khokhlov, V.N.; Glushkov, A.V.; Loboda, N.S.; Bunyakova, Y.Y. Short-range forecast of atmospheric pollutants using non-linear prediction method. Atmos. Environ. 2008, 42, 7284–7292. [Google Scholar]
- Yu, H.L.; Lin, Y.C.; Sivakumar, B.; Kuo, Y. A study of the temporal dynamics of ambient particulate matter using stochastic and chaotic techniques. Atmos. Environ. 2015, 69, 37–45. [Google Scholar]
- Furuya, K.; Kudo, Y.; Okinaga, K.; Yamuki, M.; Takahashi, S.; Araki, Y.; Hisamatsu, Y. Seasonal variation and their characterization of suspended particulate matter in the air of subway stations. J. Trace Microprobe Tech. 2001, 19, 469–485. [Google Scholar]
- Hand, J.L.; Schichtel, B.A.; Pitchford, M.; Malm, W.C.; Frank, N.H. Seasonal composition of remote and urban fine particulate matter in the United States. J. Geophys. Res. 2012, 117, D05209. [Google Scholar]
- Ho, K.F.; Lee, S.C.; Cao, J.J.; Chow, J.C.; Watson, J.G.; Chan, C.K. Seasonal variations and mass closure analysis of particulate matter in Hong Kong. Sci. Total Environ. 2006, 355, 276–287. [Google Scholar] [PubMed]
- Koelemeijer, R.B.A.; Homan, C.D.M. Comparison of spatial and temporal variations of aerosol optical thickness and particulate matter over Europe. Atmos. Environ. 2006, 40, 5304–5315. [Google Scholar]
- Mayzaud, P.; Chanut, J.P.; Ackman, R.G. Seasonal changes of the biochemical composition of marine particulate matter with special reference to fatty acids and sterols. Mar. Ecol. Prog. Ser. 1989, 56, 189–204. [Google Scholar]
- Eftaxias, K.; Sgrigna, V.; Chelidze, T. Mechanical and electromagnetic phenomena accompanying preseismic deformation: From laboratory to geophysical scale. Tectonophysics 2007, 341, 1–5. [Google Scholar]
- Eftaxias, K.; Contoyiannis, Y.; Balasis, G.; Karamanos, K.; Kopanas, J.; Antonopoulos, G.; Koulouras, G.; Nomicos, C. Evidence of fractional-Brownian-motion-type asperity model for earthquake generation in candidate pre-seismic electromagnetic emissions. Nat. Hazard Earth Syst. 2008, 8, 657–669. [Google Scholar]
- Eftaxias, K.; Balasis, G.; Contoyiannis, Y.; Papadimitriou, C.; Kalimeri, M.; Athanasopoulou, L.; Nikolopoulos, S.; Kopanas, J.; Antonopoulos, G.; Nomicos, C. Unfolding the procedure of characterizing recorded ultra low frequency, kHZ and MHz electromagnetic anomalies prior to the L’Aquila earthquake as pre-seismic ones-Part 1. Nat. Hazard Earth Syst. 2009, 9, 1953–1971. [Google Scholar]
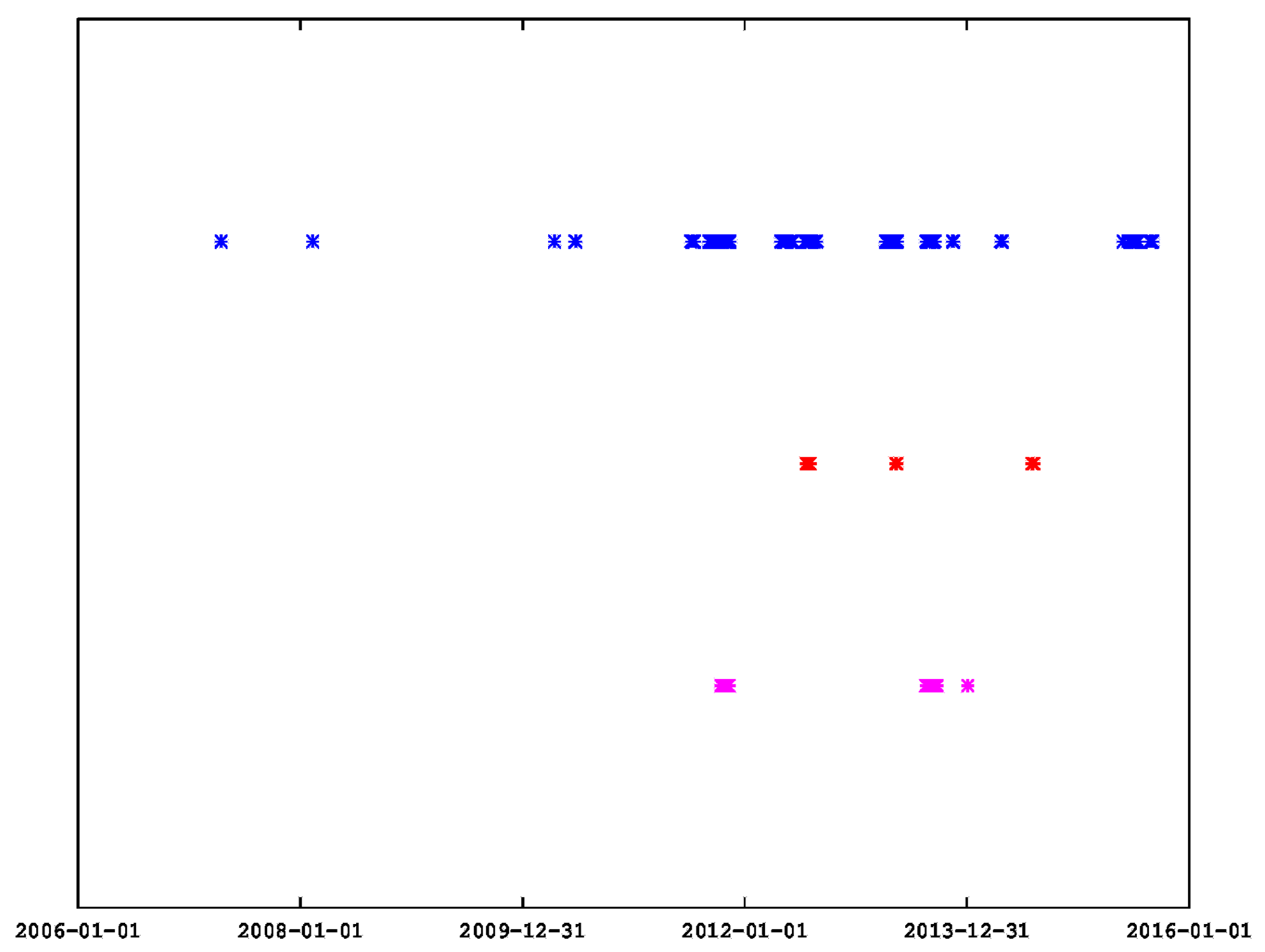

| Dates | |||
|---|---|---|---|
| 2007-7-28 | 2010-6-7 | 2010-6-9 | 2010-6-10 |
| 2010-6-11 | 2010-6-13 | 2010-6-16 | 2010-6-28 |
| 2013-8-18 | 2013-8-31 | 2013-9-1 | 2013-9-2 |
| 2013-9-3 | 2013-9-4 | 2013-9-8 | 2013-9-9 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nikolopoulos, D.; Moustris, K.; Petraki, E.; Koulougliotis, D.; Cantzos, D. Fractal and Long-Memory Traces in PM10 Time Series in Athens, Greece. Environments 2019, 6, 29. https://doi.org/10.3390/environments6030029
Nikolopoulos D, Moustris K, Petraki E, Koulougliotis D, Cantzos D. Fractal and Long-Memory Traces in PM10 Time Series in Athens, Greece. Environments. 2019; 6(3):29. https://doi.org/10.3390/environments6030029
Chicago/Turabian StyleNikolopoulos, Dimitrios, Konstantinos Moustris, Ermioni Petraki, Dionysios Koulougliotis, and Demetrios Cantzos. 2019. "Fractal and Long-Memory Traces in PM10 Time Series in Athens, Greece" Environments 6, no. 3: 29. https://doi.org/10.3390/environments6030029
APA StyleNikolopoulos, D., Moustris, K., Petraki, E., Koulougliotis, D., & Cantzos, D. (2019). Fractal and Long-Memory Traces in PM10 Time Series in Athens, Greece. Environments, 6(3), 29. https://doi.org/10.3390/environments6030029







