Abstract
Commercial microwave links have a great potential to be used as sensors for rain. However, the use of commercial microwave links to monitor the rain depends heavily on the availability of the links’ attenuation measurements. The cellular operators which provide the majority of these measurements usually make use of the standard Network Management Systems (NMS), which log only a quantized version of the minimum and the maximum attenuation values (usually in 15-min intervals). The non-linear min/max transformation, in combination with the quantizer, which are implemented on the channel attenuation measurements, should be considered during the rain-estimation procedures. In this paper, we examine actual NMS produced attenuation measurements that are taken from two commercial microwave links during multiple rain events. Using observations from two rain gauges and a weather radar, we empirically demonstrate that the output of the NMS includes bias, which in turn interferes with the rain-estimation process. We show that the detection and the compensation of this bias have the potential to increase the microwave links’ rain-estimation accuracy considerably.
1. Introduction
The potential of using standard Commercial Microwave Links (CMLs), which are part of the infrastructure of modern Microwave Communication Networks (MCNs), for rain monitoring purposes was suggested back in 2006 [1]. Since then, the capability to use the available CMLs as remote sensors for the environment has been studied by many researchers worldwide, and many achievements have been made. For instance, it has been shown that CMLs can be used to detect and classify rainy periods from dry periods [2,3,4], and to measure the rainfall accurately in various scenarios [2,5]. Algorithms for creating 2-Dimensional rain maps were presented [6], and country-wide rain mapping using CMLs was demonstrated [7]. In addition, an example of dynamic rainfall monitoring was recently demonstrated [8]. Furthermore, the integration of rain measurements that are taken by CMLs with standard radar and rain-gauge measurements was discussed [9,10], and a survey integrating three years of rain monitoring using CMLs was recently presented [11]. Ongoing collaboration of research groups in Europe and Africa presented the potential to use CMLs in Africa, where no other observation tools are available, and thus, standard rain-monitoring capabilities do not exist [12,13].
Despite the advances that have been achieved in the last decade, the fact that the major part of the available CMLs measurements are produced by the MCNs Network Management Systems (NMS), and thus, contain only a quantized version of the minimum and the maximum values of the Received Signal Level (RSL) and the Transmitted Signal Level (TSL), usually in 15-min intervals, remains challenging. Although various methodologies for treating the min/max transformation were presented (e.g., [4,14,15]), the fact that the available RSL and TSL measurements passed a quantizer, was generally ignored. These errors were considered to be unavoidable [16] and relatively small for the purpose of rain monitoring using CMLs attenuation measurements, and thus, did not attract special interest.
Nonetheless, the combination of a quantization process with a min/max transformation may introduce a high bias into the measurements [17]. This bias should not be neglected, as it can affect the rain-estimation accuracy dramatically. In this paper, we present for the first time an experimental demonstration that was designed to demonstrate how this bias affects accumulated rainfall estimations. The empirical results validate our conjecture that this bias should be detected and subtracted from the available measurements prior to the estimation process in order to increase the rainfall estimation performance.
2. Methodology
The relationship between the rain-intensity at a given time t, r(t) (in mm/h), and the CML path-averaged induced attenuation at that time, A(t) (in dB), can be expressed by the well-known Power-Law equation [18]:
where L (in km) is the CML path-length, and a and b are coefficients which depend on the CML specific signal frequency, polarization, and the drop-size-distribution of the rain. Their values are considered to remain relatively constant and are published in the technical literature [19].
For the experimental purposes of our research, we obtained the NMS based measurements from the Israeli cellular operator Cellcom™, which utilizes NMS that sample the TSL and the RSL values every 10-seconds, but produce an output log with only the observed minimum and maximum TSL and RSL values within 15-min intervals (defined for the ith interval by , , , and , respectively). The TSL measurements are quantized by a quantization level of and the RSL measurements are quantized by a quantization level of . From these available quantized extreme measurements (i.e., the minimal and the maximal TSL and RSL sampled values within 15-min intervals), the maximum and the minimum attenuation that occurred within each interval can be approximated by:
where (in dB) is the minimum observed attenuation value within the ith interval and (in dB) is the maximum observed attenuation value within the ith interval.
Based on Equations (2a) and (2b), the attenuation that was induced by the maximal observed rain-intensity in the ith interval, defined by (in dB), can be directly extracted by taking the minimal attenuation value within a fixed time-frame (in which the other-than-rain attenuation-factors’ fluctuations are small [20]), e.g., for a 30 min time-frame:
from which, the averaged rain-intensity in the ith interval, defined by (in mm/h), can be calculated using an adaptation of the Power-Law’s a coefficient [15]:
where K is the number of instantaneous samples per interval from which the maximum attenuation is extracted. For Ericsson AB MINI-LINK systems, K = 90 [21].
On the other hand, as we claim that includes bias which is to be considered, we suggest rewriting Equation (4a) as follows:
where B (in dB) is the induced bias due to the combination of the quantizer and the min/max transformation. Negative values of (), if they existed, were accounted as zeros.
Next, an experiment which emphasizes the effects of this bias, B, is presented.
3. Experimental Setup
An experiment was designed in a location where two actual operational CMLs were available and accessible. The specific CMLs were chosen based on the availability of the NMS measurements (provided by the Israeli cellular operator Cellcom™) and the availability of two nearby Rain Gauges (RGs) and weather radar coverage, all of which were controlled by the Israeli Meteorological Services (IMS). The experiment properties are:
- The minimum and the maximum TSL and RSL measurements in 15-min intervals were logged by CMLs which were located near the city of Arad, Israel. The CMLs share the same path with a path-length of 16 km and operate at a frequency of 18.6 GHz, using either Horizontal polarization (used in Events 1, 2, 3, 4 in Table 1) or Vertical polarization (used in Events 5, 6 in Table 1). Based on the literature [19], the corresponding Power-Law coefficients for these specific CMLs are a = 0.077; b = 1.074 (for the horizontally polarized CML) and a = 0.083; b = 0.999 (for the vertically polarized CML), from which the value of is directly derived using Equation (4b): (Please note that in [15], we presented a calibration procedure for the power-law coefficients and have found that for this specific horizontally polarized CML, a better suited value of the power-law coefficient a is a = 0.046. However, as we do not have the calibrated value for the vertically polarized CML, we have taken the literature values of the power-law coefficient for both CMLs. In any case, this does not affect the presented results, since . for both the horizontally and the vertically polarized CMLs, making any variation in the value of a negligible in our analysis, since the presented results throughout this manuscript are normalized).
 Table 1. Experimental results. The details of each rain event (averaged by the two available rain gauges), and the normalized Root Mean Square Error (RMSD) between the radar (RAD) and the Commercial Microwave Link (CML), and between the two Rain-Gauges (Arad and Shani) and the CML are detailed.
Table 1. Experimental results. The details of each rain event (averaged by the two available rain gauges), and the normalized Root Mean Square Error (RMSD) between the radar (RAD) and the Commercial Microwave Link (CML), and between the two Rain-Gauges (Arad and Shani) and the CML are detailed. - Two IMS controlled RGs, each located near one of the CML base-stations (in the city of Arad and the village of Shani (located roughly 4 km from each of the CML base stations)) were monitored and analyzed. The RGs reported the amount of fallen rain (in mm) in 10-min intervals.
- Unlike a RG, which provides point measurements, the CML is affected by rain throughout its path L (see Equation (1)). Due to the difficulties in comparing the point to path-integrated rainfall measurements, a weather radar was also used. Data were derived from the IMS controlled radar, which was located in Beit-Dagan (central district, roughly 85 km from the CML), from which the radar cells covering the path of the CML were utilized in order to approximate the average rainfall along the CML path, as demonstrated in an earlier study [22].
A map of the experimental setup area is depicted in Figure 1.
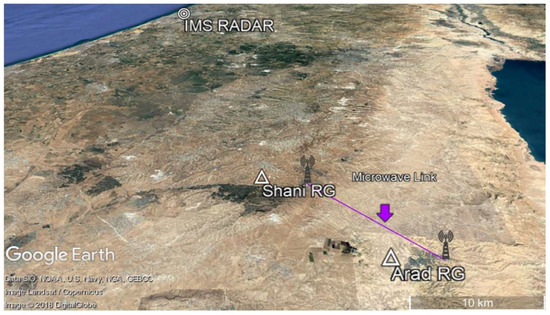
Figure 1.
The experimental setup: the location of the weather radar, the CML, and the two Rain Gauges (Arad and Shani) are marked. This image is copied from [23], where the same experimental setup was used for a different purpose.
Results
Six rain events were analyzed in order to compare the performance of the CML with and without the subtraction of the bias, B (of Equation (5)), with the different instruments. The specific events occurred on 6 November 2015; 1 January 2016; 11 January 2016; 25 January 2016; 22 February 2016; and 26 March 2016 (and are defined as Events 1, 2, 3, 4, 5, 6, respectively). The properties of each of the events are summarized in Table 1.
For each event, the available TSL and RSL data-series were used to calculate the minimum and the maximum attenuation values (of Equations (2a) and (2b)), from which the averaged rain intensities for each 15-min interval within the events, of Equation (5), were derived for the durations of the events, twice:
- No Bias Subtraction, , defined by NBS: B of Equation (5) was put to zero (i.e., no bias consideration was taken).
- Bias Subtraction, , defined by BS: B of Equation (5) was taken as 1.6 dB for the calculation of for all of the events. The value of 1.6 dB was found during dry periods prior to each event (and was found to remain constant at 1.6 dB). This value is based on the quantization levels and the specific CML additive noise [17].
The cumulative CML rain depth throughout each event was also calculated twice. In addition, for comparison, the cumulative rain depth for each event was derived both from the RGs and from the radar.
It is worth noting that comparing the monitored rain from the different sensors (i.e., CML, RG, and radar) is inherently challenging, as each sensor has different spatial and calibration properties. Thus, in order to reduce errors regarding instrumental adjustments, and to confine ourselves to comparing only the effects of the aforementioned bias, each cumulative rain depth data series was normalized to its total accumulated value. An example of the four (normalized) calculated cumulative rain depths can be seen in Figure 2 and Figure 3, for events 1 and 4, respectively (please note that during event 1, the rainfall profile was very spotty and was confined to the southern part of the CML. Thus, RG-Shani did not detect any precipitation).
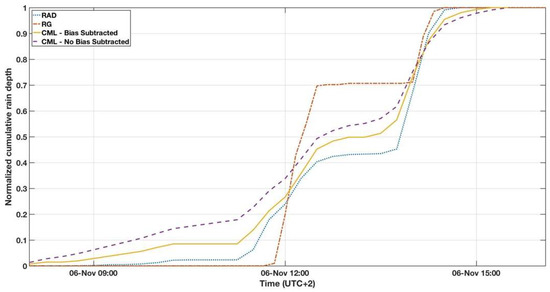
Figure 2.
Normalized accumulated rain depth for a chosen event—6 November 2015 (event 1), monitored by: radar (RAD), Arad rain gauge (RG), and CML, with and without bias subtraction.
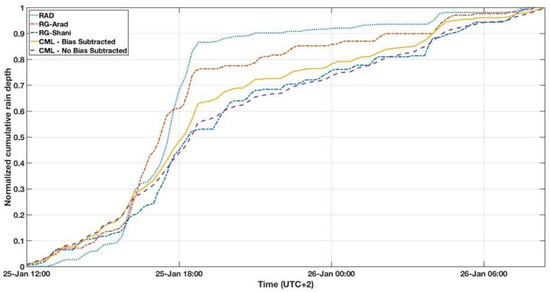
Figure 3.
Normalized accumulated rain depth for a chosen event—25 January 2016 (event 4), monitored by: radar (RAD), rain gauges (RG-Arad and RG-Shani), and CML, with and without bias subtraction.
In addition, the Root Mean Square Difference (RMSD) between the two CML based cumulative rain-depth plots (BS and NBS) and both the RGs and the radar based plots were performed for each event. The specific RMSD calculations are detailed in Table 1.
When examining normalized data, one should pay extra attention to slope differences. It is expected that, throughout the presented event duration, the subtraction of the bias indeed reduces the gap between the CML based cumulative rain estimates and that of the RGs and the radar, as a closer gap results in a lower RMSD. Furthermore, we expect to see that the gap between the NBS curve was developed during the rainy period in the beginning of the event, inferring that excess rainfall was derived (due to the bias which causes a “false alarm” of rain estimation).
An event, in which two prominent rainy periods are obvious (event 1), is presented in Figure 2. Larger slopes of the NBS curve in the “dry” periods indicate false positive rainfall detection, whereas smaller ones during the “wet” periods point on the smaller relative share of rain from the total attenuation, i.e., once other-than-rain attenuation is included. Figure 4 depicts the instantaneous normalized time-series of the rain-intensity, as observed by the available equipment, and the CML-BS and CML-NBS for the same event (event 1). As can be seen, the bias which exists in CML-NBS causes its curve to “rest” at a value which is not zero. In other words, the bias causes the CML-NBS estimate to always report a certain amount of rainfall, even during dry periods. On the other hand, once the bias is removed, the accuracy of the CML-based estimate (i.e., the CML-BS curve) is visibly higher.
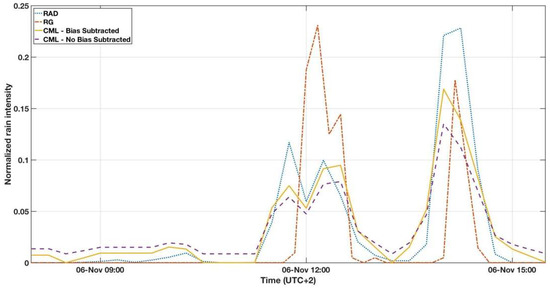
Figure 4.
Normalized instantaneous rain intensity time series for a chosen event—6 November 2015 (event 1), monitored by: radar (RAD), Arad rain gauge (RG), and CML, with and without bias subtraction.
In Figure 3, an interesting case can be visually seen, where the CML-BS plot are better fitted with both the Radar and RG-Arad data, however CML-NBS is better fitted with the northern RG, RG-Shani. This insight is directly translated into the RMSD values that are presented in Table 1, where for the 25 January 2016 event (event 4), the subtraction of the bias decreases the RMSD when compared with RG-Arad and the radar data, but increased the RMSD when compared with RG-Shani. This scenario demonstrates the difficulties and challenges of comparing point-measurement instruments such as a RG with a CML, and justifies the presentation of normalized data.
Nonetheless, as can be seen in Table 1, the benefit of subtracting the bias is not unique to this specific example: Examining the resulted RMSD, which presented for the different events, shows that the subtraction of the bias could indeed be a contributing factor to CML based rain estimation accuracy, as for most of the events, subtracting the bias improved the overall RMSDs. Indeed, in a specific case (event 2), the bias did not affect the RMSD of the CML based estimate and even seemed to improve two out of the three RMSD calculations that were made for this event (the RMSD based on the radar data and on RG-Arad measurements are better for the CML-NBS curve). However, even in this case, the subtraction of the bias did not significantly harm the calculated RMSDs.
Overall, it can be concluded that, once the bias was subtracted from the CML attenuation measurements, the resulted RMSD showed consistent improvement in the majority of the calculations that were performed per case.
4. Discussion
In Section 2, we present the methodology that was required to detect and compensate for the quantization induced bias. There, we concluded that the bias is introduced due to the fact that quantized measurements undergo a min/max transformation. Thus, in cases where the instantaneous samples of the RSL (and the TSL) are available, e.g., using direct Simple Network Management Protocol (SNMP) access [21], the quantization bias, on average, should be negligible, as the quantization-induced bias, on average, does not affect instantaneous measurements.
However, in general, the CML-based precipitation estimation process includes a pre-processing stage of extracting the base-line attenuation level (i.e., isolating the rain-induced attenuation from other attenuation sources that are not related to the rain, known as the base-line attenuation level). There are various approaches of base-line attenuation level extraction. Some of these approaches are based on the minimum attenuation values (e.g., [4,20]). Thus, even in cases where the instantaneous attenuation values are available, if one extracts the base-line attenuation using minimal attenuation values, the subtraction of the extracted base-line attenuation level will add a quantization induced bias. This bias is usually smaller than described in Section 2, as no maximum values are involved and only the biased minimum values are used. Nonetheless, this bias is then equal to . (see the definition of B in Equation (5)), and therefore, cannot be neglected.
Interaction of the Quantization Induced Bias Correction with the Wet Antenna Effect
When attributing total CML-channel attenuation to rain, a more general version of the Power-Law (of Equation (1)) can be used:
where (in dB) is the total attenuation due to the rain at time index t, which includes the direct attenuation due to rain (as described in the Power-Law—see Equation (1)), plus an additional attenuation factor, (in dB), which represents the Wet-Antenna Effect, i.e., the dampening during rainy periods, which causes additional attenuation. In [4], the authors described the wet-antenna effects and concluded that during rainy periods, the wet-antenna attenuation is relatively constant. In Overeem et al. (2013), by using a training series and side information that was based on a meteorological radar in a country-wide scale, an approximation of . was presented. There, it was concluded that the wet-antenna attenuation indeed can be considered to be constant during rainy periods and should be taken as a constant value of dB. It is important to note that this value of was established using min/max attenuation values.
However, in [24], we inspected the value of with respect to experimental E-band CMLs that were operated by Ericsson AB. Since the CMLs are owned by Ericsson, we were able to receive instantaneous measurements of the RSL (with constant TSL). Using the instantaneous samples, we found out that the value of which best fit the data was dB, or dB, depending on the specific CML. Nonetheless, both of these values are smaller by ≈1.4 dB than the value of 2.3 dB which was found in 2013. Interestingly, this 1.4 dB is almost identical to the quantization induced bias, B, which was found in the experimental demonstration of Section 3 (which equals B = 1.6 dB; see Equation (5)).
Based on the quantization induced bias analysis that was presented in this paper, we conjecture that the Wet-Antenna effect, which was found in the past using extreme attenuation values, actually included the quantization induced bias. As both the quantization induced bias, as well as the Wet-Antenna induced attenuation remain constant during a rain event, neglecting the quantization induced bias and compensating for it by choosing a higher Wet-Antenna attenuation factor still yields good and accurate results. Thus, it is suggested that the quantization induced bias was indeed taken into consideration in past studies, as it was mistakenly considered to be part of the Wet-Antenna induced attenuation, and thus, it did not affect the end result of the rain estimates.
Nonetheless, we feel that future studies should be performed in order to better understand how the quantization induced bias is introduced as a function of the manufacturer of the used hardware and the properties, location, and the specific approach that was used for rain estimation, using the CML-based extreme attenuation values.
5. Conclusions
In this paper, we examined the bias which affects the min/max quantized Received Signal Level and the Transmitted Signal Level measurements, which are used for rain monitoring. Using a specially designed experiment, we showed for the first time that this bias indeed interferes with CML based rain estimation methodologies.
We believe that the empirical results and the conclusions presented in this paper should be used as a basis for future research, both for better understanding the effects of this bias in regard to different climates and rain physical properties, and also for the implementation of new modules for bias compensation in current and future CML based rain estimation algorithms.
Author Contributions
J.O. conceived the idea and developed the theory. A.E. implemented the experiment and processed and analyzed the experimental data. Both J.O. and A.E. wrote the manuscript.
Funding
This research received no external funding.
Acknowledgments
We would like to thank Cellcom™ for giving us access to data and information that were critical for this research. The contribution to our research receives our utmost appreciation. This work was supported in part by the German Research Foundation (DFG) through the project, “Integrating Microwave Link Data for Analysis of Precipitation in Complex Terrain: Theoretical Aspects and Hydrometeorological Applications (IMAP)”.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Messer, H.; Zinevich, A.; Alpert, P. Environmental monitoring by wireless communication networks. Science 2006, 312, 713. [Google Scholar] [CrossRef] [PubMed]
- Schleiss, M.; Berne, A. Identification of dry and rainy periods using telecommunication microwave links. IEEE Geosci. Remote Sens. Lett. 2010, 7, 611–615. [Google Scholar] [CrossRef]
- Chwala, C.; Qiu, W.; Hipp, S.; Kunstmann, H.; Siart, U.; Seltmann, J.; Pohl, M. Wet/Dry-Estimation Algorithm for Commercial Backhaul Link Attenuation Data to Derive Precipitation Intensity in Alpine Terrain; European Geoscience Union General Assembly (EGU): Vienna, Austria, 2011. [Google Scholar]
- Overeem, A.; Leijnse, H.; Uijlenhoet, R. Measuring urban rainfall using microwave links from commercial cellular communication networks. Water Resour. Res. 2011, 47, W12505. [Google Scholar] [CrossRef]
- Rayitsfeld, A.; Samuels, R.; Zinevich, A.; Hadar, U.; Alpert, P. Comparison of two methodologies for long term rainfall monitoring using a commercial microwave communication system. Atmos. Res. 2012, 104–105, 119–127. [Google Scholar] [CrossRef]
- Goldstein, O.; Messer, H.; Zinevich, A. Rain rate estimation using measurements from commercial telecommunications links. IEEE Trans. Signal Process. 2009, 57, 1616–1625. [Google Scholar] [CrossRef]
- Overeem, A.; Leijnse, H.; Uijlenhoet, R. Country-wide rainfall maps from cellular communication networks. Proc. Nat. Acad. Sci. USA 2013, 110, 2741–2745. [Google Scholar] [CrossRef] [PubMed]
- Roy, V.; Gishkori, S.; Leus, G. Dynamic rainfall monitoring using microwave links. EURASIP J. Adv. Signal Process. 2016, 1, 77. [Google Scholar] [CrossRef]
- Bianchi, B.; jan van Leeuwen, P.; Hogan, R.J.; Berne, A. A variational approach to retrieve rain rate by combining information from rain gauges, radars, and microwave links. J. Hydrometeorol. 2013, 14, 1897–1909. [Google Scholar] [CrossRef]
- Liberman, Y.; Samuels, R.; Alpert, P.; Messer, H. New algorithm for integration between wireless microwave sensor network and radar for improved rainfall measurement and mapping. Atmos. Meas. Tech. Discuss. 2014, 7, 4481–4528. [Google Scholar] [CrossRef]
- Overeem, A.; Gaona, M.F.R.; Leijnse, H.; Uijlenhoet, R. Three years of country-wide rainfall maps from cellular communication networks. In EGU General Assembly Conference Abstracts; European Geosciences Union: Vienna, Austria, 2015; Volume 17, p. 15153. [Google Scholar]
- Doumounia, A.; Gosset, M.; Cazenave, F.; Kacou, M.; Zougmore, F. Rainfall monitoring based on microwave links from cellular telecommunication networks: First results from a west african test bed. Geophys. Res. Lett. 2014, 41, 6016–6022. [Google Scholar] [CrossRef]
- Gosset, M.; Cazenave, F.; Zougmore, F.; Doumounia, A.; Kacou, M. Rainfall measurements from cellular networks microwave links: An alternative ground reference for satellite validation and hydrology in Africa. In EGU General Assembly Conference Abstracts; European Geosciences Union: Vienna, Austria, 2015; Volume 17, p. 4867. [Google Scholar]
- Ostrometzky, J.; Messer, H. Accumulated Rainfall Estimation Using Maximum Attenuation of Microwave Radio Signal. In Proceedings of the 2014 IEEE 8th Sensor Array and Multichannel Signal Processing Workshop (SAM), A Coruna, Spain, 22–25 June 2014; pp. 193–196. [Google Scholar]
- Ostrometzky, J.; Raich, R.; Eshel, A.; Messer, H. Calibration of the Attenuation-Rain Rate Power-Law Parameters Using Measurements from Commercial Microwave Networks. In Proceedings of the 41st IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016. [Google Scholar]
- Kollar, I. Bias of mean value and mean square value measurements based on quantized data. IEEE Trans. Instrum. Meas. 1994, 43, 733–739. [Google Scholar]
- Ostrometzky, J.; Eshel, A.; Alpert, P.; Messer, H. Induced Bias in Attenuation Measurements Taken from Commercial Microwave Links. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017. [Google Scholar]
- Olsen, R.; Rogers, D.; Hodge, D. The relation in the calculation of rain attenuation. IEEE Trans. Antennas Propag. 1978, 26, 318–329. [Google Scholar] [CrossRef]
- P.838: Specific Attenuation Model for Rain for Use in Prediction Methods. Available online: https://www.itu.int/rec/R-REC-P.838/en (accessed on 24 May 2018).
- Ostrometzky, J.; Messer, H. Dynamic determination of the base-line level in microwave links for rain monitoring from minimum attenuation values. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 24–33. [Google Scholar]
- Chwala, C.; Keis, F.; Kunstmann, H. Real-time data acquisition of commercial microwave link networks for hydrometeorological applications. Atmos. Meas. Tech. 2016, 9, 991–999. [Google Scholar] [CrossRef]
- Eshel, A.; Messer, H.; Raich, R.; Ostrometzky, J.; Laronne, J.B.; Alpert, P. On the Use of Measurements from a Commercial Microwave link for Evaluation of Flash Floods in Arid Regions. Available online: https://www.atmos-chem-phys-discuss.net/acp-2017-963/ (accessed on 24 May 2018).
- Raich, R.; Alpert, P.; Messer, H. Vertical precipitation estimation using microwave links in conjunction with weather radar. Environments 2018, 5, 74. [Google Scholar] [CrossRef]
- Ostrometzky, J.; Raich, R.; Bao, L.J.; Hansryd, J.; Messer, H. The Wet-Antenna effect—A factor to be considered in future communication networks. IEEE Trans. Antennas Propag. 2018, 66, 315–322. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).