Prediction of Reservoir Sediment Quality Based on Erosion Processes in Watershed Using Mathematical Modelling

Abstract

Soil erosion, as a significant contributor to nonpoint-source pollution, is ranked top of sediment sources, pollutants attached to sediment, and pollutants in the solution in surface water. This paper is focused on the design of mathematical model intended to predict the total content of nitrogen (N), phosphorus (P), and potassium (K) in bottom sediments in small water reservoirs depending on water erosion processes, together with its application and validation in small agricultural watershed of the Tisovec River, Slovakia. The designed model takes into account the calculation of total N, P, and K content adsorbed on detached and transported soil particles, which consists of supplementing the soil loss calculation with a determination of the average nutrient content in topsoils. The dissolved forms of these elements are neglected in this model. Validation of the model was carried out by statistical assessment of calculated concentrations and measured concentrations in Kľušov, a small water reservoir (Slovakia), using the t-test and F-test, at a 0.05 significance level. Calculated concentrations of total N, P, and K in reservoir sediments were in the range from 0.188 to 0.236 for total N, from 0.065 to 0.078 for total P, and from 1.94 to 2.47 for total K. Measured nutrient concentrations in composite sediment samples ranged from 0.16 to 0.26% for total N, from 0.049 to 0.113% for total P, and from 1.71 to 2.42% for total K. The statistical assessment indicates the applicability of the model in predicting the reservoir’s sediment quality detached through erosion processes in the catchment.

1. Introduction

Soil erosion, as a significant contributor to nonpoint-source pollution, is ranked the top of sediment source [1], pollutants attached to sediment [2], and pollutants in the solution of surface water [3].

Worldwide, soil erosion by water affects 1094 million hectares of arable land [4]. Across Europe, data on trends in soil erosion are lacking and erosion estimates are based on modelling studies. In the 1990s, water erosion affected 105 million hectares of soil or 16% of Europe’s total land area (excluding Russia) [5]. In 2006, it was estimated that the surface area affected by water erosion in the EU-27 was 130 million hectares [6]. In 2014–2015, approximately 11.4% of the EU territory was affected by moderate to high level water erosion rate (more than five tons per hectare per year). The reduction of this rate against 1990s by 4.6% is mainly due to the application of water erosion control practices which have been applied during the last decade in the EU [7].

A significant amount of global sediment flux is retained in reservoirs [8]. It is estimated that the global annual loss in storage capacity of the world’s reservoirs due to sediment deposition is approximately 0.5–1% [9], and for individual reservoirs these values can be as high as 4–5% [10]. The useful lifetime of the reservoirs is thus reduced to only 22 years on average [11]. Other studies found in the literature [12,13] have reported that worldwide rivers carry approximately 15 billion tons of sediments to the sea annually. Walling and Webb [14] have given an overview of mean annual total suspended sediment transport to the oceans that ranged from 8 to 51 billion tons of sediments.

Together with the small fraction of sediment, pollutants including nutrients are transported via surface runoff [15] from arable land in the catchment [16] and are deposited in reservoirs [17]. The quantity of nutrient concentrations in water reservoir sediments, associated with nonpoint source pollution from agricultural catchments, is regarded as the environmental pollution index. As published by Qian et al. [18] the easier transformation of nitrogen and phosphorus from agricultural soils to freshwater bodies contributes to their accelerated eutrophication. Nutrient concentrations in runoff are affected by many factors including climate, soil characteristics, relief, land use, and chemical application [19]. Typically, the eroded soils contain about three times more nutrients per unit weight than are left in the remaining soil [20]. Pimentel and Burgess [21] summarized, that a ton of fertile topsoil averages 1 to 6 kg of nitrogen, 1 to 3 kg of phosphorus, and 2 to 30 kg of potassium, whereas the topsoil on the eroded land has an average nitrogen content of only 0.1 to 0.5 kg per ton. As reported in literature [22,23], sediments act as an efficient trap for both nutrients (nitrogen and phosphorus). For example, sediments from Gulf of Finland trap 20–50% of P and 40–65% of N in the Neva estuary and in the open Gulf, and up to 100% in the Neva Bay are buried within the accumulating sediment. The rest is released to the overlying water [22]. Similarly, [23] showed that finer sediment particles (silt and clay) transported by rivers carry the major part of nutrient loads by absorption and thus, sediment settling can remove nutrients from the water column. On the other hand, the sediment accumulation in Iron Gate reservoir (Romania) on the Danube River corresponded to 5% of total nitrogen and 12% of total phosphorus of the incoming loading [24].

In order to protect surface water resources and optimize their use, soil and nutrient losses from catchment areas must be controlled [25] and minimized [26]. Conventional methods to assess soil erosion [27] and sediment-associated chemical runoff are expensive, time-consuming, and need to be collected over many years [28,29]. Nowadays, preference is given to predict [30] and control sediment and nutrient yields from agricultural nonpoint source runoff using mathematical models [31]. Soil erosion models can assess and simulate the extent and magnitude of erosion processes in watershed. To predict soil erosion rates by water, several models exist which differ greatly in terms of complexity, inputs, and spatial and temporal scale [32]. Most have been developed for large agricultural areas and are designed to predict annual rates of soil loss from land under various cropland and rangeland management techniques [33,34]. To estimate sediment yields into small reservoirs, regression models can also be used. Most of these models are site-specific and do not permit the land and water managers to assess the impact of agronomic and mechanical changes on sediment yields [35] much less on sediment quality. Thus, there is a pressing need to extend such models to provide sediment quality prediction by integrating already available research methods with new generalization and integration techniques. Better predicting of small water reservoirs’ sediment quantity and quality is necessary, of all things, with regard to utilization or application of dredged sediment from water reservoirs [36,37].

The objective of this study is to design a mathematical model intended to predict the total content of nitrogen, phosphorus, and potassium in bottom sediments in small water reservoirs, with its application and validation in the small agricultural watershed of the Tisovec River, Slovakia. Specification of sediment quality in the reservoir depending on the main periods of the cropping cycle and distribution of erosivity during a year is the novelty of this article. Also, an average plant nutrient uptake for chosen crops divided into five crop-stage periods during growing season was devised.

2. Materials and Methods

2.1. Study Area

A prediction model was designed on the basis of the nutrient transport study carried out in the small agricultural catchment of the Tisovec River (northeast of Slovakia, the district of Bardejov) covering an area of 6.0 km². The catchment falls into the drainage basin of the Topl’a River. The average annual air temperature is 8 °C and the average annual rainfall is about 670 mm with a maximum in the summer months. Planosols, cambisols, and albic luvisols are the dominant major soil groups of the Tisovec basin with the presence of medium-textured soils (sandy loam). Non-point sources of pollution from agricultural production areas are the leading cause of the sediment and water quality degradation in this catchment. Different land uses occur within the catchment.

The upper and middle zone of the catchment consists mainly of forests (39.2%) and pastures (21.7%), 21.4% of downstream areas are covered with agricultural land. The rest of the catchment is for other uses.

For irrigation of surrounding agricultural land and accumulation of water, the Kl’ušov small water reservoir with total capacity of 72,188 m³ was built in the Tisovec River in 1986. At present, it is also used for retention of high water, suburban recreation, and as a fishery. It has a surface area of 2.2 ha, a length of about 494 m, and a mean depth of 3.5 m. At the dam, the reservoir reaches a maximum water depth of 9.57 m [38].

Because of the rough terrain, climatic conditions, and soil types, this catchment is exposed to water erosion. Eroded soil particles in this catchment greatly affect the quantity and quality of sediments in the Kl’ušov reservoir. This reservoir trapped approximately 24,500 m³ of sediments delivered from the upper catchment during 19 years of its operation and its total storage capacity decreased by about 33% [38].

2.2. Sampling Procedure and Chemical Analysis

To determine the total N, P, and K content in eroded soil particles, soil samples were collected from two parcels (1004/1 and 2001/1) of arable land situated next to the reservoir (Figure 1). Within each parcel, about 30 to 40 soil subsamples were taken and mixed into one composite sample. Considering the fact that the highest nutrient levels occur in the surface layers, sampling depth was set at 0.30 m [39].

Together with soil sampling, 21 composite (disturbed) reservoir sediment samples were taken from the drained reservoir to determine total N, P, and K content. Sampling methodology was as follows. Part of the composite sediment samples were taken from a location in proximity to the dam due to deposition of fine-grained particles (<63 µm) washed away through water erosion and preferentially attaching the nutrients [40]. Other samples were collected along the reservoir and others in different sampling depths from one location. A S9 sample was taken from the Tisovec stream.

Composite soil and sediment samples were collected in buckets; the weight of the composite samples was about 3 kg for sediment and 5 kg for soil. In laboratory conditions, the samples were air dried at room temperature, any coarse lumps were crushed and samples were homogenized.

Adsorbed forms of nutrients in soil and sediment samples were determined for total nitrogen content by elemental analysis (LECO CHN628) and for total phosphorus and potassium using an inductively coupled plasma-atomic emission spectrometry technique (Agilent 5100 ICP-OES).

To determine the amount of dissolved N and P in soil samples, laboratory leaching experiments were conducted. Leachates were prepared in a 1 to 10 proportion of soil sample to distilled water. After 24 h, leachates were subsequently filtered and total N and P contents were determined using a DR 890 (Hach Lange) portable colorimeter.

2.3. Model

The model works on the calculation of total nutrient (N, P, and K) concentrations in detached eroded soil particles in dissolved and adsorbed form of these elements.

Calculation of total N, P, and K in adsorbed form consists of supplementing the soil loss calculation with a determination of the average nutrient content in topsoils.

Soil loss from arable land is computed using the Universal Soil Loss Equation (USLE) [41] which is expressed as

$$G_{r,i}=R\ast K\ast L\ast S\ast C_{r,i}\ast P$$

(1)

where G_r,i is the potential long term average annual soil loss (tons per hectare per year); R is the rainfall erosivity factor in MJ ha⁻¹ cm h⁻¹; K is the soil erodibility factor in t ha h ha⁻¹ MJ⁻¹ mm⁻¹; L, S is the topographical factor; C_r,i is the average plant cover factor in i-year calculated as a sum of divided C_i factors; and P is the support practice factor. The generalized plant cover (C) factor values resulting from the USLE are specified and modified by their dividing into five crop-stage periods (C_i) according to Wischmeier and Smith [41] (seedbed preparation, establishment, development, maturing crop, stubble field) to take into account the height of plant cover from the ground [42] and annual rainfall distribution. To compute C_r,i, partial C_i factor is weighted according to distribution of erosivity during a year.

The calculation of average nutrient concentrations in topsoils is expressed by deducting nutrient input from fertilizer use from plant nutrient uptake (output). As in soil loss calculation, even in this case, the calculation is divided into five crop-stage periods.

Finally, the total N, P, and K content in transported soil particles from arable land to reservoir is calculated through the modification of the average N, P, and K concentrations in eroded soil particles in adsorbed form detached through water erosion by sediment enrichment ratio (SER) [43] using the proposed equation

$$C_X=\frac{{\displaystyle \sum _{i=1}^5{X}_i\cdot G_i}}{G_{r,i}}\cdot SER=\frac{{\displaystyle \sum _{i=1}^5{X}_i\cdot G_i}}{G_{r,i}}\cdot e^{2-0.2\ln (G_{r,i}.1000)}$$

(2)

$$X_i=backgroundsoilconcentration+\left(N,P,Kinput-plantN,P,Kuptake\right)$$

(3)

where C_X is an average annual concentration of total N, P, K in transported soil particles from the studied parcel (kg N,P,K ha⁻¹ or mg N,P,K kg soil⁻¹); G_i is partial soil loss in individual crop-stage periods (t ha⁻¹); G_r,i is an average soil loss from parcel in i-year (t ha⁻¹ year⁻¹); X_i is residual concentration of total N, P, K in soil in i-period (kg N,P,K ha⁻¹). The total concentrations of N, P, K in reservoir bottom sediments are computed as a weighted mean of the calculated average annual concentration of total N, P, K in transported soil particles from parcels in the watershed.

2.4. Statistical Methods

The validation of the proposed prediction model was carried out via a statistical assessment of the total N, P, and K concentrations in reservoir sediments calculated during the 10-year crop rotation system and determined nutrient concentrations in the Kl’usov small water reservoir.

It is natural to suppose that the random variables C_Xy—representing pertinent concentrations with X being N, P, or K, and y being either v for the values calculated by the proposed model or m for the measured data—exhibit a lognormal distribution. Thus the data should be logarithmically transformed.

In order to infer the proposed distribution a conformity test can be performed. The inference about the normality can be done using the Shapiro–Wilk (SW) test [44] for the transformed data. The hypothesis H₀: C_Xy ~ $𝒩$(μ(C_Xy),σ²(C_Xy)) is tested with respect to the alternative H₁: C_Xy ~ non $𝒩$(μ(C_Xy),σ²(C_Xy)). The test statistic W for the used test is given as

$$W=\frac{{\left({\displaystyle \sum _{i=1}^n{a}_i{x}_i}\right)}^2}{{\displaystyle \sum _{i=1}^n{\left(x_i-\overline{x}\right)}^2}}$$

(4)

where the values in a pertinent dataset are denoted x_i the parameters of the test a_i are obtained from the table data for the SW test [45], which in the present case of n = 20 samples are

a_i = −a_21−i, i = 1, 2, … 10, a₁₁ = 0.0140, a₁₂ = 0.0422, a₁₃ = 0.0711, a₁₄ = 0.1013, a₁₅ = 0.1334, a₁₆ = 0.1686, a₁₇ = 0.2085, a₁₈ = 0.2565, a₁₉ = 0.3211, a₂₀ = 0.4734.

(5)

The critical value for the test statistic with a significance level 0.05 is W_crit = 0.905. If W is less than W_crit, the null hypothesis is rejected.

If, as assumed, the normality is not rejected at the 0.05 significance level, the random variables’ means for each element can be compared—i.e., the calculated v and measured m—using the two-sample t-test (with the hypotheses H₀:μv = μm vs. H₁:μv ≠ μm), while for a comparison of the variances the two-sample F-test (with the hypotheses H₀:σv² = σm² vs. H₁:σv² ≠ σm²) is applied [46,47]. In all the cases, the significance level is set to the value 0.05. The parameters μ and σ are estimated by the sample mean đx̄ and sample standard deviation S, respectively.

3. Results and Analysis

3.1. Field Measurements

Chemical analyses showed that measured N, P, and K concentrations in collected average soil samples from parcel 1004/1 ranged from 0.11 to 0.22% for total N, from 0.055 to 0.082% for total P, and from 1.72 to 1.91 for total K depending on collection period (different rates and date of fertilizer application, plant cover, crop uptake rates). Determined (measured) concentrations in soil samples from parcel 2001/1 ranged from 0.12 to 0.23% for total N, from 0.049 to 0.065% for total P, and from 1.67 to 1.85 for total K.

Measured N, P, and K concentrations in composite sediment samples are given in

Table 1. Measured concentrations of total N, P, and K in reservoir sediments.

Sample	N	P	K	Sample	N	P	K
	(%)	(%)	(%)		(%)	(%)	(%)
S1	0.260	0.112	2.420	S12	0.240	0.101	2.400
S2	0.240	0.113	1.980	S13	0.250	0.103	2.420
S3	0.230	0.066	1.960	S14	0.250	0.108	1.880
S4	0.220	0.066	1.690	S15	0.150	0.049	1.940
S5	0.220	0.067	2.050	S16	0.160	0.049	1.990
S6	0.200	0.090	2.030	S17	0.180	0.052	2.020
S7	0.170	0.049	1.710	S18	0.170	0.061	2.020
S8	0.160	0.070	2.200	S19	0.160	0.055	2.000
S10	0.230	0.086	2.320	S20	0.180	0.059	2.040
S11	0.230	0.103	2.370	S21	0.190	0.077	2.330

.

3.2. Model

The dissolved concentrations of total N and P in solution from soil samples were very low (at levels 0.22–0.43% of total N and 0.45–0.86% of total P) and therefore the dissolved forms of the following elements were neglected in this model.

The proposed model takes into account the calculation of total N, P, and K content adsorbed on detached and transported soil particles via water erosion.

The individual factors entering the equation are as follows. For the whole investigated territory (Bardejov district), it is considered with the constant value of factor R = 22.43 MJ ha⁻¹ cm h⁻¹ derived by Malisek [48]. K factor data is determined considering the soil texture in watershed and range from 0.25 to 0.40 t ha h ha⁻¹ MJ⁻¹ mm⁻¹. LS factor is determined for each outflow profile. The average C_r,i values calculated are 0.25 for winter oilseed rape, 0.27 for triticale, 0.57 for corn silage, 0.17 for winter wheat, and 0.31 for spring barley. The P values are set at 1.0.

Based on the determination of a ‘divided’ C_i factor, partial soil loss G_i in individual crop-stage periods from studied parcels (1004/1 and 2001/1) are calculated and the results are given in

Table 2. Partial and average annual soil losses from 1004/1 parcel.

Year/Crop	Gi (t ha−1)					Gr,i (t ha−1 Year−1)
	Crop-Stage Period *
	1	2	3	4	5
1/winter oilseed rape	3.74	1.88	0.14	1.22	0.78	7.75
2/triticale	5.41	0.36	0.08	1.55	0.75	8.16
3/corn silage	3.41	3.50	5.35	5.47	-	17.73
4/winter wheat	-	0.03	0.06	1.75	0.07	1.91
5/winter oilseed rape	1.96	1.34	0.11	1.26	0.77	5.45
6/winter wheat	5.24	0.19	0.06	1.46	0.75	7.71
7/potatoes	3.85	1.44	4.40	5.52	-	15.22
8/winter wheat	0.04	0.15	0.08	1.42	0.76	2.44
9/spring barley	4.17	0.96	2.39	0.85	0.21	8.58
10/winter oilseed rape	3.74	2.24	0.15	1.15	0.78	8.06

* 1—seedbed preparation; 2—establishment; 3—development; 4—maturing crop; 5—stubble field.

and

Table 3. Partial and average annual soil losses from 2001/1 parcel.

Year/Crop	Gi (t ha−1)					Gr,i (t ha−1 Year−1)
	Crop-Stage Period
	1	2	3	4	5
1/corn silage	0.55	3.67	10.57	12.88	0.06	27.73
2/spring barley	0.10	0.20	1.85	2.91	0.28	5.34
3/triticale	5.88	3.99	0.21	3.07	0.14	13.28
4/winter oilseed rape	2.94	8.31	0.48	2.60	1.59	15.93
5/triticale	10.29	0.87	0.18	2.98	1.55	15.86
6/pea	8.24	1.70	4.43	1.87	1.57	17.81
7/winter wheat	8.74	0.61	0.14	4.39	0.10	13.99
8/spring barley	0.49	0.82	2.73	2.42	1.55	8.02
9/winter rye	7.57	0.67	0.15	2.88	1.85	13.12
10/winter oilseed rape	7.35	0.79	0.21	2.32	1.61	12.28

. Average annual soil loss ranged from 1.9 to 17.7 t ha⁻¹ year⁻¹ from 1004/1 parcel and from 5.34 to 27.7 t ha⁻¹ year⁻¹ for 2001/1 parcel according to used crop and management practices during the season. However, long term average annual soil loss is 8.3/14.3 t ha⁻¹ year⁻¹ from 1004/1; 2001/1 parcels depending on the crop and parcel length and slope gradient.

In terms of land management, the Tisovec River catchment falls under the authority of the Kľušov agricultural cooperative and all parcels within the catchment, with similar topographical and soil characteristics, are managed in a similar way. Consequently, calculations of total N, P, and K concentrations in eroded soil particles in adsorbed form are realized for the same (two) parcels of arable land situated next to the Kľušov reservoir.

Information about nutrient inputs is provided by the agricultural cooperative in the studied area. The fertilizers used in the watershed are primarily NPK fertilizers (8.5% or 15% N) and ammonium nitrate (27% N). Data about plant nutrient uptake are calculated according to the average yield in the Tisovec catchment’s area and the mean plant nutrient uptake values provided by The Central Control and Testing Institute in Agriculture. For crops commonly grown in our conditions, partial (divided into five periods) and average plant nutrient uptake during the crop-stage periods was designed (

Table 4. Proposed partial and average plant nutrient uptake during the crop-stage periods.

Crop	(kg ha−1)	Crop-Stage Period					${\displaystyle \sum _1^5}$
		1	2	3	4	5
spring barley	N	0.00	15.90	17.75	20.00	0.00	53.65
	P	0.00	2.05	2.50	3.70	0.00	8.25
	K	0.00	18.65	21.80	19.55	0.00	60.00
winter wheat, triticale, winter rye	N	0.00	0.00	19.10	71.35	0.00	90.45
	P	0.00	0.00	1.25	10.75	0.00	12.00
	K	0.00	0.00	9.55	67.50	0.00	77.05
winter oilseed rape	N	0.00	9.90	68.90	30.00	0.00	108.80
	P	0.00	1.40	15.90	5.00	0.00	22.30
	K	0.00	6.20	88.10	7.70	0.00	102.00
pea	N	0.00	18.30	17.70	26.30	0.00	62.30
	P	0.00	1.90	1.80	2.60	0.00	6.30
	K	0.00	8.50	8.20	12.10	0.00	28.80
potatoes	N	0.00	18.27	17.66	53.00	0.00	88.93
	P	0.00	2.61	2.52	7.58	0.00	12.71
	K	0.00	23.49	22.71	68.15	0.00	114.35
corn silage	N	0.00	16.35	16.89	50.18	0.00	83.42
	P	0.00	2.18	2.19	6.75	0.00	11.12
	K	0.00	13.62	13.67	42.22	0.00	69.51

).

The total N, P, and K content in transported soil particles from arable land to reservoir is calculated. The background concentrations of the modelled elements in topsoils from parcels 1004/1 and 2001/1 were 0.16/0.18% for N, 0.068/0.054% for P, and 1.81/1.80 for K. The values of SER ranged from 0.97 to 1.63 depending on an average soil loss from parcels in i-year.

Finally, the total nutrient contents in reservoir sediments C_Xv (

Table 5. Calculated concentrations of total N, P, and K in reservoir sediments.

Year	CXv in Reservoir (%)
	N	P	K
1	0.188	0.067	1.956
2	0.225	0.078	2.307
3	0.188	0.066	1.944
4	0.225	0.082	2.387
5	0.203	0.072	2.131
6	0.193	0.068	2.032
7	0.189	0.065	1.954
8	0.236	0.083	2.469
9	0.199	0.069	2.071
10	0.202	0.070	2.096

) are then computed as a weighted mean of the calculated average annual total nutrient concentrations in transported soil particles from investigated parcels. The area of 1004/1 parcel is 15.63 ha and 2001/1 parcel area is 18.46 ha.

3.3. Statistical Tests and Interpretation

Calculated concentrations of total N, P, and K in reservoir sediments (C_Xv) were compared with chemical analyses obtained from collected average sediment samples (C_Xm).

First, the SW test is used to surmise the normality of the distributions. The SW test statistic W (4) is calculated for each set of the logarithmic data. The results are summarized in

Table 6. The values of test statistic W (v for calculated, m for measured data) in testing of H₀ and H₁ hypotheses using the SW test of conformity and their comparison with the critical value.

Element	SW Test
	Wv		Wcrit	Wm		Wcrit
N	0.9255	>	0.905	0.9088	>	0.905
P	0.9346	>	0.905	0.9064	>	0.905
K	0.9145	>	0.905	0.9138	>	0.905

, where also the comparison with critical value set at a 0.05 W_crit significance level is introduced. In each case, the null hypothesis of the SW test is not rejected so that the samples of transformed data can be considered to have a normal distribution.

The results of the comparison of two samples for each element are shown in

Table 7. The test statistics and the F-test and t-test critical percentages for a comparison of variances in N, P, and K concentrations.

Element	Variance			Mean
	T		Percentage	T		Percentage
N	2.7161	>	2.5089	0.4956	<	2.0345
P	2.2073	<	2.5089	0.0863	<	2.0227
K	0.7173	<	2.5089	0.4078	<	2.0227

, the test statistics T are compared with critical percentages of the pertinent distributions F and t, respectively [44,46].

The results imply that for the case of nitrogen the hypothesis H₀ should be rejected, because the value of the test statistic is larger than the critical percentage. For phosphorus and potassium, however, the hypothesis H₀ cannot be rejected. This result influences the mode of the t-test for comparing the means: For N it is used with an assumption of unequal variances, while for P and K equal variances are assumed.

The results in Table 7 do not permit the rejection of the hypothesis H₀ for any of the concentrations considered. Thus, it can be supposed that the means of both results sets—i.e., measured and calculated according to the model (2)—N, P and K do not vary significantly in total concentrations. This result is also confirmed by finding the two-sided confidence intervals (CI) for distribution means μ.

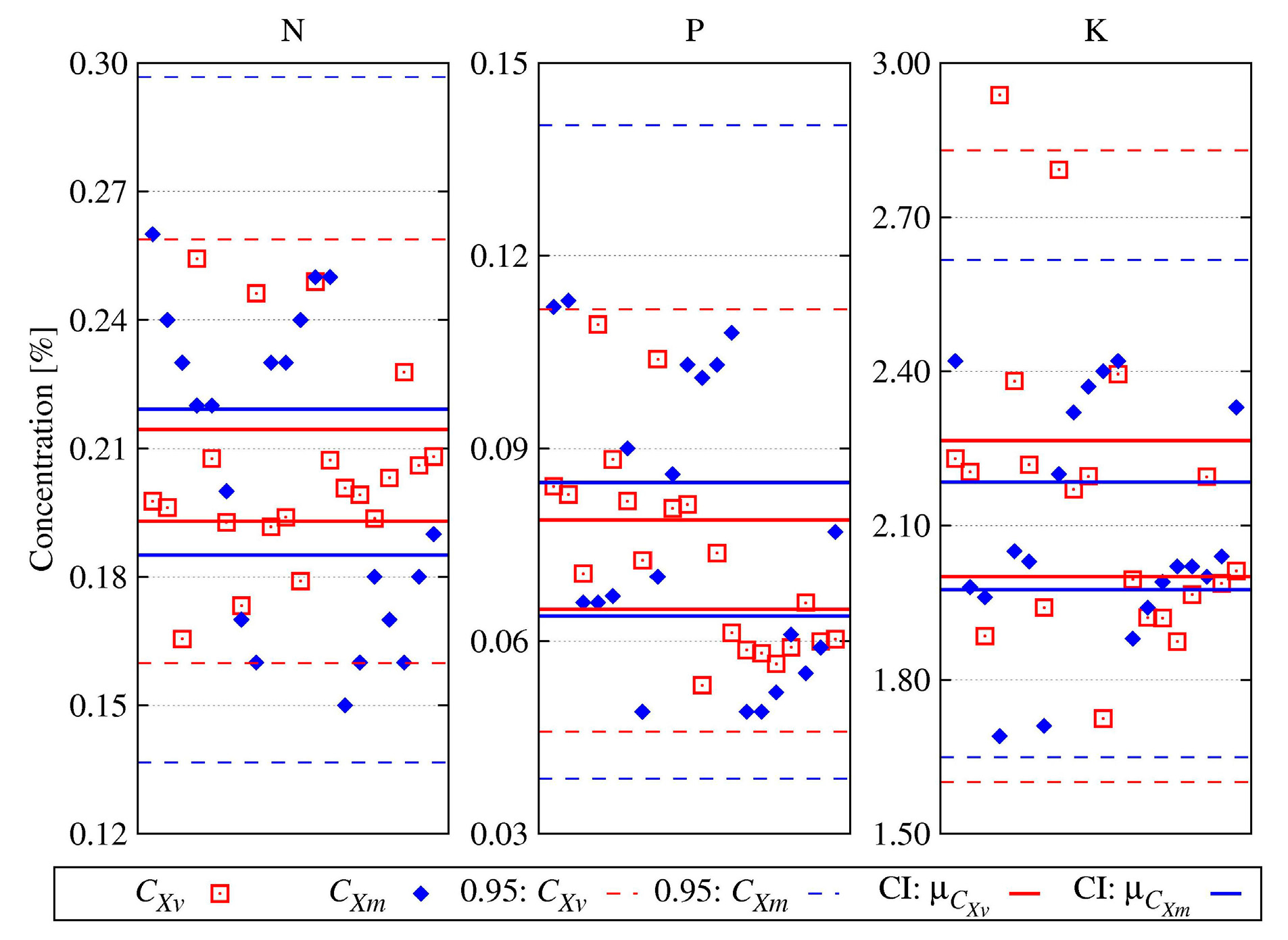
The CIs obtained for a 0.95 confidence level both for transformed and untransformed random variables were calculated. Numerical data is supported by graphs in Figure 2 which show calculated and measured concentrations of all elements and which also include CIs of pertinent distribution means.

It can be observed that the CIs are overlapping for nitrogen and phosphorus even when CIv is inside CIm, while for potassium it is reversed. The explanation of this strict inclusion takes into account the errors caused by the sample collection and its determination. The reversed situation for potassium seems to be caused by the two extreme data obtained by the model.

4. Conclusions

This paper summarizes the results of a study aimed at the design of a mathematical model to predict the nitrogen, phosphorus, and potassium concentrations in reservoir bottom sediments. The proposed model has been developed and validated for the agricultural watershed of the Tisovec River in northeast of Slovakia, where the Kľušov reservoir is located. Based on the results described above, following conclusions can be summarized:

• Prediction model of sediment quality in the reservoir was specified depending on the main five periods of the cropping cycle and distribution of erosivity during a year.
• Total N, P, and K contents in bottom sediments were calculated considering soil loss using USLE equation supplemented with a determination of the average soil nutrient concentration in topsoils.
• The generalized plant cover factor value given in the USLE calculation was modified by its dividing into five crop-stage periods. To compute C, soil loss ratios were weighted according to annual distribution of erosivity.
• For selected crops (spring barley, winter wheat, triticale, winter rye, winter oilseed rape, corn silage, potatoes, and pea) an average plant nutrient uptake during five crop-stage periods was devised.
• Validation of the proposed model using t-test and F-test at a 0.05 significance level has shown that the suggested model can be used for predicting the content of total nitrogen, phosphorus, and potassium in reservoir sediments.

The study also reveals that the model may be considered a predictor for water management enterprises and agriculturists in the future.