Sensitivity Analysis of a Riparian Vegetation Growth Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. Available Data
2.2. Vegetation Growth: Logistic Curve
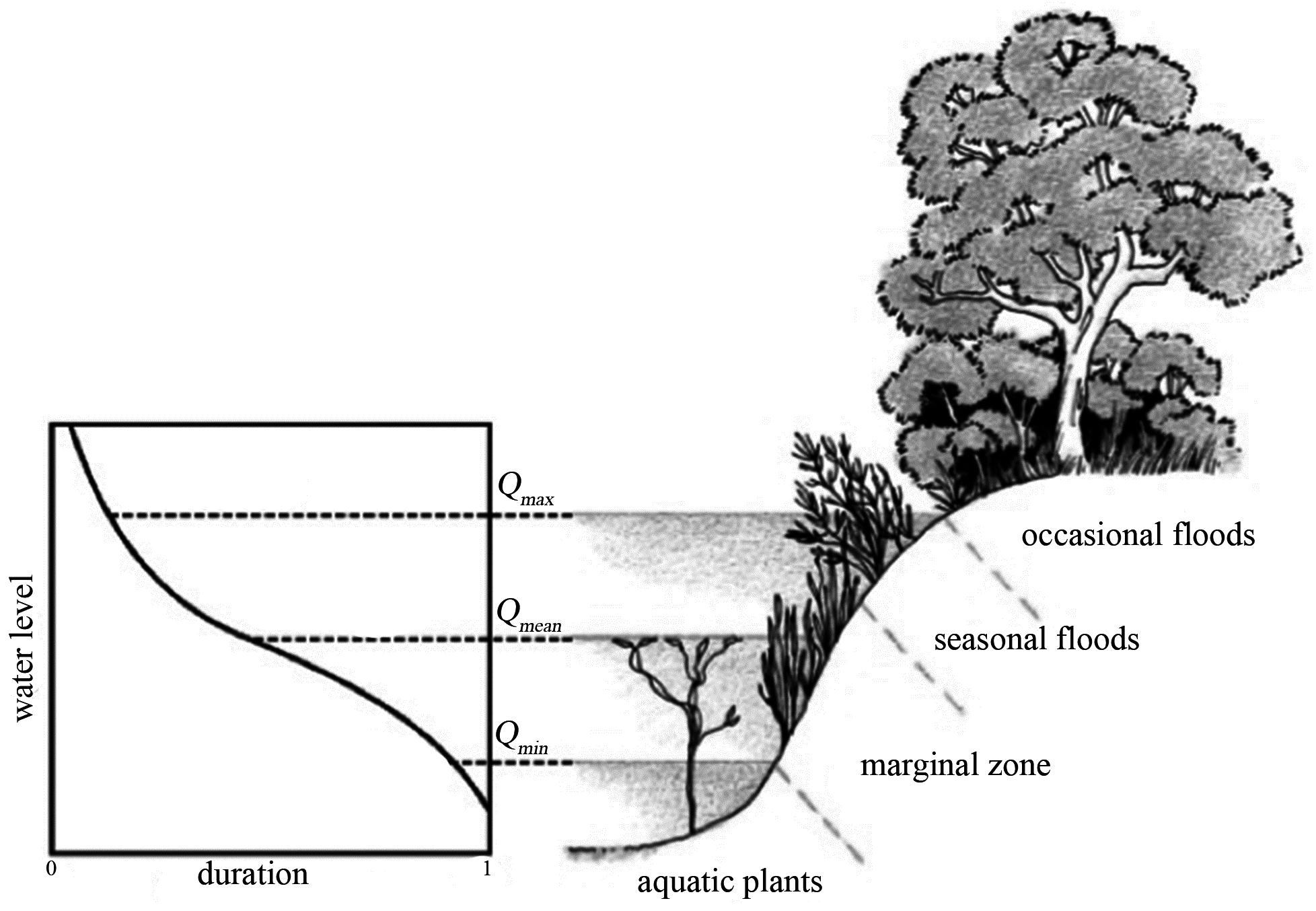
2.3. Mathematical Model
- Anoxia, depending on the submergence time;
- Wilting, depending on the vertical distance from the water table;
- Extirpation, depending on the flow velocity;
- Bank erosion, depending on the river propensity to wandering (width/depth ratio).
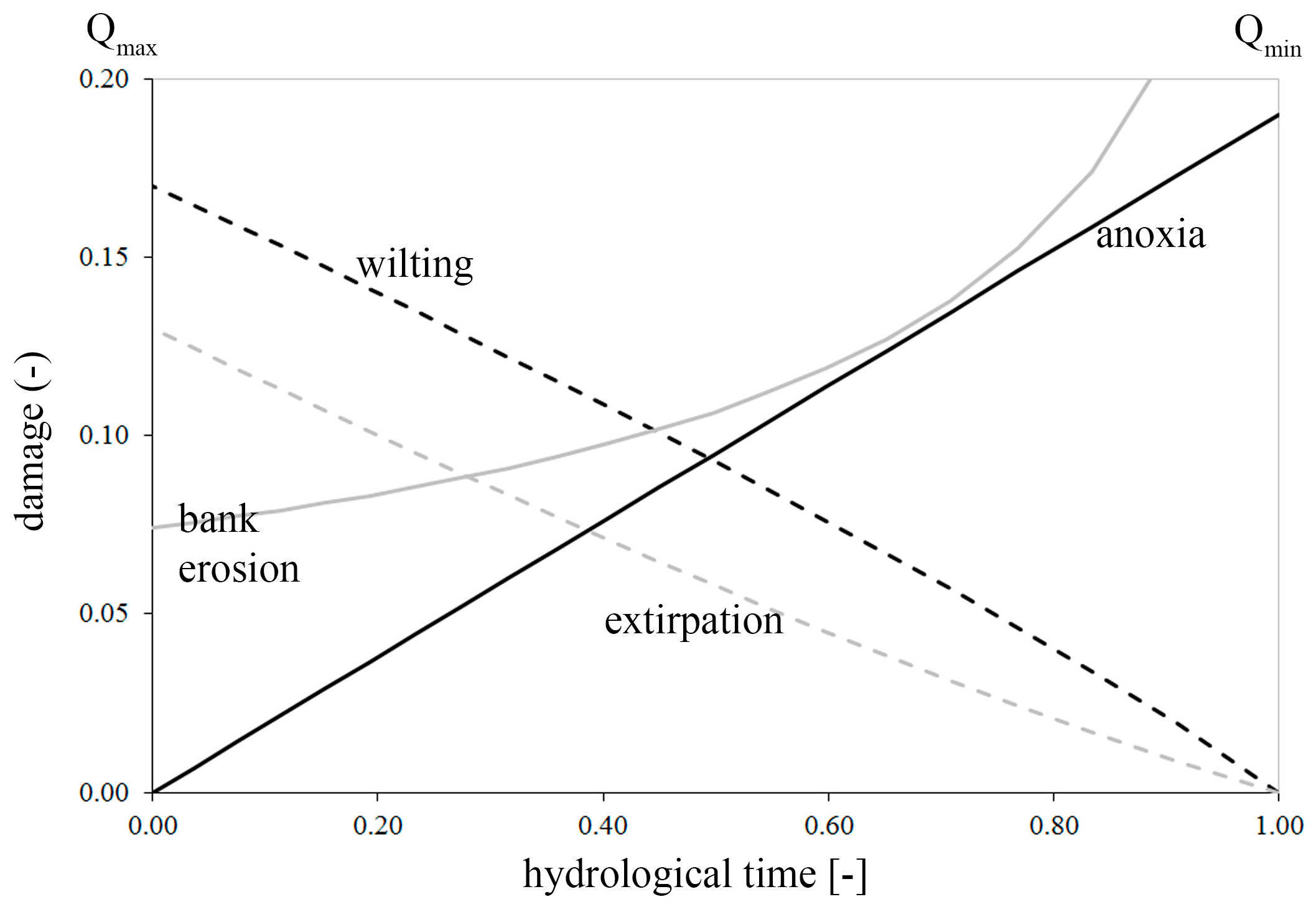
2.3.1. Anoxia
2.3.2. Wilting
2.3.3. Extirpation
2.3.4. Bank Erosion
3. Results and Discussion
3.1. Initial Population
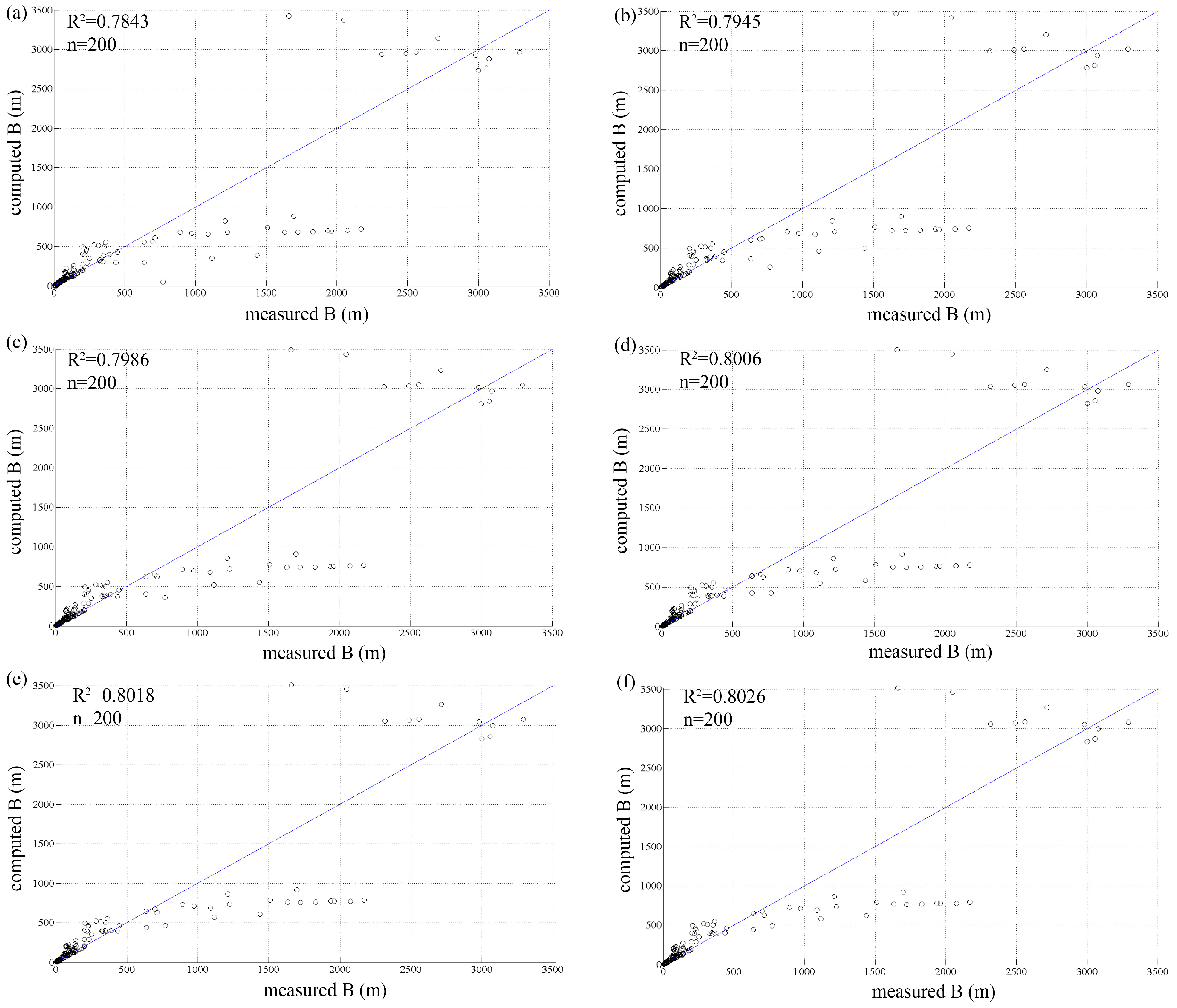
3.2. Vegetation Growth Rate
4. Conclusions
Author Contributions
Conflicts of Interest
Notation List
| B | active (transport) river width (m) |
| Bcomp | computed active river width (m) |
| Bmeas | measured active river width (m) |
| Bv | vegetated river width (m) |
| Btot | total river width (m) |
| E | mean relative error (-) |
| H | water depth (m) |
| K | carrying capacity of the riparian vegetation (-) |
| Ki | general carrying capacity (-) |
| KA | carrying capacity related to anoxia (-) |
| KW | carrying capacity related to wilting (-) |
| KE | carrying capacity related to extirpation (-) |
| KB | carrying capacity related to bank erosion (-) |
| Kopt | optimal carrying capacity (-) |
| P | population (-) |
| P0 | initial population (-) |
| Q | river discharge (m3·s-1) |
| Qmax | maximum river discharge (m3·s-1) |
| Qmin | minimum river discharge (m3·s-1) |
| Qmean | mean river discharge (m3·s-1) |
| q | coefficient (-) |
| R | coefficient of determination (-) |
| r | vegetation growth rate (-) |
| t | hydrological time (-) |
| ∆i | general damage (-) |
| ∆A | damage related to anoxia (-) |
| ∆W | damage related to wilting (-) |
| ∆E | damage related to extirpation (-) |
| ∆B | damage related to bank erosion (-) |
| α | coefficient of the width duration curve (-) |
| β | exponent of the width duration curve (-) |
| ΔA | extremal damage related to anoxia (-) |
| ΔW | extremal damage related to wilting (-) |
| ΔE | extremal damage related to an extirpation (-) |
| ΔB | extremal damage related to bank erosion (-) |
| γ | variability coefficient of river discharge (-) |
References
- Marchetti, M. Environmental changes in the central Po Plain (Northern Italy) due to fluvial modifications and anthropogenic activities. Geomorphology 2002, 44, 361–373. [Google Scholar] [CrossRef]
- Naiman, R.J.; Dècamps, H. The ecology of interfaces: Riparian zones. Annu. Rev. Ecol. Syst. 1997, 28, 621–658. [Google Scholar] [CrossRef]
- Kramer, K.; Vreugdenhil, S.J.; van der Werf, D.C. Effects of flooding on the recruitment, damage and mortality of riparian tree species: A field and simulation study on the Rhine floodplain. For. Ecol. Manag. 2008, 255, 3893–3903. [Google Scholar] [CrossRef]
- Nones, M.; Di Silvio, G. Modeling of river width variations based on hydrological, morphological and biological dynamics. J. Hydraul. Eng. 2016, 142. [Google Scholar] [CrossRef]
- Wilson, C.A.M.E.; Yagci, O.; Rauch, H.-P.; Olsen, N.R.B. 3D Numerical modelling of a willow vegetated river/floodplain system. J. Hydrol. 2006, 327, 13–21. [Google Scholar] [CrossRef]
- Li, C.W.; Zeng, C. 3D Numerical modelling of flow divisions at open channel junctions with or without vegetation. Adv. Water Resour. 2009, 32, 49–60. [Google Scholar] [CrossRef]
- Bockelmann, B.N.; Fenrich, E.K.; Lin, B.; Falconer, R.A. Development of an ecohydraulics model for stream and river restoration. Ecol. Eng. 2004, 22, 227–235. [Google Scholar] [CrossRef]
- Abu-Aly, T.R.; Pasternack, G.B.; Wyrick, J.R.; Barker, R.; Massa, D.; Johnson, T. Effects of LiDAR-derived, spatially distributed vegetation roughness on two-dimensional hydraulics in a gravel-cobble river at flows of 0.2 to 20 times bankfull. Geomorphology 2014, 206, 468–482. [Google Scholar] [CrossRef]
- Nones, M.; Guerrero, M.; Ronco, P. Opportunities from low-resolution modelling of river morphology in remote parts of the world. Earth Surf. Dyn. 2014, 2, 9–19. [Google Scholar] [CrossRef]
- Micheli, E.R.; Kirchner, J.W. Effects of wet meadow riparian vegetation on streambank erosion. 1. Remote sensing measurements of streambank migration and erodibility. Earth Surf. Process. Landf. 2002, 27, 627–639. [Google Scholar] [CrossRef]
- Mitsch, W.J.; Gosselink, J. Wetlands; Wiley & Sons: New York, NY, USA, 2007. [Google Scholar]
- Lange, C.; Schneider, M.; Mutz, M.; Haustein, M.; Halle, M.; Seidel, M.; Sieker, H.; Wolter, C.; Hinkelmann, R. Model-based design for restoration of a small urban river. J. Hydro-Environ. Res. 2015, 9, 226–236. [Google Scholar] [CrossRef]
- Manner, R.B.; Wilcox, A.C.; Kui, L.; Lightbody, A.F.; Stella, J.C.; Sklar, L.S. When do plants modify fluvial processes? Plant-hydraulic interactions under variable flow and sediment supply rates. J. Geophys. Res. 2015, 120, 325–345. [Google Scholar] [CrossRef]
- Camporeale, C.; Perucca, E.; Ridolfi, L.; Gurnell, A.M. Modeling the interactions between river morphodynamics and riparian vegetation. Rev. Geophys. 2013, 51, 379–414. [Google Scholar] [CrossRef]
- Osterkamp, W.R.; Hupp, C.R. Geomorphic and vegetative characteristics along three northern Virginia streams. Geol. Soc. Am. Bull. 1984, 95, 1093–1101. [Google Scholar] [CrossRef]
- Hupp, C.R.; Osterkamp, W.R. Bottomland vegetation distribution along Passage Creek, Virginia, in relation to fluvial landforms. Ecology 1985, 66, 670–681. [Google Scholar] [CrossRef]
- Mahoney, J.M.; Rood, S.B. Streamflow requirements for cottonwood seedling recruitment: An integrative model. Wetlands 1998, 18, 634–645. [Google Scholar] [CrossRef]
- Bendix, J.; Hupp, C.R. Hydrological and geomorphological impacts on riparian plant communities. Hydrol. Process. 2000, 14, 2977–2990. [Google Scholar] [CrossRef]
- Auble, G.T.; Friedman, J.M.; Scott, M.L. Relating riparian vegetation to present and future streamflows. Ecolog. Appl. 1994, 3, 544–554. [Google Scholar] [CrossRef]
- Friedman, J.M.; Auble, G.T. Mortality of riparian box elder from sediment mobilization and extended inundation. Regul. Rivers Res. Manag. 1999, 15, 463–476. [Google Scholar] [CrossRef]
- Johnson, W.C. Tree recruitment and survival in rivers: Influence of hydrological processes. Hydrol. Process. 2000, 14, 3051–3074. [Google Scholar] [CrossRef]
- Lite, S.J.; Bagstad, K.J.; Stromberg, J.C. Riparian plant species richness along lateral and longitudinal gradients of water stress and flood disturbance, San Pedro River, Arizona, USA. J. Arid Environ. 2005, 63, 785–813. [Google Scholar] [CrossRef]
- Tealdi, S. River-Riparian Vegetation Interactions. Ph.D. Thesis, Politecnico of Torino, Turin, Italy, May 2012. [Google Scholar]
- Tewari, S.; Kulhavy, J.; Rock, B.N.; Hadas, P. Remote monitoring of forest response to changed soil moisture regime due to river regulation. J. For. Sci. 2003, 49, 429–438. [Google Scholar]
- Yanosky, T.M. Effects of Flooding upon Woody Vegetation along Parts of the Potamac River Floodplain; U.S. Geological Survey Professional Paper; U.S. Geological Survey: Reston, VA, USA, 1982.
- Osterkamp, W.R.; Costa, J.E. Change accompanying an extraordinary flood on sandbed stream. In Catastrophic Flooding; Allen and Unwin: St. Leonards, Australia, 1987. [Google Scholar]
- Kozlowski, T.T. Responses of woody plants to flooding. In Tree Physiology Monograph; Heron Publishing: Victoria, BC, Canada, 1984. [Google Scholar]
- Naumburg, E.; Mata-Gonzales, R.; Hunter, R.G.; McLendon, T.; Martin, D.W. Phreatophytic vegetation and groundwater fluctuations: A review of current research and application of ecosystem response modelling with an emphasis on great basin vegetation. Environ. Manag. 2005, 35, 726–740. [Google Scholar] [CrossRef] [PubMed]
- Hupp, C.R. Plant ecological aspects of flood geomorphology and paleoflood history. In Flood Geomorphology; Wiley & Sons: New York, NY, USA, 1988. [Google Scholar]
- McKenney, R.; Jacobson, R.B.; Wertheimer, R.C. Woody vegetation and channel morphogenesis in low-gradient, gravel-bed streams in the Ozrak Plateaus, Missouri and Arkansas. Geomorphology 1995, 13, 175–198. [Google Scholar] [CrossRef]
- Richter, B.D.; Richter, H.E. Prescribing flood regimes to sustain riparian ecosystem along meandering rivers. Conserv. Biol. 2000, 14, 1467–1478. [Google Scholar] [CrossRef]
- Gurnell, A.M.; Petts, E.; Hannah, D.M.; Smith, B.P.G.; Edwards, P.J.; Kollmann, J.; Ward, J.V.; Tockner, K. Riparian vegetation and island formation along the gravel-bed Fiume Tagliamento, Italy. Earth Surf. Process. Landf. 2001, 26, 31–62. [Google Scholar] [CrossRef]
- Franz, E.H.; Bazzaz, F.A. Simulation of vegetation response to modified hydrological regimes: A probabilistic model based on niche differentiation in a floodplain forest. Ecology 1977, 58, 176–183. [Google Scholar] [CrossRef]
- Stromberg, J.C.; Patten, D.T. Instream flow requirements for cottonwoods at Bishop Creek, Inyo County, California. Rivers 1991, 2, 1–11. [Google Scholar]
- Pearlstine, L.; McKellar, H.; Kitchens, W. Modelling the impacts of a river diversion on bottomland forest communities in the Santee River Floodplain, South Carolina. Ecol. Model. 1985, 29, 283–302. [Google Scholar] [CrossRef]
- Brookes, C.J.; Hooke, M.J.; Mant, J. Modelling vegetation interactions with channel flow in river valleys of the Mediterranean region. Catena 2000, 40, 93–118. [Google Scholar] [CrossRef]
- Lytle, D.A.; Merritt, D.M. Hydrologic regimes and riparian forests: A structured population model for cottonwood. Ecology 2004, 85, 2493–2503. [Google Scholar] [CrossRef]
- Gran, K.; Paola, C. Riparian vegetation controls on braided stream dynamics. Water Resour. Res. 2001, 37, 3275–3283. [Google Scholar] [CrossRef]
- Camporeale, C.; Ridolfi, L. Riparian vegetation distribution induced by river flow variability: A stochastic approach. Water Resour. Res. 2006, 42, W10415. [Google Scholar] [CrossRef]
- Muneepeerakul, R.; Rinaldo, A.; Rodriguez-Iturbe, I. Effects of river flow scaling properties on riparian width and vegetation biomass. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Camporeale, C.; Ridolfi, L. Interplay among river meandering, discharge stochasticity and riparian vegetation. J. Hydrol. 2010, 382, 138–144. [Google Scholar] [CrossRef]
- Tealdi, S.; Camporeale, C.; Ridolfi, L. Modeling the impact of river damming on riparian vegetation. J. Hydrol. 2011, 396, 302–312. [Google Scholar] [CrossRef]
- Conway, D. The climate and hydrology of the Upper Blue Nile River. Geogr. J. 2000, 166, 49–62. [Google Scholar] [CrossRef]
- Pasanisi, F.; Tebano, C.; Zarlenga, F. A Survey near Tambara along the Lower Zambezi River. Environments 2016, 3, 6. [Google Scholar] [CrossRef]
- Ministero LL. PP. Servizio Idrografico. In Annali Idrologici Italia; Ministero LL. PP.: Roma, Italy, 1951. (In Italian) [Google Scholar]
- Di Silvio, G.; Nones, M. Morphodynamic reaction of a schematic river to sediment input changes: Analytical approaches. Geomorphology 2014, 215, 74–82. [Google Scholar] [CrossRef]
- Duarte, P.; Meneses, R.; Hawkins, A.J.S.; Zhu, M.; Fang, J.; Grant, J. Mathematical modelling to assess the carrying capacity for multi-species culture within coastal waters. Ecol. Model. 2003, 168, 109–143. [Google Scholar] [CrossRef]
- Bhowmik, N.G.; Stall, J.B. Hydraulic Geometry and Carrying Capacity of Floodplains; Research Report; University of Illinois: Champaign, IL, USA, 1979. [Google Scholar]
- Yalin, M.S. River Mechanics; Pergamon Press: Oxford, UK, 1992. [Google Scholar]
- Singh, V.P. On the theories of hydraulic geometry. Int. J. Sediment Res. 2003, 18, 196–218. [Google Scholar]
- Parker, G.; Wilcock, P.R.; Paola, C.; Dietrich, W.E.; Pitlick, J. Physical basis for quasi-universal relations describing bankfull hydraulic geometry of single-thread gravel bed rivers. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef]
- Vianello, A.; D’Agostino, V. Bankfull width and morphological units in an alpine stream of the dolomites (Northern Italy). Geomorphology 2007, 83, 266–281. [Google Scholar] [CrossRef]
- Valiani, A.; Caleffi, V. Analytical findings for power law cross-sections: Uniform flow depth. Adv. Water Resour. 2009, 32, 1404–1412. [Google Scholar] [CrossRef]
- Wilkerson, G.W.; Parker, G. Physical basis for quasi-universal relations describing bankfull hydraulic geometry of sand-bed rivers. J. Hydraul. Eng. 2010, 137, 739–753. [Google Scholar] [CrossRef]
- Nones, M.; Ronco, P.; Di Silvio, G. Modelling the impact of large impoundments on the lower Zambezi River. Int. J. River Basin Manag. 2013, 11, 221–236. [Google Scholar] [CrossRef]
- Verhulst, P.-F. Notice sur la loi que la population poursuit dans son accroissement. Corresp. Math. ET Phys. 1838, 10, 113–121. [Google Scholar]
- Gabriel, J.-P.; Saucy, F.; Bersier, L.-F. Paradoxes in the logistic equation? Ecol. Model. 2005, 185, 147–151. [Google Scholar] [CrossRef]
- Grime, J.P.; Hunt, T. Relative growth-rate: Its range and adaptive significance in a local Flora. J. Ecol. 1975, 63, 393–422. [Google Scholar] [CrossRef]
- Gleeson, S.K.; Tilman, D. Plant Allocation, Growth Rate and Successional Status. Funct. Ecol. 1994, 8, 543–550. [Google Scholar] [CrossRef]
- Hunt, R.; Cornelissen, J.H.C. Components of relative growth rate and their interrelations in 59 temperate plant species. New Phytol. 1997, 135, 395–417. [Google Scholar] [CrossRef]
- Karrenberg, S.; Edwards, P.J.; Kollmann, J. The life history of Salicaceae living in the active zone of floodplains. Freshw. Biol. 2002, 47, 733–748. [Google Scholar] [CrossRef]
- Merritt, D.M.; Scott, M.L.; Poff, N.L.; Auble, G.T.; Lytle, D.A. Theory, methods and tools for determining environmental flows for riparian vegetation: Riparian vegetation-flow response guilds. Freshw. Biol. 2010, 55, 206–225. [Google Scholar] [CrossRef]
- Rosgen, D.L. A classification of natural rivers. Catena 1994, 22, 169–199. [Google Scholar] [CrossRef]
- Schumm, S.A. Patterns of alluvial rivers. Annu. Rev. Earth Planet. Sci. 1985, 13, 5–27. [Google Scholar] [CrossRef]
- Nones, M. Riverine Dynamics at Watershed Scale: Hydro-Morpho-Biodynamics in Rivers; Lambert Academic Publishing: Saarbrücken, Germany, 2013; p. 140. [Google Scholar]
- Hoyos, I.C.P.; Krakauer, N.Y.; Khanbilvardi, R. Estimating the probability of vegetation to be groundwater dependent based on the evaluation of tree models. Environments 2016, 3, 9. [Google Scholar] [CrossRef]
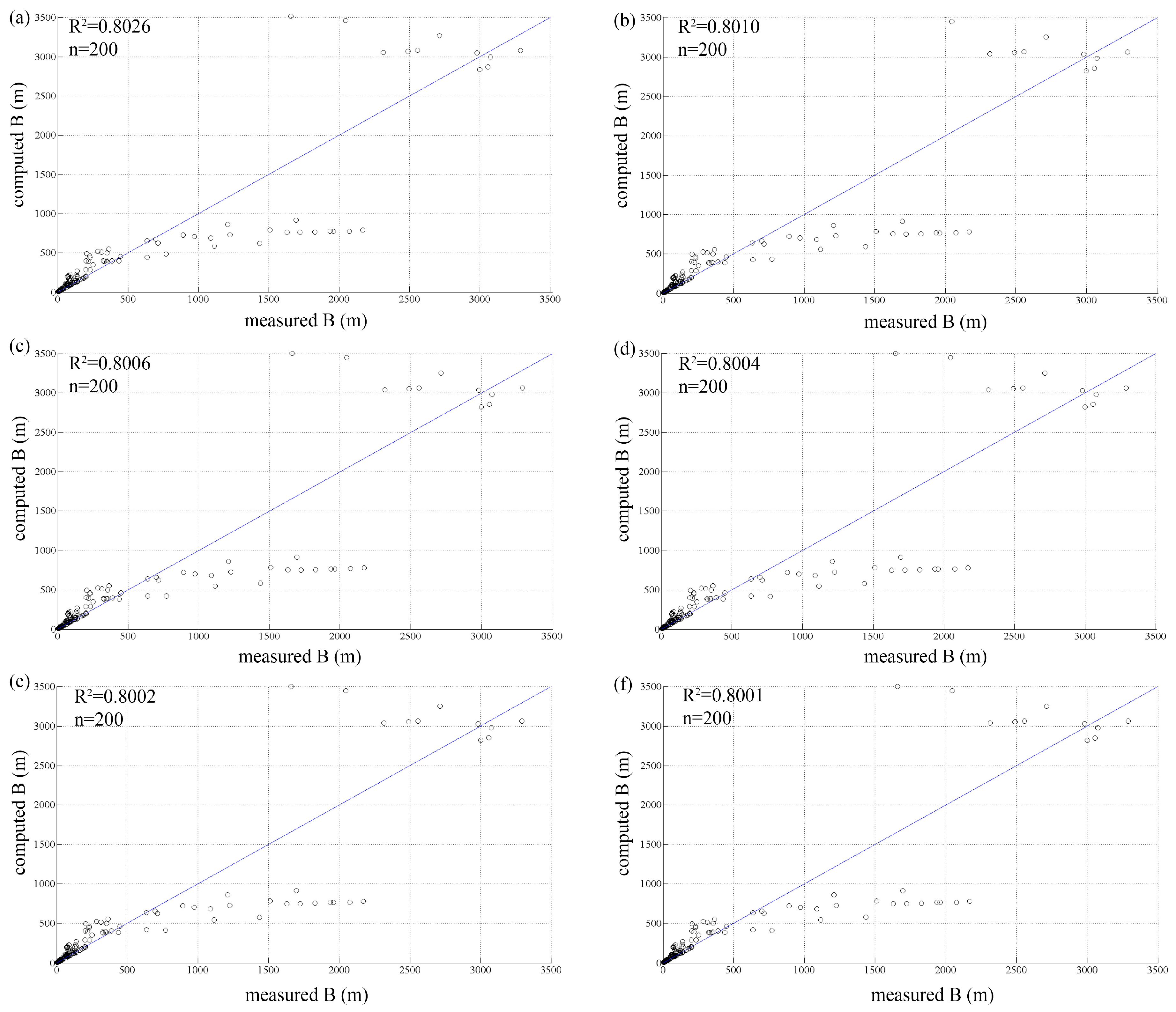
| Test | P0 | E | R2 | R2 Large Rivers |
|---|---|---|---|---|
| test 1 | 10 | 0.3452 | 0.8026 | 0.7347 |
| test 2 | 50 | 0.3405 | 0.8010 | 0.7459 |
| test 3 | 100 | 0.3394 | 0.8006 | 0.7488 |
| test 4 | 200 | 0.3388 | 0.8004 | 0.7505 |
| test 5 | 500 | 0.3382 | 0.8002 | 0.7517 |
| test 6 | 1000 | 0.3382 | 0.8001 | 0.7521 |
| Test | r | E | R2 | R2 Large Rivers |
|---|---|---|---|---|
| test 1 | 0.010 | 0.3157 | 0.7843 | 0.8544 |
| test 2 | 0.015 | 0.3223 | 0.7945 | 0.7898 |
| test 3 | 0.020 | 0.3323 | 0.7986 | 0.7630 |
| test 4 | 0.025 | 0.3394 | 0.8006 | 0.7488 |
| test 5 | 0.030 | 0.3440 | 0.8018 | 0.7401 |
| test 6 | 0.035 | 0.3474 | 0.8026 | 0.7344 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nones, M.; Varrani, A. Sensitivity Analysis of a Riparian Vegetation Growth Model. Environments 2016, 3, 30. https://doi.org/10.3390/environments3040030
Nones M, Varrani A. Sensitivity Analysis of a Riparian Vegetation Growth Model. Environments. 2016; 3(4):30. https://doi.org/10.3390/environments3040030
Chicago/Turabian StyleNones, Michael, and Arianna Varrani. 2016. "Sensitivity Analysis of a Riparian Vegetation Growth Model" Environments 3, no. 4: 30. https://doi.org/10.3390/environments3040030
APA StyleNones, M., & Varrani, A. (2016). Sensitivity Analysis of a Riparian Vegetation Growth Model. Environments, 3(4), 30. https://doi.org/10.3390/environments3040030





