Systematic Study of CDOM in the Volga River Basin Using EEM-PARAFAC
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Sampling
2.3. Absorbance and Fluorescence Measurements
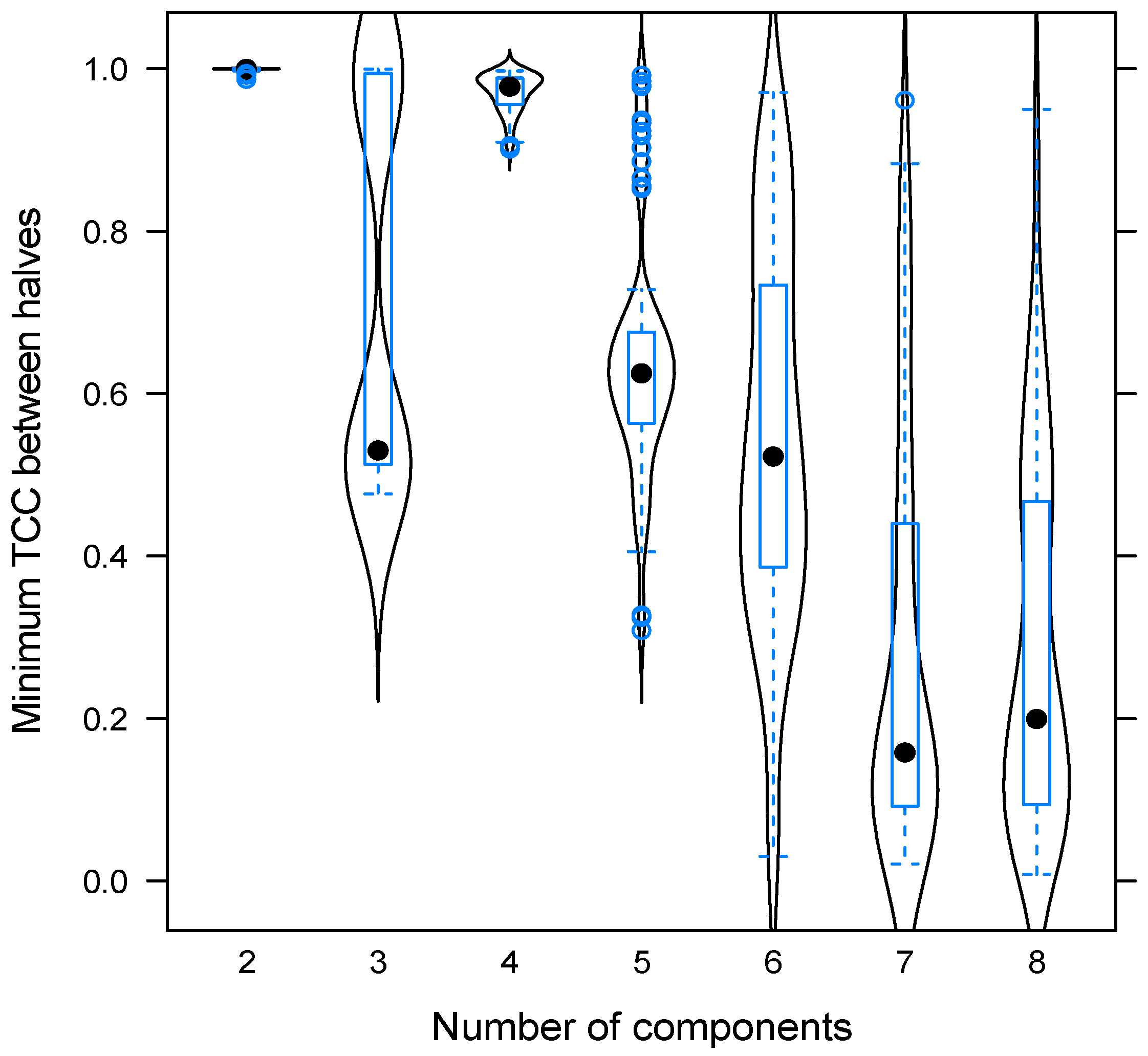
2.4. PARAFAC Decomposition of Fluorescence EEM
3. Results and Discussion
3.1. PARAFAC Components
3.2. Distribution of PARAFAC Component in the Volga River Surface Waters
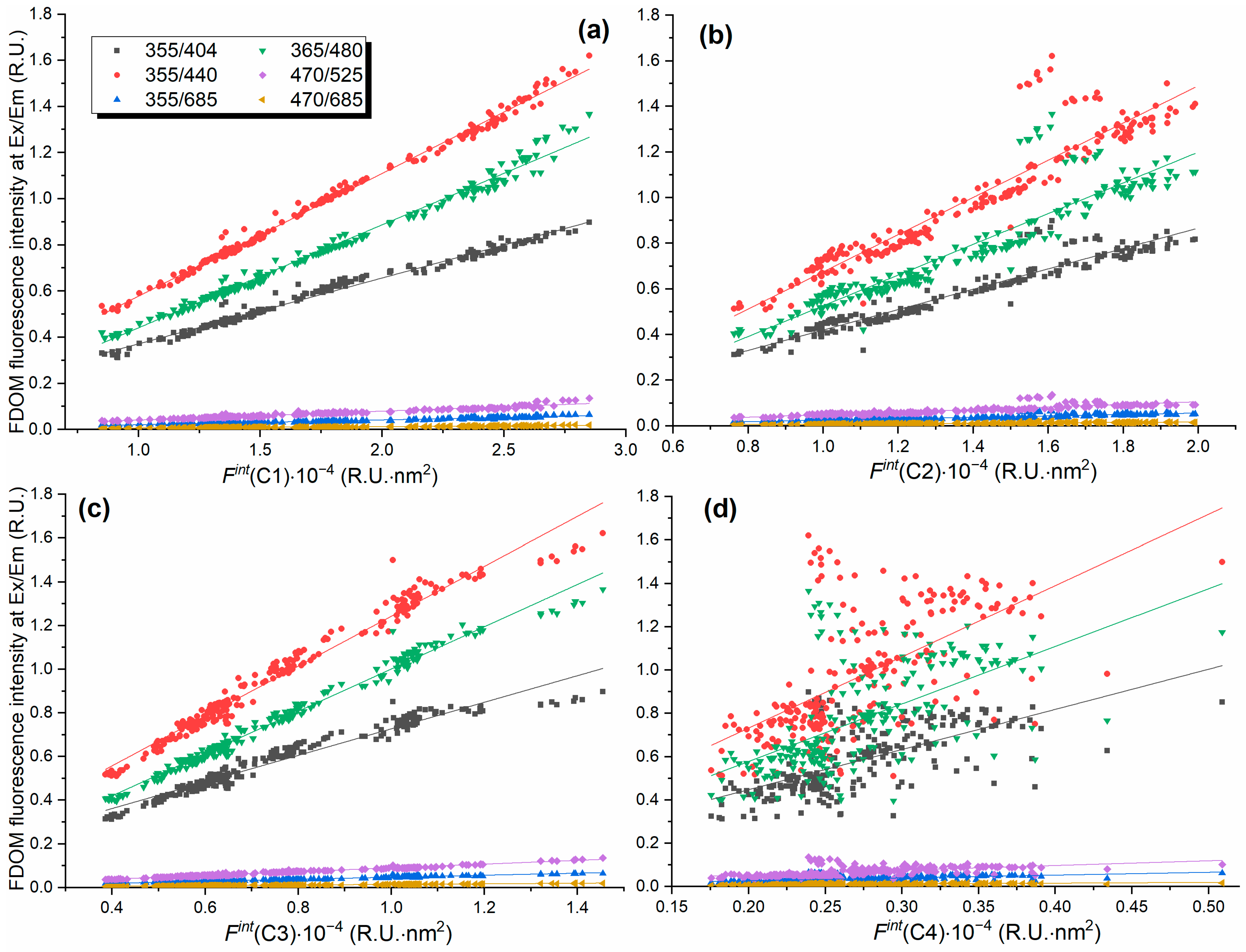
3.3. Standard Excitation/Detection Wavelengths of Fluorescence Sensors
3.4. CDOM Absorbance
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DOM | Dissolved organic matter |
| DOC | Dissolved organic carbon |
| CDOM | Colored or chromophoric dissolved organic matter |
| FDOM | Fluorescent dissolved organic matter |
| EEM | Excitation-emission matrix |
| PARAFAC | Parallel factor analysis |
| R.U. | Raman units |
References
- Wang, H.; He, G. Rivers: Linking nature, life, and civilization. River 2022, 1, 25–36. [Google Scholar] [CrossRef]
- Postel, S.; Richter, B. Rivers for Life: Managing Water for People and Nature; Island Press: Washington, DC, USA; Covelo, CA, USA; London, UK, 2012. [Google Scholar]
- Dudgeon, D.; Arthington, A.H.; Gessner, M.O.; Kawabata, Z.-I.; Knowler, D.J.; Lévêque, C.; Naiman, R.J.; Prieur-Richard, A.-H.; Soto, D.; Stiassny, M.L. Freshwater biodiversity: Importance, threats, status and conservation challenges. Biol. Rev. 2006, 81, 163–182. [Google Scholar] [CrossRef] [PubMed]
- Leopold, L.B. Rivers. Am. Sci. 1962, 50, 511–537. [Google Scholar]
- Gleick, P.H. Water use. Annu. Rev. Environ. Resour. 2003, 28, 275–314. [Google Scholar] [CrossRef]
- Meyer, A.M.; Klein, C.; Fünfrocken, E.; Kautenburger, R.; Beck, H.P. Real-time monitoring of water quality to identify pollution pathways in small and middle scale rivers. Sci. Total Environ. 2019, 651, 2323–2333. [Google Scholar] [CrossRef]
- Mezhevova, A.; Berestneva, Y.; Belyaev, A. The current chemical composition of inland water bodies of the Volga-Akhtuba floodplain (Russia). J. Geogr. Inst. "Jovan Cvijic" SASA 2024, 74, 147–164. [Google Scholar] [CrossRef]
- Savenko, A.; Brekhovskikh, V.; Pokrovskii, O. Migration of dissolved trace elements in the mixing zone between Volga River water and Caspian seawater: Results of observations over many years. Geochem. Int. 2014, 52, 533–547. [Google Scholar] [CrossRef]
- Moiseenko, T.; Gashkina, N.; Sharova, Y.N.; Pokoeva, A. Ecotoxicological assessment of after-effects of the Volga River water contamination. Water Resour. 2005, 32, 369–383. [Google Scholar] [CrossRef]
- Soomets, T.; Uudeberg, K.; Jakovels, D.; Zagars, M.; Reinart, A.; Brauns, A.; Kutser, T. Comparison of lake optical water types derived from Sentinel-2 and Sentinel-3. Remote Sens. 2019, 11, 2883. [Google Scholar] [CrossRef]
- Pahlevan, N.; Smith, B.; Schalles, J.; Binding, C.; Cao, Z.; Ma, R.; Alikas, K.; Kangro, K.; Gurlin, D.; Hà, N. Seamless retrievals of chlorophyll-a from Sentinel-2 (MSI) and Sentinel-3 (OLCI) in inland and coastal waters: A machine-learning approach. Remote Sens. Environ. 2020, 240, 111604. [Google Scholar] [CrossRef]
- Harrison, J.A.; Caraco, N.; Seitzinger, S.P. Global patterns and sources of dissolved organic matter export to the coastal zone: Results from a spatially explicit, global model. Glob. Biogeochem. Cycles 2005, 19, GB4S04. [Google Scholar] [CrossRef]
- Derrien, M.; Brogi, S.R.; Goncalves-Araujo, R. Characterization of aquatic organic matter: Assessment, perspectives and research priorities. Water Res. 2019, 163, 114908. [Google Scholar] [CrossRef]
- Glukhovets, D.; Kopelevich, O.; Yushmanova, A.; Vazyulya, S.; Sheberstov, S.; Karalli, P.; Sahling, I. Evaluation of the CDOM absorption coefficient in the Arctic seas based on Sentinel-3 OLCI data. Remote Sens. 2020, 12, 3210. [Google Scholar] [CrossRef]
- Bro, R. PARAFAC. Tutorial and applications. Chemom. Intell. Lab. Syst. 1997, 38, 149–171. [Google Scholar] [CrossRef]
- Grishin, M.Y.; Lednev, V.; Pershin, S.; Bunkin, A.; Kobylyanskiy, V.; Ermakov, S.; Kapustin, I.; Molkov, A. Laser remote sensing of an algal bloom in a freshwater reservoir. Laser Phys. 2016, 26, 125601. [Google Scholar] [CrossRef]
- Palmer, S.C.; Pelevin, V.V.; Goncharenko, I.; Kovács, A.W.; Zlinszky, A.; Présing, M.; Horváth, H.; Nicolás-Perea, V.; Balzter, H.; Tóth, V.R. Ultraviolet fluorescence LiDAR (UFL) as a measurement tool for water quality parameters in turbid lake conditions. Remote Sens. 2013, 5, 4405–4422. [Google Scholar] [CrossRef]
- Kokhanenko, G.; Balin, Y.S.; Penner, I.; Shamanaev, V. Lidar and in situ sensing of the upper layers of Baikal Lake water. Opt. Atmos. Okeana 2011, 24, 377–385. [Google Scholar]
- Chen, P.; Mao, Z.; Zhang, Z.; Liu, H.; Pan, D. Detecting subsurface phytoplankton layer in Qiandao Lake using shipborne lidar. Opt. Express 2020, 28, 558–569. [Google Scholar] [CrossRef]
- Mineeva, N.; Lazareva, V.; Litvinov, A.; Stepanova, I.; Chuiko, G.; Papchenkov, V.; Korneva, L.; Shcherbina, G.; Pryanichnikova, E.; Perova, S. The Volga River. In Rivers of Europe; Elsevier: Amsterdam, The Netherlands, 2022; pp. 27–79. [Google Scholar]
- Litvinov, A.S.; Mineeva, N.M.; Papchenkov, V.G.; Korneva, L.G.; Lazareva, V.I.; Shcherbina, G.K.; Gerasimov, Y.V.; Dvinskikh, S.A.; Noskov, V.M.; Kitaev, A.B.; et al. Volga River Basin. In Rivers of Europe; Academic Press: London, UK, 2009; pp. 23–57. [Google Scholar]
- Terskii, P.N.; Ermakova, G.S.; Gorelits, O.V. Hydropower in Russia: Case Study on Hydrological Management of the Volga-Kama Cascade. In Technological Innovations and Advances in Hydropower Engineering; IntechOpen: Rijeka, Croatia, 2022; pp. 20–29. [Google Scholar]
- Lakowicz, J.R. Principles of Fluorescence Spectroscopy; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- De Haan, H.; De Boer, T. Applicability of light absorbance and fluorescence as measures of concentration and molecular size of dissolved organic carbon in humic Lake Tjeukemeer. Water Res. 1987, 21, 731–734. [Google Scholar] [CrossRef]
- Peuravuori, J.; Pihlaja, K. Molecular size distribution and spectroscopic properties of aquatic humic substances. Anal. Chim. Acta 1997, 337, 133–149. [Google Scholar] [CrossRef]
- Krylov, I.N.; Labutin, T.A. Recovering fluorescence spectra hidden by scattering signal: In search of the best smoother. Spectrochim. Acta Part A: Mol. Biomol. Spectrosc. 2023, 293, 122441. [Google Scholar] [CrossRef] [PubMed]
- Krylov, I.N.; Drozdova, A.N.; Labutin, T.A. Albatross R package to study PARAFAC components of DOM fluorescence from mixing zones of arctic shelf seas. Chemom. Intell. Lab. Syst. 2020, 207, 104176. [Google Scholar] [CrossRef]
- Murphy, K.R.; Stedmon, C.A.; Graeber, D.; Bro, R. Fluorescence spectroscopy and multi-way techniques. PARAFAC. Anal. Methods 2013, 5, 6557–6566. [Google Scholar] [CrossRef]
- Murphy, K.R.; Stedmon, C.A.; Wenig, P.; Bro, R. OpenFluor–an online spectral library of auto-fluorescence by organic compounds in the environment. Anal. Methods 2014, 6, 658–661. [Google Scholar] [CrossRef]
- Coble, P.G. Characterization of marine and terrestrial DOM in seawater using excitation-emission matrix spectroscopy. Mar. Chem. 1996, 51, 325–346. [Google Scholar] [CrossRef]
- Lobus, N.V.; Glushchenko, A.M.; Osadchiev, A.A.; Maltsev, Y.I.; Kapustin, D.A.; Konovalova, O.P.; Kulikovskiy, M.S.; Krylov, I.N.; Drozdova, A.N. Production of Fluorescent Dissolved Organic Matter by Microalgae Strains from the Ob and Yenisei Gulfs (Siberia). Plants 2022, 11, 3361. [Google Scholar] [CrossRef]
- Marcé, R.; Verdura, L.; Leung, N. Dissolved organic matter spectroscopy reveals a hot spot of organic matter changes at the river–reservoir boundary. Aquat. Sci. 2021, 83, 67. [Google Scholar] [CrossRef]
- Williams, C.J.; Yamashita, Y.; Wilson, H.F.; Jaffé, R.; Xenopoulos, M.A. Unraveling the role of land use and microbial activity in shaping dissolved organic matter characteristics in stream ecosystems. Limnol. Oceanogr. 2010, 55, 1159–1171. [Google Scholar] [CrossRef]
- Lin, H.; Guo, L. Variations in colloidal DOM composition with molecular weight within individual water samples as characterized by flow field-flow fractionation and EEM-PARAFAC analysis. Environ. Sci. Technol. 2020, 54, 1657–1667. [Google Scholar] [CrossRef] [PubMed]
- Yamashita, Y.; Maie, N.; Briceño, H.; Jaffé, R. Optical characterization of dissolved organic matter in tropical rivers of the Guayana Shield, Venezuela. J. Geophys. Res. Biogeosci. 2010, 115, G00F10. [Google Scholar] [CrossRef]
- Yan, C.; Sheng, Y.; Ju, M.; Ding, C.; Li, Q.; Luo, Z.; Ding, M.; Nie, M. Relationship between the characterization of natural colloids and metal elements in surface waters. Environ. Sci. Pollut. Res. 2020, 27, 31872–31883. [Google Scholar] [CrossRef]
- Thuile Bistarelli, L.; Poyntner, C.; Santín, C.; Doerr, S.H.; Talluto, L.; Singer, G.; Sigmund, G. Wildfire-derived pyrogenic carbon modulates riverine organic matter and biofilm enzyme activities in an in situ flume experiment. ACS EsT Water 2021, 1, 1648–1656. [Google Scholar] [CrossRef] [PubMed]
- Parr, T.B.; Cronan, C.S.; Ohno, T.; Findlay, S.E.; Smith, S.M.; Simon, K.S. Urbanization changes the composition and bioavailability of dissolved organic matter in headwater streams. Limnol. Oceanogr. 2015, 60, 885–900. [Google Scholar] [CrossRef]
- Gold-Bouchot, G.; Polis, S.; Castañon, L.E.; Flores, M.P.; Alsante, A.N.; Thornton, D.C.O. Chromophoric dissolved organic matter (CDOM) in a subtropical estuary (Galveston Bay, USA) and the impact of Hurricane Harvey. Environ. Sci. Pollut. Res. 2021, 28, 53045–53057. [Google Scholar] [CrossRef]
- Brogi, S.R.; Balestra, C.; Casotti, R.; Cossarini, G.; Galletti, Y.; Gonnelli, M.; Vestri, S.; Santinelli, C. Time resolved data unveils the complex DOM dynamics in a Mediterranean river. Sci. Total Environ. 2020, 733, 139212. [Google Scholar] [CrossRef] [PubMed]
- Castillo, C.R.; Sarmento, H.; Alvarez-Salgado, X.A.; Gasol, J.M.; Marraséa, C. Production of chromophoric dissolved organic matter by marine phytoplankton. Limnol. Oceanogr. 2010, 55, 446–454. [Google Scholar] [CrossRef]
- Osburn, C.L.; Oviedo-Vargas, D.; Barnett, E.; Dierick, D.; Oberbauer, S.F.; Genereux, D.P. Regional groundwater and storms are hydrologic controls on the quality and export of dissolved organic matter in two tropical rainforest streams, Costa Rica. J. Geophys. Res. Biogeosci. 2018, 123, 850–866. [Google Scholar] [CrossRef]
- Kowalczuk, P.; Durako, M.J.; Young, H.; Kahn, A.E.; Cooper, W.J.; Gonsior, M. Characterization of dissolved organic matter fluorescence in the South Atlantic Bight with use of PARAFAC model: Interannual variability. Mar. Chem. 2009, 113, 182–196. [Google Scholar] [CrossRef]
- Cawley, K.M.; Butler, K.D.; Aiken, G.R.; Larsen, L.G.; Huntington, T.G.; McKnight, D.M. Identifying fluorescent pulp mill effluent in the Gulf of Maine and its watershed. Mar. Pollut. Bull. 2012, 64, 1678–1687. [Google Scholar] [CrossRef]
- Berggren, M.; Gudasz, C.; Guillemette, F.; Hensgens, G.; Ye, L.; Karlsson, J. Systematic microbial production of optically active dissolved organic matter in subarctic lake water. Limnol. Oceanogr. 2020, 65, 951–961. [Google Scholar] [CrossRef]
- Graeber, D.; Gelbrecht, J.; Pusch, M.T.; Anlanger, C.; von Schiller, D. Agriculture has changed the amount and composition of dissolved organic matter in Central European headwater streams. Sci. Total Environ. 2012, 438, 435–446. [Google Scholar] [CrossRef]
- Osburn, C.L.; Handsel, L.T.; Mikan, M.P.; Paerl, H.W.; Montgomery, M.T. Fluorescence tracking of dissolved and particulate organic matter quality in a river-dominated estuary. Environ. Sci. Technol. 2012, 46, 8628–8636. [Google Scholar] [CrossRef]
- Yang, J.; Gong, W.; Shi, S.; Du, L.; Zhu, B.; Sun, J.; Song, S. Excitation wavelength analysis of laser-induced fluorescence LiDAR for identifying plant species. IEEE Geosci. Remote Sens. Lett. 2016, 13, 977–981. [Google Scholar] [CrossRef]
- Weiser, M.W.; Swanson, J.; Ghosh, N.; Hong, J.; Harringmeyer, J.P.; Kaiser, K.; Fichot, C.G. Improving estimates of dissolved organic carbon (DOC) concentration from in situ fluorescence measurements across estuaries and coastal wetlands. Environ. Sci. Technol. 2024, 58, 9213–9226. [Google Scholar] [CrossRef]
- Hoffmeister, S.; Murphy, K.; Cascone, C.; Ledesma, J.L.; Köhler, S. Evaluating the accuracy of two in situ optical sensors to estimate DOC concentrations for drinking water production. Environ. Sci. Water Res. Technol. 2020, 6, 2891–2901. [Google Scholar] [CrossRef]
- Houskeeper, H.F.; Hooker, S.B.; Kudela, R.M. Spectral range within global aCDOM (440) algorithms for oceanic, coastal, and inland waters with application to airborne measurements. Remote Sens. Environ. 2021, 253, 112155. [Google Scholar] [CrossRef]
- Kowalczuk, P.; Cooper, W.J.; Durako, M.J.; Kahn, A.E.; Gonsior, M.; Young, H. Characterization of dissolved organic matter fluorescence in the South Atlantic Bight with use of PARAFAC model: Relationships between fluorescence and its components, absorption coefficients and organic carbon concentrations. Mar. Chem. 2010, 118, 22–36. [Google Scholar] [CrossRef]
- Wünsch, U.J.; Murphy, K.R.; Stedmon, C.A. Fluorescence quantum yields of natural organic matter and organic compounds: Implications for the fluorescence-based interpretation of organic matter composition. Front. Mar. Sci. 2015, 2, 98. [Google Scholar] [CrossRef]
- Mineeva, N.; Poddubny, S.; Stepanova, I.; Tsvetkov, A. Abiotic factors and their role in phytoplankton development in reservoirs of the Middle Volga River, Russia. Inland Water Biol. 2022, 15, 729–739. [Google Scholar] [CrossRef]
- Nemirovskaya, I.; Lisitzin, A. Spatial variability of different compounds in water, suspension, and sediments of the Volga River. Dokl. Earth Sci. 2011, 437, 537–543. [Google Scholar] [CrossRef]
- Nagai, S.; Nasahara, K.N.; Akitsu, T.K.; Saitoh, T.M.; Muraoka, H. Importance of the collection of abundant ground-truth data for accurate detection of spatial and temporal variability of vegetation by satellite remote sensing. In Biogeochemical Cycles: Ecological Drivers and Environmental Impact; Wiley Online Library: Hoboken, NJ, USA, 2020; pp. 223–244. [Google Scholar]
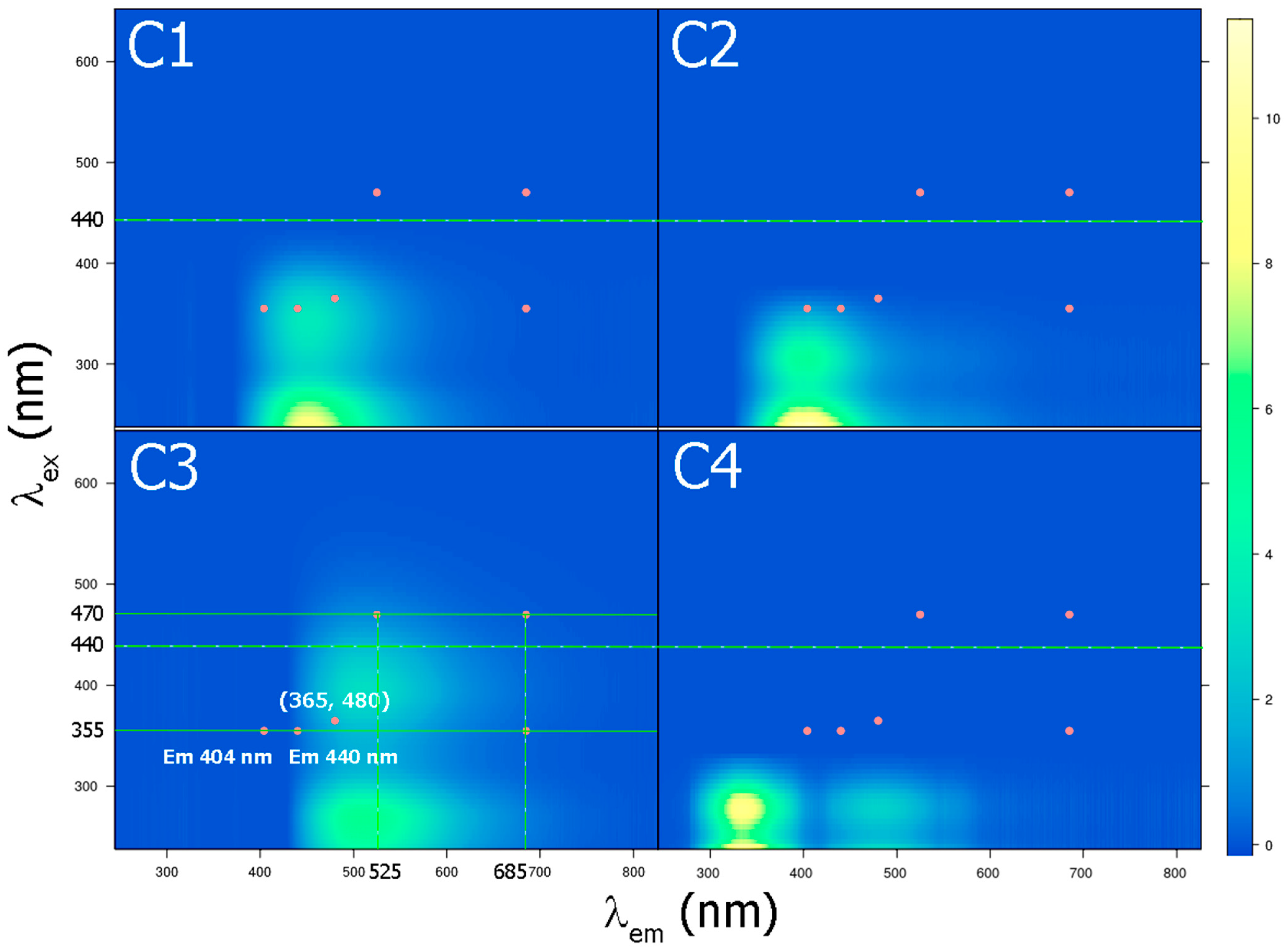
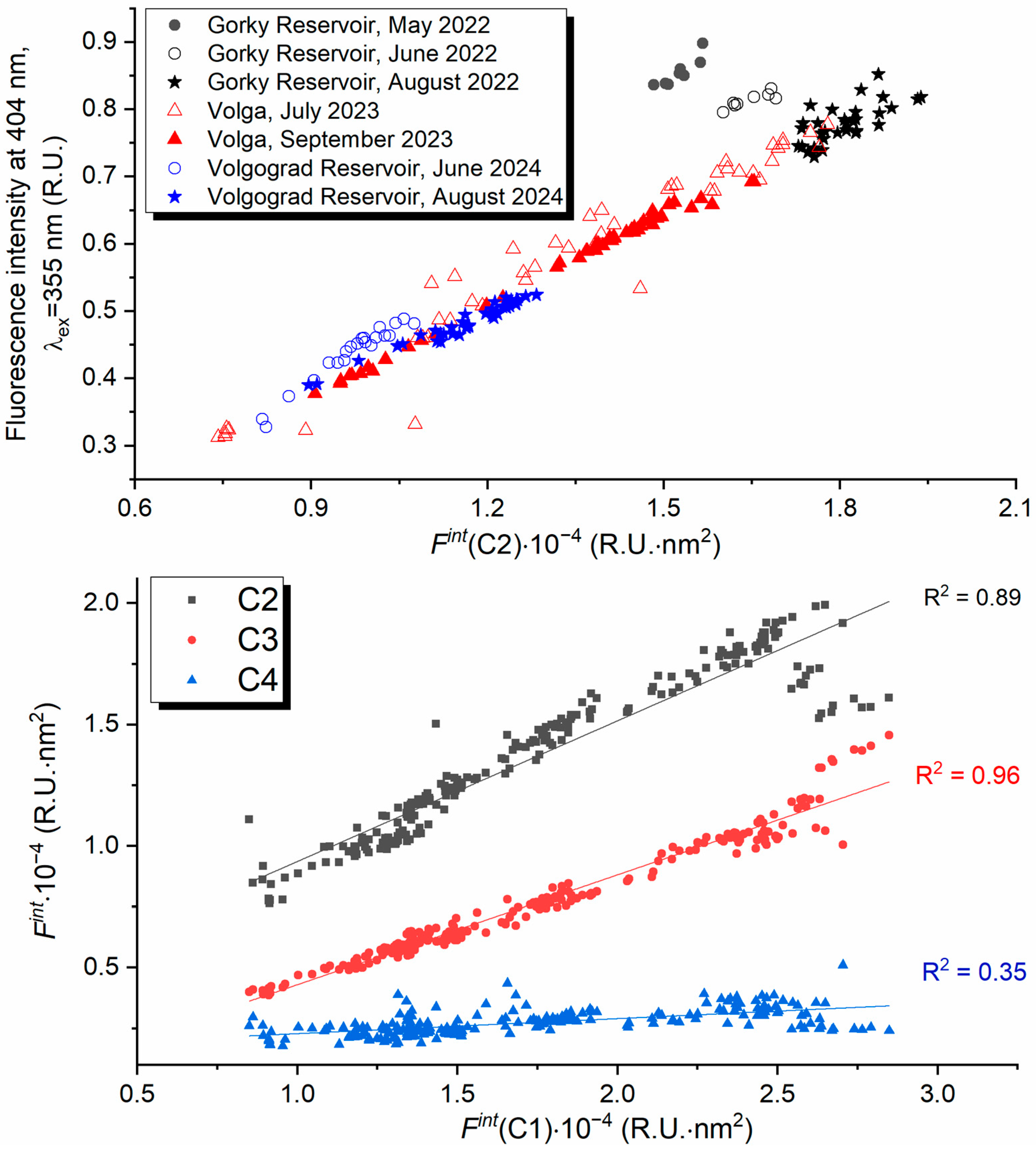
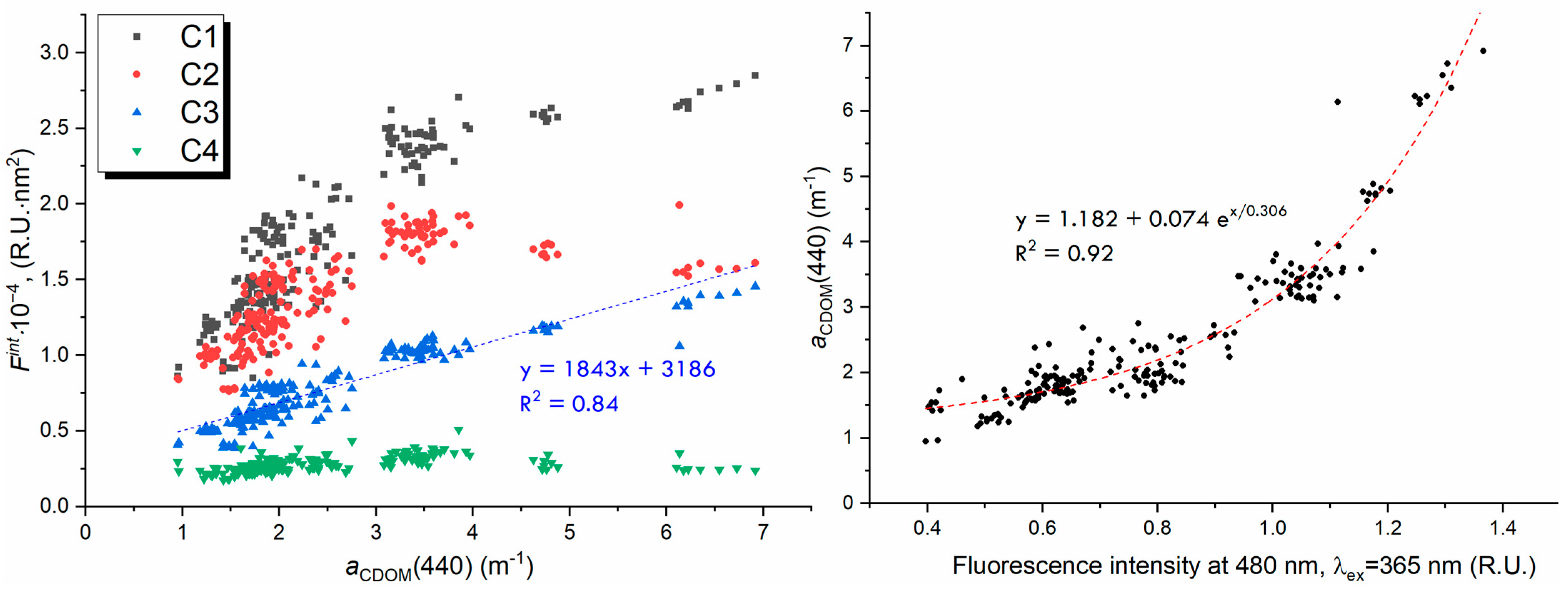
| Component | Excitation, nm | Emission, nm | Number of Matches in OpenFluor | Description |
|---|---|---|---|---|
| C1 | <280, 343 | 453 | 107 | Humic-like, terrestrial |
| C2 | <260, 304 | 403 | 131 | Humic-like, terrestrial, or microbial |
| C3 | 269, 397 | 511 | 76 | Humic-like, terrestrial, sediment/soil fulvic-like |
| C4 | <245, 277 | 334 | 33 | Protein-like, autochthonous |
| Date | n | Fraction, % | Average , 103 R.U.⋅nm2 | aCDOM(440), m−1 | E2:E3 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | C1 | C2 | C3 | C4 | ||||
| Gorky Reservoir | |||||||||||
| 2022/05 | 8 | 46 | 27 | 22–23 | 4–5 | 27.2 ± 0.8 | 15.7 ± 0.3 | 13.7 ± 0.5 | 2.5 ± 0.1 | 6.4 ± 0.3 | 5.29 ± 0.04 |
| 2022/06 | 8 | 45 | 30 | 19–20 | 4–6 | 25.8 ± 0.3 | 16.9 ± 0.4 | 11.8 ± 0.2 | 2.8 ± 0.3 | 4.8 ± 0.1 | 5.78 ± 0.04 |
| 2022/08 | 32 | 41–43 | 33–34 | 16–18 | 6–7 | 24.5 ± 0.9 | 18.5 ± 0.6 | 10.4 ± 0.3 | 3.5 ± 0.4 | 3.5 ± 0.5 | 6.52 ± 0.20 |
| Between Gorky Reservoir and confluence with the Oka River | |||||||||||
| 2023/07 | 12 | 42–44 | 32–33 | 18–19 | 5–7 | 23.1 ± 1.0 | 17.3 ± 0.7 | 10.2 ± 0.3 | 3.1 ± 0.3 | 3.4 ± 0.2 | 6.74 ± 0.12 |
| Oka River | |||||||||||
| 2023/08 | 2 | 39 | 34 | 18 | 9 | 13.5 ± 0.1 | 11.6 ± 0.3 | 6.4 ± 0.1 | 3.0 ± 0.3 | 1.9 ± 0.1 | 6.39 ± 0.06 |
| Confluence with the Oka River—Cheboksary Reservoir | |||||||||||
| 2023/08 | 5 | 41–43 | 33 | 18–19 | 5–8 | 18.5 ± 2.3 | 14.5 ± 1.3 | 8.4 ± 0.9 | 2.9 ± 0.1 | 2.6 ± 0.3 | 6.56 ± 0.09 |
| 2023/09 | 14 | 41–42 | 34–35 | 17–18 | 6–8 | 17.9 ± 1.1 | 14.7 ± 0.7 | 7.8 ± 0.5 | 2.8 ± 0.1 | 2.0 ± 0.1 | 7.32 ± 0.7 |
| Cheboksary Reservoir | |||||||||||
| 2023/09 | 7 | 41 | 35 | 17 | 7 | 18.5 ± 0.6 | 15.5 ± 0.6 | 7.9 ± 0.1 | 3.0 ± 0.2 | 1.9 ± 0.1 | 7.42 ± 0.11 |
| Cheboksary Reservoir—Kazan | |||||||||||
| 2023/09 | 8 | 41–42 | 34–35 | 17 | 6–7 | 18.8 ± 0.3 | 15.3 ± 0.2 | 7.9 ± 0.2 | 3.0 ± 0.2 | 2.0 ± 0.2 | 7.33 ± 0.11 |
| Kama River | |||||||||||
| 2023/07 | 7 | 37–41 | 34–38 | 16–17 | 8–9 | 9.2 ± 0.2 | 8.0 ± 0.6 | 4.0 ± 0.1 | 1.9 ± 0.2 | 1.5 ± 0.1 | 7.16 ± 0.07 |
| 2023/09 | 11 | 41 | 35 | 17 | 7–8 | 11.9 ± 0.4 | 10.0 ± 0.4 | 5.0 ± 0.1 | 2.1 ± 0.2 | 1.3 ± 0.1 | 7.62 ± 0.20 |
| Confluence of the Volga and Kama rivers | |||||||||||
| 2023/07 | 10 | 40–42 | 34–35 | 16–18 | 6–9 | 14.7 ± 1.3 | 11.9 ± 0.8 | 6.2 ± 0.6 | 2.4 ± 0.3 | 2.0 ± 0.2 | 7.06 ± 0.13 |
| 2023/09 | 12 | 41 | 35 | 17 | 7–8 | 15.2 ± 1.8 | 12.7 ± 1.6 | 6.4 ± 0.8 | 2.6 ± 0.3 | 1.7 ± 0.2 | 7.39 ± 0.10 |
| Volgograd Reservoir | |||||||||||
| 2024/06 | 19 | 38–42 | 32–34 | 17–18 | 7–12 | 12.8 ± 0.9 | 10.2 ± 0.5 | 5.6 ± 0.4 | 2.7 ± 0.5 | 1.8 ± 0.3 | 6.72 ± 0.30 |
| 2024/09 | 37 | 40–42 | 34–36 | 16–19 | 6–8 | 14.3 ± 0.8 | 12.1 ± 0.5 | 6.3 ± 0.3 | 2.4 ± 0.1 | 1.8 ± 0.2 | 7.40 ± 0.20 |
| Confluence with Yeruslan River | |||||||||||
| 2024/06 | 2 | 36–38 | 35–36 | 16–17 | 10–12 | 8.9 ± 0.4 | 8.4 ± 0.04 | 4.2 ± 0.1 | 2.6 ± 0.4 | 0.96 ± 0.01 | 8.53 ± 0.50 |
| 2024/08 | 3 | 38–39 | 35–36 | 17 | 8–9 | 11.5 ± 1.0 | 10.4 ± 0.7 | 5.2 ± 0.3 | 2.5 ± 0.1 | 1.3 ± 0.1 | 8.16 ± 0.30 |
| C1 | C2 | C3 | C4 | ||
|---|---|---|---|---|---|
| 355 | 404 | 0.43–0.64 | 0.36–0.57 | 0 | 0 |
| 355 | 440 | 0.73–0.84 | 0.13–0.25 | 0.02–0.03 | 0 |
| 355 | 685 | 0.29–0.36 | 0.11–0.22 | 0.48–0.58 | 0 |
| 365 | 480 | 0.75–0.80 | 0.02–0.06 | 0.16–0.21 | 0 |
| 470 | 525 | 0 | 0 | 1 | 0 |
| 470 | 685 | 0 | 0 | 1 | 0 |
| Component | Parameter | 355/404, R.U. | 355/440, R.U. | 355/685, R.U. | 365/480, R.U. | 470/525, R.U. | 470/685, R.U. | , m−1 |
|---|---|---|---|---|---|---|---|---|
| C1 | Slope∙105 | 2.86 | 5.32 | 0.211 | 4.46 | 0.387 | 0.061 | 20 |
| Intercept | 0.085 | 0.046 | −0.001 | −0.006 | 0.002 | 0.000 | −1.06 | |
| R2 | 0.99 | 0.99 | 0.95 | 0.99 | 0.94 | 0.93 | 0.75 | |
| C2 | Slope∙105 | 4.53 | 8.28 | 0.320 | 6.83 | 0.574 | 0.093 | n/a |
| Intercept | −0.037 | −0.161 | −0.008 | −0.165 | −0.010 | −0.002 | n/a | |
| R2 | 0.90 | 0.87 | 0.78 | 0.83 | 0.74 | 0.75 | 0.47 | |
| C3 | Slope∙105 | 6.02 | 11.33 | 0.46 | 9.63 | 0.860 | 0.137 | 45.7 |
| Intercept | 0.126 | 0.110 | 0.001 | 0.038 | 0.004 | 0.000 | −1.06 | |
| R2p87 | 0.94 | 0.97 | 0.97 | 0.98 | 0.98 | 0.97 | 0.84 | |
| C4 | R2 | 0.38 | 0.35 | 0.33 | 0.32 | 0.27 | 0.29 | 0.14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Drozdova, A.N.; Molkov, A.A.; Kapustin, I.A.; Ermoshkin, A.V.; Leshchev, G.V.; Krylov, I.N.; Labutin, T.A. Systematic Study of CDOM in the Volga River Basin Using EEM-PARAFAC. Environments 2025, 12, 309. https://doi.org/10.3390/environments12090309
Drozdova AN, Molkov AA, Kapustin IA, Ermoshkin AV, Leshchev GV, Krylov IN, Labutin TA. Systematic Study of CDOM in the Volga River Basin Using EEM-PARAFAC. Environments. 2025; 12(9):309. https://doi.org/10.3390/environments12090309
Chicago/Turabian StyleDrozdova, Anastasia N., Aleksandr A. Molkov, Ivan A. Kapustin, Alexey V. Ermoshkin, George V. Leshchev, Ivan N. Krylov, and Timur A. Labutin. 2025. "Systematic Study of CDOM in the Volga River Basin Using EEM-PARAFAC" Environments 12, no. 9: 309. https://doi.org/10.3390/environments12090309
APA StyleDrozdova, A. N., Molkov, A. A., Kapustin, I. A., Ermoshkin, A. V., Leshchev, G. V., Krylov, I. N., & Labutin, T. A. (2025). Systematic Study of CDOM in the Volga River Basin Using EEM-PARAFAC. Environments, 12(9), 309. https://doi.org/10.3390/environments12090309










